Алгебра логики: Конъюнкция, Дизъюнкция, Импликация, Эквивалентность
Лада Есакова, преподаватель информатики и математики, автор книги «Информатика. Полный курс подготовки к ЕГЭ».
Ну а теперь, ребята, самая «вкусная» тема теоретической части ЕГЭ – это булева алгебра, она же алгебра логики.
Сначала я хочу задать вам вопрос: для чего вообще придумали такой аппарат как булева алгебра, кроме того, чтобы мучить маленьких детей?
Раз у нас есть такая возможность пообщаться с компьютером, поручить ему какие-то задачи на выполнение, неплохо бы нам научиться говорить с ним на одном языке. То есть перевести наши желания и намерения на его компьютерный язык.
А кто такой компьютер? Если очень упрощенно, то это некоторое устройство, у которого на проводники подается либо не подается ток. Так вот в зависимости от того, есть ток или его нет на входящих проводниках, происходят определенные действия.
Рассматривая задачи, в том числе и 27, сложную задачу, считаем, что мы крутые программисты, если мы написали программный код на каком-то языке программирования. А компьютер нас поймет? Нет. Он знает только 0 и 1. Как же нам тогда до него достучаться?
После программистов высокого уровня в дело вступают Боги от программирования – это люди, которые пишут компиляторы, драйверы, операционные системы и которые уже непосредственно пытаются достучаться до компьютерного железа.
Что такое уже перевод программы в машинные коды? У меня нет цели рассказать, как это работает детально, я расскажу очень упрощенно, чтобы просто было понятно, для чего это нужно.
Если на один компьютерный разъем ток не поступил, а на другой поступил, мне нужно, чтобы получился 0. Я уже говорю терминами 0 и 1, нет тока или есть ток.
Если на оба разъема ток не поступил, тоже будет 0.
Если наоборот на первый поступил, а на второй не поступил, – то я тоже хочу 0. И в случае, если на оба разъема ток поступил, тогда пусть будет у меня 1
Например, у меня другая схема, в которую входит три проводника, и, в зависимости от того, что пришло на входы, я тоже хочу какое-то значение. Например, вот так. Не буду расписывать все варианты
По сути, у меня единственный возможный способ общаться с компьютером – это завести много функций от разного числа переменных, которые могут быть только 0 и 1 и которые на выходе дают тоже 0 или 1.
Можно посмотреть функцию от двух переменных и назвать ее f(1), функцию от трех переменных назовем f(2). Будут и другие функции, которые запишем в таблицы, переплету в многотомники и поставлю на полку. В случае, если мне нужно найти какую-то схему, достаю том, листаю страницы и нахожу то, что мне нужно.
Для компьютера это будет нормально, его устроит, если я выстрою с ним такой диалог. А вот человека такая схема работы не устроит, потому что людям очень сложно оперировать большими объемами информации без логического обоснования.
Наверняка вы помните детсадовские игры, когда можно задавать только вопросы, на которые можно ответить «да» или «нет», и нужно что-то угадать. Наверное, у детей изначально подсознательно заложена склонность к двоичному коду.
Поэтому человек поставил в соответствие аппарат логических высказываний, и теперь за 0 мы принимаем ложь, за 1 – истину. И выяснилось, что если я такими операциями буду оперировать, то все операции от трех, четырех, пяти и т. д. переменных я могу свести к функциям от двух переменных. А к каким же функциям?
Первая функция – это функция отрицания. Ее можно обозначить несколькими способами — .
Посмотрим, как это работает.
Если у меня высказывание ложное (например, я показываю маркер, а говорю, что это апельсин)
| 0 | |
| 1 |
А если я показываю маркер и говорю, что это не апельсин, то это истина
| 0 | 1 |
Если я наоборот говорю, что это маркер и показываю его, то это истина, а если я говорю, что это не маркер, это будет ложь
| 0 | 1 |
| 1 | 0 |
Следующая операция – это логическое ИЛИ, она же записывается как .
Покажу как это работает.
Функция от двух переменных работает следующим образом: например, я говорю, что это апельсин или это яблоко (то есть два ложных высказывания), в сумме получается 0; если я говорю, что это апельсин или это маркер, в целом я сказала правду, потому что одно из утверждений является истинным, то получается 1; если я говорю, что это маркер или это банан, опять же это правда; и наконец, если я говорю, что это маркер или это маркер, то есть два верных утверждения, это тоже правда
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 1 |
Вот таким образом работает функция. Акцентирую ваше внимание, что мне ненужно запоминать эти наборы. Конечно, они запомнятся после несколько десятков прорешанных задач, но эту таблицу истинности не надо запоминать, это вытекает из логики.
Далее логическое И — , &, знак умножения.
Посмотрим, как оно работает. Если я говорю два ложных утверждения – это яблоко и это банан – это ложь. Если я говорю, что это яблоко и это маркер – одно высказывание истина, но я же настаиваю на том, что и то, и другое должно выполняться, поэтому это ложь. Если я говорю, что это маркер и это банан, то это тоже ложь. И если я говорю два истинных утверждения – это маркер и это маркер – да, это правда
| 00 | 0 |
| 01 | 0 |
| 10 | 0 |
| 1 |
А умножение, потому что если 1 умножить на 0 или 0 на 1, то тоже будет 0, и только в случае умножения 1 на 1 получится 1.
Вот именно к этим операциям можно свести и все остальные, но не всегда удобно, поэтому еще две функции используется в курсе школьной программы – это импликация и эквивалентность.
Импликацию можно свести к вышеперечисленным, но удобнее ее использовать по-другому.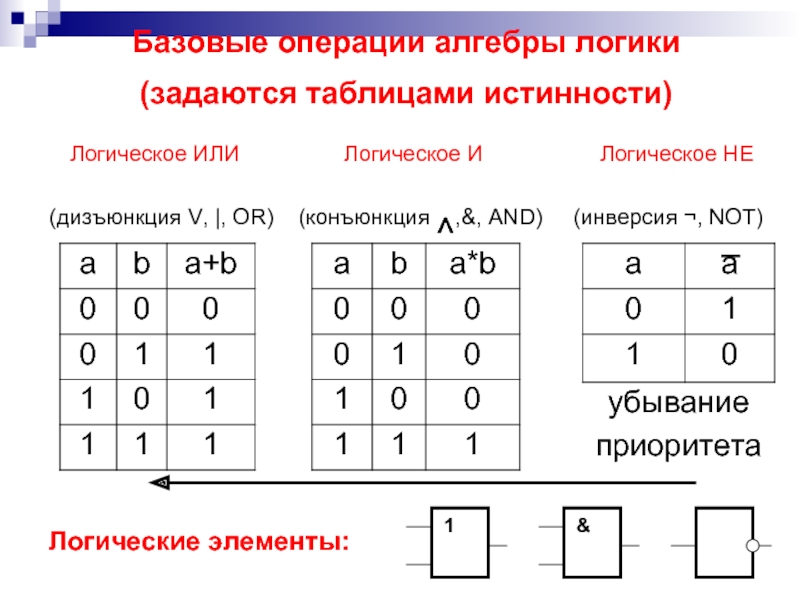
Импликация – это логическое следование
Не будем зубрить таблицу истинности, а попробуем понять.
Если у меня есть ложное высказывание (например, 2 больше 5), могу ли я получить из него ложь разрешенными функциями? Легко! Добавлю к двум частям неравенства единицу и получу ложь: 2>5, 3>6.
То есть мы можем получить изо лжи ложь.
А могу ли я изо лживого высказывания получить истину? Тоже могу. -5 больше -3. Это ложь? Ложь. А применим-ка разрешенную операцию – возведение в квадрат. И запросто получим истину: -5>-3, 25>9. То есть изо лжи истину мы тоже можем получить.
А вот из истины получить ложь никак не получится. Из истины можно получить только истину.
Ну и из истины истину получить, конечно же, возможно.
| 00 | 1 |
| 01 | 1 |
| 0 | |
| 11 | 1 |
То есть не всегда удобно приводить импликацию к другим функциям.
Потому что это замечательная функция, которая 0 дает в единственном случае, когда из истины следует ложь.
И последняя функция, часто употребляемая, – это функция эквивалентности, обозначается логическим равенством или взаимными стрелками
Здесь все очень просто. 0 равен 0? Да. 0 = 1? Нет. 1 равна 0? Нет. 1 равна 1? Да.
| 00 | 1 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
Мы логически обосновали все пять функций, и это избавляет нас от необходимости зубрить таблицы истинности. Да, мы их запомним в процессе решения задач, но гораздо проще логически понять, в чем суть вопроса.
Теперь приоритеты этих функций.
Если у нас не стоят никакие скобки, то все действия, как и в математике, имеют некоторый приоритет.
Вот такая cтрока без скобок
Первый приоритет имеет отрицание , оно прямо приклеивается к тому высказыванию, рядом с которым стоит , поэтому я всегда настаиваю использовать вот такой символ, черточку сверху , потому что это гораздо понятнее, что оно относится к высказыванию.
Следующий приоритет – умножение . То есть в нашем выражении у нас будет вот так
Третий приоритет у сложения , То есть вот так .
А дальше одинаковый приоритет имеют эквивалентность и импликация , слева на право. В нашем случае сначала выполнится сравнение на эквивалентность, а потом из этого импликация .
Все видео по информатике
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Алгебра логики: Конъюнкция, Дизъюнкция, Импликация, Эквивалентность» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 08.05.2023
7.2. Логические операции (отрицание, конъюнкция, дизъюнкция, импликация, эвиваленция).
Правила записи и истинности.1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
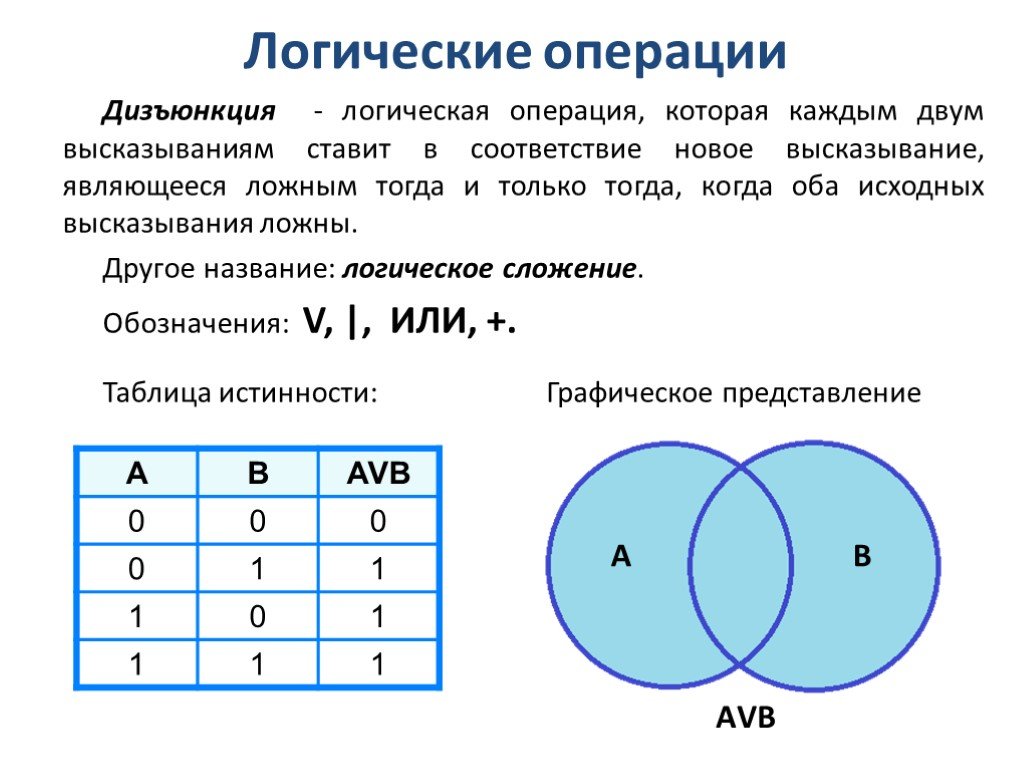
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
3) Логическое отрицание или инверсия:
Инверсия
— это сложное логическое выражение, если
исходное логическое выражение истинно,
то результат отрицания будет ложным, и
наоборот, если исходное логическое
выражение ложно, то результат отрицания
будет истинным. Другими простыми слова,
данная операция означает, что к исходному
логическому выражению добавляется
частица НЕ или слова НЕВЕРНО, ЧТО.
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
5)Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Порядок выполнения логических операций в сложном логическом выражении.
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
7.3. Логическая формула. Тождественно истинные и тождественно лонные формулы
7.4. Связь между алгеброй логики и двоичным кодированием.
7.5. Логические элементы компьютера и их таблицы истинности
7.
5.1.
Схема «И»
7.5.2. Схема «ИЛИ»
7.5.3. Схема «НЕ»
7.5.4. Схема «И-НЕ»
7.5.5. Схема «ИЛИ-НЕ»
7.5.6. RS-триггер и его таблица истинности.
Особенность RS-триггера заключается в том, что при подаче одновременно на входы R и S сигнала, соответствующего логической 1, состояние триггера становится неопределенным: на обоих выходах Q и `Q установится уровень “1”, а после снятия со входов управляющих сигналов, в силу случайных причин, триггер может установиться в состояние “0” либо “1”. Очевидно, что для нормальной работы триггера необходимо исключить указанное сочетание входных сигналов, приводящее к неопределенному состоянию, что можно осуществить, предусмотрев выполнения запрещающего условия R × S=0.
7.5.7. Сумматор и его таблица истинности.
7.6. Основные законы алгебры логики и упрощение логических формул.
7.7. Переключательная схема
8. Алгоритмы и алгоритмизация
8.
1.
Понятие алгоритма
8.2. Свойства алгоритма (понятность, дискретность, определенность, результативность, массовость)
Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
Определенность — каждое правило алгоритма должно быть четким, однозначным. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
Результативность (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов.
Массовость
— алгоритм решения задачи разрабатывается
в общем виде, то есть он должен быть
применим для некоторого класса задач,
различающихся только исходными данными.
При этом исходные данные могут выбираться
из некоторой области, которая называется
областью применимости алгоритма.
8.3. Формы представления алгоритмов
8.4. Составление блок-схем.
8.5. Линейная алгоритмическая конструкция
8.6. Ветвящаяся алгоритмическая конструкция
8.7. Цикл с предусловием
8.8. Цикл с постусловием
8.9. Массив
9. Основы программирования
9.1. Машинный код процессора (триггеры, венили)
9.2. Общее понятие языка программирования (метаязык, синтаксис, семантика, операторы, отладка)
Программи́рование
— в обычном понимании, это процесс
создания компьютерных программ. Иногда
под программированием понимают настройку
электронных устройств и программно-аппаратных
комплексов (например, программирование
цифровых АТС, программирование бытовых
приборов конечным пользователем, запись
информации в ПЗУ). Разработку логической
схемы для ПЛИСтоже называют
программированием. В общем понимании,
программирование — это процесс создания
алгоритма функционирования устройства,
который может быть выражен либо в
структуре самого устройства, либо в
виде последовательности выполняемых
устройством элементарных инструкций.
Программирование сочетает в себе
элементы науки (логика, математика,
информатика, кибернетика, психология)
и искусства.
Обычно,
основным инструментом программирования
является среда программирования, которая
включает себя текстовый редактор и
компилятор или интерпретатор. Текстовый
редактор среды программирования может
иметь специфичную функциональность,
такую как индексация имен, отображение
документации, средства визуального
создания пользовательского интерфейса.
С помощью текстового редактора программист
производит набор программы в виде
текста, который называют исходным кодом.
Язык программирования определяет
синтаксис и изначальную семантику
исходного кода, семантика языка
программирования может расширяться
текстом программы, дополнительными
библиотеками и программно-аппаратным
окружением, в котором исполняется
программа. Компилятор преобразует текст
программы в машинный код, непосредственно
исполняемый электронными компонентам
и компьютера. Интерпретатор либо явно
не преобразует текст программы в машинный
код, либо делает такое преобразование
в процессе выполнения программы.
Программирование можно разбить логически на несколько стадий:
Анализ
Проектирование — разработка комплекса алгоритмов
Кодирование и компиляцию — написание исходного текста программы и преобразование его в исполнимый код с помощью компилятора
Тестирование и отладку — выявление и устранение ошибок в программах
Испытания и сдачу программ
Сопровождение
9.3. Компиляторы и интерпретаторы
9.4. Уровни языков программирования (низкий, высокий)
1.7 Таблицы истинности: отрицание, соединение, дизъюнкция
Цели обучения
- Что такое таблица истинности?
- Основные таблицы истинности для
- Отрицание
- Соединение
- Разъединение
- Порядок логических операций
- Соединение (отрицание, конъюнкция, дизъюнкция)
Поскольку сложно представить сложные утверждения, мы можем создать таблицу истинности , чтобы разбить сложное утверждение на простые утверждения и определить, являются ли они истинными или ложными.
Таблица поможет отслеживать все значения истинности простых утверждений, составляющих сложное утверждение, что приведет к анализу всего утверждения.
Таблица истинности
Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности простых утверждений.
Пример
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный 9».0035 или что-нибудь с фаэтоном». Постройте таблицу истинности, описывающую элементы условий этого утверждения и соблюдение условий.
Показать решениеОтрицание говорит нам: «Это не так, что…»
Соединение говорит нам: «И то, и другое… имеет место». Союзы истинны только тогда, когда оба союза истинны.
Дизъюнкция говорит нам, что «верно хотя бы одно…» Дизъюнкции ложны только тогда, когда ложны оба дизъюнкции.
Основные таблицы истинности
Обратите внимание, что столбец b имеет шаблон TFTF.
Тогда столбец A имеет шаблон TTFF.
| и | б | [латекс]а\клин{б}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
Думая о ситуациях «и», часто полезно представить сценарий. Представьте, что вы арендатор и заключили договор с арендодателем. Вы договорились, что будете выносить мусор и косить газон. Теперь, если А выносит мусор, а Б косит газон, вы выполняете свою часть сделки только тогда, когда делаете и то, и другое. Значения истинности будут ложными, за исключением случаев, когда вы выполняете оба действия, и в этом случае они будут истинными.
| и | б | [латекс]а\ви{б}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
При обдумывании ситуаций «или» также полезно подумать о сценарии.
Представьте, что вы арендатор (как в предыдущем примере), и ваш арендодатель попросил вас заплатить 1-го числа за плату 2-го числа. Предположим, что A заплатит за первое, а B заплатит за второе. Результат будет верным во всех сценариях, за исключением случаев, когда вы не платите ни в первый, ни во второй раз. В этом случае результат ложный.
| и | [латекс]\sim{а}[/латекс] |
|---|---|
| Т | Ф |
| Ф | Т |
Я просто думаю о противоположном дне, когда дело доходит до отрицаний. Все противоположно тому, что было изначально.
Примечание:
Когда мы создаем таблицу истинности, нам нужно перечислить все возможные комбинации значений истинности для A и B. Обратите внимание, что первый столбец содержит 2 значения True (T), за которыми следуют 2 значения False (F). Во втором столбце чередуются T, F, T, F. Этот шаблон гарантирует, что будут учтены все 4 комбинации.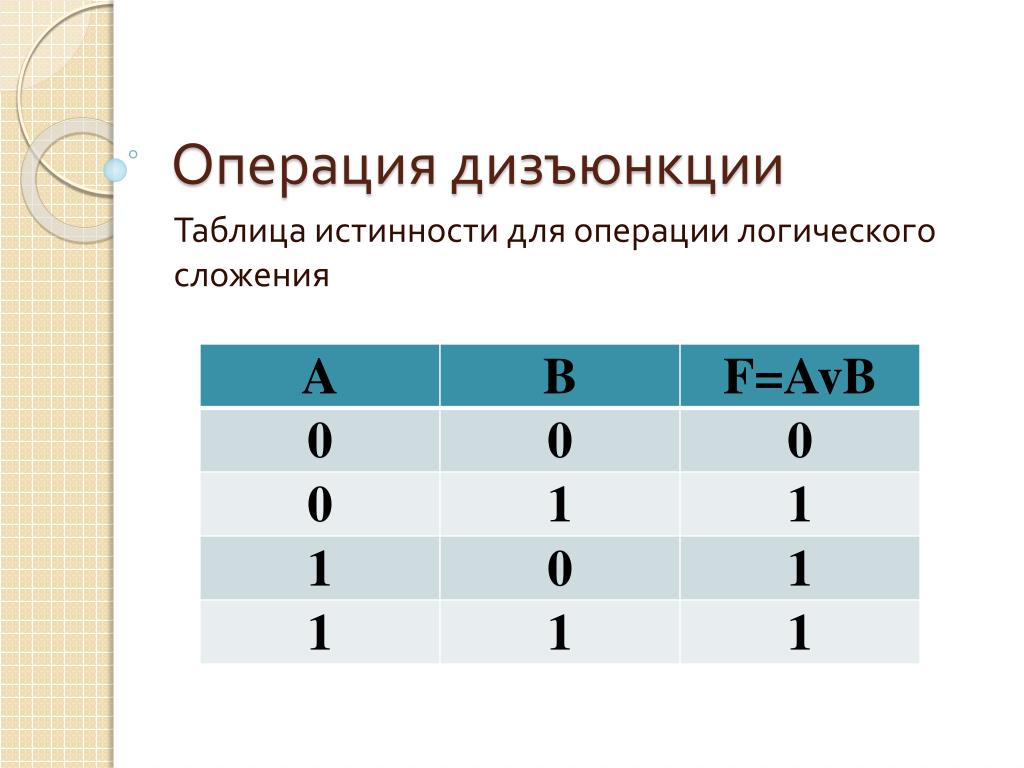
| А | Б |
| Т | Т |
| Т | Ф |
| Ф | Т |
| Ф | Ф |
Попробуйте
Это конец раздела. Закройте эту вкладку и перейдите к соответствующему заданию.
Сравнение конъюнкций и дизъюнкций в таблице истинности
Изучая логику в курсе конечной математики, вы, вероятно, будете работать с таблицами истинности. Таблица истинности — это визуальное представление всех возможных комбинаций значений истинности для данного составного утверждения.Два типа связок, которые часто встречаются в составных операторах, — это конъюнкции и дизъюнкции, обозначаемые символами ∧ и ∨ соответственно.
Важно знать разницу между этими двумя связками.
Идентификация соединения
Соединение, 9 q неверно.
Используя утверждения (4) и (2), союз звучит так: «Сан-Франциско — это город во Флориде, а красный цвет — это цвет американского флага».И, наконец, когда оба утверждения ложны, их соединение ложно. Используя утверждения (3) и (4), союз звучит так: «7 + 3 = 11, а Сан-Франциско — город во Флориде».
По сути, здесь вы видите, что для того, чтобы конъюнкция была истинной, оба утверждения компонента должны быть истинными.
Идентификация дизъюнкции
В дизъюнкции p ∨ q используется слово or для создания составного утверждения.Таблица истинности для дизъюнкции показана здесь:
Чтобы дизъюнкция была истинной, только одно из составляющих утверждений должно быть истинным. Рассмотрим следующие составные операторы, представляющие четыре строки.
Оба варианта верны; составное утверждение истинно.
TF: «На Гавайях идет дождь, или у всех коров семь ног». Первое утверждение истинно, поэтому составное утверждение истинно.
