1. Последовательный колебательный контур
Последовательный колебательный контур – это цепь, состоящая из катушки индуктивности (L), конденсатора (С) и активного сопротивления (R), соединенных последовательно относительно входных зажимов, к которым можно подключать генератор (рис. 1).
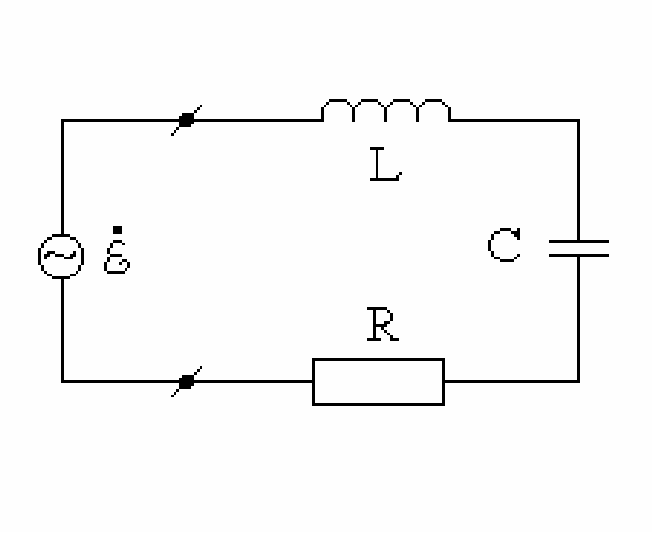
Рис. 1. Последовательный колебательный контур.
Для нахождения тока в цепи составляем уравнение второго закона Кирхгофа для комплексных амплитуд: 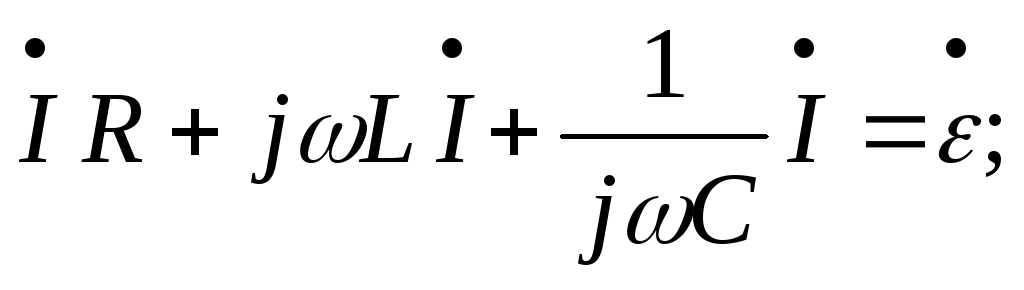
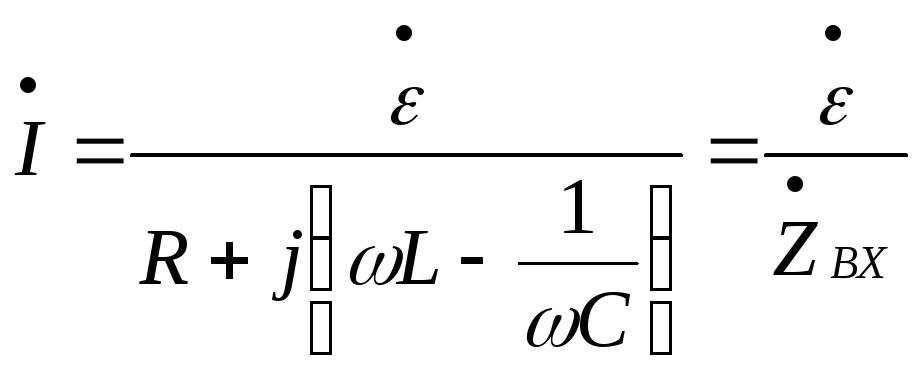
где 
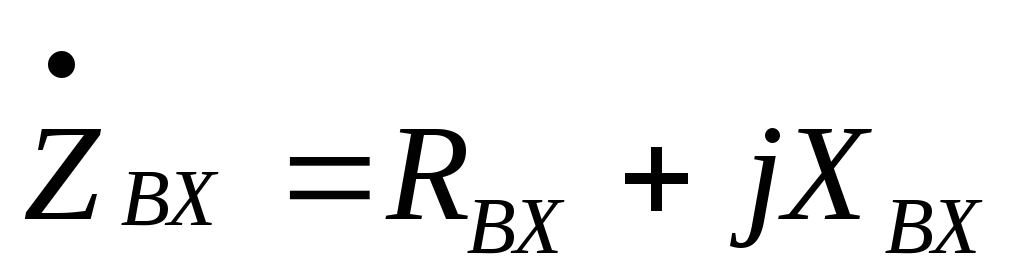 – входное комплексное сопротивление
контура;
– входное комплексное сопротивление
контура;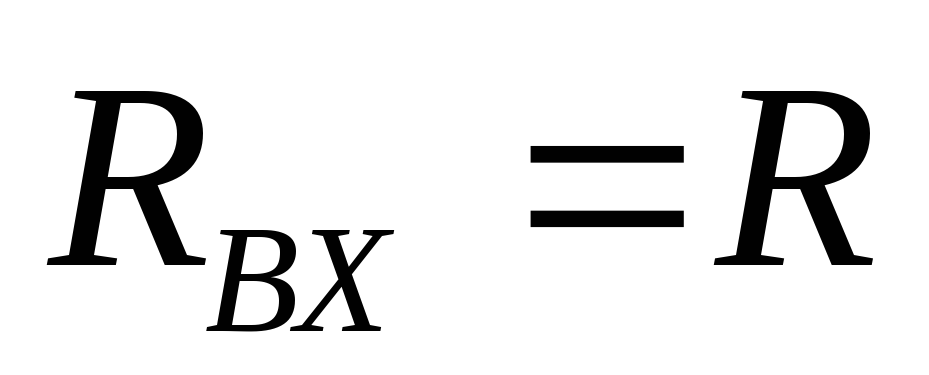 – активная составляющая входного
сопротивления;
– активная составляющая входного
сопротивления;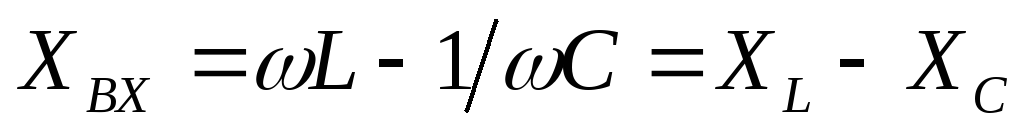 – реактивная составляющая входного
сопротивления.
– реактивная составляющая входного
сопротивления. Векторная
диаграмма токов и напряжений в
последовательном контуре (рис. 2) построена
с учетом того, что напряжение на
индуктивности опережает ток по фазе на 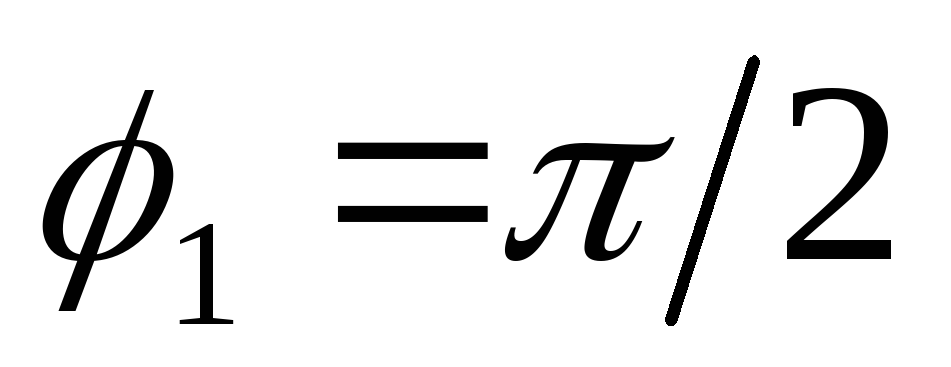
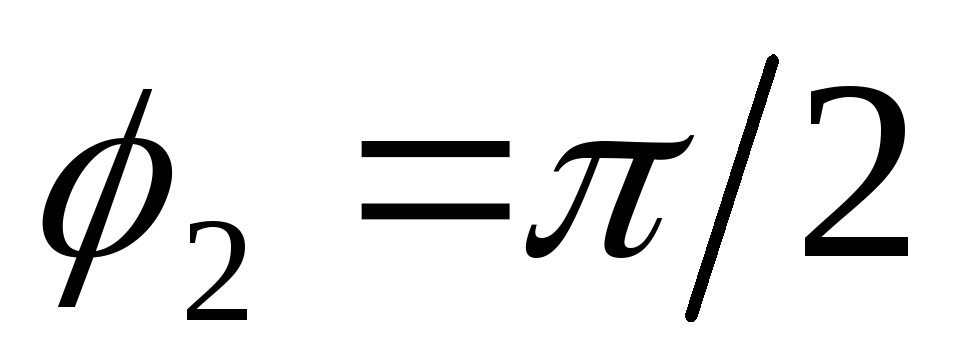 .
. 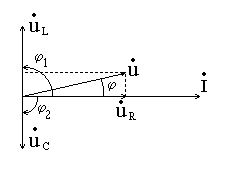
Рис. 2. Векторная диаграмма тока и напряжений в последовательном колебательном контуре.
Возможны три случая: 1)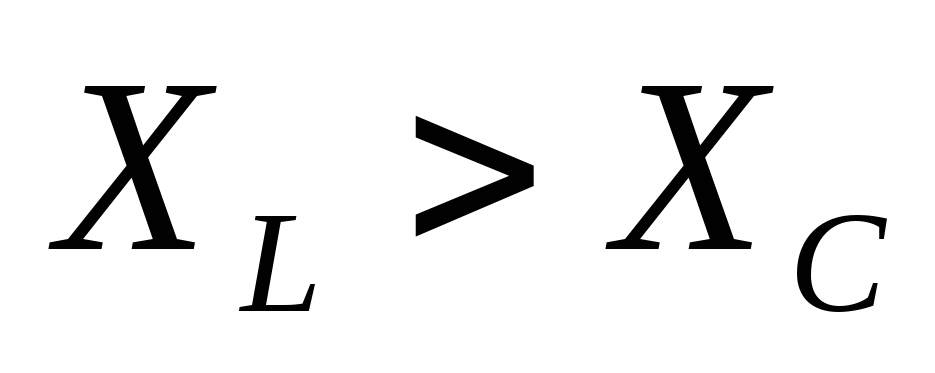 ,
,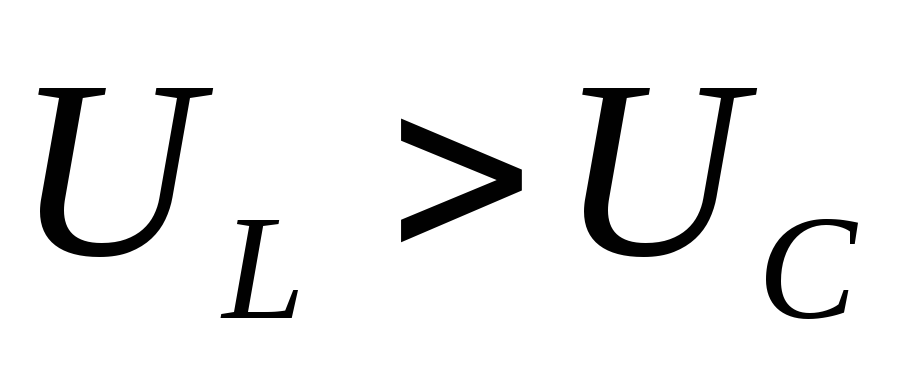
2)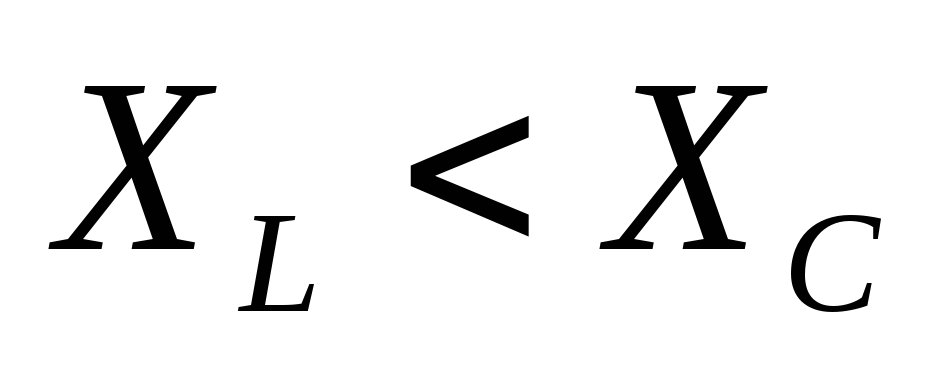
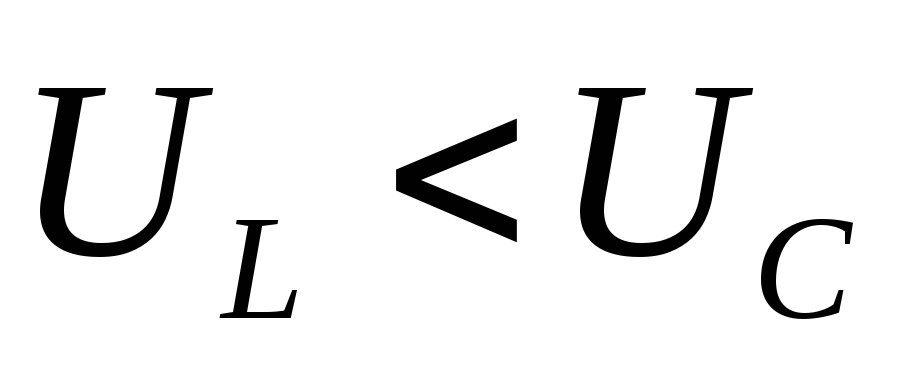
3) 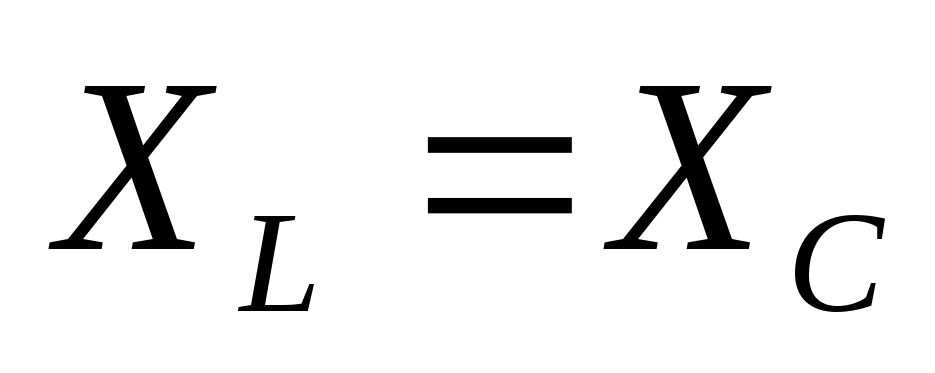 ,
,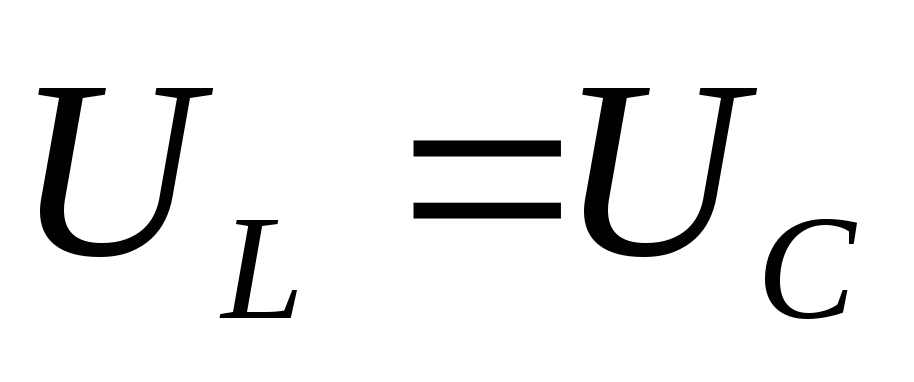
На
рис. 2 представлена векторная диаграмма
для первого случая. Здесь  – сдвиг фаз между током в контуре и
напряжением на нем:
– сдвиг фаз между током в контуре и
напряжением на нем:
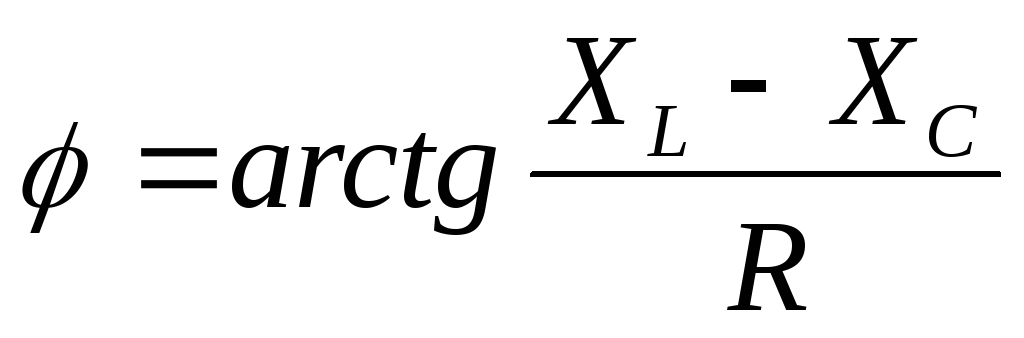
Особый
интерес представляет случай, когда 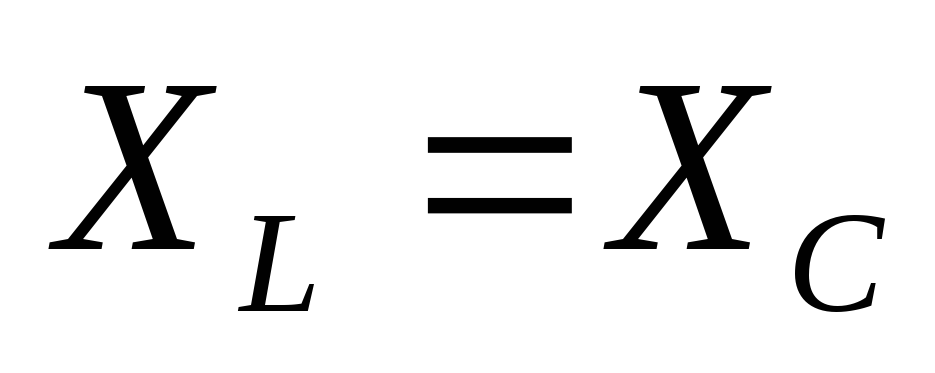 ,
при этом
,
при этом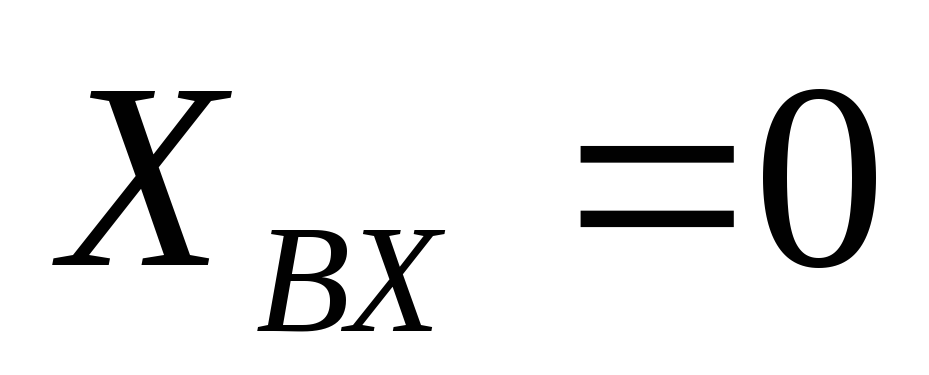 .
Режим цепи, при котором
.
Режим цепи, при котором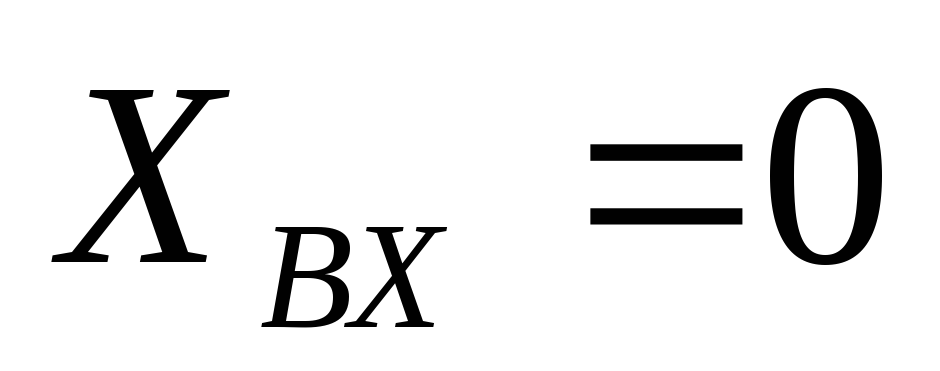 ,
несмотря на наличие реактивных элементов,
называется резонансом.Для
последовательного контура говорят о
резонансе напряжений, так как
,
несмотря на наличие реактивных элементов,
называется резонансом.Для
последовательного контура говорят о
резонансе напряжений, так как 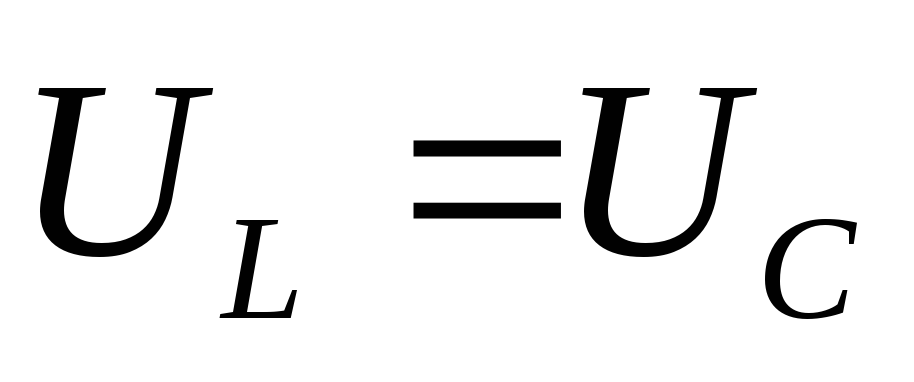 . Векторная диаграмма резонанса представлена
на рис. 3.
. Векторная диаграмма резонанса представлена
на рис. 3.
В
контуре с заданными 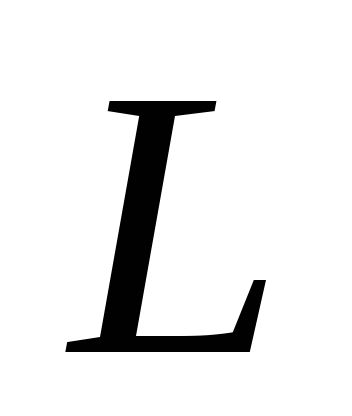
 резонанс наступает при определенной
частоте
резонанс наступает при определенной
частоте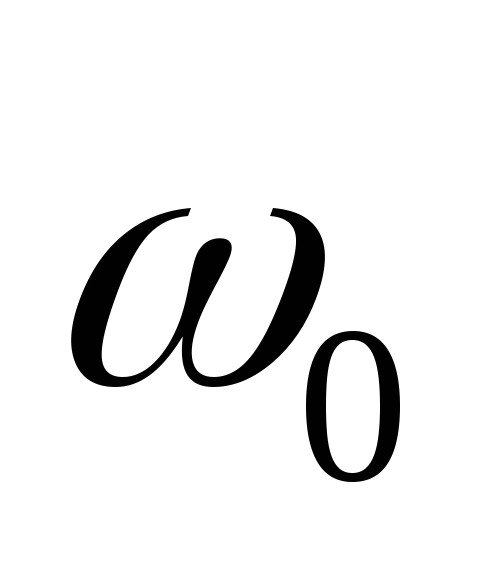 :
: 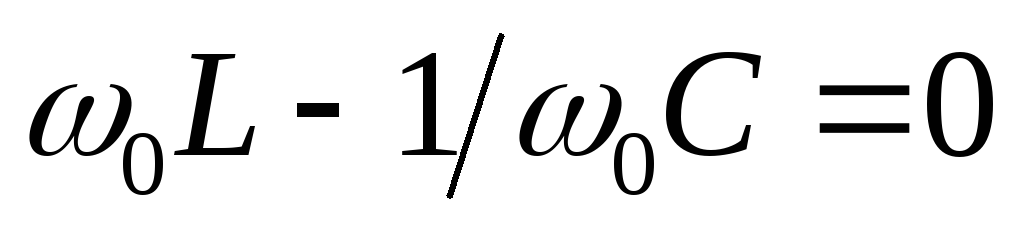 ;
; 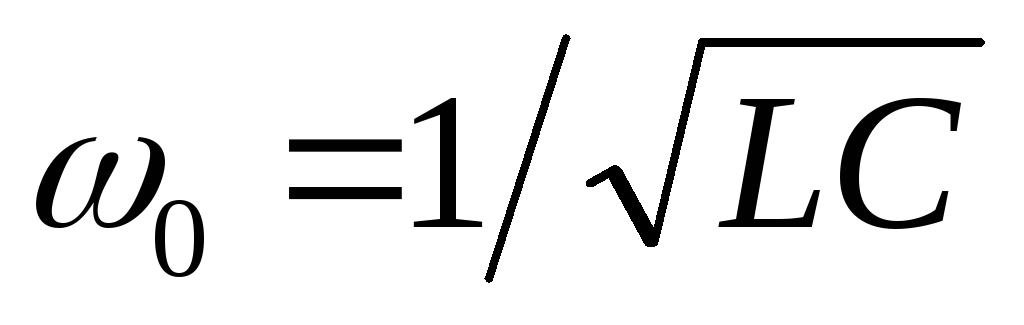 .
.
В
настроенном в резонанс контуре 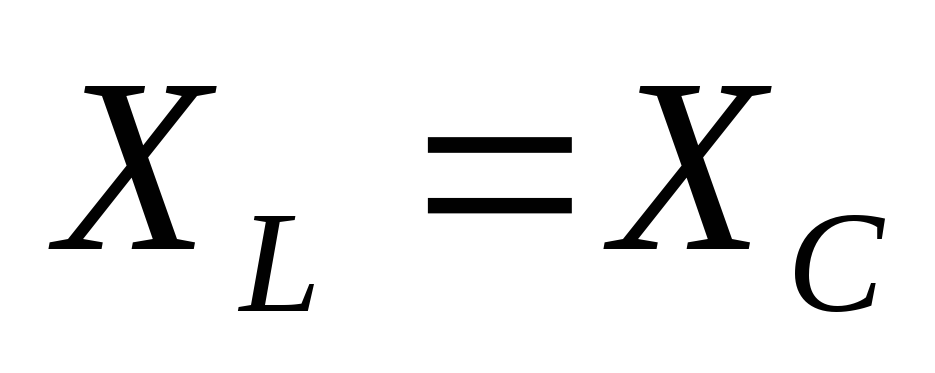 ,
,
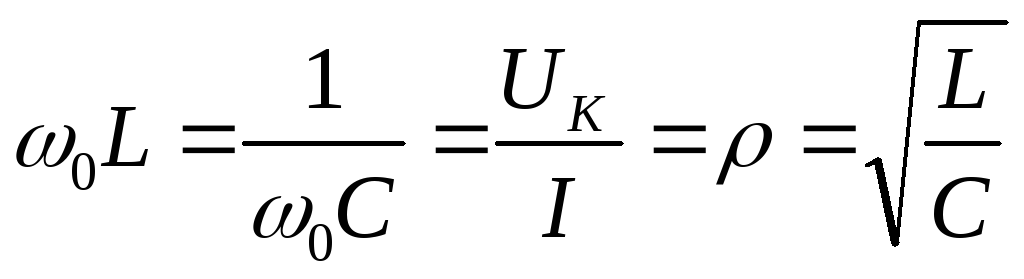
где — характеристическое сопротивление контура.
Рис. 3. Векторная диаграмма тока и напряжений в последовательном контуре при резонансе.
Энергетические соотношения в контуре характеризуются величиной его добротности ,
которая равна отношению энергии,
запасенной в реактивном элементе
контура, к энергии, расходуемой за период
при резонансе, умноженному на
,
которая равна отношению энергии,
запасенной в реактивном элементе
контура, к энергии, расходуемой за период
при резонансе, умноженному на :
: 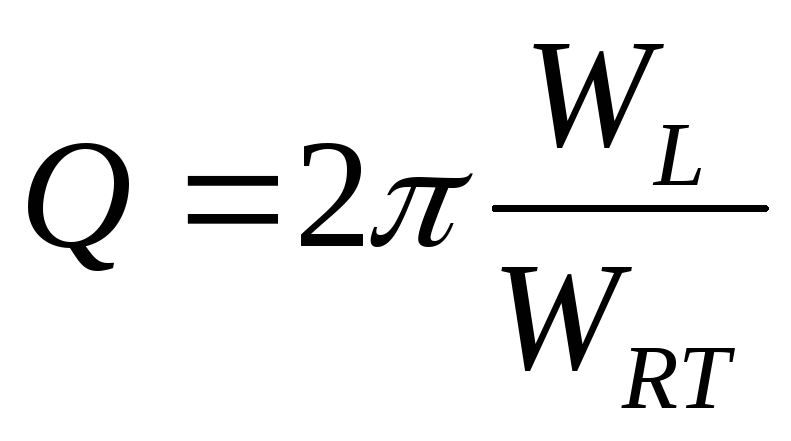
Так
как 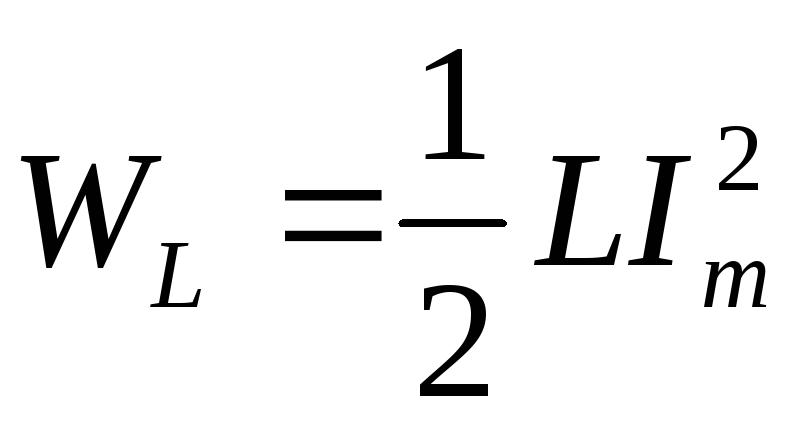 ,
, ,
где
,
где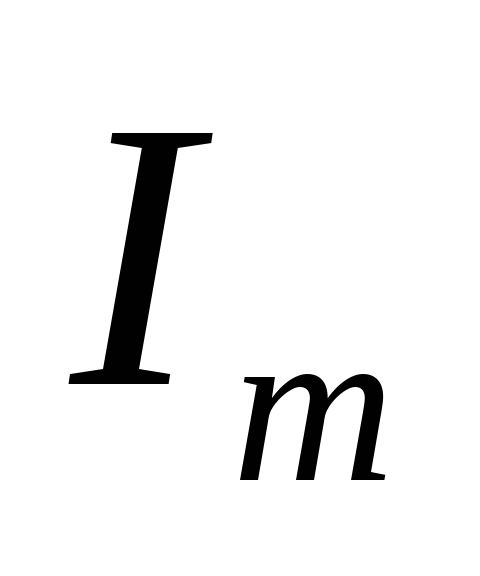 – амплитуда тока,
– амплитуда тока,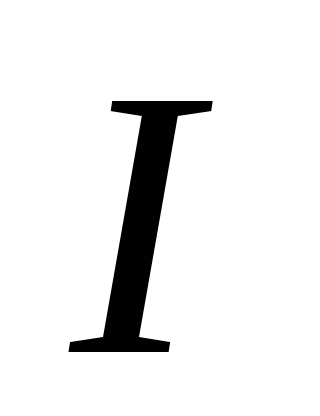 – среднеквадратическое (действующее)
значение тока, а для синусоидального
тока
– среднеквадратическое (действующее)
значение тока, а для синусоидального
тока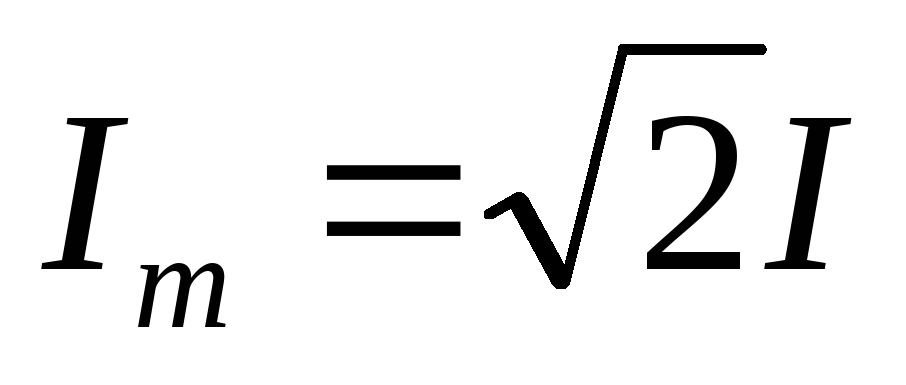 , то
, то
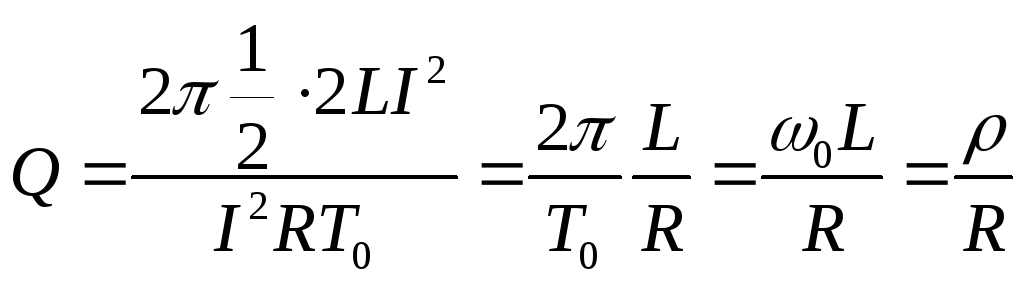
Обратная
величина добротности называется
декрементом затухания 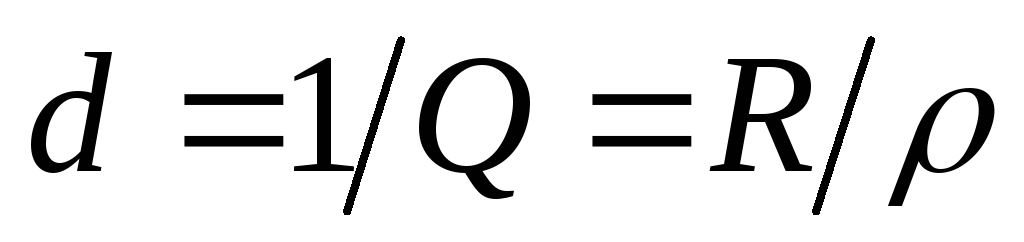 .
.
Рассмотрим входное сопротивление ненагруженного последовательного контура:
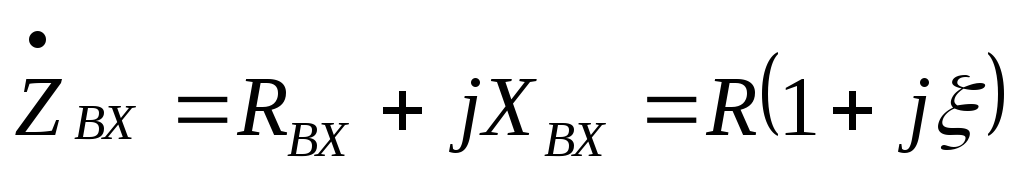
где 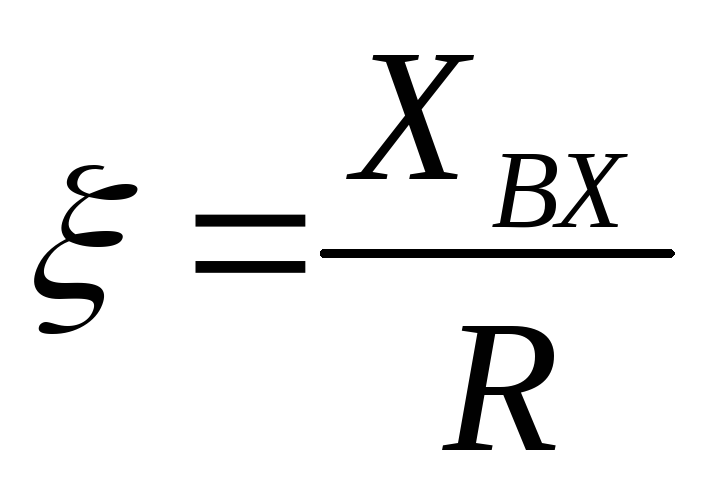 – обобщенная растройка контура.
– обобщенная растройка контура.
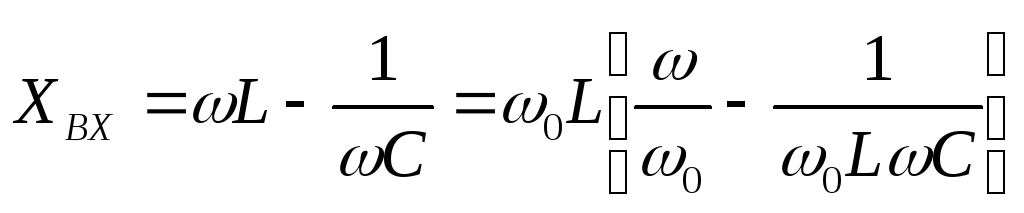
Так
как 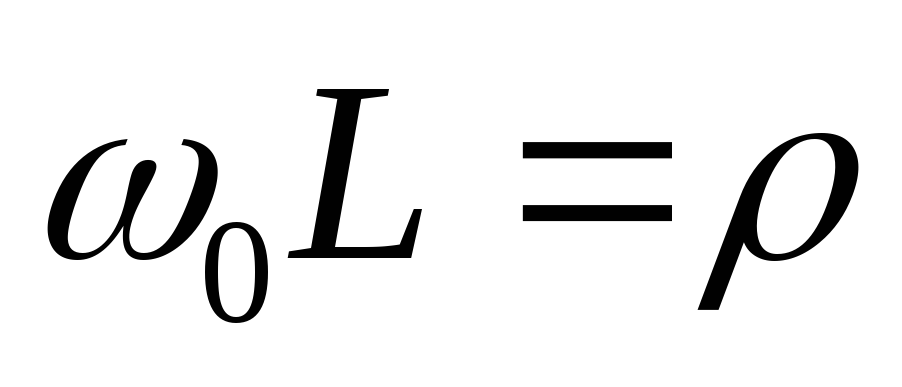 ,
,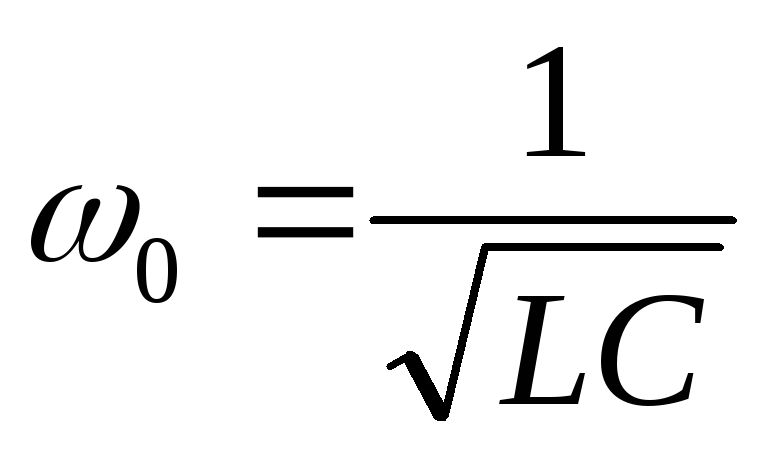 ,
то
,
то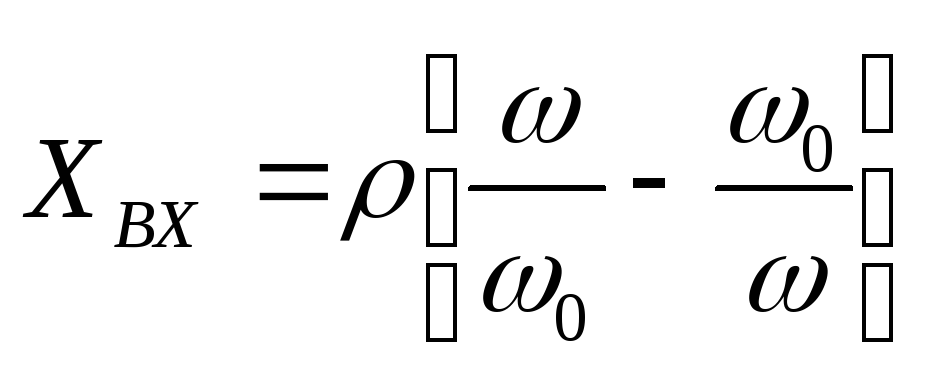
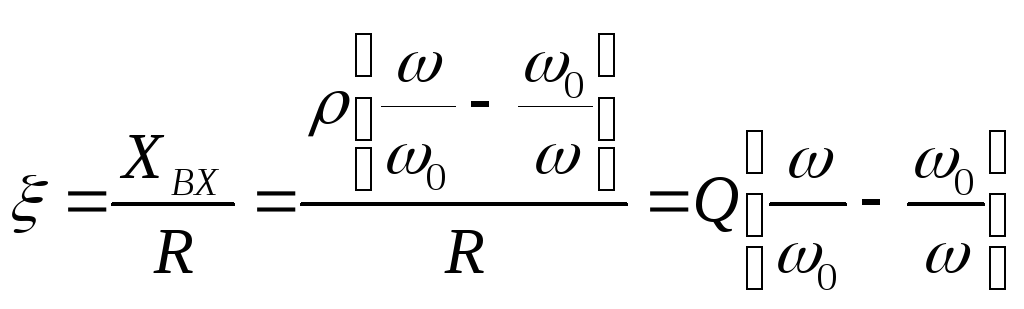
Обычно
исследуют контура вблизи резонансной
частоты 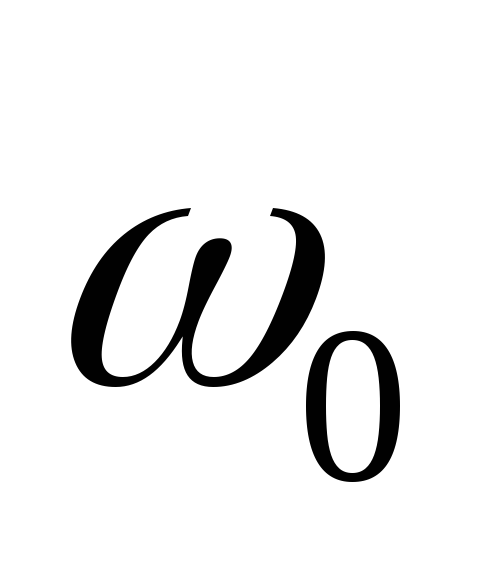 ,
то есть при малых расстройках частоты
(при малом уходе от резонансной частоты)
,
то есть при малых расстройках частоты
(при малом уходе от резонансной частоты)
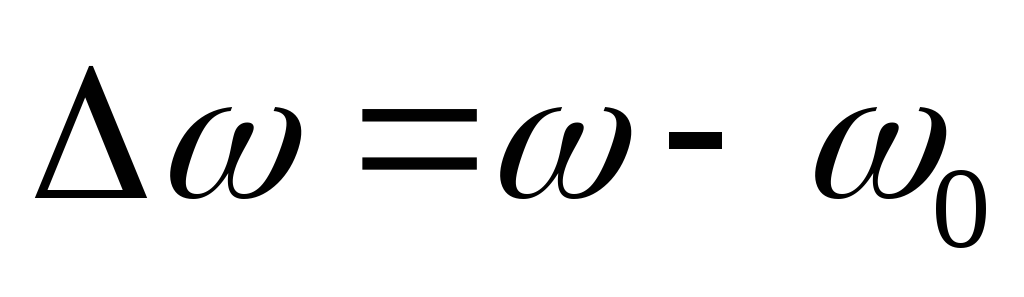 .
.
Тогда 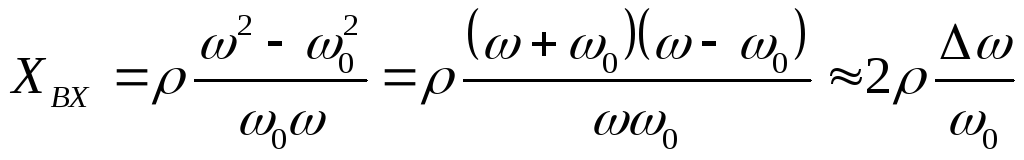 .
.
Зависимость
модуля 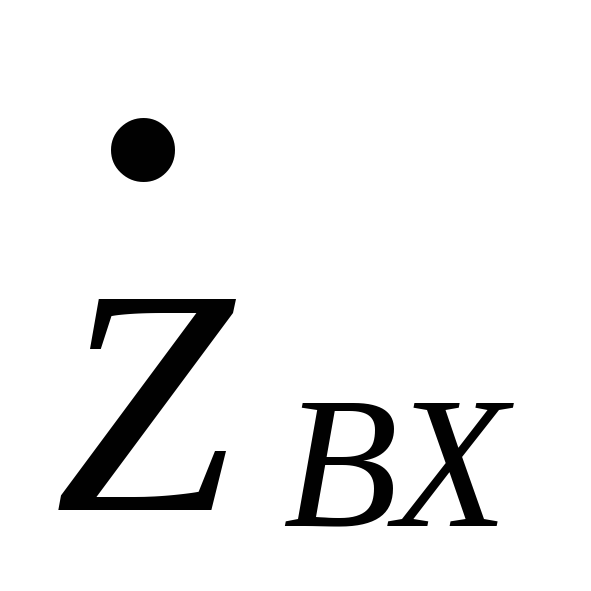 от расстройки представленна на рис. 4.
от расстройки представленна на рис. 4.
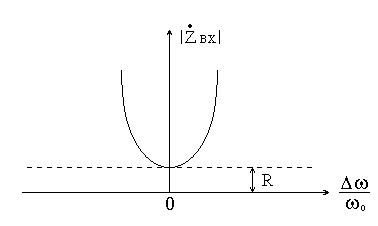
Рис. 4.
Ток в контуре определяется выражением
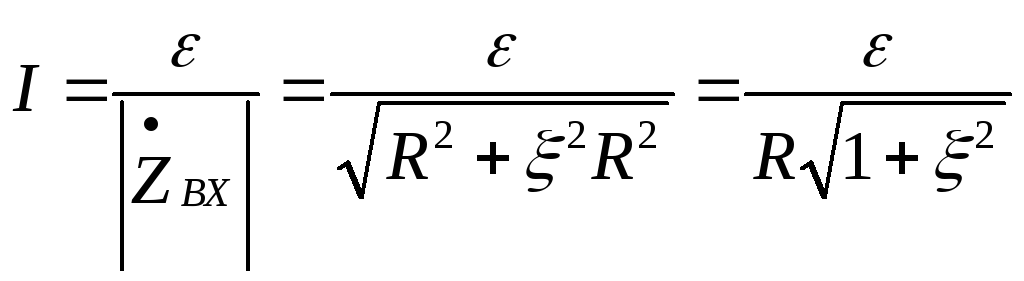
При
резонансе ток достигает максимального
значения 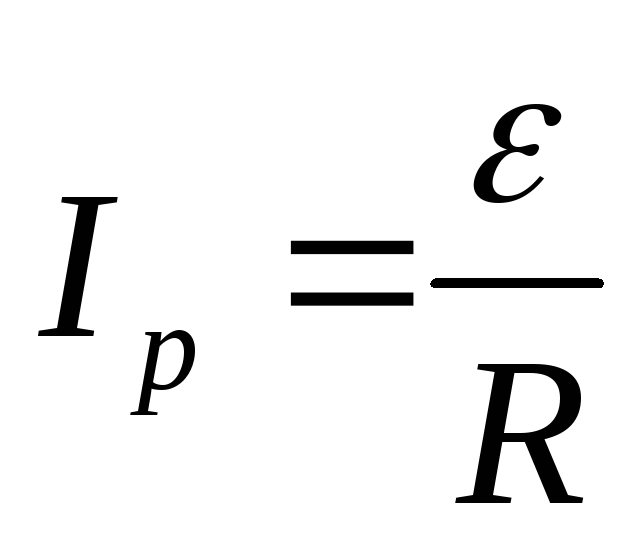 .
Кривая, показывающая отношение
.
Кривая, показывающая отношение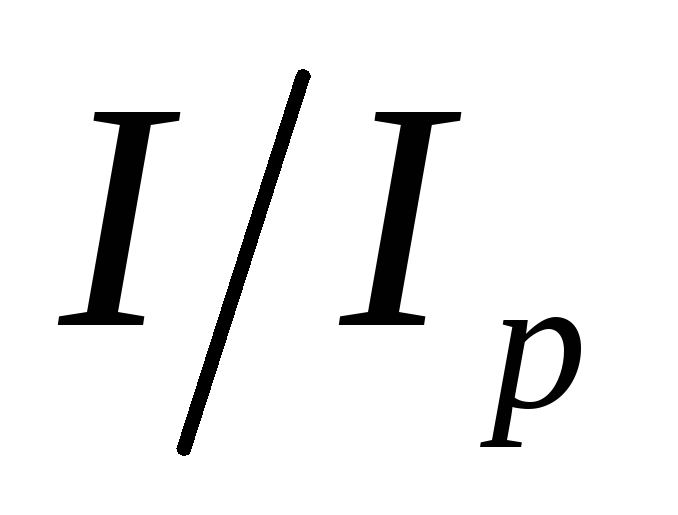 ,
называется резонансной кривой контура
(рис. 5).
,
называется резонансной кривой контура
(рис. 5).
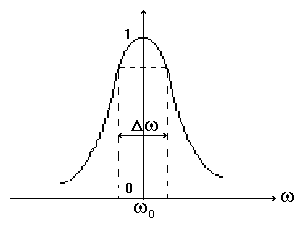
Рис. 5.
Для сравнения работы последовательных контуров вводится понятие полосы пропускания по уровню 0.7, как интервала частот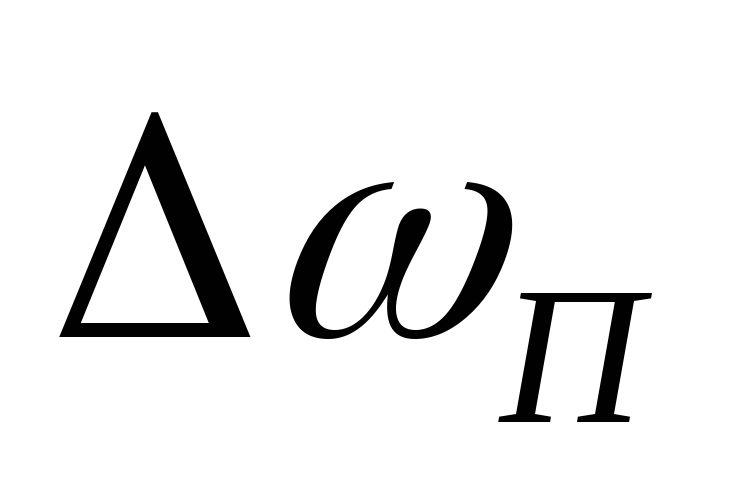 ,
для которых отношение
,
для которых отношение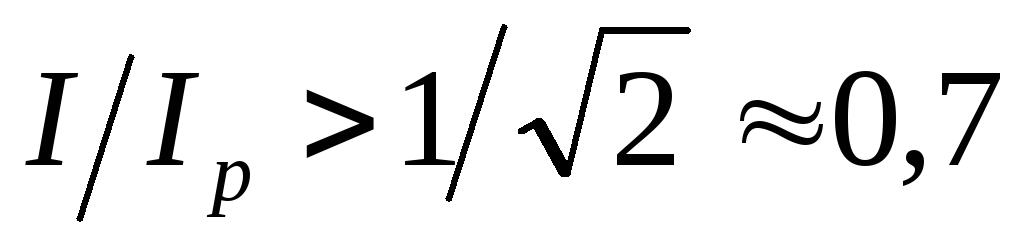
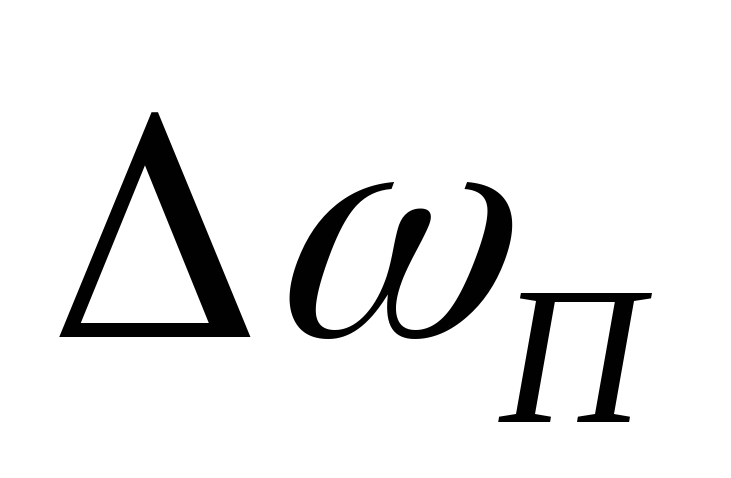 :
: 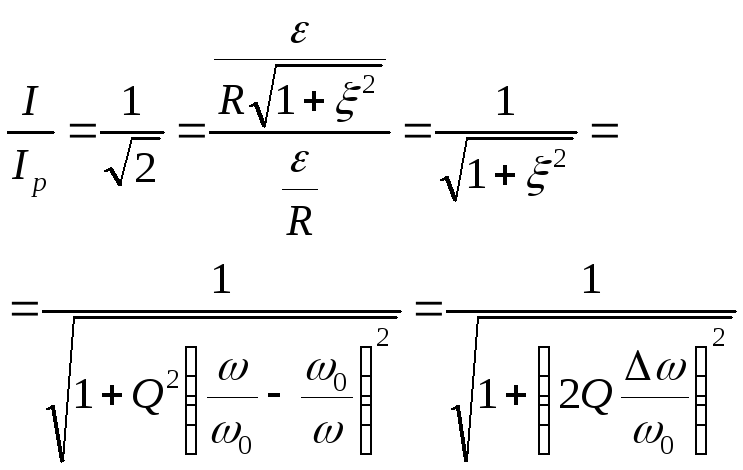
или 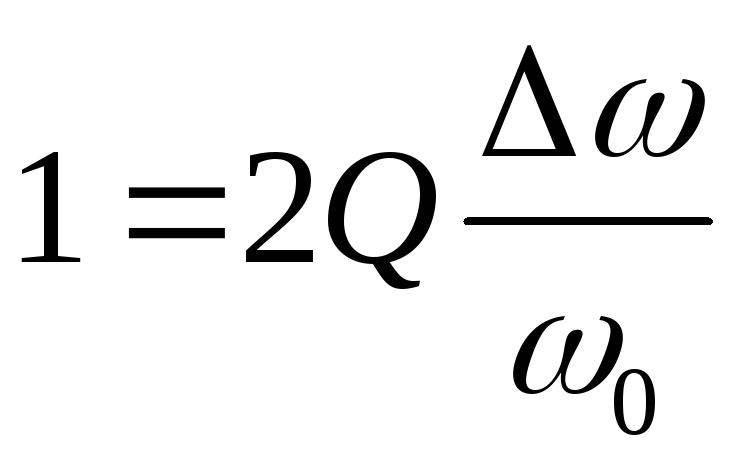 ,
отсюда
,
отсюда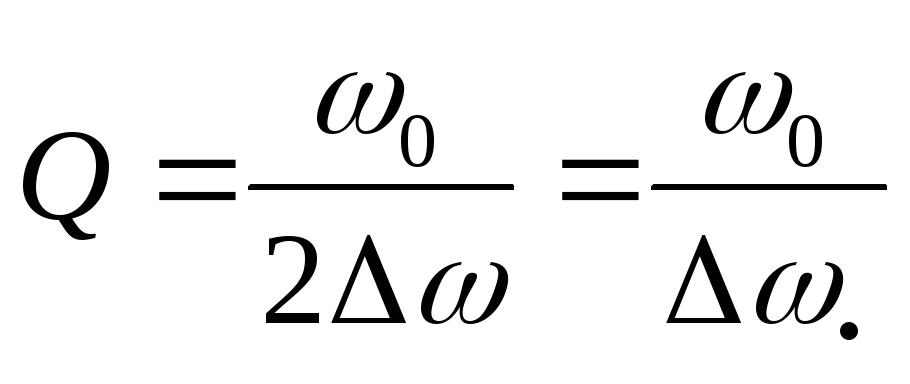 ,
где
,
где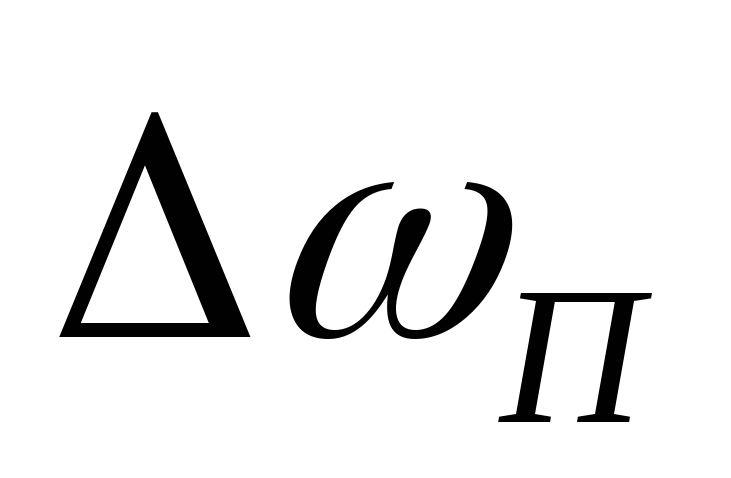
Вынужденные
колебания в контуре создаются генератором
с определенным внутренним сопротивлением 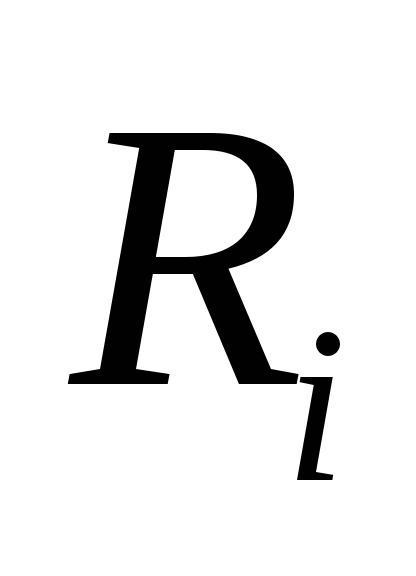 (рис. 6). Внутреннее сопротивление
генератора ухудшает избирательные
свойства контура, т.е. делает резонансную
кривую более пологой (рис. 7), т.е. уменьшает
добротность контура, т.к.
(рис. 6). Внутреннее сопротивление
генератора ухудшает избирательные
свойства контура, т.е. делает резонансную
кривую более пологой (рис. 7), т.е. уменьшает
добротность контура, т.к.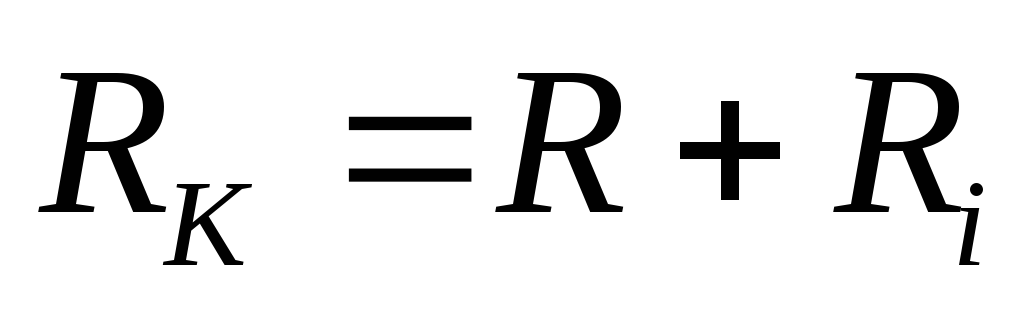 .
.
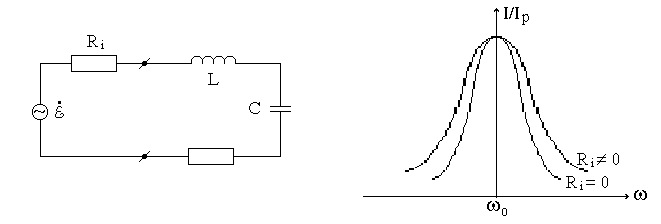
Откуда 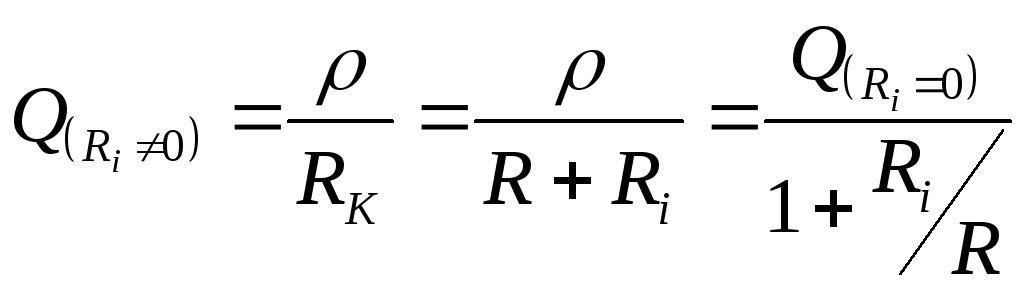
Кривые зависимостей напряжений на индуктивности и емкости от частоты выглядят аналогично, по ним так же можно определить добротность контура.
Колебательные контуры — RadioRadar
Документация
Главная Справочник Документация
«Документация» — техническая информация по применению электронных компонентов, особенностях построения различных радиотехнических и электронных схем, а также документация по особенностям работы с инженерным программным обеспечением и нормативные документы (ГОСТ).
Оглавление
Материал предоставлен журналом Радиолюбитель
Последовательный колебательный контур
Как известно, простейшими резонансными (или колебательными) цепями являются последовательный и параллельный колебательные контуры. Рассмотрим цепь, состоящую из последовательно включенных катушки индуктивности и конденсатора (рис. 1). При воздействии на такую цепь переменного (в простейшем случае гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина (амплитуда) которого может быть вычислена согласно закону Ома: I = U/|ХΣ| , где |ХΣ| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора. На рис. 2 приведены зависимости реактивных сопротивлений катушки XL и конденсатора ХC от круговой частоты ω, а также график зависимости от частоты ω их алгебраической суммы ХΣ Последний график, по сути, показывает зависимость от частоты общего реактивного сопротивления цепи, изображенной на рис. 1. Из этого графика видно, что на некоторой частоте ω=ωр , на которой реактивные сопротивления катушки и конденсатора равны по модулю, общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи, а саму цепь, изображенную на рис. 1, принято называть последовательным колебательным контуром. Также из рис. 2 видно, что на частотах ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах — индуктивный. Что касается самой резонансной частоты, то она может оыть вычислена при помощи известной формулы Томсона: ωр = 1/√(LC).
Рис. 1
Последовательный колебательный контур
Рис. 2
Зависимости реактивных сопротивлений катушки XL и конденсатора ХC от круговой частоты ω
На рис.3 изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь r, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Модуль полного сопротивления (импеданса) такой цепи определяется следующим образом: |z| = √(r2+|XΣ|2), где |XΣ| = ωL-1/ωC. Очевидно, что на резонансной частоте, когда величины реактивных сопротивлений катушки XL = jωL и конденсатора ХC= -j/ωС равны по модулю, величина |XΣ| обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/r. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение UL=UC=I|XL|=I|XC|. На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы — они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений |XL| и |XC| .Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. С учетом приведенной записи для импеданса цепи можно привести часто встречающееся определение резонансной частоты: резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер.
Рис. 3
Эквивалентная схема последовательного резонансного контура
Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое сопротивление ρ и добротность Q. Характеристическим сопротивлением контура ρ называется величина модуля реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = |ХL| =|ХC| при ω =ωр . В общем случае характеристическое сопротивление может быть вычислено следующим образом: ρ = √(LC). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура — катушкой (энергия магнитного поля) WL= (LI2)/2 и конденсатором (энергия электрического поля) WC=(CU2)/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает «качество». Величину, обратную добротности d=1/Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q=ρ/r, где r-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р=I2r. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.
Рис.4 а
Рис.4 б
| Рис. 5 а | Рис. 5 б |
Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ). На рис. 4а и рис. 4б представлены два простейших четырехполюсника, содержащих последовательный колебательный контур. АЧХ этих цепей приведены (показаны сплошными линями) на рис. 5а и рис. 5б соответственно. По вертикальной оси отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному. Для пассивных цепей (не т.е. содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Очевидно, что сопротивление цепи на рис. 4а переменному току будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля. При резонансе в цепи, изображенной на рис. 4б, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. Чаще всего за полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение — в зависимости от вида цепи) коэффициента передачи относительного его значения на резонансной частоте, не превышает величины 0,707 (3дБ).
Пунктирными линиями на рис. 5а и рис. 5б показаны АЧХ точно таких же цепей, как на рис. 4а и рис. 4б соответственно, колебательные контуры которых имеют такие же резонансные частоты, как и для случая рассмотренного выше, но обладающие меньшей добротностью (например, катушка индуктивности намотана проводом, обладающим большим сопротивлением постоянному току). Как видно из рис. 5а и рис. 5б, при этом расширяется полоса пропускания цепи и ухудшаются ее селективные (избирательные) свойства. Исходя из этого, при расчете и конструировании колебательных контуров нужно стремиться к повышению их добротности. Однако, в ряде случаев, добротность контура, наоборот, приходится занижать (например, включая последовательно с катушкой индуктивности резистор небольшой величины сопротивления), что позволяет избежать искажений широкополосных сигналов. Хотя, если на практике требуется выделить достаточно широкополосный сигнал, селективные цепи, как правило, строятся не на одиночных колебательных контурах, а на более сложных связанных (многоконтурных) колебательных системах, в т.ч. многозвенных фильтрах.
Параллельный колебательный контур
В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рис. 6 приведена принципиальная схема параллельного колебательного контура Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя — можно лишь складывать проводимости На рис. 7 приведены графические зависимости реактивных проводимостей катушки индуктивности BL = j/ωL, конденсатора ВC = -jωC, а также суммарной проводимости ВΣ, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току. Действительно, если построить зависимость реактивного сопротивления контура от частоты XΣ=1/BΣ, эта кривая (рис. 8) в точке ω = ωр будет иметь разрыв второго рода. Сопротивление реального параллельного колебательного контура (т.е с потерями), разумеется, не равно бесконечности — оно тем меньше, чем больше омическое сопротивление потерь в контуре, т.е уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический смысл понятий добротности, характеристического сопротивления и резонансной частоты колебательного контура, а также их расчетные формулы, справедливы как для последовательного, так и для параллельного колебательного контура.
Рис. 6
Параллельный колебательный контур
Рис. 7
Зависимости реактивных поводимостей катушки и конденсатора и суммарная проводимость этих двух элементов
Рис. 8
Зависимость реактивного сопротивления контура от частоты
Рассмотрим цепь, состоящую из генератора гармонических колебаний и параллельного колебательного контура. В случае, когда частота колебаний генератора совпадает с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут одинаковыми. В этом случае говорят, что в цепи имеет место резонанс токов. Как и в случае последовательного колебательного контура, реактивности катушки и конденсатора компенсируют друг друга, и сопротивление контура протекающему через него току становится чисто активным (резистивным). Величина этого сопротивления, часто называемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление Rэкв=Q·ρ. На частотах, отличных от резонансной, сопротивление контура уменьшается и приобретает реактивный характер (рис. 8) на более низких частотах — индуктивный (поскольку реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких — наоборот, емкостной (т к реактивное сопротивление емкости падает с ростом частоты). В процессе работы контура, дважды за период колебаний, происходит энергетический обмен между катушкой и конденсатором (рис. 9). Энергия поочередно накапливается то в виде энеогии электрического поля заряженного конденсатора, то в виде энергии магнитного поля катушки индуктивности. При этом в контуре протекает собственный контурный ток Iк, превосходящий по величине ток во внешней цепи I в Q раз. В случае идеального контура (без потерь), добротность которого теоретически бесконечна, величина контурного тока также будет бесконечно большой.
Рис. 9
Процесс работы контура
| Рис. 10 а | Рис. 10 б |
Рассмотрим, как изменяются коэффициенты передачи четырехполюсников, аналогичных приведенным на рис. 4а и рис. 4б, от частоты, при включении в них не последовательных колебательных контуров, а параллельных. Четырехполюсник, изображенный на рис. 10а, на резонансной частоте контура представляет собой огромное сопротивление току, поэтому при ω=ωр его коэффициент передачи будет близок к нулю (с учетом омических потерь). На частотах, отличных от резонансной, сопротивление контура будет уменьшатся, а коэффициент передачи четырехполюсника — возрастать. Этот случай соответствует графику АЧХ, приведенному на рассмотренном ранее рис. 5б. Для четырехполюсника, приведенного на рис. 10б, ситуация будет противоположной — на резонансной частоте контур будет представлять собой очень большое сопротивление и практически все входное напряжение поступит на выходные клеммы (т.е коэффициент передачи будет максимален и близок к единице). При значительном отличии частоты входного воздействия от резонансной частоты контура, источник сигнала, подключаемый к входным клеммам четырехполюсника, окажется практически закороченном накоротко, а коэффициент передачи будет близок к нулю. АЧХ такого четырехполюсника соответствует изображенной на рис. 5а.
В заключении настоящего экскурса отметим тот факт, что достаточно часто в реальной радиоэлектронной аппаратуре приходится сталкиваться с необходимостью перестройки колебательных контуров — например, в приемнике, для обеспечения возможности приема радиостанций, работающих на разных частотах В этом случае емкостные элементы контуров выполняются в виде конденсаторов переменной емкости, либо специальных диодов — варикапов, обладающих большой барьерной емкостью, зависящей от приложенного к ней запирающего напряжения В ряде случаев применяют и перестраиваемый катушки индуктивности — вариометры.
Дата публикации: 09.09.2003
Оглавление
Мнения читателей
- Павел / 12.01.2017 — 09:20
Спасибо! - Поиск / 14.01.2016 — 21:21
подскажите как вычислить частоту контура, если включить катушку параллельно последовательному контуру? - Кирилл / 18.02.2014 — 22:22
Мужики дайте схему подключения аудиомодуляции к первичке тесла? Хочу переделать Ионофон под поющий транс тесла. Или подскажите где такие схемы найти если они есть? Пожалуйста и заранее спасибо! - николай / 21.10.2013 — 07:32
подскажите как вычислить частоту контура, если включить конденсатор параллельно последовательному контуру - sad / 10.07.2013 — 13:22
Ыыыы!!! - Денис / 20.06.2013 — 09:43
Как изменится период колебаний контура, если пластины конденсатора, включенного в контур сблизить между собой: а) уменьшится ; б) увеличится Дать математически обоснованный ответ. Помогите я в физике дуб дубом.. 🙁 Зарание спасибо - витя / 19.04.2013 — 11:51
спасибо за информацию - Влад… / 23.11.2012 — 17:41
Спасибо, очень доходчиво написано. - ааааааа / 04.10.2012 — 10:24
ааааааа - Света / 18.09.2012 — 15:06
колебательній контур состоит из конденсатора емкостью 2 Пф и катушки с индуктивностью 0,50 мкГн,какова частота колебаний в контуре - серегей / 15.09.2012 — 11:51
помогите пожалуста .как отличается зависимость полного сопротивления от частоты для последовательного и параллельного контуров? - Срез умоляю помогите / 05.06.2012 — 05:57
колебательный контур излучает в воздухе электромагнитные войны длиной 150м. Какая емкость включена в контур, если его индуктивноть равна 0,25 мГн? Активным сопротивлением пренебречь - Денис / 13.05.2012 — 19:09
ребят, подскажите плиз) эт вопрос на билет к экзамену( не могу нигде найти( Реальный колебательный контур.Свободные колебание в контуре с потерями. Характеристики оценивающие реальный колебательный контур. - Денис / 13.05.2012 — 19:00
ребят, подскажите плиз) эт вопрос на билет к экзамену( не могу нигде найти( Реальный колебательный контур.Свободные колебание в контуре с потерями. Характеристики оценивающие реальный колебательный контур. - Ann / 11.05.2012 — 15:31
как изменится форма резонансной кривой,если в колебательный контур включить резистор? - Ann / 11.05.2012 — 15:29
как изменится форма резонансной кривой,если в колебательный контур включить резистор? - василий / 16.04.2012 — 10:11
обьясните пожалуста как рабтает колебательный контур ? - Сергей,Ужгород / 10.02.2012 — 13:33
Спасибо автору. Простое и понятное объяснение без заумной теории и формул. Кому надо более глубокий анализ — изучайте курс ЛРТУ (линейные радиотехнические устройства). А всякие придирки типа «Скажите, где вы видите контур на рис.1. Лично я вижу там двухполюсник» — чепуха, игра слов. Все изожено просто и понятно. - Саша / 19.12.2011 — 09:35
Ну что,могу сказать только одно,отличный сайт!Очень познавательный,вот только если б кто подкрепил теорию вечного двигателя основанного на резонансе,практикой,и выложил бы материалы на сайт,я думаю было бы ещё интересней.должен же кто нибудь когда нибудь до этого дойти.Я поддерживаю идею этого,по сути простейшего,вечного двигателя.И Теслу уважаю,он был прав на счет всего о чем сейчас ведутся разговоры.Его ещё вспомнят!Я считаю,что от наших разговоров о резонансе и получении на выходе мощности больше чем на входе,закон сохранения энергии уже канул в лето,вопреки всему,свободная энергия существует!!!:)как сказал один … :»и всё таки она вертится!»,только в нашем случае:»и всё таки она существует!!!» - Алекс / 16.09.2011 — 12:16
Здравствуйте. Характеристическое сопротивление равно корень квадратный из отношения L/С (а не произведения LC)
Вы можете оставить свой комментарий, мнение или вопрос по приведенному вышематериалу:
2.2.4 Последовательный колебательный контур
В
последовательной цепи, состоящей из 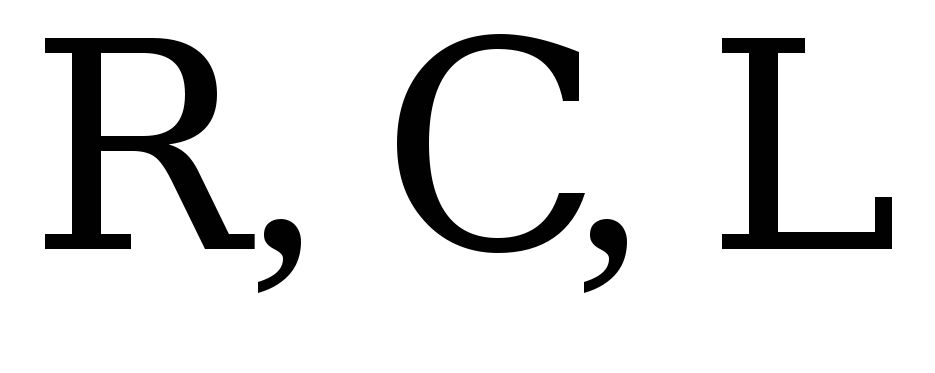 элементов, возникает явление, называющееся
резонансом напряжений, когда напряжения
на конденсаторе и катушке индуктивности
равны по модулю и в десятки–сотни раз
превосходят входное напряжение. Условием
резонанса напряжений является отсутствие
сдвига фаз между током и напряжением
источника сигнала
элементов, возникает явление, называющееся
резонансом напряжений, когда напряжения
на конденсаторе и катушке индуктивности
равны по модулю и в десятки–сотни раз
превосходят входное напряжение. Условием
резонанса напряжений является отсутствие
сдвига фаз между током и напряжением
источника сигнала ,
т.е.
,
т.е.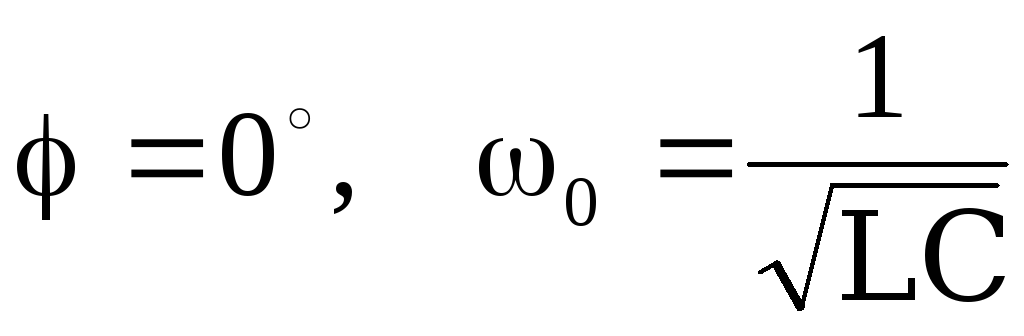 – резонансная частота колебательного
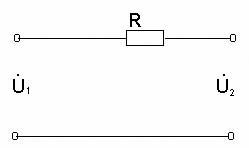
контура. Представим последовательный
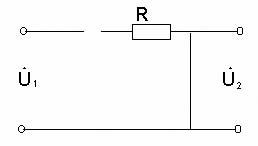
колебательный контур в виде четырехполюсника
(рис.17), где выходное напряжение
– резонансная частота колебательного
контура. Представим последовательный
колебательный контур в виде четырехполюсника
(рис.17), где выходное напряжение 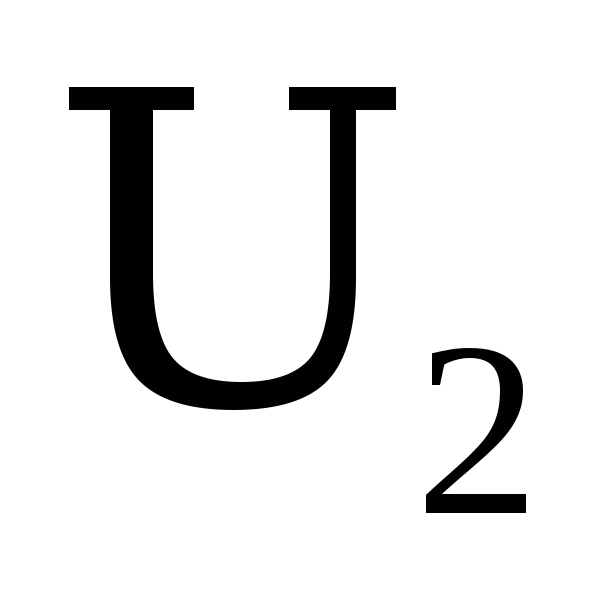 снимается с конденсатора
снимается с конденсатора .
Определим комплексный коэффициент
передачи этой цепи.
.
Определим комплексный коэффициент
передачи этой цепи.
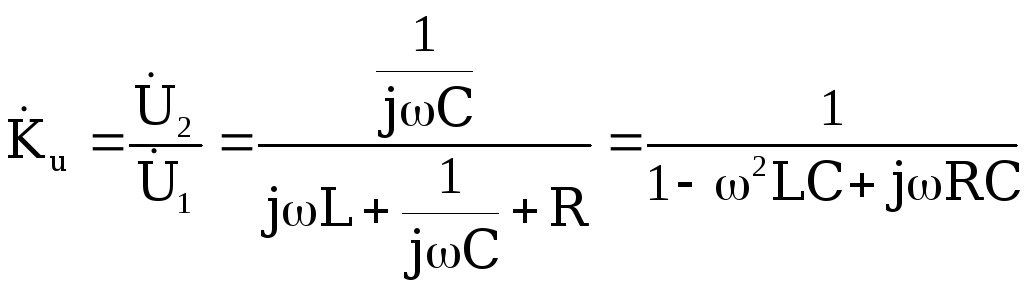 .
.
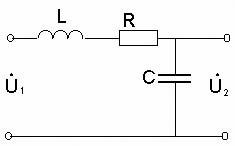
Рисунок 17 Схема последовательного колебательного контура
Отсюда
видно, что комплексный коэффициент
передачи этой цепи зависит от частоты 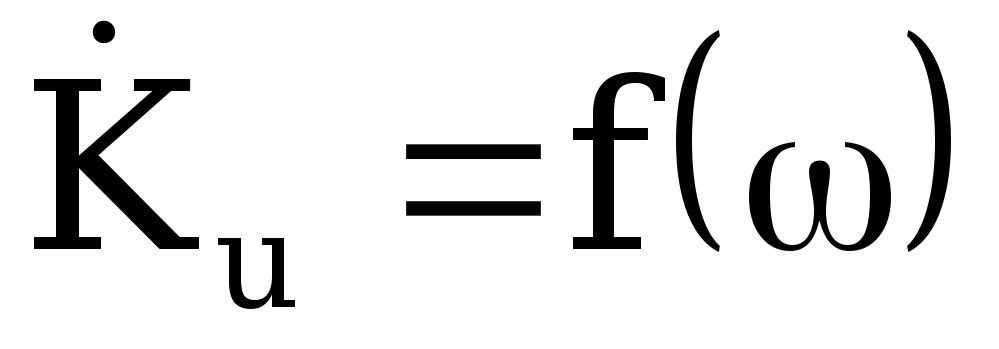 .
Найдем модуль коэффициента передачи последовательного
колебательного контура:
.
Найдем модуль коэффициента передачи последовательного
колебательного контура:
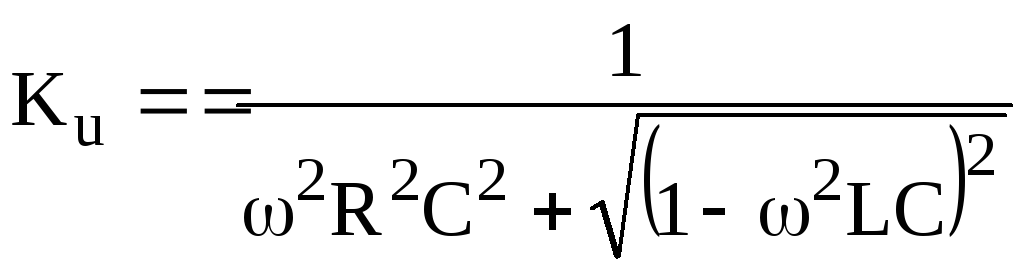 .
.
Проведём анализ полученной формулы:
при
 ;
;при
 ;
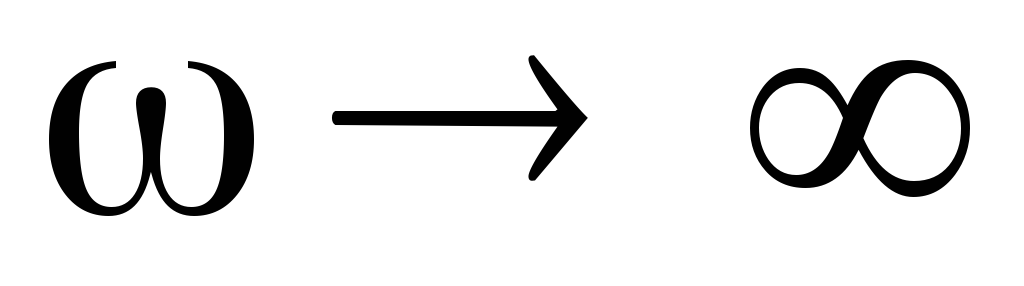
;при
 .
.
При 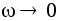 и
и 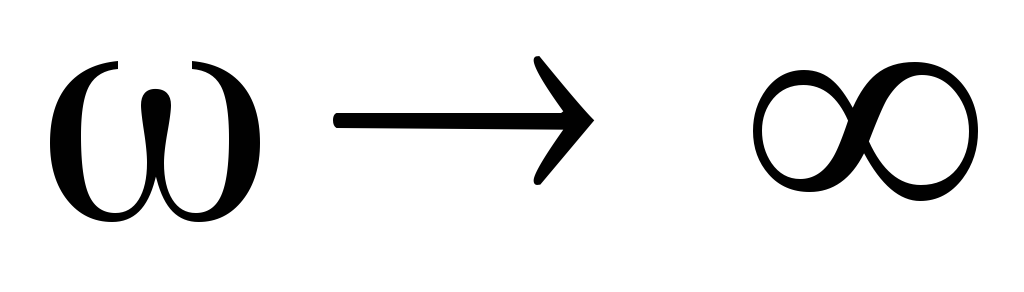 реактивное сопротивление конденсатора
стремится к бесконечности и нулю, а
сопротивление катушки к нулю и
бесконечности, соответственно. В схемах
это эквивалентно разрыву цепи и короткому
замыканию, соответственно.Проводя
последующие рассуждения, можем изобразить
эквивалентные схемы последовательного
колебательного контура:
реактивное сопротивление конденсатора
стремится к бесконечности и нулю, а
сопротивление катушки к нулю и
бесконечности, соответственно. В схемах
это эквивалентно разрыву цепи и короткому
замыканию, соответственно.Проводя
последующие рассуждения, можем изобразить
эквивалентные схемы последовательного
колебательного контура:
Рис.
18 Эквивалентная
схема последовательного колебательного
контура при | Рис.
19 Эквивалентная
схема последовательного колебательного
контура при |
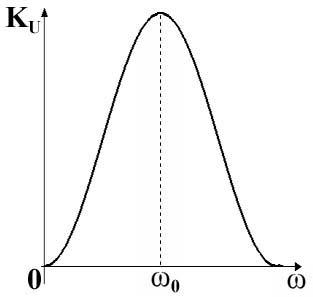
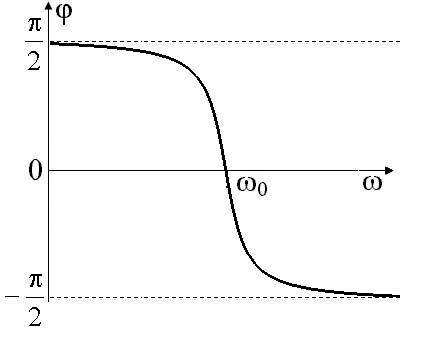
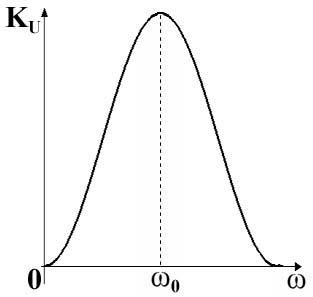
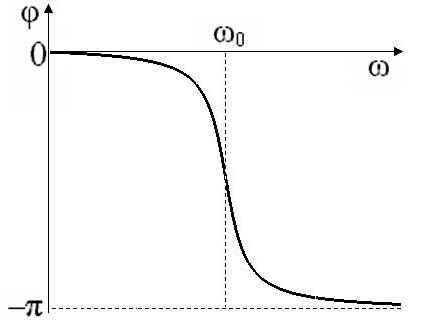
Рисунок 20 – Амплитудно-частотная характеристика последовательного колебательного контура | Рисунок 21 – Фазочастотная характеристика последовательного колебательного контура |
Таким образом, амплитудно-частотная характеристика последовательного колебательного контура имеет вид резонансной кривой, изображённой на рис. 20.
Из
выражения для комплексного коэффициента
передачи получим зависимость фазы от
частоты 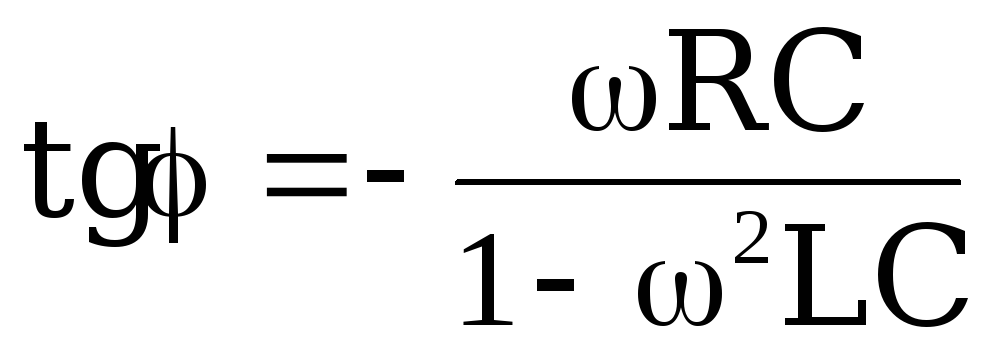 .
Откуда следует, что фазочастотная
характеристика контура
имеет вид, представленный на рисунок 21.
.
Откуда следует, что фазочастотная
характеристика контура
имеет вид, представленный на рисунок 21.
2.2.5 Параллельный колебательный контур
Параллельный
колебательный контур представляет
собой электрическую схему, где конденсатор
и катушка включены параллельно, а к ним
подводится напряжение от генератора.
Эта схема интересна тем, что на некоторой
частоте, называемой резонансной, в
контуре возникает резонанс токов, т.е.
в подводящих к контуру проводах ток
практически равен нулю, в то время как
через конденсатор и катушку циркулируют
огромные токи. На резонансной частоте
сопротивление параллельного колебательного
контура велико, что используется для
получения большого коэффициента усиления
по напряжению в резонансных усилителях,
где в качестве нагрузки включается
параллельный колебательный контур. На
практике катушка индуктивности и
подводящие провода обладают омическим
сопротивлением  .
Поэтому схему параллельного колебательного
контура в виде четырехполюсника с учетом
активного сопротивления можно представить
следующим способом (рисунок 22):
.
Поэтому схему параллельного колебательного
контура в виде четырехполюсника с учетом
активного сопротивления можно представить
следующим способом (рисунок 22):
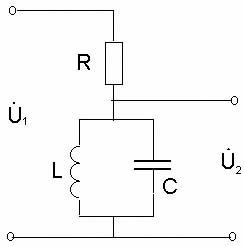
Рисунок 22. Схема параллельного колебательного контура в виде 4-х полюсника
Определим
комплексный коэффициент передачи этой
цепи: 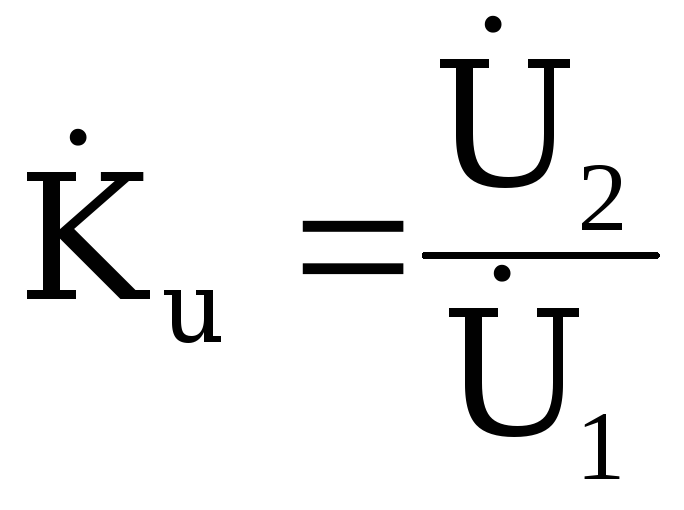 .
Обозначим сопротивление параллельно
соединенных катушки индуктивности и
конденсатора, как
.
Обозначим сопротивление параллельно
соединенных катушки индуктивности и
конденсатора, как .
Тогда
.
Тогда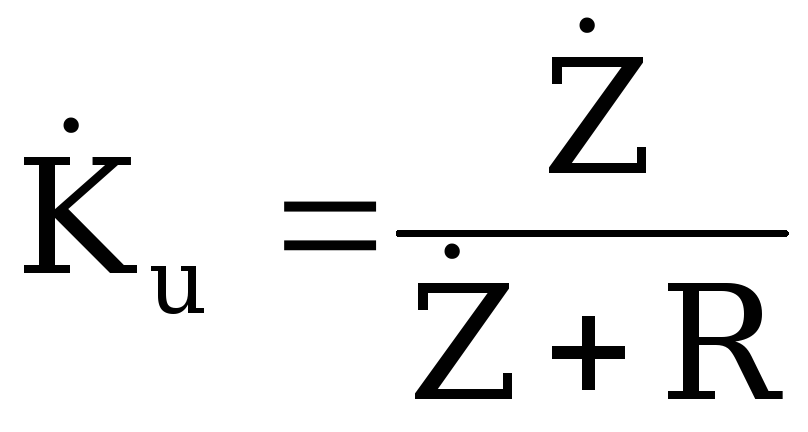 или
с учетом того, что
или
с учетом того, что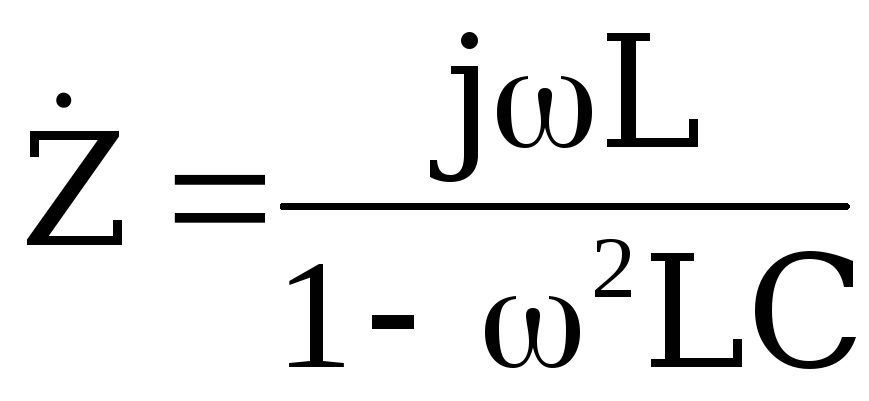 получим
получим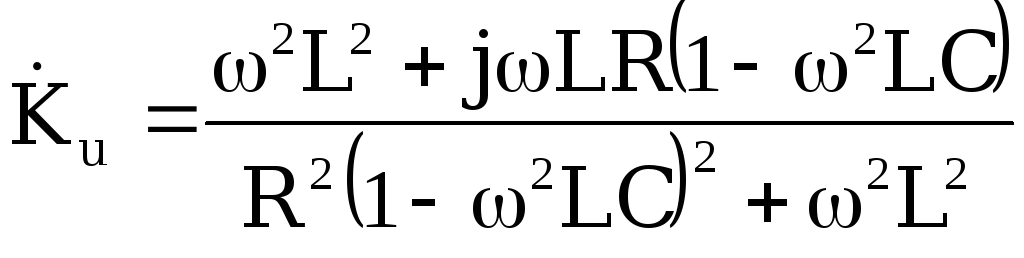 .
Модуль коэффициента передачи этой цепи
имеет вид:
.
Модуль коэффициента передачи этой цепи
имеет вид: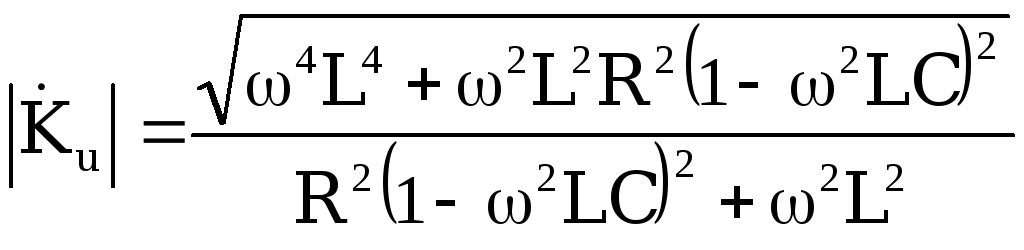 или
или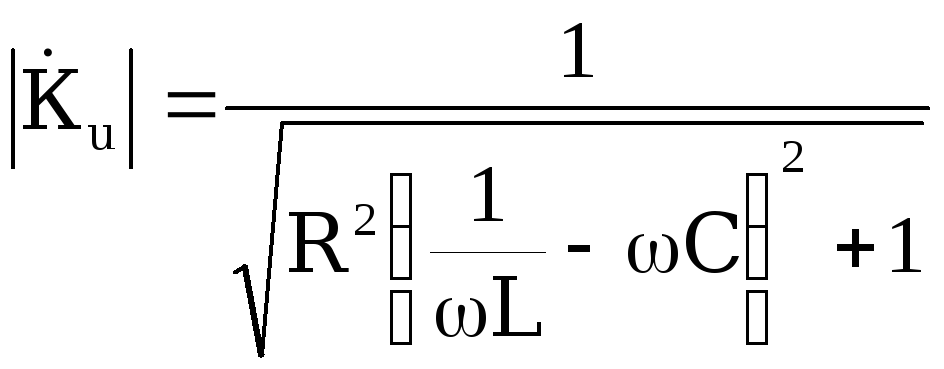 .
Проведём анализ полученной формулы:
.
Проведём анализ полученной формулы:
при
 ;
;при
 ;
;при
 .
.
Таким образом, амплитудно-частотная характеристика имеет вид резонансной кривой, изображённой на рис. 23.
Из
формулы (4) получим зависимость фазы от
частоты. 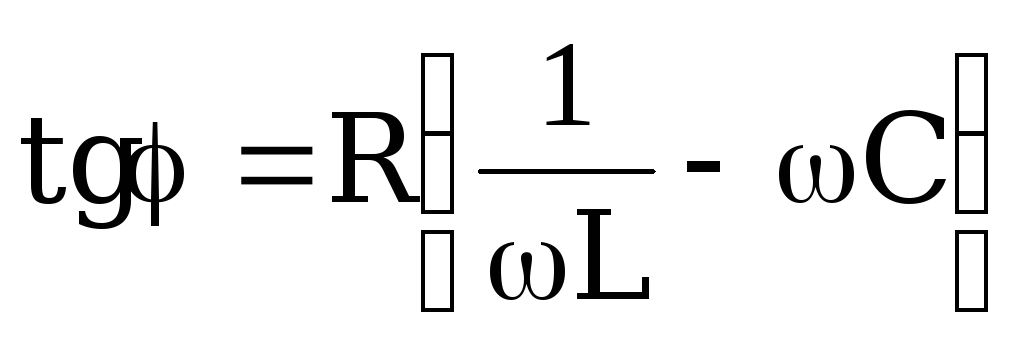 .
Проведём анализ полученной формулы
.
Проведём анализ полученной формулы
Фазочастотная характеристика параллельного колебательного контура имеет вид, представленный на рисунок 24.
Рисунок 23 – Амплитудно-частотная характеристика параллельного колебательного контура | Рисунок 24 – Фазочастотная характеристика параллельного колебательного контура |
Резонанс напряжений в последовательном колебательном контуре
В радиотехнике широкое применение имеют электрические цепи, составленные из катушки индуктивности и конденсатора. Такие цепи в радиотехнике называются колебательными контурами. Источник переменного тока к колебательному контуру может быть присоединен двумя способами: последовательно (рисунок 1а) и параллельно (рисунок 1б).
Рисунок 1. Схемотическое обозначение колебательного контура. а) последовательный колебательный контур; б) параллельный колебательный контур.
Рассмотрим поведение колебательного контура в цепи переменного тока при последовательном соединении контура и источника тока (рис 1а).
Мы знаем, что такая цепь оказывает переменному току реактивное сопротивление, равное:
где RL— активное сопротивление катушки индуктивности в ом;
ωL,-индуктивное сопротивление катушки индуктивности в ом;
1/ωC-емкостное сопротивление конденсатора в ом.
Активное сопротивление катушки RL практически очень мало изменяется при изменении частоты (если пренебречь поверхностным эффектом). Индуктивное и емкостное сопротивления в очень сильной степени зависят от частоты, а именно: индуктивное сопротивление ωL увеличивается прямо пропорционально частоте тока, а емкостное сопротивление 1/ωC уменьшается при повышении частоты тока, т. е. оно связано с частотой тока обратно пропорциональной зависимостью.
Отсюда непосредственно следует, что реактивное сопротивление последовательного колебательного контура также зависит от частоты, и колебательный контур будет оказывать токам разных частот неодинаковое сопротивление.
Если мы будем измерять реактивное сопротивление колебательного контура при различных частотах, то обнаружим, что в области низких частот сопротивление последовательного контура очень велико; при увеличении частоты оно уменьшается до некоторого предела, а затем начинает снова возрастать.
Объясняется это тем, что в области низких частот ток испытывает большое сопротивление со стороны конденсатора, при увеличении же частоты начинает действовать индуктивное сопротивление, компенсирующее действие емкостного сопротивления.
При некоторой частоте индуктивное сопротивление становится равным емкостному, т. е.
Они будут взаимно компенсировать друг друга и общее реактивное сопротивление контура станет равным нулю:
При этом реактивное сопротивление последовательного колебательного контура будет равно только его активному сопротивлению, так как
При дальнейшем повышении частоты ток будет испытывать все большее и большее сопротивление со стороны индуктивности катушки, при одновременном уменьшении компенсирующего действия емкостного сопротивления. Поэтому реактивное сопротивление контура начнет снова возрастать.
На рисунке 2а приведена кривая, показывающая изменение реактивного сопротивления последовательного колебательного контура при изменении частоты тока.
Рисунок 2. Резонанс напряжений. а) зависимость изменения полного сопротивления от частоты; б) зависимость реактивного сопротивления от активного сопротивления контура; в) кривые резонанаса.
Частота тока, при которой сопротивление колебательного контура делается наименьшим, называется частотой резонанса или резонансной частотой колебательного контура.
При резонансной частоте имеет место равенство:
пользуясь которым, нетрудно определить частоту резонанса:
(1)
Единицами в этих формулах служат герцы, генри и фарады.
Из формулы (1) видно, что чем меньше величины емкости и самоиндукции колебательного контура, тем больше будет его резонансная частота.
Величина активного сопротивления RL не влияет на резонансную частоту, однако от нее зависит характер изменения Z. На рисунке 2б приведен ряд графиков изменения реактивного сопротивления колебательного контура при одних и тех же величинах L и С, но при разных RL. Из этого рисунка видно, что чем больше активное сопротивление последовательного колебательного контура, тем тупее становится кривая изменения реактивного сопротивления.
Теперь рассмотрим, как будет изменяться сила тока в колебательном контуре, если мы будем изменять частоту тока. При этом мы будем считать, что напряжение, развиваемое источником переменного тока, остается все время одним и тем же.
Так как источник тока включен последовательно с L и С контура, то сила тока, протекающего через катушку и конденсатор, будет тем больше, чем меньше реактивное сопротивление колебательного контура в целом, так как
Отсюда непосредственно следует, что при резонансе сила тока в колебательном контуре будет наибольшей. Величина тока при резонансе будет зависеть от напряжения источника переменного тока и от активного сопротивления контура:
На рисунке 2г изображен ряд графиков изменения силы тока в последовательном колебательном контуре при изменении частоты тока так называемых кривых резонанса. Из этого рисунка видно, что чем больше активное сопротивление контура, тем тупее кривая резонанса.
При резонансе сила тока может достигать огромных значений при сравнительно малой внешней ЭДС. Поэтому падения напряжения на индуктивном и емкостном сопротивлениях контура, т. е. на катушке и на конденсаторе, могут достигать очень больших величии и далеко превосходить величину внешнего напряжения.
Последнее утверждение на первый взгляд может показаться несколько странным, однако нужно помнить, что фазы напряжений на емкостном и индуктивном сопротивлениях сдвинуты друг относительно друга на 180°, т. е. мгновенные значения напряжений на катушке и конденсаторе направлены всегда в противоположные стороны. Вследствие этого большие напряжения, существующие при резонансе внутри контура на его катушке и конденсаторе, ничем не обнаруживают себя вне контура, взаимно компенсируя друг друга.
Разобранный нами случай последовательного резонанса называется резонансом напряжений, так как в этом случае в момент резонанса имеет место резкое увеличение напряжения на L и С колебательного контура.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
последовательный контур тока — со всех языков на русский
1 последовательный контур
Большой англо-русский и русско-английский словарь > последовательный контур
2 последовательный контур
Англо-русский словарь технических терминов > последовательный контур
3 Serienstromkreis
Универсальный немецко-русский словарь > Serienstromkreis
4 series circuit
Универсальный англо-русский словарь > series circuit
5 «in-line» hydraulic circuit
Англо-русский словарь технических терминов > «in-line» hydraulic circuit
6 series circuit
Англо-русский словарь технических терминов > series circuit
7 acceptor circuit
Универсальный англо-русский словарь > acceptor circuit
8 in-line hydraulic circuit
Универсальный англо-русский словарь > in-line hydraulic circuit
9 Serienkreis
сущ.электр. последовательная цепь, последовательный контур
Универсальный немецко-русский словарь > Serienkreis
10 Stromkreis
сущ.2) тех. контур, электрический контур
3) электр. контур тока, токовая цепь, электрическая цепь, цепь тока
6) океаногр. водоворот, круговое движение воды
9) судостр. контур цепи, фидер
Универсальный немецко-русский словарь > Stromkreis
11 Stromschleife
сущ.2) электр. контур тока, петля тока
Универсальный немецко-русский словарь > Stromschleife
12 Vorschaltnetzwerk
сущ.электр. последовательный контур, предвключённый контур
Универсальный немецко-русский словарь > Vorschaltnetzwerk
13 geschlossener Stromkreis
прил.3) электр. замкнутая цепь тока, замкнутый контур тока
Универсальный немецко-русский словарь > geschlossener Stromkreis
14 offener Stromkreis
прил. 1) тех. разомкнутый контур3) радио. открытый контур, разомкнутая цепь
4) электр. незамкнутая цепь тока, открытый контур тока, разомкнутая цепь тока
Универсальный немецко-русский словарь > offener Stromkreis
15 unbelasteter Stromkreis
прил.2) электр. ненагруженная цепь тока, ненагруженный контур тока
Универсальный немецко-русский словарь > unbelasteter Stromkreis
16 Serienkreis
(m)
последовательная цепь
последовательный контур
Deutsch-Russische Wörterbuch der Automatisierung und Fernsteuerung > Serienkreis
17 Längskreis
m
последовательный контур; последовательная цепь
Deutsch-Russische Wörterbuch polytechnischen > Längskreis
18 Serienkreis
m
последовательный контур; последовательная цепь
Deutsch-Russische Wörterbuch polytechnischen > Serienkreis
19 Stromkreis
Deutsch-Russische Wörterbuch polytechnischen > Stromkreis
20 series circuit
English-russian dictionary of physics > series circuit
См. также в других словарях:
Резонанс — (франц. resonance, от лат. resono звучу в ответ, откликаюсь) явление резкого возрастания амплитуды вынужденных колебаний (См. Вынужденные колебания) в какой либо колебательной системе (См. Колебательные системы), наступающее при… … Большая советская энциклопедия
ГОСТ 16110-82: Трансформаторы силовые. Термины и определения — Терминология ГОСТ 16110 82: Трансформаторы силовые. Термины и определения оригинал документа: 8.2. Аварийный режим трансформатора Режим работы, при котором напряжение или ток обмотки, или части обмотки таковы, что при достаточной… … Словарь-справочник терминов нормативно-технической документации
РЕЗОНАНС — (франц. resonance, от лат. resono звучу в ответ, откликаюсь), относительно большой селективный (избирательный) отклик колебательной системы (осциллятора) на периодич. воздействие с частотой, близкой к частоте её собств. колебаний. При Р.… … Физическая энциклопедия
Электрический конденсатор — У этого термина существуют и другие значения, см. Конденсатор (значения). См. также: варикап Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик … Википедия
блок — 23.02.13 блок* [block]: Часть текста, определенная пользователем, с которой проводят операции обработки текста. Источник: ГОСТ Р ИСО/МЭК 2382 23 2004: Информационная технология. Словарь. Часть 23. Обработка текста … Словарь-справочник терминов нормативно-технической документации
Конденсатор — Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик Слева конденсаторы для поверхностного монтажа; справа конденсаторы для объёмного монтажа; сверху керамические; снизу электролитические … Википедия
Конденсатор (электрический) — Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик Слева конденсаторы для поверхностного монтажа; справа конденсаторы для объёмного монтажа; сверху керамические; снизу электролитические … Википедия
Конденсатор (электронный компонент) — Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик Слева конденсаторы для поверхностного монтажа; справа конденсаторы для объёмного монтажа; сверху керамические; снизу электролитические … Википедия
Конденсатор (электронный элемент) — Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик Слева конденсаторы для поверхностного монтажа; справа конденсаторы для объёмного монтажа; сверху керамические; снизу электролитические … Википедия
Конденсатор электрический — Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик Слева конденсаторы для поверхностного монтажа; справа конденсаторы для объёмного монтажа; сверху керамические; снизу электролитические … Википедия
Подстроечный конденсатор — Основа конструкции конденсатора две токопроводящие обкладки, между которыми находится диэлектрик Слева конденсаторы для поверхностного монтажа; справа конденсаторы для объёмного монтажа; сверху керамические; снизу электролитические … Википедия
Резонанс токов в параллельном колебательном контуре
Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.
Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.
При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений. Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).
Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.
Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру. При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.
Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.
Сопротивление колебательного контура при параллельном резонансе равно:
где L выражено в гн, С—в ф, RL—в ом.
Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.
Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.
Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.
При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.
Явление резонанса имеет огромнейшее значение в радиотехнике. На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!


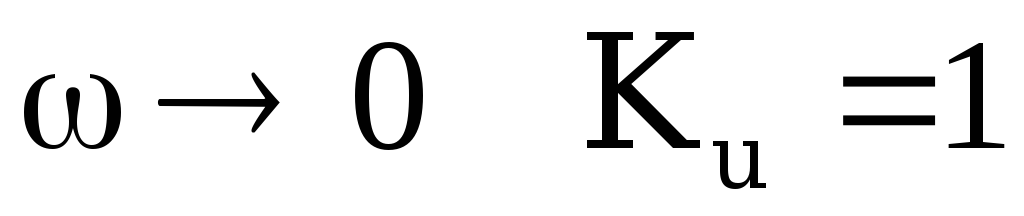 ;
;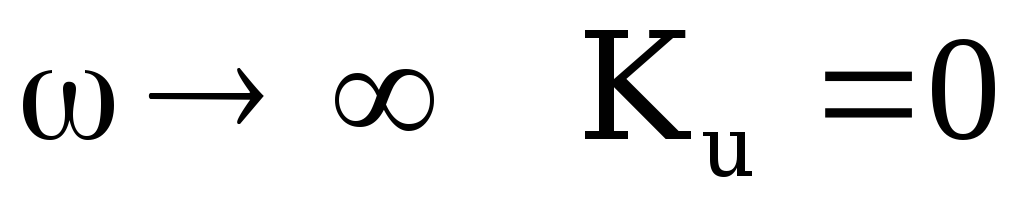 ;
;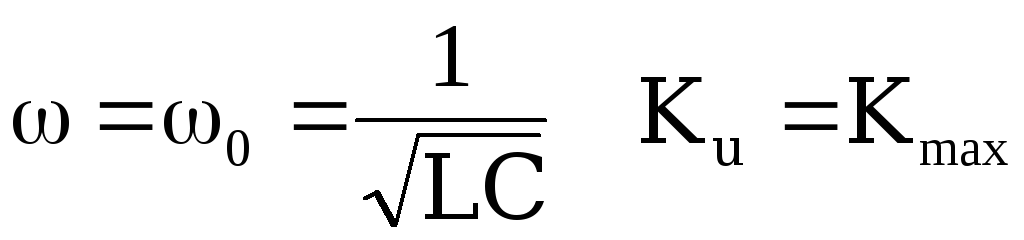 .
.
 .
.
 .
.
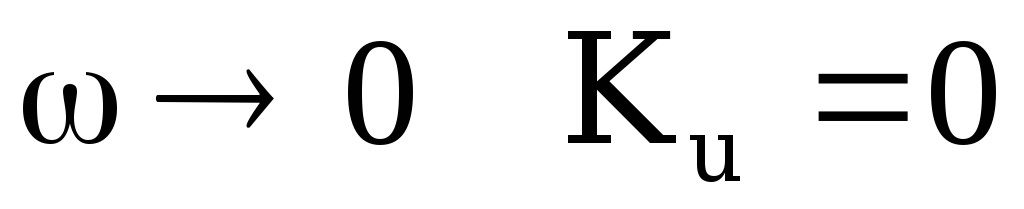 ;
;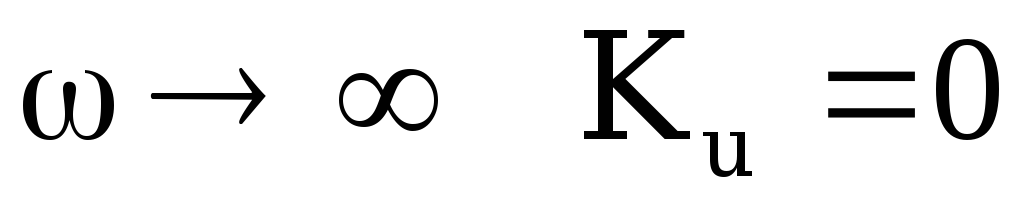 ;
;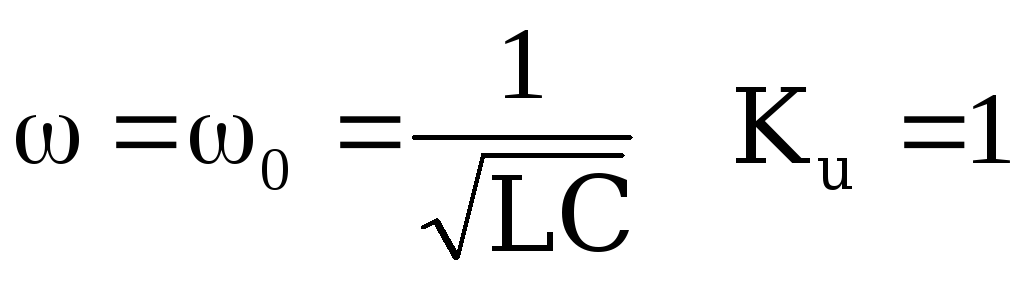 .
.