Параллельный колебательный контур (простой)
1. Идеализированный контур
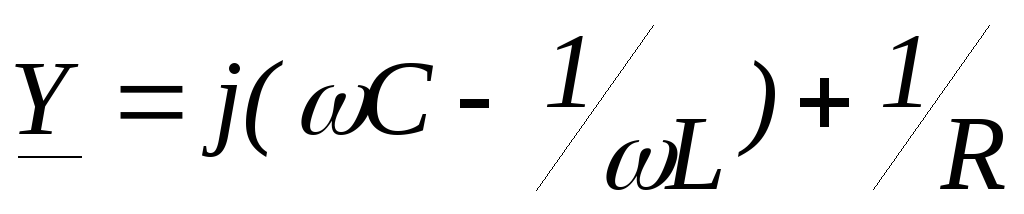 —
комплексная проводимость.
—
комплексная проводимость.
 —
резонансная частота
—
резонансная частота 
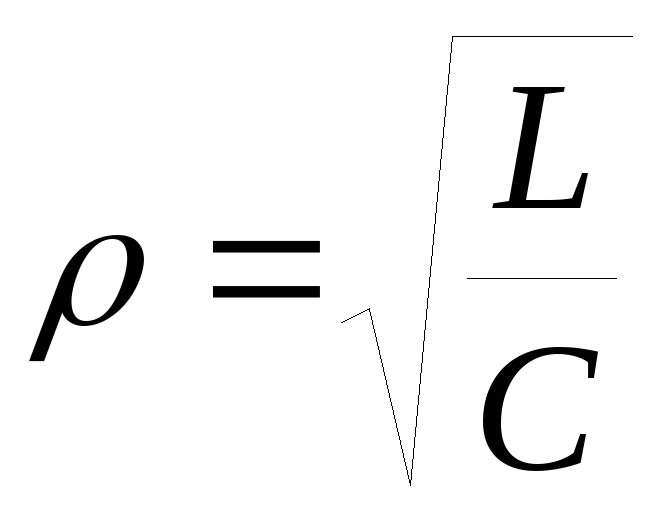 — характеристическое сопротивление,
сопротивление реактивного элемента на
резонансной частоте,
— характеристическое сопротивление,
сопротивление реактивного элемента на
резонансной частоте,
 ,
— усилительная способность контура где IL0, IC
,
— усилительная способность контура где IL0, IC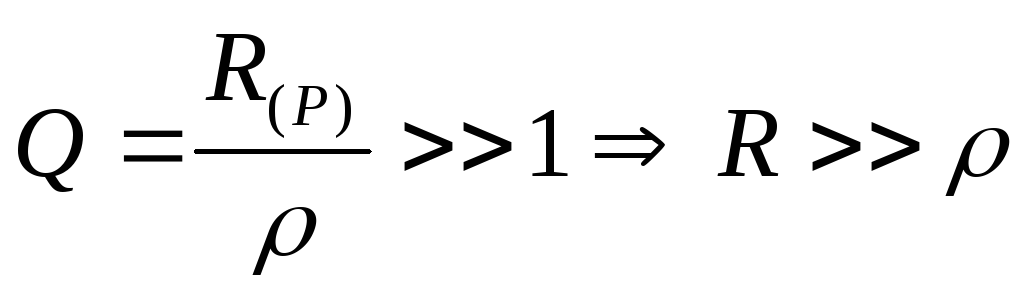 ,
,  .
При резонансе емкостной ток компенсируется
индуктивным и поэтому резонанс в
параллельном контуре называется
резонансом токов.
.
При резонансе емкостной ток компенсируется
индуктивным и поэтому резонанс в
параллельном контуре называется
резонансом токов.
Полоса
пропускания П определяется аналогично,
как для последовательного контура по
уровню половинной активной мощности.
Коэффициент подавления помехи:  Рассчитаем токи в ветвях идеального
параллельного контура при резонансе.
При резонансе (
Рассчитаем токи в ветвях идеального
параллельного контура при резонансе.
При резонансе (

 и
вQ раз больше тока в общей ветви.
и
вQ раз больше тока в общей ветви. 2. Реальный параллельный контур — это цепь из параллельно соединенных конденсатора и катушки индуктивности.
Схема замещения:
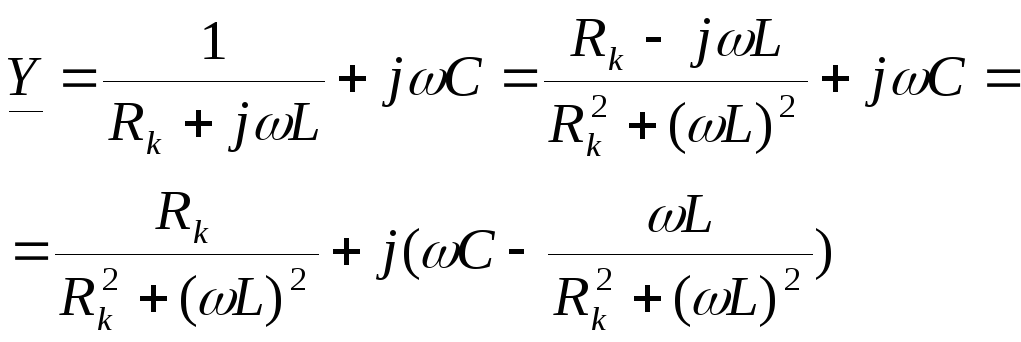
Условие
резонанса: 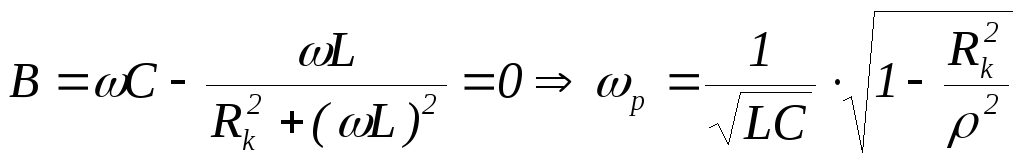 ,
,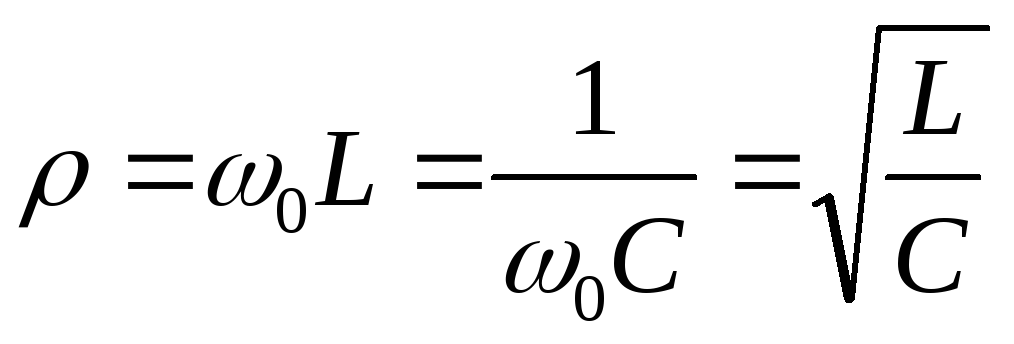
Условие
приближения к идеальному контуру: 
Резонансное сопротивление:
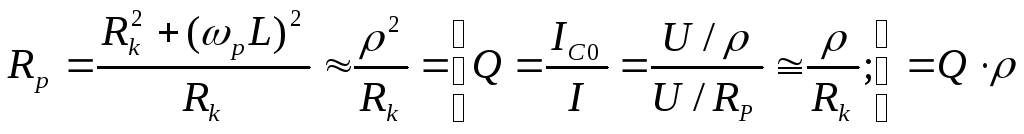
Векторная диаграмма:
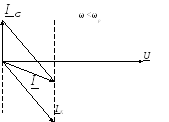
3. Частотные зависимости параллельного контура
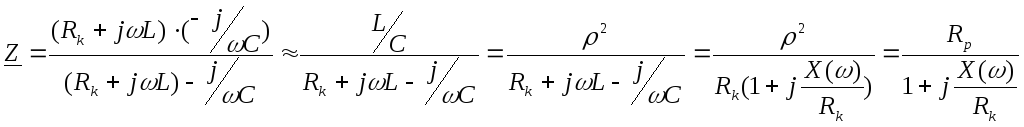
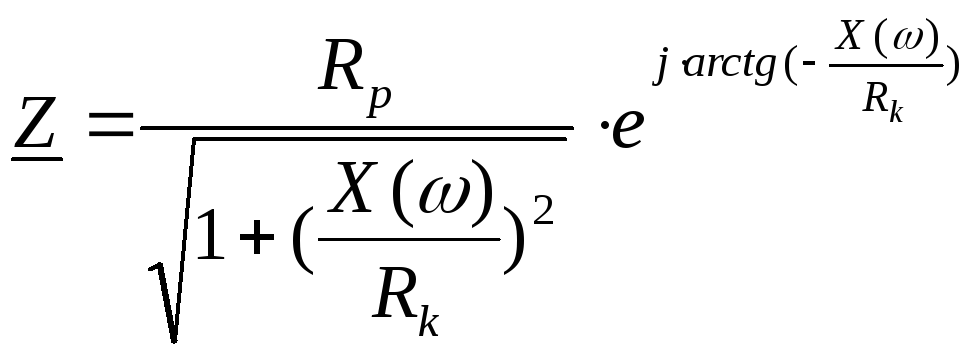

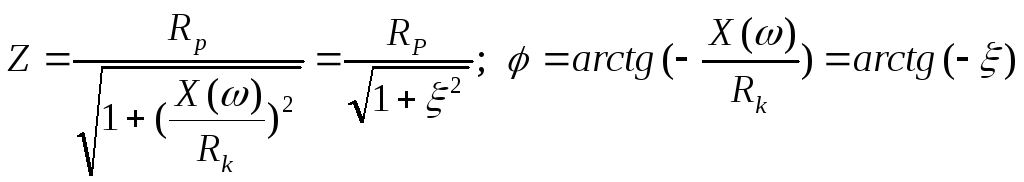
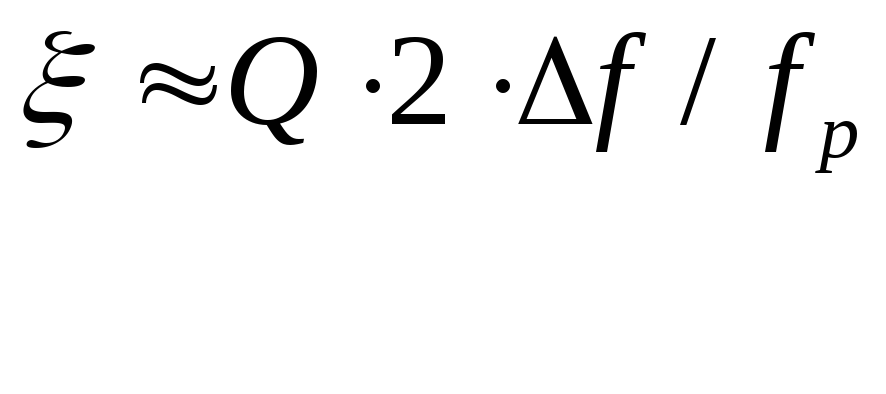
0
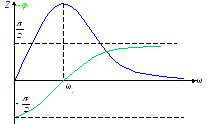
Если действует гармонический ток на контур, то при значении I(m)=const действующее напряжение на контуре и амплитудное будет повторять зависимость величины Z от .
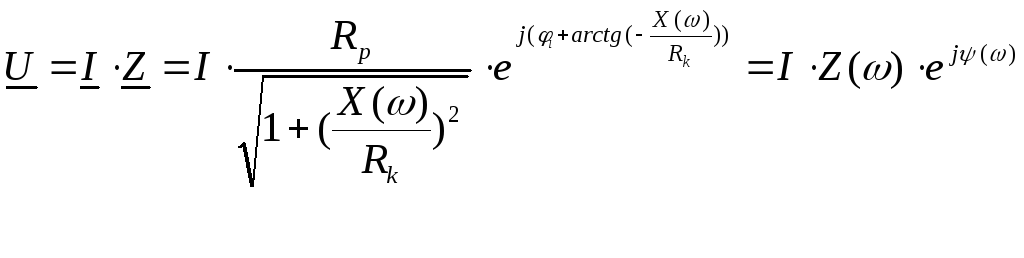
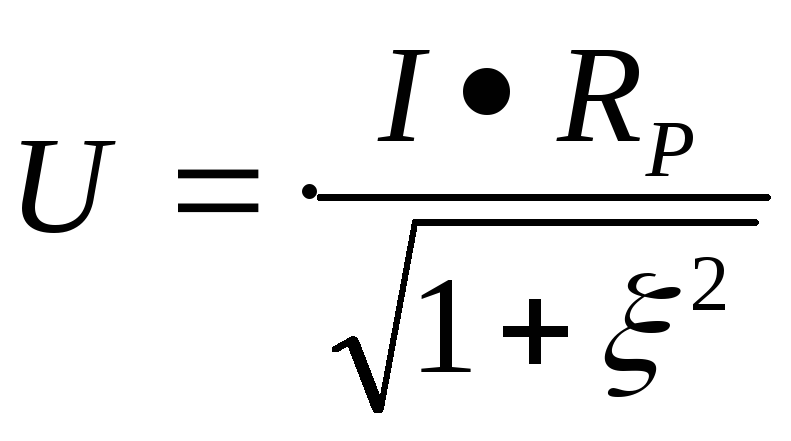
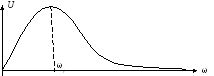


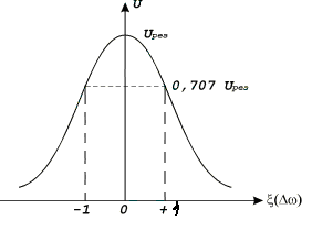
П=ω2 – ω1 (f2 – f1) Здесь полоса пропускания определяется по уровню 0,707 от максимального значения напряжения на контуре и обобщенная расстройка на границах равна +,- 1.
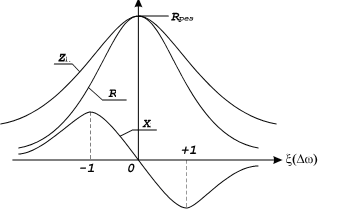
При резонансе (=0) Х=0. Зависимость Х от показана ниже . Параллельный колебательный контур на частоте ниже резонансной (<0) ведет себя как некоторая индуктивность (Х>0), на частоте выше резонансной (>0) – некоторая емкость (Х<0).
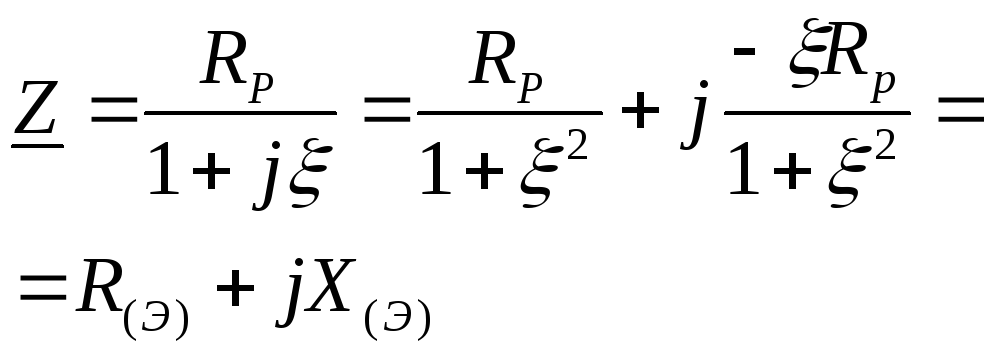
Здесь 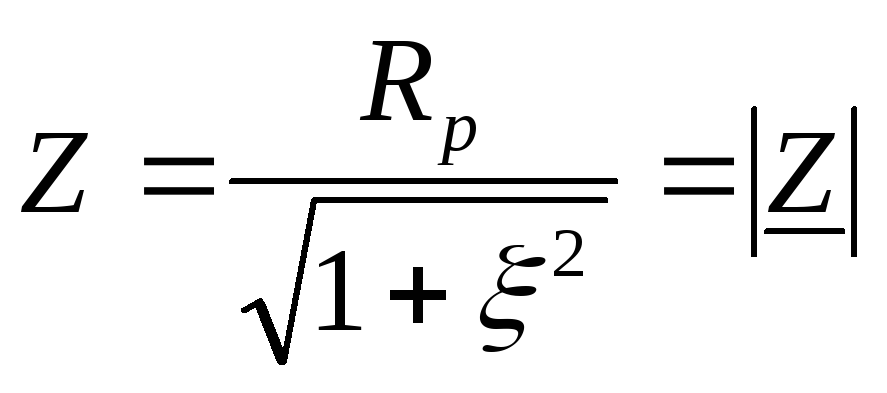 ,R(Э)=Re(Z),
,R(Э)=Re(Z),
X(Э)=Im(Z).
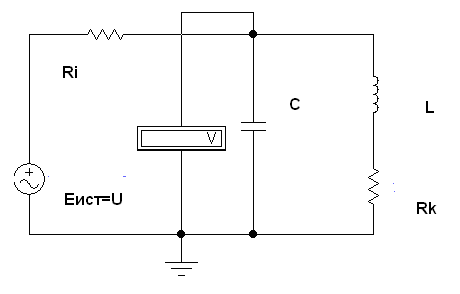
Схема исследования параллельного контура в
Здесь показан источник напряжения (идеальный), его сопротивление Ri, вольтметр V. который надо настроить на измерение переменного напряжения и установить большое внутреннее сопротивление ( 1000 Мом) для большей точности. Так же здесь включены идеальные емкость С и индуктивность L и резистор, имитирующий сопротивление катушки (Rk).
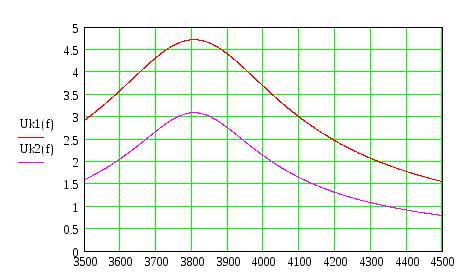
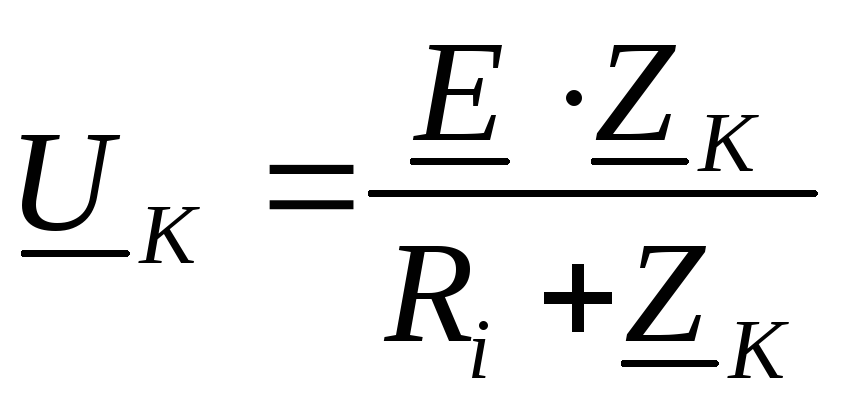
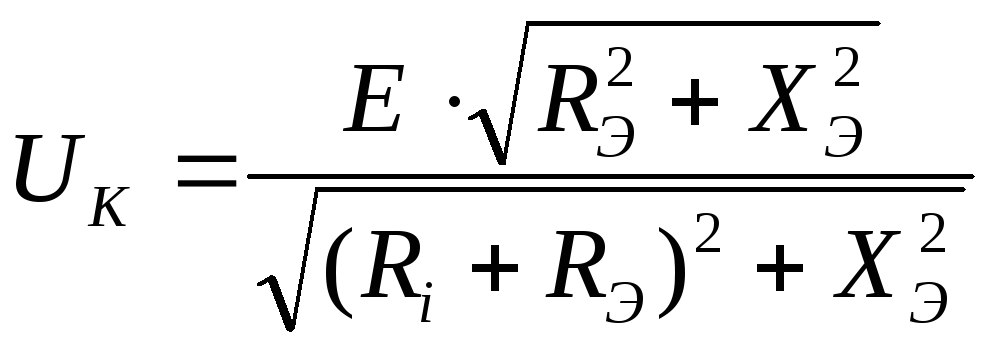
Гц
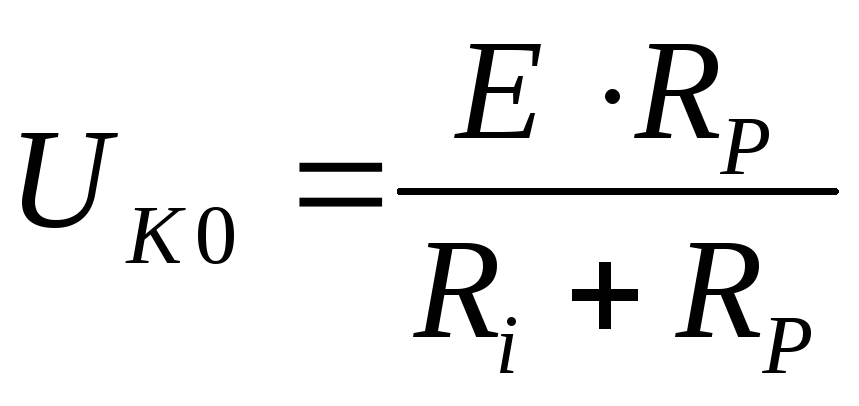
Расчетные графики частотных зависимостей напряжения
на параллельном контуре при разных Ri
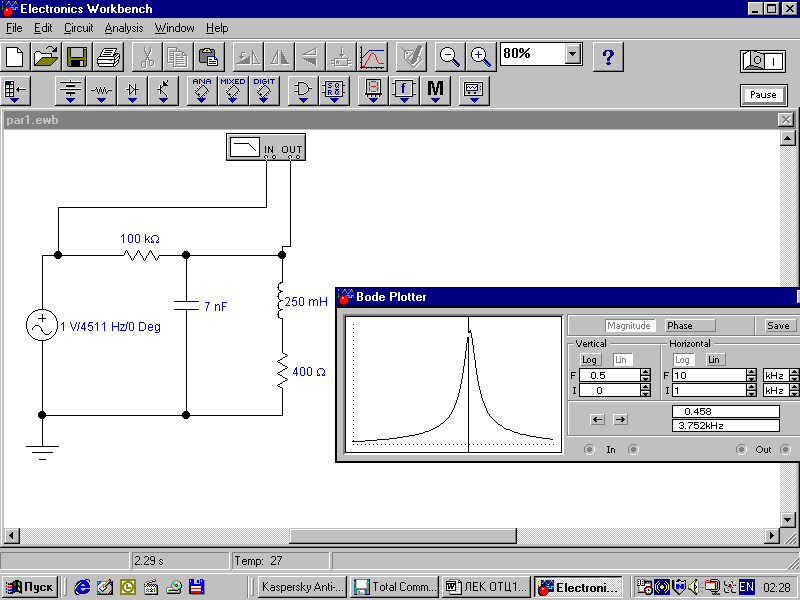
Вид экрана ЭВМ при исследовании частотной зависимости Uкон/Uист
в EWB-5 c использованием автоматического ИЧХ (Bode plotter)
Влияние внешних сопротивлений
на избирательность контура
(Добротность, полоса пропускания, коэффициент подавления)
Внешним сопротивлением является сопротивление источника и нагрузки.
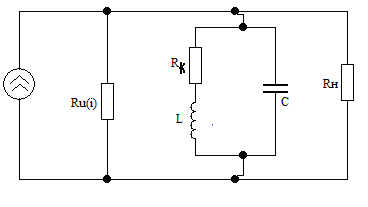
Определим эквивалентную добротность с учетом сопротивления источника
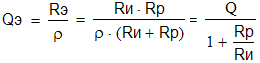
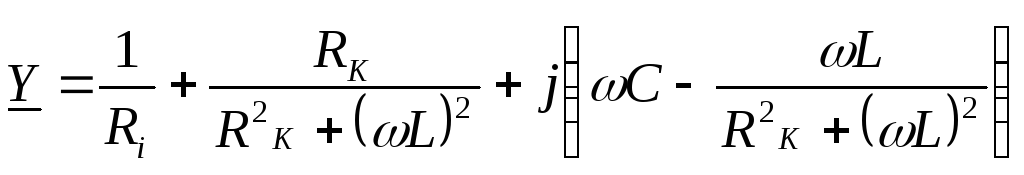
где — характеристическое сопротивление контура,
Q — исходная добротность.( RP / )
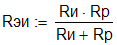
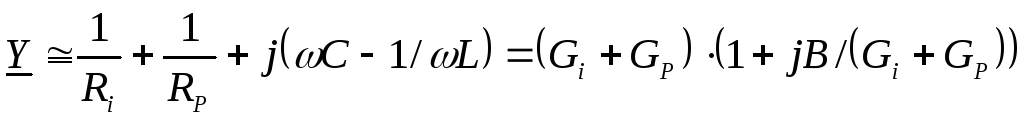
Аналогично
с нагрузкой. вместо RИ
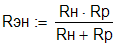
А если необходимо учесть и то и другое, то получаем формулу
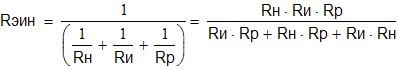
Полоса пропускания относительная находится по формуле:
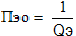
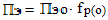
Величина обратная коэффициенту подавления помехи равна:
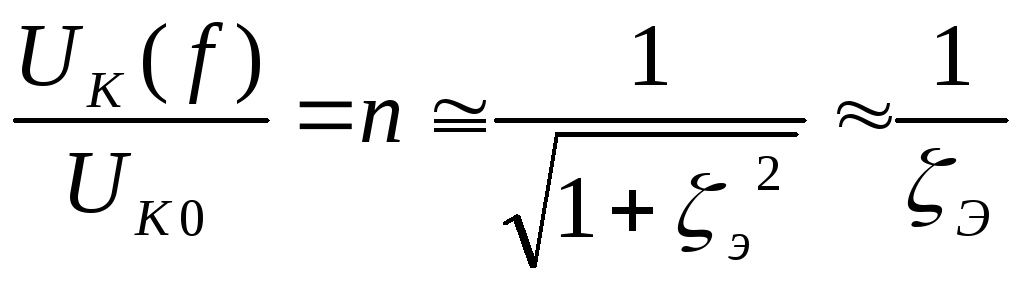
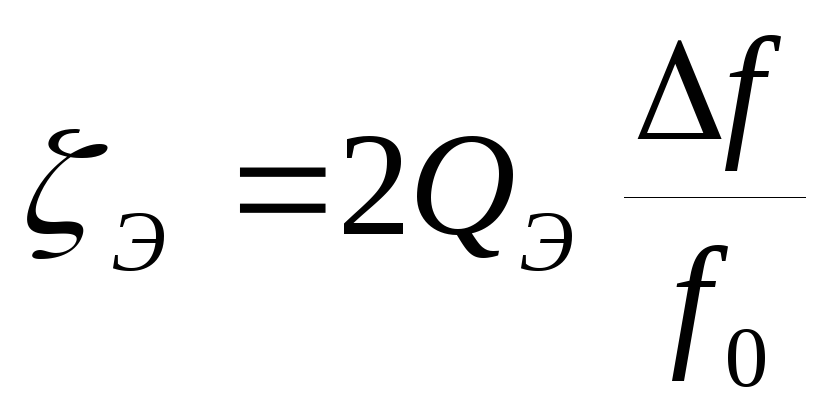
Коэффициент подавления помехи КПЭ ≈ Э
 Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Параллельным колебательным контуром называется двухполюсная электрическая цепь, подключенная к источнику гармонического сигнала и содержащая в своем составе резистор, конденсатор и индуктивность, соединенные параллельно (рис. 3.11). Резистор в контур может специально не включаться, но в контуре он всегда будет присутствовать, отражая потери, имеющие место в реальных реактивных элементах. Комплексная проводимость параллельного контура определяется следующими соотношениями
Изобразим для параллельного колебательного контура график зависимости реактивной проводимости Y от частоты (рис. 3.12), учитывая, что
Рис. 3.11. Параллельный колебательный контур
Анализ графика показывает, что на частоте ω0реактивная проводимость контура становиться равной нулю. Это свидетельствует о том, что сопротивление цепи становиться чисто резистивным (активным) и сдвиг фаз между напряжением и током в контуре равен нулю. Следовательно, в параллельном контуре также имеет место явление электрического резонанса. Резонансная частота параллельного контура определяется той же формулой что и резонансная частотота последовательного контура
В диапазоне частот, когда частота источника сигнала меньше резонансной частоты f<f0 , преобладает реактивное сопротивление индуктивности, сопротивление контура имеет активно — индуктивный характер и фазовый сдвиг между напряжением и током есть величина положительная.
Рис. 3.12. График зависимости реактивной проводимости параллельного контура от частты
В области частот f>f0 преобладает реактивное сопротивление конденсатора, сопротивление контура активно – емкостное, ток источника опережает по фазе напряжение на выводах. Если рассмотреть, что происходит в параллельном контуре с энергией, то можно установить, что и при параллельном соединении реактивных элементов на резонансной частоте происходит непрерывный периодический процесс обмена энергиями между электрическим полем конденсатора и магнитным полем индуктивности, который сопровождается необратимыми потерями части энергии на резисторе. Энергия, поступающая от источника электрической энергии в контур, компенсирует тепловые потери на сопротивлении контура. Контур оценивается добротностью, показывающей отношение (с учетом 2π) величин энергий, накапливаемых на резонансной частоте в реактивных элементах параллельного контура к энергии, расходуемой в цепи в виде необратимых потерь, за период. Добротность параллельного контура определяется формулой
Следует иметь в виду, что, величины R, входящие в формулу добротности в параллельном (3.36) и последовательном (3.27, 3.28) контуре, существенно различны. Если не включать в контур дополнительный резистор, а учитывать только потери реактивных элементов, величины R в формулах добротности последовательного и параллельного контуров будут различаться на несколько порядков. При последовательном соединении L и C величина R = r, определяясь сопротивлением провода катушки r, будет составлять несколько десятков Ом. В параллельном контуре потери на тепловыделение за счет нагревания провода пересчитывают по формуле R =ρ2 /r, поэтому его величина десятки кОм. Отметим, что величина добротности параллельных контуров в зависимости от качества конденсатора и катушки индуктивности составляет Q =50 – 120. Поскольку реактивные проводимости на резонансной частоте равны и на них одно и тоже напряжение, то амплитуды токов на реактивных элементах контура равны ImL = ImC . К тому же,
Следовательно, на резонансной частоте амплитуды токов на реактивных элементах в Q раз превышают амплитуду тока, поданного на контур от источника. Комплексное сопротивление параллельного контура, если его выразить через добротность, равно
Тогда полное сопротивление цепи равно
График зависимости полного сопротивления параллельного контура от частоты показан на рис.3.13.
Рис. 3.13. График зависимости полного сопротивления параллельного контура от частоты
Полное сопротивление контура на резонансной частоте максимально и равно сопротивлению R. С отклонением от резонансной частоты (с увеличением расстройки относительно резонансной частоты) полное сопротивление контура уменьшается. Если параллельный контур подключить к реальному источнику гармонического тока, то можно утверждать, что параллельный контур «выделяет» напряжение резонансной частоты, а также сигналы, частоты которых находятся в полосе (диапазоне) частот примыкающей к резонансной частоте. Этот диапазон частот называют полосой пропускания контура. Границы полосы пропускания определяют частоты f1 и f2. Полоса пропускания контура определяется формулой
Резюмируя сказанное отметим, что параллельный колебательный контур обладает следующими свойствами. 1. В контуре наблюдается явление электрического резонанса. Поскольку ток на реактивных элементах увеличиваются в Q раз по сравнению с током источника, то правильнее говорить, что в контуре имеет место явление электрического резонанса токов. 2. В случае высокой добротности контура явление резонанса характеризуется тем, что контур мало энергии потребляет от источника, а внутри него идет непрерывно периодический процесс обмена энергиями реактивных элементов. Контур как бы становиться генератором гармонической ЭДС. 3. Ток на реактивных элементах может почти в 100 раз (точнее в Q раз) превышать ток источника. 4. Если источник гармонического тока вырабатывает сигналы с несколькими частотами, то параллельный контур выделяет сигналы, частоты которых лежат в его полосе пропускания. Выделение сигналов будет тем лучше, чем больше величина добротности контура. Это свойство можно использовать для выделения полезных сигналов, например в радиовещательном приемнике. 5. Сопротивление параллельного контура на резонансной частоте максимально. Для обеспечения передачи энергии от источника в нагрузку параллельный контур, при работе на резонансной частоте, должен подключаться к реальному источнику тока, обладающему большим внутренним сопротивлением. При малых величинах внутренних сопротивлений источника добротность контура существенно уменьшается.
|
2. Простой параллельный резонанс (колебательный контур) | 6. Резонанс | Часть2
2. Простой параллельный резонанс (колебательный контур)
Простой параллельный резонанс (колебательный контур)
Колебательный контур перейдет в состояние резонанса только в том случае, если реактивные сопротивления конденсатора и катушки индуктивности будут равны друг другу. Поскольку при увеличении частоты реактивное сопротивление катушки индуктивности возрастает, а реактивное сопротивление конденсатора уменьшается, существует только одна частота, при которой оба этих сопротивления будут равны.
В приведенной выше схеме мы имеем конденсатор 10 мкФ и катушку индуктивности 100 мГн. Так как мы знаем уравнения для расчета реактивных сопротивлений этих компонентов на заданной частоте, нам нужно найти значение, при котором два реактивных сопротивления будут равны друг другу. Для этого нам нужно приравнять две формулы, и рассчитать частоту алгебраически:
В результате проведенных манипуляций мы получили формулу, при помощи которой можно рассчитать резонансную частоту контура. Подставив в нее значения L и C из нашей схемы, мы получим резонансную частоту, равную 159,155 Гц.
Явления, происходящие при резонансе, довольно интересны. Если реактивные сопротивления конденсатора и катушки индуктивности равны друг другу, то общий импеданс контура увеличивается до бесконечности, означая отсутствие потребления тока от источника! Мы можем подтвердить это математически, рассчитав отдельные импедансы конденсатора (10 мкФ) и катушки индуктивности (100 мГн), и подставив их в формулу параллельного импеданса:
Как вы наверное догадались, величины компонентов были подобраны таким образом, чтобы с полученными значениями импедансов было легко работать (100 Ом). Теперь можно воспользоваться формулой параллельного импеданса, чтобы увидеть что произойдет с общим значением Z:
Мы не можем разделить какое либо число на ноль и прийти к значимому результату. Но мы можем сказать, что при равенстве двух параллельных инмпедансов, результат будет близок к бесконечности. С практической точки зрения это означает, что общий импеданс контура в состоянии резонанса имеет бесконечное значение (ведет себя как обрыв цепи). Давайте смоделируем поведение колебательного контура в широком диапазоне частот питающего напряжения при помощи программы SPICE:
freq i(v1) 3.162E-04 1.000E-03 3.162E-03 1.0E-02 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 1.000E+02 9.632E-03 . . . . * 1.053E+02 8.506E-03 . . . . * . 1.105E+02 7.455E-03 . . . . * . 1.158E+02 6.470E-03 . . . . * . 1.211E+02 5.542E-03 . . . . * . 1.263E+02 4.663E-03 . . . . * . 1.316E+02 3.828E-03 . . . .* . 1.368E+02 3.033E-03 . . . *. . 1.421E+02 2.271E-03 . . . * . . 1.474E+02 1.540E-03 . . . * . . 1.526E+02 8.373E-04 . . * . . . 1.579E+02 1.590E-04 . * . . . . 1.632E+02 4.969E-04 . . * . . . 1.684E+02 1.132E-03 . . . * . . 1.737E+02 1.749E-03 . . . * . . 1.789E+02 2.350E-03 . . . * . . 1.842E+02 2.934E-03 . . . *. . 1.895E+02 3.505E-03 . . . .* . 1.947E+02 4.063E-03 . . . . * . 2.000E+02 4.609E-03 . . . . * . - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
tank circuit frequency sweep v1 1 0 ac 1 sin c1 1 0 10u * rфиктив. необходим для устранения прямой связи * между v1 и l1, с которой SPICE не имеет возможности справиться rbogus 1 2 1e-12 l1 2 0 100m .ac lin 20 100 200 .plot ac i(v1) .end
Резистор сопротивлением 1 пОм позволяет устранить прямую связь между напряжением источника питания и катушкой индуктивности, которую SPICE обрабатывать не умеет. Очень низкое значение сопротивления минимизирует влияние резистора на поведение цепи.
Это SPICE моделирование за 20 шагов отрисовывает график тока схемы в частотном диапазоне от 100 до 200 Гц (100 и 200 Гц включительно). Величина тока на графике увеличивается слева направо, а частота увеличивается сверху вниз. Из данного графика можно увидеть резкое падение тока в районе частоты 157,9 Гц (которая близка к рассчитанной нами частоте резонанса 159,155 Гц). Именно в этот момент общий ток, забираемый от источника питания, падает до нуля.
Гораздо нагляднее будет график, произведенный при помощи графического постпроцессора «Nutmeg», являющегося частью пакета SPICE. Следующие команды произведут отображенный ниже график:
spice -b -r resonant.raw resonant.cir
( -b batch mode, -r raw file, input is resonant.cir)
nutmeg resonant.raw
From the nutmeg prompt:
>setplot ac1 (setplot {enter} for list of plots)
>display (for list of signals)
>plot mag(v1#branch)
(magnitude of complex current vector v1#branch)
Кстати, этот график, построенный программой SPICE, более известен как диаграмма Боде. В этой диаграмме на одной оси откладываются амплитуда или фазовый сдвиг, а на другой — частота. Крутизна кривой диаграммы Боде характеризует «частотную характеристику» цепи (насколько цепь чувствительна к изменениям частоты).
13. Подключение параллельного колебательного контура к источникам напряжения и тока. Избирательность параллельного колебательного контура
Питание параллельного контура от источника напряжения и источника тока
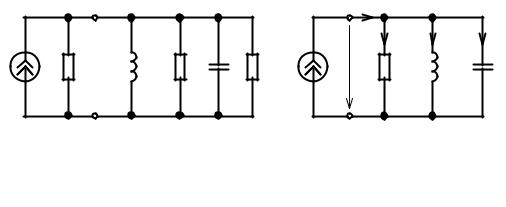
Если параллельный контур питается от источника напряжения с малым внутренним сопротивлением, то (видно из схемы), избирательности по напряжению нет.
в момент резонанса будет минимальный ток.
Вывод: при питании от источника напряжения с малым внутренним сопротивлением параллельный контур обладает избирательностью по току, но не обладает избирательностью по напряжению.
Чтобы он обладал избирательностью по напряжению, последовательно с ним включают очень большое внутреннее сопротивление , которое:
При этом источник напряжения превращается в источник тока, ток которого не зависит от сопротивления нагрузки.
, а т. к. , то будет повторять по форме .
Вывод: если параллельный контур питается от источника тока, то он обладает избирательностью по напряжению.
14. Входные ачх и фчх параллельного колебательного контура. Характер реактивного сопротивления параллельного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной
, и в числителе им можно пренебречь
Воспользовавшись формулой , получим формулу входной АЧХ параллельного контура:
— формула входной АЧХ параллельного контура
Вывод: параллельный контур имеет максимальное сопротивление на резонансной частоте. По мере увеличения расстройки сопротивление параллельного контура падает.
ФЧХ:
— входная ФЧХ параллельного контура
Вывод: на резонансной частоте сопротивление контура чисто активное . На частотах больше резонансной — активно-емкостное, , а на частотах меньше резонансной — активно-индуктивное, .
15. Передаточные ачх параллельного колебательного контура. Эквивалентная добротность, полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы
Для этой схемы вводят понятие эквивалентной добротности:
, где
— собственная добротность параллельного контура
Появляется понятие эквивалентной обобщённой расстройки:
,
тогда передаточная АЧХ параллельного контура в абсолютных координатах рассчитывается:
, где
Передаточная АЧХ в относительных координатах параллельного контура имеет вид:
Для этой схемы токи ветвей и общий ток в момент резонанса можно рассчитать по формулам:
16. Виды параллельных колебательных контуров. Контуры с неполным включением
Автотрансформаторное (неполное) включение контура
Схема контура I-го вида
Эта цепь удовлетворительно работает, если соблюдается условие .
На практике — внутреннее сопротивление лампы или транзистора, т. е. вполне определённая величина. — тоже определённая величина, поэтому это равенство может не соблюдаться.
Чтобы это равенство соблюдалось, уменьшают . Для этого используют неполное (автотрансформаторное) включение контура. Часть индуктивности катушки или ёмкости конденсатора переносят из одной ветви в другую так, чтобы общая ёмкость или индуктивность контура, а значит и резонансная частота, не изменились.
Схема контура II-го вида
Вводят понятие коэффициент включения контура:
Доказано, что контура II вида равно:
Т. к. , то
Схема контура III вида
Т. к. , то
Неполное включение контура служит для уменьшения входного сопротивления контура на резонансной частоте.
Дополнение. Сравнение последовательного и параллельного контуров
Последовательный контур | Параллельный контур |
1. Резонанс напряжений | 1. Резонанс токов |
2. | 2. |
3. | 3. |
4. В последовательном контуре добротность показывает, во сколько раз напряжение на реактивных элементах (на выходе) больше, чем напряжение на входе. Поэтому это явление называется резонанс напряжений. | 4. В параллельном контуре добротность показывает, во сколько раз ток ветвей больше общего тока в момент резонанса. Поэтому это явление называется резонанс токов. |
17. Электронные аналоги колебательных контуров. Электронный колебательный контур, его избирательные свойства. Достоинства электронного колебательного контура по сравнению с пассивными колебательными контурами. Гиратор
Электронный колебательный контур
Начертим схему последовательного контура, чтобы на выходе стоял резистор:
Известно, что последовательный контур обладает избирательностью по напряжению. Докажем, при каких условиях это будет. Рассмотрим, какой вид имеет комплексная передаточная характеристика контура:
Вывод: если знаменатель комплексного коэффициента передачи цепи имеет вид квадратного уравнения , то эта цепь обладает избирательностью по напряжению. Выражают некоторые величины через B и D:
Можно получить избирательные свойства цепи, используя активные элементы ОУ с отрицательными обратными связями:
Для этой цепи рассчитан комплексный коэффициент передачи, считая :
Из формулы видно, что знаменатель передаточной функции имеет вид квадратного уравнения, значит электронный контур обладает избирательностью по напряжению, и его передаточная характеристика имеет резонансный вид:
Рассчитаем некоторые величины через коэффициенты B и D:
Электронный контур имеет следующие преимущества перед обычными контурами:
можно регулировать , , Q и П резисторами;
большое входное сопротивление кОм, малое выходное сопротивление;
схема компактная, т. к. нет катушек индуктивности.
Электронная индуктивность (гиратор)
Обычные катушки индуктивности обладают рядом недостатков:
сказываются помехи, создаваемые магнитными полями других катушек или цепей;
большие габариты;
магнитная проницаемость, а значит и индуктивность катушки, зависят от частоты, поэтому используют схему, состоящую из активных элементов (ОУ), резисторов и конденсаторов.
Электронные цепи, обладающие индуктивными свойствами, называются гираторами. Если считать все сопротивления R приблизительно одинаковыми, то входное сопротивление такой цепи: .
Известно, что входное сопротивление индуктивности , значит входное сопротивление такой цепи изменяется по закону индуктивности, где в качестве LЭ существует:
, тогда .
Электронная индуктивность имеет малые габариты, может быть выполнена в микроэлектронном исполнении и не подвержена влиянию внешних электромагнитных полей.
18. Реактивные двухполюсники. Определение. Одно-, двух-, трехэлементные реактивные двухполюсники. Построение характеристик, χ = F(ω), φ = F(ω). Нулевые и полюсные частоты
Реактивные двухполюсники
Реактивными двухполюсниками называются цепи, имеющие 2 входных зажима и состоящие из индуктивностей и емкостей.
Главной зависимостью двухполюсника является зависимость его реактивного сопротивления от частоты, т. е. , где x — реактивное сопротивление.
Одноэлементные реактивные двухполюсники
Двухэлементные реактивные двухполюсники
Последовательное соединение L и C
На некоторой частоте . Наступает резонанс напряжений. Такие частоты называются нулями функции и обозначаются кружком .
Признак последовательного двухполюсника:
нет пути прохождения постоянному току.
Параллельное соединение L и C
На некоторой частоте наступает резонанс токов, . Такие частоты называются полюсами функции и обозначаются крестиком .
Признак параллельности двухполюсника:
Есть путь прохождения постоянному току.
Трёхэлементные реактивные двухполюсники
Порядок построения характеристик :
Резонансных частот на 1 меньше числа элементов.
Нулевые и полюсные частоты всегда чередуются.
Если есть путь прохождения постоянному току, то первым будет резонанс токов, характеристика начинается с нулевого сопротивления.
Если постоянный ток не проходит, то первым будет резонанс напряжений, т. е. характеристика начинается из .
Постоянный ток по данной цепи проходит, значит первым будет резонанс токов, характеристика начинается с 0. Это собственный резонанс параллельного контура LC. Вторым будет резонанс напряжений. Это резонанс между L0 и параллельным контуром, когда его сопротивление носит емкостной характер.
Т. к. есть путь для прохождения постоянного тока, то первым будет резонанс токов. Характеристика начинается с 0. Это коллективный резонанс параллельного контура между L0 и последовательным контуром, когда его сопротивление носит емкостной характер. Вторым будет резонанс напряжений. Это собственный резонанс последовательного контура. Входная АЧХ и ФЧХ будут такими же, как и для пункта 1.
Т. к. нет пути прохождения постоянному току, первым будет резонанс напряжений. Это собственный резонанс последовательного контура LC. Вторым будет резонанс токов. Это коллективный резонанс между C0 и последовательным контуром, когда его сопротивление носит индуктивный характер.
Т. к. нет пути для прохождения постоянного тока, то первым будет резонанс напряжений. Это коллективный резонанс между C0 и параллельным контуром, когда его сопротивление носит индуктивный характер. Вторым будет резонанс токов. Это собственный резонанс параллельного контура.
Модуль 3.3. Параллельный колебательный контур
Цель модуля: изучение амплитудно частотных и фазо частотных характери стик параллельного колебательного контура.
Схемы замещения
Параллельным колебательным контуром называется электрическая цепь, в
которой индуктивные катушки и конденсаторы размещены в двух ветвях, подклю ченных параллельно источнику энергии. Принципиальные электрические схемы параллельных колебательных контуров различных видов приведены на рис. 3.20, б
— д.
Знакомство с параллельными колебательными контурами начнем с простого параллельного контура (рис. 3.20, б). В соответствии с основным методом теории цепей заменим реальные элементы контура их упрощенными моделирующими це пями, а принципиальную электрическую схему контура — его схемой замещения. Используя параллельные схемы замещения источника энергии, индуктивной ка тушки и конденсатора, получаем один из вариантов схемы замещения контура (рис. 3.34, а). Ограничим рассмотрение случаем, когда элементы контура имеют высокую добротность, при этом зависимостью Lпар от частоты ω можно пренебречь и в соот ветствии с (3.20), (3.21) считать, что параметры реактивных элементов параллель ной и последовательной схем замещения индуктивной катушки и конденсатора имеют одинаковые значения:
пар | посл | ; пар | посл | . | 3.76 |
Заменяя сопротивления потерь одним элементом
1 | 1 | 3.77 | |
пар |
| пар | |
и пренебрегая внутренней проводимостью источника энергии, получаем простей шую схему замещения параллельного контура основного вида (рис. 3.34, б).
Рис. 3.34. Схемы замещения параллельного колебательного контура основного вида, полу ченные при использовании параллельных схем замещения элементов
Если каждый из пассивных элементов контура заменить последовательной схемой замещения, то при тех же допущениях получим несколько более сложную схему замещения контура (рис. 3.35, а). В теории цепей в зависимости от характера решаемой задачи нашли применение оба варианта схем замещения.
273

Параллельный колебательный контур основного вида
Ранее было установлено, что идеализированные цепи, схемы которых приве дены на рис. 3.23, б и 3.34, б, являются дуальными, поэтому при рассмотрении про цессов в параллельном колебательном контуре основного вида с помощью про стейшей схемы замещения (рис. 3.34, б) можно использовать все выражения, полу ченные для последовательного колебательного контура, произведя в них взаимные замены токов и напряжений, сопротивлений и проводимостей, емкостей и индук тивностей. Действительно, выражения для комплексной входной проводимости па
раллельной | RLС | цепи (2.100) и комплексного входного сопротивления последова | ||||
тельной | RLС | цепи (2.96) имеют одинаковую структуру и могут быть получены од | ||||
но из другого путем упомянутых замен. На резонансной частоте ( | ω = | р) мнимая со | ||||
| ||||||
ставляющая входной проводимости параллельной RLC цепи должна быть равна ну лю:
|
|
| Im | р | Im |
|
|
|
|
| 1 |
|
|
|
|
| р |
|
| р | 1 | 0. | 3.78 | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| р | ||||||||||||||
| Решая уравнение (3.78), находим, что резонансная частота параллельного ко | |||||||||||||||||||||||||||||||
лебательного0 | контура | р совпадает с резонансной частотой последовательного кон | ||||||||||||||||||||||||||||||
тура | ω | , составленного из тех же элементов: | 1 | . |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| р |
| √ |
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
| На резонансной частоте полные проводимости емкости |
|
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
|
| | |
| р | | |
|
| р | р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.35. Схема замещения параллельного колебательного контура основного вида, полученные при использовании последовательных схем замещения элементов

и индуктивности
равны характеристической проводимости параллельного колебательного контура σ, которая является величиной, обратной характеристическому сопротивлению кон тура ρ (выражения для характеристических сопротивлений параллельного и после довательного колебательных контуров совпадают). Как видно из векторных диа грамм параллельной RLC цепи (рис. 2.23, в), при ω = р действующее значение тока емкости равно действующему значению тока индуктивности: IC = IL = σU, а входной ток контура (ток неразветвленной части параллельной RLC цепи) равен току прово димости: I = IG = GU.
Отношение действующего значения тока реактивного элемента к входному то ку параллельного колебательного контура на резонансной частоте называется доб ротностью параллельного колебательного контура:
Выражение (3.79) имеет такую же структуру, как и выражение (3.32), и может быть получено из него заменой сопротивления потерь R и характеристического со противления ρ последовательного контура на проводимость потерь G и характери стическую проводимость σ параллельного контура.
Рис. 3.36. К определению эквивалентной добротности параллельного колебательного кон тура
Из выражения (3.79) следует, что с увеличением проводимости потерь доброт ность параллельного колебательного контура падает. Таким же образом на доброт ность контура влияют внутренняя проводимость источника энергии Gi и проводи мость нагрузки GH , подключенная к зажимам контура 1 — 1’ (рис. 3.36). Добротность параллельного колебательного контура с учетом внутренней проводимости источ ника Gi , и проводимости нагрузки Gн определяется выражением
эк |
| 1 |
|
| н | , | 3.80 |
н |
|
| |||||
|
где Q — добротность параллельного контура без учета Gi и Gн.

Таким образом, для повышения эквивалентной добротности параллельного ко лебательного контура желательно, чтобы проводимости источника энергии и на грузки были бы близки к нулю, т. е. чтобы свойства источника энергии, к которому подключен контур, приближались к свойствам идеального источника тока, а сопро тивление нагрузки контура было бы бесконечно большим.
При исследовании комплексных частотных характеристик параллельного кон тура внешнее воздействие на контур обычно задают в виде тока идеального источ ника тока, подключенного к зажимам 1 — 1’, а в качестве реакции контура рассмат ривают напряжение u на этих же зажимах (см. рис. 3.34, б). В ряде случаев в ка честве реакции контура рассматривают ток емкости iC C или ток индуктивности iL L . Следовательно, параллельный колебательный контур, подобно последова тельному, обладает как входными, так и передаточными характеристиками.
К входным характеристикам параллельного колебательного контура относится его комплексное входное сопротивление в режиме холостого хода (Gн = 0)
н
Выражения для нормированного модуля и аргумента комплексного входного сопротивления параллельного колебательного контура
1 |
| 1 | р |
| р |
| 1 | 1 | ; | 3.82 |
|
| |||||||||
arctg |
|
|
| р |
|
| arctg |
|
|
|
р |
|
|
|
|
|
полностью совпадают с выражениями (3.54) для нормированного модуля и аргу мента комплексной входной проводимости последовательного колебательного кон тура. Следовательно, нормированные АЧХ и ФЧХ входного сопротивления парал лельного колебательного контура совпадают с соответствующими характеристика ми входной проводимости последовательного колебательного контура (рис. 3.28, 3.29).
На частоте резонанса токов ω = ωP входное сопротивление параллельного ко лебательного контура имеет чисто резистивный характер (φ = 0), а модуль входного сопротивления достигает максимального значения:
На частотах ниже резонансной входное сопротивление контура имеет рези стивно индуктивный характер (0<φ<π/2), а на частотах выше резонансной — рези стивно емкостный (—π/2< φ <0).
276

Можно показать, что выражения для коэффициентов передачи параллельного колебательного контура по току GC(ω) и GL(ω) совпадают с выражениями для коэф фициентов передачи последовательного контура по напряжению KL(ω) и KC(ω):
|
|
|
| ; | |
| р | р | |||
|
|
|
|
| |
и иллюстрируются теми же кривыми (рис. 3.31, а). (При этом напряжению емкости последовательного контура соответствует ток индуктивности параллельного кон тура, а напряжению индуктивности последовательного контура — ток емкости па раллельного.) Все, что ранее говорилось о передаточных характеристиках последо вательного контура, справедливо и для передаточных характеристик параллельного
контура. ВGчастностиL( С | , при высокой добротности контура на частотах, близких к ре | ||||
зонансной | ω | ) | G (ω | ω | |
|
| ) | Q ( ). | ||
В связи с тем, что нормированные входные и передаточные характеристики последовательного и параллельного колебательных контуров совпадают, их изби рательные свойства одинаковы. Полоса пропускания параллельного колебательного контура, если пренебречь внутренней проводимостью источника и проводимостью нагрузки, определяется выражением (3.69). Если необходимо учесть влияние прово димости нагрузки и внутренней проводимости источника энергии на избиратель ные свойства контура, то вместо Q в выражение (3.69) подставляют эквивалентную добротность Qэк рассчитываемую с помощью выражения (3.80).
Таким образом, применение простейшей схемы замещения параллельного ко лебательного контура позволяет существенно упростить процесс рассмотрения его свойств путем использования соответствующих выражений, полученных при иссле довании последовательного колебательного контура. Однако непосредственное применение этих выражений на практике, в частности выражений (3.79), (3.80) и (3.83), в значительной степени затруднено в связи с тем, что в них входит проводи мость потерь контура G, которая зависит от частоты. [Напомним, что проводимость потерь контура G определяется выражением (3.77), причем с учетом соотношений (3.23) она практически совпадает с величиной, обратной сопротивлению потерь ин дуктивной катушки в параллельной схеме замещения (3.20)] Этого недостатка ли шены выражения для сопротивления контура на резонансной частоте и добротно сти, полученные с помощью схемы замещения рис. 3.35, а, в которой индуктивная катушка и конденсатор представлены последовательными схемами замещения.
Используя эту схему, найдем комплексное входное сопротивление параллель ного колебательного контура

|
|
|
|
|
|
| посл | посл | 1 | . | 3.84 | ||||
|
|
|
|
|
|
| посл | посл |
| 1 | |||||
Ограничимся, как и ранее, случаем, когда элементы контура имеют высокую | |||||||||||||||
добротность [ Р | L | >> | посл, 1/( Р | C | )>> | посл], а частота внешнего воздействия нена | |||||||||
|
| ||||||||||||||
много отличается от резонансной ( | Р . Тогда выражение (3.84) можно преоб | ||||||||||||||
разовать к более простому виду : |
|
| 1 |
| , |
|
| 3.85 | |||||||
где ρ = | / | и |
|
|
|
|
|
|
|
|
| ||||
|
| посл | посл — характеристическое | сопротивление и сопротив | |||||||||||
ление потерь последовательного контура, составленного из тех же элементов, что и рассматриваемый параллельный контур, или, точнее, характеристическое сопро тивление и сопротивление потерь одиночного колебательного контура (рис. 3.19). С учетом соотношений (3.23) можно считать, что сопротивление R практически равно RL посл и не зависит от частоты. Таким образом, эквивалентная схема, приведенная на рис. 3.35, а, в большинстве важных для практики случаев может быть заменена бо лее простой схемой (см. рис. 3.35, б), в которую входят те же элементы, что и в экви валентную схему последовательного колебательного контура, причем параметры элементов можно считать не зависящими от частоты.
На резонансной частоте мнимая составляющая комплексного входного сопро тивления контура должна быть равна нулю, что возможно только в том случае, ко гда мнимая составляющая знаменателя выражения (3.85) равна нулю:
Из выражения (3.86) следует, что условие резонанса токов в параллельном ко лебательном контуре при высокой добротности элементов имеет такой же вид, как условие резонанса напряжений в последовательном колебательном контуре (3.26), и, следовательно, частота резонанса токов совпадает с резонансной частотой после довательного контура, составленного из тех же элементов:
Если элементы контура имеют невысокую добротность, для определения час тоты резонанса токов необходимо приравнять нулю мнимую составляющую вход ного сопротивления, определяемую из выражения (3.84). При этом частота резо нанса токов несколько отличается от резонансной частоты последовательного кон тура:

|
| р | посл | , |
однако при | посли | посл | ||
посл этим различием можно пренебречь. | ||||
Как отмечалось выше, характеристическое сопротивление параллельного кон тура, равное абсолютному значению мнимых составляющих сопротивлений ветвей контура на резонансной частоте, определяется тем же выражением, что и характе ристическое сопротивление последовательного контура:
| | | р | | | р | р | 1 |
|
| . |
р |
|
|
Входное сопротивление параллельного колебательного контура на резонанс ной частоте R0 (резонансное сопротивление контура) имеет чисто резистивный характер и, как следует из (3.85), может быть найдено с помощью выражения
Следовательно, ток i и напряжение u на зажимах 1 — 1’ (рис. 3.35, б) на резо нансной частоте совпадают по фазе, а их действующие значения I0 = I|ω=ωр, U0=U|ω=ωр, связаны между собой соотношением U0 = R0I0 = ρ2I0/R.
Действующие значения токов ветвей контура на резонансной частоте имеют одинаковые значения:
| | р | | | р |
|
|
| . | 3.89 |
|
|
Используя выражение (3.89), находим добротность параллельного колебатель ного контура:
рр
Таким образом, добротность параллельного колебательного контура основно го вида совпадает с добротностью последовательного колебательного контура, со ставленного из тех же элементов.
Аналогичный результат может быть получен и из соотношения (3.42), пригод ного для определения добротности любых колебательных систем.
С учетом выражений (3.88) и (3.90) представим комплексное сопротивление параллельного контура в следующем виде:
279



 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.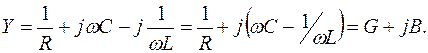 (3.33)
(3.33)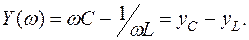 (3.34)
(3.34)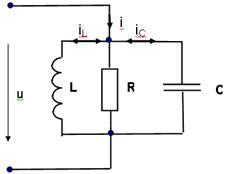
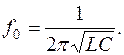 (3.35)
(3.35)

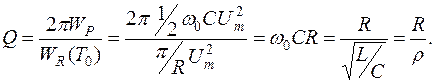 (3.36)
(3.36)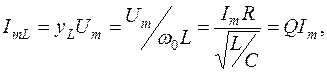 (3.37)
(3.37)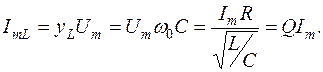 (3.38)
(3.38)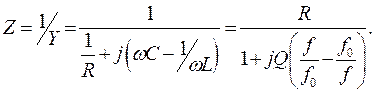 (3.39)
(3.39)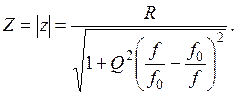 (3.40)
(3.40)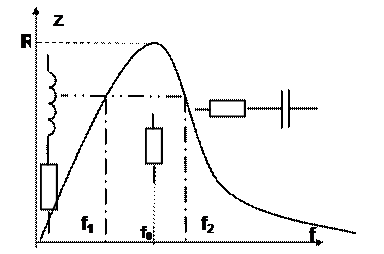

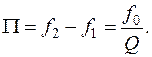 (3.41)
(3.41)