План-конспект занятия на тему: Лекции, электротехника.

Лекции по курсу основы электротехники

Эквивалентные преобразования схем

         Эквивалентным называется преобразование, при котором напряжения и токи в частях схемы, не подвергшихся преобразованию, не меняются.

Последовательное соединение элементов
электрических цепей

   На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.

Рис. 2.1

Напряжение на зажимах источника ЭДС равно величине электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам

В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи.

        где   — эквивалентное сопротивление.

    Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.

2.2. Параллельное соединение элементов
электрических цепей

На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.

Рис. 2.2

Токи в параллельных ветвях определяются по формулам:

        где — проводимости 1-й, 2-й и n-й ветвей.

      В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.

        где 

     Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости

  Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость

  Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента

Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.

Рис. 2.3 Эквивалентная проводимость схемы

,

    а эквивалентное сопротивление

      Напряжение на входе схемы

       Токи в параллельных ветвях

       Аналогично

      Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.

2.3.Преобразование треугольника сопротивлений
в эквивалентную звезду

Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.

Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:

    Эквивалентное соединение полученной схемы определяется по формуле

       Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.

2.4.Преобразование звезды сопротивлений
в эквивалентный треугольник

Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между узлами 1-2-3.

2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник

Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:

      Эквивалентное сопротивление преобразованной схемы равно

Анализ сложных электрических цепей с несколькими источниками энергии

Метод непосредственного применения законов Кирхгофа

       На рис. 4.1 изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи.
В схеме имеются четыре узла, можно составить четыре уравнения по первому закону Кирхгофа.

   Укажем произвольно направления токов. Запишем уравнения::

               (4.1)

                    Рис. 4.1

Сложим эти уравнения. Получим тождество 0 = 0. Система уравнений (4.1) является зависимой.
Если в схеме имеется n узлов, количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n — 1.
Для схемы на рис. 4.1 число независимых уравнений равно трем.

       (4.2)

Недостающее количество уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров. Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры.
Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа.

       (4.3)

       Решив совместно системы уравнений (4.2) и (4.3), определим токи в схеме.
Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.

Метод контурных токов

    Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.
Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I11 и I22 — контурные токи.

Рис. 4.2
Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно.

Порядок расчета

    Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

Перегруппируем слагаемые в уравнениях

     (4.4)

     (4.5)

 Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы

,     .

    Сопротивление R3, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.

,

  где R12 — общее сопротивление между первым и вторым контурами;
R21 — общее сопротивление между вторым и первым контурами.
E11 = E1 и E22 = E2 — контурные ЭДС.
В общем виде уравнения (4.4) и (4.5) записываются следующим образом:

,

.

       Собственные сопротивления всегда имеют знак «плюс».
Общее сопротивление имеет знак «минус», если в данном сопротивлении контурные токи направлены встречно друг другу, и знак «плюс», если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (4.4) и (4.5) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.
        В схеме на Рис. 4.2

.

Рекомендации

Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам.
Контурные токи желательно направлять одинаково (по часовой стрелке или против).
Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным.
Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.

 

4.3. Метод узловых потенциалов

    Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы ?4 = 0.

                                
Рис. 4.3

Запишем уравнение по первому закону Кирхгофа для узла 1.

    (4.6)

    В соответствии с законами Ома для активной и пассивной ветви

,

     где — проводимость первой ветви.

,

      где — проводимость второй ветви.

  Подставим выражения токов в уравнение (4.6).

    (4.7)

    где g11 = g1 + g2 — собственная проводимость узла 1.

Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.
g12 = g2 — общая проводимость между узлами 1 и 2.
Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.

      — сумма токов источников, находящихся в ветвях, сходящихся в узле 1.
Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком «плюс», если от узла — со знаком «минус».
По аналогии запишем для узла 2:

    (4.8)
    для узла 3:

    (4.9)
       Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы ?1, ?2, ?3, а затем по закону Ома для активной или пассивной ветви найдем токи.
Если число узлов схемы — n, количество уравнений по методу узловых потенциалов — (n — 1).

Замечание.

Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше.

4.4. Метод двух узлов

     Схема на рис. 4.4 имеет два узла. Потенциал точки 2 примем
равным нулю ?2 = 0. Составим узловое уравнение для узла 1.

,

,

      Рис. 4.4

                                               где  , , — проводимости ветвей.

В общем виде:

.

     В знаменателе формулы — сумма проводимостей параллельно включенных ветвей. В числителе — алгебраическая сумма произведений ЭДС источников на проводимости ветвей, в которые эти ЭДС включены. ЭДС в формуле записывается со знаком «плюс», если она направлена к узлу 1, и со знаком «минус», если направлена от узла 1.
После вычисления величины потенциала ?1 находим токи в ветвях, используя закон Ома для активной и пассивной ветви.

4.5. Метод эквивалентного генератора

    Этот метод используется тогда, когда надо определить ток только в одной ветви сложной схемы.
Чтобы разобраться с методом эквивалентного генератора, ознакомимся сначала с понятием «двухполюсник».
Часть электрической цепи с двумя выделенными зажимами называется двухполюсником. Двухполюсники, содержащие источники энергии, называются активными. На рис. 4.5 показано условное обозначение активного двухполюсника.
Двухполюсники, не содержащие источников, называются пассивными. На эквивалентной схеме пассивный двухполюсник может быть заменен одним элементом — внутренним или входным сопротивлением пассивного двухполюсника Rвх. На рис. 4.6 условно изображен пассивный двухполюсник и его эквивалентная схема.

        Рис. 4.5 Рис. 4.6

Входное сопротивление пассивного двухполюсника можно измерить.
Если известна схема пассивного двухполюсника, входное сопротивление его можно определить, свернув схему относительно заданных зажимов.
Дана электрическая цепь. Необходимо определить ток I1 в ветви с сопротивлением R1 в этой цепи. Выделим эту ветвь, а оставшуюся часть схемы заменим активным двухполюсником (рис. 4.7).
Согласно теореме об активном двухполюснике, любой активный двухполюсник можно заменить эквивалентным генератором (источником напряжения) с ЭДС, равным напряжению холостого хода на зажимах этого двухполюсника и внутренним сопротивлением, равным входному сопротивлению того же двухполюсника, из схемы которого исключены все источники (рис. 4.8). Искомый ток I1 определится по формуле:

     (4.10)

              Рис. 4.7 Рис. 4.8

Параметры эквивалентного генератора (напряжение холостого хода и входное сопротивление) можно определить экспериментально или расчетным путем.
Ниже показан способ вычисления этих параметров расчетным путем в схеме на рис. 4.2. Изобразим на рис. 4.9 схему, предназначенную для определения напряжения холостого хода. В этой схеме ветвь с сопротивлением R1 разорвана, это сопротивление удалено из схемы. На разомкнутых зажимах появляется напряжение холостого хода. Для определения этого напряжения составим уравнение для первого контура по второму закону Кирхгофа

,

    откуда находим

,     (4.11)

        где определяется из уравнения, составленного по второму закону Кирхгофа для второго контура

.     (4.12)

    Так как первая ветвь разорвана, ЭДС Е1 не создает ток. Падение напряжения на сопротивлении Rвн1 отсутствует.
На рис. 4.10 изображена схема, предназначенная для определения входного сопротивления.

.

                      Рис. 4.9 Рис. 4.10

Из схемы на рис. 4.9 удалены все источники (Е1 и Е2), т.е. эти ЭДС мысленно закорочены. Входное сопротивление Rвх определяют, свертывая схему относительно зажимов 1-1′

.     (4.13)

      Для определения параметров эквивалентного генератора экспериментальным путем необходимо выполнить опыты холостого хода и короткого замыкания.
При проведении опыта холостого хода от активного двухполюсника отключают сопротивление R1, ток I1 в котором необходимо определить. К зажимам двухполюсника 1-1′ подключают вольтметр и измеряют напряжение холостого хода Uxx (рис. 4.11).
При выполнении опыта короткого замыкания соединяют проводником зажимы 1-1′ активного двухполюсника и измеряют амперметром ток короткого замыкания I1кз (рис. 4.12).

                                  Рис. 4.11 Рис. 4.12

        откуда

                     (4.14)

Конспект по электротехнике на тему » Электрические цепи постоянного тока»

ЛЕКЦИЯ № 2

Электрические цепи постоянного тока.

ПЛАН

1. Понятие об электрических цепях, электрический ток, электродвижущая сила, закон Ома, электрическое сопротивление и проводимость.

Электрическая цепь – это совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, электрическом токе и электрическом напряжении.

Любая электрическая цепь состоит из следующих трех групп элементов, выполняющих определенную функцию:

— источники электрической энергии;

— приемники электрической энергии;

— вспомогательные элементы.

Источники электрической энергии (активные элементы) – это элементы электрической цепи, в которых происходит преобразование химической, тепловой, механической и других видов энергии в электрическую. Источниками электрической энергии являются, например, гальванические элементы, аккумуляторы, солнечные батареи, генераторы электрических станций и др.

Приемники электрической энергии (пассивные элементы) – это элементы электрической цепи, в которых происходит преобразование электрической энергии в другие виды энергии, а также ее запасание. Приемниками электрической энергии являются электрические двигатели, лампы накаливания, нагревательные элементы, громкоговорители, резисторы, конденсаторы, индуктивные катушки и др.

Вспомогательные элементы – это элементы электрической цепи, предназначенные для защиты, измерения, соединения источников и приемников электроэнергии и других вспомогательных функций. Вспомогательными элементами являются выключатели, предохранители, измерительные приборы, соединительные провода, разъемы и др. Для подключения к остальной части цепи каждый элемент цепи имеет внешние выводы, называемые также зажимами или полюсами. В зависимости от числа внешних выводов различают двухполюсные (резистор, конденсатор, катушка индуктивности) и многополюсные (транзистор, трансформатор, электронная лампа и др.) элементы.

В теории цепей предполагается, что каждый элемент цепи полностью характеризуется зависимостью между током и напряжениями на его зажимах, при этом процессы, имеющие место внутри элементов, не рассматриваются. В основе теории электрических цепей лежит принцип моделирования. В соответствии с этим принципом реальные элементы цепи заменяются их упрощенными моделями, построенными из идеализированных элементов. Используют пять основных типов идеализированных двухполюсных элементов: — идеальный резистор; — идеальный конденсатор; — идеальная индуктивная катушка; — идеальный источник напряжения; — идеальный источник тока.

В простейшем случае модель реального элемента может состоять из одного идеализированного элемента, в более сложных случаях она представляет собой соединение нескольких идеализированных элементов. Например, моделью реальной индуктивной катушки может быть последовательное соединение идеальной индуктивности и идеального резистора, учитывающего сопротивление проводов катушки. Кроме двухполюсных использую также многополюсные идеализированные элементы – управляемые источники тока и напряжения, идеальные трансформаторы и др.

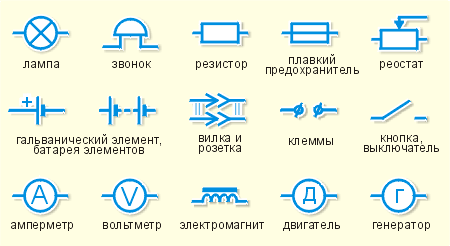
Графические обозначения в электрических схемах

Направленное движение заряженных частиц  называется электрическим током.

За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

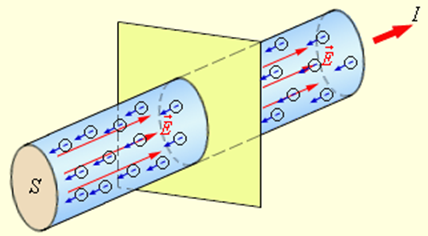
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1) за интервал времени Δt, к этому интервалу времени: I=ΔqΔt

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.

Рисунок 1.Упорядоченное движение электронов в металлическом проводнике и ток

I. S – площадь поперечного сечения проводника, E−→ – электрическое поле

В Международной системе единиц СИ сила тока измеряется в Амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током.

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

I=1RU;U=IR

где R = const.

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит Ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме: IR=U12=ϕ1−ϕ2+E=Δϕ12+E; I=UR

Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.

На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.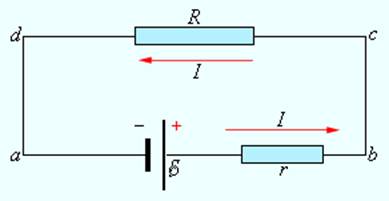

Рисунок 1.8.2.

Цепь постоянного тока По закону Ома

IR=Δϕcd

Участок (ab) содержит источник тока с ЭДС, равной E.

По закону Ома для неоднородного участка, Ir=Δϕab+E

Сложив оба равенства, получим: I(R+r)=Δϕcd+Δϕab+E

Но Δϕcd=Δϕba=−Δϕab.

Поэтому : I=ER+r

Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи (внутреннего сопротивления источника).

Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R ≪r), тогда в цепи потечет ток короткого замыкания

Iкз=Er

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой E и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

Конспект лекций электротехника — Стр 2

ЛЕКЦИЯ № 2

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ОДНОФАЗНОГО ТОКА

Переменный ток широко применяется в различных областях электротехники. Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока. Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации.

Генерирование переменного электрического тока практически легче осуществляется в машинах с вращающимися проводниками.

Переменный ток, меняет свое значение и направление определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебания. Вследствие своей малой скорости движения (Vэл = 10-4 м/с = 0,1 мм/с ) электроны при таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода.

Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, э.д.с.) со временем показывает плавная кривая линия, называемая синусоидой.

Электрические цепи, в которых значения и направления э.д.с., напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.

Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.

Кроме того именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы входящие в состав электрических цепей не изменяют синусоидальной формы.

В большинстве стран выбрана частота переменного тока 50 Гц (США и Канада — 60 Гц). Эта частота является наиболее оптимальной, поскольку переменные токи низкой частоты 25 — 40 Гц вызывают заметное для глаза мигание электрических ламп накаливания, а повышение частоты приводит к росту э.д.с. самоиндукции и дополнительным потерям при передаче электроэнергии.

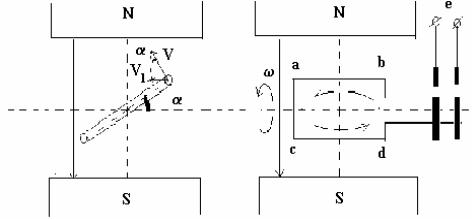
Рассмотрим процесс возникновения синусоидальной э.д.с. Простейшим генератором синусоидальной э.д.с. может служить прямоугольная рамка, равномерно вращающаяся в однородном магнитном поле с угловой скоростью . Пронизывающий катушку (рамку) магнитный поток во время вращения рамки abcd индуцирует в ней на основании закона электромагнитной индукции э.д.с. е.

Нагрузку подключают к генератору с помощью щеток, прижимающихся к двум контактным кольцам, которые соединены с катушкой (рамкой).

Значение наведенной в рамке э.д.с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части рамки l = ab + cd , скорости пересечения магнитных линий VH :

e = BlVH.

Причем скорость VH зависит от ориентации рамки :

VH = V sin ,

где V — линейная скорость движения рамки, — угол описывающий положение рамки (ориентацию относительно вектора магнитной индукции).

В случае равномерного вращения рамки угол поворота зависит от времени следующим образом :

= t.

Следовательно, э.д.с. индуцируемая в равномерно вращающейся рамке определяется : e = BlVsin t.

Сомножители, стоящие перед sin t представляют собой максимальное значение наведенной э.д.с. :

em = BlV.

Тогда

e = emsin t.

Если в начальный момент времени рамка распологалась не по нормали к силовым линиям, а под углом

e то = t + e и

e = emsin ( t+ e ).

Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности, во-вторых тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения.

Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется.

Врезисторах в цепях постоянного тока электрическая энергия преобразуется в тепловую. В цепях переменного тока помимо преобразования электрической энергии в тепловую происходит накапливание энергии в магнитном и электрическом полях, то есть кроме параметра сопротивления R, цепь характеризуется еще и параметрами индуктивности и емкости L, C.

Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи.

Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений : сдвиг фаз, явление резонанса, появление реактивных мощностей.

При расчете режимов цепи синусоидального тока максимально используются понятия, формулы и методы расчета цепей постоянного тока.

Вцепях переменного тока направление э.д.с., токов и напряжений изменяются два раза за период. Однако при расчете цепи синусоидального тока необходимо составлять уравнения по законам Кирхгофа, а они требуют задания определенных направлений э.д.с., токов и напряжений. Поєтому положительные направления токов, как и для цепи постоянного тока, выбирают произвольно.

Законы Кирхгофа, расмотренные ранее для цепей постоянного тока, справедливы и для мгновенных значений синусоидальных токов, напряжений и э.д.с.

Первый закон Кирхгофа :

Алгебраическая сумма мгновенных значений токов в узле равна нулю :

N

ik 0,

k 1

где N — число ветвей, соединенных в узле.

Второй закон Кирхгофа :

Алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах контура в данный момент времени равна алгебраической сумме э.д.с. в том же контуре в тот же момент времени.

При составлении уравнений контур обходят в одном произвольно выбранном направлении, алгебраически суммируя напряжения и э.д.с. Если положительное направление напряжения и э.д.с. совпадает с направлением обхода, то это напряжение или э.д.с. записываются со знаком “ + ” плюс, если не совпадает, то со знаком “ — ”.

Закон Ома для мгновенных значений напряжения и тока справедлив только для резистивных элементов ( I = U/R ).

ПАРАМЕТРЫ ПЕРЕМЕННОГО ТОКА.

Для количественной характеристики переменного тока служат служат следующие параметры. Мгновенные значения тока, напряжений и э.д.с. — это их значения в любой момент времени:

i = imsin ( t+ i ), u = umsin ( t+ u ),

e = emsin ( t+ e ).

Амплитудные значения тока, напряжения и э.д.с. im ,um ,em — максимальные значения мгновенных значений.

Период Т — промежуток времени, в течение которого ток совершает полное колебание и принимает прежнее по величине мгновенное значение. Период измеряется в секундах.

Угловая частота — характеризует скорость вращения катушки генератора в магнитном поле. Измеряется в рад/с. Связана с периодом следующей формулой :

= 2 /Т.

Циклическая частота (частота) f — величина, обратная периоду и характеризующая число полных колебаний тока за 1с. Частота измеряется [Гц] = 1/с и определяется :

f = 1/Т.

Частота и угловая частота связаны между собой следующим образом :

= 2 f.

Фаза. Аргументы периодических функций называют фазой. Фазы характеризуют значения соответствующих величин в заданный момент времени. Значение фазы в начальный момент времени называется начальной фазой. Начальная фаза определяет значение соответствующей величины в начальный момент времени.

Действующие значения I, U, E. Пользоваться амплитудными значениями тока и напряжения не всегда удобно. Например, очевидно, что переменный ток с амплитудой 10 А имеет меньшую мощность, чем постоянный ток 10 А. Значение постоянного тока все время равно 10 А, а переменный ток достигает 10 А только в моменты, соответствующие амплитудному значению. В другие моменты ток меньше 10 А и даже доходит до нуля.

За основу для измерения постоянного тока положено сопоставление его среднего теплового действия с тепловым действием постоянного тока. Определенное посредством такого сравнения значение силы тока называется действующим значением.

Действующим значением переменного тока называется такой постоянный ток, при котором выделяется в резистивном элементе с активным сопротивлением R за период то же количество энергии, что и при действии переменного тока.

Энергия, которая выделяется в резистивном элементе при переменном токе :

T	T
W i 2Rdt im2		sin2 tRdt.
0	0

При постоянном токе выделяется энергия :

W I 2RT .

Приравнивая правые части получим действующее значение тока :

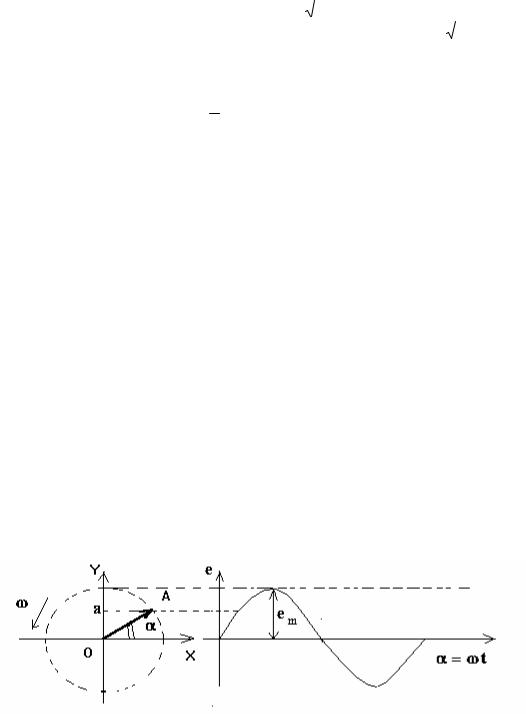
		T	i
I (	1	im2 sin2 tdt)1/ 2		m		0707,im.
	T
			2
0
Таким образом, действующее значение тока меньше			амплитудного в				2	раз. Аналогично
определяются действующие значения э.д.с. и напряжения.

Когда говорят о значении напряжения, э.д.с. и тока в цепях переменного тока, то имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока проградуированы в действующих значениях. Например, если прибор показывает 10 А, то это значит, что амплитуда тока : im = 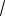2I = 1,41 10 = 14,1 A,

Напряжение в сети 220 В означает, что действующее напряжение в осветительной сети составляет 220 В. Амплитудное значение напряжения в осветительной сети равно 311 В. Амплитудное значение напряжения нужно принимать во внимание, например при выборе изоляции.

МЕТОД ВЕКТОРНЫХ ДИАГРАММ.

Электрическое состояние цепей переменного тока, так же как и цепей постоянного тока, описывается уравнениями Кирхгофа. Однако при анализе цепей переменного синусоидального тока математический аппарат становится очень громоздким, так как все уравнения содержат электрические величины, изменяющиеся по гармоническому закону.

Для упрощения анализа и расчета цепей переменного тока в электротехнике используют метод

векторных диаграмм.

В электротехнике векторами изображаются изменяющиеся гармонически э.д.с., напряжения и токи, но в отличие от векторов, которыми изображались силы и скорости в механике, эти вектора вращаются с постоянной угловой скоростью и не означают направления действия.

Допустим, что радиус-вектор ОА, представляющий собой в определенном масштабе амплитудное значение э.д.с. em вращается с постоянной угловой частотой = 2 f против часовой стрелки. Проекция ОА на OY будет равна

Oa = OA sin .

Выразив ОА через амплитудное значение э.д.с. em и угол через t , получим выражение мгновенного значения э.д.с. изменяющейся синусоидально :

e = em sin t.

График мгновенных значений э.д.с. изображен в правой части рисунка.

За начало отчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью ( ось Х ). Если в начальный момент времени t = 0, ОА совпадает с линией, расположенной под углом к оси Х, то проекция ОА, а следовательно, и э.д.с. будут соответственно равны :

Oa = OA sin ( t + ), e = em sin ( t + е).

Аналогично можно представить в виде векторов, вращающихся против часовой стрелки с постоянной угловой частотой , напряжение и ток.

Совокупность нескольких вращающихся векторов, в начальный момент времени, соответствующих уравнениям электрической цепи, называется векторной диаграммой.

Обычно векторные диаграммы строят не для амплитудных значений, а для действующих значений. При построении векторных диаграмм обычно один из векторов распологают на плоскости

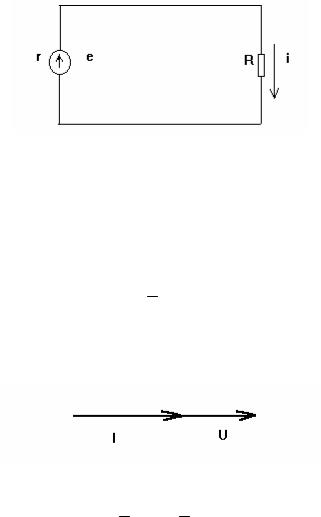
произвольно, остальные же вектора — под соответствующими углами к исходному. При этом в подавляющем большинстве случаев можно обойтись без нанесения осей координат.

Векторные диаграммы позволяют, не прибегая к вычислениям, исследовать характер изменений той или иной величины, определяющей режим работы электрической цепи.

АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО СИНУСОИДАЛЬНОГО ТОКА.

В общем случае электрическая цепь переменного тока может содержать резистивные, индуктивные и емкостные элементы, параметрами которых являются сопротивление, индуктивность и емкость. Анализ и расчет таких цепей значительно сложней, чем цепей постоянного тока. Прежде чем разбирать общий случай цепи содержащей все выше перечисленные элементы рассмотрим частные случаи.

1.Электрическая цепь с активным сопротивлением.

Рассмотрим электрическую цепь, содержащую только резистивный элемент с активным сопротивлением. Под активным сопротивлением понимают сопротивление проводников переменному току. Активные сопротивления непрерывно потребляют энергию.

Сопротивление резистора в цепи переменного тока может отличаться от сопротивления того же резистора в цепи постоянного тока. Это различие обусловлено поверхностным эффектом, при котором ток вытесняется к поверхности проводника, и зависит от частоты. С увеличением частоты сопротивление растет. Однако при относительно небольших частотах, например 50 Гц, его увеличением можно пренебречь.

Рассмотрим цепь состоящую из источника э.д.с.

e = em sin t.

и резистора сопротивлением R :

Если r << R, то ток в цепи зависит главным образом от э.д.с. и сопротивления нагрузки — источник в этом случае называют источником э.д.с. или напряжения, так как на его выводах

e= u.

Поэтому в цепи переменного тока действует напряжение :

u = um sin t.

Мгновенное значение силы тока в цепи с активным сопротивлением определяется законом Ома:

i = u / R = um sin t /R = im sin t.

Отсюда следует закон Ома для амплитудных значений : im = um / R,

а разделив левую и правую части равенства на 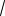2, получим закон Ома для действующих значений :

I = U / R.

Сопоставляя выражения для мгновенных и действующих значений тока и напряжения, можно прийти к выводу, что токи и напряжения в цепи с активным сопротивлением совпадают по фазе.

Векторная диаграмма для цепи с активным сопротивлением имеет вид :

Мгновенная мощность цепи равна произведению мгновенных значений тока и напряжения. Мощность определяет скорость расхода энергии, и следовательно, для цепей переменного тока является величиной переменной. Мгновенная мощность по определению равна :

P =ui= um im sin2 t = (um /2) ( im /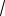2)(1 — cos 2 t) = UI — UIcos2 t.

Мгновенная мощность, оставаясь все время положительной колеблется около уровня UI.

В цепи с активным сопротивлением энергия все время поступает от источника к приемнику и необратимо преобразуется в нем в теплоту и рассеивается в окружающей среде.

Для определения расхода энергии за длительное время целесообразно пользоваться средним значением мощности. Для вывода выражения средней мощности найдем сначала расход энергии в цепи за полупериод :

		T / 2		T / 2			T / 2	T / 2		T
	W		Pdt	(UI	UI	cos2 t)dt	UIdt	UI	cos2 tdt		UI
		0		0			0	0	2

Разделив полученное выражние на Т / 2, получим среднюю скорость расхода

энергии:

P UI .

Электрическая энергия, которая преобразуется на активном сопротивлении в тепловую называется

активной мощностью.

Активная мощность измеряется ваттметром.

2.Электрическая цепь с индуктивным элементом.

Огромное влияние на процессы протекающие в цепях имеет явление электромагнитной индукции. Явление электромагнитной индукции заключается в том, что изменение магнитного поля вокруг проводника, связанное с пересечением проводника магнитными силовыми линиями, вызывает появление э.д.с. в этом проводнике.

При этом безразлично, будет ли изменяться магнитное поле относительно проводника или проводник будет перемещаться в магнитном поле.

При изменении тока в проводнике изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока индуцирует в проводнике э.д.с., действие которой по правилу Ленца направлено на поддержание предшествующего состояния поля (Правило Ленца: Индуцируемая э.д.с. стремится противодействовать причине, ее вызывающей). Такое явление называется самоиндукцией. Явление самоиндукции в проводниках характеризуется индуктивностью L. Индуктивность это размерный коэффициент пропорциональности между скоростью изменения тока во времени и индуцируемой при этом э.д.с.

e = — L (di / dt)

Знак минус в формуле отражает правило Ленца. Индуктивность измеряется в Генри.

Значение индуктивности L зависит от конструкции элементов цепи. Так для катушки с числом витков

N, магнитопроводом длины l, площади S и магнитной проницаемостью :

L = 0 N2 S / l

Индуктивностью обладают также одиночный прямой провод, двухпроводная линия, коаксиальный кабель.

Обмотки электрических машин, трансформаторов, реле, катушки индуктивности обладают значительной индуктивностью.

Переменный ток встречает в проводниках не только омическое сопротивление. Непрерывное противодействие э.д.с., препятствующее изменению переменного тока, создает в цепи дополнительное сопротивление. Это дополнительное сопротивление называют индуктивным сопротивлением. Таким образом, катушки и разные обмотки, поскольку в них есть индуктивность, оказывают большее сопротивление переменному току, чем постоянному.

Параметрами катушек индуктивности являются активное сопротивление и индуктивность. Рассмотрим вначале катушку, активное сопротивление которой настолько мало, что им можно пренебречь. Применим к рассматриваемому замкнутому контуру второй закон Кирхгофа.

Вслучае цепей переменного тока второй закон Кирхгофа формулируется для мгновенных значений следующим образом:

Алгебраическая сумма напряжений на всех элементах контура в данный момент времени равна алгебраической сумме э.д.с. в том же контуре, в тот же момент времени.

При составлении уравнений контур обходят в одном произвольно выбранном направлении, алгебраически суммируя напряжения и э.д.с.

Если положительное направление напряжения и э.д.с. совпадает с направлением обхода контура, то это напряжение или э.д.с. записываются со знаком “ + “, если не совпадают, то со знаком » — «.

Под действием синусоидального напряжения в цепи с катушкой протекает синусоидальный ток :

i= im sin t.

Врезультате вокруг этой катушки возникает переменное магнитное поле и в катушке наводится э.д.с.

самоиндукции.

e + eL = 0.

При исследовании цепей с э.д.с. самоиндукции условились положительное направление э.д.с. самоиндукции брать совпадающим, с положительным направлением тока, который наводит эту э.д.с. Но э.д.с. источника равна его внешнему напряжению (у источника э.д.с. внутреннее сопротивление r 0 и э.д.с. не зависит от тока нагрузки проходящего через источник e = u = const):

e = u,

а э.д.с. самоиндукции и ток связаны уравнением :

eL = — L di/dt.

Если ток со временем увеличивается, то di/dt > 0 и eL < 0, то есть ток самоиндукции направлен навстречу току, обусловленному внешним источником, и тормозит его возростание. Если ток со временем падает, то di/dt < 0 и eL > 0, то есть индукционный ток имеет тоже направление как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность.

Второй закон Кирхгофа для рассматриваемой электрической цепи : u = -eL.

Напряжение источника целиком идет на уравновешивание eL.

u = L di/dt = im L cos t = um sin ( t + /2 ),

где

um = im L.

Сопоставляя мгновенные значения тока и напряжения приходим к выводу, что ток в цепи с индуктивным элементом отстает по фазе от напряжения на /2.

Векторная диаграмма цепи с индуктивным элементом имеет вид :

Выведем закон Ома для этой цепи. Из um = im L следует, что

im=um/ L. Введем обозначение:

ХL = L.

Эта величина называется реактивным индуктивным сопротивлением, или просто индуктивным сопротивлением.

Закон Ома для мгновенных значений:

im=um / ХL

Закон Ома для действующих значений :

I= U / ХL.

Сувеличением частоты тока индуктивное сопротивление увеличивается. Физически это объясняется тем, что возрастает скорость изменения тока, а следовательно, и э.д.с. самоиндукции.

Иногда необходимо увеличить сопротивление в цепи переменного тока, в этом случае в цепь включают катушку со стальным сердечником, называемую дросселем. Большая самоиндукция мешает увеличению тока и поддерживает его в моменты спада. Дроссели применяются: в электросварке, в различных выпрямителях, в радиотехнических устройствах. Для защиты электрических сетей от токов короткого замыкания устанавливают реакторы — большие катушки из толстого медного провода. Для обычного перменного тока они представляют очень небольшое сопротивление. При мгновенном увеличении тока короткого замыкания в реакторе индуктируется большая э.д.с. самоиндукции. Она противодействует этому увеличению и ограничивает ток короткого замыкания до безопасной величины, чем защищает ценное оборудование — генераторы, трансформаторы, электродвигатели — от разрушения.

Обычно катушки и обмотки имеют значительное индуктивное сопротивление. Когда нужно, чтобы катушка в цепи переменного тока не имела индуктивного сопротивления, а только активное, то провод на катушку накладывают так: весь провод складывают вдвое и тогда наматывают на катушку. Обмотка выполненная таким образом, называется бифилярной, или двухвитковой.

Осутствие индуктивности в таких катушках обьясняется тем, что магнитные поля, создающиеся противоположно направленными токами в двух половинах обмотки, взаимно компенсируются. Поэтому катушка в целом не создает магнитного потока и в ее витках не индуктируется э.д.с.

Как и для цепи с активным элементом, мгновенное значение мощности определяется произведением мгновенных значений напряжений и тока :

p =ui = um im sin t sin ( t + /2 ) = (um /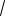2)( im /2) sin t cos t) = UI sin 2 t.

Среднее значение мощности:

			1	T
				uidt 0.
	P
		T
				0

Физически это объясняется преобразованием энергии источника в энергию магнитного поля катушки и возвращением накопленной энергии источнику. В среденем катушка не потребляет энергии, и следовательно, активная мощность P = 0.

Для количественной характеристики интенсивности обмена энергией между источником и индуктивными элементами служит величина называемая реактивной мощностью:

Q = UI.

Измеряется реактивная мощность в единицах, которые называются вольт-ампер реактивный или сокращенно вар.

Реактивными называются сопротивления, которые в среднем не потребляют энергию.

3.Электрическая цепь с емкостным элементом.

Если в цепь постоянного тока подключить конденсатор, то тока в цепи не будет, так как она разрывается диэлектриком, находящимся между пластинами конденсатора.

При включении конденсатора в цепь переменного тока обнаружим, что ток проходит по цепи, несмотря на ее разрыв диэлектриком в конденсаторе.

Чтобы понять, почему переменный ток проходит по цепи, рассмотрим работу установки; изображенную на рисунке:

Поршень П двигается в цилиндре вправо и влево. В сосуде С имеется упругая перепонка М, которая делит цепь на две части. При перемещении поршня влево вода, опускаясь по трубе Т1, начнет давить на перепонку М, которая, выгнувшись, займет положение М1; в трубе Т2 вода в этот момент будет подниматься вверх.

Непрерывное перемещение поршня создает непрерывное движение жидкости в цепи. Перепонка периодически выгибается то вправо, то влево, создавая давление на воду.

Источник переменного тока выполняет работу, подобную поршню, а конденсатор в цепи переменного тока можно сравнить с упругой перепонкой. Напряжение электрической цепи похоже на давление поршня на воду, а перемещение воды имеет сходство с током в электрической цепи. Напряжение источника периодически меняет свой знак. Поэтому за первый полупериод одна обкладка конденсатора заряжается положительно, а другая — отрицательно.

В начале следующего полупериода меняется знак напряжения источника, и конденсатор перезаряжается.

При каждой перезарядке конденсатора по цепи то в одном, то в другом направлении будет проходить ток. Этот ток не проходит сквозь диэлектрик конденсатора, так же, как вода не проходит сквозь перепонку М. Когда ток перезарядки конденсатора проходит через лампу, то он накаляет ее нить.

Такой ток называют емкостным током. Таким образом, переменный ток по цепи с конденсатором проходит.

Проанализируем процессы в цепи емкостным элементом. Зададимся напряжением на зажимах источника

u = um sin t,

тогда ток в цепи также будет изменяться по синусоидальному закону. Ток определяется по формуле : i = dq/dt.

Электрический заряд на обкладках конденсатора связан с напряжением на конденсаторе и его емкостью формулой :

q = Cu.

Следовательно :

i = dq/dt = Cdu/dt = um С cos t = um С sin ( t + /2 ).

Таким образом, ток в цепи с емкостью опережает по фазе напряжение на угол /2.

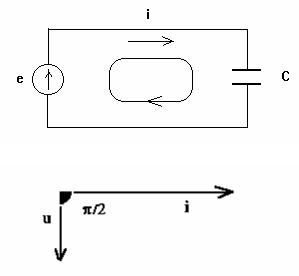
Векторная диаграмма напряжения и тока для цепи с емкостным элементом имеет вид :

Физически это объясняется тем, что напряжение на конденсаторе возникает за счет разделения зарядов на его обкладках в результате протекания тока. Следовательно, напряжение появляется только после возникновения тока.

Получим закон Ома для цепи с емкостным элементом. В формуле :

i = um С sin ( t + /2 )

введем обозначение

Хc = 1 / С,

где Хc — емкостное сопротивление.

Закон Ома для амплитудных и действующих значений имеет вид :

im = um / Хc,

I = U / Xc.

Емкостное сопротивление уменьшается с ростом частоты. Это объясняется. тем что при большой частоте через поперечное сечение диэлектрика в единицу времени протекает больший заряд при том же напряжении, что эквивалентно уменьшению сопротивления в цепи.

Рассмотрим энергетические характеристики в цепи с емкостью. Пусть начальная фаза тока в цепи равна нулю, тогда

i = im sin t .

Поскольку напряжение на емкости отстает от тока на угол /2 , то

u = um sin ( t — /2 ) = — um сos t.

Мгновенная мощность вычисляется по формуле :

p = ui = — um im sin t сos t = — UI sin 2 t.

Графики напряжения, тока и мгновенной мощности показаны ниже на рисунке. В цепи с емкостью, так же как в цепи с индуктивностью, происходит переход энергии от источника к нагрузке, и наоборот. В данном случае энергия источника преобразуется в энергию электрического поля конденсатора и наоборот. Средняя активная мощность в цепи с емкостью также равна нулю.

Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность:

Q = UI.

Лекции по электротехнике (1 часть)

ЛЕ К Ц И Я 1

1.Введение. Цели, задачи и структура курса.

2.Линейные цепи постоянного тока — основные понятия и определения.

3.Схемы электрических цепей и их элементы.

4.Законы Ома и Кирхгофа.

1.Введение

Электротехника — техническая дисциплина, которая занимается анализом и

практическим использованием для нужд промышленного производства и быта всех физических явлений, связанных с электрическими и магнитными полями.

Область практического применения электротехники имеет четыре связанные друг с другом направления :

1.Получение электрической энергии.

2.Передача энергии на расстояние.

3.Преобразование электромагнитной энергии.

4.Использование электроэнергии.

Научно-технический прогресс происходит при все более широком исполь- зовании электрической энергии во всех отраслях отечественной промышлен- ности. Поэтому электротехническая подготовка инженеров не электротехниче-

ских специальностей должна предусматривать достаточно подробное изучение вопросов теории и практики использования различных электроустановок. Ин- женер любой специальности должен знать устройство, принцип действия, характеристики и эксплуатационные возможности электрических цепей, элек- трических машин, различных аппаратов и другого электрооборудования, спо- собы регулирования и управления ими.

История развития электротехники как науки связана с важнейшими иссле- дованиями и открытиями. Это исследования атмосферного электричества, появление источников непрерывного электрического тока — гальванических элементов (1799 г.), открытие электрической дуги (1802 г.) и возможность ее использования для плавки металлов и освещения, открытие закона о направле- нии индуцированного тока (1832 г.) и принципа обратимости электрических машин, в 1834 г. впервые осуществлен электропривод судна, открытие закона теплового действия тока — закона Джоуля — Ленца (1844 г.), в 1876 г. положе- но начало практическому применению электрического освещения с изобрете- нием электрической свечи, в 1889-1891 гг. созданы трехфазный трансформа- тор и асинхронный двигатель.

Внастоящее время отечественная электроэнергетика занимает передовые позиции в мире по созданию мощных ГЭС и каскадов электростанций, произ- водству мощных гидрогенераторов, высоким темпам теплофикации, строи-

тельству высоковольтных линий электропередач и мощных объединенных энергосистем, высокому техническому уровню электросетевого хозяйства.

Всовременных производственных машинах с помощью электротехнической

иэлектронной аппаратуры осуществляется управление ее механизмами, авто- матизация их работы, контроль за ведением производственного процесса, обеспечивается безопасность обслуживания и т.д. Все шире используется в технологических установках электрическая энергия, например, для нагрева из- делий, плавления металлов, сварки.

Основной задачей данного курса является получение основных сведений и формирование знаний, умений и навыков по электротехнике, электронным устройствам и электроприводу.

Всостав курса входят следующие разделы:

1.Электрические цепи постоянного тока.

2.Электрические цепи переменного тока.

3.Переходные процессы в электрических цепях.

4.Основы электроники.

5.Магнитные цепи и электромагнитные устройства.

6.Трансформаторы.

7.Электрические машины.

8.Основы электропривода.

2. Линейные цепи постоянного тока — основные понятия и определения.

Электрической цепью называется совокупность источников и потребителей электрической энергии, соединенных друг с другом с помощью проводников.

Электрический ток — направленное движение заряженных частиц (элек- тронов или ионов ).

Постоянный ток — ток, неизменный по величине и направлению.

Ветвью называется участок цепи между двумя соседними узлами, содержа- щий последовательное соединение элементов.

Точка, где соединяются три и более ветвей называется узлом.

Любой замкнутый путь, проходящий по ветвям данной цепи, называется контуром.

Основными параметрами, характеризующими электрические цепи постоян- ного тока, являются: I(А)- сила тока — количество электричества, проходяще- го через поперечное сечение проводника за единицу времени, U(В) — напря- жение на некотором участке электрической цепи, равное разности потенциалов на концах этого участка, R(Ом) — сопротивление, Р(Вт)- мощность. Все обо-

значения основных физических величин предусмотрены государственным стандартом. Единицы измерения диктуются международной системой единиц.

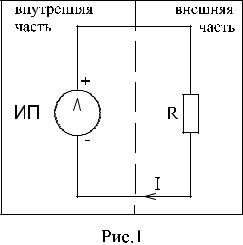
3. Схемы электрических цепей и их элементы.

Графическое изображение электрической цепи и ее элементов называется электрической схемой (рис. 1)

На любую машину, в состав которой входят электрические устройства, кроме конструкторских чертежей имеется элек- тродокументация, состоящая из различных

электрических схем. Электрические функ-

циональные схемы раскрывают принцип действия устройства. Существуют элек- тромонтажные схемы, в которых раскры- вается монтаж (соединение) электриче-

ских элементов цепи.

Электрические принципиальные схемы раскрывают электрические связи всех от-

дельных элементов электрической цепи между собой.

Все схемы вычерчиваются по определенным стандартам- ГОСТам. ГОСТы являются основой технического языка, применяемого в масштабе всей стра- ны.

Кроме основных электрических схем существуют схемы замещения, по ко- торым наиболее удобно составлять математические уравнения, описания элек- трических и энергетических процессов. Такие схемы являются эквивалентными моделями электрической цепи. Схемы максимально упрощены и по ним удоб- нее провести анализ отображаемых ими сложных электрических цепей.

Все элементы электрических цепей можно разделить на три группы: ис- точники (активные элементы), потребители и элементы для передачи элек- троэнергии от источников к потребителю (пассивные элементы).

Источником электрической энергии (генератором) называют устройство, преобразующее в электроэнергию какой-либо другой вид энергии (электро- машинный генератор — механическую, гальванический элемент или аккумуля- тор — химическую, фотоэлектрическая батарея — лучистую и т.п.).Источники делятся на источники напряжения (Е,U=соnst, при изменении и I) и источники тока (I=соnst, при изменении U). Все источники имеют внутреннее сопротив- ление Rвн, значение которого невелико по сравнению с сопротивлением других элементов электрической цепи .

Приемником электрической энергии (потребителем) называют устройство, преобразующее электроэнергию в какой-либо другой вид энергии (электро- двигатель — в механическую, электронагреватель — в тепловую, источник света — в световую (лучистую) и т.п.).

Элементами передачи электроэнергии от источника питания к приемнику служат провода, устройства, обеспечивающие уровень и качество напряжения и др.

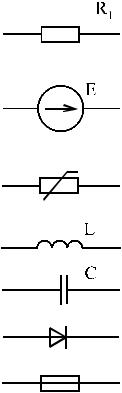
Условные обозначения элементов электрической цепи на схеме стандарти- зованы. Примеры:

— резистивный элемент (линейный),

— идеальный источник ЭДС, условно положи- тельное направление ЭДС принято от отрица- тельного полюса к положительному (и совпа- дает с положительным направлением тока)

— нелинейный элемент,

— индуктивный элемент, — емкостной элемент,

— полупроводниковый диод, — плавкий предохранитель

4. Законы Ома и Кирхгофа

Закон Ома в простейшем случае связывает величину тока через сопротив- ление с величиной этого сопротивления и приложенного к нему напряжения:

Сила тока на некотором участке электрической цепи прямо пропорциональ-

на напряжению на этом участке и обратно пропорциональна сопротивлению этого участка.

Закон Ома справедлив для любой ветви (или части ветви) электрической цепи, в таких случаях его называют обобщенным законом Ома. Для ветви, не содержащей ЭДС, закон Ома запишется:

I =	ϕa −ϕb	=	Uab	.
	n		n
	åRi		åRi
	1		1

Здесь ϕа ,ϕb — потенциалы крайних точек ветви, их разность можно заменить напряжением Uab.

Обобщенный закон Ома для ветви, содержащей ЭДС (т.е. для активной вет- ви):

		k			k
	I =	ϕa −ϕb + åEj	=	Uab + åEj
		1		1
		n			n
		åRi			åRi
		1		1

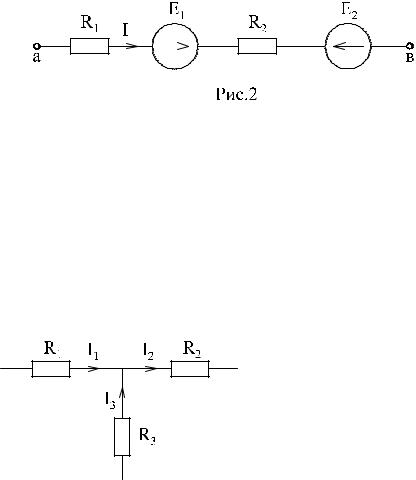
Пример: Записать закон Ома для активной цепи на рис. 2.

I = ϕa −ϕb + E1 − E2

R1 − R2

Первый закон Кирхгофа

Алгебраическая сумма токов, сходящихся в любом узле электрической цепи равна нулю. При этом токи, текущие к узлу считаются положительными, а от узла — отрицательными. Другая формулировка: сумма токов, подходящих к уз- лу, равна сумме токов, отходящих от узла.

n
åIk = 0
k =1		+ I3 = 0 или
I1	− I2
I1	+ I3	= I2

Первый закон Кирхгофа по сути является законом баланса токов в узлах цепи.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма па- дений напряжений на элементах, входящих в контур, равна алгебраической сумме ЭДС.

m	n
åRk Ik = åE j
k =1	j=1

Второй закон Кирхгофа по сути является законом баланса напряжений в контурах электрических цепей.

Для составления уравнения по 2-му закону Кирхгофа выбирается произ- вольное направление обхода контура. Тогда, если направление тока в цепи совпадает с направлением обхода, то соответствующее слагаемое берется со знаком «+», а если не совпадает, то со знаком «-«. Аналогичное правило рас- становки знаков справедливо и для ЭДС.

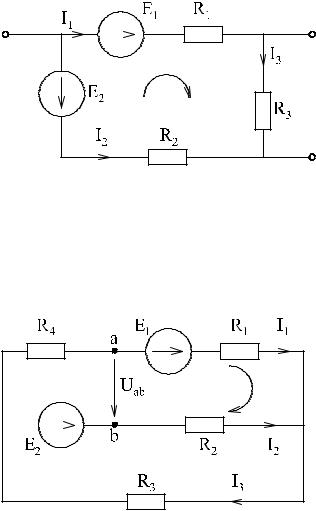
Пример:

R1I1 + R3I3 − R2 I2 = E1 − E2

Уравнение по 2-му закону Кирхгофа может быть записано и для контура, имеющего разрыв цепи, однако при этом необходимо в уравнении учитывать напряжение между точками разрыва.

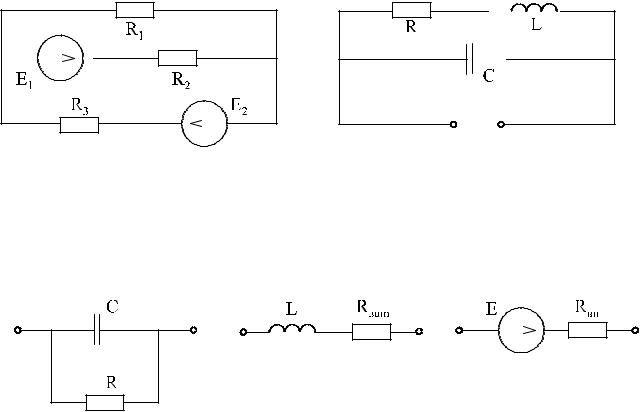
Пример:

R1I1 − R2 I2 −Uab = E1

ЛЕ К Ц И Я 2

1.Схемы замещения электрических цепей.

2.Эквивалентные преобразования пассивных электрических цепей.

3.Расчет цепей посредством двух законов Кирхгофа.

4.Мощность в цепях постоянного тока.

5.Баланс мощностей.

1.Схемы замещения электрических цепей.

Схемой электрической цепи называется ее графическое изображение с ис- пользованием обозначений идеальных элементов. Например:

Если учесть сопротивление утечки реального конденсатора, сопротивление

витков реальной индуктивной катушки и внутреннее сопротивление реального источника ЭДС, то можно составить соответствующие схемы замещения этих элементов:

Отсюда следует, что все схемы по сути дела являются лишь более или ме- нее точными схемами замещения реальных электрических цепей.

Представленный на рис.2 контур содержит три участка: участок с посто- янным напряжением U = Е, не зависящим от тока источника, и участки с на- пряжениями RвхI и U на нагрузке Rн.

Направление ЭДС выбрано совпадающим с направлением тока, но оно противоположно напряжению на этом элементе.

Для определения параметров схемы замещения источника электрической энергии с линейной внешней характеристикой нужно провести два опыта — холостого хода (I=0; U=Uх=Е) и короткого замыкания (I=Iк; U=Е-RвнI).

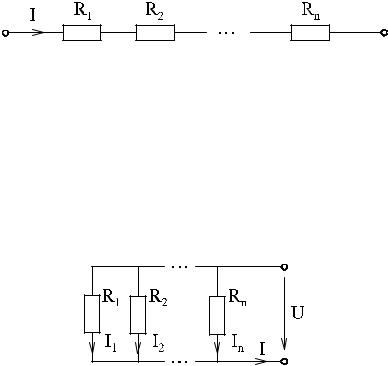
2. Эквивалентные преобразования пассивных электрических цепей.

Для упрощения анализа сложных электрических цепей отдельные их уча- стки, не содержащие ЭДС, или пассивные цепи целиком можно заменить од- ним эквивалентным сопротивлением. Под эквивалентным понимают такое сопротивление, которое, будучи включенным в цепь вместо заменяемой группы сопротивлений, не изменяет распределение токов и напряжений в ос- тальной части цепи.

При последовательном соединении сопротивлений по каждому из них

протекает один тот же ток, следовательно, падение напряжения на эквива- лентном сопротивлении должно быть равно сумме падений напряжений на ис- ходных сопротивлениях:

IRэкв = IR1 + IR2 +…+ IRn

отсюда получаем:

n

Rэкв = R1 + R2 +…+ Rn = åRi

1

Если группа заменяемых сопротивлений соединена параллельно, то

напряжения на каждом из них и на эквивалентном сопротивлении одинаковы. Условия эквивалентности будут выполнены, если ток через искомое сопро- тивление будет равен сумме токов через отдельные параллельные сопротив- ления:

I = I1 + I2 +…+ In

Используя закон Ома для отдельного сопротивления, можем записать:

U

=

U

+

U

+…+

U

R

R

R

R

Окончательно получаем:

экв

1

2

n

1

1

1

1

n

1

=

+

+…+

= å

R

R

R

R

R

экв

1

2

n

1

i

Поскольку величина, обратная сопротивлению, есть проводимость, то, вводя обозначения для проводимости Gi =1/ Ri , получим:

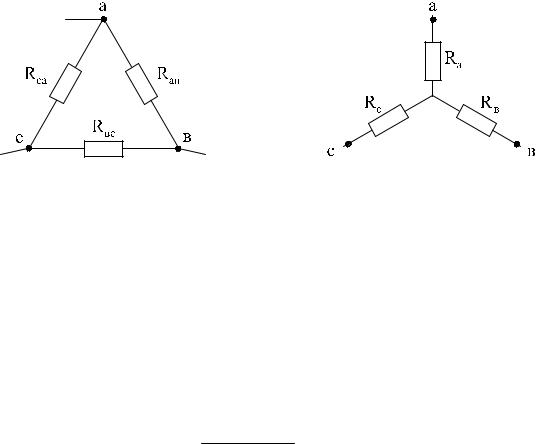
n

Gэкв = åGi

1

При анализе сложных схем встречаются случаи, когда часть схемы образу- ет так называемый треугольник сопротивлений:

Схема упрощается, если треугольник с сопротивлениями Rав, Rвс, Rса за- менить эквивалентной звездой с сопротивлениями Rа, Rв, Rс. Иногда, наобо- рот, необходимо обратное преобразование звезды в треугольник. Схемы тре- угольника и звезды считаются эквивалентными, если после преобразования все токи и напряжения в остальных частях схемы (не затронутых преобразова- ниями) остаются неизменными.

Очевидно, условия эквивалентности должны выполняться и при обрыве проводов, подходящих к узлам «а», «в», «с». Например, при обрыве провода, подходящего к узлу «а», сопротивления между точками «в» и «с» в треуголь- нике и звезде должны быть одинаковы, т.е.:

Rbc (+Rac ++Rab ) = Rb + Rc ;

Rbc Rca Rab

Рассуждая аналогичным образом, можно записать:

Rca (Rab + Rbc )	= R + R ;
	c	a
Rca + Rab + Rbc
Rab (Rbc + Rca )	= R + R ;
	a	b
Rab + Rbc + Rca

Решая полученную систему уравнений относительно Rа, Rв и Rс, получим формулы эквивалентного преобразования треугольника в звезду:

	Ra =	Rab Rca	;
		Rab + Rbc + Rca

	Rb =		Rbc Rab	;
			Rab + Rbc + Rca
	Rc =		Rca Rbc	;
			Rab + Rbc + Rca

Решая систему относительно Rab , Rbc и Rca получим формулы преобразова- ния звезды в треугольник:

Rab = Ra + Rb + Ra Rb ;

Rc

Rbc = Rb + Rc + Rb Rc ;

Ra

Rca = Rc + Ra + RRc Ra ;

b

В частном случае, когда сопротивления звезды или треугольника одина- ковы, эти формулы упрощаются:

RY = 13 R

R= 3RY

3.Расчет цепей посредством двух законов Кирхгофа.

Порядок расчета:

а) произвольно задаются положительными направлениями токов во всех ветвях схемы,

б) для всех узлов схемы кроме одного составляются уравнения по 1-му за- кону Кирхгофа,

в) для всех независимых контуров составляются уравнения по 2-му закону Кирхгофа (контур будет считаться независимым от остальных, если в него вхо- дит хотя бы одна новая ветвь, т.е. не вошедшая в состав других контуров).

Общее число уравнений, составленных по 1 и 2-му законам Кирхгофа должно быть равно числу неизвестных токов. Полученная система линейных уравнений разрешается относительно токов с использованием известных ме- тодов решения систем уравнений (например, с помощью определителей)

Лекции по электротехнике | Учебные материалы

Выберите предметВысшая математикаЭкономикаИнформатикаФизикаМеханикаНачертательная геометрияТеоретическая механикаСопротивление материаловАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАрхитектура и строительствоБазы данныхВысшая математикаГеометрияГидравликаДетали машинИздательское делоИнформатикаИнформационная безопасностьИнформационные технологииМатериаловедениеМашиностроениеМеталлургияМетрологияМеханикаМорская техникаНаноинженерияНачертательная геометрияПолиграфияПриборостроение и оптотехникаПрограммированиеПроцессы и аппаратыРабота на компьютереРадиофизикаСопротивление материаловТелевидениеТеоретическая механикаТеория вероятностейТеория машин и механизмовТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТранспортные средстваФизикаХолодильная техникаЧертежиЧерчениеЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЯдерная энергетика и теплофизикаЯдерные физика и технологииАнализ хозяйственной деятельностиАнтикризисное управлениеБанковское делоБизнес-планированиеБухгалтерский учет и аудитВнешнеэкономическая деятельностьГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиИнвестицииИнновационный менеджментКредитЛогистикаМаркетингМеждународные рынкиМенеджментМенеджмент организацииМикро-, макроэкономикаНалогиОрганизационное развитиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментСервисСтандартизацияСтатистикаСтратегический менеджментСтрахованиеТаможенное делоТеория управленияТовароведениеТорговое делоТуризмУправление персоналомФинансовый менеджментФинансыЦенообразование и оценка бизнесаЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализАрхеологияАстрономияБезопасность жизнедеятельностиБиологияБиотехнологияВетеринарияВоспроизводство и переработка лесных ресурсовГеографияГеодезияГеологияГидрометеорологияЕстествознаниеКартография и геоинформатикаМедицинаНефтегазовое делоПочвоведениеПриродообустройство и водопользованиеСельское и рыбное хозяйствоХимияХирургияЭкологияБиблиотечно-информационная деятельностьДизайнДокументоведение и архивоведениеЖурналистикаИскусствоИсторияКонфликтологияКриминалистикаКультурологияЛитератураЛогикаМеждународные отношенияМузыкаПедагогикаПолитологияПраво и юриспруденцияПсихологияРежиссураРеклама и PRРелигияСвязи с общественностьюСоциальная работаСоциологияСтрановедениеТеатроведениеФизическая культураФилософияЭтикаЯзыки (переводы)Языкознание и филология

Выберите вид работы…Дипломная работаРешение задачКонтрольная работаКурсовая работаРефератПомощь онлайнОтветы на вопросыОтчёт по практикеЧертёжМонографияБизнес-планТворческая работаЭссеСочиненияРецензияДокладНабор текстаМагистерская диссертацияКандидатская диссертацияСтатьяЛабораторная работаПереводПрезентацииПовышение уникальности текстаДругое

Краткий конспект лекций к первой части курса «Теоретические основы электротехники»

85

Павлов В. ЭС-104

Оглавлени

Краткий конспект лекций 1

1

2

Павлов В. ЭС-104 2

Введение 5

Общие определения цепей и их параметров 5

Активные элементы 7

Эквивалентные преобразования источников электрической энергии 8

Свойства линейных электрических цепей 9

Основные уравнения электрических цепей. Законы Кирхгофа. 10

ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА 12

Эквивалентные преобразования пассивных цепей 12

Расчет цепей по законам Кирхгофа 14

Метод контурных токов 15

Метод узловых напряжений 17

Метод наложения 18

Свойство взаимности 20

Теорема о компенсации 22

Метод эквивалентного источника напряжения 23

(теорема Гельмгольца-Тевенена) 23

Метод эквивалентного источника тока 26

(теорема Нортона) 26

Потенциальная диаграмма. 28

Баланс мощностей 29

Топология электрической цепи 30

Топологические матрицы графов 32

ЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ЭДС И ТОКОВ 36

Периодические напряжения и токи 36

Генератор синусоидального напряжения 37

37

Временная диаграмма 38

Векторная диаграмма 38

Действующие и средние значения периодических ЭДС и токов 39

Разность фаз напряжения и тока. Параметры цепей переменного тока. 41

Активное сопротивление в цепи переменного тока. 41

Индуктивное сопротивление в цепи переменного тока. 41

Емкостное сопротивление в цепи переменного тока. 42

Установившийся режим в цепи с последовательным соединением активного сопротивления, индуктивности и емкости 43

Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости 45

Энергетические соотношения в цепях синусоидального тока 47

Комплексный метод расчета электрических цепей 50

Комплексные сопротивления и проводимости 53

Перевод комплексных величин в показательную форму: 55

Перевод показательных величин в комплексную форму: 55

Основные законы электрических цепей в комплексной форме 55

Мощность в комплексной форме. Баланс мощностей 57

Резонансные явления в электрических цепях. 58

Частотные характеристики. 58

Резонанс напряжений 59

Частотные характеристики последовательного R-L-C контура. 61

Резонансные характеристики 61

Параллельный колебательный контур. Резонанс токов. 63

Частотные характеристики цепи с параллельным соединением элементов. 64

Резонансные кривые при параллельном соединении элементов 64

Цепи с взаимной индукцией 65

Последовательное и параллельное соединения 65

индуктивно связанных катушек 65

Векторные диаграммы: 66

При параллельном соединении катушек их напряжение одинаково. 67

Трансформатор без стального сердечника 68

Трехфазные системы токов и напряжений 71

Энергия и мощность в трехфазных цепях 74

ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ 75

Уравнения четырехполюсников 75

Холостой ход и короткое замыкание четырехполюсника 77

Определение параметров четырехполюсника 78

ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ НАПРЯЖЕНИЯ И ТОКИ 81

В ЛИНЕЙНЫХ ЦЕПЯХ 81

Разложение периодических функций в ряд Фурье 81

Действующее значение и мощность при несинусоидальных 83

напряжениях и токах 83

Расчет линейных цепей при несинусоидальных напряжениях и токах 84

Введение 4

Общие определения цепей и их параметров 4

Активные элементы 6

Эквивалентные преобразования источников электрической энергии 7

Свойства линейных электрических цепей 7

Основные уравнения электрических цепей. Законы Кирхгофа. 9

ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА 10

Эквивалентные преобразования пассивных цепей 10

Расчет цепей по законам Кирхгофа 12

Метод контурных токов 13

Метод узловых напряжений 15

Метод наложения 16

Свойство взаимности 18

Теорема о компенсации 19

Метод эквивалентного источника напряжения 20

(теорема Гельмгольца-Тевенена) 20

Метод эквивалентного источника тока 23

(теорема Нортона) 23

Потенциальная диаграмма. 25

Баланс мощностей 26

Топология электрической цепи 27

Топологические матрицы графов 29

ЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ЭДС И ТОКОВ 33

Периодические напряжения и токи 33

Генератор синусоидального напряжения 34

Временная диаграмма 34

Векторная диаграмма 35

Действующие и средние значения периодических ЭДС и токов 36

Разность фаз напряжения и тока. Параметры цепей переменного тока. 37

Активное сопротивление в цепи переменного тока. 37

Индуктивное сопротивление в цепи переменного тока. 37

Емкостное сопротивление в цепи переменного тока. 38

Установившийся режим в цепи с последовательным соединением активного сопротивления, индуктивности и емкости 38

Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости 40

Энергетические соотношения в цепях синусоидального тока 42

Комплексный метод расчета электрических цепей 45

Комплексные сопротивления и проводимости 48

Перевод комплексных величин в показательную форму: 49

Перевод показательных величин в комплексную форму: 49

Основные законы электрических цепей в комплексной форме 49

Мощность в комплексной форме. Баланс мощностей 50

Резонансные явления в электрических цепях. 51

Частотные характеристики. 51

Резонанс напряжений 52

Частотные характеристики последовательного R—L—C контура. 54

Резонансные характеристики 54

Параллельный колебательный контур. Резонанс токов. 55

Частотные характеристики цепи с параллельным соединением элементов. 57

Резонансные кривые при параллельном соединении элементов 57

Цепи с взаимной индукцией 58

Последовательное и параллельное соединения 58

индуктивно связанных катушек 58

Векторные диаграммы: 59

При параллельном соединении катушек их напряжение одинаково. 60

Трансформатор без стального сердечника 61

Трехфазные системы токов и напряжений 63

Энергия и мощность в трехфазных цепях 66

ОСНОВЫ ТЕОРИИ ЧЕТЫРЕХПОЛЮСНИКОВ 67

Уравнения четырехполюсников 67

Холостой ход и короткое замыкание четырехполюсника 69

Определение параметров четырехполюсника 70

ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ НАПРЯЖЕНИЯ И ТОКИ 72

В ЛИНЕЙНЫХ ЦЕПЯХ 72

Разложение периодических функций в ряд Фурье 72

Действующее значение и мощность при несинусоидальных 74

напряжениях и токах 74

Расчет линейных цепей при несинусоидальных напряжениях и токах 75

Конспект лекций электротехника — Стр 5

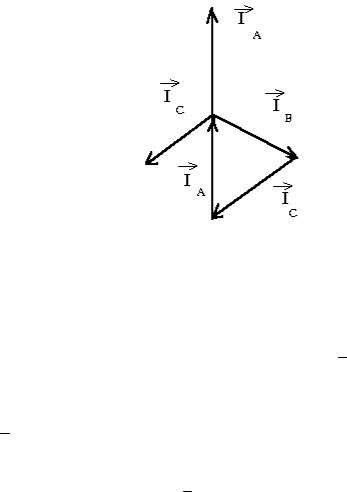
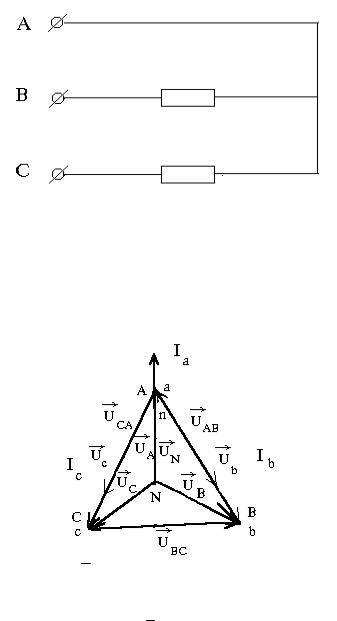
Ia = Ua/Za; Ib = Ub/Zb; Ic = Uc/Zc;

cos a = Ra/Za; cos b = Rb/Zb; cos c = Rc/Zc.

При симметричной нагрузке достаточно выполнить расчет для одной фазы.

Найдем для такой цепи напряжение между нейтральными точками. Так как для симметричной нагрузки Ya = Yb = Yc, то смещение нейтрали определяется:

UN = Yа(UA + UB + UC)/( YN + 3Ya ),

но при симметричной системе напряжений

UA + UB + UC = 0.

Поэтому при симметричной нагрузке нейтральные точки генератора и приемника совпадают и напряжение между ними равно нулю. Отсюда следует, что при симметричной нагрузке ток в нулевом проводе будет равен нулю. К такому же выводу можно прийти рассмотрев векторную диаграмму токов из которой так же следует равенство нулю тока в нулевом проводе

IN = Ia + Ib + Iс = 0

Таким образом, если нагрузка равномерная, то необходимость в нейтральном проводе отпадает. Трехфазная цепь без нейтрального провода является трехпроводной.

Соединения звездой при несимметричной нагрузке.

При несимметричной нагрузке сопротивления приемников не одинаковы. Для несимметричных нагрузок применяют только четырехпроводные цепи, так как между нейтральными точками появляется напряжение и напряжения на фазах нагрузки становятся различными. При этом нарушается

соотношение между фазными и линейными напряжениями UЛ = 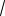3 UФ, причем на одних фазах нагрузки напряжение становиться большим, а на других — меньшим.

Наличие нейтрального провода в цепи с несимметричной нагрузкой позволяет выравнивать напряжение на фазах приемника и поддерживать их неизменными, равными фазным напряжениям

источника UЛ/3, то есть нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда ZN=0, даже при несимметричной нагрузке фазные напряжения приемника равны друг другу и соблюдается соотношение между

фазными и линейными напряжениями UЛ = 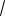3 UФ.

Если нагрузка несимметричная и нейтральный провод имеет конечное сопротивление ZN 0, то токи в фазах приемника и нулевом проводе будут определяться выражениями:

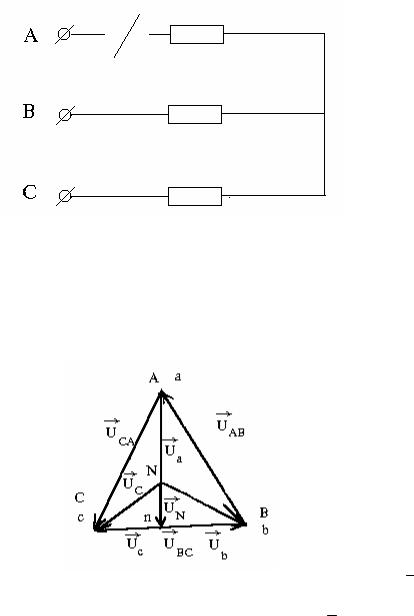
IA = Ua/Za = (UA — UN)Ya

IB = Ub/Zb = (UB — UN)Yb

IC = Uc/Zc = (UC — UN)Yc

IN = UN/ZN = UNYN = IA + IB + IC.

Рассмотрим аврийные ситуации в трехпроводной системе.

1.Обрыв одной из фаз нагрузки. В исходном состоянии нагрузка симметричная (для простоты считаем ее активной), система фазных токов симметрична, нейтрали совпадают и система фазных напряжений приемника также симметрична. Рассмотрим случай обрыва линейного провода А.

В этом случае Ya = 0, Yb = Yc = Y0 , смещение нейтрали определяется:

UN = Y0( UB + UC)/2Y0 = — UA/2

поскольку UA + UB + UC = 0.

Этому случаю соответствует такая векторная диаграмма:

При этом фазное напряжение UA увеличивается в 1,5 раза, а UB и UC уменьшаются в 2/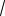3, так как они становятся равными половине линейного напряжения.

Ток в фазе А равен нулю, а токи в фазах В и С уменьшаются в 2/ 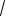3 раза из-за уменьшения напряжений UB и UC. Так как нагрузка активная, то токи будут совпадать по фазе с фазными напряжениями.

2. Короткое замыкание одной из фаз приемника. Например Za = 0 => Ya = .

Напряжение смещения нейтрали:

UN = (UA + UBYb/Ya + UCYc/Ya)/( 1 + Yb/Ya + Yc/Ya) = UA.

Следовательно, нейтральная точка приемника переместится в точку а — напряжение в фазе а будет равно нулю, а фазы нагрузки b и с будут находиться под линейными напряжениями. Этому случаю соответствует такая векторная диаграмма:

Фазные токи Iс и Ib возростают в 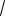3, совпадая по фазе со своими напряжениями. Ток в проводе а находится из уравнения:

Ia = — ( Ib + Iс).

Как видно из векторной диаграммы ток ia в 3 раз больше токов Ib и Ic и в 3 раза больше тока в исходном режиме.

Трехфазные цепи при соединении приемников треугольником.

При соединении приемников электрической энергии треугольником отдельные фазы приемника присоединяются к линейным проводам, идущим от генератора:

При этом каждая фаза приемника непосредственно включается на линейное напряжение, которое в то же время будет и фазным:

Ua = Uab; Ub = Ubc; Uc = Uca;

Для определения связи между линейными и фазными токами воспользуемся I законом Кирхгофа. Применим его к узлам: a, b, c.

За положительное направление фазных токов выбирается направление от начала фазы к ее концу. С учетом того что фазы нагрузки у нас соединены последовательно положительными направлениями будут: a b, b c, c a.

За положительные направления линейных токов принимают направление от генератора к приемнику. Тогда получим

для узла а		Ia + Ica = Iab	Ia = Iab — Ica
для узла b		Ib + Iab = Ibc	Ib = Ibc — Iab
для узла с		Ic + Ibc = Ica	Ic = Ica — Ibc

Этим уравнениям соответствует векторная диаграмма:

Если нагрузка фаз симметричная ( Za = Zb = Zc; a = b = c ), то действующие значения фазных токов равны между собой и токи сдвинуты по фазам на одинаковые углы от соответствующих напряжений. Рассмотрим треугольник, образованный векторами Ia, Iab, -Ica:

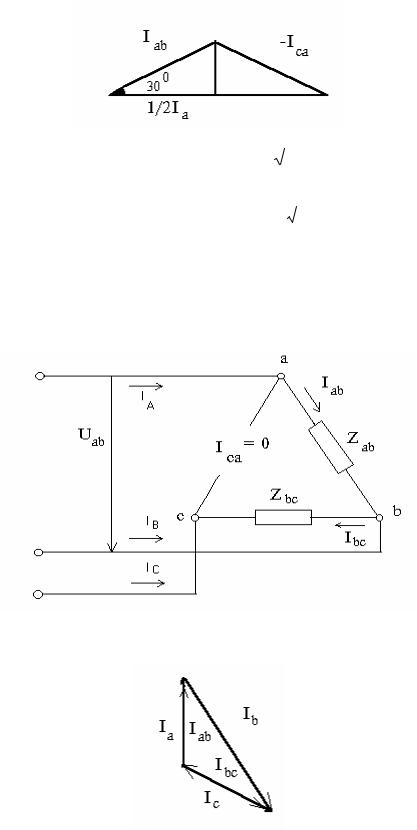
Из этого треугольника следует, что
1/2 Ia = Iab cos 300 Ia =	3	Iab.
При симметричной нагрузке:
Ia = Ib = Ic = IЛ, Iab = Ibc = Iac = IФ
Действующие значения линейных токов больше, чем фазные в			3	.

Из векторной диаграммы видно, линейные токи отстают от фазных на 300. Рассмотрим аврийные ситуации при соединении приемников треугольником.

1.Обрыв одной из фаз нагрузки.

При обрыве фазы са фазный ток Ica = 0. Другие фазные токи не изменяются. Линейный провод оказывается включенным последовательно с фазой ab , поэтому линейный ток Ia = Iab. По этой же причине Ic = -Ibc . Таким образом, Ia и Ic по значению становятся равными фазным токам.

Линейный ток Ib определяется так же как и в исходном режиме Ib = Ibc — Iab , и поэтому остается неизменным. Этому случаю соответствует векторная диаграмма:

2.Обрыв линейного провода.

При обрыве провода а (перегорание предохранителя) трехфазная цепь преобразуется в однофазную цепь:

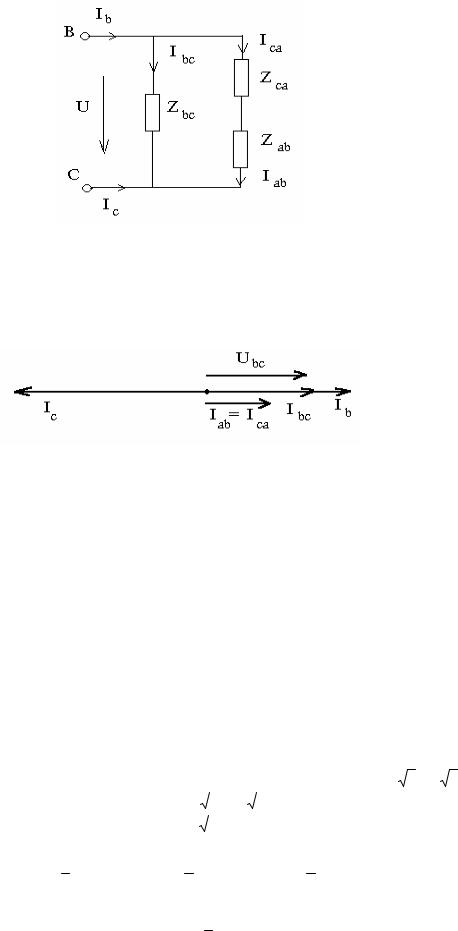
Фазы приемника образуют две параллельные ветви, к которым подводится напряжение Ubc. Ток в ветви Zbc остается неизменным, так как по-прежнему определяется тем же напряжением Ubc. Ток в ветвях Zab и Zca , включенных последовательно, совпадает по фазе с током Ibc , так как тоже определяется напряжением Ubc. По значению он в два раза меньше тока Ibc , так как Zab = Zca = Zbc.

Линейный ток Ib = Ibc + Iab совпадает по фазе с током Ibc , а по значению в 1,5 раза больше тока Ibc. Ток Ic равен по значению Ib , а по фазе ему противоположен. Векторная диаграмма токов такой однофазной цепи изображена на рисунке:

МОЩНОСТЬ ТРЕХФАЗНЫХ ЦЕПЕЙ.

Активная мощность трехфазного тока равна сумме мощностей всех трех фаз, а именно

P = Pa + Pb + Pc = UaIa cos a + UbIb cos b + UcIc cos c

При симметричной нагрузке

P = 3Pф = 3UфIф cos .

Реактивная мощность трехфазной цепи

Q = Qa + Qb + Qc = UaIa sin a + UbIb sin b + UcIc sin c

При симметричной нагрузке

Q = 3Qф = 3UфIф sin .

Полная мощность

S = ( P2 + Q2)1/2.

Полная мощность при симметричной нагрузке

S = 3UфIф.

Обычно в качестве паспортных данных для трехфазных приемников приняты линейные напряжения и токи. Поэтому мощности трехфазных приемников целесообразно выражать через линейные напряжения и токи. При таких обозначениях индекс “л” у линейного напряжения и тока не указывают.

Так как при соединении симметричной нагрузки треугольником Uф=Uл=U и Iф=Iл/						3=I/	3, а при
соединении симметричной нагрузки звездой Uф=Uл/	3		=U/	3	и Iф=Iл=I, то независимо от схемы
соединения фаз приемника произведение UфIф=UI/	3	оказывается одинаковым.				Таким	образом,

независимо от схемы соединения симметричной нагрузки имеет место следующие выражения для мощностей

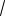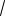P = 3UI cos , Q = 3UI sin , S = 3UI.

Если известны активная мощность, линейные напряжения и ток при симметричной нагрузке, то коэффициент мощности определяется по формуле:

cos = P/(3UI)

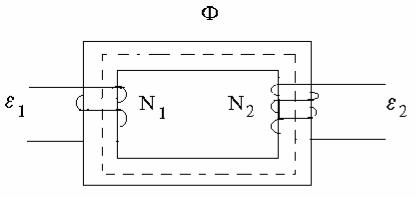
ЛЕКЦИЯ № 6

ТРАНСФОРМАТОРЫ

Электрическая энергия вырабатывается на электростанциях синхронными генераторами с напряжением до 35 кВ. Для непосредственного безопасного использования потребителями это напряжение очень велико (220В, 380В, 660В) а для экономичной передачи на большие расстояния, поскольку обычно приемники электрической энергии расположены на некотором расстоянии от электростанций, очень низкое (1150 кВ). При заданной передаваемой мощности линией электропередачи, чем выше напряжение, тем меньше будет значение тока и тем меньше получается требуемое сечение проводов линии электропередачи. Поэтому в месте производства электрической энергии — на электрических станциях — выгодно повышать напряжение до сотен тысяч Вольт и выше, а затем передавать энергию по проводам потребителям.

Изменение напряжения до необходимых значений осуществляется с помощью трансформаторов.

Трансформатором называется статическое электротехническое устройство, служащее для преобразования переменного тока одного напряжения в переменный ток другого напряжения той же частоты.

Электрическая энергия при передаче от электростанции до потребителей преобразуется с помощью тансформаторов около 5 — 7 раз.

В цепях переменного тока использование трансформаторов позволяет изменять напряжения, ток и число фаз.

Трансформаторы относятся к высоконадежным электротехническим устройствам, поскольку они не имеют движущихся частей и скользящих контактных соединений.

По назначению трансформаторы делятся на силовые и специального назначения. Силовые трансформаторы служат для передачи и распределения электрической энергии, а также для питания различных электротехнических устройств. К трансформаторам специального назначения относятся измерительные, сварочные трансформаторы, для прогрева бетона, для перносных светильников, питания электроинструментов и другие.

По числу фаз трансформаторы делятся на однофазные и трехфазные.

УСТРОЙСТВО ТРАНСФОРМАТОРОВ.

Трансформатор состоит из стального магнитопровода, на который намотаны обмотки :

Обмотка, подключаемая к источнику электрической энергии, называется первичной обмоткой, а обмотка к которой подключается нагрузка называется вторичной.

Если через трансформатор необходимо осуществить питание двух и более нагрузок с разным напряжением, то выполняется соответствующее число вторичных обмоток. Такие трансформаторы называются многообмоточными.

Существуют тансформаторы состоящие из одной обмотки. Такие трансформаторы называются автотрансформаторами. В случае повышающего авторансформатора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается с части обмотки. В понижающем автотрансформаторе

напряжение сети подается на всю обмотку, а вторичная э.д.с. снимается с части обмотки. Автотрансформаторы позволяют регулировать напряжение в широких пределах.

Магнитопровод трансформаторов изготавливают из стальных листов толщиной 0,35 — 0,5 мм. Стальные пластины сердечника трансформатора изолируют друг от друга бумажной, лаковой изоляцией или окалиной, что позволяет уменьшить потери мощности в магнитопроводе за счет того, что вихревые токи замыкаются в плоскости поперечного сечения отдельной пластины. Чем меньше толщина листа, тем меньше сечение проводника, по которому протекает вихревой ток, и тем болше его сопротивление. В результате вихревой ток и потери мощности на нагрев магнитпровода уменьшаются. Обмотки трансформаторов обычно выполняют из медного провода круглого или прямоугольного сечения. Для лучшей магнитной связи между обмотками их стремятся расположить как можно ближе друг к другу. Обычно их распологают на одном стержне. Обмотки изолируют как от стержня магнитопровода, так и друг от друга. В качестве изоляции применяют электротехнический картон, специальную бумагу или ткань, пропитанную лаком.

По расположению обмоток относительно друг от друга различают концентрические, изготовленные в виде цилиндров, и чередующиеся, когда обмотки расположены друг за другом. В случае концентрической намотки обмоток первой

наматывается обмотка низшего напряжения, а поверх нее размещается обмотка высшего напряжения. По способу охлаждения трансформаторы делятся на сухие и маслянные. Сухие трансформаторы имеют естественное воздушное охлаждение, которое может быть ипользовано только для трансформаторов малой мощности. При увеличении мощности увеличивается нагрев обмоток. Чтобы обеспечить допустимую для изоляции температуру нагрева, применяют более интенсивные способы отвода тепла. Для этого магнитопровод с обмотками помещают в специальный бак, заполненный трансформаторным маслом. Масло является одновременно и охлаждающей и изолирующей средой. Интенсивность охлаждения обеспечивается как за счет большей по сравнению с воздухом теплопроводности масла, так и за счет того, что поверхность бака по сравнению с поверхностью тансформатора значительно больше. Этот способ охлаждения называется естественным маслянным охлаждением. В трансформаторах большой мощности применяют систему принудительного масляного охлаждения при котором масло специальными насосами прокачивается через специальные теплообменники, которые в свою очередь охлаждаются водой или воздухом.

ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРОВ.

Принцип действия трансформаторов основан на явлении взаимной индукции.

При подсоединении первичной обмотки трансформатора к источнику переменного напряжения с э.д.с.1 в ней возникает переменный ток, создающий в магнитном сердечнике переменный магнитный поток, который практически полностью локализован в железном сердечнике и, следовательно почти целиком пронизывает витки вторичной обмотки. Применение магнитопровода с большой магнитной проводимостью способствует увеличению магнитного потока и усилению электромагнитной связи между обмотками. Замыкаясь магнитный поток оказывается сцепленным как с первичной, так и вторичной обмотками.

Изменение этого магнитного потока вызывает во вторичной обмотке появление э.д.с. взаимной индукции, а в первичной э.д.с. самоиндукции.

Ток в первичной обмотке определяется по второму закону Кирхгофа :

е1 + еi1 = i1R1 ==> е1 — d(N1 Ф) / dt = i1R1,

где R1 — активное сопротивление первичной обмотки. Из-за малости R1 падение напряжения I1R1 мало по сравнению с каждой из двух э.д.с. Поэтому

e1 N1 dФ/dt.

Во вторичной обмотке возникает э.д.с. взаимной индукции :

e2 = -N2 dФ/dt.

Сравнивая две последние формулы мы можем найти э.д.с., возникающую во вторичной обмотке :

e2 = -N2 e1/ N1,

где знак «минус», что э.д.с. в первичной и вторичной обмотках отличаются по фазе на 1800. Отношение вторичной э.д.с. к первичной называется коэффициентом трансформации трансформатора

:

k = e2/e1 = N2/N1

При незначительном активном сопротивлении источника. э.д.с. примерно равна напряжению в цепи. Э.д.с. вторичной обмотки при разомкнутой вторичной обмотке (то есть при отсутствии в ней тока и падения напряжения) равна напряжению на концах обмотки. Тогда

k = e2/e1 =u2 /u1 = N2/N1

Коэффициент трансформации может быть определен на основании измерений напряжения на входе и выходе ненагруженного трансформатора.

Коэффициент трансформации может быть как больше, так и меньше единицы.

Если необходимо повысить напряжение источника питания, то число витков вторичной обмотки делают больше числа витков первичной обмотки. Такой трансформатор называется повышающим. Если напряжение надо понизить, то необходимо, чтобы число витков в первичной обмотке было больше, чем во вторичной обмотке. В этом случае трансформатор будет понижающим.

Учитывая высокий к.п.д. трансформаторов, можно считать, что мощность потребляемая из сети примерно равна мощности отдаваемой нагрузке :

S1 S2 ===> i1 u1 i2 u2 .

Отсюда следует:

i1/i2 = u2 /u1.

Мы видим, что во сколько раз увеличивается напряжение во столько же раз уменьшается ток.

По обмотке высшего напряжения проходит меньший ток, поэтому ее делают из провода соответственно меньшего сечения, но она имеет меньшее большее число витков. Обмотка низшего напряжения — с большим током — имеет большее сечение провода, но меньшее число витков. По сечению провода легко отличить обмотку высшего напряжения от обмотки низшего напряжения трансформатора.

Если ко вторичной обмотке трансформатора подключены потребители, через которые замыкается цепь этой обмотки, то по ней проходит ток i2 , направленный (по закону Ленца) противоположно току в первичной обмотке i1 .

Эти токи создают в сердечнике трансформатора два противоположно направленных магнитных потока Ф1 и Ф2, которые вместе образуют общий магнитный поток

Ф = Ф1 — Ф2

Этот общий поток и индуктирует э.д.с. в обмотках трансформатора. Поскольку Е1 = U1, а напряжение U1, которое подводится от источника, обычно не изменяется, то и Е1 почти всегда неизменна. Э.д.с. Е1 индуктируется магнитным потоком Ф, который также вследствие этого должен быть постоянной величиной.

Таким образом, величина общего потока в сердечнике трансформатора всегда постоянна.

При холостом ходе трансформатора, когда i2 = 0, магнитный поток Ф2 также равен нулю. Общий поток Ф трансформатора равен потоку Ф1.

Если же цепь вторичной обмотки замкнуть на потребитель, то возникший ток i2 вторичной обмотки создаст, поток Ф2, противоположный потоку Ф1. Поток Ф2 будет размагничивать сердечник трансформатора.

Так как общий поток Ф = Ф1 — Ф2 не изменяется, то размагничивающее действие потока Ф1 должно быть уравновешено увеличенным намагничивающим потоком Ф1. Таким образом, всякое увеличение тока i2 и его потока Ф2 способствует увеличению потока Ф1, до такой величины, чтобы разность этих потоков Ф1 — Ф2 была равна общему неизменному потоку трансформатора Ф.

Поскольку увеличение потока Ф1 возможно только вследствие увеличения тока i1, который создает этот поток, то всякое увеличение или уменьшение нагрузки (тока i2) во вторичной обмотке трансформатора вызывает соответствующее увеличение или уменьшение тока i1, в первичной обмотке трансформатора. Иногда это явление называют «саморегулированием» трансформатора. Оно основано на законе сохранения и преобразования энергии.

РЕЖИМЫ РАБОТЫ ТРАНСФОРМАТОРОВ

1.Номинальный режим, режим при номинальных значениях тока и напряжения первичной обмотки трансформатора.

2.Рабочий режим (основной режим), при котором напряжение первичной обмотки близко к номинальному значению или равно ему, а ток определяется нагрузкой трансформатора.

3.Режим холостого хода — это режим ненагруженного трансформатора при котором цепь вторичной обмотки разомкнута или подключена к приемнику с очень большим сопротивлением, например, к вольтметру.

4.Режим короткого замыкания трансформатора, режим при котором его вторичная обмотка закорочена или подключена к приемнику с очень маленьким сопротивлением нагрузки, например к амперметру. Короткое замыкание трансформатора в условиях эксплуатации создает аварийный режим,

так как токи в первичной и вторичной обмотках возростают в несколько десятков раз по сравнению с номинальным. Поэтому в цепях с трансформаторами предусматривается защита, которая при коротком замыкании автоматически отключает трансформатор.

Режимы короткого замыкания и холостого хода возникают при аварийных ситуациях или специально создаются при испытании трансформаторов.

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ

При работе трансформаторов возникают потери в ферромагнитном сердечнике при перемагничивании (потери в стали Рст) и электрические потери в обмотках (потери в меди Рэл). Поэтому активная мощность потребляемая трансформатором из сети отличается от активной мощности отдаваемой трансформатором нагрузке.

Отношение активной мощности отдаваемой трансформатором приемнику к активной мощности подведенной к трансформатору из сети называется его коэффициентом полезного действия.

= Р2 / Р1 = Р2 / (Р2 + Рст + Рэл).

К.П.Д. трансформаторов зависит так же от загруженности трансформатора и от характера нагрузки, то есть коэфициента мощности приемника.

Загрузка трансформатора в рабочем режиме оценивается коэффициентом

= Р2 /Sн cos = I2 / I2н

где Р2 — полезная мощность трансформатора; Sн — номинальная полная мощность; cos — коэффициент мощности нагрузки; I2 — ток во вторичной обмотке; I2н — номинальный ток вторичной обмотки.

Активная мощность отдаваемая трансформатором приемнику при любом характере нагрузки и произвольной загруженности определяется выражением:

P2 = I2U2cos 2 = I2U2cos 2 = Sн cos 2

Потери в стали не зависят от нагрузки и загруженности трансформатора и равны потерям холостого хода. Потери в меди пропорциональны квадрату тока и определяются мощностью потребляемой трансформатором при опыте короткого замыкания. ( Рк ). При произвольной нагрузке трансформатора потери в меди расчитываются с учетом загруженности трансформатора:

Pэл = 2 Рк .

Поэтому в общем случае для произвольной нагрузки К.П.Д. трансформатора определяется:

= Sн cos 2 / ( Sн cos 2 + Рст + 2 Рк).

Потери в стали не зависят от нагрузки. Потери в меди увеличиваются одновременно с увеличением тока нагрузки. При небольших нагрузках преобладают индуктивные потери в стали, cos трансформатора небольшой и работа его неэкономична. Следовательно, нужно стремиться к наиболее полной нагрузке трансформатора, так как при этом потери в меди хотя и увеличиваются, но по отношению ко всей мощности они будут составлять меньшую их часть. Поэтому при увеличении нагрузки к.п.д. трансформатора увеличивается.

К.П.Д. у мощных трансформаторов достигает 95 — 99 %, а у трансформаторов малой и средней мощности 70 — 90 %.