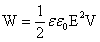Соединение конденсаторов Параллельное соединение конденсаторов
П
 ри
параллельном соединении конденсаторов
к каждому конденсатору приложено
одинаковое напряжениеU, а
величина заряда на обкладках каждого
конденсатора Q пропорциональна
его емкости (рис. 2).
ри
параллельном соединении конденсаторов
к каждому конденсатору приложено
одинаковое напряжениеU, а
величина заряда на обкладках каждого
конденсатора Q пропорциональна
его емкости (рис. 2).
Рис.2 U=U1=U2=U3
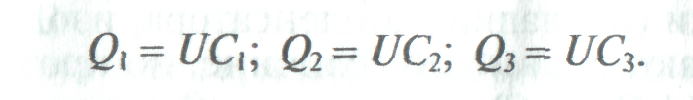
Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.
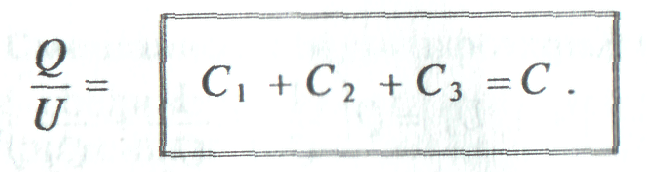
Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.
4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением
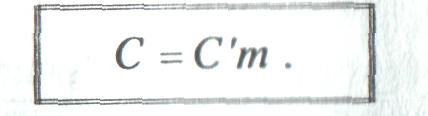
Последовательное соединение конденсаторов

Рис.3
На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.
Q=Q1=Q2=Q3
Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

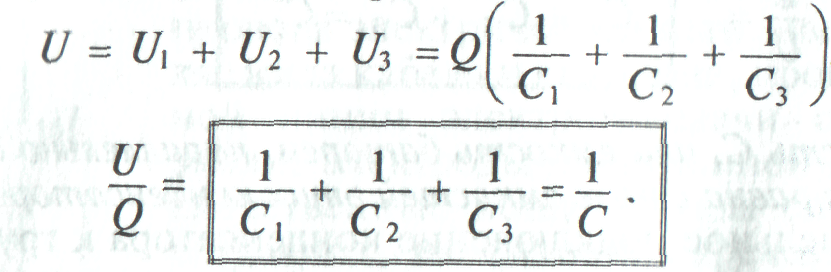
Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:
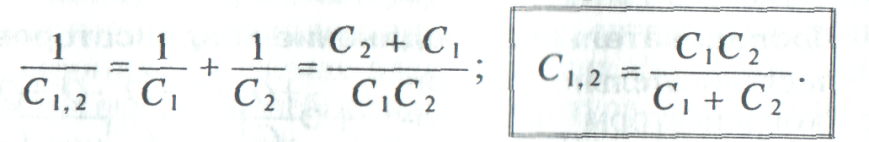
Если в цепь включены последовательно п одинаковых конденсаторов емкостью

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.
На практике может оказаться , что допустимое рабочее напряжение Up конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего
Смешанное соединение конденсаторов
Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.
Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.
Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым приложено напряжение U; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U.
Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.
15.Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)
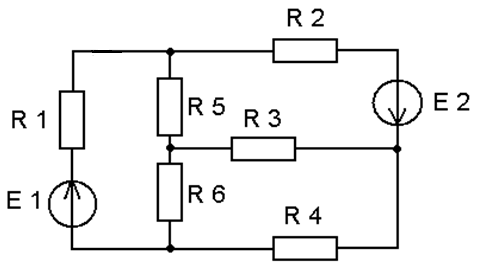
Рисунок 5- Схема электрическая
6.СХЕМЫ ЗАМЕЩЕНИЯ
Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.
На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.
1.Схемы замещения элементов электрических цепей
На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

напряжение на зажимах источника при любом токе равно
ЭДС: U=E=const.
В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияIK, а вместо внутреннего сопротивления в расчет вводится внутренняя проводимость
Возможность такой замены можно доказать, разделив равенство (3.1) на r:
U/r = E/r—I,
где U/r = Io—некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E/r = IK — ток короткого замыкания источника;
Вводя новые обозначения, получим равенство IK = Io + I, которому удовлетворяет эквивалентная схема рис. 3.14,
В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):
I=Iк=const.
Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.
Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику ЭДС/тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на Q, получим знакомую формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов


Пример 1
Какова результирующая емкость 4 конденсаторов включенных последовательно и параллельно, если известно что С1 = 10 мкФ, C2 = 2 мкФ, C3 = 5 мкФ, а C4 = 1 мкФ?
При последовательном соединении общая емкость равна:

При параллельном соединении общая емкость равна:

Пример 2
Определить результирующую емкость группы конденсаторов подключенных последовательно-параллельно, если известно, что С1 = 7 мкФ, С2 = 2 мкФ, С3 = 1 мкФ.

Сначала найдем общую емкость параллельного участка цепи:

Затем найдем общую емкость для всей цепи:

По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Советуем прочесть — Заряд и разряд конденсатора
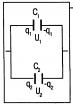
Соединения конденсаторов . | |
Параллельное соединение конденсаторов |
|
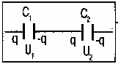
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора |
|
|
|
Вывод: При параллельном соединении конденсаторов
Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов |
|
Последовательное соединение конденсаторов |
|
Производят только одно соединение, а две оставшиеся обкладки — одна от конденсатора С1 другая от конденсатора С2 — играют роль обкладок нового конденсатора. |
|
|
|
Вывод: При последовательном соединении конденсаторов
Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов. |
|
Энергия электрического поля конденсатора. Под энергией электрического поля конденсатора будем понимать энергию одной его обкладки, находящейся в поле, созданном другой обкладкой. Тогда: Формулы справедливы для любого конденсатора. | Пример: С=2мкФ; U=1000В. t=10-6c.W=1 Дж |
|
|
Плотность энергии. Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических). |
|
Параллельное соединение конденсаторов напряжение. Соединение конденсаторов Как правильно соединять конденсаторы
В электрических цепях применяются различные способы соединения конденсаторов . Соединение конденсаторов может производиться: последовательно , параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельное (смешанное) соединение конденсаторов
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.
У начинающих электронщиков при сборке любого самодельного устройства могут возникнуть проблемы с соединением конденсатора. Ведь даже у заядлого любителя электроники может не оказаться под рукой конденсатора с нужным номиналом, особенно когда нужно срочно отремонтировать бытовой прибор. Из сложившейся проблемы легко выйти, соединив последовательно или параллельно несколько конденсаторов.
Приготовьте:
- конденсаторы;
- вольтметр;
- провода;
- кусачки.
Параллельное и последовательное соединение конденсаторов: способы, правила, формулы
Любая электроника в доме может выйти из строя. Однако сразу бежать в сервис не стоит – простейшие приборы может продиагностировать и починить даже начинающий радиолюбитель. К примеру, сгоревший конденсатор виден невооружённым глазом. Но как быть, если под рукой нет детали подходящего номинала? Конечно, соединить 2 и более в цепь. Сегодня поговорим о таких понятиях, как параллельное и последовательное соединение конденсаторов, разберемся, как его выполнить, узнаем о способах соединения, правилах его выполнения.
 Не всегда удаётся подобрать конденсатор нужного номинала
Не всегда удаётся подобрать конденсатор нужного номиналаЧитайте в статье:
Нет конденсатора нужного номинала: что делать
Очень часто начинающие домашние мастера, обнаружив поломку прибора, стараются самостоятельно обнаружить причину. Увидев сгоревшую деталь, они стараются найти подобную, а если это не удаётся, несут прибор в ремонт. На самом деле, не обязательно, чтобы показатели совпадали. Можно использовать конденсаторы меньшего номинала, соединив их в цепь. Главное – сделать это правильно. При этом достигается сразу 3 цели – поломка устранена, приобретён опыт, сэкономлены средства семейного бюджета.
Попробуем разобраться, какие способы соединения существуют и на какие задачи рассчитаны последовательное и параллельное соединение конденсаторов.
 Часто без соединения конденсаторов в батарею не обойтись. Главное – сделать это правильно
Часто без соединения конденсаторов в батарею не обойтись. Главное – сделать это правильноСоединение конденсаторов в батарею: способы выполнения
Существует 3 способа соединения, каждый из которых преследует свою определённую цель:
- Параллельное – выполняется в случае необходимости увеличить ёмкость, оставив напряжение на прежнем уровне.
- Последовательное – обратный эффект. Напряжение увеличивается, ёмкость уменьшается.
- Смешанное – увеличивается как ёмкость, так и напряжение.
Теперь рассмотрим каждый из способов более подробно.
Параллельное соединение: схемы, правила
На самом деле всё довольно просто. При параллельном соединении расчёт общей ёмкости можно вычислить путём простейшего сложения всех конденсаторов. Итоговая формула будет выглядеть следующим образом: Собщ= С₁ + С₂ + С₃ + … + Сn. При этом напряжение на каждом их элементов будет оставаться неизменным: Vобщ= V₁ = V₂ = V₃ = … = Vn.
Соединение при таком подключении будет иметь следующий вид:

Получается, что подобный монтаж подразумевает подключение всех пластин конденсаторов к точкам питания. Такой способ встречается наиболее часто. Но может произойти ситуация, когда важно увеличить напряжение. Разберёмся, каким образом это сделать.
Последовательное соединение: способ, используемый реже
При использовании способа последовательного подключения конденсаторов напряжение в цепи возрастает. Оно складывается из напряжения всех элементов и выглядит так: Vобщ= V₁ + V₂ + V₃ +…+ Vn. При этом ёмкость изменяется в обратной пропорции: 1/Собщ= 1/С₁ + 1/С₂ + 1/С₃ + … + 1/Сn. Рассмотрим изменения ёмкости и напряжения при последовательном включении на примере.
Дано: 3 конденсатора с напряжением 150 В и ёмкостью 300 мкф. Подключив их последовательно, получим:
- напряжение: 150 + 150 + 150 = 450 В;
- ёмкость: 1/300 + 1/300 + 1/300 = 1/С = 299 мкф.
Внешне подобное подключение обкладок (пластин) будет выглядеть так:

Выполняют такое соединение в том случае, если есть опасность пробоя диэлектрика конденсатора при подаче напряжения в цепь. Но ведь существует и ещё один способ монтажа.
Полезно знать! Применяют также последовательное и параллельное соединение резисторов и конденсаторов. Это делается с целью снижения подаваемого на конденсатор напряжения и исключения его пробоя. Однако следует учитывать, что напряжения должно быть достаточно для работы самого прибора.
Смешанное соединение конденсаторов: схема, причины необходимости применения
Такое подключение (его ещё называют последовательно-параллельным) применяют в случае необходимости увеличения, как ёмкости, так и напряжения. Здесь вычисление общих параметров немного сложнее, но не настолько, чтобы нельзя было разобраться начинающему радиолюбителю. Для начала посмотрим, как выглядит такая схема.

Составим алгоритм вычислений.
- всю схему нужно разбить на отдельные части, высчитать параметры которых просто;
- высчитываем номиналы;
- вычисляем общие показатели, как при последовательном включении.
Выглядит подобный алгоритм следующим образом:

Преимущество смешанного включения конденсаторов в цепь по сравнению с последовательным или параллельным
Смешанное соединение конденсаторов решает задачи, которые не под силу параллельным и последовательным схемам. Его можно использовать при подключении электродвигателей либо иного оборудования, его монтаж возможен отдельными участками. Монтаж его намного проще за счёт возможности выполнения отдельными частями.
Интересно знать! Многие радиолюбители считают этот способ более простым и приемлемым, чем два предыдущих. На самом деле, так и есть, если полностью понять алгоритм действий и научиться пользоваться им правильно.
Смешанное, параллельное и последовательное соединение конденсаторов: на что обратить внимание при его выполнении
Соединяя конденсаторы, в особенности электролитические, обратите внимание на строгое соблюдение полярности. Параллельное присоединение подразумевает подключение «минус/минус», а последовательное – «плюс/минус». Все элементы должны быть однотипны –плёночные, керамические, слюдяные либо металлобумажные.
 А вот что умеют делать всем известные китайские «изобретатели» – такой конденсатор явно долго не протянет
А вот что умеют делать всем известные китайские «изобретатели» – такой конденсатор явно долго не протянетПолезно знать! Выход из строя конденсаторов часто происходит по вине производителя, экономящего на деталях (чаще это приборы китайского производства). Поэтому правильно рассчитанные и собранные в схему элементы будут работать намного дольше. Конечно, при условии отсутствия замыкания в цепи, при котором работа конденсаторов невозможна в принципе.
Калькулятор расчёта ёмкости при последовательном соединении конденсаторов
А что делать, если необходимая ёмкость неизвестна? Не каждому хочется самостоятельно рассчитывать необходимую ёмкость конденсаторов вручную, а у кого-то на это просто нет времени. Для удобства производства подобных действий редакция Seti.guru предлагает нашему уважаемому читателю воспользоваться онлайн-калькулятором расчёта конденсаторов при последовательном соединении или вычисления ёмкости. В работе он необычайно прост. Пользователю необходимо лишь ввести в поля необходимые данные, после чего нажать кнопку «Рассчитать». Программы, в которые заложены все алгоритмы и формулы последовательного соединения конденсаторов, а также вычислений необходимой ёмкости, моментально выдаст необходимый результат.
Как рассчитать энергию заряженного конденсатора: выводим окончательную формулу
Первое, что для этого необходимо сделать – рассчитать, с какой силой притягиваются обкладки друг к другу. Это можно сделать по формуле F = q₀ × E, где q₀ является показателем величины заряда, а E – напряжённостью обкладок. Далее нам необходим показатель напряжённости обкладок, который можно вычислить по формуле E = q / (2ε₀S), где q – заряд, ε₀ – постоянная величина, S – площадь обкладок. В этом случае получим общую формулу для расчёта силы притяжения двух обкладок: F = q₂ / (2ε₀S).
Итогом наших умозаключений станет вывод выражения энергии заряженного конденсатора, как W = A = Fd. Однако это не окончательная формула, которая нам необходима. Следуем далее: учитывая предыдущую информацию, мы имеем: W = dq₂ / (2ε₀S). При ёмкости конденсатора, выражаемой как C = d / (ε₀S) получаем результат W = q₂ / (2С). Применив формулу q = СU, получим итог: W = CU² /2.
 Редакция Seti.guru советует сохранить эту памятку
Редакция Seti.guru советует сохранить эту памяткуКонечно, для начинающего радиолюбителя все эти расчёты могут показаться сложными и непонятными, но при желании и некоторой усидчивости с ними можно разобраться. Вникнув в смысл, он поразится, насколько просто производятся все эти расчёты.
Для чего нужно знать показатель энергии конденсатора
По сути, расчёт энергии применяется редко, однако есть области, в которых это знать необходимо. К примеру, фотовспышка камеры – здесь вычисление показателя энергии очень важно. Она накапливается за определённое время (несколько секунд), а вот выдаётся мгновенно. Получается, что конденсатор сравним с аккумулятором – разница лишь в ёмкости.
 Ни одна фотовспышка не сможет работать без накопителя энергии, такого, как конденсатор
Ни одна фотовспышка не сможет работать без накопителя энергии, такого, как конденсаторПодводя итог
Порой без соединения конденсаторов не обойтись, ведь не всегда можно подобрать подходящие по номиналам. Поэтому знание того как это сделать может выручить при поломке бытовой техники или электроники, что позволит значительно сэкономить на оплате труда специалиста по ремонту. Как наверняка уже понял Уважаемый читатель, сделать это несложно и под силу даже начинающим домашним мастерам. А значит стоит потратить немного своего драгоценного времени и разобраться в алгоритме действий и правилах их выполнения.
 Правильность соединения конденсаторов гарантирует их долгую бесперебойную работу
Правильность соединения конденсаторов гарантирует их долгую бесперебойную работуНадеемся, что информация, изложенная в сегодняшней статье, была полезна нашим читателям. Возможно, у Вас остались какие-либо вопросы? В этом случае их можно изложить в обсуждении ниже. Редакция Seti.guru с удовольствием на них ответит в максимально короткие сроки. Если же Вы имеете опыт самостоятельного соединения конденсаторов (неважно, положительный он или отрицательный), убедительная просьба поделиться им с другими читателями. Это поможет начинающим мастерам более полно понять алгоритм действий и избежать ошибок. Пишите, делитесь, спрашивайте. А напоследок мы предлагаем посмотреть короткий, но довольно информативный видеоролик по сегодняшней теме.
Как решать задачи со смешанным соединением конденсаторов — MOREREMONTA

Преподаватель междисциплинарного курса
Практическое занятие №4
Тема: Расчет общей емкости конденсатора
Цель: рассчитать напряжение, заряд, емкость конденсаторов и их энергию в электрических цепях постоянного тока с последовательным, параллельным и смешанным соединением конденсаторов.
1. Изучить краткие теоретические сведения.
2. Рассмотреть примеры выполнения задания.
3. Выполнить индивидуальное задание.
1. Краткие теоретические сведения
 Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
где С емкость конденсатора, Ф
Q – заряд конденсатора, Кл
U – напряжение на конденсаторе, В
Энергия конденсатора зависит от его емкости. Поэтому при изменении емкости заряженного конденсатора будем изменяться его энергия:

где W – энергия конденсатора, Дж
В электрических цепях применяются различные способы соединения конденсаторов.
Соединение конденсаторов может производиться: последовательно, параллельно и смешанно (то есть последовательно-параллельно). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока.
U = UC1 = UC2 = UC3 = …
Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы:
Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
Собщ = С1 + С2 + С3 + …
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Рисунок 3. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д. Всю группу конденсаторов, соединенных последовательно, можно рассмотреть как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Напряжения на различных конденсаторах будут различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
U = UC1 + UC2 + UC3 + …
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:

Для частного случая двух последовательно соединенных конденсаторов рисунок 4

Рисунок 4. Последовательное соединение двух конденсаторов
Формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 5 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 5. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов.
Всякое смешанное соединение конденсаторов путем упрощений может быть сведено либо к параллельному соединению, либо к последовательному.
Алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 6.


Рисунок 6. Алгоритм сворачивания схемы при смешанном соединении конденсаторов
2. Пример выполнения задания
 |
 Дано: Решение:
Дано: Решение:
 U = 36 В 1. Конденсаторы С1 и С2 соединены параллельно:
U = 36 В 1. Конденсаторы С1 и С2 соединены параллельно:
Собщ, q1, q2, q3, С1,2 = С1 + С2 = 8×10-6 + 4×10-6 = 12×10-6 Ф = 12 мкФ
q4, q, W1, W2, 2. Конденсаторы С3 и С4 соединены последовательно:
W3, W4, W — ? 
3. Общая емкость:
Собщ = 
4. Определим заряд цепи:
q = Собщ×U = 2×10-6×36 = 72×10-6 Кл = 72 мкКл
При последовательном соединении конденсаторов:
q = q1,2 = q3 = q4 = 72 мкКл
Тогда, напряжение на участках цепи
U1,2 = 
U3 = 
U4 = 
U1,2 = U1 = U2 = 6 В, тогда
q1 = C1×U1 = 8×10-6×6 = 48×10-6 Кл = 48 мкКл
q2 = C2×U2 = 4×10-6×6 = 24×10-6 Кл = 24 мкКл
5. Энергия всей цепи:
W =  = 1,29 мДж
= 1,29 мДж
Энергия электрического поля каждого конденсатора:
W1 = 
W2 = 
W3 = 
W4 = 
Ответ: Собщ =  , q1 = 48 мкКл, q2 = 24 мкКл, q = q3 = q4 = 72 мкКл,
, q1 = 48 мкКл, q2 = 24 мкКл, q = q3 = q4 = 72 мкКл,
W1  , W2
, W2  , W3
, W3  , W4
, W4  ,
,

Эквивалентная емкость верхней ветви

Эквивалентная емкость нижней цепи

Теперь это смешанное соединение конденсаторов может быть приведено к параллельному соединению. Эквивалентная емкость всей батареи конденсаторов


Эквивалентная емкость между точками 1 и 2:
Эквивалентная емкость между точками 2 и 3
Теперь это смешанное соединение конденсаторов может быть приведено к последовательному соединению

Эквивалентная емкость батареи конденсаторов

Конденсатор емкостью С=2 мкф и номинальным рабочим напряжением Up=600 в вышел из строя.
Составить схему замены его конденсаторами емкостью С=1 мкФ и номинальным рабочим напряжением Up=200 В.
Р е ш е н и е. Конденсаторы с номинальным рабочим напряжением 200 В нельзя включать под напряжение 600 В. Поэтому прежде всего необходимо обеспечить электрическую прочность батареи. Для этого конденсаторы надо соединить последовательно. Число последовательно соединенных конденсаторов должно быть

Емкость такой ветви

Для обеспечения емкости батареи необходимо соединить несколько параллельных ветвей. Число параллельных ветвей

Общая схема замены конденсатора

3. Индивидуальные задания для обучающихся
Задание: Определить эквивалентную емкость цепи, напряжение на каждом конденсаторе, заряд и энергию электрического поля в цепи и для каждого конденсатора.
Варианты задания, номера схемы и исходные данные для расчета приведены в таблице 1.

- Попроси больше объяснений
- Следить
- Отметить нарушение
VeronikaRov 13.09.2016
Ответ
Проверено экспертом
Конденсаторы С₂ и С₃ соединены ПОСЛЕДОВАТЕЛЬНО, поэтому
С₂₃ = 0,45*0,15/(0,45+0,15)=0,1125 мкФ
Конденсаторы С₄ и С₅ тоже соединены последовательно, поэтому
С₄₅ = 0,2*0,6/(0,2+0,6) = 0,15 мкФ
Конденсаторы С₁, С₂₃ и С₄₅ соединены ПАРАЛЛЕЛЬНО, поэтому
С₀ = 0,35+0,1125+0,15 ≈0,61 мкФ = 0,61*10⁻⁶ Ф
Общий заряд
Q = C₀*U = 0,61*10⁻⁶*75 ≈ 0,46 мкКл
Теперь осталось «обратным» ходом вычислить заряды на каждом конденсаторе. Вот и всё!
Лабораторная работа №3
Тема: «Соединение конденсаторов»
Цель: изучить параллельное, последовательное и смешанное соединение конденсаторов.
Оборудование: мультиметр, источник переменного напряжения, конденсаторы.
Теоретический материал
Электроемкость — это скалярная величина, характеризующая способность проводника накапливать электрический заряд
Электроемкость зависит от формы проводника.
Поэтому для каждого вида существует своя формула расчета электроемкости.
Конденсатор — это система, состоящая из двух или более проводников.
Плоский конденсатор — две параллельные металлические пластины (обкладки), между которыми находится диэлектрик.
В быту можно встретить подобные конденсаторы
На схеме конденсатор обозначается следующим образом:
Электроемкость плоского конденсатора
Используя общую формулу нахождения электроемкости, можно получить
Поле между обкладками конденсатора однородно, поэтому напряжение можно определить как
Несколько конденсаторов, соединенных вместе, образуют батарею конденсаторов.
Различают последовательное, параллельное и смешанное соединение конденсаторов
Порядок выполнения
Задание 1. Последовательное соединение конденсаторов
1. Собрать схему:
2. Емкость конденсаторов Сконд и напряжение Uист на источнике переменного тока установить по указанию преподавателя.
3. Измерьте напряжение Uконд с помощью вольтметра на каждом конденсаторе.
4. Вычислите заряд каждого конденсатора qконд
5. Вычислите общую емкость Собщ батареи конденсаторов.
6. Найдите общее напряжение Uобщ и сравните его с напряжением источника Uист переменного напряжения.
7. Заполните таблицу:
| № конд | Сконд, Ф | Uконд, В | qконд, Кл | Собщ, Ф | Uобщ, В | Uист, В |
Задание 2. Параллельное соединение конденсаторов
1. Собрать схему:
2. Емкость конденсаторов Сконд и напряжение Uист на источнике переменного тока установить по указанию преподавателя.
3. Измерьте напряжение Uконд с помощью вольтметра на каждом конденсаторе.
4. Вычислите заряд каждого конденсатора qконд
5. Вычислите общую емкость Собщ батареи конденсаторов.
6. Найдите общий заряд на конденсаторах qобщ
7. Заполните таблицу:
| № конд | Сконд, Ф | Uконд, В | qконд, Кл | Собщ, Ф | qобщ, Кл | Uист, В |
Задание 3. Смешанное соединение конденсаторов
1. Собрать схему:
2. Емкость конденсаторов Сконд установить по указанию преподавателя, напряжение Uист на источнике переменного тока установить самостоятельно.
3. Измерьте напряжение Uконд с помощью вольтметра на каждом конденсаторе.
4. Вычислите заряд каждого конденсатора qконд
5. Вычислите общую емкость Собщ батареи конденсаторов.
6. Найдите общий заряд на конденсаторах qобщ
7. Найдите общее напряжение Uобщ и сравните его с напряжением источника Uист переменного напряжения.
1.4. Способы соединения конденсаторов
Возможны параллельное и последовательное соединения конденсаторов.
П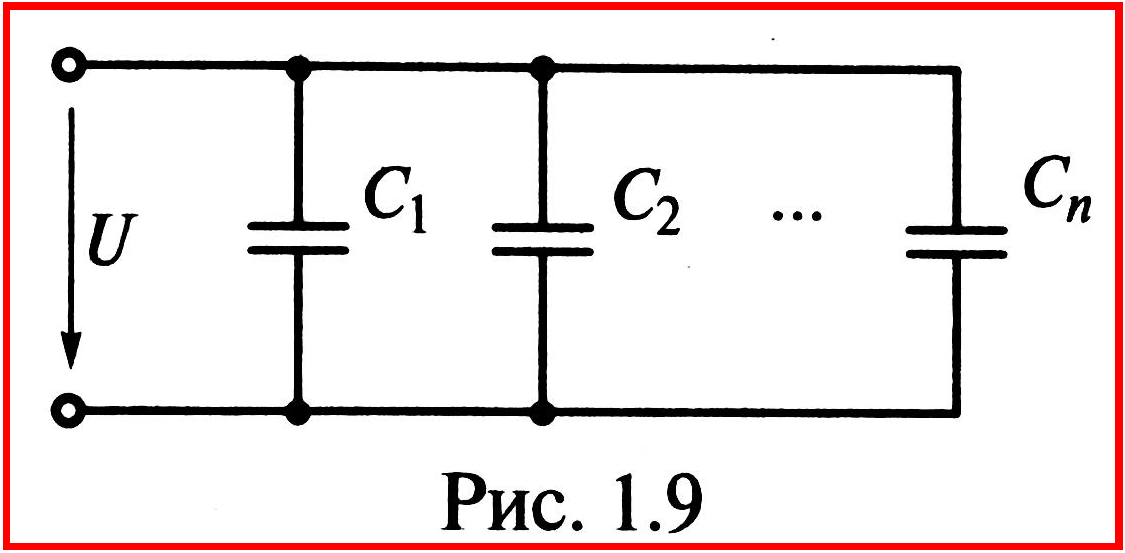 рипараллельном соединении (рис. 1.9) все конденсаторы находятся под
одним напряжением U, а
заряд, который они получают от источника
энергии, равен сумме зарядов отдельных
конденсаторов
рипараллельном соединении (рис. 1.9) все конденсаторы находятся под
одним напряжением U, а
заряд, который они получают от источника
энергии, равен сумме зарядов отдельных
конденсаторов
г деп —
число конденсаторов;
деп —
число конденсаторов;
к — порядковый номер конденсатора.
Следовательно, общая емкость параллельно соединенных конденсаторов по (1.9)равна сумме емкостей отдельных конденсаторов.
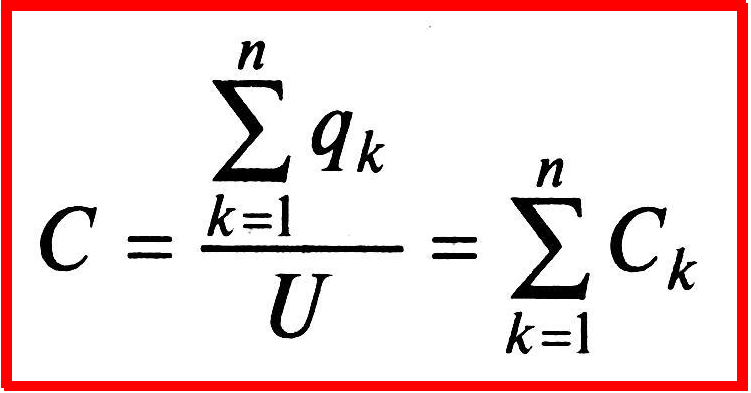
П рипоследовательном соединении
конденсаторов (рис. 1.10) общее напряжение равно сумме
напряжений на отдельных конденсаторах
рипоследовательном соединении
конденсаторов (рис. 1.10) общее напряжение равно сумме
напряжений на отдельных конденсаторах
где п — число конденсаторов;
к — порядковый номер конденсатора.
Н о
заряд от источника энергии получают
лишь внешние электроды двух крайних
конденсаторов. На остальных попарно
электрически
соединенных электродах заряды создаются
переносом положительного заряда на
один электрод и отрицательного — на
второй, которые равны между собой. Таким
образом, при
последовательном соединении конденсаторов их заряды одинаковы.
о
заряд от источника энергии получают
лишь внешние электроды двух крайних
конденсаторов. На остальных попарно
электрически
соединенных электродах заряды создаются
переносом положительного заряда на
один электрод и отрицательного — на
второй, которые равны между собой. Таким
образом, при
последовательном соединении конденсаторов их заряды одинаковы.
Так как заряд конденсатора равен произведению его емкости на приложенное к нему напряжение
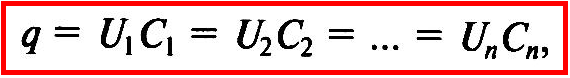
то напряжения на конденсаторах равны

а общая емкость последовательно соединенных конденсаторов — Собщ
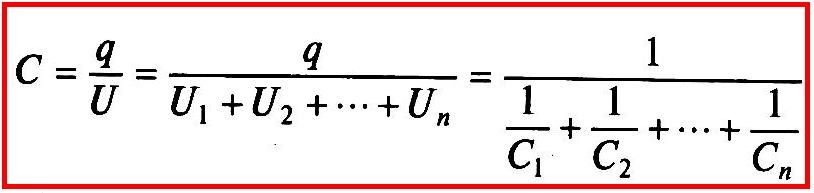
Если последовательно соединены n одинаковых конденсаторов каждый емкостью С0, то их общая емкость будет равна

1.5. Зарядка и разрядка конденсатора
Ч тобы
изменить скачком энергию конденсатора,
необходим источник бесконечной мощности
что невозможно.
тобы
изменить скачком энергию конденсатора,
необходим источник бесконечной мощности
что невозможно.
Поэтому при зарядке и разрядке конденсатора его энергия, а следовательно, и напряжение на нем Uс не могут изменяться скачком. Это условие называется первым законом коммутации и записывается в виде
(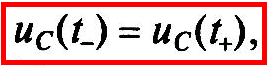 1.16)
1.16)
где 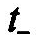 и
и — моменты времени, непосредственно
предшествующий моменту времени
— моменты времени, непосредственно
предшествующий моменту времени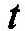 и непосредственно следующий за моментом
времениt, в
который начинается зарядка или разрядка
конденсатора.
и непосредственно следующий за моментом
времениt, в
который начинается зарядка или разрядка
конденсатора.
Зарядка конденсатора.
Рассмотрим процесс зарядки конденсатора от источника постоянного напряжения Е=U (см. подразд. 2.7) через резистор сопротивлением R (см. подразд. 2.4) при замыкании в момент времени t=0 ключа К (рис. 1.11, а).
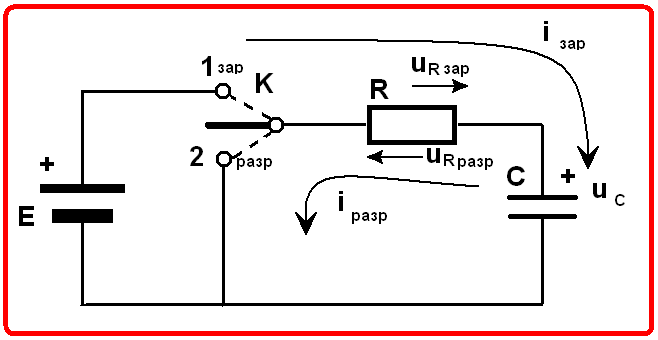
Напряжение источника равно сумме напряжений на резисторе и конденсаторе

или с учетом (2.1) и (1.13)
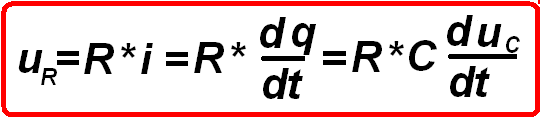
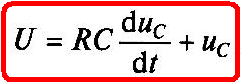 (1.17)
(1.17)
Разделим переменные в (1.17)

(1.18)
и проинтегрируем (1.18)
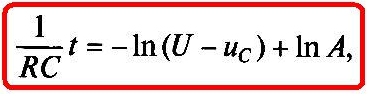 (1.19)
(1.19)
где неизвестная постоянная интегрирования записана в виде In А.
Умножив обе части равенства (1.19) на (-1) и заменив разность логарифмов логарифмом частного, после потенцирования получим

или
 (1.20)
(1.20)

Для определения постоянной А в (1.20) обратимся к закону коммутации для емкостного элемента (1.16). Примем, что емкостный элемент до замыкания ключа, т. е. и в момент времени /= 0_, не был заряжен. Поэтому
ис(0_) = 0 = ис(0+) = Е+А, откуда А = -Е.
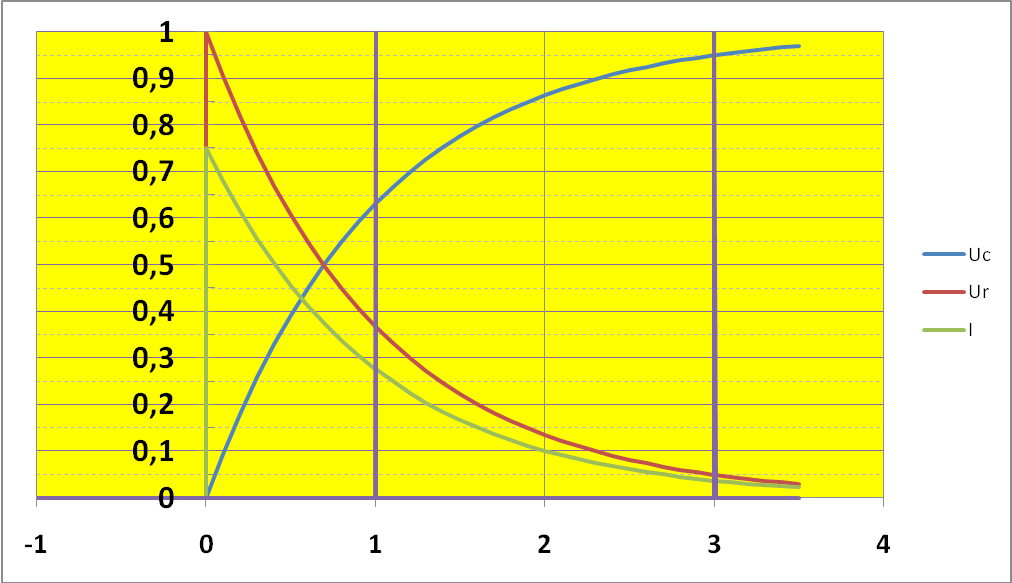
Подставив значение постоянной А в (1.20), найдем напряжение на емкостном элементе во время его зарядки (рис. 1.11, б):
 (1.21)
(1.21)
где τ = RC имеет размерность времени (Ом • Ф = Ом • А • с/В = с) и называется постоянной времени цепи. Она определяет скорость переходного процесса.
Напряжение на емкостном элементе (1.21) определяет зависимости от времени тока зарядки и напряжения на резисторе (рис. 1.11,5):
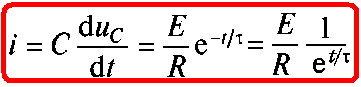
тогда
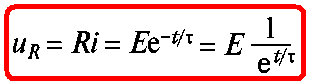
В первый момент после замыкания ключа t=0+ ток заряда в цепи скачком возрастает
от нуля i (0_) = 0
до i (0+) = E/R.
При малом сопротивлении R в цепи может наблюдаться значительный скачок тока.
Процесс зарядки можно считать практически закончившимся через интервал времени Зτ, (при этом uc=0,95 E) который может быть достаточно большим, что используется, например, в реле времени — устройствах, срабатывающих по истечении определенного времени.
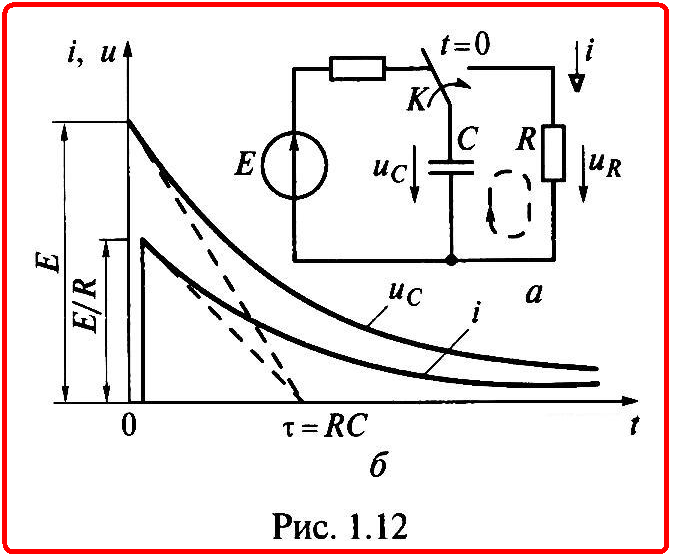
Разрядка конденсатора.
В электрическом поле заряженного емкостного элемента сосредоточена энергия (1.15), за счет которой емкостный элемент в течение некоторого времени сам может служить источником энергии. После подключения емкостного элемента, предварительно заряженного до напряжения ис= Е, к резистивному элементу сопротивлением R (рис. 1.12, а) ток в цепи будет обусловлен изменением заряда q емкостного элемента (1.13):
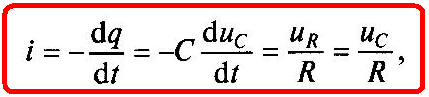 (1.22)
(1.22)
где знак минус указывает на то, что ток i — это ток разрядки в контуре цепи, обозначенном на рисунке штриховой линией, направленный навстречу напряжению на емкостном элементе.
Разделим переменные в (1.22)
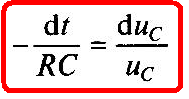
и проинтегрируем (1.23)
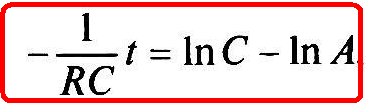 (1.24)
(1.24)
где неизвестная постоянная интегрирования записана в виде (-In А).
После потенцирования (1.24) получим
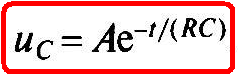 (1.25)
(1.25)
Для определения постоянной А в (1.25) обратимся к закону коммутации для емкостного элемента (1.16). Так как до коммутации, т.е. и в момент времени t=0_, емкостный элемент был заряжен до напряжения источника, то
ис (0_) = Е=ис (0+)=А.
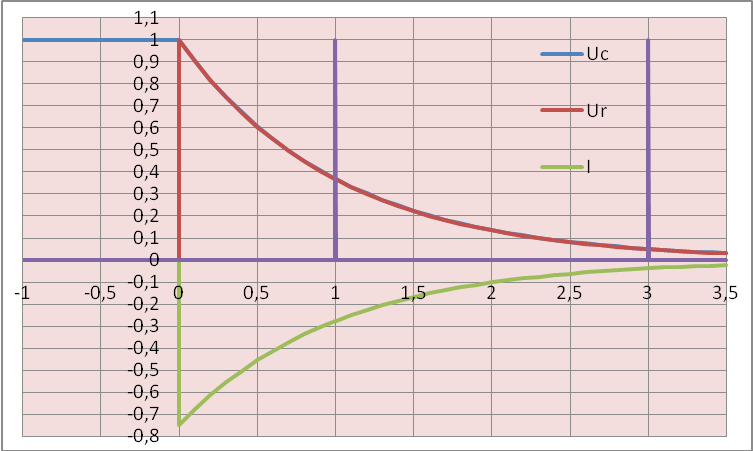
Подставив значение постоянной А в (1.25), получим зависимость изменения напряжения на емкостном элементе при его разрядке (рис. 1.12, б):
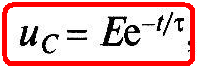 (1.26)
(1.26)
где τ = RC — постоянная времени цепи.
Ток разрядки найдем по (1.22):

Ток разрядки скачком возрастает от нуля
i(0_) = 0 до i(0+) = E/R, а затем убывает экспоненциально (см. рис. 1.12, б).
Зарядка конденсатора при малых значениях тока и больших значениях ЭДС Ев цепи на рис. 1.12, а позволяет накопить в нем большую энергию, которая может использоваться при разрядке большим током в импульсных источниках.
ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1.1. Конденсатор емкостью С = 1 Ф, имеющий заряд q = 1 Кл, в момент времени t= 0 начинает разряжаться через резистор сопротивлением R= 1 Ом (см. рис. 1.12). Определите ток в резисторе в момент времени i=0,5 с.
Ответ: 0,6065 А.
1.2. Сохранив условия задачи 1.1, определите энергию конденсатора в момент времени t=0,5 с.
Ответ: 0,183 Дж.
1.3. Сохранив условия задачи 1.1, определите, какое количество энергии выделится в виде тепла в резисторе к моменту времени t= 0,5 с.
Ответ: 0,317 Дж.
1.4. Плоский конденсатор (см. рис. 1.7, а) состоит из двух листов фольги каждый площадью 20 см2, разделенных слоем парафина (см. табл. 1.1) толщиной 0,05 мм с относительной диэлектрической проницаемостью εr = 2,1. Определите емкость конденсатора.
Ответ: 0,745 нФ.
Дайте определения электрического потенциала и разности электрических потенциалов.
Дайте определения линейных и нелинейных емкостных элементов.
Определите общую емкость двух конденсаторов, включенных параллельно, емкостью 1 мкФ каждый (см. рис. 1.9).
Ответ: 2 мкФ.
1.8. Определите общую емкость двух конденсаторов, включенных последовательно, емкостью 2 мкФ каждый (см. рис. 1.10).
Ответ: 1 мкФ.
3


 ри
параллельном соединении конденсаторов
к каждому конденсатору приложено
одинаковое напряжениеU, а
величина заряда на обкладках каждого
конденсатора Q пропорциональна
его емкости (рис. 2).
ри
параллельном соединении конденсаторов
к каждому конденсатору приложено
одинаковое напряжениеU, а
величина заряда на обкладках каждого
конденсатора Q пропорциональна
его емкости (рис. 2).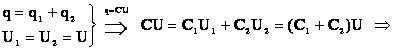
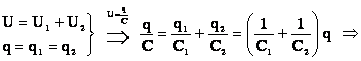
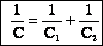
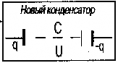
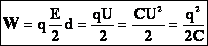
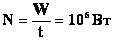 — опасно для жизни!
— опасно для жизни!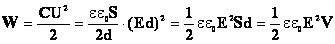
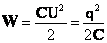
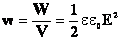 — плотность энергии (энергия единицы объема).
— плотность энергии (энергия единицы объема).