Последовательное и параллельное соединение конденсаторов
Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.
Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов, получаемая цепь выглядит следующим образом:
Эта схема состоит из следующих элементов: трех конденсаторов C1, C2, С3 и источника электрической энергии E.
Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2, ну а конец конденсатора C2 соединен с началом третьего конденсатора C3.
Стоит обратить внимание на то, как распределяются ёмкости каждого.
При таком соединении, все ёмкостя следующим образом.
Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.
Общую емкость можно рассчитать по следующей формуле:
Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:
Параллельное соединение конденсаторов
При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:
Так при параллельном соединении, емкости всех конденсаторов складываются:
То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.
Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.
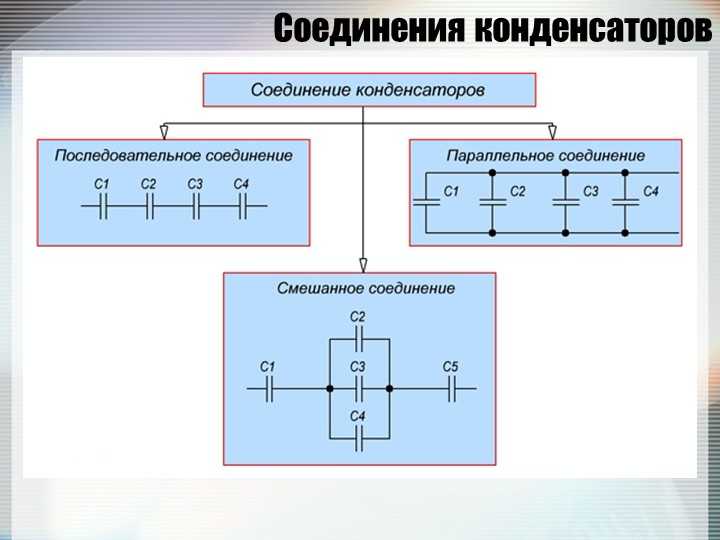
Смешанное соединение конденсаторов
Смешанное соединение конденсаторов выглядит следующим образом:
И представляет с собой различные сочетания параллельного и последовательного соединений.
Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.
Например, дана следующая схема и следующие данные:
C1=0.4Ф
C2=0.8Ф
C3=0,73Ф
Необходимо найти общую емкость всех трех конденсаторов.
Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.
Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.
Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.
Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.
Последовательное и параллельное соединение конденсаторов – формулы и схемы кратко
4
Средняя оценка: 4
Всего получено оценок: 228.
Обновлено 20 Ноября, 2020
4
Средняя оценка: 4
Всего получено оценок: 228.
Обновлено 20 Ноября, 2020
Схемы любой сложности в электротехнике можно представить в виде множества звеньев, связанных узлами. Отдельные звенья и элементы могут быть связаны последовательно или параллельно. Рассмотрим особенности параллельного и последовательного подключения конденсаторов.
Последовательное и параллельное соединение
Соединение двух двухвыводных деталей в электрической схеме можно выполнить двумя способами.
Во-первых, можно соединить детали одним выводом, а оставшиеся свободные выводы подключить к схеме. Такое соединение называется последовательным.
Во-вторых, можно соединить оба вывода обоих деталей, а к линии подключить точки соединения. Такое соединение называется параллельным.
В последовательном и параллельном соединении может участвовать более двух деталей. В первом случае детали соединяются «цепочкой». Во втором случае все детали соединяются одноименными выводами, и две точки соединения подключаются к схеме.
Большинство электрических схем разлагаются на ряд последовательных и параллельных звеньев. Даже если это не так (когда есть узлы или компоненты с нечетным количеством выводов), в схеме всё равно, как правило, имеется множество последовательно и параллельно соединенных участков.
Рис. 1. Пример принципиальной электрической схемы.
Емкость соединенных конденсаторов
Заметим, что как бы ни были соединены конденсаторы, если в рассматриваемом соединении нет других элементов, то такой участок схемы может только накапливать и отдавать заряд. Никаких других электрических преобразований здесь нет. А значит, с точки зрения внешней схемы, несколько конденсаторов представляют также конденсатор некоторой емкости. Однако эта емкость будет, конечно, отличаться от емкости составляющих конденсаторов. Формулы последовательного и параллельного соединений конденсаторов также будут различны.
Емкость параллельного соединения конденсаторов находится по формуле:
$$C_{пар}=C_1+C_2+…+C_n$$
Емкость последовательного соединения конденсаторов находится по формуле:
$${1\over C_{посл}}={{1\over C_1}+{1\over C_1}+…{1\over C_n}}$$
Запомнить сами формулы несложно: в обоих случаях результат равен сумме составляющих. Разница в том, что для первого случая составляющие и результат формулы — это сами емкости. А для второго случая — это обратные величины.
А для второго случая — это обратные величины.
Запомнить, где какая формула используется, можно, учитывая два момента:
- емкость характеризует легкость зарядки конденсатора;
- при обычной сумме результат становится больше, при суммировании же обратных величин результат будет меньше.
Теперь остается представить, как распределяется общий заряд по параллельному и по последовательному соединению.
Если конденсаторы соединены параллельно, то это эквивалентно увеличению площади их обкладок. Большие по размеру обкладки «вмещают» больше электронов, зарядить их легче, емкость будет больше. Справедлива формула с суммой емкостей.
Рис. 2. Параллельное соединение конденсаторов.Если конденсаторы соединены последовательно, то для заряда каждого конденсатора необходимо преодолеть напряжение, которое имеется на всех остальных конденсаторах (они ведь тоже заряжаются), и по мере заряда это напряжение растет. Следовательно, последовательные конденсаторы зарядить труднее, емкость будет меньше.
Формулы последовательного и параллельного соединения конденсаторов аналогичны формулам общего сопротивления для соединений резисторов, но используются «наоборот»: у резисторов формула с суммой значений используется в последовательном соединении, а формула с суммой обратных величин — в параллельном.
Что мы узнали?
Конденсаторы могут быть соединены последовательно или параллельно. В обоих случаях с точки зрения внешней схемы результатом будет некоторая электроемкость. Ее значение равно сумме емкостей для параллельного соединения. Если соединение последовательно, то обратная величина общей емкости будет равна сумме обратных величин отдельных емкостей.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 228.
А какая ваша оценка?
Конденсаторы, включенные последовательно и параллельно
Цели обучения
К концу этого раздела вы сможете:
- Выводить выражения для полной емкости последовательно и параллельно.
- Определите последовательное и параллельное соединение конденсаторов.
- Рассчитайте эффективную емкость при последовательном и параллельном подключении, учитывая отдельные емкости.
Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9.0015 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.
Емкость в серии
На рис. 1а показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]C=\frac{Q}{V}\\[/latex].
Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обеим сторонам первоначально незаряженной комбинации конденсаторов, когда приложено напряжение В . Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1b.) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.
Рис. 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d. Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.
Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанное на рисунке 1. Решение [latex]C=\frac{Q}{V}\\[/latex] для В дает [ латекс]V=\frac{Q}{C}\\[/латекс]. Таким образом, напряжения на отдельных конденсаторах равны [latex]V_1=\frac{Q}{C_1},V_2=\frac{Q}{C_2},\text{ и }V_3=\frac{Q}{C_3}\\ [/латекс].
Общее напряжение равно сумме отдельных напряжений:
В = В 1 + В 2 + В 3 9
Теперь, назвав общую емкость C S для последовательной емкости, учтите, что
[латекс]V=\frac{Q}{C_{\text{S}}}=V_1+V_2+V_3\\ [/латекс].
Ввод выражений для В 1 , В 2 и В 3 , получаем
[латекс]\frac{Q}{C_{\text{S}}}=\frac{Q}{C_{1}}+\frac{Q}{C_{2} }+\frac{Q}{C_{3}}\\[/latex].
Отменив Q с, получим уравнение для полной емкости в ряду C S равной
[латекс]\frac{1}{C_{\text{S}}}=\frac {1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots,\\[/latex]
, где «…» означает что выражение справедливо для любого числа последовательно соединенных конденсаторов. Выражение этой формы всегда приводит к полной емкости C S меньше любой из отдельных емкостей C 1 , C 2 , …, как показано в Примере 1.
Полная последовательная емкость,
C сПолная последовательная емкость:
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1 }}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots\\[/latex]
Пример 1. Что такое последовательная емкость?
Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 мкФ.
Стратегия
Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.
Решение
Ввод данных емкостей в выражение для [латекс]\фракция{1}{С_{\текст{S}}}\\[/латекс] дает [латекс]\фракция{1}{С_{\ text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\\[/latex].
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{1,000 \mu\text{F}}+\frac{1}{5,000 \mu\text{F }}+\frac{1}{8.000 \mu\text{F}}=\frac{1.325}{\mu\text{F}}\\[/latex]
Инвертирование для нахождения C S дает [латекс] C _ {\ text {S}} = \ frac {1,325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [ /латекс].
Обсуждение
Общая емкость серии C s меньше, чем наименьшая индивидуальная емкость, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,
Таким образом,
[латекс]\frac{1}{C_{\text{S}}}=\frac{40}{40 \mu\text{F}}+\frac{8}{40 \mu\text{F }}+\frac{5}{40 \mu\text{F}}=\frac{53}{40\mu\text{F}}\\[/latex]
, так что
[latex]C_ {\text{S}}=\frac{40\mu\text{F}}{53}=0,755\mu\text{F}\\[/latex]
Параллельные конденсаторы
На рисунке 2a показана параллель соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную полную емкость C p , сначала отметим, что напряжение на каждом конденсаторе равно В , такое же, как и у источника, так как они соединены с ним непосредственно через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий сбор Q представляет собой сумму отдельных сборов: 9.
Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.
Используя отношение Q = CV , we see that the total charge is Q = C p V , and the individual charges are Q 1 = C 1 V , Q 2 = C 2 V , и Q 3 = C 3 V . Ввод их в предыдущее уравнение дает
C p В = С 1 В + С 2 В + С
1
Canceling V from the equation, we obtain the equation for the total capacitance in parallel
C p : C p = C 1 + C 2 + C 3 + ….
Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять « … ” указывает, что выражение справедливо для любого количества параллельно соединенных конденсаторов.) Так, например, если бы конденсаторы в примере 1 были соединены параллельно, их емкость была бы
C p = 1,000 мкФ + 5.000 мкФ + 8.000 мкФ = 14.000 мкФ.
Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластин и, следовательно, большую емкость, как показано на рис. 2b.
Суммарная емкость при параллельном подключении,
C P Общая емкость в параллельной C P = C 1 + C 2 + C 3 2 + C 3 . быть комбинациями последовательного и параллельного. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.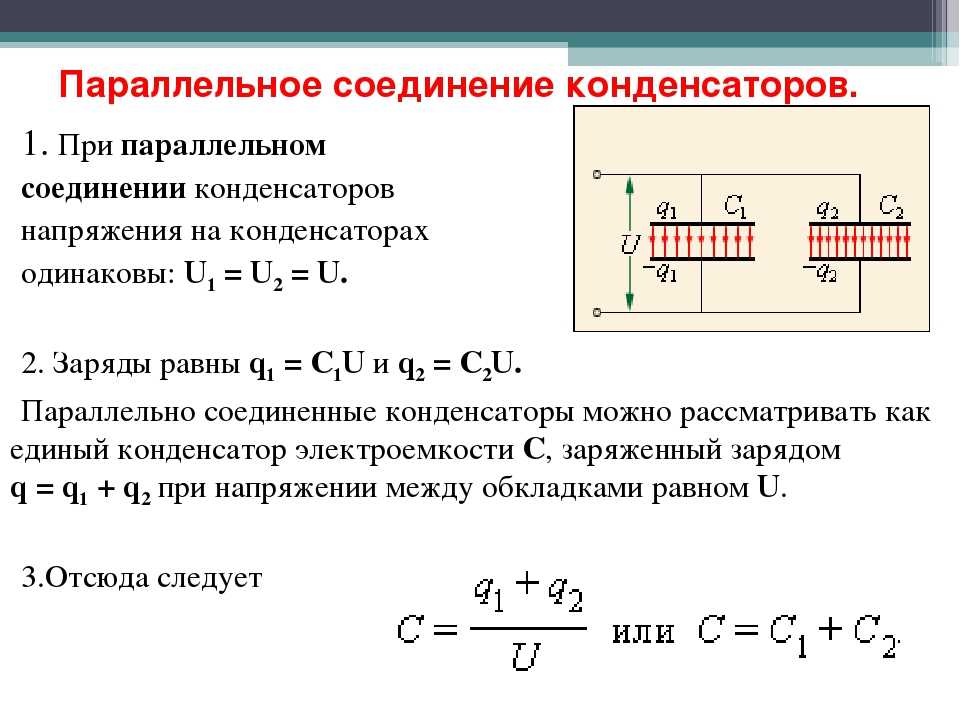
Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (б) C 1 и C 2 последовательно; их эквивалентная емкость C S меньше любого из них. (c) Обратите внимание, что C S находится параллельно с C 3 . Таким образом, общая емкость равна сумме Кл С и Кл 3 .
Пример 2. Смесь последовательных и параллельных емкостей
Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ( C 1 = 1,000 мкФ, C 2 = 3,000 мкФ и C 3 = 8,000 мкФ), и округлите ответ до трех знаков после запятой.
Стратегия
Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно.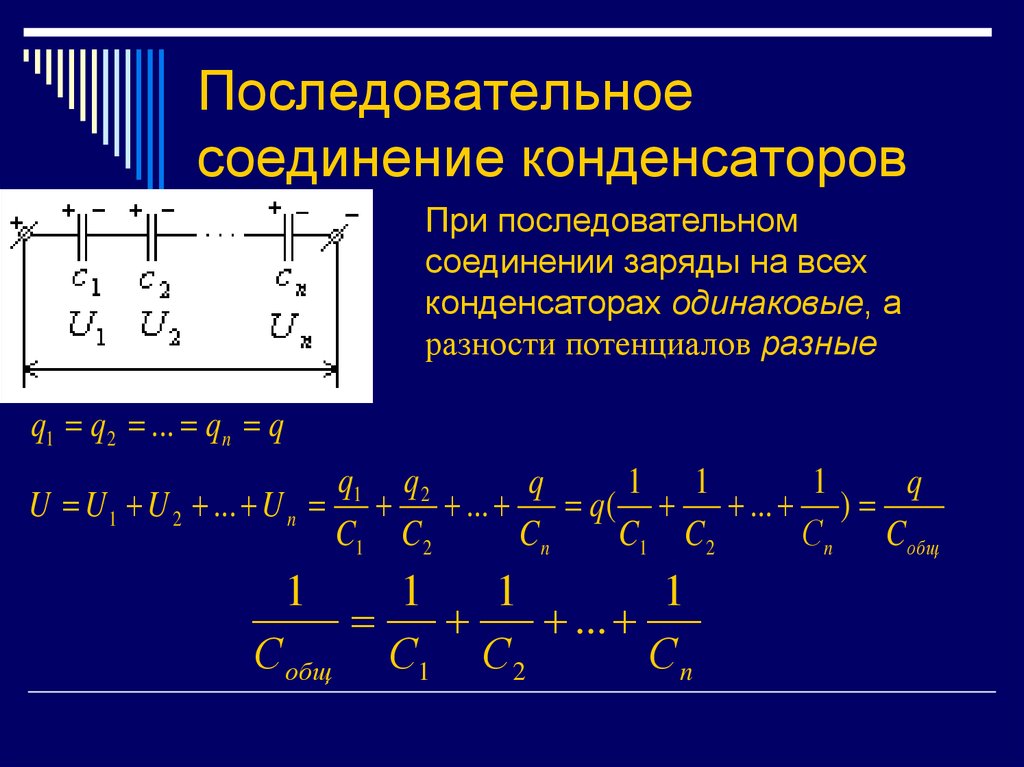 Конденсаторы С 1 и С 2 включены последовательно. Их комбинация, обозначенная на рисунке C S , идет параллельно с С 3 .
Конденсаторы С 1 и С 2 включены последовательно. Их комбинация, обозначенная на рисунке C S , идет параллельно с С 3 .
Решение
Поскольку C 1 и C 2 соединены последовательно, их общая емкость определяется выражением [латекс]\frac{1}{C_{\text{S}}}=\frac {1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\\[/latex]. Ввод их значений в уравнение дает
[латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2} }=\frac{1}{1.000\mu\text{F}}+\frac{1}{5.000\mu\text{F}}=\frac{1.200}{\mu\text{F}}\\ [/латекс].
Инвертирование дает C S = 0,833 мкФ.
Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общее количество равно сумме
[латекс]\begin{array}{lll}C_{\text{tot}}&=&C_{\text{S}}+C_{\text{S}}\\\ текст { }&=&0,833\мю\текст{F}+8,000\мю\текст{F}\\\текст{ }&=&8,833\мю\текст{F}\конец{массив}\\[ /latex]
Обсуждение
Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к большим комбинациям конденсаторов.
Резюме сечения
- Суммарная емкость последовательно [латекс]\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{ 2}}+\frac{1}{C_{3}}+\dots\\[/latex]
- Суммарная емкость при параллельном подключении C p = C 1 + C 2 + C 3 + …
- Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.
Концептуальные вопросы
- Если вы хотите хранить большое количество энергии в батарее конденсаторов, вы бы соединили конденсаторы последовательно или параллельно? Объяснять.
Задачи и упражнения
- Найдите общую емкость комбинации конденсаторов на рисунке 4.
Рисунок 4. Сочетание последовательного и параллельного соединения конденсаторов.
- Предположим, вам нужна батарея конденсаторов общей емкостью 0,750 Ф, и у вас есть несколько конденсаторов емкостью 1,50 мФ.
 Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?
Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили? - Какую общую емкость можно получить, соединив вместе конденсаторы емкостью 5,00 мкФ и 8,00 мкФ?
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 5.
Рисунок 5. Сочетание последовательного и параллельного соединения конденсаторов.
- Найдите общую емкость комбинации конденсаторов, показанной на рисунке 6.
Рисунок 6. Сочетание последовательного и параллельного соединения конденсаторов.
- Необоснованные результаты. (a) Конденсатор емкостью 8,00 мкФ подключен параллельно другому конденсатору, что дает общую емкость 5,00 мкФ. Какова емкость второго конденсатора? б) Что неразумного в этом результате? (c) Какие предположения являются необоснованными или непоследовательными?
Избранные решения задач и упражнений
1. 0,293 мкФ
3. 3,08 мкФ в последовательном соединении, 13,0 мкФ в параллельном соединении
4. 2,79 мкФ
2,79 мкФ
–3,0 (a мкФ) –3,0; (b) У вас не может быть отрицательного значения емкости; (c) Предположение, что конденсаторы были подключены параллельно, а не последовательно, было неверным. Параллельное соединение всегда дает большую емкость, а здесь предполагалась меньшая емкость. Это могло произойти только при последовательном соединении конденсаторов.
Параллельные конденсаторы — Видео физики от Brightstorm
Параллельные конденсаторы позволяют заряжать конденсаторы на выбор. Разница потенциалов одинакова с несколькими параллельными конденсаторами, но заряд увеличивается. Как и при последовательном сопротивлении, параллельное подключение конденсаторов увеличивает эффективную емкость. Формула для определения эффективной емкости: эффективная емкость = емкость 1 + емкость 2 .
параллельные конденсаторы емкость фарад
Итак, давайте поговорим о параллельном добавлении конденсаторов.
Итак, заряд увеличивается, разность потенциалов такая же. Итак, давайте посмотрим, что произойдет, q равно q1 плюс q2, поэтому, поскольку q равно емкости, умноженной на разность потенциалов, мы пишем, что c параллельная дельта v равна c1 дельта v плюс с2 дельта v разность потенциалов одинакова, поэтому дельта v отменяется.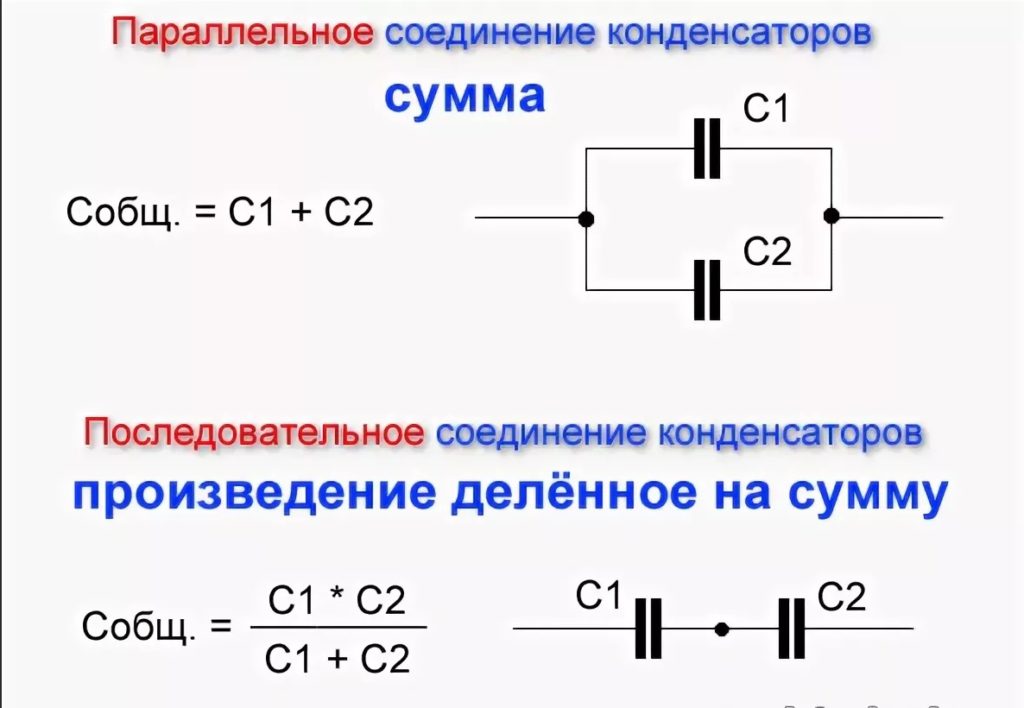 И это дает нам удивительно простую формулу, в которой параллельное добавление конденсаторов равно c1 плюс c2. Это означает, что все, что мне нужно сделать, это просто добавить, что всегда приятно. Это похоже на резисторы, соединенные последовательно, поэтому, если я добавлю больше конденсаторов параллельно, емкость увеличится. И это на самом деле часто использовалось в начале создания компьютеров; вы бы поставили кучу конденсаторов параллельно, и тогда вы смогли бы получить гораздо большую емкость, чем вы могли бы получить любым другим способом. Итак, мы собираемся добавить эти 2 конденсатора параллельно, и я хочу определить, каков будет общий заряд, если разность потенциалов на этих конденсаторах составляет 6 вольт.
И это дает нам удивительно простую формулу, в которой параллельное добавление конденсаторов равно c1 плюс c2. Это означает, что все, что мне нужно сделать, это просто добавить, что всегда приятно. Это похоже на резисторы, соединенные последовательно, поэтому, если я добавлю больше конденсаторов параллельно, емкость увеличится. И это на самом деле часто использовалось в начале создания компьютеров; вы бы поставили кучу конденсаторов параллельно, и тогда вы смогли бы получить гораздо большую емкость, чем вы могли бы получить любым другим способом. Итак, мы собираемся добавить эти 2 конденсатора параллельно, и я хочу определить, каков будет общий заряд, если разность потенциалов на этих конденсаторах составляет 6 вольт.
Хорошо, давайте сделаем это двумя разными способами, если разность потенциалов составляет 6 вольт, то это должна быть разность потенциалов на конденсаторе емкостью 3 фарад, а это означает, что заряд, удерживаемый на конденсаторе емкостью 3 фарад, будет равен разности потенциалов, умноженной на емкость 18.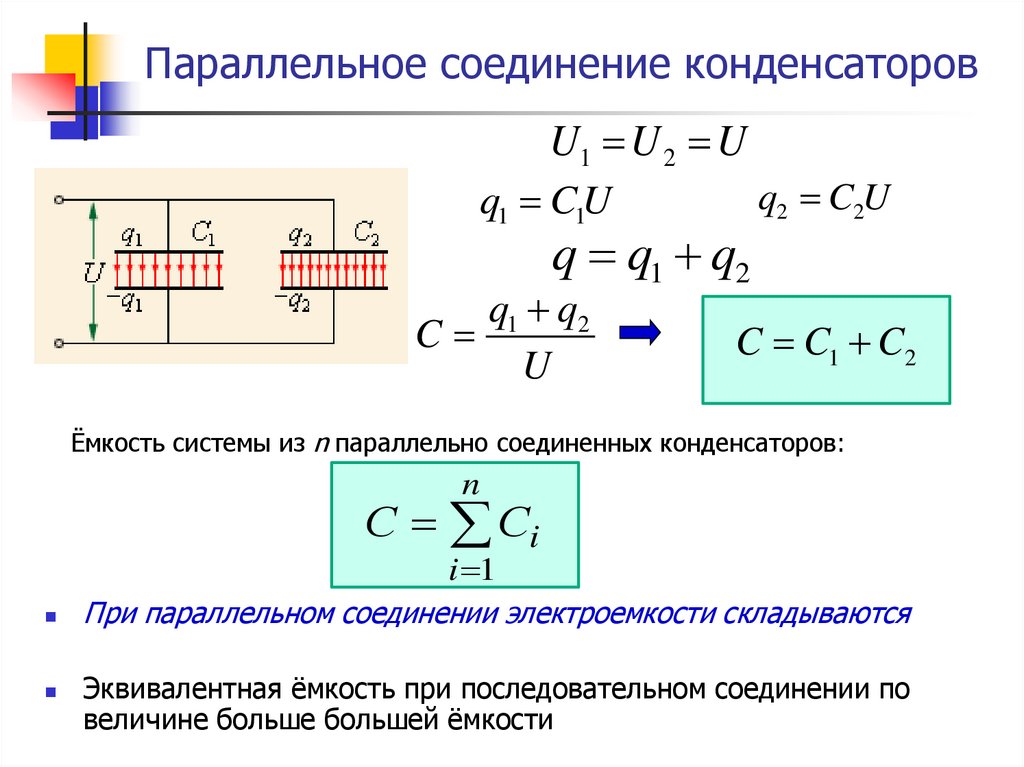 джоули. Хорошо, и заряд, удерживаемый конденсатором емкостью 2 фарад, снова будет равен емкости, умноженной на разность потенциалов, умноженной на 2, умноженной на 6, 12 джоулей. Итак, общая сумма, извините, не в джоулях, а в кулонах, поэтому общая сумма заряда, которую я собираюсь удерживать, равна 18 плюс 12, что составляет 30 кулонов, хорошо, теперь давайте сделаем это, сначала добавив их параллельно. Ну я добавляю их параллельно тогда я говорю знаете что я очень просто хочу рассмотреть один конденсатор емкостью 5 фарад. Если разность потенциалов на нем 6 вольт намного проще. Хорошо, теперь еще одна вещь, о которой следует подумать, когда у вас есть конденсаторы, подключенные параллельно, самый большой конденсатор будет хранить больше всего энергии, и это потому, что конденсаторы, соединенные параллельно треугольником, одинаковы. Итак, мы говорим, что энергия равна половине c дельта v в квадрате, это константа, поэтому чем больше c, тем больше энергия, и именно так конденсаторы складываются параллельно.
джоули. Хорошо, и заряд, удерживаемый конденсатором емкостью 2 фарад, снова будет равен емкости, умноженной на разность потенциалов, умноженной на 2, умноженной на 6, 12 джоулей. Итак, общая сумма, извините, не в джоулях, а в кулонах, поэтому общая сумма заряда, которую я собираюсь удерживать, равна 18 плюс 12, что составляет 30 кулонов, хорошо, теперь давайте сделаем это, сначала добавив их параллельно. Ну я добавляю их параллельно тогда я говорю знаете что я очень просто хочу рассмотреть один конденсатор емкостью 5 фарад. Если разность потенциалов на нем 6 вольт намного проще. Хорошо, теперь еще одна вещь, о которой следует подумать, когда у вас есть конденсаторы, подключенные параллельно, самый большой конденсатор будет хранить больше всего энергии, и это потому, что конденсаторы, соединенные параллельно треугольником, одинаковы. Итак, мы говорим, что энергия равна половине c дельта v в квадрате, это константа, поэтому чем больше c, тем больше энергия, и именно так конденсаторы складываются параллельно.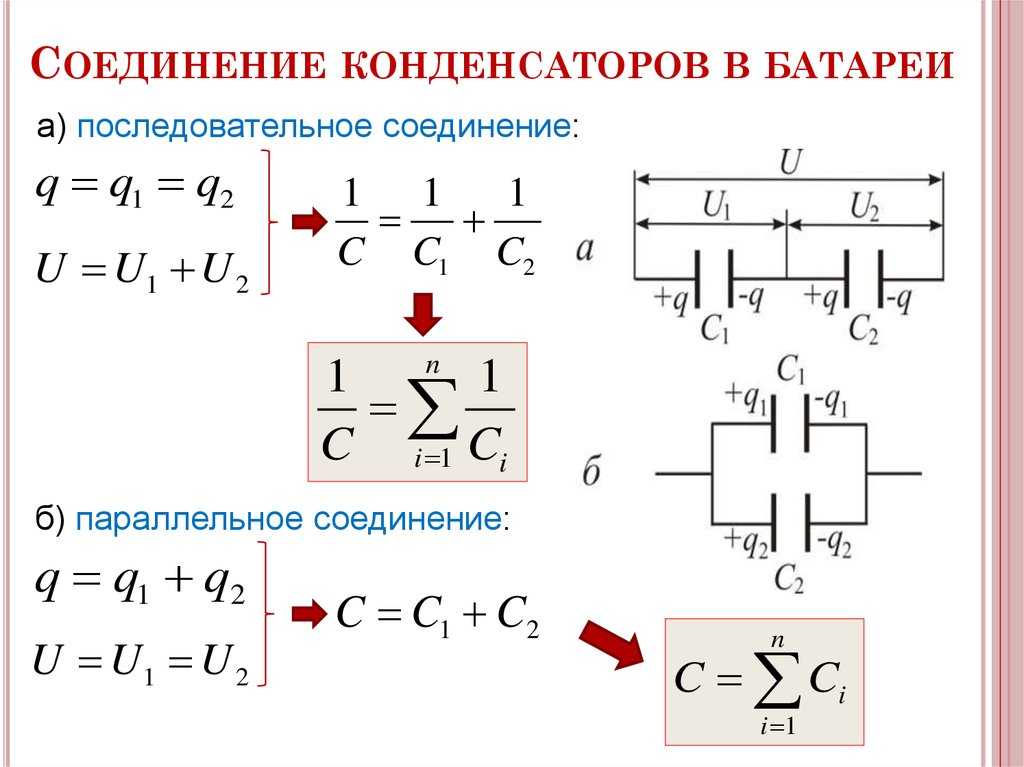


 Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?
Какое наименьшее число вы могли бы соединить вместе, чтобы достичь своей цели, и как бы вы их соединили?