значение формулы заряда, принцип работы
Конденсаторы часто встречающийся элемент в электрических схемах.
Они нужны для накопления заряда, сглаживания пульсаций электрического тока, фильтрация отдельных видов частот,
создание фазовых сдвигов обеспечивающих работу электрических двигателей и для других технических решений.
Содержание
- Что такое конденсатор
- От чего зависит емкость и заряд конденсатора
- Как устроен конденсатор
- Виды конденсаторов
- Плоский
- Сферический
- Цилиндрический
- Полярные
- Танталовые
- Ионисторы
- Электролитические
- Неполярные
- Керамические
- Пленочные
- Smd
- Переменные
- Максимальное рабочее напряжение на конденсаторе
- Величина и значение потери у конденсатора
- Конденсатор в цепи электрического тока
- Постоянного
- Переменного
- Сопротивления конденсатора в зависимости от
- Частоты и сдвига фаз
- Номинала конденсатора
- Последовательное и параллельное соединение конденсаторов
- Формулы для вычисления
- Посредством математических выражений
- Как зависит емкость от среды диэлектрика
- Как измерить емкость
- Мультиметром
- Осциллографом
- Тестером не имеющим прямой функции
- Мостовыми измерителями
- Единицы расчета
- Математическое выражение фарада
- Диэлектрическая проницаемость
- Маркировка конденсаторов
- Способы обозначения конденсатора
- Код конденсаторов импортных
- Кодовая для конденсаторов поверхностного монтажа
Что такое конденсатор
Конденсаторы — это компоненты в электронике, которые могут накапливать электрические заряды.
Эти детали используются в любом электронном устройстве.
Свойство конденсатора – это накопление заряда и последующая его отдача.
От чего зависит емкость и заряд конденсатора
Емкость конденсатора это физическая величина по которой производится оценка его возможностей выполнять свои функциональные задачи.
Практическое значение емкости выражается в способности электрического устройства к накоплению заряда.
Величина напряжения на пластинах в прямой пропорции влияет на количественные характеристики заряда на обкладках.
Формула определения емкости выглядит как
C = q/U,
где С — емкость конденсатора,
q — означает количество заряда на одной из пластин,
U — разница потенциалов на обкладках.
Приведенная формула расчета имеет в большей степени теоретический характер.
Существует иное определение емкости, которое полезнее в практическом смысле.
В формуле C = єS/d обозначена ее связь с площадью S обкладок, расстоянием между пластинами d и свойствами диэлектрика є.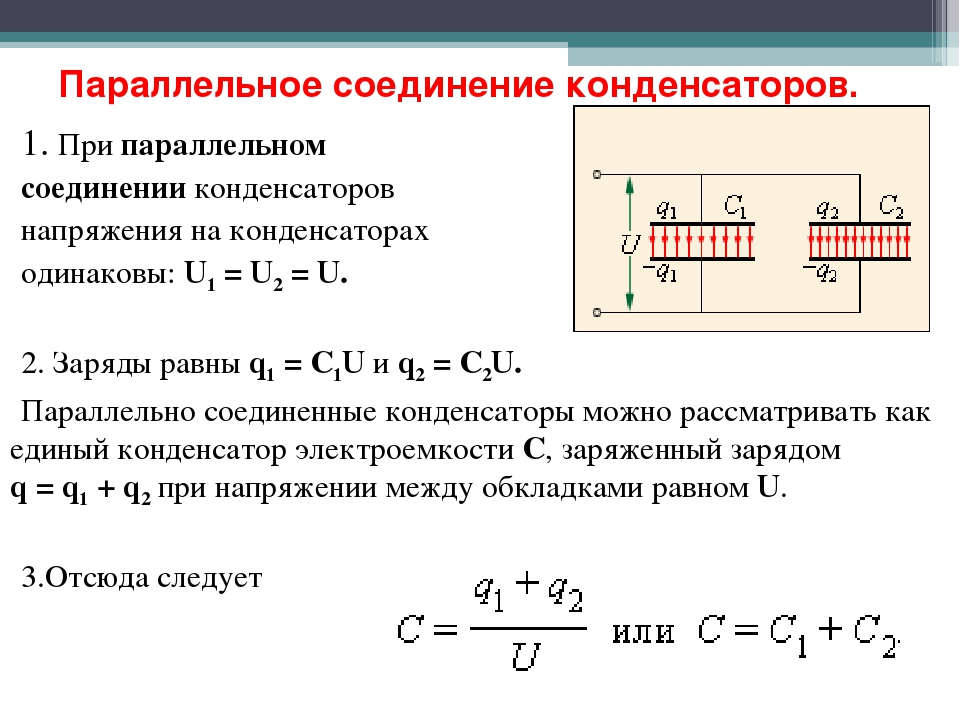
Из формулы следует, что чем больше площадь обкладок, тем больший заряд может на них разместиться и чем больше расстояние между пластинами,
тем слабее заряженные частицы будут притягиваться друг к другу, увеличивая их шансы покинуть обкладку.
Максимальная диэлектрическая проницаемость материала, расположенного между пластинами, увеличивает емкость конденсатора без изменения габаритных характеристик.
Как устроен конденсатор
Конденсатор состоит из двух или нескольких металлических пластин, между которыми располагается диэлектрический материал.
Электроны начинают двигаться, но не в состоянии преодолеть диэлектрик, из-за этого между пластинами накапливается электрический заряд.
Хорошими диэлектрическими свойствами обладают бумага покрытая оксидом алюминия, слюда, электролит, керамика и подобные материалы.
Заряды на разных обкладках одинаковые по величине, но противоположные по знаку.
Виды конденсаторов
Конденсаторы различаются по целому ряду параметров: по конфигурации, по типу диэлектрика,
по материалу обкладок, по виду изменения емкости (постоянные, переменные, подстрочные),
по рабочему напряжению.
Ниже на рисунке рассмотрим основные виды электрических устройств различной конфигурации.
Плоский
Плоский вид устройства, – это две пластины, которые располагаются параллельно друг против друга.
Они отличаются компактностью, сохраняя при этом большую емкость.
Емкость плоского конденсатора возрастает по мере увеличения площади пластин и при уменьшении расстояния между ними.
Для расчета емкости плоского конденсатора следует пользоваться формулой C = ε0 εS / d
Сферический
Сферический конденсатор это две концентрично расположенные сферы с находящимся между ними тонким диэлектриком.
Наружную поверхность внешней обкладки заземляют для создания электрического поля непосредственно между обкладками.
С учетом геометрии обкладок расчет емкости сферического конденсатора производится по формуле
C = 4πεε0 Rr/ R — r, где R — радиус наружной обкладки, r — радиус внутренней.
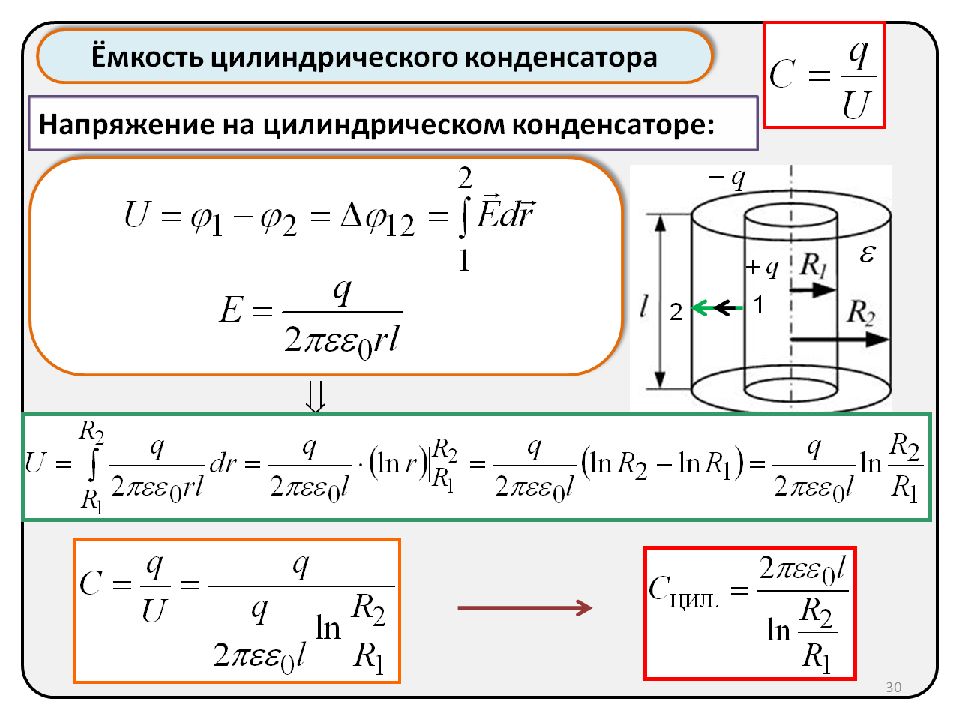
Цилиндрический
Цилиндрический конденсатор выполнен из двух полых цилиндров с разными радиусами образующих их окружностей с общей осью.
Между наружной поверхностью малого цилиндра и внутренней поверхностью большого находится диэлектрик.
Для расчета емкости цилиндрического конденсатора можно воспользоваться формулой
C = 2πєє0L/ ln (R2/R1),
где L — длина цилиндрических обкладок,
R2 — радиус наружного цилиндра,
R1 — радиус внутреннего цилиндра,
ln — обозначение логарифмического действия.
Полярные
Полярные конденсаторы – это приборы, имеющие полярность, а именно плюс и минус.
Важно чтобы плюсовой контакт был соединен с «плюсом» источника питания, а минусовой с его «минусом».
Нарушение полярности может привести даже к взрыву конденсатора.
К полярным принадлежат танталовые, ионисторы, конденсаторы с электролитическим диэлектриком.
Танталовые
В танталовых конденсаторах, относящихся к электролитическому типу, в качестве диэлектрика используется спеченный танталовый порошок оксид тантала, отсюда происходит их название.
Такой диэлектрик сводит практически к нулю ток утечки.
Недостаток заключается в невозможности работать в электрических цепях с высоким напряжением.
Танталовый конденсатор включает в себя 4 элемента – анод, диэлектрик, электролит и катод.
В отличие от электролитических танталовые имеют меньшую собственную индуктивность, благодаря чему их можно применять на высоких частотах.
Компактность танталовых устройств позволяет их использовать в качестве составляющих монтажных схем.
Ионисторы
Ионисторы принадлежат к разряду электрохимических конденсаторов.
Особенность конструкции заключается в сочетании свойств обычного конденсатора и аккумуляторной батареи.
Пространство между электродами заполняется твердым электролитом на основе рубидия и аналогичных материалов.
Такая конструкция исключает самопроизвольный разряд ионистора.
Быстрая разрядка и зарядка делают возможным его использование в некоторых видах электрических схем вместо аккумулятора.
Аккумулятор, в отличие от ионистора, потребует значительное время для своей зарядки.
Емкость ионистора отличается повышенным значением среди всех электролитических устройств.
Работает ионистор только с источником постоянного напряжения.
Электролитические
Большое распространение получили электролитические конденсаторы, у которых одна из обкладок выполнена в виде алюминиевой фольги.
Другой обкладкой служит твердый или жидкий электролит обеспечивающий движение заряженных частиц для сохранения оксидной пленки.
Емкость электролитического конденсатора на сегодняшний день является наибольшей при соотношении емкости и объема элемента.
Электролитические элементы устанавливаются в фильтрах, но важно соблюдение полярности.
По сравнению с танталовыми конденсаторами в электролитических идут значительный ток утечки.
Процессы переноса заряженных частиц происходят медленно, что увеличивает количество выделяемого тепла.
Отсюда перегрев и низкий срок службы.
Неполярные
Неполярные конденсаторы корректно работают при любых вариантах подключения их в электрическую схему.
Это связано с похожей структурой материалов образующих границу между обкладкой и диэлектриком.
Стороны одинаковы. Все это приводит к тому, что во время установки конденсатора нет необходимости соблюдать полярность.
В качестве неполярных электрических устройств в основном используются сухие, реже электролитические, изготовленные по измененной технологии.
Керамические
Керамические конденсаторы имеют высокие электрические показатели, маленькие габариты и приемлемую стоимость.
Устанавливаются элементы в контурах радиоаппаратуры.
Керамические конденсаторы подразделяются на
- с постоянной емкостью
- подстроечные.
Элементы с постоянной емкостью – устанавливают в контурах генераторов и гетеродинов.
Подстроечные – используются для подгонки параметров колебательных контуров.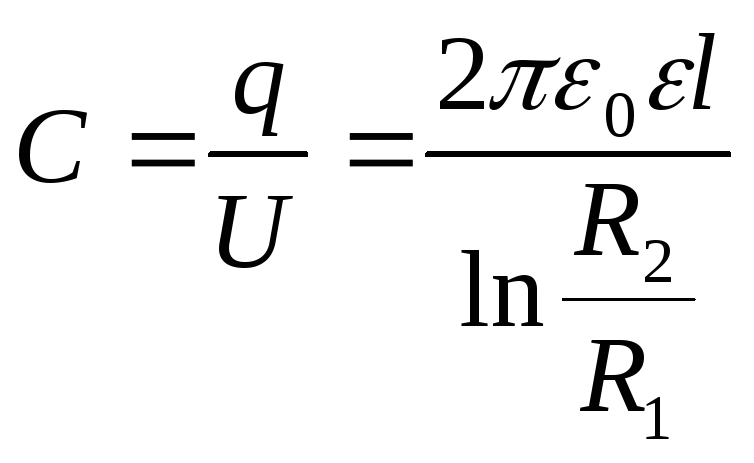
Широкое распространение получили благодаря разнообразию емкостей, широкому диапазону рабочих напряжений,
стандартными типоразмерами аналогичными керамическим устройствам разных производителей.
Пленочные
Особенностью таких устройств будет диэлектрик в виде пленки.
Пленка изготавливается из фторопласта, металлизированной бумаги, полипропилена, поликарбоната и подобных материалов.
Металлическая пленка или фольга напыляются или напрессовываются на диэлектрик.
Благодаря большому количества слоев – получается увеличение площади, соответственно, существенно увеличивается емкость.
Из достоинств пленочного конденсатора следует отметить сравнительно высокую надежность, стабильность теплового состояния при действии нагрузок вызванных переменным током.
К недостаткам можно отнести невысокое значение диэлектрической проходимости.
Пленочные конденсаторы используются в цепях постоянного тока, всевозможных фильтрах и резонансных схемах.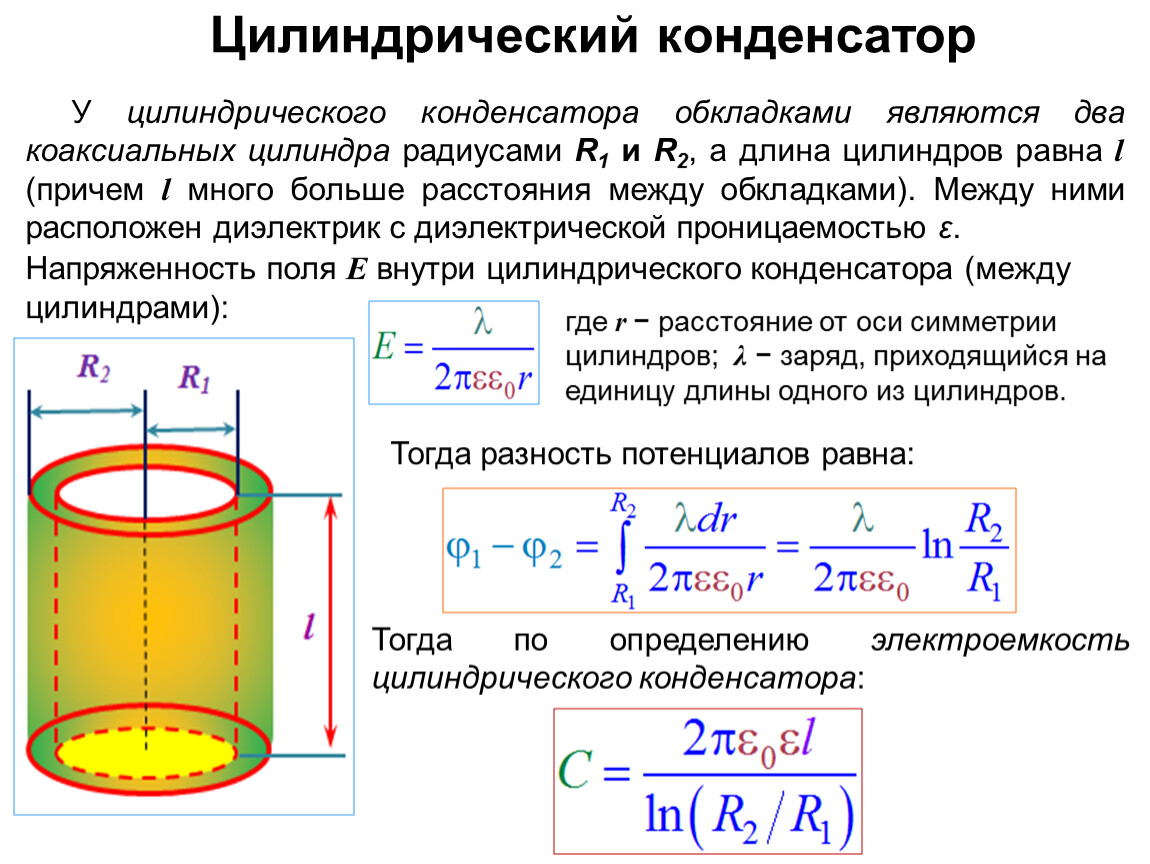
Smd
В цепях управления некоторых видов плат используются небольшие по размерам Smd конденсаторы, имеющие форму маленьких кирпичиков.
На плату радиоэлемент устанавливается посредством правила поверхностного монтажа.
Smd устройства бывают следующих видов:
- электролитические
- керамические;
- танталовые.
Керамические SMD конденсаторы, имеющие диэлектрик с высокой проницаемостью, маркируются тремя буквами.
Первыми двумя буквами обозначается нижняя и верхняя предельно допустимая граница рабочего диапазона температур,
третья буква используется при обозначении отклонений изменения емкости для измеряемых диапазонов.
Маленькие размеры Smd конденсаторов не всегда позволяют нанести маркировку на корпус или она будет очень мелкая.
В таких случаях без специального измерительного прибора, например, мультиметра не обойтись.
Переменные
Конденсаторы переменной емкости (КПЕ) состоят из части секций металлических пластин.
Одна из них двигается плавно по отношению ко второй.
Во время передвижения получается, что подвижные пластины (ротора), попадают в зазоры неподвижной пластины (статора).
Благодаря процессу площадь перекрытия одних пластин другими изменяется, в результате чего изменяется у конденсатора емкость.
Слоем диэлектрика в этом случае является воздух.
В конденсаторах, установленных в небольших устройствах, используется твердый диэлектрик, например, фторопласт или полиэтилен.
В старых радиоприемниках устройство применялось для настройки на определенную частоту колебательного контура работающей радиостанции.
Максимальное рабочее напряжение на конденсаторе
Напряжение, подаваемое на конденсатор, не должно превышать максимальное, так как может произойти пробой диэлектрика и выход элемента из строя.
Для анализа работы конденсатора в цепи переменного тока, критерием для сравнения следует брать максимальную амплитудную величину напряжения.
Это значит, что если на нем обозначено какое то максимальное напряжение DC WV , то в действительности при включении в сеть оно должно быть на 1,4 меньше.
Величина и значение потери у конденсатора
Ток утечки конденсатора – критический фактор для использования, особенно если его применяют для силовой электроники.
Потеря напрямую завязана со свойствами диэлектрика.
Никакой диэлектрик не способен гарантировать на 100% изоляцию металлических обкладок.
Через изолятор всегда будет проходить ток, меньший или больший в зависимости от свойств диэлектрика и теряться энергия.
Кроме изолирующих способностей диэлектрика на ток утечки влияют факторы:
- температура окружающего пространства;
- срок годности конденсатора без напряжения, температура;
- величина тока утечки прямо пропорциональна приложенному к обкладкам напряжению.
Восстановить работоспособность конденсатора после длительного хранения можно, приложив к нему рабочее напряжение с выдержкой в течение нескольких минут.
При этом этапе окислительный слой заново накапливается и восстанавливает работоспособность конденсатора.
Конденсатор в цепи электрического тока
Принцип работы конденсатора простой – подается напряжение и накапливается заряд.
Накопитель по-разному ведет себя в двух вариантах электрической цепи.
Постоянного
Если в цепь с присоединенным к ней конденсатором подать ток, то стрелка на амперметре придет в движение и быстро вернется в предыдущее положение.
Это связано с тем, что прибор быстро заряжается и ток исчез.
Через обкладки разделенные диэлектриком постоянный ток проходить не может.
Практическое применение конденсатора в такой цепи вызывает много вопросов.
В условиях постоянного тока конденсатор функционирует, но непродолжительное время.
Переходные процессы в виде зарядки и разрядки снимают все сомнения.
В электронных схемах на постоянном токе конденсаторы один из самых распространенных компонентов.
Переменного
При подключении переменного напряжения полюса конденсатора меняют плюс на минус с частотой подачи напряжения.
В данном случае электроны передвигаются сначала в одну, а потом в другую.
На обкладках при такой смене остаются излишки заряда, которые собственно и создают ток во внешней цепи.
Конденсатор в цепи переменного тога выступает в качестве резистора.
Сопротивления конденсатора в зависимости от
Сопротивление конденсатора зависит от частоты подаваемого на него напряжения и показателя емкости.
Частоты и сдвига фаз
Устройство накопления зарядов одинаковой емкости на разных частотах оказывает различный уровень сопротивления.
Оно растет или уменьшается.
При повышении частоты входного напряжения сопротивление, называемое емкостным уменьшается.
На низких частотах имеется сдвиг по фазе входного напряжения и напряжения на нагрузке.
С увеличением частоты сдвиг по фазе уменьшается.
При достижении частоты определенного уровня фазовый сдвиг стремиться к нулю.
Хс = 1/ωС,
где ω — круговая частота, равная произведению 2πf,
С—емкость цепи в фарадах.
Номинала конденсатора
Емкость конденсатора влияет на процесс зарядки и разрядки при прохождении через него переменного тока.
Устройство с меньшей емкостью будет быстрее отдавать заряд и вновь заряжаться.
Сопротивление переменному току будет выше, чем при медленной зарядке и разрядке.
Отсюда вывод: емкостное сопротивление находится в обратной зависимости от номинала конденсатора.
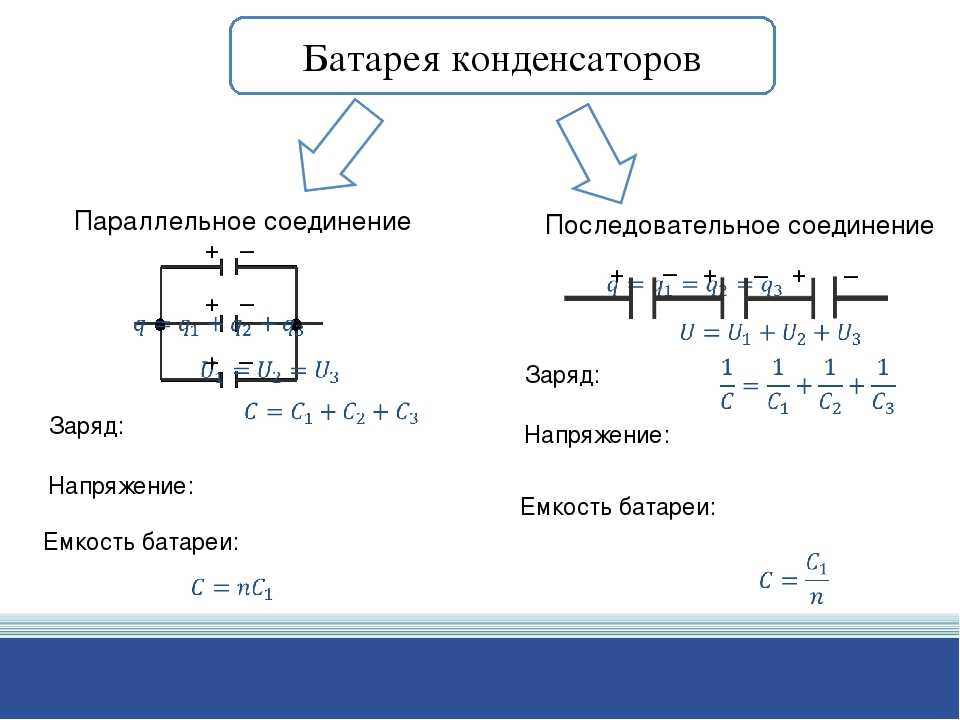
Последовательное и параллельное соединение конденсаторов
Наиболее популярным типом соединения конденсаторов является параллельное.
При этом подключении электроемкость повышается, а напряжение остается исходным.
К одной точке может подключаться несколько конденсаторов.
Так как электрическая емкость конденсаторов равна площади обкладок, общая емкость при таком виде соединения пропорциональна сумме емкостей всех конденсаторов в цепи.
Собщ.= C1+C2.
При последовательном соединении конденсаторов общая емкость снижается, а напряжение работы конденсатора возрастает.
Конденсаторы подключены так, что только первый и последний имеют доступ к источнику ЭДС/тока одной из своих пластин.
Заряд одинаковый на всех пластинах, но наружные получают заряд от источника, а внутренние образуются благодаря разделению зарядов ранее нейтрализовавших друг друга.
Емкость последовательного соединения двух конденсаторов мы можем вычислить по формуле
Собщ.= С1*С2/ C1+C2.
Формулы для вычисления
Измерения емкости осуществляется по специально выведенной формуле.
Электрическая емкость (С) — это отношение сообщенного заряда (Q) к образующему в результате этого потенциалу (U).
Формулу, которую используют, чтобы измерить емкость, выглядит следующим образом:
C=Q/V .
Единицей измерения служит фарада, которая обозначается буквой Ф.
Емкость величиной 1 фарада будет хранить заряд q = 1 кулон при напряжении на обкладках U =1 Вольт.
Так как конденсаторы имеют разные виды, формулы также используются разные.
Посредством математических выражений
Математическое выражение для определения емкости конденсатора С = q*U в единицах измерения в системе СИ каждой из входящих в формулу
физических величин определяет значение 1 фарады.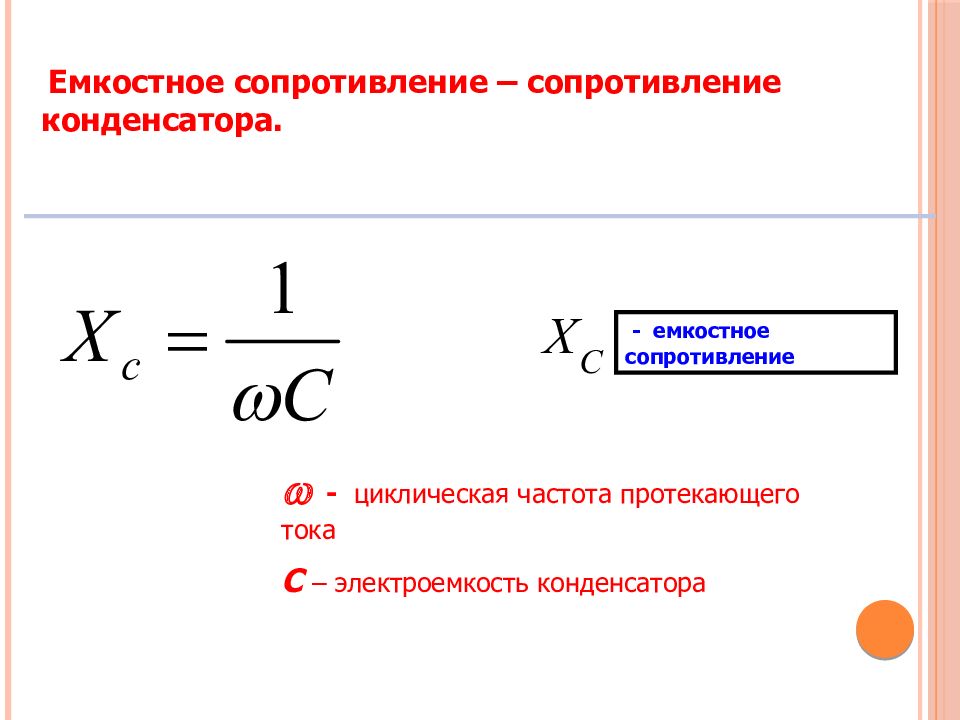
Как зависит емкость от среды диэлектрика
Влияние изолятора на емкость конденсатора зависит от проводящих свойств вещества внутри этой прокладки.
Способность межпластинного проводника на изоляцию называют диэлектрической проницаемостью.
С учетом характеристик диэлектрика формула емкости плоского устройства станет:
С = є0є S/d,
где под буквой є стоит значение диэлектрической проницаемости изолятора,
а є0 — постоянная величина равная диэлектрической проницаемости вакуума (воздуха).
На практике применяется коэффициент, обозначающий во сколько раз применяемый диэлектрик уменьшает электрическое поле по сравнению с воздухом.
Таблица:
Как измерить емкость
Существует некоторое количество способов измерения емкости конденсатора с помощью приборов и различных методик.
В статье описывается использование мультиметра, осциллографа, тестера и мостовых измерителей.
Мультиметром
В начале, прежде чем начать измерение емкости конденсатора, его необходимо разрядить до полного исчезновения тока.
Как пример: сделать это с путем замыкания выводов отверткой.
Если пренебречь этим нюансом, то мультиметр может поломаться.
Измерить емкость с помощью мультиметра можно следующим образом:
активируйте режим «Сх» и установите предел замера 2000 пФ, если он есть.
На стандартном устройстве он равный 20 мкФ;
Установите конденсатор в соответствующие гнезда в мультиметре или используйте щупы для подключения конденсатора.
На экране прибора будет отображено значение емкости.
Осциллографом
Для измерения понадобиться кроме осциллографа собрать схему из тестируемого конденсатора, резистора и генератора синусоидальных колебаний.
Точки подключения осциллографа к схеме находятся до резистора и после конденсатора.
Частота колебаний генератора изменяется до получения на экране осциллографа одинаковых по амплитуде синусоидальных кривых.
Это делается для точности измерений.
Представьте как рассчитать емкость конденсатора с помощью амплитудных значений напряжений?
Для этого требуется воспользоваться формулой UR/UC*2πfR подставив в нее измеренные значения.
С его помощью также рассчитывается ток утечки конденсатора косвенным способом – через снижение напряжения на предварительно известном сопротивлении.
Осциллограф способен вычислить емкость конденсаторов от 20 pF до 200 mkF.
Тестером не имеющим прямой функции
Для нахождения варианта определения емкости с помощью тестера, но без функции замера емкости,
обратите внимание на формулу мгновенного значения тока во время его зарядки или разрядки i = С dU/dt.
Здесь дело в том, что кроме тестера, секундомера следует собрать схему с источником питания,
конденсатором и резистором с большим сопротивлением для увеличения времени процесса зарядки или разрядки.
После снятия всех показаний с тестера и секундомера можно, достаточно приближенно вычислить и узнать емкость.
Зная, как определить емкость конденсатора современными приборами, будет несложно разобраться и с устройством со времен СССР.
На экране происходит вывод не цифр, а отклонения стрелки, за которой важно внимательно следить.
Измерение емкости осуществляется только на разряженном конденсаторе.
Щупы выведите к контактам конденсатора, если он рабочий, то стрелка изначально отклонится и по мере заряда займет исходную позицию.
Скорость передвижения стрелки зависит от объема емкости.
Если стрелка тестера не сдвинулась с места, либо эта величина минимальная или отклонилась и зависла в одном положении – это показатель неисправности конденсатора.
Мостовыми измерителями
Емкость конденсатора измеряется методом сравнения с эталонной емкостью.
Для чего выполняется мостовая схема, где одно плечо работает с образцовым электрическим устройством, другое с тестируемым.
Показания моста могут быть реализованы на цифровых носителях.
Единицы расчета
Математическое выражение фарада
C=Q/V, где С – электрическая емкость, Q – сообщенный заряд, V – приложенное напряжение.
Диэлектрическая проницаемость
D = εF, где D – электрическая индукция в среде, ε — диэлектрическая проницаемость среды, F — сила взаимодействия между зарядами в вакууме.
Маркировка конденсаторов
На корпусе каждого конденсатора имеется специальная маркировка – буква и цифра.
По сравнению с резисторами, маркировка конденсатора, обозначающая емкость и код отклонения емкости, довольно-таки сложная и разнообразная.
Иногда обозначения наносятся прописными буквами – MF (микрофарады), fd – фарады.
Также на корпусе указаны положительные и отрицательные символы, помогающие определить полярность конденсатора.
Способы обозначения конденсатора
Единицей измерения емкости конденсатора является фарад, поэтому на корпусе элемента обязательно присутствует буква Ф или F:
- 1 миллифарад = 10-3 фарад = 1мФ;
- 1 микрофарад = 10-6 фарад = 1 мкФ;
- 1 нанофарад = 10-9 фарад = 1 нФ;
- 1 пикофарад = 10-12 фарад = 1 пФ.
Если на элементе не обозначен номинал, то целое значение свидетельствует о том, что емкость указана в пикофарадах.
На корпусе емкость указывается с отклонением, если указана буква J – то диапазон отклонения менее 5%, буква М – 20%.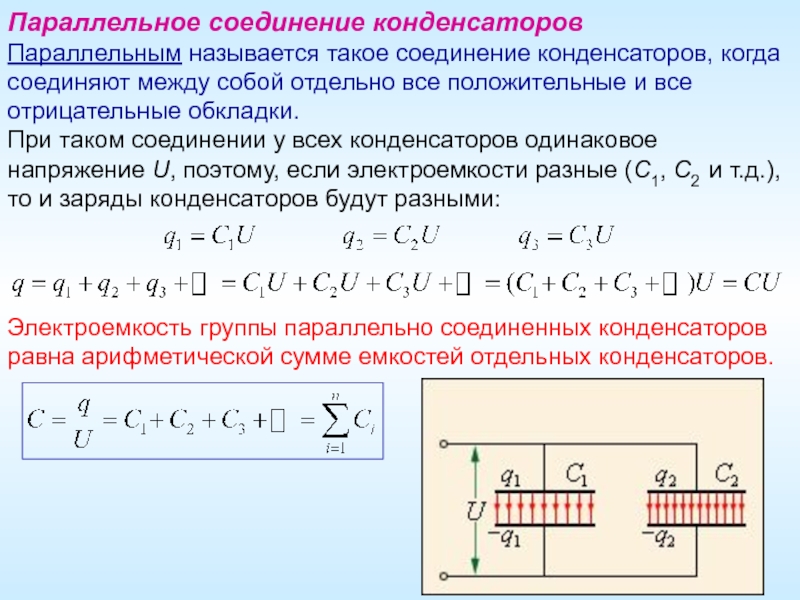
Код конденсаторов импортных
Устройства зарубежного производства, так же как и российские, имеют маркировку согласно международных стандартов.
Данный нормативный документ предполагает нанесение кода из трех цифр. Первые две цифры обозначают емкость в пикофарадах.
Третья цифра говорит о количестве нулей, например, если емкость будет меньше 1 пикофарады, цифра будет выглядеть как «0».
Кодовая для конденсаторов поверхностного монтажа
Маркировка электролитических SMD конденсаторов состоит из емкости и рабочего напряжения.
Например,108V, где закодирована электроемкость 10 пф и рабочее напряжение 8 Вольт.
Знак плюс находится рядом с полоской.
Есть три основных способа кодировки:
код из двух или трех знаков (буквы или цифры), которые указывают на рабочее напряжение и номинальную емкость.
Показатели указываются буквой, а цифра является множителем;
четыре знака, обозначающие напряжение и номинальную емкость.
Первая буква – это рабочее напряжение, следующие символы – емкость в пикофарадах, последняя цифра – количество нулей;
если площадь корпуса большая, кода располагают на две строки.
Верхняя строка – номинал емкости, нижняя – рабочее напряжение.
формулы и примеры определения емкости
Мы все знаем об электрическом токе, проводимости и сопротивлении. Но емкость является еще одной важной частью понимания концепции электричества. Возможно, вы слышали, что ничто не может хранить электричество. Однако это не так — конденсаторы способны накапливать электрический заряд. Давайте подробнее рассмотрим концепцию конденсаторов и емкости. Начнем с конденсатора.
Конденсатор образован двумя обращенными друг к другу проводниками, между которыми вставлен диэлектрик, то есть изолирующий материал. Эти два проводника называются обкладками конденсатора.
Главной характеристикой конденсаторов является величина емкости.
Емкость конденсатора — формула
Определение
Емкость конденсатора — это ничто иное, как умение конденсатора накапливать энергию в виде электрического заряда. Другими словами, емкость — это запоминающая способность конденсатора. Измеряется емкость в фарадах.
Измеряется емкость в фарадах.
Емкость может быть рассчитана, когда известны заряд Q и напряжение V конденсатора:
Емкость используется для описания того, сколько заряда может удерживать любой проводник. Он представляет собой отношение заряда к приложенному потенциалу.
Любой объект, который может быть электрически заряжен, показывает емкость. Конденсатор с двумя параллельными пластинами — это обычная форма накопителя энергии. Емкость отображается параллельным расположением пластин и определяется с точки зрения накопления заряда. Когда конденсатор заряжен полностью, между его пластинами имеется разность потенциалов, и чем больше площадь пластин и чем меньше расстояние между ними, тем больше будет заряд конденсатора и тем больше будет его Емкость.
Если конденсаторы соединены последовательно, формула емкости выражается следующим образом:
Если конденсаторы подключены параллельно, формула емкости выражается следующим образом:
Где C1, C2, C3 ……. Cn — конденсаторы, а емкость выражается в фарадах.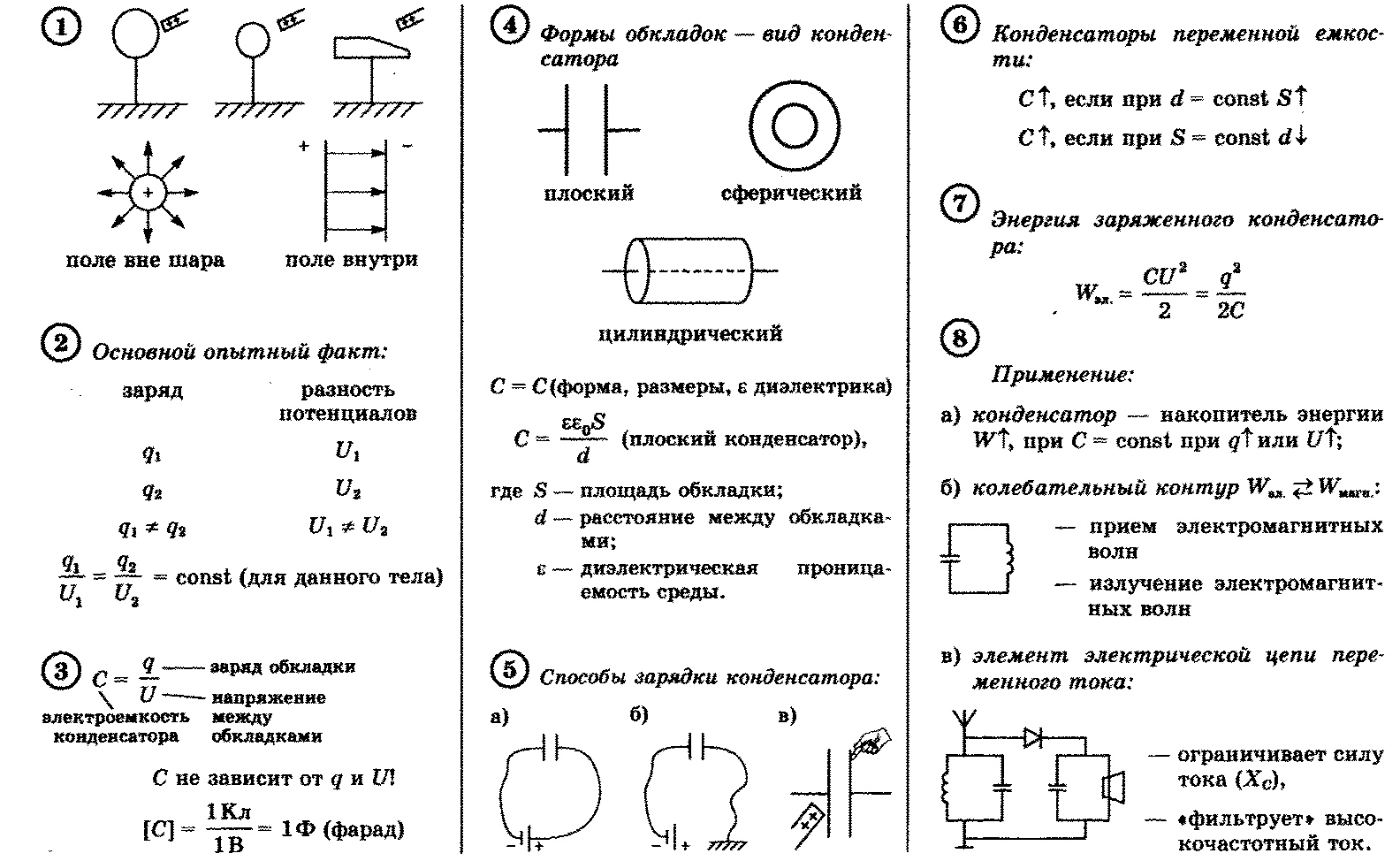
Примеры решения:
Пример 1
Определите емкость конденсатора, если течет 5 кулонов заряда и приложен потенциал 2 В.
Решение
Приведенные параметры
Заряд Q составляет 5 C,
Приложенное напряжение V равно 2 В.
Формула емкости определяется как
C=Q/V
= 5/2
= 2,5 F
Пример 2
Определите емкость, если подключены конденсаторы 6 Ф и 5 Ф.
a) последовательно;
b) параллельно
Решение
Формула последовательной емкости определяется как
Cs = 1 / C1 + 1 / C2
= C1 + C2 / C1C2
= 6 + 5/30
Cs = 0,367 F
Емкость в параллельной формуле определяется как
Ср = С1 + С2
= 6 + 5
Cp = 11 F
Различают три вида конденсаторов:
- Конденсатор плоский;
- Конденсатор цилиндрический
- Конденсатор сферический.
Конденсатор плоский
Данный конденсатор образован двумя металлическими пластинами, которые мы называем A и B, расположенными на расстоянии d.
Две проводящие пластины A и B являются пластинами конденсатора, d — их расстояние, более того, поскольку две пластины параллельны, их поверхности равны.
Мы знаем, что внутри двух поверхностей электрическое поле однородно, а снаружи равно нулю
Рассчитываем разность потенциалов между двумя пластинами
Как только разность потенциалов известна, мы можем рассчитать емкость плоского конденсатора.
Заменим найденную ранее разность потенциалов
Конденсатор цилиндрический
Конденсатор используется для хранения большого количества электрического тока в небольшом пространстве. Цилиндрический конденсатор включает полый или сплошной цилиндрический проводник, окруженный концентрическим полым сферическим цилиндром. Конденсаторы широко используются в электродвигателях, мельницах, электрических соковыжималках и других электрических инструментах. Разность потенциалов между конденсаторами различна. Существует множество электрических цепей, в которых конденсаторы должны быть сгруппированы соответствующим образом, чтобы получить желаемую емкость. Есть два общих режима, включая конденсаторы, включенные последовательно, и конденсаторы, подключенные параллельно. Единица измерения емкости — Фарад (Ф).
Есть два общих режима, включая конденсаторы, включенные последовательно, и конденсаторы, подключенные параллельно. Единица измерения емкости — Фарад (Ф).
Его часто используют для хранения электрического заряда. Цилиндрический конденсатор — это тип конденсатора, который имеет форму цилиндра, имеющую внутренний радиус как a и внешний радиус как b.
Формула для цилиндрического конденсатора:
C = емкость цилиндра
L = длина цилиндра
a = внутренний радиус цилиндра,
b = внешний радиус
εₒ= диэлектрическая проницаемость свободного пространства (8.85×10ˉ¹²)
Пример
Цилиндрический конденсатор длиной 8 см состоит из двух колец с внутренним радиусом 3 см и внешним радиусом 6 см. Найдите емкость конденсатора.
Дано:
Длина L = 8 см
внутренний радиус a = 3 см
внешний радиус b = 6 см
Решение
Формула для конденсатора цилиндрического:
Конденсатор сферический
Данный конденсатор состоит из сплошного или полого сферического проводника, окруженного другой полой концентрической сферической формой другого радиуса.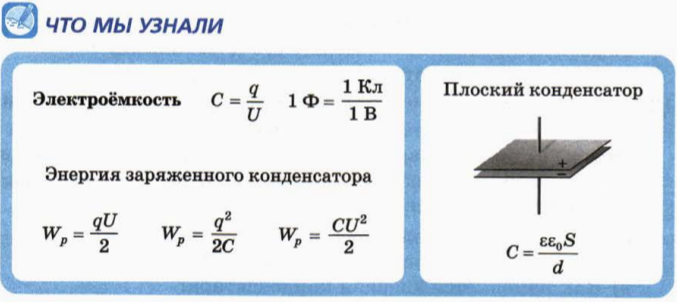
Формула для определения емкости сферического конденсатора
Где,
C = емкость
Q = заряд
V = напряжение
r 1 = внутренний радиус
r 2 = внешний радиус
ε 0 = диэлектрический потенциал (8,85 x 10-12 Ф / м)
Значение емкости двух разных конденсаторов может быть одинаковым, а номинальное напряжение двух конденсаторов может быть разным. Возьмем два конденсатора — один с малым номинальным напряжением, а другой с высоким. Если мы заменим конденсатор с меньшим номинальным напряжением на конденсатор с более высоким номинальным напряжением, то получится конденсатор меньшего размера. Это может произойти из-за неожиданного повышения напряжения.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Влияние диэлектрика на емкость
Плотности поверхностного заряда равны σ p и — σ p.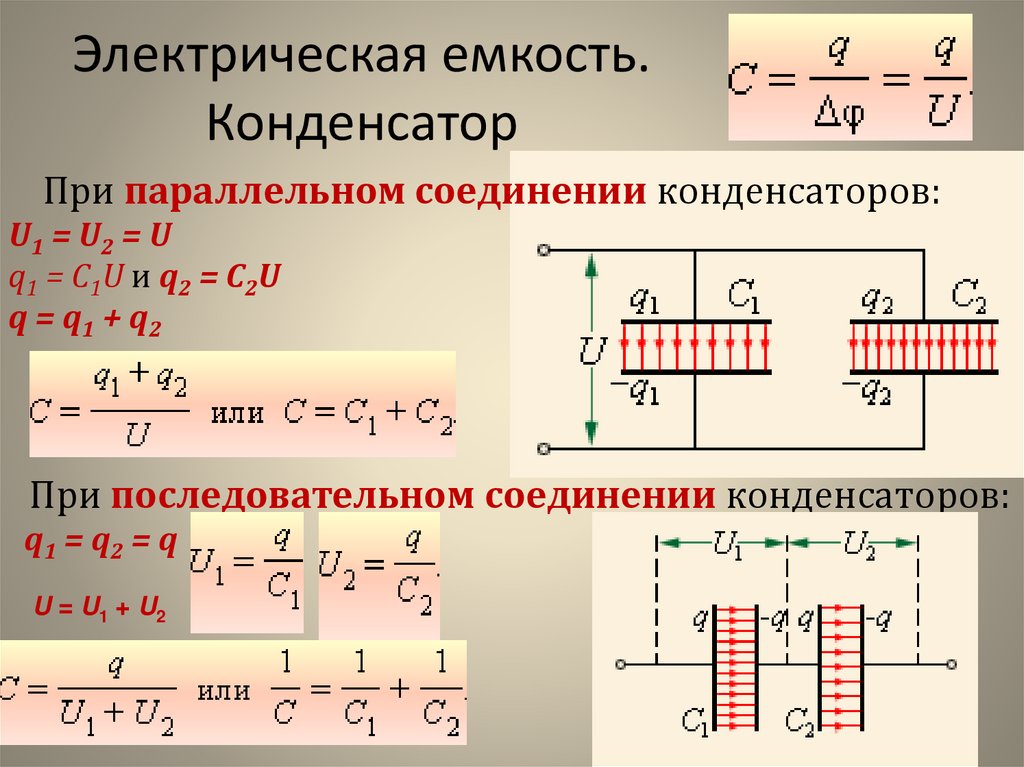 Когда мы полностью помещаем диэлектрик между двумя пластинами конденсатора, его диэлектрическая проницаемость увеличивается по сравнению с вакуумным значением.
Когда мы полностью помещаем диэлектрик между двумя пластинами конденсатора, его диэлектрическая проницаемость увеличивается по сравнению с вакуумным значением.
Внутри конденсатора следующее электрическое поле:
Следовательно, мы имеем:
а именно:
Ɛ — диэлектрическая проницаемость. Разность потенциалов между пластинами задаются
Для линейных диэлектриков:
Где k — диэлектрическая проницаемость вещества, K = 1.
Электрическое поле между пластинами конденсатора прямо пропорционально емкости конденсатора. Напряжение электрического поля снижается из-за наличия диэлектрика. Если общий заряд на пластинах поддерживается постоянным, то уменьшается разность потенциалов на пластинах конденсатора. Таким образом, диэлектрик увеличивает емкость конденсатора.
Конденсаторыпоследовательно и параллельно: формула
Возможно, вы уже знакомы с термином «конденсатор». Это электрическое устройство, которое может быть подключено к цепи для накопления энергии в электрическом поле, фильтрации переменного тока и многих других функций. Конденсаторы в основном известны своей способностью накапливать электрический заряд. Электрический заряд накапливается в конденсаторе во время прохождения электрического тока, когда этот ток прекращается, конденсатор затем разряжает этот электрический заряд обратно в цепь, чтобы поддерживать поток электрического тока в течение некоторого времени. Эту особенность конденсатора можно использовать для преобразования постоянного тока в переменный.
Конденсаторы в основном известны своей способностью накапливать электрический заряд. Электрический заряд накапливается в конденсаторе во время прохождения электрического тока, когда этот ток прекращается, конденсатор затем разряжает этот электрический заряд обратно в цепь, чтобы поддерживать поток электрического тока в течение некоторого времени. Эту особенность конденсатора можно использовать для преобразования постоянного тока в переменный.
Рис. 1. На рисунке показаны конденсаторы, используемые для подключения к электрической цепи, размещенные на зеленой поверхности
Функцию этих конденсаторов можно регулировать и улучшать, соединяя их в определенных схемах. Мы можем увеличить чистую емкость цепи, подключив конденсаторы параллельно батарее. Точно так же мы можем сохранить одинаковое количество заряда во всех конденсаторах, соединив их последовательно. В этой статье мы подробно узнаем о последовательном и параллельном соединении конденсаторов и их преимуществе в электрических цепях.
Конденсатор в последовательной и параллельной формуле
Давайте сначала посмотрим на формулу для конденсаторов в параллельном, это станет яснее позже, почему мы сначала выбираем параллельное.
Параллельные конденсаторы
На рисунке ниже мы видим два параллельных пластинчатых конденсатора, соединенных параллельно.
Рис. 2 — Конденсаторы с параллельными пластинами в параллельной ориентации, соединенные двумя проводами.
В параллельной цепи ток подается к двум компонентам независимо друг от друга с помощью соединения. Чтобы рассчитать общую емкость этой установки, мы можем использовать следующее уравнение
\[ C_{\text{p}} = \sum_{\text{i}} C_{\text{i}} ,\]
где \(C_{\text{p}}\) общая параллельная емкость, измеренная в фарадах \(\mathrm{F}\), \(C_{\text{i}}\) — индивидуальная емкость конденсаторов, также измеренная в фарадах \(\mathrm{F}\), и знак суммы \(\sum_{\text{i}}\) указывает на то, что мы суммируем отдельные емкости. Из этого уравнения мы можем видеть сходство между уравнением параллельной емкости и уравнением последовательного резистора. Важная вещь, которую следует отметить в отношении этого уравнения, заключается в том, что емкость группы конденсаторов, включенных параллельно, всегда будет больше, чем емкость любого из задействованных конденсаторов, даже того, который имеет наибольшую емкость.
Из этого уравнения мы можем видеть сходство между уравнением параллельной емкости и уравнением последовательного резистора. Важная вещь, которую следует отметить в отношении этого уравнения, заключается в том, что емкость группы конденсаторов, включенных параллельно, всегда будет больше, чем емкость любого из задействованных конденсаторов, даже того, который имеет наибольшую емкость.
Конденсаторы в серии
Давайте теперь введем правило последовательной емкости. Мы увидим, что оно имеет ту же форму, что и общее сопротивление набора резисторов, соединенных в параллельно . На рисунке ниже мы видим те же два конденсатора \(C_1\) и \(C_2,\), теперь соединенные последовательно.
Рис.3 — Конденсаторы расположены последовательно, соединены одним проводом.
В этом случае элементы соединяются один за другим, стыка нет. Уравнение для последовательно соединенных конденсаторов
\[ \frac{1}{C_{\text{s}}} = \sum_{\text{i}} \frac{1}{C_{\text{i}}} ,\]
где \(C_{\text{s}}\) — последовательная емкость, измеренная в фарадах \(\mathrm{F}\), \(C_{\text{i}}\) — отдельная емкость, измеренная в \(\ mathrm{F}\), и снова \(\sum_{\text{i}}\) обозначает сумму всех емкостей. Как мы видим, оно похоже на уравнение для параллельных конденсаторов, за исключением того, что теперь мы добавляем обратные величины отдельных емкостей, чтобы получить обратную общую емкость. Емкость группы конденсаторов, соединенных последовательно, всегда меньше емкости любого из задействованных конденсаторов, даже конденсатора с наименьшей емкостью.
Как мы видим, оно похоже на уравнение для параллельных конденсаторов, за исключением того, что теперь мы добавляем обратные величины отдельных емкостей, чтобы получить обратную общую емкость. Емкость группы конденсаторов, соединенных последовательно, всегда меньше емкости любого из задействованных конденсаторов, даже конденсатора с наименьшей емкостью.
Конденсатор в последовательном и параллельном выводе
Во-первых, давайте посмотрим на вывод конденсаторов в параллельном соединении.
Конденсаторы в параллельном выводе
Используя уравнение конденсатора, мы находим, что первый конденсатор подчиняется уравнению первого конденсатора, \(Q_1\) — величина заряда на пластинах первого конденсатора, а \(V_1\) — напряжение на первом конденсаторе. Аналогично со вторым конденсатором находим
\[ C_2 = \frac{Q_2}{V_2} ,\]
где \(C_2\) — вторая емкость, \(Q_2\) — величина заряда на обкладках второго конденсатора, а \(V_2\) — напряжение на втором конденсаторе.
Когда у нас есть электрические компоненты, соединенные параллельно друг с другом, мы знаем, что напряжение на них равно и эквивалентно общему напряжению на параллельном участке. Таким образом, мы можем написать, что
\[ V_1 = V_2 = V_{\text{T}} .\]
Кроме того, мы можем переписать полное напряжение на параллельном участке как
\[ V_{\text{T}} = \frac{Q_{\text{T}}}{C_{\text{T}}} .\]
Общий заряд \(Q_{\text{ T}}\) определяется суммированием зарядов на обоих конденсаторах с параллельными пластинами, это связано с тем, что ток в двух ветвях параллельной цепи является общим. Таким образом, мы находим, что
\[ \begin{align} Q_\text{T} &= Q_1 + Q_2 \\ C_{\text{T}} V_{\text{T}} &= \left(C_1 V_1 \ вправо) + \влево( C_2 V_2 \вправо) \\ C_{\text{T}} &= \frac{1}{V_{\text{T}}} ( \left(C_1 V_{\text{T}) } \right) + \left( C_2 V_{\text{T}} \right}} \\ C_{\text{T}} &= \frac{\bcancel{V_{\text{T}}}}{ \bcancel{V_{\text{T}}}} (C_1 + C_2) \\ C_{\text{T}} &= C_1 + C_2, \end{align} \]
, что дает нам уравнение для параллельных конденсаторов.
Конденсаторы в последовательном выводе
Подобно выводу конденсаторов в параллельном соединении, давайте применим уравнение для конденсаторов к обоим последовательно включенным конденсаторам. Это приводит к
\[ C_1 = \frac{Q_1}{V_1} ,\]
и
\[ C_2 = \frac{Q_2}{V_2} .\]
Когда электрические компоненты соединены последовательно с одним в другом их общее напряжение является общим, в то время как ток на обоих компонентах равен. Поскольку ток равен, это также означает, что заряд на обеих пластинах конденсаторов будет одинаковым, что позволяет нам написать
\[ Q_1 = Q_2 = Q_{\text{T}} .\]
Затем мы также можем записать, что общее напряжение на комбинации конденсаторов как
\[ V_{\text{T}} = V_1 + V_2 .\]
Таким образом, переставляя наши уравнения для отдельных конденсаторов и подставляя их в уравнение для полного напряжения, мы находим, что
\[ \begin{align}V_{\text{T}} &= V_1+V_2\\ V_ {\text{T}} &= \frac{Q_1}{C_1} + \frac{Q_2}{C_2} \\ V_{\text{T}} &= \frac{Q_{\text{T}}} {C_1} + \ frac {Q _ {\ text {T}}} {C_2} \\ \ frac {V _ {\ text {T}}} {Q _ {\ text {T}}} &= \ frac {1} {C_1} + \frac{1}{C_2} \\ \frac{1}{C_{\text{T}}} &= \frac{1}{C_1} + \frac{1}{C_2} , \ конец {выравнивание} \]
, что дает нам уравнение последовательного конденсатора.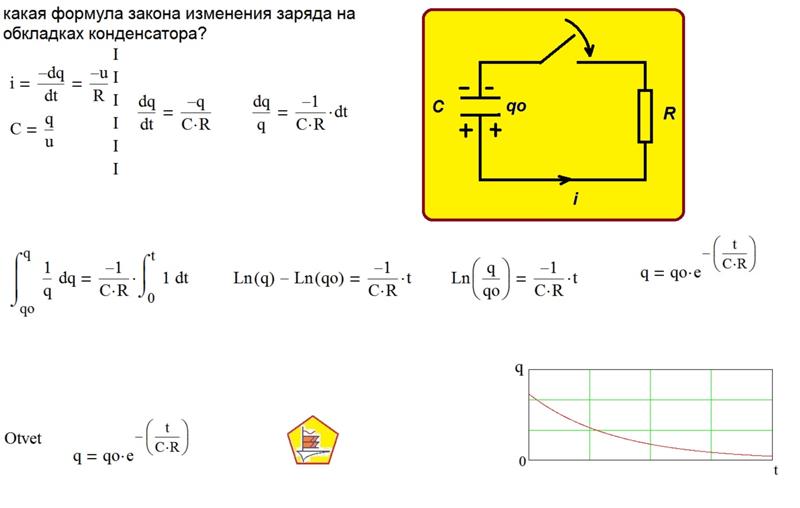
Конденсатор в последовательном и параллельном соединении
Теперь, когда мы установили правила для конденсаторов как в последовательном, так и в параллельном расположении, давайте рассмотрим объединение двух случаев и определим, как рассчитать общую емкость. Ссылаясь на диаграмму ниже, мы видим, что конденсатор \(C_1\) подключен последовательно, а \(C_2\) и \(C_3\) подключены параллельно.
Рис. 4 — Конденсаторы теперь объединены как последовательно, так и параллельно.
Во-первых, мы определяем емкости каждого из конденсаторов как \(C_1 = 2,0 \, \mathrm{\mu F}\), \(C_2 = 9,6 \, \mathrm{\mu F}\) и \ (C_3 = 4,3 \, \mathrm{\mu F}\). Теперь мы можем рассчитать общую емкость \(C_2\) и \(C_3\), используя правило параллельного конденсатора, как
\[ C_{\text{p}} = 9,6 \, \mathrm{\mu F} + 4,3 \, \mathrm{\mu F} = 13,9 \, \mathrm{\mu F} .\]
Теперь мы можем применить правило последовательной емкости, чтобы найти общую емкость конфигурации. Это приводит к 92}{C} ,\]
где \(U_{\text{C}}\) — энергия, запасенная в одном конденсаторе, измеряемая в джоулях \(\mathrm{J}\), \(Q\) величина заряда на параллельных пластинах, измеренная в кулонах \(\mathrm{C}\), а \(C\) — емкость конденсатора, измеренная в фарадах \(\mathrm{F}\).
Энергия, накопленная в последовательно соединенных конденсаторах
Подобно тому, как мы рассчитывали общую емкость последовательно соединенных конденсаторов, мы рассчитываем общую энергию двух последовательно соединенных конденсаторов. Первый конденсатор подчиняется уравнению 92 \влево(C_1 + C_2\вправо) . \end{align} \]
Свойства конденсаторов, соединенных последовательно и параллельно
Давайте вспомним некоторые важные свойства конденсаторов, соединенных последовательно и параллельно.
Емкость группы конденсаторов, соединенных последовательно, всегда меньше емкости любого из задействованных конденсаторов, даже конденсатора с наименьшей емкостью.
Емкость группы конденсаторов, включенных параллельно, всегда будет больше, чем у любого из задействованных конденсаторов, даже у конденсатора с наибольшей емкостью.
Конденсаторы в последовательном и параллельном соединении – основные выводы
- Конденсаторы накапливают энергию за счет электрического поля, создаваемого противоположно заряженными параллельными пластинами.
 2}{C}\).
2}{C}\). - Емкость группы конденсаторов, соединенных последовательно, всегда меньше емкости любого из задействованных конденсаторов.
- Емкость группы конденсаторов, включенных параллельно, всегда будет больше емкости любого из задействованных конденсаторов.
Каталожные номера
- Ничего впереди (https://www.pexels.com/@ian-panelo/) под лицензией Pexels (https://www.pexels.com/license/).
- Рис. 2. Параллельные конденсаторы, StudySmarter Originals.
- Рис. 3. Конденсаторы последовательно, StudySmarter Originals.
- Рис. 4. Конденсаторы последовательно и параллельно, StudySmarter Originals.
Емкость
ЕмкостьЕмкость характеризуется параллельное расположение пластин и определяется с точки зрения заряда хранилище:
| Указатель Концепции емкости Концепции индуктивности | |||||
| Назад |
Конденсаторы параллельно добавить…
| Указатель Концепции емкости Концепции индуктивности | ||
| Назад |
|






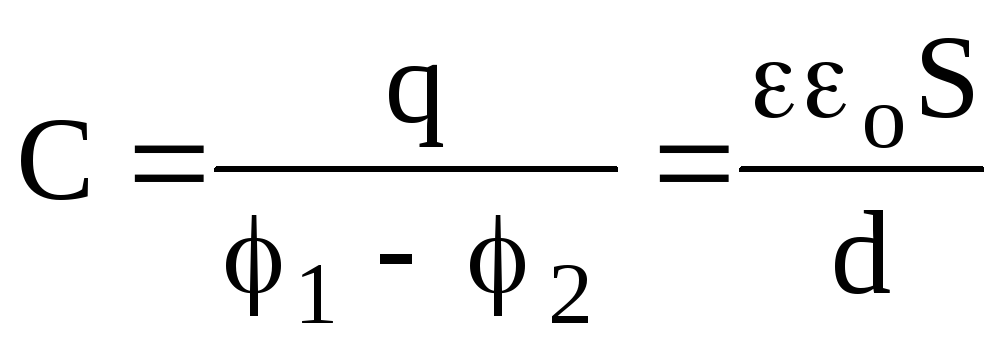
 2}{C}\).
2}{C}\).