Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры.
Напишите сочинение о том как вы выполняете любимую или необходимую работу готовите какое-то блюдо убираете Квартиру комнату заботьтесь И домашних животных например чистить аквариум ухаживать
Вычислить площадь треугольника с вершинами А(7;3;4), В(1;0;6), С(4;5;-2)
Сколько молекул содержится в 1 кг водорода(н2)?
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
| ||||||||||||
| Специальный поиск | ||||||||||||
|
Физика Теория вероятностей и мат. Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||
конденсатора заряженного разности потенциалов Задача 10711 К воздушному конденсатору, заряженному до разности потенциалов U = 500 В и отключенному от источника напряжения, присоединен параллельно второй конденсатор таких же размеров и формы, но с другим диэлектриком (стекло). Определить диэлектрическую проницаемость e стекла, если после присоединения второго конденсатора разность потенциалов уменьшилась до U2 = 70 В.
Задача 60031 Плоский конденсатор заряжен до разности потенциалов U = 1 кВ.
Задача 60175 Плоский воздушный конденсатор заряжен до разности потенциалов 100 В и отключен от источника. Для увеличения расстояния между обкладками в 3 раза была совершена работа 50 мДж. Найти первоначальную емкость конденсатора. Задача 60302 Какой энергией обладает заряженный до разности потенциалов 177 В конденсатор с площадью пластин 8866 кв.см, если расстояние между пластинами , заполненного диэлектриком с относительной диэлектрической проницаемостью 27, равно 470 мкм?
Задача 60429 Плоский слюдяной конденсатор, заряженный до разности потенциалов 600 В, обладает энергией 40 мкДж. Площадь пластин составляет 100 см2.
Задача 11897 Конденсатор электроемкостью С1 = 0,2 мкФ был заряжен, до разности потенциалов U1 = 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U2 = 450 В, напряжение U на нем изменилось до 400 В. Вычислить емкость С2 второго конденсатора.
Задача 26281 Пластины воздушного конденсатора площадью S = 300 см2 отдалены друг от друга на расстояние d = 3,0 мм. Между ними находится изолированная металлическая пластина той же площади толщиной d’ = 1,0 мм. Конденсатор заряжен до разности потенциалов U = 600 В и отсоединен от источника напряжения. Какую работу нужно совершить, чтобы извлечь изолированную пластину из конденсатора?
Задача 12028 Один конденсатор заряжен до разности потенциалов U1 = 60 В, а другой — до U2 = 20 В.
Задача 16112 Сколько электронов содержит пылинка массой 2·10–14 кг, если она находится в равновесии в поле плоского конденсатора, заряженного до разности потенциалов 150 В. Расстояние между пластинами конденсатора 4·10–3 м. Поле считать однородным. 2) Какое ускорение приобретет пылинка при изменении знаков на пластинах конденсатора? 3) Какая сила будет действовать на пылинку, если пластины конденсатора установить вертикально?
Задача 20392 Между горизонтально расположенными пластинами конденсатора, заряженного до разности потенциалов 600 В, висит капелька ртути, несущая некоторый заряд и удерживаемая силами электростатического поля.
Задача 22656 Имеются два конденсатора емкостью 200 пФ и 100 пФ. Первый конденсатор заряжен до разности потенциалов 100 В, второй – незаряженный. Конденсаторы соединили между собой, образовав замкнутую цепь. Найти заряд и разность потенциалов каждого конденсатора в цепи и энергию, израсходованную на образование искры.
| ||||||||||||
Конденсаторы
Конденсатор — это устройство, в котором две проводящие поверхности накапливают электрический заряд. Однако у него есть зазор между двумя поверхностями, который изолирует их друг от друга. Расстояние между зазором и материалом в зазоре (воздух, стекло, минерал, жидкость и т. д.) не слишком велико, чтобы предотвратить достаточно сильное электрическое поле, которое толкает электрические заряды и заставляет их собираться на поверхностях.
Из чего состоит конденсатор?
В простом конденсаторе используются две параллельные пластины из проводящего материала, разделенные изолятором. Изолятор называется диэлектрик и представляет собой материал, препятствующий прохождению через него электрического тока. Способность электрического поля проходить через диэлектрический материал определяется значением измерения, известным как ε , называемым диэлектрической проницаемостью . Это, наряду с размерами пластин конденсатора, определяет, сколько заряда он может хранить. Имеет значение площадь пластин ( A ) и расстояние между ними ( d ). Вот иллюстрация того, как части конденсатора связаны вместе с их важными свойствами:
Величина емкости ( C ) конденсатора зависит от способности электрического поля влиять на заряды на его пластин, умноженное на площадь проводящей поверхности, деленную на расстояние между пластинами.
C = ε * A / d
Емкость измеряется в единицах Фарад (Ф) . Большинство конденсаторов, используемых в небольших современных электронных схемах, имеют емкость микрофарад (мкФ) или пикофарад (пФ) . Пикофарад очень мал, это 1/1000000000000 фарада.
Электрическое поле
Сначала конденсатор имеет одинаковое количество положительных и отрицательных зарядов на каждой пластине. Заряды не могут перейти на другую пластину из-за зазора между ними, который изолирует пластины друг от друга. Зазор может быть воздухом или другим непроводящим материалом. Однако внутри зазора есть электрическое поле ( E ), который направляет силу от батареи, чтобы подтолкнуть противоположный электрический заряд к пластинам.
Зарядка
Наличие электрического поля между этими поверхностями заставляет заряды на пластинах располагаться ближе всего к направлению противоположного заряда. Это происходит до тех пор, пока пластины конденсатора не заполнятся противоположными зарядами. На приведенном ниже рисунке показан конденсатор с двумя пластинами, которые заряжаются противоположно за счет силы приложенного к ним напряжения. Заряды перемещаются и движутся к пластине в направлении своего притяжения.
Это происходит до тех пор, пока пластины конденсатора не заполнятся противоположными зарядами. На приведенном ниже рисунке показан конденсатор с двумя пластинами, которые заряжаются противоположно за счет силы приложенного к ним напряжения. Заряды перемещаются и движутся к пластине в направлении своего притяжения.
Время RC
На самом деле конденсатор не заряжается сразу. Для зарядки требуется время из-за некоторого сопротивления току, протекающему к его пластинам или от них. При любом напряжении на обкладках конденсатора потребуется некоторое время, пока он полностью зарядится. Как только конденсатор полностью зарядится, к нему перестанет поступать ток, потому что больше нет места для новых зарядов. На следующей схеме показана простая схема для зарядки конденсатора.
Специальная величина для цепи зарядки конденсатора находится путем умножения ее сопротивления на емкость. Результатом является значение времени, называемое постоянной времени RC . Например, если резистор 20 кОм, а конденсатор 200 пФ (пФ), постоянная времени RC будет:
Например, если резистор 20 кОм, а конденсатор 200 пФ (пФ), постоянная времени RC будет:
20000 Ом * 2e-10 фарад = 4 микросекунды
Используя свойства времени заряда , мы можем определить, что конденсатор будет иметь более 99% его заряда через 5 постоянных времени, или 5 * RC секунд. На этой диаграмме первая цепь показывает момент замыкания цепи. Ток только начинает течь с 0 вольт через конденсатор, и он имеет сбалансированный заряд. На второй диаграмме показан полный заряд и отсутствие тока после периода 5 постоянных времени RC.
На второй схеме вы видите, что когда конденсатор полностью заряжен и ток прекращается, напряжение на нем становится таким же, как напряжение питания, обеспечивающее заряд. Используя значения сопротивления и емкости, упомянутые в предыдущем примере, конденсатор будет заряжаться примерно за 20 микросекунд:
5 * RC = 5 * 4 микросекунды = 20 микросекунд
Следующие графики показывают, как конденсатор заряжается и разряжается во времени: время идет. Напряжение на конденсаторе с течением времени следует «естественной» схеме, пока конденсатор полностью не зарядится или не разрядится. Из графиков видно, что скорость заряда или разряда действительно замедляется по мере приближения к
Напряжение на конденсаторе с течением времени следует «естественной» схеме, пока конденсатор полностью не зарядится или не разрядится. Из графиков видно, что скорость заряда или разряда действительно замедляется по мере приближения к 5 * RC количество времени, в данном случае 20 микросекунд .
Специальный номер, называемый и , используется для расчета напряжения конденсатора в любой конкретный момент после начала зарядки или разрядки. Это число известно как Число Эйлера и используется в математических формулах для моделирования поведения в естественном мире. Значение этого числа приблизительно равно 2,71828 и в сочетании с R и C значений в цепи зарядки, используется для определения напряжения на конденсаторе. Напряжение на конденсаторе рассчитывается по следующим формулам:
- Зарядка:
В пост. заряжать с - Разрядка:
Vc=Vstart*(e**(t/(R*C))), гдеVstart- напряжение перед разрядом
Эксперимент: имитация заряда и разряда
Используя значения для R и C вместе с числом Эйлера, вы можете составить график заряда и разряда конденсатора, чтобы увидеть, как он ведет себя во времени. Кроме того, множители постоянной времени RC можно сопоставить с уровнем напряжения, чтобы увидеть, когда конденсатор почти полностью заряжен. Для моделирования модели значение
Кроме того, множители постоянной времени RC можно сопоставить с уровнем напряжения, чтобы увидеть, когда конденсатор почти полностью заряжен. Для моделирования модели значение 20 кОм используется для R и 200 пФ используется для C . Зарядное и пусковое напряжение 3.3v .
Настройка : Скопируйте следующий код в редактор.
пусть е = 2,71828
пусть R = 20000
пусть С = 2e-10
пусть Vc = 0
пусть Вин = 3,3
пусть т = 0
для (пусть я = 0; я < 75; я ++) {
Vc = Vin*(1 - e**(t/(R*C)))
т += -0,0000005
console.logValue("ВК", ВК)
пауза(100)
}
т = 0
Вин = Вк
для (пусть я = 0; я < 75; я ++) {
Vc=Vin*(e**(t/(R*C)))
т += -0,0000005
console.logValue("ВК", ВК)
пауза(100)
} Тест : Запустите код и переключитесь в режим просмотра данных, чтобы увидеть вывод консоли на диаграмме.
Результат : Диаграмма показывает схемы заряда и разряда в течение 37,5 микросекунд каждый. Форма графика показывает, как работает «естественная» скорость заряда и разряда.
Форма графика показывает, как работает «естественная» скорость заряда и разряда.
Эксперимент: Детектор заряда
Уровень заряда конденсатора можно отслеживать, проверяя, какое напряжение на нем в данный момент. Цифровой выходной контакт может служить источником заряда, а аналоговый входной контакт может измерять напряжение на конденсаторе. Конденсатор заряжается через резистор. Чтобы иметь возможность наблюдать за изменением уровня заряда, используется конденсатор на 100 мкФ и сопротивление от 10 кОм до 40 Ом. Если вы сделали свой собственный резистор, он будет хорошо работать в этом эксперименте.
Материалы :
- (4) Зажимы типа «крокодил»
- Резистор с сопротивлением от 10 кОм до 40 кОм — используйте собственный графитовый резистор
- Конденсатор 100 мкФ
Настройка :
- Подсоедините один конец зажима типа «крокодил» к выводу (-) конденсатора (на некоторых конденсаторах это более короткий провод).
 Подключите другой конец провода типа «крокодил» к контакту GND на плате.
Подключите другой конец провода типа «крокодил» к контакту GND на плате. - Подсоедините один конец другого провода типа «крокодил» к выводу конденсатора (+) (на некоторых конденсаторах это более длинный провод). Подключите другой конец провода типа «крокодил» к одному концу вашего резистора.
- Возьмите третий провод типа «крокодил» и подключите один его конец к выводу (+) конденсатора. Подключите другой конец этого провода типа «крокодил» к контакту A5 на плате.
- Возьмите еще один провод типа «крокодил» и прикрепите его к другому концу резистора. Прикрепите несвязанный конец шнура «крокодил» к А4 пин на плате.
- Загрузите на плату следующий код:
пин.A4.digitalWrite(false)
input.buttonA.onEvent (ButtonEvent.Click, функция () {
контакты.A4.digitalWrite(true)
})
input.buttonB.onEvent (ButtonEvent.Click, функция () {
контакты. A4.digitalWrite(false)
})
навсегда (функция () {
light.graph(pins.A5.analogRead(), 1010)
пауза(200)
})
A4.digitalWrite(false)
})
навсегда (функция () {
light.graph(pins.A5.analogRead(), 1010)
пауза(200)
}) Тест : Нажмите кнопку A , чтобы зарядить конденсатор, и наблюдайте, как загораются пиксели, показывающие уровень заряда. Нажмите кнопку B , чтобы разрядить конденсатор и наблюдать, как пиксели гаснут, когда заряд уходит.
Дополнительный тест : Измените значение сопротивления и повторите тест. Обратите внимание, как время заряда и разряда отличается от первого теста.
Результат : Пиксели на плате загорятся, показывая уровень заряда конденсатора. Каждый пиксель представляет еще 10% заряда. Каждый пиксель будет светиться (или отключаться при разрядке) дольше, чем предыдущий, поскольку скорость заряда замедляется. Последнему пикселю требуется гораздо больше времени, чтобы загореться, чем другим пикселям. Это будет относиться ко времени зарядки последних 10%, как показано на плоской части графика из предыдущего эксперимента.
Изменить эту страницу на GitHub
Изменить шаблон этой страницы на GitHub
Как конденсатор заряжается в цепи постоянного тока?
Введение
Конденсаторы в настоящее время широко используются в качестве развязывающих конденсаторов, разделительных конденсаторов по постоянному току или согласующих конденсаторов из-за их характеристик , блокирующих постоянный ток при прохождении переменного тока . Но в практических приложениях постоянный ток может заряжать конденсатор и проходить через него. Это противоречит его характеристикам? Почему постоянный ток может заряжать конденсатор? Здесь мы подробно обсудим этот вопрос.
Charging and Discharging of Capacitor -RC Circuit
Catalog
Introduction |
Ⅰ Capacitor Charging Principle |
Ⅱ Why Capacitor Charges in DC? |
Ⅲ Переходные и установившиеся процессы в конденсаторах |
Ⅳ Анализ и расчет конденсаторных цепей |
Ⅰ Принцип зарядки конденсатора
Конденсатор — это компонент, который может накапливать электрическую энергию. Как один из наиболее часто используемых электронных компонентов, простейший конденсатор состоит из пластин на обоих концах и изолирующего диэлектрика (включая воздух) в середине. После включения пластины заряжаются, образуя напряжение (разность потенциалов), но из-за изоляционного материала в середине весь конденсатор не проводит ток. Однако эта ситуация возникает при условии, что критическое напряжение (напряжение пробоя) конденсатора не превышено. На самом деле любое вещество является относительно изолирующим. Когда напряжение на веществе увеличивается до определенного уровня, вещество может проводить электричество. Мы называем это напряжение напряжением пробоя.
Как один из наиболее часто используемых электронных компонентов, простейший конденсатор состоит из пластин на обоих концах и изолирующего диэлектрика (включая воздух) в середине. После включения пластины заряжаются, образуя напряжение (разность потенциалов), но из-за изоляционного материала в середине весь конденсатор не проводит ток. Однако эта ситуация возникает при условии, что критическое напряжение (напряжение пробоя) конденсатора не превышено. На самом деле любое вещество является относительно изолирующим. Когда напряжение на веществе увеличивается до определенного уровня, вещество может проводить электричество. Мы называем это напряжение напряжением пробоя.
То же самое для конденсатора. После того, как конденсатор вышел из строя, он не является изолятором. В цепи переменного тока, потому что направление тока изменяется со временем как определенная функция. Процесс зарядки и разрядки конденсатора требует времени. В это время между пластинами образуется изменяющееся электрическое поле, также являющееся функцией времени. Так ток проходит между конденсаторами в виде электрического поля. Конденсаторы
Так ток проходит между конденсаторами в виде электрического поля. Конденсаторы
аналогичны батареям тем, что у них также есть два электрода. Внутри конденсатора два электрода соединены с двумя металлическими пластинами, разделенными диэлектриком. Когда конденсатор подключен к источнику питания, под действием силы электрического поля свободные электроны пластины конденсатора, подключенной к положительному электроду источника питания, будут двигаться к отрицательному электроду. Положительный электрод заряжен положительно из-за потери отрицательных электронов, а отрицательный электрод заряжен отрицательно из-за своих отрицательных электронов. Кроме того, заряды на положительной и отрицательной пластинах равны и имеют разные знаки.
Направленное движение заряда образует ток. Из-за отталкивания одинаковых зарядов ток сначала наибольший, а затем постепенно уменьшается. Во время движения заряда заряд, хранящийся в пластине конденсатора, продолжает увеличиваться, и заряд прекращает движение, когда напряжение между двумя пластинами конденсатора становится равным напряжению источника питания. То есть ток I=0, ключ замкнут, а плюсовая и минусовая пластины конденсатора нейтрализованы соединением проводов. Когда переключатель замкнут, положительный заряд положительного полюса конденсатора может быть перемещен к отрицательному полюсу и нейтрализован. Когда заряд постепенно уменьшается, ток уменьшается, а напряжение постепенно уменьшается до нуля.
То есть ток I=0, ключ замкнут, а плюсовая и минусовая пластины конденсатора нейтрализованы соединением проводов. Когда переключатель замкнут, положительный заряд положительного полюса конденсатора может быть перемещен к отрицательному полюсу и нейтрализован. Когда заряд постепенно уменьшается, ток уменьшается, а напряжение постепенно уменьшается до нуля.
Ⅱ Почему конденсатор заряжается постоянным током?
Почему зарядный ток сохраняется в течение определенного периода времени при использовании постоянного тока для зарядки конденсатора? В это время цепь эквивалентна разомкнутой цепи, непрерывный ток без петли отсутствует, а зарядка конденсатора происходит во времени, а не мгновенно, поэтому мгновенный ток не является ответом. Как при наличии разности потенциалов цепь без замкнутого контура создает зарядный ток, который длится в течение определенного периода времени?
Рис. 1. Процесс перехода при зарядке конденсатора
Напряжение на конденсаторе не должно резко изменяться. Таким образом, когда питание включено, напряжение на конденсаторе равно нулю, а затем напряжение растет экспоненциально, пока не войдет в установившееся состояние. Конденсатор после входа в установившееся состояние эквивалентен разомкнутой цепи. Фактически конденсатор может блокировать постоянный постоянный ток и отключаться при полной зарядке в цепи. В зависимости от сопротивления утечки конденсатора заряд может сохраняться в конденсаторе в течение длительного периода времени.
Таким образом, когда питание включено, напряжение на конденсаторе равно нулю, а затем напряжение растет экспоненциально, пока не войдет в установившееся состояние. Конденсатор после входа в установившееся состояние эквивалентен разомкнутой цепи. Фактически конденсатор может блокировать постоянный постоянный ток и отключаться при полной зарядке в цепи. В зависимости от сопротивления утечки конденсатора заряд может сохраняться в конденсаторе в течение длительного периода времени.
Когда Usr мгновенно добавляется в цепь резистор-конденсатор, поскольку напряжение на конденсаторе не может внезапно измениться, конденсатор в это время эквивалентен короткому замыканию. Таким образом, в момент времени 0 ток, протекающий через конденсатор и резистор R, равен .
Потом начался процесс заряда конденсатора, и ток становился все меньше и меньше. После 5-кратного времени RC зарядка конденсатора в основном заканчивается, а ток снижается до нуля. С тех пор он вошел в устойчивое состояние. RC(τ) здесь называется постоянной времени.
Мы знаем, что сопротивление равно отношению напряжения к току, то есть R=U/I. Мы также знаем, что емкость C равна отношению количества электричества Q к напряжению U, а количество электричества Q равно произведению тока I на время t.
Получается, что произведение сопротивления на емкость есть время. Единицей измерения сопротивления является ом, а единицей измерения емкости - фарад, поэтому единицей измерения времени являются секунды.
На рисунке 1, когда конденсатор заряжен, напряжение на нем равно .
Находим Uc при t=0, 1RC, 2RC, 3RC, 4RC и 5RC следующим образом:
Видно, что при времени t=0 напряжение на конденсаторе равно нулю; при t=5RC напряжение на конденсаторе почти равно входному напряжению.
Посмотрим на ток, протекающий через конденсатор, его выражение выглядит следующим образом:
При t=5RC, где .
Видно, что ток в это время практически равен нулю. Поэтому необходимо четко различать переходный процесс и установившийся процесс конденсатора.
1) Имеются переходные и установившиеся процессы в цепи заряда конденсаторов.
2) В начале заряда конденсатора необходимо учитывать, что напряжение на конденсаторе не допускает резких изменений, что является важным принципом.
3) Переходный процесс обычно заканчивается после 5τ.
4) Для рисунка 1 в момент переходного пуска напряжение на конденсаторе Uc равно нулю, а ток Ic равен максимальному значению. Из закона Ома известно, что эквивалентное сопротивление конденсатора равно нулю. Обычно мы говорим, что емкость в это время равна короткому замыканию i. В установившемся режиме в конце переходного процесса напряжение конденсатора Uc равно входному напряжению Usr, а ток конденсатора Ic=0. По закону Ома эквивалентное сопротивление конденсатора равно бесконечности. В это время емкость эквивалентна разомкнутой цепи.
5) Если напряжение входного сигнала является коротким импульсом, конденсатор может передать сигнал на нагрузку; если входной сигнал представляет собой постоянное напряжение, конденсатор сработает только при кратковременном переходе, а затем заблокирует входной сигнал; если входной сигнал представляет собой сигнал переменного тока, который находится точно посередине двух вышеуказанных ситуаций.
Чем выше частота сигнала переменного тока, тем легче он проходит через конденсатор. Мы называем эту функцию функцией фильтра верхних частот. Хотя сигнал переменного тока может проходить через конденсатор, будет определенное ограничение. Это показывает, что конденсатор имеет функцию изоляции постоянного тока в установившемся режиме и характеристику верхних частот. Таким образом, мы можем дополнительно проанализировать любую цепь с конденсатором и катушкой индуктивности, мы должны проанализировать цепь в соответствии с переходным состоянием и установившимся состоянием, чтобы получить правильный результат анализа.
Ⅳ Анализ и расчет конденсаторной цепи
Анализ доступен на рисунке ниже:
R1 и R2 оба по 1 кОм, тогда как проанализировать значение Usc?
Шаг 1: Определите постоянную времени конденсатора.
Рисунок 3. Usr при коротком замыкании
Из анализа приведенного выше рисунка видно, что постоянная времени составляет 20 миллисекунд, а время для 5-кратного увеличения постоянной времени составляет 0,1 секунды.
Шаг 2: Рассчитаем конкретное значение Usc.
Когда Usr на рисунке только что установлен, падение напряжения на конденсаторе равно нулю, т.е.
Через 5τ конденсатор заполнен напряжением, и его значение равно Uc=Usr, поэтому Usc=0, .
Когда начинается зарядка, t=0,
Когда время прошло 0,1 секунды, имеем , а Usc в это время практически равен нулю.
Теперь давайте соединим R1 и C параллельно и посмотрим, что получится:
Рисунок 4. R1 и C подключены параллельно
Мы видим, что если Usr на рисунке закорочено, R1 и R2 соединены параллельно, поэтому постоянная времени равна
В начале включения питания Usr C эквивалентно короткому замыканию, а Usr напрямую нагружен на обоих концах резистора R2, так что в это время Usc=Use
Когда схема входит в установившееся состояние, Usc эквивалентно парциальному давлению Usr на резисторах R2 и R1, а именно
На основании этого можно вывести следующее уравнение: .
В приведенной выше формуле первый член справа от знака равенства представляет собой изменение напряжения на конденсаторе, отражающее переходный процесс. Второй член справа от знака равенства представляет собой конечное установившееся напряжение.
Второй член справа от знака равенства представляет собой конечное установившееся напряжение.
Подставьте параметры и сначала рассчитайте постоянную времени: .
Другими словами, при времени 5τ, то есть 25 мкс, выходное напряжение имеет тенденцию к стабилизации. Окончательное значение .
Это все еще 5В, но процесс перехода составляет всего 25 микросекунд, что намного короче предыдущих 0,1 секунды.
Ⅴ Часто задаваемые вопросы
1. Когда конденсатор заряжается в цепи постоянного тока?
В этот момент электрическое поле между пластинами нейтрализует действие электрического поля, создаваемого аккумулятором, и дальнейшее движение заряда прекращается. Таким образом, если конденсатор поместить в цепь постоянного тока, то, как только его обкладки зарядятся, конденсатор фактически ведет себя как разрыв в цепи.
2. Что происходит с током в цепи постоянного тока после зарядки конденсатора?
Для заряда конденсатора Q = емкость C, умноженная на напряжение V. Это просто означает, что скорость изменения напряжения вызывает ток. Если напряжение растет линейно со временем, конденсатор будет потреблять постоянный ток, и как только напряжение перестанет изменяться, ток будет равен нулю.
Это просто означает, что скорость изменения напряжения вызывает ток. Если напряжение растет линейно со временем, конденсатор будет потреблять постоянный ток, и как только напряжение перестанет изменяться, ток будет равен нулю.
3. Течет ли ток в цепи постоянного тока при зарядке конденсатора?
Да. Для цепей постоянного тока, когда конденсатор заряжается или разряжается, ток течет в него и из него. Для цепей переменного тока конденсатор может действовать почти как «резистор», но вместо этого он называется реактивным сопротивлением. Но, увы, ток течет через конденсатор.
4. Конденсаторы заряжаются от переменного или постоянного тока?
Когда постоянный ток подается на цепь только с сопротивлением и емкостью, конденсатор заряжается до уровня приложенного напряжения. Поскольку постоянный ток течет только в одном направлении, после полной зарядки конденсатора ток больше не течет.
5. Можно ли использовать конденсатор в постоянном токе?
Можно ли использовать конденсатор в постоянном токе?
Конденсаторы могут использоваться во многих различных приложениях и схемах, таких как блокирование постоянного тока при передаче аудиосигналов, импульсов или переменного тока или других форм волны, изменяющихся во времени. ... На постоянном токе конденсатор имеет бесконечное сопротивление (разомкнутая цепь), на очень высоких частотах сопротивление конденсатора равно нулю (короткое замыкание).
6. Можно ли заряжать конденсатор постоянным током?
Когда конденсатор подключен к источнику постоянного напряжения, конденсатор начинает заряжаться. Это создаст напряжение на конденсаторе. Как только конденсатор приобретает достаточный заряд, начинает течь ток, и вскоре напряжение на конденсаторе достигает значения, приблизительно равного напряжению источника постоянного тока.
7. Почему через конденсатор проходит переменный ток, а не постоянный?
Конденсаторы имеют две параллельные металлические пластины, расположенные близко друг к другу, и между пластинами имеется зазор.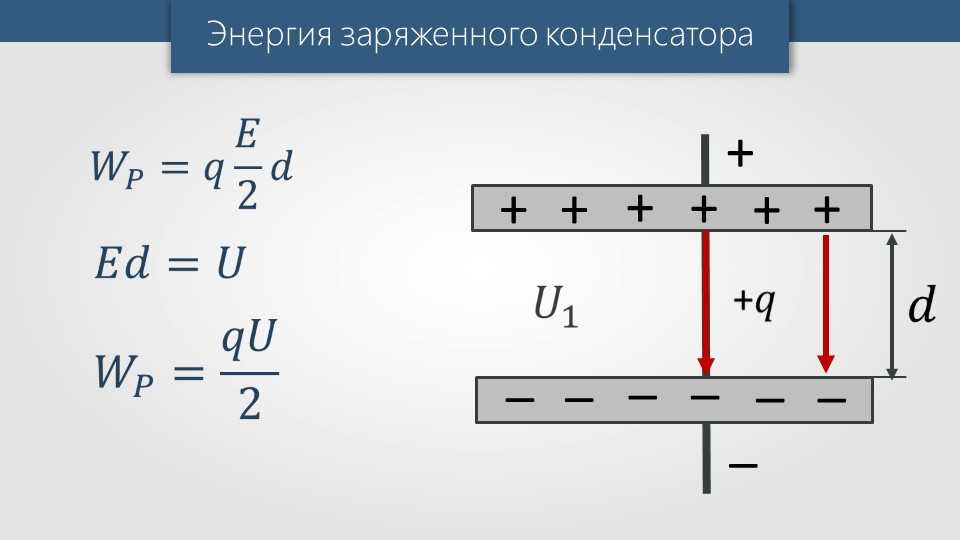 Конденсатор блокирует постоянный ток, но пропускает переменный ток. ... Поэтому электроны, текущие в одном направлении (т.е. постоянном токе), не могут пройти через конденсатор. Но кажется, что электроны от источника переменного тока текут через C.
Конденсатор блокирует постоянный ток, но пропускает переменный ток. ... Поэтому электроны, текущие в одном направлении (т.е. постоянном токе), не могут пройти через конденсатор. Но кажется, что электроны от источника переменного тока текут через C.
8. Что происходит, когда конденсатор подключен к постоянному току?
Когда конденсаторы подключены к постоянному напряжению питания постоянного тока, их пластины заряжаются до тех пор, пока значение напряжения на конденсаторе не станет равным внешнему приложенному напряжению. ... Затем емкость в цепях переменного тока зависит от частоты, поскольку конденсатор постоянно заряжается и разряжается.
9. Почему в цепи постоянного тока используется конденсатор?
Конденсаторы используются для уменьшения пульсаций напряжения. При подаче на параллельную цепь высокого напряжения конденсатор заряжается, а с другой стороны, разряжается при низком напряжении. В то время как вытекающий ток представляет собой переменный ток, большинство электронных схем работают с постоянным током.
10. Почему конденсаторы блокируют постоянный ток?
Мы знаем, что в источнике постоянного тока нет частоты, т.е. частота 0 Гц. Если мы поместим частоту «f = 0» в формулу индуктивного сопротивления (которое представляет собой сопротивление переменному току в емкостной цепи). Если мы положим XC как бесконечность, значение тока будет равно нулю. Это точная причина, по которой конденсатор блокирует постоянный ток.
11. Как заряжается конденсатор в цепи постоянного тока?
При использовании в цепи постоянного тока или цепи постоянного тока конденсатор заряжается до напряжения питания, но блокирует протекание через него тока, поскольку диэлектрик конденсатора является непроводящим и, по сути, является изолятором. ... В этот момент говорят, что конденсатор «полностью заряжен» электронами.
12. Какой конденсатор используется в цепи постоянного тока?
Развязывающий конденсатор используется для развязки двух электронных цепей.


 01.19
01.19 01.19
01.19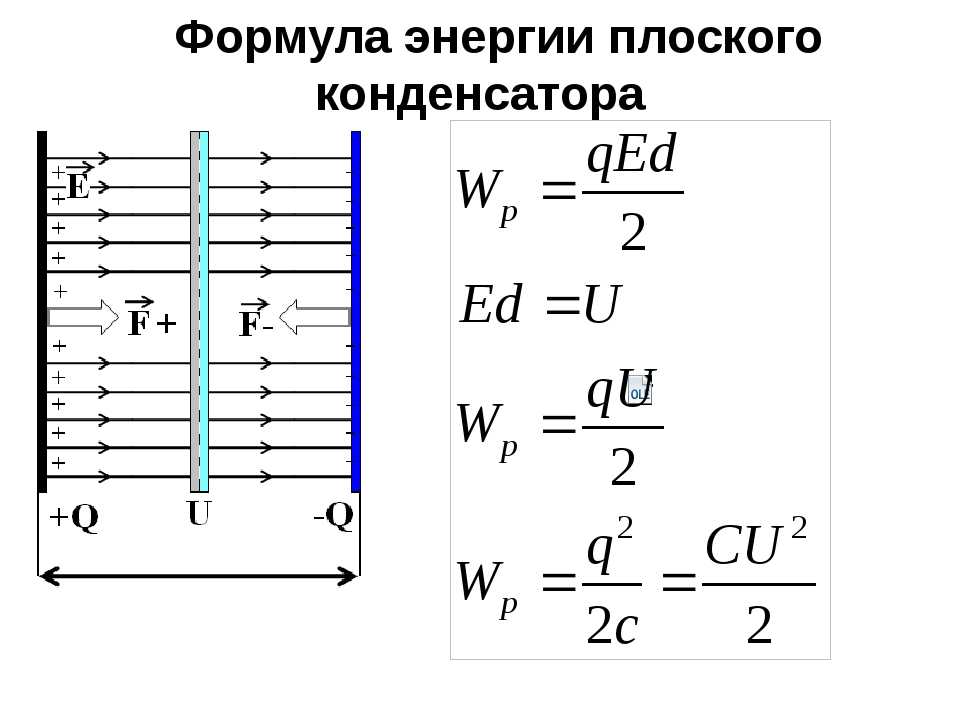 статистика
статистика Расстояние d между пластинами равно 1 см. Диэлектрик — стекло. Определить объемную плотность энергии поля конденсатора.
Расстояние d между пластинами равно 1 см. Диэлектрик — стекло. Определить объемную плотность энергии поля конденсатора. Определить расстояние между пластинами, напряженность и объемную плотность энергии электрического поля конденсатора.
Определить расстояние между пластинами, напряженность и объемную плотность энергии электрического поля конденсатора.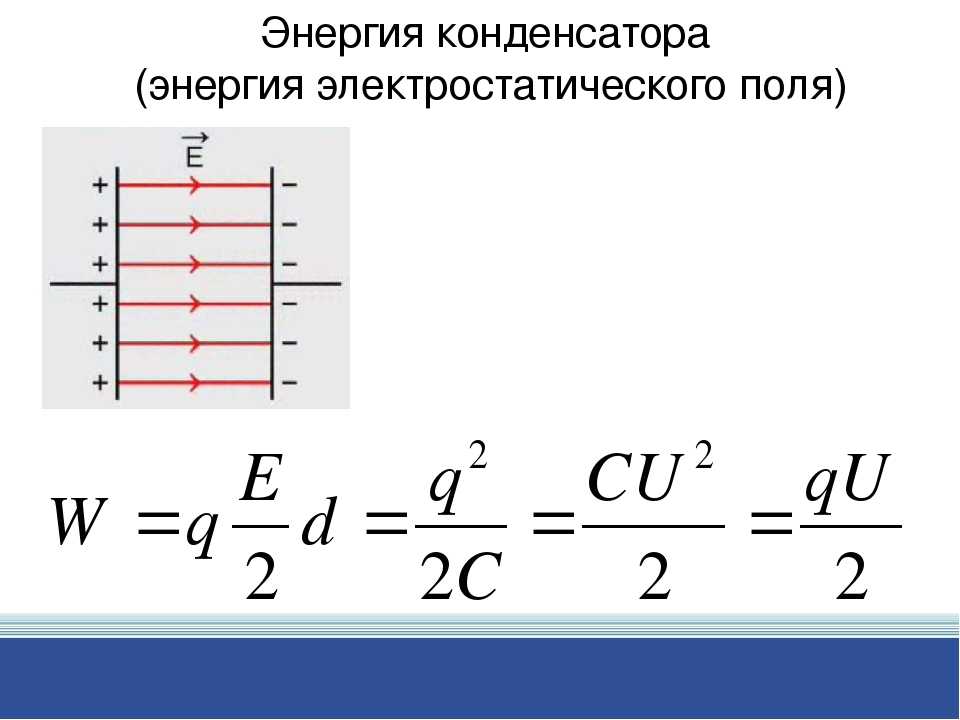 Конденсаторы соединили параллельно одноименно заряженными обкладками, и разность потенциалов оказалась равной U = 50 В. Определить отношение емкостей этих конденсаторов.
Конденсаторы соединили параллельно одноименно заряженными обкладками, и разность потенциалов оказалась равной U = 50 В. Определить отношение емкостей этих конденсаторов. Найдите этот заряд. Расстояние между пластинами равно 0,5 см, масса капельки равна 3,8·10–11 кг.
Найдите этот заряд. Расстояние между пластинами равно 0,5 см, масса капельки равна 3,8·10–11 кг. Подключите другой конец провода типа «крокодил» к контакту GND на плате.
Подключите другой конец провода типа «крокодил» к контакту GND на плате. A4.digitalWrite(false)
})
навсегда (функция () {
light.graph(pins.A5.analogRead(), 1010)
пауза(200)
})
A4.digitalWrite(false)
})
навсегда (функция () {
light.graph(pins.A5.analogRead(), 1010)
пауза(200)
})