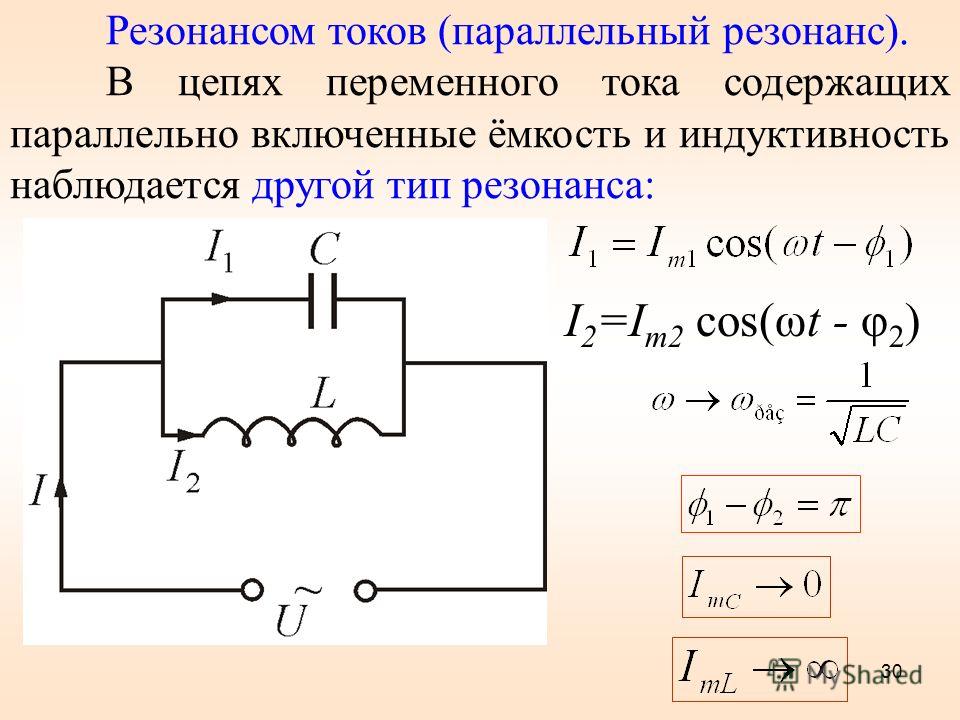
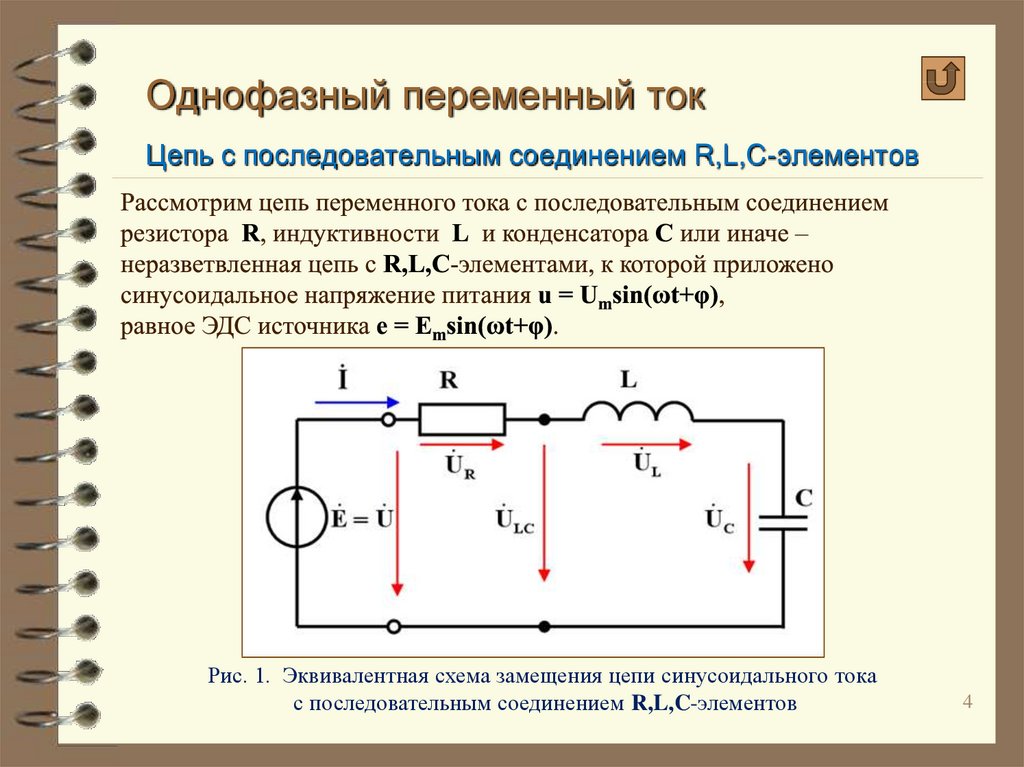
Конденсатор включен в цепь переменного тока стандартной ч… -reshimne.ru
Новые вопросы
Ответы
Решение на картинке.
Похожие вопросы
Вычисли мощность устройства,если оно совершает работу за 30 секунд работу 2 кДж…
Определить частоту свободных электромагнитных колебаний в контуре с параметрами: 2 мкГн и 0,5 пФ…
Как можно узнать по графику зависимости координаты от времени в какой момент времени расстояние между телами будет равно начпльному…
Двигатель трактора развивает мощность 200кВт.Какую работу совершит двигатель в течение одного часа.
Ответ дай в киловатт-часах….
Протон в однородном магнитном поле с индукцией 4 мТл движется по окружности. Найти радиус и период его обращения….
Игрушечный автомобиль прикладывает к прицепу силу 20 Н и проделал путь 10 м. Какой величины работу совершил автомобиль?…
Математика
Литература
Алгебра
Геометрия
Английский язык
Химия
Физика
Другие предметы
История
Обществознание
Окружающий мир
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АРХАНГЕЛЬСКОЙ ОБЛАСТИ Государственное автономное профессиональное образовательное учреждение Архангельской области «Северодвинский техникум социальной инфраструктуры» (ГАПОУ АО «СТСИ») УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС УЧЕБНОЙ ДИСЦИПЛИНЫ ОДП. Северодвинск 2014
УМК учебной дисциплины рассмотрен и рекомендован к использованию на заседании предметно-цикловой комиссии естественно-научного цикла Протокол № 4 от «09» апреля 2014 г.
— извлечение из ФГОС СПО — требования к знаниям, умениям по дисциплине; — рабочие учебные программы дисциплины. ФЕДЕРАЛЬНЫЙ ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ (10-11 КЛ.) от 12.04.2012 Требования к результатам освоения основной образовательной программы «Физика» (базовый уровень) – требования к предметным результатам освоения базового курса физики должны отражать: 1) сформированность представлений о роли и месте физики в современной научной картине мира; понимание физической сущности наблюдаемых во Вселенной явлений; понимание роли физики в формировании кругозора и функциональной грамотности человека для решения практических задач; 2) владение основополагающими физическими понятиями, закономерностями, законами и теориями; уверенное пользование физической терминологией и символикой; 3) владение основными методами научного познания, используемыми в физике: наблюдение, описание, измерение, эксперимент; умения обрабатывать результаты измерений, обнаруживать зависимость между физическими величинами, объяснять полученные результаты и делать выводы; 4) сформированность умения решать физические задачи; 5) сформированность умения применять полученные знания для объяснения условий протекания физических явлений в природе и для принятия практических решений в повседневной жизни; 6) сформированность собственной позиции по отношению к физической информации, получаемой из разных источников. 1) сформированность системы знаний об общих физических закономерностях, законах, теориях, представлений о действии во Вселенной физических законов, открытых в земных условиях; 2) сформированность умения исследовать и анализировать разнообразные физические явления и свойства объектов, объяснять принципы работы и характеристики приборов и устройств, объяснять связь основных космических объектов с геофизическими явлениями; 3) владение умениями выдвигать гипотезы на основе знания основополагающих физических закономерностей и законов, проверять их экспериментальными средствами, формулируя цель исследования; 4) владение методами самостоятельного планирования и проведения физических экспериментов, описания и анализа полученной измерительной информации, определения достоверности полученного результата; 5) сформированность умений прогнозировать, анализировать и оценивать последствия бытовой и производственной деятельности человека, связанной с физическими процессами, с позиций экологической безопасности. МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АРХАНГЕЛЬСКОЙ ОБЛАСТИ Государственное автономное профессиональное образовательное учреждение Архангельской области «Северодвинский техникум социальной инфраструктуры » (ГАПОУ АО «СТСИ») | ||||||||||||||||||
| Котчет у об основной деятельности государственного бюджетного учреждения… План развития архивного дела за 2016 год Государственным бюджетным учреждением Архангельской области «Государственный архив Архангельской… | О структуре агентства стратегических разработок Архангельской области | |||||||||||||||||
| Документация об открытом аукционе в электронной форме Пцн) Государственного учреждения «Управления вневедомственной охраны при Управлении внутренних дел по Архангельской области» (гу… | Документация об открытом аукционе в электронной форме «Управления вневедомственной охраны при Управлении внутренних дел по Архангельской области» (гу «уво при увд» по Архангельской области).  | |||||||||||||||||
| Документация об открытом аукционе в электронной форме Пцн) соответствующих подразделений Государственного учреждения «Управления вневедомственной охраны при Управлении внутренних дел… | 1. Настоящее Положение разработано в соответствии со статьями 135,… Архангельской области, Отраслевым примерным положением об оплате труда в государственных бюджетных и автономных учреждениях Архангельской… | |||||||||||||||||
| Руководство пользователя 10 1 Операция «Прием запроса на согласование» Администрация Губернатора Архангельской области и Правительства Архангельской области | Документация об открытом аукционе в электронной форме Пцн) Государственного учреждения «Управления вневедомственной охраны при Управлении внутренних дел по Архангельской области» (гу… | |||||||||||||||||
| К извещению об аукционе в электронной форме Архангельской области и помещений Управления Судебного департамента в Архангельской области и нао к отопительному периоду 2015– 2016.  .. | Документация об открытом аукционе в электронной форме Лот №1: поставка картриджей для факсов и копировальных аппаратов в количестве – 56 шт для нужд районных (городских) и гарнизонных… | |||||||||||||||||
| Организация работы врачебно-сестринской бригады службы медицины катастроф Архангельской области: Методические указания. Архангельск. Министерство здравоохранения и социального развития Архангельской области…. | Документация об аукционе в электронной форме на электронной площадке… Закупка у субъектов малого предпринимательства, социально ориентированных некоммерческих организаций принтеров для нужд федеральных… | |||||||||||||||||
| Цель: развитие познавательного интереса учащихся к изучению достопримечательностей… Данное мероприятие приурочено к празднованию 80 – летия Архангельской области. В игре семь станций, количество участников 3 команд…. | Об утверждении программы государственных гарантий оказания гражданам. ..Российской Федерации бесплатной медицинской помощи и контроле за их реализацией» и от 4 октября 2010 года n 782 «о программе государственных… | |||||||||||||||||
| Агентство по организационному обеспечению деятельности мировых судей… Утвердить прилагаемые изменения, которые вносятся в Инструкцию по судебному делопроизводству у мирового судьи, утвержденную постановлением… | Агентство по организационному обеспечению деятельности мировых судей… Приказ Управления по организационному обеспечению деятельности мировых судей Архангельской области от 23 декабря 2003 года №68-од… |
03 ФИЗИКА
23.12 Цепи переменного тока серии RLC — College Physics: OpenStax
Глава 23 Электромагнитная индукция, цепи переменного тока и электрические технологии
Сводка
- Вычислите импеданс, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и/или ток в последовательной цепи RLC.
- Нарисуйте принципиальную схему последовательной цепи RLC.
- Объясните значение резонансной частоты.
Катушки индуктивности, конденсаторы и резисторы в цепи переменного тока сами по себе препятствуют току. Как они ведут себя, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в омах не просто складываются. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично или полностью компенсируют эффект друг друга. На рис. 1 показана цифра 9.0017 Цепь серии RLC с источником переменного напряжения, поведение которой рассматривается в этом разделе. Суть анализа схемы RLC заключается в частотной зависимости [latex]\boldsymbol{X_L}[/latex] и [latex]\boldsymbol{X_C}[/latex] и их влиянии на фазу зависимости напряжения от тока (установлено в предыдущем разделе). Это приводит к частотной зависимости схемы с важными «резонансными» свойствами, которые лежат в основе многих приложений, таких как радиотюнеры.
Суммарный эффект сопротивления [латекс]\boldsymbol{R}[/латекс], индуктивного сопротивления [латекс]\boldsymbol{X_L}[/латекс] и емкостного сопротивления [латекс]\boldsymbol{X_C}[/латекс] составляет определяется как импеданс , аналог переменного тока для сопротивления в цепи постоянного тока. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс]\boldsymbol{I_0 =}[/латекс][латекс]\boldsymbol{\frac{V_0}{Z}}[/латекс][латекс]\boldsymbol{\textbf{или} \; I _{\textbf{rms}} =}[/latex][latex]\boldsymbol{\frac{V _{\textbf{rms}}}{Z}}.[/latex]
Здесь [latex]\boldsymbol{I_0}[/latex] — пиковый ток, [latex]\boldsymbol{V_0}[/latex] — пиковое напряжение источника, а [latex]\boldsymbol{Z}[/latex] — импеданс цепи. Единицами импеданса являются омы, и его влияние на цепь, как и следовало ожидать: чем больше импеданс, тем меньше ток.
Чтобы получить выражение для [латекс]\boldsymbol{Z}[/латекс] через [латекс]\жирныйсимвол{R}[/латекс], [латекс]\жирныйсимвол{X_L}[/латекс] и [латекс] \boldsymbol{X_C}[/latex], теперь мы рассмотрим, как напряжения на различных компонентах связаны с напряжением источника. Эти напряжения помечены как [latex]\boldsymbol{V_R}[/latex], [latex]\boldsymbol{V_L}[/latex] и [latex]\boldsymbol{V_C}[/latex] на рисунке 1.
Сохранение заряда требует, чтобы ток был одинаковым в каждой части цепи все время, так что мы можем назвать токи в [латекс]\boldsymbol{R}[/латекс], [латекс]\boldsymbol{L}[ /latex] и [latex]\boldsymbol{C}[/latex] равны и совпадают по фазе. Но из предыдущего раздела мы знаем, что напряжение на индукторе [латекс]\boldsymbol{V_L}[/latex] опережает ток на одну четвертую периода, напряжение на конденсаторе [латекс]\boldsymbol{V_C}[ /latex] соответствует току на одну четвертую цикла, а напряжение на резисторе [latex]\boldsymbol{V_R}[/latex] точно совпадает по фазе с током. На рис.
2 эти отношения показаны на одном графике, а также показано общее напряжение вокруг цепи [latex]\boldsymbol{V = V_R + V_L + V_C}[/latex], где все четыре напряжения являются мгновенными значениями. Согласно петлевому правилу Кирхгофа, полное напряжение вокруг цепи VV также является напряжением источника. 92}},[/латекс]
, где [латекс]\boldsymbol{V_{0R}}[/латекс], [латекс]\boldsymbol{V_{0L}}[/латекс] и [латекс]\boldsymbol{V_{0C}}[/латекс] пиковые напряжения на [латекс]\boldsymbol{R}[/латекс], [латекс]\boldsymbol{L}[/латекс] и [латекс]\boldsymbol{C}[/латекс] соответственно. Теперь, используя закон Ома и определения из главы 23.11 «Реактивное, индуктивное и емкостное сопротивление», подставим [латекс]\boldsymbol{V_0 = I_0Z}[/latex] в приведенное выше, а также [латекс]\boldsymbol{V_{0R} = I_0R}[/latex], [latex]\boldsymbol{V_{0L} = I_0X_L}[/latex] и [latex]\boldsymbol{V_{0C} = I_0X_C}[/latex], что дает 92}},[/латекс]
, который представляет собой импеданс цепи переменного тока серии RLC .
Для цепей без резистора возьмите [latex]\boldsymbol{R = 0}[/latex]; для тех, у кого нет индуктора, возьмите [латекс]\boldsymbol{X_L = 0}[/латекс]; а для тех, у кого нет конденсатора, возьмите [латекс]\boldsymbol{X_C = 0}[/латекс].
Пример 1. Расчет импеданса и тока
Цепь серии RLC имеет резистор [латекс]\boldsymbol{40,0 \;\Омега}[/латекс], катушку индуктивности 3,00 мГн и [латекс]\boldsymbol{5,00 \;\mu F}[/latex] конденсатор. (a) Найдите полное сопротивление цепи при частотах 60,0 Гц и 10,0 кГц, учитывая, что эти частоты и значения для [latex]\boldsymbol{L}[/latex] и [latex]\boldsymbol{C}[/latex] одинаковы. как в главе 23.11 Пример 1 и главе 23.11 Пример 2. (b) Если источник напряжения имеет [латекс]\жирный символ{I_{\textbf{rms}}}[/латекс] на каждой частоте? 92}}[/latex], чтобы найти импеданс, а затем закон Ома, чтобы найти силу тока.
2}}[/ латекс] дает 92}} \\[1em] & \boldsymbol{190 \;\Omega \;\textbf{at} \; 10,0 \;\textbf{кГц}}. \end{array}[/latex]
Обсуждение для (a)
В обоих случаях результат почти одинаков для наибольшего значения, а импеданс определенно не является суммой отдельных значений. Ясно, что [латекс]\boldsymbol{X_L}[/латекс] доминирует на высокой частоте, а [латекс]\жирныйсимвол{X_C}[/латекс] доминирует на низкой частоте.
Решение для (b)
Текущий [латекс]\boldsymbol{I _{\textbf{среднеквадратичное значение}}}[/латекс] можно найти, используя версию закона Ома для переменного тока в уравнении [латекс]\жирныйсимвол{ I_{rms} = V_{rms} / Z}[/латекс]:
[латекс]\boldsymbol{I _{\textbf{rms}} =}[/latex][латекс]\boldsymbol{\frac{V _{\textbf{rms}}}{Z}}[/latex][латекс ]\boldsymbol{=}[/латекс][латекс]\boldsymbol{\frac{120 \;\textbf{V}}{531 \;\Omega}}[/latex][латекс]\boldsymbol{= 0,226 \; \textbf{A}}[/latex] при 60,0 Гц
Наконец, при 10,0 кГц мы находим
[латекс]\boldsymbol{I _{\textbf{rms}} =}[/latex][latex]\boldsymbol {\ frac {V _ {\ textbf {rms}}} {Z}} [/latex][latex]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{120 \;\textbf{V} }{190 \;\Omega}}[/latex][latex]\boldsymbol{= 0,633 \;\textbf{A}}[/latex] при 10,0 кГц
Обсуждение для (a)
Ток при 60,0 Гц такой же (с точностью до трех цифр), что и для одного конденсатора в примере 1.
2}}[/латекс] дает 92}}}.[/латекс]
Реактансы зависят от частоты: [latex]\boldsymbol{X_L}[/latex] велики на высоких частотах и [latex]\boldsymbol{X_C}[/latex] велики на низких частотах, как мы видели в трех предыдущих примерах. . На некоторой промежуточной частоте [latex]\boldsymbol{f_0}[/latex] реактивные сопротивления будут равны и сокращаются, что дает [latex]\boldsymbol{Z = R}[/latex] — это минимальное значение импеданса, и максимальное значение для результатов [latex]\boldsymbol{I_{\textbf{rms}}}[/latex]. Мы можем получить выражение для [латекс]\boldsymbol{f_0}[/латекс], взяв
[латекс]\boldsymbol{X_L = X_C}.[/латекс]
Замена определений [латекс]\boldsymbol{X_L}[/латекс] и [латекс]\жирныйсимвол{X_C}[/латекс],
[латекс]\boldsymbol{2 \pi f_0 L =}[/latex][латекс]\boldsymbol{\frac{1}{2 \pi f_0 C}}.[/latex]
Решение этого выражения для [латекс]\boldsymbol{f_0}[/латекс] дает
[латекс]\boldsymbol{f_0 =}[/латекс][латекс]\boldsymbol{\frac{1}{2 \pi \sqrt{LC}}},[/latex]
, где [латекс]\boldsymbol{f_0}[/латекс] – резонансная частота цепи серии RLC .
Это также собственная частота , при которой схема будет колебаться, если не будет управляться источником напряжения. В точке [latex]\boldsymbol{f_0}[/latex] эффекты катушки индуктивности и конденсатора компенсируются, так что [latex]\boldsymbol{Z = R}[/latex] и [latex]\boldsymbol{I_{\ textbf{rms}}}[/latex] — это максимум.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания — в данном случае вызванные источником напряжения — на собственной частоте системы. Приемник в радио — это Цепь RLC , которая лучше всего колеблется в своем [латексе]\boldsymbol{f_0}[/латекс]. Переменный конденсатор часто используется для настройки [latex]\boldsymbol{f_0}[/latex] для получения желаемой частоты и отклонения других. Рисунок 3 представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в [латекс]\boldsymbol{I_{\textbf{rms}}}[/latex] в [латекс]\boldsymbol{f_0}[/latex] . Две кривые относятся к двум разным цепям, которые отличаются только величиной сопротивления в них.
Пик ниже и шире для схемы с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не резонирует так сильно и не будет такой избирательной, например, в радиоприемнике.
Пример 2: Расчет резонансной частоты и тока
Для той же цепи серии RLC , имеющей резистор [латекс]\boldsymbol{40,0 \;\Омега}[/латекс], катушку индуктивности 3,00 мГн и [латекс]\ boldsymbol{5.00 \;\mu F}[/latex] конденсатор: (a) Найдите резонансную частоту. (b) Рассчитайте [латекс]\boldsymbol{I_{\textbf{rms}}}[/latex] в резонансе, если [латекс]\boldsymbol{V_{\textbf{rms}}}[/латекс] равно 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex]\boldsymbol{f_0 = \frac{1}{2 \pi \sqrt{LC}}}[/latex].
Ток на этой частоте такой же, как если бы в цепи был только резистор.
Решение для (a)
Ввод заданных значений для [латекс]\жирныйсимвол{L}[/латекс] и [латекс]\жирныйсимвол{С}[/латекс] в выражение, данное для [латекс]\ boldsymbol{f_0}[/latex] в [latex]\boldsymbol{f_0 = \frac{1}{2 \pi \sqrt{LC}}}[/latex] дает 9{-6} \;\textbf{F})}} = 1,30 \;\textbf{кГц}.} \end{array}[/latex]
Обсуждение для (a)
Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, две частоты, выбранные в предыдущих примерах. Этого и следовало ожидать, поскольку на низкой частоте преобладал конденсатор, а на высокой частоте — катушка индуктивности. Их эффекты одинаковы на этой промежуточной частоте.
Решение для (b)
Ток определяется законом Ома. В резонансе два реактивных сопротивления равны и компенсируются, так что импеданс равен одному сопротивлению. Таким образом,
[латекс]\boldsymbol{I _{\textbf{rms}} =}[/latex][латекс]\boldsymbol{\frac{V _{\textbf{rms}}}{Z}}[/latex][латекс ]\boldsymbol{=}[/latex][latex]\boldsymbol{\frac{120 \;\textbf{V}}{40,0 \;\Omega}}[/latex][latex]\boldsymbol{= 3,00 \; \textbf{A}}.
[/latex]
Обсуждение для (b)
В резонансе ток больше, чем на более высоких и более низких частотах, рассмотренных для той же цепи в предыдущем примере.
Если ток зависит от частоты в RLC , то подаваемая на него мощность также зависит от частоты. Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рис. 2, напряжение и ток не совпадают по фазе в цепи RLC . Существует фазовый угол [латекс]\boldsymbol{\phi}[/латекс] между напряжением источника [латекс]\жирныйсимвол{V}[/латекс] и током [латекс]\жирныйсимвол{I}[/латекс ], который можно найти из
[латекс]\boldsymbol{\textbf{cos} \;\phi =}[/latex][латекс]\boldsymbol{\frac{R}{Z}}.[/latex] 9{\circ}}[/latex] и что напряжение и ток совпадают по фазе, как и ожидается для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Это связано как с тем, что напряжение и ток не совпадают по фазе, так и с тем, что [латекс]\жирный символ{I _{\textbf{среднеквадратичное значение}}}[/латекс] ниже.
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
[латекс]\boldsymbol{P_{\textbf{ave}} = I_{\textbf{rms}} V_{\textbf{rms}} \textbf{cos} \;\phi},[/latex]
Таким образом, [latex]\boldsymbol{\textbf{cos} \;\phi}[/latex] называется коэффициентом мощности , который может варьироваться от 0 до 1. При проектировании эффективного двигателя желательны коэффициенты мощности, близкие к 1, Например. На резонансной частоте [латекс]\boldsymbol{\textbf{cos} \;\phi = 1}[/латекс].
Пример 3: Расчет коэффициента мощности и мощности
Для той же цепи серии RLC , имеющей резистор [латекс]\boldsymbol{40,0 \;\Омега}[/латекс], катушку индуктивности 3,00 мГн, [латекс]\ boldsymbol{5,00 \;\mu F}[/latex] конденсатор и источник напряжения с [латекс]\boldsymbol{V _{\textbf{rms}}}[/latex] 120 В: (a) Рассчитайте мощность коэффициент и фазовый угол для [латекса]\boldsymbol{f = 60,0 \textbf{Гц}}[/латекс].
(b) Какова средняя мощность при 50,0 Гц? в) Найдите среднюю мощность на резонансной частоте контура.
Стратегия и решение для (a)
Коэффициент мощности при 60,0 Гц определяется из
[латекс]\boldsymbol{\textbf{cos} \;\phi =}[/latex][латекс]\boldsymbol {\frac{R}{Z}}.[/latex]
Мы знаем [латекс]\boldsymbol{Z = 531 \;\Omega}[/latex] из примера 1, так что
[латекс]\boldsymbol {cos \;\phi =}[/латекс][латекс]\boldsymbol{\frac{40,0 \;\Omega}{531 \;\Omega}}[/latex][латекс]\boldsymbol{= 0,0753 \;\ текстбф{ат} \; 60,0 \;\textbf{Гц}}.[/latex]
9{\circ}}[/latex] не в фазе).Стратегия и решение для (b)
Средняя мощность при 60,0 Гц составляет
[латекс]\boldsymbol{P_{ave} = I_{\textbf{rms}}V_{\textbf{rms}} \ текстбф{кос} \; \phi}[/latex]
[latex]\boldsymbol{I_{\textbf{rms}}}[/latex] в примере 1 равно 0,226 А. Ввод известных значений дает
[latex]\boldsymbol {P_{\textbf{ave}} = (0,226 \;\textbf{A})(120 \;\textbf{V})(0,0753) = 2,04 \;\textbf{W at} \; 60,0 \;\textbf{Гц}}.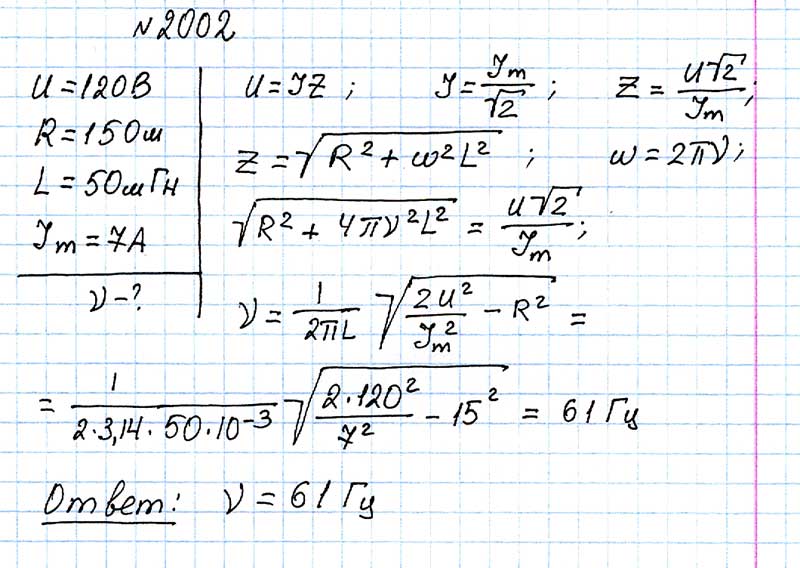
[/latex]
Стратегия и решение для (c)
На резонансной частоте мы знаем [латекс]\boldsymbol{\textbf{cos} \;\phi = 1}[/латекс] и [латекс]\boldsymbol{ I_{\textbf{rms}}}[/latex] оказалось равным 6,00 А в примере 2. Таким образом,
[латекс]\boldsymbol{P_{\textbf{ave}} = (3,00 \;\textbf{A })(120 \;\textbf{V})(1) = 360 \;\textbf{W}}[/latex] в резонансе (1,30 кГц)
Обсуждение
И ток, и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на более высоких и более низких частотах.
Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, при этом резистор рассеивает именно то, что источник напряжения помещает в цепь. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, такого как радиоволны.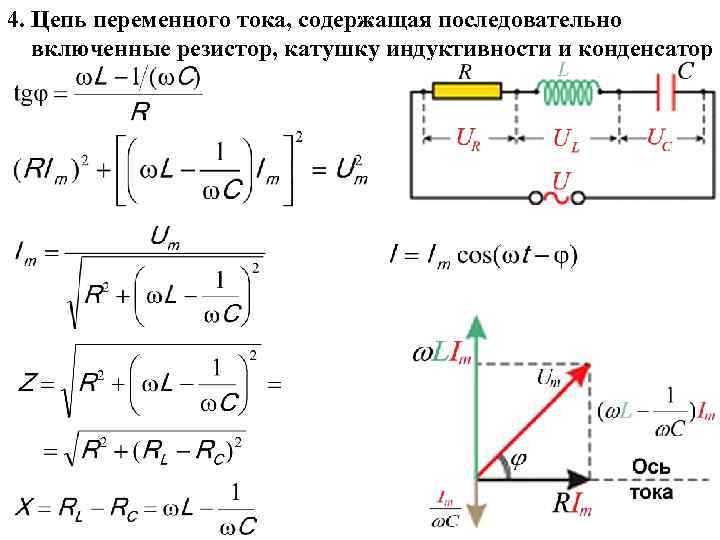
Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но его также можно подавить, как в случае с этой главой. Схема аналогична колесу автомобиля, движущегося по неровной дороге, как показано на рис. 4. Равномерно расположенные неровности на дороге аналогичны источнику напряжения, приводящему в движение колесо вверх и вниз. Амортизатор аналогичен сопротивлению, демпфирующему и ограничивающему амплитуду колебаний. Энергия в системе переходит туда и обратно между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если удары о неровности дороги происходят на резонансной частоте.
Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.Чистая цепь LC с незначительным сопротивлением колеблется на частоте [latex]\boldsymbol{f_0}[/latex], той же резонансной частоте, что и цепь RLC . Он может служить эталоном частоты или тактовой схемой, например, в цифровых наручных часах. При очень малом сопротивлении для поддержания колебаний требуется лишь очень небольшая затрата энергии. Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рис. 5 показана аналогия между LC схема и масса на пружине.
Рисунок 5. Цепь LC аналогична массе, колеблющейся на пружине без трения и движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
PhET Explorations: Набор для построения цепей (AC+DC), виртуальная лаборатория
Создавайте схемы с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных приборов, таких как вольтметры и амперметры.
Рис. 6. Набор для построения схемы (AC+DC), виртуальная лаборатория- Аналогом сопротивления переменного тока является импеданс [латекс]\boldsymbol{Z}[/латекс], комбинированный эффект резисторов, катушек индуктивности и конденсаторов, определяемый версией закона Ома для переменного тока:
[латекс]\boldsymbol{I_0 =}[/латекс][латекс]\boldsymbol{\frac{V_0}{Z}}[/латекс][латекс]\boldsymbol{\textbf{или} \; I _{\textbf{rms}} =}[/latex][латекс]\boldsymbol{\frac{V _{\textbf{rms}}}{Z}},[/latex]
, где [latex]\boldsymbol{I_0}[/latex] — пиковое значение тока, а [latex]\boldsymbol{V_0}[/latex] — пиковое напряжение источника. 92}}[/латекс].
- Резонансная частота [латекс]\boldsymbol{f_0}[/латекс], при которой [латекс]\boldsymbol{X_L = X_C}[/латекс], равна
[латекс]\boldsymbol{f_0 =}[/латекс][латекс]\boldsymbol{\frac{1}{2 \pi \sqrt{LC}}}[/латекс].
- В цепи переменного тока существует фазовый угол [latex]\boldsymbol{\phi}[/latex] между напряжением источника [latex]\boldsymbol{V}[/latex] и током [latex]\boldsymbol{I} [/latex], который можно найти в
[латекс]\boldsymbol{\textbf{cos} \;\phi =}[/латекс][латекс]\boldsymbol{\frac{R}{Z}}[/латекс], 9{\ circ}} [/latex] для чисто резистивной цепи или цепи RLC в резонансе.
- Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс]\boldsymbol{P_{\textbf{ave}} = I_{\textbf{rms}}V_{\textbf{rms}} \;\textbf{cos} \;\phi},[/latex]
[latex]\boldsymbol{\textbf{cos} \;\phi}[/latex] называется коэффициентом мощности, который принимает значения от 0 до 1.
Задачи и упражнения
1: Цепь RL состоит из резистора [латекс]\boldsymbol{40,0 \;\Омега}[/латекс] и катушки индуктивности 3,00 мГн. (a) Найдите его импеданс [латекс]\boldsymbol{Z}[/латекс] на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [latex]\boldsymbol{Z}[/latex] со значениями, найденными в примере 1, в котором также был конденсатор.
2: Цепь RC состоит из резистора [латекс]\boldsymbol{40,0 \;\Omega}[/latex] и резистора [латекс]\boldsymbol{5,00 \;\мкФ[/latex] конденсатор. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [латекс]\boldsymbol{Z}[/латекс] с найденными в примере 1, в котором также был индуктор.
3: Цепь LC состоит из катушки индуктивности [латекс]\boldsymbol{3,00 \;\textbf{мГн}}[/латекс] и [латекс]\boldsymbol{5,00 \;\mu F}[ /латексный] конденсатор. (а) Найдите его импеданс на частотах 60,0 Гц и 10,0 кГц. (b) Сравните эти значения [latex]\boldsymbol{Z}[/latex] со значениями, найденными в примере 1, в котором также был резистор.
4: Какова резонансная частота катушки индуктивности 0,500 мГн, подключенной к [латексу]\boldsymbol{40,0 \; \mu F}[/latex] конденсатор?
5: Для приема AM-радио вам понадобится схема RLC , которую можно заставить резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированного [латексного]\boldsymbol{1.00 \;\mu \textbf{H}}[/латексного] индуктора, соединенного с переменным конденсатором. Какой диапазон емкости нужен?
6: Предположим, у вас есть запас катушек индуктивности от 1,00 нГн до 10,0 Гн и конденсаторов емкостью от 1,00 пФ до 0,100 Ф. один конденсатор?
7: Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8: Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ2,00 мкФ?
9: Самая низкая частота в диапазоне FM-радио — 88,0 МГц. а) Какая индуктивность необходима для получения этой резонансной частоты, если он подключен к конденсатору емкостью 2,50 пФ? (b) Конденсатор переменный, что позволяет регулировать резонансную частоту до 108 МГц. Какая должна быть емкость на этой частоте?
10: Цепь серии RLC имеет [латекс]\boldsymbol{2,50 \;\Омега}[/латекс] резистор, [латекс]\boldsymbol{100 \;\mu \textbf{H}} [/latex] индуктор и конденсатор [latex]\boldsymbol{80,0 \;\mu \textbf{F}}[/latex]. (a) Найдите полное сопротивление цепи на частоте 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет [latex]\boldsymbol{V_{\textbf{rms}} = 5,60 \;\textbf{V}}[/latex], что такое [latex]\boldsymbol{I _{\textbf{ rms}}}[/latex] на каждой частоте? г) Какова резонансная частота цепи? (e) Что такое [латекс]\boldsymbol{I_{\textbf{rms}}}[/латекс] в резонансе?
11: Цепь серии RLC имеет [латекс]\boldsymbol{1.00 \;\textbf{k} \Omega}[/latex] резистор, [латекс]\boldsymbol{150 \;\mu \ textbf{H}}[/latex] индуктор и конденсатор 25,0 нФ. а) Найдите полное сопротивление цепи на частоте 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет [latex]\boldsymbol{V_{\textbf{rms}} = 408 \;\textbf{V}}[/latex], что такое [latex]\boldsymbol{I _{\textbf{ rms}}}[/latex] на каждой частоте? г) Какова резонансная частота цепи? (e) Что такое [латекс]\boldsymbol{I_{\textbf{rms}}}[/латекс] в резонансе?
12: Цепь серии RLC имеет [латекс]\boldsymbol{2. 50 \;\Omega}[/latex] резистор, [латекс]\boldsymbol{100 \;\mu H}[/latex] индуктор и конденсатор [латекс]\boldsymbol{80,0 \;\mu \textbf{F}}[/латекс]. (a) Найдите коэффициент мощности при [латекс]\boldsymbol{f = 120 \;\textbf{Гц}}[/латекс]. (b) Каков фазовый угол на частоте 120 Гц? в) Какова средняя мощность на частоте 120 Гц? г) Найдите среднюю мощность на резонансной частоте контура.
13: Ан Цепь серии RLC имеет [латекс]\boldsymbol{1.00 \;\textbf{k} \Omega}[/latex] резистор, [латекс]\boldsymbol{150 \;\mu \textbf{H}}[/ латекс] индуктор и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при [латекс]\boldsymbol{f = 7,50 \;\textbf{Гц}}[/латекс]. б) Каков фазовый угол на этой частоте? в) Какова средняя мощность на этой частоте? г) Найдите среднюю мощность на резонансной частоте контура.
14: Цепь серии RLC имеет резистор [латекс]\boldsymbol{200 \;\Омега}[/латекс] и катушку индуктивности 25,0 мГн. При частоте 8000 Гц фазовый угол равен [латекс]\boldsymbol{45,0^{\circ}}[/латекс]. а) Чему равно сопротивление? б) Найдите емкость цепи. (c) Если применяется [латекс]\жирный символ{V_{\textbf{rms}} = 408 \;\textbf{V}}[/латекс], какова средняя подаваемая мощность? 92}}[/латекс]
- резонансная частота
- частота, при которой импеданс в цепи минимален, а также частота, при которой цепь колебалась бы, если бы она не приводилась в действие источником напряжения; рассчитано по формуле [латекс]\boldsymbol{f_0 = \frac{1}{2 \pi \sqrt{LC}}}[/latex]
- фазовый угол
- обозначается [latex]\boldsymbol{\phi}[/latex], величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
- коэффициент мощности
- величина, на которую мощность, подаваемая в цепь, меньше теоретического максимума цепи из-за несовпадения по фазе напряжения и тока; рассчитано по [латексу]\boldsymbol{\textbf{cos} \;\phi}[/латекс]
Расчет мощности переменного тока для конденсаторов постоянного тока
Доступно в формате PDF
Конденсаторы обычно оцениваются по напряжению постоянного тока. Этот рейтинг означает, что можно ожидать, что деталь будет надежно работать в течение длительного времени при этом напряжении постоянного тока и при номинальной температуре конденсатора. Поскольку в большинстве приложений используется некоторая составляющая переменного напряжения, важно понимать факторы, которые определяют, какое количество переменного тока может выдержать данная деталь с номинальным постоянным током. Эти факторы включают частоту, напряжение, номинальную мощность (размер), значение емкости и диэлектрические характеристики.
Влияние переменного тока на характеристики и надежность конденсатора частично зависит от типа используемого диэлектрика. Для керамических конденсаторов все три первичных диэлектрика (NPO, X7R и Z5U) имеют разные характеристики изменения по отношению к приложенному переменному току. Например, с диэлектриком NPO значения емкости и коэффициента рассеяния останутся относительно постоянными при подаче различных сигналов переменного тока. X7R, однако, будет демонстрировать небольшие изменения в зависимости от приложенной частоты и значительные изменения в зависимости от величины приложенного напряжения. Z5U еще больше изменится как по частоте, так и по напряжению. Конкретные конструкции конденсаторов будут влиять на степень изменения этих параметров, поскольку они зависят как от используемого диэлектрика, так и от толщины этого диэлектрика при заданном напряжении. Эти цифры относятся только к диэлектрику X7R. NPO не покажет никаких измеримых изменений ни напряжения, ни частоты. Z5U продемонстрирует изменения, аналогичные X7R, но гораздо более масштабные. По этой причине Z5U редко используется в приложениях переменного тока.
В то время как изменения, связанные с частотой, можно легко изобразить на графике для X7R (см. рис. 1), изменения, связанные с уровнем напряжения, зависят от напряжения диэлектрика (вольт на мил толщины диэлектрика) и будут разными для каждого номинального напряжения. Типичные значения для X7R показаны на рисунках с 2 по 5.
Для данного применения мощность, рассеиваемая в конденсаторе, может быть рассчитана по формуле P=i² R, где P = мощность в ваттах, i = среднеквадратичное значение тока через конденсатор и R = эквивалентное последовательное сопротивление (ESR) конденсатора. Тогда я = 2 pie fCE, где f = частота в герцах, C = емкость в фарадах и E = среднеквадратичное приложенное напряжение. Наконец, R = d/(2 pie fC), где d = коэффициент рассеяния. Объединив эти три уравнения, мы получим окончательную формулу мощности: P=2 pie fCE²d.
Теперь необходимо определить значения емкости и коэффициента диэлектрических потерь, предполагая, что мы знаем приложенное напряжение и частоту. Емкость можно определить по рисункам 1, 2 и 3, изменив номинальную емкость на изменения, показанные для данной частоты и нагрузки по напряжению. Аналогичным образом можно определить коэффициент рассеяния по рисункам 1, 4 и 5. Обратите внимание, что эти значения являются типичными и варьируются от одного производителя к другому. Изменение крышки из-за напряжения также может быть изменено производителем для удовлетворения требований конкретного применения.
После внесения указанных выше поправок на емкость и коэффициент рассеяния на основе напряжения и частоты цепи фактическое потребление энергии конденсатором можно рассчитать по формуле P=2 pie fCE²d. Обратите внимание, что и значение емкости, и частота напрямую влияют на мощность при заданном напряжении. Вот почему невозможно назначить общий номинал переменного тока (или коэффициент, применяемый к рейтингу постоянного тока) для конденсаторов. Это можно сделать только тогда, когда эти значения известны (как в приложениях с постоянным значением 60 Гц).
После определения мощности необходимо выяснить, сможет ли данный конденсатор ее выдержать. Компания Johanson Dielectrics разработала таблицу номинальной мощности для конденсаторов различных размеров, чтобы ее можно было легко сравнить с расчетной мощностью (см. Таблицу 1).
Эти номинальные мощности основаны на повышении температуры на 25°C, измеренной на поверхности конденсатора при подаче питания. Номинальные значения также основаны на стандартном монтаже на печатной плате, отсутствии поблизости источников тепла и отсутствии внешнего покрытия или герметизации, которые могут препятствовать теплопроводности.
Вот пример: 0,1 мкФ, 500 В, X7R, размер микросхемы 2520 для поверхностного монтажа и работы при среднеквадратичном напряжении 30 В и частоте 10 кГц. В каталоге Johanson Dielectrics выберите номер детали Johanson 501h57W104KV4. Чтобы использовать формулу P=2 pie fCE²d, значения f (10 000) и E (30) известны, а значения C и d должны быть определены из рисунков с 1 по 5.
Соответственно, емкость к изменениям частоты –2 % из-за частоты (рис. 1) и +25 % из-за напряжения (используйте кривую 500 В пост. тока на рис. 2). Это делает «C» фактической емкостью (0,1) (0,98)(1,25)=0,123 мкФ. Точно так же «d», коэффициент рассеяния с использованием большего из двух значений на рисунках 1 и 4, составляет 8% (0,08).
Значения теперь известны:
f=10000
C=0,123 (e-6)
E=30
d=0,08
Расчетная мощность 0,56 Вт. Согласно Таблице 1, номинальная мощность для размера h57 составляет 1,3 Вт, поэтому конструкция подходит для этого приложения.
Области применения Инженерная поддержка доступна на заводе для других конкретных применений или вопросов.
Примечание. Технические характеристики могут быть изменены без предварительного уведомления.
