Ключевые моменты при решении задач повышенного уровня по теме «Конденсаторы и их соединения»

Ключевые слова: ЕГЭ, ЕГЭ по физике, конденсаторы

При подготовке к ЕГЭ по физике и решении задач повышенной сложности очень часто обучающиеся сталкиваются с трудностями анализа физических процессов в конденсаторах. Целью данной работы является некоторая систематизация и выделение ключевых позиций при решении задач повышенной сложности по теме «Конденсаторы и их соединение». Реализовывая системно-деятельностный подход к изучению физики, возможно рассмотрение следующих ситуаций анализа решаемых задач, а также вариативных вопросов к ним.

I. Рассмотрим известную задачу, которая раскрывает взаимосвязь физических характеристик конденсатора и последовательность их изменений [2]:

Плоский конденсатор, между пластинами которого находится воздух, заряжен от источника питания. Как меняются заряд конденсатора, напряженность электрического поля, разность потенциалов между пластинами, энергия и плотность энергии электрического поля, если увеличить в n раз расстояние между пластинами в ситуациях, если а) конденсатор отключить от источника питания и б) с включенным источником питания.

Рассмотрим первую ситуацию: изменяем расстояние между пластинами при отключенном источнике.

В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик

— Что остается неизменным в данном процессе. (q = const, заряд на пластинах конденсатора при отключении источника тока)

— Что происходит с емкостью конденсатора (Конденсатор плоский: d увеличивается,

C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) Напряженность электрического поля конденсатора E = ϭ/(2ε₀) (не изменяется)

2) Разность потенциалов между пластинами C = q/U (С уменьшается, U увеличивается в n раз)

3) Энергия электрического поля W = qU/2 (U увеличивается в n раз, W увеличивается в n раз)

4) Плотность энергии ω = ε₀E²/2 (не изменяется)

Рассмотрим вторую ситуацию: изменяем расстояние между пластинами при включенном источнике питания.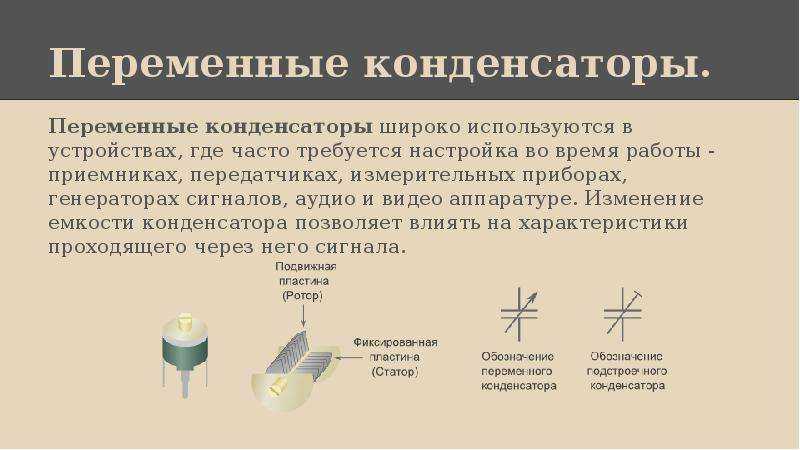

В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик

— Что остается неизменным в данном процессе. (U = const, напряжение на пластинах конденсатора при включении источнике тока)

— Что происходит с емкостью конденсатора (Конденсатор плоский: d увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) При неизменном напряжении и уменьшении емкости, заряд конденсатора должен уменьшиться в n раз (анализ C = q/U)

2) Напряженность электрического поля конденсатора E = ϭ/(2ε₀) (E уменьшается в n раз при уменьшении заряда в n раз)

3) Энергия электрического поля W = qU/2 (q уменьшается в n раз, W уменьшается в n раз)

4) Плотность энергии ω = ε₀E²/2 уменьшается в n² раз (при уменьшении напряженности)

Особое внимание следует обратить на энергетические превращения в конденсаторе.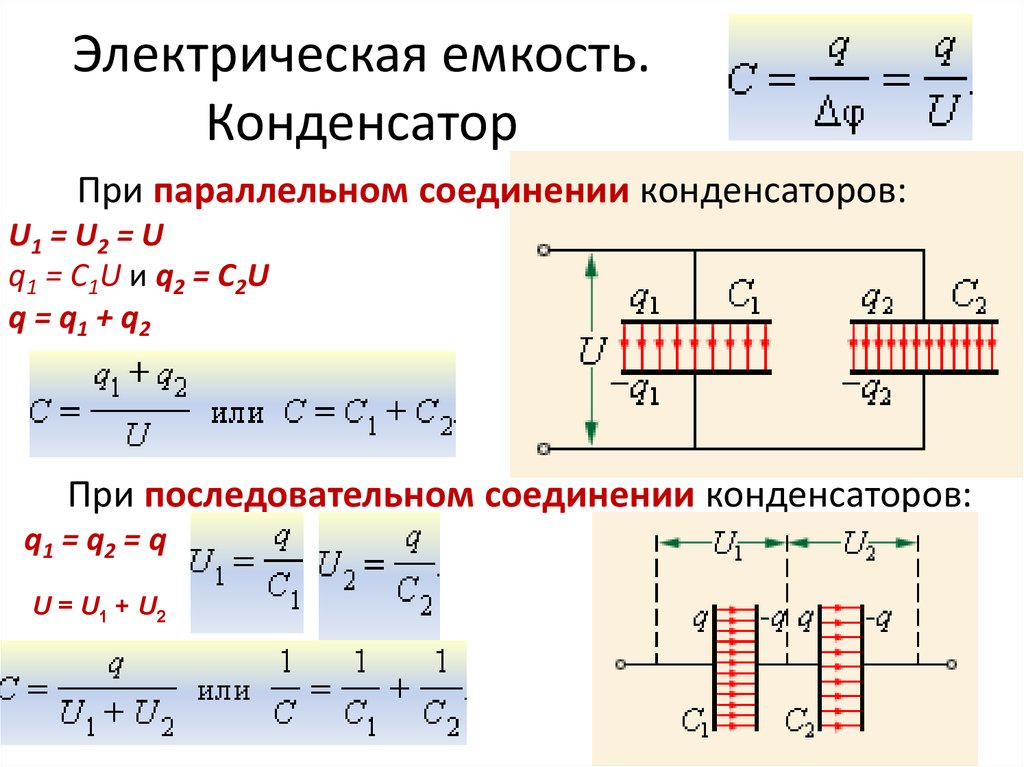 При увеличении расстояния между пластинами совершается положительная механическая работа, но энергия конденсатора уменьшается. Согласно закону сохранения энергии источник должен забирать энергию, равную убыли энергии конденсатора и механической работы внешних сил. Иначе, если источник является аккумулятором, то он будет заряжаться от конденсатора. Если источником является гальванический элемент, то на нем будет выделяться тепло.

Поставленную задачу можно не ограничивать данными изменениями, а можно выполнить анализ при изменении площади пластин конденсатора или замене диэлектрика между пластинами. В результате поможет сформировать у обучающихся целостное и устойчивое представление физических процессов и их характеристик в конденсаторе, варьируя ситуации.

II. Рассмотрим две возможные ситуации при параллельном подключении одного конденсатора к другому, если обкладки конденсаторов соединены одноименными зарядами и разноименными зарядами [2]:

Конденсатор емкостью C₁ заряжен до разности потенциалов U₁.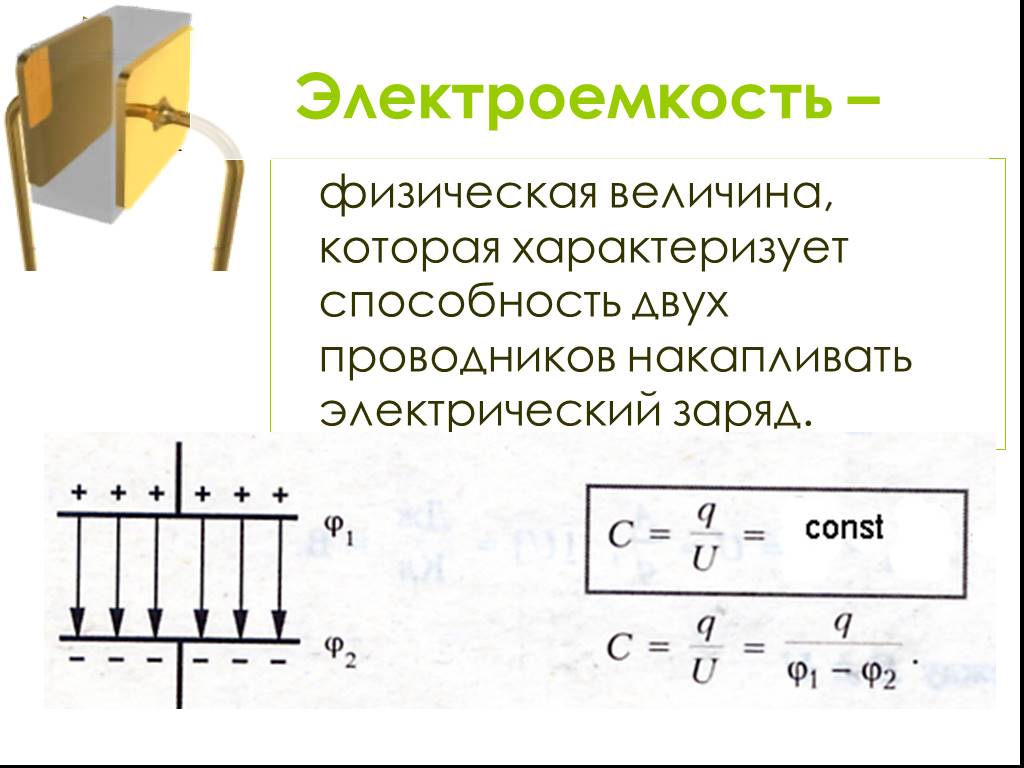 Какой заряд и каково напряжение будет на обкладках конденсатора, если к нему подключить параллельно другой конденсатор емкостью C₂, заряженный до разности потенциалов U₂.

Если обкладки конденсаторов соединены одноименными зарядами, то решение задачи сводится к составлению уравнения закона сохранения заряда до соединения и после соединения конденсаторов. Закон сохранения заряда будет ключевым моментом анализа задачи. Второй момент — равенство напряжений на конденсаторах при параллельном подключении, дает возможность упростить и решить данную задачу.

Иначе дело обстоит, если обкладки конденсаторов соединены разноименными зарядами. При соединении двух конденсаторов возникает ситуация, когда при распределении зарядов после подключения происходит перезарядка одного из конденсаторов и смена знаков зарядов на его обкладках. В этом случае при составлении уравнения закона сохранения заряда как ключевого момента следует не забыть изменить знак заряда на противоположный. Положим, в данном примере U₂ > U

1, то при соединении конденсаторов, первый конденсатор перезарядится, и знаки зарядов на его пластинах сменятся. Поэтому удобно при составлении закона сохранения заряда, принять заряд первого конденсатора, до соединения к нему второго, за отрицательный заряд.

Закон сохранения заряда для данного примера будет выглядеть: -q₁+ q₂ = q₁‘+ q₂‘. Последующее равенство напряжений на конденсаторах при параллельном подключении дает возможность упростить и решить данную задачу.

III. Рассмотрим анализ схемы соединения конденсаторов, где их соединения не сводятся к совокупности параллельных и последовательных соединений.

Например, в разветвленной схеме требуется найти напряжения на конденсаторах. Данный пример подробно описан [1]. Из данного примера выделим следующие ключевые моменты:

1) Составляем независимые уравнения, связывающие напряжения на конденсаторах с электродвижущими силами, выбрав точки разности потенциалов.

А) Между точками F и D: Ɛ₁+ Ɛ₂= U₁+ U₂

Б) Между точками F и A: Ɛ₁= U

₁+ U₃

2) Составляем уравнение алгебраической суммы зарядов в узле точки B:

q₁— q₂ — q₃= 0 или C₁U₁— C₂U₂ — C₃U₃= 0

Система трех независимых уравнений с тремя неизвестными дает их решение. Если схема симметрична (Ɛ₁ = Ɛ₂, C₁ = C₂), то U₃(Напряжение между точками A и B) равно нулю, а напряжение U

₁= U₂.

В связи с данным примером, возникает упрощенный анализ схем при переключении в цепи с конденсаторами, например [1]:

Для положения ключа в состоянии A и B между точками F и D выражение Ɛ₁ + Ɛ₂ = U₁ + U₂справедливо в обоих случаях. Следовательно, U₂не изменяется при переключении.

Для узла N сумма зарядов в узле равна нулю: q₁— q₂ ± q₃= 0. Следовательно, не изменится заряд третьего конденсатора, а вместе с ним и не изменится напряжение

U₃.

После переключения U₂= U₃, конденсаторы соединены параллельно.

В данном примере интересен вывод: точки A и B имеют одинаковый потенциал, следовательно Ɛ₂= 0.

IV. Рассмотрим некоторые варианты изменения энергии конденсатора с точки зрения закона сохранения энергии, подробные объяснения которых обсуждаются в источнике [3].

Изменение энергии конденсатора можно произвести от источника питания или путем совершения механической работы внешними силами.

Увеличение энергии конденсатора при зарядке конденсатора в общем виде можно определить из уравнения закона сохранения:

Aист. = ΔWк + A + Q,

где Aист. – работа источника при зарядке конденсатора, ΔWк – изменение энергии конденсатора, A – механическая работа сил электрического поля, Q – выделяющееся тепло. В идеальном случае, при отсутствии потерь энергии от источника: Aист. = ΔWк

Однако наиболее часто встречаются задания, где изменение энергии заряженного конденсатора происходит путем совершения работы внешней силы в ситуациях с отключенным и подключенным источником тока.

Рассмотрим первую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при отключенном источнике питания.

— обращаем внимание на то, что в данной ситуации остается неизменным заряд q конденсатора.

— обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε₀S/d)

Формируем вывод исходя из формулы энергии при неизменном заряде: W = q₂/2C – энергия конденсатора увеличивается. Увеличение энергии произошло за счет работы внешней силы. ΔWк = Aвнеш.

Рассмотрим вторую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при включенном источнике питания.

— обращаем внимание на то, что в данной ситуации остается неизменным напряжение U на обкладках конденсатора.

— обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε₀S/d)

Формируем вывод исходя из формулы энергии при неизменном напряжении: W = CU²/2 – энергия конденсатора уменьшается. Уменьшение энергии произошло за счет того, что источник совершает отрицательную работу, забирая часть заряда с обкладок конденсатора при положительной работе внешних сил:. ΔWк = Aист. + Aвнеш.

Возможны и другие очевидные вариации изменения энергии конденсатора с помощью работы внешних сил.

В данной работе рассмотрена лишь небольшая часть анализа ключевых ситуаций по данной теме. Но все рассмотренные ситуации являются опорными для формирования разбора задач и их решения.

Литература

1. Е.И.Бутиков, А.А.Быков, А.С.Кондратьев. Физика в примерах и задачах, МЦНМО, Пероглиф, 2019, стр. 297-301.

2. А.С.Кондратьев, В.М.Уздин. Физика. Сборник задач, М., ФИЗМАТЛИТ, 2020, стр.67-69.

3. А.С.Кондратьев, Л.А.Ларченкова, В.А.Ляпцев. Методы решения задач по физике. М., ФИЗМАТЛИТ, 2019, стр.149-154.

Конденсатор

24 марта 1896 года Александр Степанович Попов с помощью изобретённого им радиопередатчика передал на расстояние в 250 метров азбукой Морзе первую в мире радиограмму из двух слов: «Генрих Герц». В то время это было воспринято как чудо. Сейчас же мы настолько привыкли к тому, что можем не только слышать, но и видеть то, что происходит за многие километры от нас, что это не вызывает ни малейшего удивления. Но чтобы понять физические процессы, лежащие в основе приёма и передачи звука и изображения, нам сначала следует познакомиться с одним важным устройством — конденсатором.

Конденсатор — это устройство, служащее для накопления заряда и энергии электрического поля.

История конденсаторов началась в тысяча семьсот сорок пятом году в городе Ле́йдене, где местный учёный Пи́тер ван Му́шенбру́к и его ученик Кюне́ус заряжали электричеством воду в банке. Зарядка осуществлялась при помощи цепочки, присоединённой к электрофорной машине. Цепочка спускалась через горлышко колбы в воду. Когда, по мнению Кюне́уса, зарядка воды была завершена, он решил вынуть цепочку рукой из сосуда и тут получил «такой страшный электрический удар, что чуть не скончался».

Так была изобретена лейденская банка (по названию города Лейден в Голландии), — первый простейший конденсатор, и одно из самых распространённых электротехнических устройств нашего времени.

Позже данный опыт был повторен в присутствии французского короля аббатом Нолле. Он образовал цепь из 180 гвардейцев, взявшихся за руки, причём первый держал банку в руке, а последний прикасался к проволоке, извлекая искру. «Удар почувствовался всеми в один момент; было забавно наблюдать разнообразие жестов и слышать мгновенный вскрик десятков людей». Кстати, говорят, что именно от этой цепи солдат и произошёл термин «электрическая цепь».

Но мы слегка отвлеклись. Итак, простейший конденсатор представляет собой две металлические пластины, называемые обкладками, разделённые между собой слоем диэлектрика. При этом толщина слоя диэлектрика намного меньше, чем размеры обкладок.

Если обкладки конденсатора подсоединить к полюсам источника тока, например, батарейки, то на обкладках появятся равные по модулю, но противоположные по знаку электрические заряды.

Модуль заряда любой из обкладок конденсатора называется зарядом конденсатора. Как показали различные опыты, заряды распределены на внутренних поверхностях пластин конденсатора. А созданное ими электрическое поле в основном сосредоточено внутри конденсатора.

Если отключить конденсатор от источника тока, то заряд с его обкладок никуда не исчезнет, в чём легко убедиться, если присоединить к обкладкам лампочку, которая на мгновение вспыхивает.

Для характеристики свойства проводника накапливать электрический заряд ввели физическую величину — электрическую ёмкость или просто — ёмкость. Для объяснения её физического смысла проведём такой опыт: возьмём конденсатор, одну из пластин которого соединим со стержнем электрометра, а другую — с его корпусом.

Возьмём три одинаково заряженных шара и будем последовательно сообщать конденсатору одинаковые положительные электрические заряды, увеличивая его суммарный заряд в целое число раз.

Из результатов опыта не трудно увидеть, что чем больше сообщённый конденсатору электрический заряд, тем больше напряжение между его обкладками. При этом, обратите внимание, напряжение увеличивается во столько же раз, во сколько раз увеличивается заряд. Но отношение электрического заряда к напряжению остаётся постоянным.

Таким образом, электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к напряжению на его пластинах.

Обозначается ёмкость конденсатора большой латинской буквой С. А единицей ёмкости в СИ является фарад (Ф), названная так, как вы догадались, в честь Майкла Фарадея. 1 Ф — это такая ёмкость конденсатора, при которой заряд, равный 1 Кл, создаёт между обкладками конденсатора напряжение 1 В.

1 Ф — это очень большая электроёмкость. Например, в вакууме электроёмкостью один фарад обладал бы шар радиусом 9 000 000 километров (для сравнения: радиус Солнца примерно равен 696 000 километрам, а нашей планеты — всего 6400 километров). Поэтому на практике применяют дольные единицы фарада:

Например, электроёмкость такого огромного конденсатора, как земной шар, составляет 710 мкФ.

Но вернёмся к нашему опыту и попытаемся выяснить, от чего зависит ёмкость конденсатора. Для этого зарядим конденсатор и отметим показания электрометра.

Теперь сблизим пластины — не трудно увидеть, что напряжение между пластинами уменьшилось. Поскольку заряд на пластинах оставался неизменным, то уменьшение напряжения связано с увеличением ёмкости конденсатора. Таким образом, чем меньше расстояние между обкладками конденсатора, тем больше его ёмкость.

Теперь будем изменять площадь пластин конденсатора.

Как видим, при уменьшении площади пластин напряжение между ними увеличивается, значит, ёмкость конденсатора уменьшается.

И наконец, внесём между пластинами конденсатора диэлектрик, например, лист стекла.

Как видим, напряжение уменьшилось, следовательно, ёмкость конденсатора увеличилась. Значит, ёмкость зависит и от свойств используемого диэлектрика.

Физическая величина, характеризующая свойства изолирующей (диэлектрической) среды, называется диэлектрической проницаемостью. Она показывает, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме.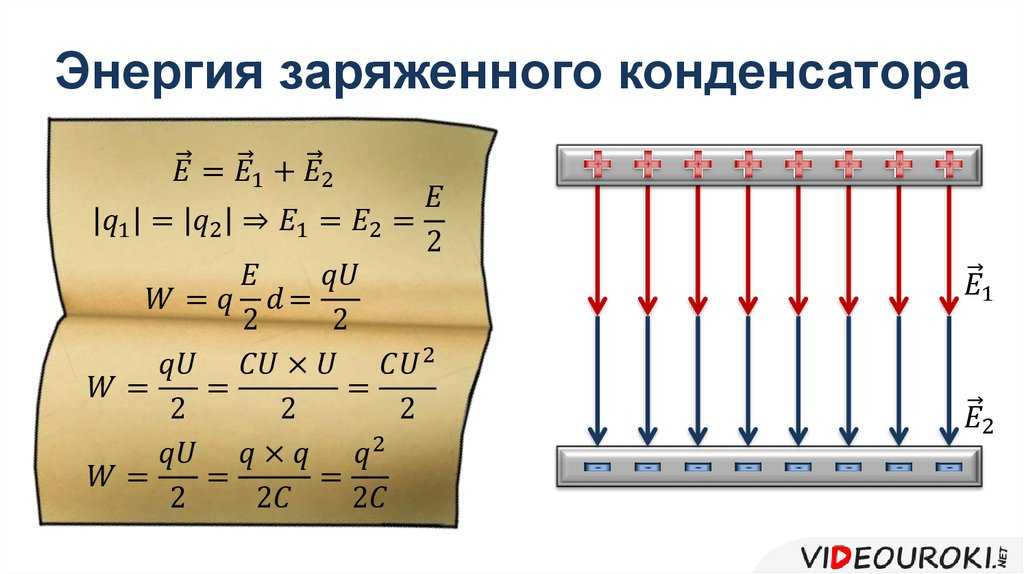

Таким образом, ёмкость плоского конденсатора зависит от площади пластин, расстояния между ними и свойств внесённого в конденсатор диэлектрика. Она прямо пропорциональна площади пластин и обратно пропорциональна расстоянию между ними.

В СИ коэффициентом пропорциональности между электроёмкостью конденсатора и определяющими её величинами является электрическая постоянная.

Полученный нами экспериментальным путём вывод о зависимости ёмкости плоского конденсатора от его параметров очень важен в практическом отношении. Он указывает способы изменения ёмкости. Например, в одних конденсаторах ёмкость можно изменить, повернув рукоятку и уменьшив или увеличив при этом площадь пластин.

А в других используется зависимость электроёмкости от расстояния между обкладками. Такие конденсаторы используют, например, в схемах кодирования клавиатуры персонального компьютера. Под каждой клавишей находится конденсатор, электроёмкость которого изменяется при нажатии на клавишу. Микросхема, подключённая к каждой клавише, при изменении электроёмкости выдаёт кодированный сигнал, соответствующий данной букве.

Идём дальше. Вы знаете, что любые заряженные тела создают в пространстве вокруг себя электростатическое поле, силовой характеристикой которого является напряжённость.

Напомним, что напряжённость — это физическая векторная величина, характеризующая электрическое поле в данной точке и численно равная отношению силы, действующей на неподвижный пробный заряд, помещённый в эту точку поля, к величине заряда.

Рассмотрим электростатическое поле заряженного плоского конденсатора.

Как видно, оно в основном сосредоточено между его обкладками. Обратите внимание, что линии напряжённости электрического поля плоского конденсатора параллельны и расположены на одинаковом расстоянии друг от друга. Значит поле такого конденсатора однородно. Но вблизи краёв пластин однородность поля нарушается, однако этим часто пренебрегают, когда расстояние между пластинами значительно меньше их размеров.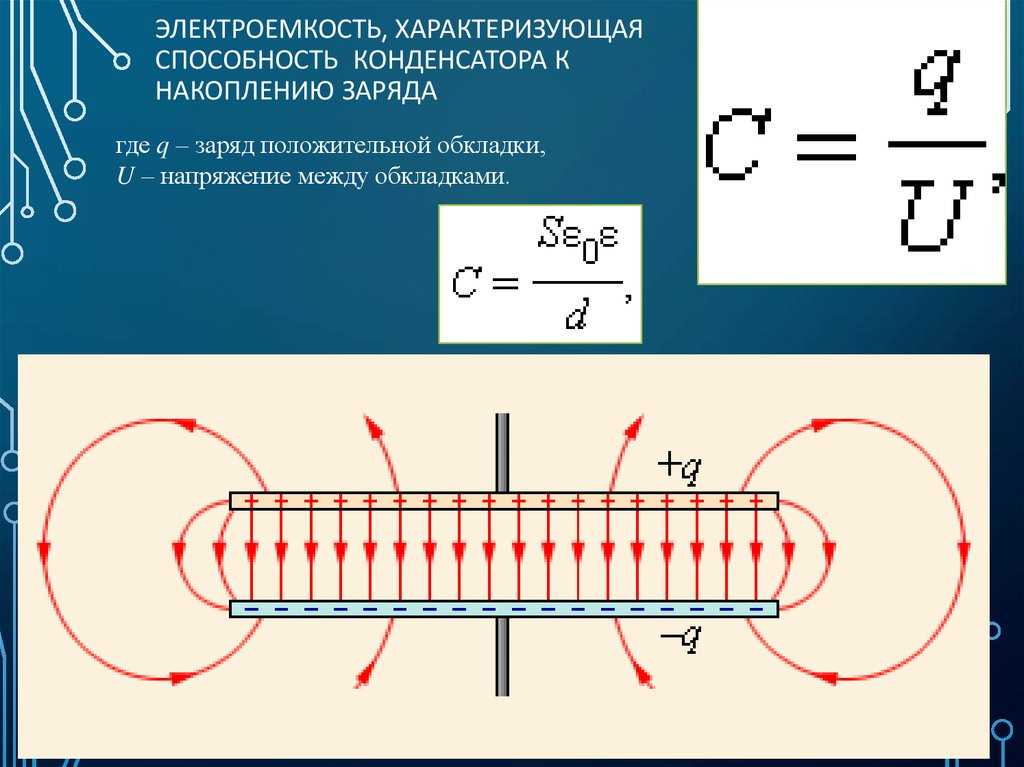

При зарядке конденсатора внешними силами совершается работа по разделению положительных и отрицательных зарядов. По закону сохранения, работа внешних сил равна энергии поля конденсатора. Значит, при разрядке конденсатора за счёт этой энергии может быть совершена работа.

Убедиться в том, что заряженный конденсатор действительно обладает энергией, можно на простом опыте. Соберём электрическую цепь, состоящую из источника тока, конденсатора и электрической лампы. Зарядим конденсатор, подсоединив его к источнику тока. Затем, отключив конденсатор от источника тока, подсоединим его к лампе. При этом наблюдаем кратковременную вспышку света. В данном случае во время разрядки конденсатора его энергия превратилась во внутреннюю энергию спирали лампы.

Энергию электрического поля конденсатора можно рассчитать по формуле:

Воспользовавшись формулой для электроёмкости, можно получить ещё две формулы для расчёта энергии электрического поля конденсатора.

В настоящее время конденсаторы находят широкое применение во многих областях науки и техники. В связи с этим конденсаторы можно классифицировать по следующим признакам и свойствам:

по назначению — это конденсаторы постоянной и переменной ёмкости.

по форме обкладок — различают конденсаторы плоские, сферические, цилиндрические и другие;

а также по типу диэлектрика — это, например, бумажные, керамические, электролитические конденсаторы и так далее.

Наиболее распространённым типом конденсаторов является бумажный конденсатор. Он представляет собой две ленты металлической фольги, разделённые тонкой парафинированной бумагой, полистиролом, слюдой или другим диэлектриком, которые свёрнуты в тугую спираль и запаяны.

Для получения очень больших электроёмкостей используют электролитические конденсаторы. В качестве диэлектрика в них применяют тонкую плёнку окиси алюминия, нанесённую на металлическую пластину, являющуюся одной из обкладок. Роль второй обкладки играет электролит, контактирующий с металлическим корпусом. Ёмкость таких конденсаторов может достигать сотен и тысяч микрофарад.

В последнее время широкое применение находят керамические конденсаторы. Диэлектриком в них служит специальная керамика. Электрическая ёмкость таких конденсаторов достигает сотен пикофарад.

Закрепления материала.

Физика конденсаторов — 2022

Определение конденсатора

Конденсатор можно определить как устройство, которое может накапливать электрическую энергию. Он состоит в основном из двух металлических пластин, разделенных изолятором. Изолятор называется диэлектрическим материалом. Когда конденсатор подключен к источнику pd, противоположные заряды постепенно накапливаются на каждой из пластин.

Конденсатор

Отношение заряда Q  накопленного на конденсаторе к разности потенциалов между обкладками называется емкость конденсатора. Единица емкости называется фарад.

C=QV ———(i)

Q — это заряд, а В — это pd между пластинами.

Наиболее распространенным типом конденсатора является конденсатор с плоскими пластинами. Емкость конденсатора с плоскими пластинами зависит от следующих факторов:

(i) Площадь перекрытия пластин : емкость конденсатора с плоскими пластинами прямо пропорциональна площади перекрытия пластин.

C∝A

(ii)  Расстояние между пластинами : емкость плоского конденсатора обратно пропорциональна расстоянию между пластинами.

C∝1d

(iii)  Диэлектрическая проницаемость изолятора между пластинами : емкость конденсатора прямо пропорциональна диэлектрической проницаемости изолятора. Диэлектрическая проницаемость — это диэлектрическая проницаемость изолятора по отношению к электрической линии потока.

C∝ε

Суммарно емкость конденсатора дается как:

C=εAd ——–(ii)

ОЦЕНКА (ОТВЕТЬТЕ ВАШИ ОТВЕТЫ, ИСПОЛЬЗУЯ ВОПРОС НИЖЕ ДЛЯ ОЦЕНКИ И ОБСУЖДЕНИЯ):

90663 900 диэлектрическое вещество?

Перечислите факторы, определяющие емкость плоского конденсатора, и укажите влияние каждого из них на емкость.

Объясните, что подразумевается под утверждением « емкость конденсатора 5 мкФ ’

Энергия, накопленная в конденсаторе

Конденсатор хранит электрическую энергию. Когда конденсатор подключен к источнику pd, заряд на его пластине постепенно увеличивается от нуля до Q. Работа, совершаемая при заряде при среднем напряжении, равна:

Вт=12QVW=12CV2W=1Q22C———(iii)

Процесс зарядки и разрядки конденсатора приведен ниже:

Расположение конденсаторов

Конденсаторы могут быть расположены в цепи параллельно или последовательно.

Последовательное расположение

Здесь конденсаторы соединены встык, как показано ниже.

Для последовательно включенных конденсаторов;

(i) В конденсаторе сохраняется равный заряд Q.

Q1=Q2=Q3

(ii) Сумма разности потенциалов на каждой пластине равна разности потенциалов от источника.

V=V1+V2+V3

а,

C=QV

Следовательно, V=QC

Подставляя это в выражение для V,

QC=QC1+QC2+QC3

Отмена Q out,

1C=1C1+1C2+1C3 ———(iv)

Обратная величина эквивалентной емкости последовательно соединенных конденсаторов равна сумме обратны отдельным конденсаторам в серии.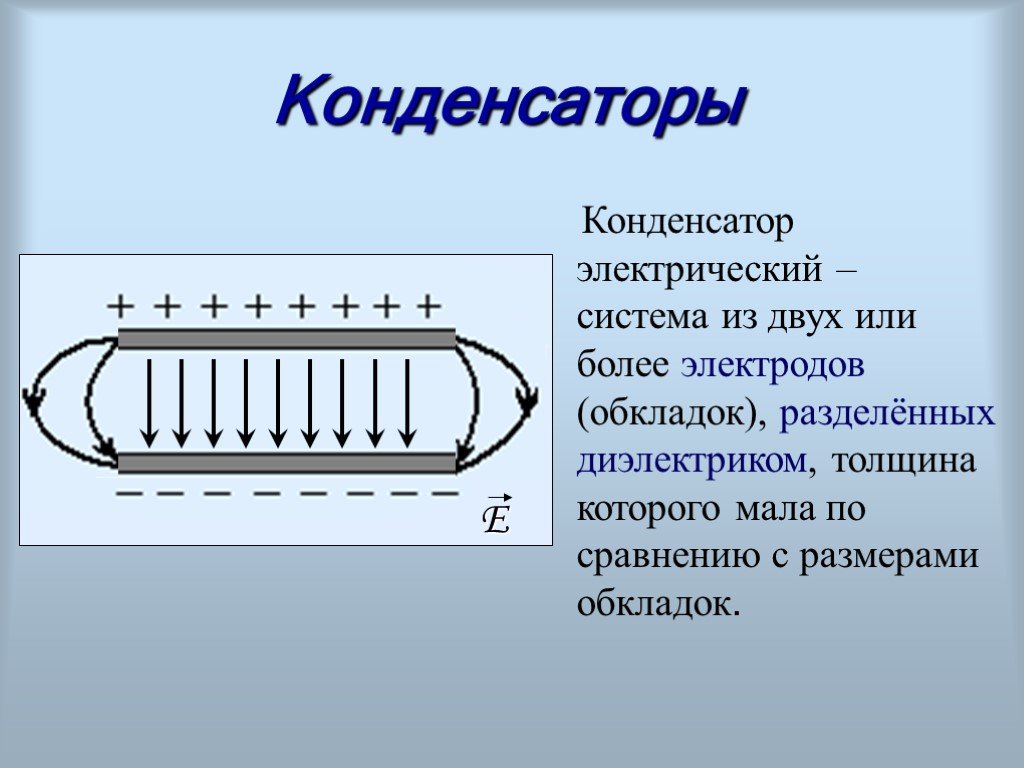

Параллельное расположение

Здесь конденсаторы расположены, как показано ниже.

Для конденсатора, подключенного параллельно,

(i) Разность потенциалов между пластинами конденсатора одинакова.

V=V1=V2=V3

(ii) Общий накопленный заряд представляет собой сумму всех зарядов, хранящихся в каждом конденсаторе.

Q=Q1+Q2+Q3

но,

C=QV

Следовательно, Q=CV

подставив это в выражение для Q,

CV=C1V+C2V+C3VC=C1+C2 ——–(v)

Эквивалентная емкость для параллельно включенных конденсаторов представляет собой сумму емкостей отдельных конденсаторов.

Решенные вопросы

1. Для переноса заряда 5 мКл из точки В в точку А в электрическом проводе совершается работа в 30 Дж. Потенциал между В и А равен

Решение:

Заряд Q = 5 мКл

Работа = 30J

Обратите внимание, что W = QV

V=WQ=305×10−3=6000V

2. На конденсатор емкостью 3,0 мкФ действует разность потенциалов 2000 В. Рассчитайте энергию, запасенную в конденсаторе

Решение:

Емкость C = 3,0 мкФ

Разность потенциалов В = 2000 В

Энергия E =?

Напомним, что E=12CV2E=3,0×10−6×600022E=54 Дж

3. Три конденсатора емкостью 8 мкФ, 12 мкФ и 24 мкФ соединены последовательно с батареей 90 В.

(i) Нарисуйте схему разомкнутой цепи для этого устройства

(ii) Рассчитайте эффективную емкость в цепи

(iii) При замкнутой цепи рассчитайте заряд каждого конденсатора при полной зарядке

(iv) Определите напряжение на 8 мкФ

Решение:

2. Для последовательно соединенных конденсаторов эффективная емкость определяется как:

1C=1C1+1C2+1C31C=18+112+124=3+2 +1241C = 624

, принимая взаимные с обеих сторон,

C1 = 246

Эффективная емкость C = 4 мкф

3. Отзыв для конденсаторов последовательно,

. Зарядка на каждом конденсаторе равной 9004

Q =CVQ=4µ×90Q=4×10−6×90Q=3,6×10−4C

4. Напомним, Q=CVV=QCV=3,6×10−48×10−6В=0,45×102=45В

ВАШИ ОТВЕТЫ, ИСПОЛЬЗУЯ ВОПРОС НИЖЕ ДЛЯ ОЦЕНКИ И ОБСУЖДЕНИЯ):

1. Пластины конденсатора с плоскими пластинами, расположенные на расстоянии 5,0 x 10 ^-3 м друг от друга, поддерживаются при разности потенциалов 5,0 x 10 ⁴ . из:

• напряженность электрического поля между пластинами
• сила, действующая на электрон
• ускорение электрона

(Заряд электрона = -1,6 x 10 ^-19 Кл, масса электрона = 9,1 x 10 ^-31 кг) мкФ подвергается разности потенциалов 200 В. Рассчитайте энергию, запасенную в конденсаторе

Присоединяйтесь к форуму и выполните задание : Найдите вопросы в конце каждого урока. Щелкните здесь, чтобы обсудить свои ответы на форуме

Вы хотите учиться в Великобритании или КАНАДЕ? : Воспользуйтесь нашим БЕСПЛАТНЫМ калькулятором, чтобы узнать, сколько вам нужно будет показать посольству! Это БЕСПЛАТНО Нажмите здесь, чтобы начать путешествие за границу.

Объявление: Получите БЕСПЛАТНУЮ Библию : Обрести истинный покой. Нажмите здесь, чтобы узнать, как получить БЕСПЛАТНУЮ Библию.

Для размещения рекламы/партнерства WhatsApp +2348157171707

Загрузите наше бесплатное мобильное приложение для Android : Сохраняйте свои данные при использовании нашего бесплатного приложения. Нажмите на картинку, чтобы скачать. Нет подписки.

Мы заинтересованы в продвижении БЕСПЛАТНОГО обучения. Расскажите своим друзьям о Stoplearn.com. Нажмите кнопку «Поделиться» ниже!

Конденсаторная физика | Видео TI.com

1. Учебный дом TI
2. Учебная программа по экспериментальной силовой электронике и справочник
3. Конденсаторы
4. Конденсаторная физика

Учебная программа по экспериментальной силовой электронике и справочник

МЕНЮ

• Введение и математические инструменты для силовой электроники (9)

• Преобразователи с широтно-импульсной модуляцией (ШИМ) (9)

• Реализация переключателя и коммутационные потери (11)

• Драйверы ворот (6)

• Терморегулирование в силовых преобразователях (6)

• Конденсаторы (9)

• Основы магнетизма (9)

• Дроссели индуктивности (4)

• Схема и паразитные помехи в силовых преобразователях (8)

• Моделирование слабосигнальных преобразователей ШИМ (4)

• Управление преобразователями ШИМ (5)

• Электромагнитные помехи в силовых преобразователях (6)

• Инструменты и программное обеспечение для силовой электроники (5)

• Проект: Проект CCM PWM (1)

Электронная почта

Всем привет. Меня зовут Алекс Хансен, и в этом видео мы поговорим о самых основах физики конденсаторов и о том, как они работают. Мы собираемся рассмотреть эту емкость как понятие, связанное с количеством заряда, хранящегося на двух узлах или двух металлических пластинах при заданном напряжении. Мы также немного поговорим о диэлектрических материалах, которые находятся между этими пластинами, и о том, как они влияют на емкость. И мы увидим, что накопление энергии конденсаторами или, на самом деле, их способность обработки энергии масштабируется вместе с объемом. И это будет важно, когда мы сравним магнитные материалы и магнитные компоненты с конденсаторами. Мы можем изучить концепцию емкости, взглянув на две параллельные пластины. Теперь не все конденсаторы являются конденсаторами с параллельными пластинами. На самом деле емкость появляется между любыми двумя проводниками. Но это сделает нашу жизнь немного проще, если рассмотреть случай с параллельными пластинами. Мы собираемся подать напряжение между этими двумя пластинами, и интуитивно понятно, что заряды будут накапливаться на этих пластинах. Положительные заряды на положительной пластине, отрицательные заряды на отрицательной пластине. И это приведет к возникновению электрического поля между двумя пластинами. Хорошо, вот мои электрические поля. Это электрические поля, а это заряды, и я обозначу их буквой q. Теперь я могу понять, как работает конденсатор из первых принципов. Уравнение Максвелла, которое я хочу применить, состоит в том, что интеграл от D dot dA по замкнутой поверхности равен интегралу от плотности заряда внутри этой поверхности. Поэтому мне нужно назначить закрытую поверхность, которая включает или инкапсулирует некоторое количество заряда. Итак, что я собираюсь сделать, так это нарисовать коробку вокруг некоторых из этих зарядов, трехмерную коробку, которая частично проникает в пластину. Теперь я знаю, что на большинстве поверхностей этого ящика поля нет. Из дна выходит электрическое поле, но из-за симметрии проблемы на самом деле нет электрического поля, выходящего из стенок коробки. Я также знаю, что на верхней стороне коробки не может быть никакого электрического поля, потому что эта сторона коробки находится внутри хорошего проводника.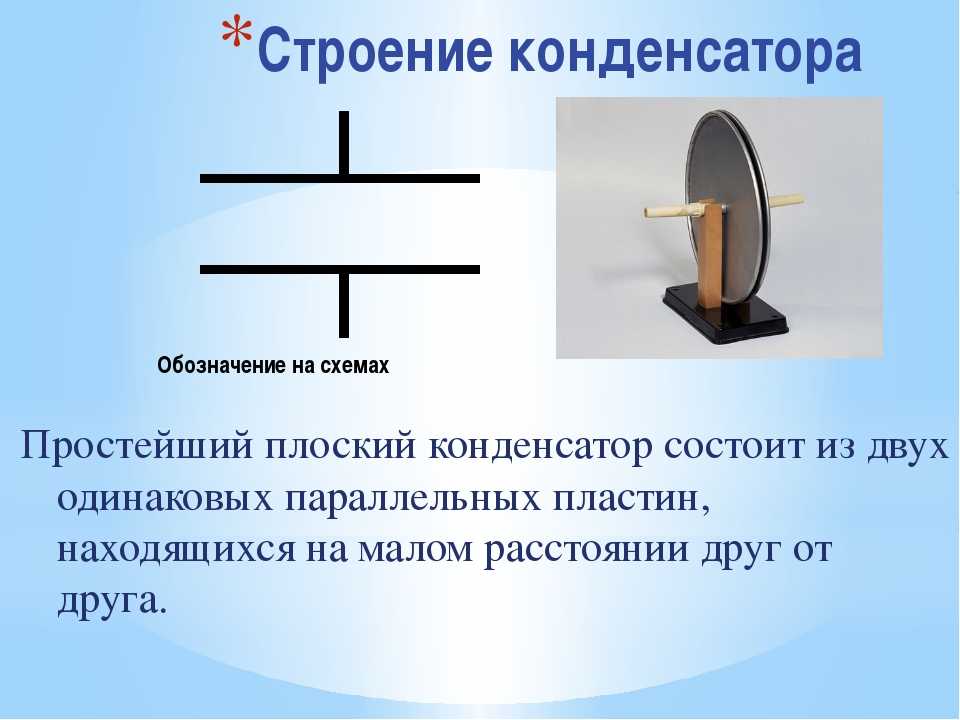 И если бы существовало электрическое поле, это означало бы, что протекал ток, но ясно, что в этой цепи ток не может течь. Таким образом, ни на одной из поверхностей ящика, кроме дна, не может быть никакого электрического поля. Таким образом, этот интеграл на самом деле довольно прост. Это просто поле D, умноженное на площадь коробки. И под площадью коробки я подразумеваю площадь этой нижней поверхности коробки. А это равно общему количеству заряда, хранящегося в ящике. Теперь я могу позволить площади блока быть площадью всего конденсатора, просто увеличив блок, и этот блок площади будет просто площадью конденсатора. Мы назовем это A. А q box — это просто заряд конденсатора. Далее я напишу, что поле D равно диэлектрической проницаемости, умноженной на электрическое поле. Это обычно имеет место для линейного диэлектрического материала. Время, когда площадь конденсатора равна общему заряду конденсатора. Вот одно выражение, которое мы получаем из закона Гаусса. Мы также можем использовать тот факт, что интеграл от E dot dl равен напряжению, и он будет равен электрическому полю, умноженному на расстояние между двумя пластинами здесь, D. Вы можете думать об этом как о KVL вокруг контура. . Вы также можете думать об этом как о применении закона Фарадея. В любом случае, мы приходим к этому второму уравнению. И, конечно же, объединив их, мы получим, что заряд конденсатора равен эпсилону А, умноженному на D, умноженному на напряжение на конденсаторе. Итак, прежде всего, мы пришли к выводу, что заряд и напряжение линейно связаны друг с другом. Эта линейная зависимость известна как емкость. Таким образом, мы не только вывели понятие емкости, но и вывели ее значение. Мы знаем, что емкость C равна эпсилон A относительно d в случае этого плоского конденсатора. Емкость увеличивается с площадью. В этом есть интуитивный смысл. Если у вас большие пластины, у вас должна быть большая емкость. Емкость также увеличивается при уменьшении разделительного расстояния. Таким образом, когда вы приближаете эти пластины друг к другу, ожидается, что емкость также увеличится. Третье, что влияет на емкость, — это диэлектрическая проницаемость промежуточного материала. И чтобы понять, как это работает, мы должны действительно посмотреть, что делает диэлектрический материал. Итак, позвольте мне нарисовать здесь упрощенную схему. Вот мои две тарелки. А когда между ними просто воздух или даже вакуум, скажем, вакуум, диэлектрическая проницаемость — это просто диэлектрическая проницаемость свободного пространства. Но когда у меня есть какой-то диэлектрический материал между ними, это добавляет кое-что интересное в уравнение. Теперь у меня есть маленькие электрические диполи по всему материалу, и, по крайней мере, когда они неполяризованы, все эти диполи обращены в несколько случайных направлениях, так что в целом от них нет никакого эффекта. Рядом с одним диполем будут другие диполи, которые находятся в противоположной ориентации, и они как бы компенсируют друг друга. Однако, когда я прикладываю электрическое поле или напряжение к конденсатору, многие из этих диполей будут вращаться, чтобы выровняться с электрическим полем. Этот диполь уже в основном выровнен с электрическим полем. Этот диполь может вращаться полностью или почти полностью в соответствии с электрическим полем, как и этот, и так далее, и тому подобное. И теперь диполи больше не ориентированы случайным образом. На самом деле, они все как бы согласованы друг с другом. И когда они выровнены друг с другом, их собственные электрические поля указывают от положительного к отрицательному, и, поскольку все они выровнены, они имеют тенденцию усиливать друг друга. Итак, теперь у меня есть приложенное электрическое поле, направленное вниз, но все эти диполи генерируют свои собственные электрические поля, направленные вверх. Это означает, что мне нужно предъявить еще больше обвинений. Раньше у меня были некоторые заряды, но мне нужно внести еще больше зарядов, чтобы общее электрическое поле дало мне определенное напряжение. Я должен применить больше зарядов, чтобы получить заданное напряжение. И, конечно же, помните, что емкость — это отношение между зарядом и напряжением, эпсилон А к dV. И мы только что физически поспорили, что, когда у меня есть эти диполи в моем материале, мне потребуется больше зарядов, чтобы развить достаточное сильное общее поле, чтобы напряжение между пластинами было определенной величины.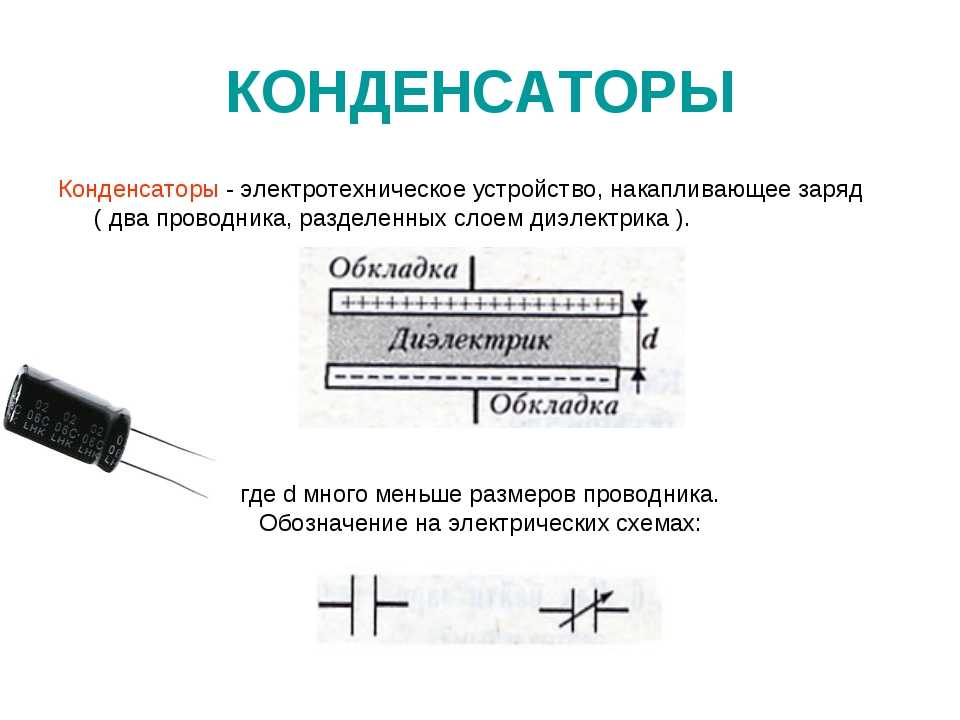 Мне нужно больше зарядов на единицу напряжения. Это проявляется в диэлектрической проницаемости. Это диэлектрическая проницаемость материала. Итак, для диэлектрика диэлектрическая проницаемость, эпсилон, равная некоторой относительной диэлектрической проницаемости — это безразмерное число, умноженное на диэлектрическую проницаемость свободного пространства, больше, чем диэлектрическая проницаемость самого свободного пространства. И это из-за действия этих электрических диполей, которые плавают в материале. Большинство конденсаторов, которые вы используете в цепи, состоят из пластин и диэлектрических материалов. И вам могут не сказать, что такое диэлектрическая проницаемость, но именно так они получают конденсатор с такой емкостью, вставляя между пластинами что-то, что имеет более высокую диэлектрическую проницаемость, чем воздух. Также важно отметить, что мы имеем дело со многими конденсаторами, особенно когда мы занимаемся высокочастотной силовой электроникой, и когда мы переходим к радиочастотной электронике, многие из этих конденсаторов не являются преднамеренными. Они паразитируют между двумя узлами. И чтобы действительно понять эти конденсаторы, мы должны понять физику того, как работает конденсатор, потому что между этими конденсаторами могут быть диэлектрические материалы. В них может быть воздух. И у них может быть какая-то комбинация материалов, а не просто система материалов. Теперь еще одна вещь, на которую мы, возможно, захотим обратить внимание, это то, сколько энергии вы можете обрабатывать с помощью конденсатора. Под этим я подразумеваю, что мы хотим посмотреть на максимальную величину напряжения, которое может быть приложено к конденсатору, и мы хотим посмотреть на максимальную величину тока, который может быть пропущен через конденсатор. Ну, максимальная величина напряжения будет связана с некоторым максимальным электрическим полем. Это максимальное электрическое поле может вызвать разрушение материала. Это может вызвать насыщение. И получается, что диэлектрическое насыщение — это такая же вещь, как и магнитное насыщение. Но каким бы ни было это E max, если вы умножите его на d, это будет максимальное напряжение, которое вы можете подать на конденсатор. Точно так же количество тока, которое вы можете пропустить через конденсатор, может быть связано с некоторой максимальной плотностью тока. Почему должна быть максимальная плотность тока? Ну и чем больше тока на единицу площади протолкнешь, например, металл, тем больше потерь получишь на единицу объема. А отводить тепло становится сложно, когда у вас большие потери на единицу объема. Так что это может привести к некоторой максимальной плотности тока. И тогда, конечно, общий ток будет равен плотности тока, умноженной на площадь. Таким образом, максимальная мощность, которую может обработать конденсатор… и под обрабатываемой мощностью я имею в виду величину напряжения, умноженную на величину тока. Это будет равно максимальному полю Е, умноженному на максимальное J, а это оба свойства материала, свойство диэлектрика и свойство металла, умноженное на объем конденсатора. И, конечно же, масштабы объема, такие как длина в кубе. Сейчас это может показаться интуитивно понятным. Объем — это валюта королевства, и если у меня в два раза больше объема, то логично, что я должен обрабатывать в два раза больше энергии с этим объемом. Причина, по которой я вхожу в это, заключается в том, что это становится важным сравнением, когда вы смотрите на магнитные компоненты. В усовершенствованном магнитном модуле мы обнаружим, что магнитные компоненты не масштабируются, как куб длины. Фактически, их длина часто увеличивается до четверти, что дает магнетикам огромное преимущество при больших размерах. Подумайте о сетевых трансформаторах. Но это дает конденсаторам огромное преимущество при небольших размерах. Подумайте о том, что, если вы посещаете занятия по интегральным схемам, вы почти никогда не видели там катушки индуктивности. А если и есть, то только как паразитический компонент. Таким образом, понимание этого масштабирования также может быть важной частью понимания того, когда использовать конденсаторы и когда конденсаторы будут важны. Итак, мы рассмотрели, что емкость в основном является коэффициентом масштабирования. Это постоянное масштабирование между зарядом и напряжением. И поскольку заряд связан с током, он также связан с законом определения конденсатора: I равно C dv/dt.