Конденсаторы в цепи постоянного тока
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
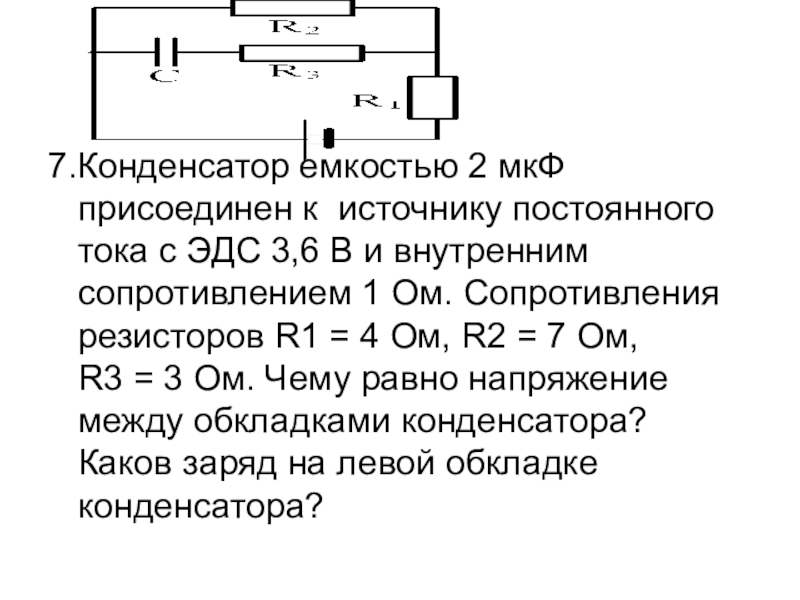
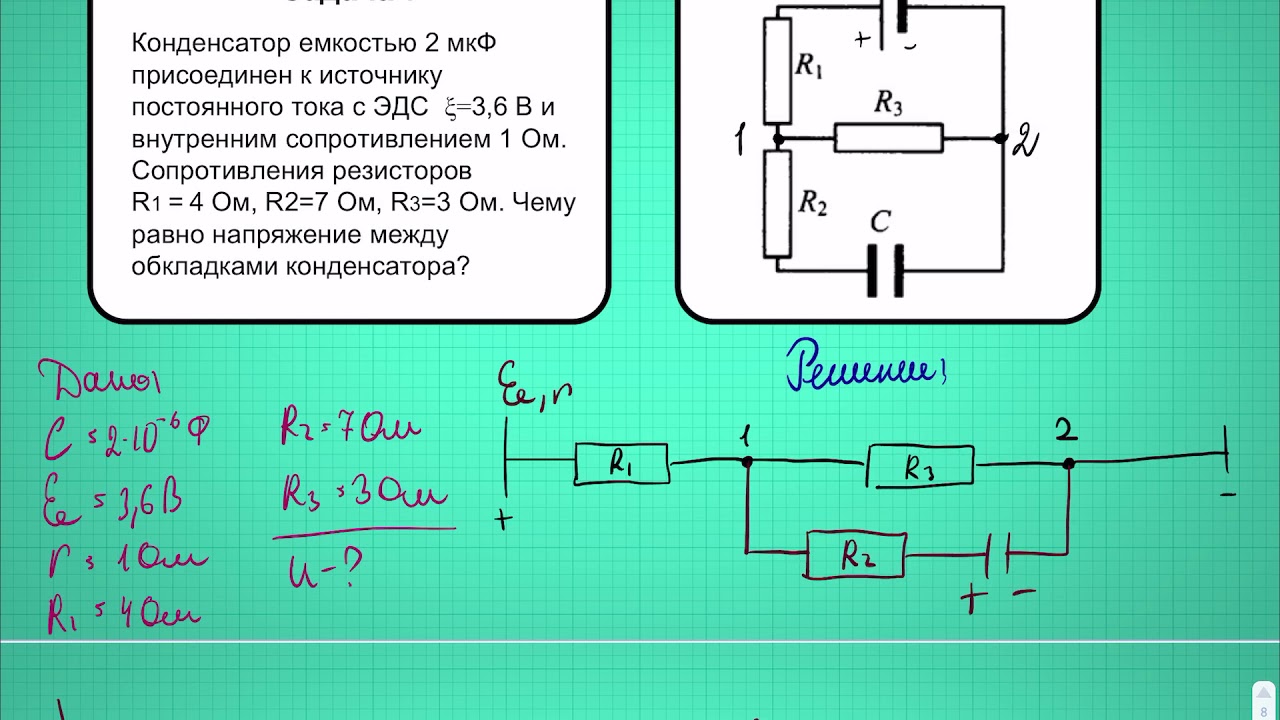
1. Задача № 1
Определить энергию конденсатора емкостьюС =200 мкф, включенного в цепь, схема которой
изображена на рисунке. ЭДС источника 5 В, его
внутреннее сопротивление 0,5 Ом. Сопротивление
резистора
R1 = 2 Ом,
R2 =2,5 Ом.
С
R2
R1
2. Решение задачи №1:
В стационарном режиме через конденсатор ток не идет.Поэтому электрическую цепь можно представить проще:
Ток в этой цепи определяется
I = E/ R1 +R2 + r.

Напряжение на участке ав – напряжение на резисторе R2 , а значит и на конденсаторе:
U = IR2.=R2 E/ R1 +R2 + r.
W= СU2/2
W= С(R 2) 2E2/2(R1 +R2 +r )2=
6,25/10000Дж
Ответ:
а
Е
R2
R1
в
W =6,25/10000Дж
3. Задача № 2 Попробуйте решить самостоятельно.
Конденсаторы С1 и С2 и резисторы, сопротивлениякоторых равны R1, R2, R3 включены в электрическую цепь,
как показано на рисунке. Найдите установившийся заряд
на конденсаторе С, если ЕДС источника Е, а его
внутреннее сопротивление равно нулю.
C1
R3
R2
R1
C2
E
4. Решение задачи №2 Ток в стационарном режиме идет по цветной ветке. I =E/ R1+R2+R3 = 1A Напряжение на конденсаторе С2 равно
напряжению на резисторах R2 и R3q2=C2U23 = C2 I R23 = 2мкф 1А 10ом = 20мкКл
Ответ:q2 = 20мкКл
С1
R3
R3
R2
R1
R2
R1
С2
Е
Е
5. Следующий тип задач позволяет определить разность потенциалов в электрической цепи содержащей конденсаторы.
 Задача № 3
Задача № 3Найти разность потенциалов между точками А и В в
цепи. Внутренним сопротивлением источника можно
пренебречь. ЭДС источника равна Е=10В, R1 = 2 ом, R2 = 3
ом. Емкость конденсаторов С1 = 0,5мкф,
С1
С2
С2 = 2 мкф
А
+
+
R1
R2
В
—
+
E
6. Решение задачи №3:
Ток в стационарном режиме идет от источника через сопротивление R1 и R2I = E/R1 +R2 = 10B/5ом = 2А . Ur1 = I R1 = 4В
По верхней ветке, через конденсаторы ток не идет.
Правые пластины конденсатора заряжены положительно, левые отрицательно от источника
тока. Если идти от точки А против часовой стрелки до точки В потенциал изменяется:
при переходе через конденсатор С1 потенциал (энергия) уменьшается от + к -, при переходе по
резистору R1 к точке В потенциал возрастает:
Yа – Uc1 + Ur1 = Yв :
Yа –Yв = Uc1 — Ur1
По законам последовательного соединения конденсаторов:
q1 = q2,
следовательно: С1U1 = C2U2, Откуда: U1 С1/ C2 = U2
Е = U1 +U2 = U1 + U1 С1/ C2 = U1 ( 1 + С1/ C2 ).

Uc1 = Е/ ( 1 + С1/ C2 ) = 10В /( 1+ 0,5мкф/2мкф) = 8В
Yа –Yв = Uc1 — Ur1 = 8В – 4В = 4В
Ответ: Yа –Yв = 4В
7. Задача №4.Определить заряд конденсатора С в схеме, представленной на рисунке. Внутренним сопротивлением батареи пренебречь.
EРешение задачи:
—
+
3C
2C
+
Обозначим заряды
конденсаторов С, 2С и
3С через q1,q2 и q3
соответственно.
2R
+
C
+
R
Предположим, что у конденсатора С положительный заряд находится на нижней пластине.
Тогда из закона сохранения заряда
–q2 – q1 + q3 = 0
( в выделенном квадрате пластины конденсаторов не соединены с источником, значит
заряд этих пластин до зарядки конденсаторов и после зарядки остается равны нулю
1) q2 + q1 = q3
В стационарном режиме ток идет только через источник тока R и 2R. Через конденсаторы
ток не идет. R и 2R соединены последовательно, поэтому ток в цепи:
I = E/3R
8. Продолжение решения задачи №4
Выберем обход в правом контуре по часовой стрелке, тогда по 2 –му правилу Кирхгоффа:2) – Uc+ U2c = IR = E/3; q2/2c — q1/c = E/3; q2/2C — q1/C = E/3; — 2q1 + q2 =2CE/3
q2 = 2q1 +2CE/3
( конденсатор — накопитель энергии, здесь в роли источника тока)
Аналогично в левом контуре:
3C
3) U3c + Uc = I2R = 2E/3
q3/3c + q1/c = 2 E/3
2C
+
2R
+
C
+
R
С учетом первого уравнения:
3) q 1 /3c + q2/3c + q1/c = 2E/3;
q2 + q1 +3q1 = 2CE
4q1 + 2 q1 + 2CE/3 = 2CE
6q1 =2CE – 2CE/3 = 6CE/3 -2CE/3 = 4CE/3
q1 = 4CE/18 = 2CE/9
Ответ: Заряд на конденсаторе С: q1 = 2CE/9
Примечание: Следует обратить внимание на то, что q1 положительный.
 Это означает, что предположение о знаке
Это означает, что предположение о знакезаряда на обкладках конденсатора С было правильным (от этого предположения зависит расстановка знаков в
первом уравнении). Понятно, что если бы было сделано другое предположение, ответ имел бы другой знак.
English Русский Правила
Переходные процессы в цепях постоянного тока с конденсатором
ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными
РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи
Согласно закону Ома для однородного участка цепи
IR=U,
где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что и , преобразуем закон Ома к виду
(1)
В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем
, (2)
где q0 — начальный заряд конденсатора, е — основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t . Продифференцировав выражение (2) по времени, найдём закон изменения тока:
, (3)
где I0 — сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.
Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:
(4)
ЗАРЯДКА КОНДЕСАТОРА.
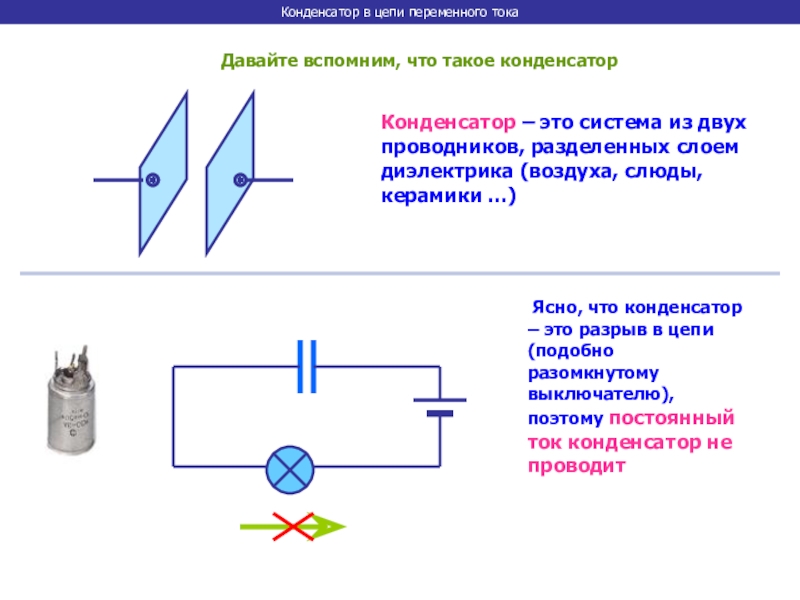
Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи:
.
После разделения переменных уравнение примет вид:
Проинтегрировав это уравнение с учётом начального условия
q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим
, или после потенцирования
q = . (4)
Анализ этого выражения показывает, что заряд приближается к своему максимальному значению, равному С, асимптотически при t ® ?.
Подставляя в формулу (4) функцию I(t) = dq/dt, получим
. (5)
(5)
Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dАист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW:
dAист= dQ + dW,
где dAист =Idt, dQ =I2Rdt, dW =d. Тогда для произвольного момента времени t имеем:
Аист(t)===С. (6)
Q(t)==С. (7)
W(t) ==. (8)
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
В реальных электрических цепях постоянного тока, содержащих конденсаторы, переходные процессы разрядки и зарядки конденсаторов проходят за время порядка 10–6 – 10-3 с.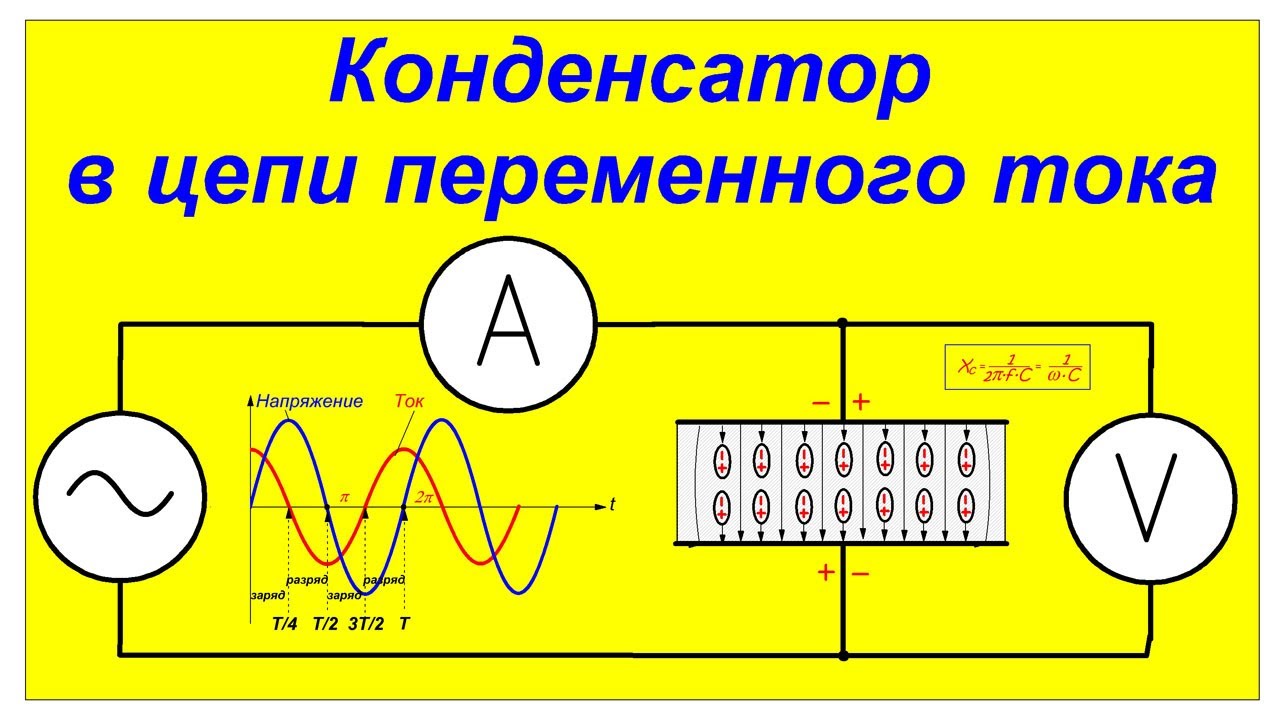 Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
ЭКСПЕРИМЕНТ 1
1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.
Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), Ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).
2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.
3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.
4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.
5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I0. Запишите это значение в таблицу 3.
6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.
7. Для каждого опыта рассчитайте It=
Для каждого опыта рассчитайте It=
8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.
9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к It. Запишите это значение времени t1 в таблицу 3.
10. Проделайте опыты п.п.8, 9 ещё 4 раза.
Таблица 1. Суммарное значение э.д.с. источников тока
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Э. |
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
Таблица 2. Определение сопротивления лампы.
|
№п/п |
I, А |
U, В |
R, Ом |
|
Номер опыта |
1 |
2 |
3 |
4 |
5 |
Среднее значение |
|
I0, А |
||||||
|
It, А |
||||||
|
t, с |
||||||
|
C, Ф |
Таблица 3. Результаты измерений и расчётов.
Результаты измерений и расчётов.
ОБРАБОТКА РЕЗУЛЬТАТОВ:
1. По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.
2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.
3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.
ЭКСПЕРИМЕНТ 2
Изучение зависимости от времени количества тепла, выделившегося на нагрузке при разряде конденсатора
- Выполняя действия, аналогичные описанным в эксперименте 1, зарядите конденсатор до напряжения, соответствующего суммарному значению э.д.с. для вашего варианта.
- Нажмите кнопку «Стоп» и отключите ключ К.
- Проведите 5-ти секундный процесс частичного разряда конденсатора через подключённые лампы.
 Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора. - Запишите показания амперметра в таблицу 4 и вновь зарядите конденсатор до первоначального напряжения.
- Последовательно увеличивая длительность процесса разрядки конденсатора на 5 с, проделайте эти опыты до времени разрядки, соответствующему полному исчезновению заряда на конденсаторе. (Напряжение на конденсаторе и ток разрядки через лампы должен быть близким к нулю). Результаты измерений тока разрядки запишите в соответствующие ячейки таблицы 4.
Таблица 4. Результаты измерений и расчетов
|
Время разрядки t, с |
5 |
10 |
15 |
20 |
… |
5n |
|
Ток разряда I через |
||||||
|
Кол-во тепла Q за t с, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- Для каждого времени разрядки вычислите по формуле (4) количество тепла, выделившегося на шести лампах и запишите эти значения в соответствующие ячейки третьей строки табл.
 4. Полезный совет: для расчёта Q воспользуйтесь программой
4. Полезный совет: для расчёта Q воспользуйтесь программой - Постройте график зависимости количества выделившегося тепла Q к данному моменту времени от длительности процесса разрядки конденсатора t.
- Сравните рассчитанное количество тепла, выделившееся к моменту полного разряда конденсатора с его теоретическим значением, равным .
- Сделайте выводы по графику и ответу и проведите расчёт погрешностей измерений.
ЭКСПЕРИМЕНТ 3
Проверка закона сохранения энергии в процессе зарядки конденсатора через сопротивление
Рис.3
- Соберите в рабочей части экрана опыта схему, показанную на рис.3. Вольтметр, включённый параллельно 5-ти лампам, будет показывать напряжение на внешнем сопротивлении, а амперметр – силу тока через нагрузку и источники тока. Напряжение на конденсаторе определяется программой автоматически и указывается в вольтах на экране монитора над конденсатором.

- Установите суммарную э.д.с. источников тока, соответствующую значению, приведённому в табл.1 для вашего варианта.
- При разомкнутом ключе К нажмите кнопку «Старт».
- Нажатием кнопки мыши замкните ключ К и начните процесс зарядки конденсаторов. Одновременно с замыканием ключа включите секундомер.
- Через время релаксации t = RС нажатием кнопки «Стоп» остановите процесс и запишите показания электроизмерительных приборов в таблицу 5.
- Нажмите кнопку «Выбор» и обнулите показания напряжений на всех конденсаторах и на электроизмерительных приборах.
- Повторите эти измерения ещё 4 раза и заполните две верхних строки таблицы 5.
Таблица 5. Результаты измерений и расчетов
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
Среднее |
|
I, A |
||||||
|
Uc, B |
||||||
|
UR, B |
||||||
|
Аист, Дж |
||||||
|
DW, Дж |
||||||
|
Q, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- По формулам 6, 7, 8 и измеренным значениям напряжения на конденсаторе Uc рассчитайте величины работу источника тока Аист, изменение энергии конденсатора DW и выделившегося на нагрузке количества тепла Q через время заряда, равного времени релаксации.

- Проверьте выполнение закона сохранения энергии в процессе зарядки конденсатора по формуле: Аист =DW + Q.
- Сделайте выводы по итогам работы.
Вопросы и задания для самоконтроля
Вопросы и задания для самоконтроля
- Что представляет собой конденсатор и от чего зависит его ёмкость?
- Выведите формулы ёмкости плоского, цилиндрического и сферического конденсаторов.
- Как изменяется разность потенциалов на обкладках конденсатора при его зарядке и разрядке?
- Какой ток называется квазистационарным?
- Выведите формулы электроёмкости батареи последовательно и параллельно соединённых конденсаторов
- Что такое время релаксации?
- Объясните принцип работы экспериментальной установки.
- Нарисуйте графики зависимости силы тока и напряжения от времени при зарядке и разрядке конденсатора.

- Соберите на мониторе такую цепь, состоящую из источника тока, двух ламп, выключателя и соединительных проводов, чтобы с выключением лампы в одной цепи загоралась лампа в другой.
- Определите заряд, который пройдёт через гальванометр в схеме, показанной на рис. 2, при замыкании ключа.
- Конденсатор ёмкости С = 300 пФ подключается через сопротивление R =500 Ом к источнику постоянного напряжения U0. Определите: а) время, по истечению которого напряжение на конденсаторе составит 0,99 U0; в) количество тепла, которое выделится на этом сопротивлении при разрядке конденсатора за это же время.
- Имеется ключ, соединительные провода и две электрические лампочки. Составьте на мониторе электрическую схему включения в сеть этих лампочек, которая должна удовлетворять следующему условию: при замкнутом ключе горит только первая лампочка, при размыкании ключа первая гаснет, а вторая загорается.

- Конденсатору ёмкостью С сообщают заряд q, после чего обкладки конденсатора замыкают через сопротивление R. Определите: а) закон изменения силы тока, текущего через сопротивление; б) заряд, прошедший через сопротивление за время t; в) количество тепла, выделившееся в сопротивлении за это время.
- Определите количество тепла, выделившегося в цепи (рис. 4-6) при переключении ключа К из положения 1 в положение 2. Параметры цепи обозначены на рисунках.
Конденсаторы в цепях постоянного тока
Конденсатор и емкость
Когда любые две проводящие поверхности разделены изоляционным материалом, это называется конденсатором . Проводящие поверхности известны как обкладки конденсатора , а изоляционный материал известен как диэлектрик .
Способность конденсатора накапливать заряд называется емкостью конденсатора. Он обозначается буквой C и измеряется в фарадах (F).
Экспериментально установлено, что заряд (Q), запасенный в конденсаторе, прямо пропорционален разности потенциалов на нем, т. е.
$$Q\varpropto\:V$$
$$\Rightarrow\:Q=CV$$
$$\Rightarrow\:C=\frac{Q}{V}\:\:\:\ :…(1)$$
Где C – постоянная, известная как емкость конденсатора.
Таким образом, емкость (C) конденсатора определяется как отношение заряда (Q) на любой пластине конденсатора к разности потенциалов (V) на ней.
Единицей емкости является
$$\because\:C=\frac{Q}{V}$$
$$\следовательно\:Единица\:of\:C=\frac{Кулон} {Вольт}=Фарад$$
Как конденсатор накапливает заряд?
Рассмотрим плоский конденсатор, подключенный к батарее V вольт через переключатель. Зарядку конденсатора можно понять следующим образом: −
Шаг 1 − При разомкнутом переключателе S пластины конденсатора не заряжаются.
Шаг 2 − Когда переключатель S замкнут, положительный полюс батареи притягивает электроны с пластины A и накапливает эти электроны на пластине B. Это приводит к тому, что пластина A становится все больше и больше положительным, а пластина В становится все более и более отрицательной. Это действие называется зарядка конденсатора . Этот процесс зарядки конденсатора продолжается до тех пор, пока разность потенциалов на конденсаторе не станет равной напряжению батареи (В).
Это приводит к тому, что пластина A становится все больше и больше положительным, а пластина В становится все более и более отрицательной. Это действие называется зарядка конденсатора . Этот процесс зарядки конденсатора продолжается до тех пор, пока разность потенциалов на конденсаторе не станет равной напряжению батареи (В).
Шаг 3 — Как только конденсатор заряжается до напряжения батареи (В), ток прекращается.
Шаг 4 – Теперь, если переключатель S разомкнут, пластины конденсатора сохранят заряд. Поэтому говорят, что в это время конденсатор заряжен.
Важные моменты
Следующее можно отметить относительно действия конденсатора −
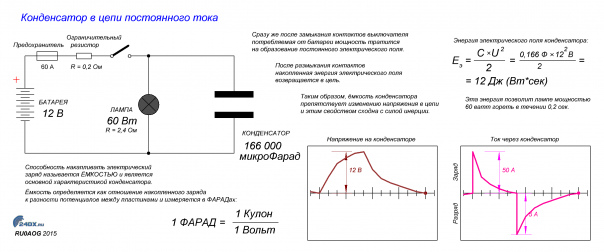
Когда на конденсатор подается постоянное напряжение, зарядный ток будет течь до тех пор, пока конденсатор полностью не зарядится, когда ток остановится. Этот процесс зарядки будет происходить за очень короткое время, доли секунды. Следовательно, полностью заряженный конденсатор блокирует прохождение постоянного тока.

Происходит только перенос электронов с одной пластины на другую по внешней цепи. Ток между пластинами конденсатора не течет.
Когда конденсатор заряжен, две пластины несут одинаковый и противоположный заряд. Таким образом, заряд на конденсаторе означает заряд на любой пластине.
Энергия, необходимая для зарядки конденсатора, поступает от внешнего источника.
Поведение конденсатора в цепи постоянного тока
Поведение конденсатора в цепи постоянного тока можно понять из следующих пунктов: −
$$i=\frac{dQ}{dt}=\frac{d(CV) }{dt}=C\frac{dV}{dt}\:\:\:\:(2)$$
Когда конденсатор полностью заряжен, напряжение на конденсаторе становится постоянным и равняется приложенному напряжению. Следовательно, (dV/dt = 0) и, следовательно, зарядный ток.
Напряжение на незаряженном конденсаторе равно нулю, что эквивалентно короткому замыканию, если речь идет о постоянном напряжении.

Когда конденсатор полностью заряжен, ток в цепи отсутствует. Следовательно, полностью заряженный конденсатор выглядит как разомкнутая цепь для постоянного тока.
Зарядка конденсатора
Рассмотрим незаряженный конденсатор емкостью C, подключенный к батарее с напряжением V вольт (постоянного тока) через последовательный резистор R для ограничения зарядного тока в безопасных пределах. Когда ключ S замкнут, в цепи протекает зарядный ток, и конденсатор начинает заряжаться.
Зарядный ток максимален в момент замыкания ключа и постепенно уменьшается по мере увеличения напряжения на конденсаторе. Когда конденсатор полностью заряжен до приложенного напряжения (В), зарядный ток уменьшается до нуля.
В момент замыкания ключа
В момент замыкания ключа напряжение на конденсаторе равно нулю (поскольку в начале конденсатор не заряжен). Все напряжение V возникает на резисторе R, а зарядный ток максимален. Следовательно,
Следовательно,
$$Исходное\:зарядка\:ток,I_{m}=\frac{V}{R}$$
$$Напряжение\:accross\:конденсатор,v=0$$
$$ Заряд\:на\:конденсатор,Q=0$$
В любой момент времени, t
После замыкания ключа зарядный ток начинает уменьшаться, а напряжение на конденсаторе постепенно увеличивается. Следовательно, в любой момент времени t,
$$voltage\:накрест\:capacitor=v$$
$$charge\:on\:capacitor,q=Cv$$
$$The\:charging\: ток,i=C\frac{dv}{dt}$$
Напряжение на конденсаторе −
Применяя KCL в цепи, мы можем написать,
$$V=V_{R}+v$$
$$\Rightarrow\:V=iR+v=(C\frac{dv}{dt})R+v\:\:\:\:\:…(3)$$
$$\Rightarrow\:\frac{dv}{V-v}=\frac{dt}{RC}$$
Интегрируя обе стороны,
$$\int\frac{dv}{V-v}= \int\frac{dt}{RC}$$
Решая это интегрирование, получаем
$$-\log_{e}{(V-v)}=\frac{t}{RC}+K\: \:\:\:…(4)$$
Значение K можно определить из начальных условий. В момент замыкания ключа t = 0 и v = 0. Следовательно, из уравнения (4)
В момент замыкания ключа t = 0 и v = 0. Следовательно, из уравнения (4)
$$-\log_{e}{V}=K$$
Подставляем значение K в уравнение (4), получаем, 9{-t/RC}\:\:\:\:…(7)$$
Где I m — начальный зарядный ток. Также из ур. (7) видно, что зарядный ток уменьшается экспоненциально. Уравнения зарядного напряжения и зарядного тока также могут быть представлены графически, как показано ниже.
Постоянная времени −
Постоянная времени может быть определена как время, необходимое для того, чтобы напряжение на конденсаторе (v) поднялось до своего окончательного установившегося значения V. Оно обозначается Тау (τ) и определяется как,
$$Time\:Constant,\tau=RC\:seconds\:\:\:\:…(8)$$
Разрядка конденсатора
Рассмотрим заряженный конденсатор C фарад, соединенный последовательно с резистор R через переключатель S. Когда переключатель разомкнут, напряжение на конденсаторе составляет V вольт.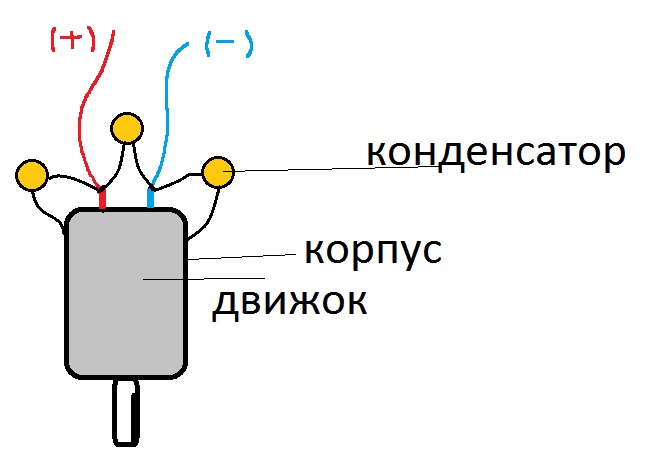 При замыкании ключа в цепи начинает протекать ток разряда и конденсатор начинает разряжаться, т.е. напряжение на нем начинает уменьшаться. Разрядный ток мгновенно возрастает до значения I м и затем сводится к нулю.
При замыкании ключа в цепи начинает протекать ток разряда и конденсатор начинает разряжаться, т.е. напряжение на нем начинает уменьшаться. Разрядный ток мгновенно возрастает до значения I м и затем сводится к нулю.
Напряжение разряда −
Учитывать в любой момент времени t во время разряда,
трещина { dV}{dt}$$
Применяя КВЛ в схеме, получаем,
$$V+iR=0$$
$$\Rightarrow\:v+CR\frac{dV}{cdt}= 0$$
$$\Rightarrow\:\frac{dV}{v}=-\frac{dt}{RC}$$
Интегрируя в обе стороны, получаем,
9{-t/RC}\:\:\:…(11)$$Уравнения напряжения разряда и тока разряда также можно представить графически, как показано ниже.
Числовой пример
Конденсатор емкостью 4 мкФ подключен к источнику постоянного тока 120 В через сопротивление 1 МОм.
Определите следующее −
Постоянная времени
Начальный зарядный ток
Напряжение на конденсаторе через 5 секунд после замыкания ключа 9{-5/4})=85,62 В$$
Время, необходимое для полной зарядки конденсатора = 5 × Постоянная времени
$$\следовательно\:t_{полный\:заряженный}=5\раз\:4 =20\:sec$$
Конденсаторы для питания переменного или постоянного тока
Серия E50
Конденсаторы постоянного тока с малой индуктивностью
От 600 В до 3600 В, до 7400 мкФ, Irms до 120 А на конденсаторE50 конденсатор (PK16™) может универсально использоваться для сборки буферных цепей постоянного тока с низкой индуктивностью и фильтров промежуточного контура; благодаря своей высокой плотности энергии он может заменить батареи последовательно соединенных электролитических конденсаторов, а также большие пленочные конденсаторы в прямоугольных корпусах.
 Благодаря компактному цилиндрическому алюминиевому (N1/N5) или пластиковому (N4) корпусу этот конденсатор идеально подходит как для электрических, так и для механических требований высокоскоростных IGBT-преобразователей.
Благодаря компактному цилиндрическому алюминиевому (N1/N5) или пластиковому (N4) корпусу этот конденсатор идеально подходит как для электрических, так и для механических требований высокоскоростных IGBT-преобразователей.Его прочные клеммы и крепкая фиксирующая шпилька обеспечивают очень простой и надежный монтаж, который сочетает в себе самую низкую индуктивность и самую высокую силу тока.
Серия E51
Осевые малоиндуктивные конденсаторы постоянного или переменного/постоянного тока
от 1300 до 50000 В пост. тока, до 700 мкФ
от 2350 до 35000 В перем. тока, до 5 мкФКонденсаторы серии Е51 в первую очередь подходят для использования в буферных цепях с низкой индуктивностью с более высокими напряжениями, а также в разрядных цепях, и они подходят для использования в силовой электронике в целом.
Несмотря на высокое номинальное напряжение, изготавливаются по сухой технологии и без дорогостоящих вводов. Внутри корпуса, изготовленного из самозатухающего пластика, конденсаторный элемент заключен в твердую смолу (PUR).
Загрузить брошюру Подключение осуществляется через прочные клеммы с внутренней резьбой. Наряду с очень хорошим отношением емкости к объему эти конденсаторы также обладают высокой силой импульса и очень хорошими характеристиками самовосстановления без потери емкости.
Подключение осуществляется через прочные клеммы с внутренней резьбой. Наряду с очень хорошим отношением емкости к объему эти конденсаторы также обладают высокой силой импульса и очень хорошими характеристиками самовосстановления без потери емкости.Серия E53
Радиальные и осевые малоиндуктивные конденсаторы переменного/постоянного тока
9 Конденсаторы 0004 E53 имеют особенно низкое последовательное сопротивление и высокую импульсную сила; они особенно подходят для буферных цепей с низкой индуктивностью и высокими среднеквадратичными значениями тока, а также для демпфирования тиристоров GTO.
280–2100 В переменного тока / 550–5000 В постоянного тока, до 250 мкФНаряду с очень хорошим отношением емкости к объему эти конденсаторы также обладают очень хорошими характеристиками самовосстановления без потери емкости. Их очень низкая собственная индуктивность делает их пригодными для использования в сильноточных приложениях со средними частотами.
Загрузить брошюру
Серии E56 и E59
Конденсаторы постоянного тока/фильтра постоянного тока в прямоугольном корпусе
До 25 000 В постоянного тока или до 10 000 В переменного тока, до 60,0 00 мкФБлагодаря особому виду пленок и покрытий, используемых в наших конденсаторах Е56/Е59, они сочетают в себе большую емкость, низкую собственную индуктивность и способность выдерживать высокие импульсные токи (до 750 кА), а также возможность работы с высокими среднеквадратичными значениями тока (до 1000 А). Специальные плоские клеммы дополнительно снижают самоиндукцию.
Эти конденсаторы имеют высокое удельное отношение емкости к объему. В то же время они чрезвычайно устойчивы к перенапряжению. Конденсаторы помещены в стальные или алюминиевые корпуса, заполненные твердой смолой, т.е. полностью сухие и герметичные. Даже при высоких рабочих температурах и после повышенного количества самовосстанавливающихся пробоев емкость остается стабильной.
Загрузить брошюру
Серия E57
Конденсаторы DC-link/DC-Filter в прямоугольном пластиковом корпусе
Рабочая температура до 105°CЭта серия была создана специально для применения в автомобильной промышленности, где ключевыми требованиями часто являются высокое рабочее напряжение и очень компактная конструкция.
Загрузить брошюруСерия E61
Конденсаторы постоянного тока с низкой индуктивностью для монтажа на печатной плате
От 500 В до 1300 В, до 260 мкФ, Irms до 35 А на конденсаторКонденсатор E61 основан на той же философии, что и наш Модельный ряд PK16™, но подготовленный для непосредственного монтажа на печатных платах. Функции и преимущества такие же, как и у PK16™, только в меньшем масштабе.
Серия E62
AC/DC-конденсаторы общего назначения
420–5000 В переменного токаБлагодаря высокой нагрузочной способности переменного напряжения и исключительной пригодности для высоких среднеквадратичных значений и импульсных токов, серия E62 конденсаторы широко используются в приложений силовой электроники.

Заполненные жидкой смолой на растительной основе, эти конденсаторы имеют высокое удельное отношение емкости к объему. Очень хорошие характеристики самовосстановления и встроенная защита от избыточного давления (механизм размыкания) обеспечивают безопасную работу и контролируемое отключение в случае перегрузки или отказа в конце срока службы. Все конструкции с металлической крышкой могут быть выполнены в том же размере и исполнении, что и E65 с газовым наполнением.
Загрузить брошюруСерия E63
Конденсаторы постоянного тока общего назначения
800–6300 В пост. тока, до 1800 мкФСпециализированные пленки и покрытия Использование в наших конденсаторах E63 делает их интересными, в частности, для приложений с высокими действующие токи.
Заполненные жидкой смолой на растительной основе, эти конденсаторы имеют высокое удельное отношение емкости к объему. В то же время они чрезвычайно устойчивы к перенапряжению. Очень хорошие характеристики самовосстановления и встроенная защита от избыточного давления (механизм размыкания) обеспечивают безопасную работу и контролируемое отключение в случае перегрузки или отказа в конце срока службы.
Загрузить брошюру
Серия E62-3ph/276 (275)
Трехфазные конденсаторы с фильтром переменного тока
От 640 до 1700 В перем. 3 x 200 мкФЭти конденсаторы, разработанные специально для фильтрации гармоник в трехфазных сетях, отличаются высокой нагрузочной способностью переменного напряжения и подходят для высоких среднеквадратичных значений и импульсных токов. Благодаря своей конструкции они имеют очень низкое последовательное сопротивление и низкую собственную индуктивность.
Три емкостных элемента соединены треугольником внутри; заливка жидкой смолой служит для улучшения отвода тепла. Защищенные от прикосновения винтовые клеммы конструкций CAPAGRIPTM K, L и M (степень защиты IP20) упрощают подключение.
Загрузить брошюруСерия E70
Самовосстанавливающиеся конденсаторы для индукционных печей
900 04 Резонансные конденсаторы / коррекция коэффициента мощности в печах Загрузить брошюру
От 400 В до 800 В, до 230 кВАрСерия E90
Самовосстанавливающиеся конденсаторы среднего напряжения сухого типа
От 3000 до 12000 В (среднеквадратичное значение), до 400 кВАр (3 фазы)Эти конденсаторы самовосстанавливаются и чрезвычайно долговечны.



 д.с.,В
д.с.,В Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора. 4. Полезный совет: для расчёта Q воспользуйтесь программой
4. Полезный совет: для расчёта Q воспользуйтесь программой 




 Благодаря компактному цилиндрическому алюминиевому (N1/N5) или пластиковому (N4) корпусу этот конденсатор идеально подходит как для электрических, так и для механических требований высокоскоростных IGBT-преобразователей.
Благодаря компактному цилиндрическому алюминиевому (N1/N5) или пластиковому (N4) корпусу этот конденсатор идеально подходит как для электрических, так и для механических требований высокоскоростных IGBT-преобразователей. Подключение осуществляется через прочные клеммы с внутренней резьбой. Наряду с очень хорошим отношением емкости к объему эти конденсаторы также обладают высокой силой импульса и очень хорошими характеристиками самовосстановления без потери емкости.
Подключение осуществляется через прочные клеммы с внутренней резьбой. Наряду с очень хорошим отношением емкости к объему эти конденсаторы также обладают высокой силой импульса и очень хорошими характеристиками самовосстановления без потери емкости.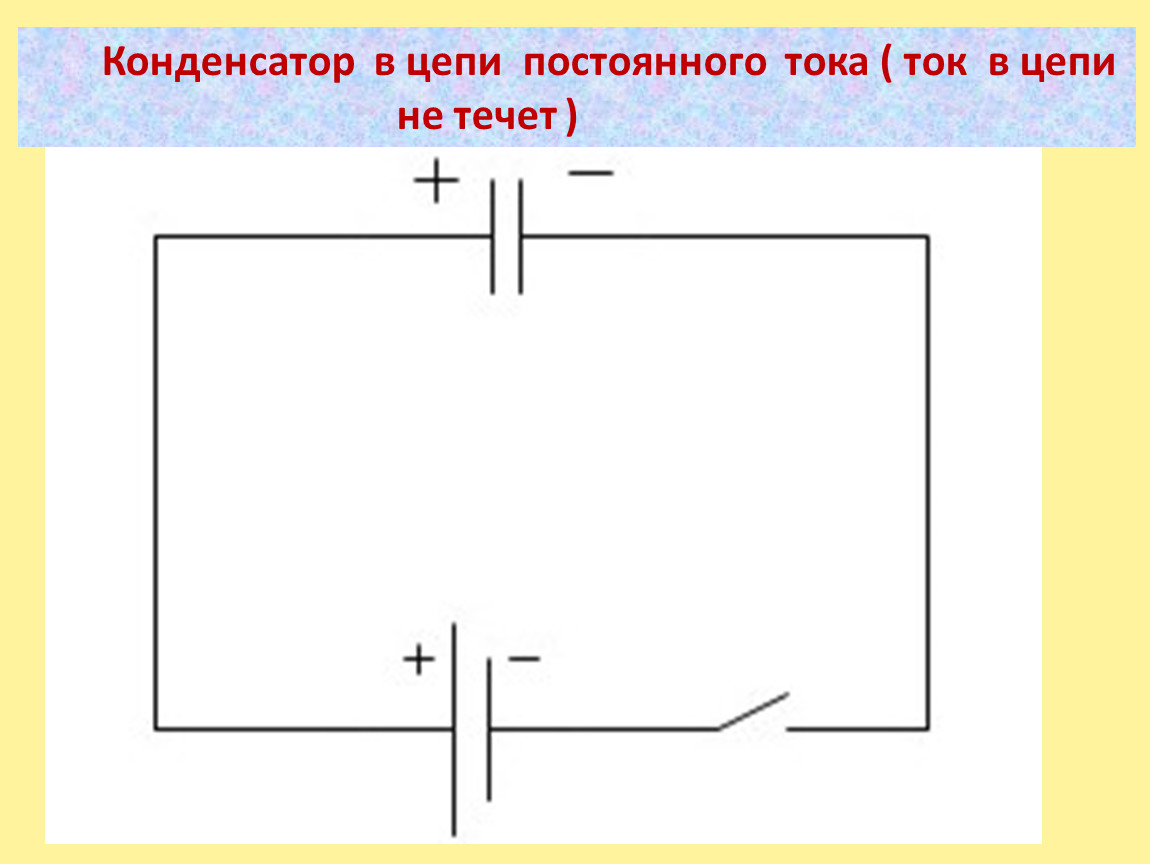

2016.ppt_images/306-elektrotehnika_(dlya_zanyatiy)2016.ppt_7.jpg)

