определение, основные понятия и примеры решений
Содержание:
- Плоские конденсаторы
- Конденсатор сферического типа
- Конденсатор цилиндрического типа
- Расчёт емкостных батарей, соединений конденсаторов
Определение 1
Конденсатором называют любые два проводника, разделённые диэлектрическим слоем. Такие проводники должны обладать зарядами одинаковыми по величине, но противоположными по знаку.
Возникающее электрическое поле будет полностью расположено внутри, между проводниками. По этой причине на электрическую ёмкость конденсатора не влияет его внешнее окружение. А на разность потенциалов между пластинами не влияет величина заряда.
Выражение для электроёмкости выглядит так:
$ C=\frac{q}{\phi_1-\phi_2} = \frac{q}{U} $
Величины $ {\phi_1-\phi_2=U}$ определяют разность потенциалов, которая также носит название «напряжение» и обозначается «U». Как следует из определения, ёмкость — положительная величина.
Существуют три основных типа конденсаторов: плоские, сферические, цилиндрические. Вычислить ёмкость можно, если найти напряжение на обкладках и определить величину заряда.
Плоские конденсаторы
Определение 2
Плоский конденсатор — элемент состоящий из двух или нескольких плоских пластин, расположенных друг напротив друга, имеющих одинаковый по величине, но разный по знаку заряд. Чтобы не возникало воздушного разряда, пластины разделяют слоем диэлектрика.
Чтобы не возникало воздушного разряда, пластины разделяют слоем диэлектрика.
Для вычисления ёмкости плоского конденсатора используется выражение:
$C=\frac{\epsilon\epsilon_0 S}{d}$.
Здесь S — площадь пластин, чем она больше, тем выше ёмкость. Величина зазора между пластинами — d. Чем меньше d, тем больше ёмкость. Диэлектрическая проницаемость — ε. Она также оказывает значительное влияние на величину ёмкости.
Пример 1
Возьмём конденсатор состоящий из двух пластин, между которыми воздух, и определим его ёмкость. Затем поместим между пластинами диэлектрик, параметр ε которого выше, чем у воздуха. Измерения показывают, что ёмкость конденсатора увеличивается существенно, прямо пропорционально повышению диэлектрической проницаемости.
Чаще всего, при создании плоских конденсаторов делают не две пластины, а «пакет» обкладок в несколько слоёв. Электрическая ёмкость такого элемента, имеющего n слоёв, вычисляется с учётом толщины каждого i-го слоя $d_i$, а также диэлектрической проницаемости каждого слоя $ε_i$.
Конденсатор сферического типа
Определение 3
Сферический конденсатор отличается формой обкладок, у него они представляют собой сферы. И внешняя, и внутренняя — обе оболочки выполнены в виде сфер.
В отличии от плоского конденсатора, в сферическом площадь поверхности разнозаряженных пластин отличается. И формула для вычисления ёмкости элемента изменится:
$ C = 4\pi\epsilon\epsilon_0\frac{R_1 R_2}{R_2-R_1} $,
где $ R_1 $ и $ R_2 $ являются радиусами обкладок.
Конденсатор цилиндрического типа
Отдельная формула используется для вычисления параметров конденсатора цилиндрической формы:
$ C = 2\pi\epsilon\epsilon_0 \frac{l}{ln{\frac{R_2}{R_1}}} $.
В уравнении использованы следующие параметры: l — высота, $R_1 и R_2$ – радиусы пластин. Конденсатор цилиндрического вида выполнен в виде вложенных друг в друга соосных цилиндрических пластин. Они выполнены из проводящего материала, а между ними находится диэлектрик.
Определение 4
Параметр, характеризующий конденсаторы — пробивное напряжение. 4 \frac{В}{м}$
4 \frac{В}{м}$
Страница не найдена — РОО «Ассоциация победителей олимпиад»
Ваши ФИО*
Ваш email*
Ваш номер телефона*
Какой предмет вы хотели бы преподавать?*
Расскажите кратко о своих олимпиадных достижениях*
Приложите резюме*
Объём файлов не должен превышать 20 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt
Please leave this field empty.
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
Ваша электронная почта*
Из какого вы региона?*
Расскажите, как мы могли бы сотрудничать*
Please leave this field empty.
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО*
Ваша электронная почта*
Ваш номер телефона*
Образовательное учреждение*
Расскажите кратко, какая у вас сложилась ситуация с олимпиадным движением в школе и какого результата вы ожидаете от сотрудничества с АПО*
Please leave this field empty.
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
Ваш email
Каким предметом вы интересуетесь
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО ученика
Дата рождения ученика
Класс
Образовательное учреждение
Город образовательного учреждения
ФИО родителя
Телефон родителя
Email родителя
Выберите группу Группа не выбрана
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО ученика
Дата рождения ученика
Класс
Образовательное учреждение
Город образовательного учреждения
ФИО родителя
Телефон родителя
Email родителя
Выберите группу Группа не выбрана
Мотивационное письмо Объём файла не должен превышать 2 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО
Телефон
Образовательное учреждение
Город образовательного учреждения
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО
Телефон
Проект / отдел
Должность
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
ФИО ребенка
Название образовательного учреждения
Город образовательного учреждения
ФИО родителя
Телефон родителя
Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.
Войти
Родитель
Буду покупать курсы для своего ребёнка ЗарегистрироватьсяОбучающийся
Сам буду проходить курсы ЗарегистрироватьсяПредставитель школы
Буду заказывать услуги для своего образовательного учреждения и контролировать их исполнение ЗарегистрироватьсяСлушатель КПК
Буду проходить курсы повышения квалификации для учителей ЗарегистрироватьсяФормула сферического конденсатора — GeeksforGeeks
Конденсатор — это просто электрическое устройство, состоящее из двух клемм, способных накапливать энергию в виде электрического заряда. Его можно сконструировать, просто разместив два электрических проводника на расстоянии друг от друга. Пустое пространство между проводниками может быть заполнено вакуумом (или воздухом) или изоляционным материалом, известным как диэлектрик. Способность конденсатора накапливать заряды называется емкостью.
Его можно сконструировать, просто разместив два электрических проводника на расстоянии друг от друга. Пустое пространство между проводниками может быть заполнено вакуумом (или воздухом) или изоляционным материалом, известным как диэлектрик. Способность конденсатора накапливать заряды называется емкостью.
В конденсаторе две клеммы с противоположными зарядами расположены на расстоянии друг от друга, что позволяет ему генерировать (хранить) энергию. Простейшая конструкция конденсатора представляет собой параллельную пластину, состоящую из двух металлических пластин с зазором между ними. Следует отметить, что конденсатор может быть любой формы или размера или быть изготовлен из любого материала, пока его клеммы не будут накапливать противоположные заряды и, таким образом, накапливать энергию.
Емкость конденсатора
Рассмотрим конденсатор, положительные и отрицательные пластины которого удерживают заряд +q и -q соответственно. На него подается источник постоянного напряжения, который создает разность потенциалов V на пластинах. Теперь, как мы знаем,
Теперь, как мы знаем,
Q α V
Ввод константы C в это отношение.
Q=CV.
Примечание: Емкость каждого материала уникальна, и ее единицей СИ является Фарад (Ф).
Работа конденсатора
Предположим, что нам дана простейшая форма конденсатора, то есть конденсатор с параллельными пластинами. Он состоит из двух параллельных пластин, разделенных небольшим расстоянием, и этот зазор заполнен диэлектриком. Затем нам дан источник постоянного напряжения, подключенный через конденсатор, где одна пластина прикреплена к положительному концу (пластина I), а другая пластина подключена к отрицательному концу (пластина II). Когда потенциал батареи приложен к конденсатору, пластина I становится положительной по отношению к пластине II. В установившемся режиме ток пытается пройти через конденсатор от положительной пластины к отрицательной. Однако из-за зазора между ними с изолирующим слоем (диэлектриком) он не может течь.
Структура простого конденсатора.
Некоторое время конденсатор продолжает заряжаться набегающим потоком тока. Но через некоторое время он достигает состояния, когда он удерживает максимально возможное количество заряда. Вот как конденсатор накапливает энергию. Время, необходимое для достижения этого состояния максимального заряда, называется временем зарядки конденсатора. Далее отключаем от цепи источник напряжения и вставляем в него нагрузочный резистор. Теперь ток начинает течь от положительно заряженного вывода конденсатора к отрицательно заряженному выводу и теряет при этом всю свою энергию. Этот период времени называется временем разрядки конденсатора.
Разряд конденсатора.
Формула сферического конденсатора
Как упоминалось ранее, емкость возникает, когда между двумя пластинами есть разделение. Итак, для изготовления сферического конденсатора возьмем полую сферу, у которой внутренняя поверхность заряжена положительно, а внешняя поверхность сферы заряжена отрицательно.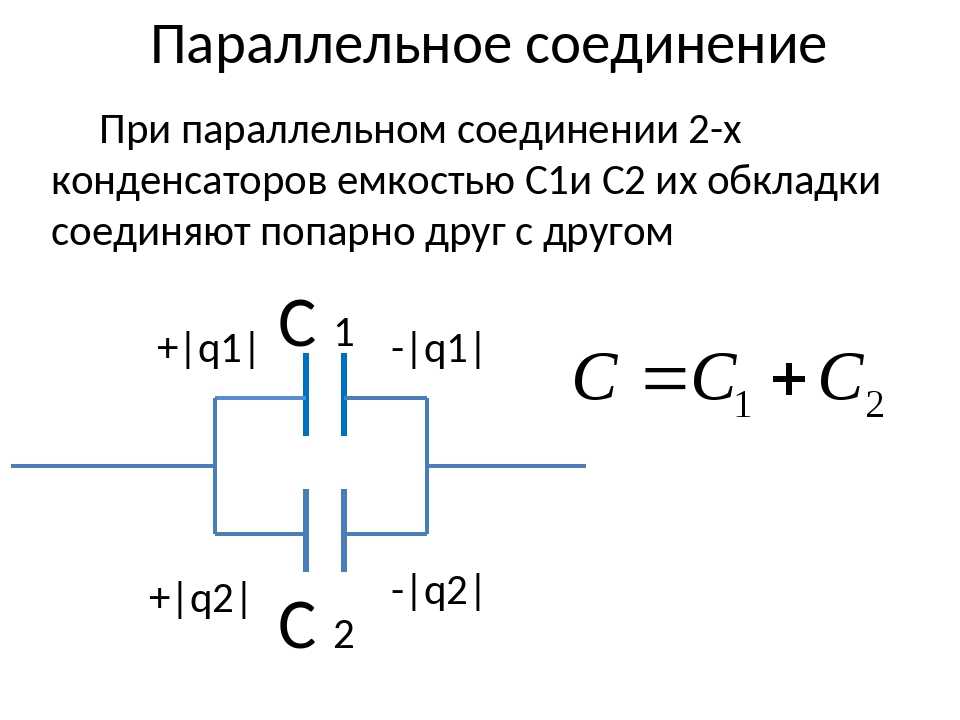 Внутренний радиус сферы равен r, а внешний радиус равен R. Расстояние R-r между двумя противоположно заряженными поверхностями действует как диэлектрик. Предположим, что внутренняя сферическая поверхность имеет потенциал В 1 и V 2.
Внутренний радиус сферы равен r, а внешний радиус равен R. Расстояние R-r между двумя противоположно заряженными поверхностями действует как диэлектрик. Предположим, что внутренняя сферическая поверхность имеет потенциал В 1 и V 2.
Сферический конденсатор
Далее, электрическое поле, создаваемое заряженной сферой (полой) радиусом r, имеющей заряд Q, определяется выражением
E= . ⇢ (1)
Кроме того, мы знаем, что генерируемое электрическое поле связано с разностью потенциалов как
E= . ⇢ (2)
Сравнивая (1) и (2),
Интегрируя в обе стороны в пределах V, V и r, R.
⇢ (3)
— это изменение потенциала при движении из сферы внутрь сферы наружу. Теперь емкость конденсатора определяется,
⇢ (4)
Сравнение (3) и (4),
Упрощение. t быть отрицательным, берется положительное значение. Это выражение для емкости сферического конденсатора.
t быть отрицательным, берется положительное значение. Это выражение для емкости сферического конденсатора.
Примеры вопросов
Вопрос 1. Сферический конденсатор имеет внутренний радиус 7 см и внешний радиус 10 см. Найдите емкость шара. Предположим, что диэлектриком между ними является воздух.
Решение:
емкость сферы определяется,
C =
здесь ∈ 0 = 8,85 × 10 -12 , R = 7, R = 10
C =
С = 2,593 × 10 -12 F
Вопрос 2. В приведенной выше задаче найдите, сколько заряда потребуется конденсатору, чтобы поднять его потенциал с 0 до 10 000 В.
Решение:
× 10 -12 F.
Требуемый заряд можно найти, используя Q = CV. где V — разность потенциалов.
Разность потенциалов V в этом случае равна 1000-0 = 1000В
Следовательно, Q = 3,7052 × 10 -12 × 1000
Q = 2,593 × 10 -9 C
Вопрос 3. Внутренний радиус сферического конденсатора равен x м, а его внешний радиус равен 5/4 x м, если внешний радиус увеличить до 3/2x м, найти, во сколько раз изменится его емкость.
Внутренний радиус сферического конденсатора равен x м, а его внешний радиус равен 5/4 x м, если внешний радиус увеличить до 3/2x м, найти, во сколько раз изменится его емкость.
Solution:
In this case
=
= 20 πε o x F
= 20 πε o x F
So the capacitance decreases as the внешний радиус увеличен. 9-8 C.
Решение:
C = 4 πε O x F
C = 4 × 3,14 × 8,85 × 10 —12 × 10 × 10 –2
C = C = C = C = C = C = C = C = C =
9000 2
9000 2 9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 × 10 × –2 9000 2 . 111.156 × 10 −13C = 1,11 × 10 −11 F
Теперь Q = CV
Следовательно,
Следовательно V = 900,9 В
Вопрос 5: Оверт -диал.
на 10 % больше, чем его внутренний радиус. Емкость этого конденсатора 10 -8 F. Найдите значение его внутреннего и внешнего радиусов.
Ответ:
Здесь R = x, R = 1,1x и C = 10 -8 F
SO,
x = 0,009 M
SO. равен 0,09 см, а внешний радиус равен 0,099 см.
Вопрос 6: Внутренний и внешний радиусы сферического конденсатора равны 5см и 6см. Найдите энергию конденсатора, если к нему приложена разность потенциалов 1000 В.
Solution:
The capacitance of this capacitor is calculated as,
C = 3.3363 × 10 −12 F
U = 1/2 CV 2
U = 21 × 3,3363 × 10 −12 × (1000) 2
U = 1,66815 × 10 −9 Дж
см -8 Дж . Найдите его напряжение.
Solution:
Lets find the capacitance first,
C = 4.
446 × 10 -9 F
U = 1/2 CV 2
V = 2.12 V
Зарядка конденсатора Формула График и пример
Конденсатор представляет собой компонент пассивной схемы , используемый в ввести емкость. Емкость
определяется как свойство вещества, благодаря которому оно запасает электрическую энергию в виде электростатическое поле . Типовой конденсатор состоит из двух металлических пластин, разделенных диэлектрическим материалом. Это диэлектрический материал, обладающий способностью накапливать электрическую энергию в виде электростатических разрядов. заряжать.
Процесс накопления электрической энергии в виде электростатического поля, когда конденсатор подключение к источнику электроэнергии называется зарядкой конденсатора . Это сохранено энергия в электростатическом поле может быть доставлена в цепь в более поздний момент времени.
В этой статье мы обсудим зарядку конденсатора и выведем уравнение напряжение, ток и электрический заряд, хранящийся в конденсаторе во время зарядки.
Что такое зарядка конденсатора?
Как обсуждалось ранее, зарядка конденсатора представляет собой процесс накопления энергии в виде электростатического заряда в диэлектрической среде конденсатора.
Рассмотрим незаряженный конденсатор емкостью C фарад. Этот конденсатор подключен к источнику постоянного напряжения V вольт через резистор R и переключатель S, как показано на рисунке-1.
При замыкании ключа S начинается зарядка конденсатора, т.е. начинается зарядный ток течет по цепи. Этот зарядный ток максимален в момент переключения и постепенно уменьшается с увеличением напряжения на конденсаторе. Как только конденсатор заряжается до напряжения, равного напряжению источника V, зарядный ток станет равным нулю.
Следовательно, для понимания процесса зарядки конденсатора рассмотрим следующие два момента −
Момент 1 − При замыкании ключа
В момент переключения напряжение на конденсаторе равно нулю, т.к. полностью разряженный конденсатор.
В этот момент все напряжение источника V падает на резистор R, а зарядный ток максимален (допустим I
м ). Таким образом,
$$\mathrm{Исходный\: зарядка\: ток,\, I_{m}=\frac{V}{R}}$$
$$\mathrm{Напряжение\: поперек\: конденсатор, V_{C} = 0}$$
$$\mathrm{Charge\: on\: конденсатор, Q_{C} = 0}$$
Момент 2: Любой Мгновенный «t»
После замыкания переключателя S напряжение на конденсаторе начинает увеличиваться и зарядный ток в цепи начинает постепенно уменьшаться. Пусть в любой момент времени t в течение зарядка конденсатора,
$$\mathrm{Зарядка\: ток = i}$$
$$\mathrm{Напряжение\: через\: конденсатор, V_{C} = v}$$
$$\ mathrm{Заряд\: вкл\: конденсатор, Q_{C} = q = Cv}$$
Теперь, применив в схеме КВЛ, можно записать,
$$\mathrm{V=v+iR\: \cdot \cdot \cdot (1)}$$
$$\mathrm{\because Current \: in\: конденсатор,\, i=C\frac{dv}{dt}}$$
$$\mathrm{\следовательно, V=v+CR\frac{dv}{dt}}$$
Преобразовывая уравнение, получаем,
$$\mathrm{\frac{dv}{V-v}=\frac{dt}{RC}}$$
Интегрируя с обеих сторон, получаем,
$$\mathrm {\ int \ frac {dv} {Vv} = \ int \ frac {dt} {RC}} $ $
$ $ \ mathrm {\ потому что \ int \ frac {dx} {1-x} = — log_ { e}\left|1-x \right|}$$
Используя это интегрирование, мы получаем,
$$\mathrm{-log_{e}\left ( V-v \right )=\frac{t}{RC}+K}$$
Где K — это постоянная, значение которой можно определить из начальных условий конденсатор.
Таким образом, при t = 0 v = 0. $$\mathrm{\следовательно, K=-log_{e}V }$$
Подставив это значение K в приведенное выше выражение, мы получим,
$$ \mathrm{-log_{e}\left (Vv \right)=\frac{t}{RC}-log_{e}V}$$
$$\mathrm{\Rightarrow log_{e}\left (Vv \right )-log_{e}V=-\frac{t}{RC}}$$ 9{-\frac{t}{RC}} \right )\: \cdot \cdot \cdot \left ( 2 \right )}$$
Выражение в уравнении (2) дает напряжение на конденсаторе при в любое время т. Он показывает, что увеличение напряжения на конденсаторе во время заряда происходит по экспоненциальному закону.
Уравнение (2) также показывает, что по мере увеличения t экспоненциальный член e -t/RC уменьшается и напряжение на конденсаторе увеличивается. Когда член e -t/RC становится равным нулю, напряжение на конденсатор станет равным напряжению источника V, и говорят, что конденсатор полностью заряжен. Когда конденсатор полностью заряжен, падение напряжения на резисторе R равно нулю.


 на 10 % больше, чем его внутренний радиус. Емкость этого конденсатора 10 -8 F. Найдите значение его внутреннего и внешнего радиусов.
на 10 % больше, чем его внутренний радиус. Емкость этого конденсатора 10 -8 F. Найдите значение его внутреннего и внешнего радиусов.  446 × 10 -9 F
446 × 10 -9 F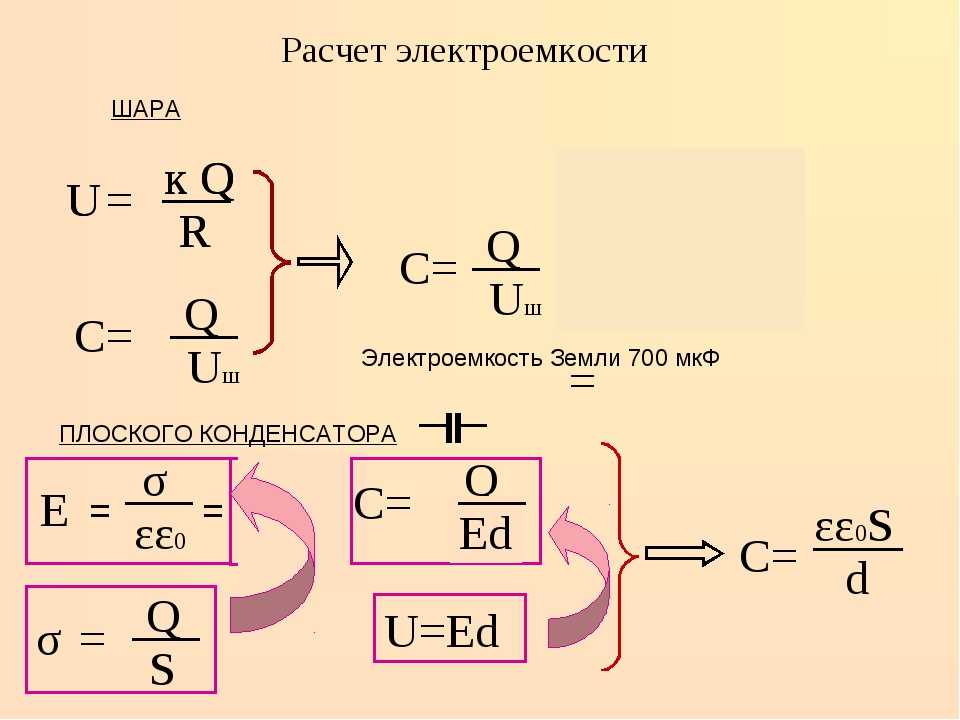
 В этот момент все напряжение источника V падает на
резистор R, а зарядный ток максимален (допустим I
В этот момент все напряжение источника V падает на
резистор R, а зарядный ток максимален (допустим I 
