Емкость конденсаторов: определение, формулы, примеры.
Определение 1Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Определение 2Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Определение 3Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:
Емкость рассчитывается по формуле:
C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.
Рисунок 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C=2πεε0llnR2R1, где l — высота цилиндров, R1 и R2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.
Рисунок 3
Определение 4Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.
Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:
C=∑i=1NCi.
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Пример 1Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
C=εε0Sd.
Значения:
ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
Подставим числовые выражения и вычислим:
C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
Ответ: C≈0,9 пФ.
Пример 2Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м.
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x — расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
q=CU.
Для сферического конденсатора предусмотрена формула вида
C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
Производим подстановку выражений для получения искомой напряженности:
E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
Ответ: E=3,45·104 Вм.
Автор: Роман Адамчук
Преподаватель физики
4.
 Электрическая емкость. Конденсатор. Способы изменения электрической емкости конденсаторов. Параллельное и последовательное соединения конденсаторов.
Электрическая емкость. Конденсатор. Способы изменения электрической емкости конденсаторов. Параллельное и последовательное соединения конденсаторов.Проводники различной формы и различного размера, заряженные одинаковым количеством электричества, приобретают различные потенциалы. Это является следствием того, что такие проводники обладают различной электроемкостью. При одной и той же форме большую емкость будут иметь тела больших размеров. Так, например, емкость шара прямо пропорциональна его емкости.
Емкость тел зависит от близости окружающих предметов и их физических свойств. При приближении к проводнику другого проводника его емкость увеличивается.
В международной системе единиц за единицу емкости принята емкость такого проводника, потенциал которого при увеличении заряда на 1 кулон повышается на 1 вольт. Эта единица называется фарадой (Ф).
1фарад=1кулон/1вольт.
Это
очень большая величина. На практике
применяются меньшие единицы: микрофарада
(мкФ), равная 10^-6Ф и пикофарада (пФ), равная
10^-12 Ф.
Два проводника, изолированные один от другого и помещенные в непосредственной близости, образуют конденсатор. Емкость конденсатора зависит от площади поверхности проводников, которые выполняются в виде пластин. Для увеличения емкости увеличивают число пластин, соединяя их вместе с одной стороны (рис 1 а)
Пластины называют обкладками конденсатора. Они могут быть самых различных форм.
Емкость конденсатора С численно равна заряду, который ему надо сообщить, чтобы разность потенциалов между его обкладками равнялась 1 вольту: C=q/(2—1)=q/U (1.3)
Электрическое поле конденсатора сосредоточено между обкладками и поэтому окружающие конденсатор тела практически не влияют на его емкость.
При введении между обкладками конденсатора диэлектрика его емкость увеличивается. Степень увеличения емкости зависит от типа диэлектрика, т.е. от его диэлектрической проницаемости:
=C/C0,
где,
C0 — емкость конденсатора с воздушным
диэлектриком; С — емкость того же
конденсатора с твердым или жидким
диэлектриком. 2, d-
расстояние между пластинами (толщина
диэлектрика) , см,
—
диэлектрическая проницаемость.
2, d-
расстояние между пластинами (толщина
диэлектрика) , см,
—
диэлектрическая проницаемость.
Для увеличения площади обкладок последние выполняются в виде двух полосок фольги, свернутых в рулон и изолированных друг от друга бумажной лентой. При этом увеличиваются габариты конденсатора.
Уменьшение расстояния между обкладками конденсатора с целью увеличения его емкости наиболее эффективным сказывается в электролитических (оксидных) конденсаторах, в которых в качестве диэлектрика используется тонкая пленка окисла аммония. Однако уменьшение d уменьшает электрическую прочность конденсатора (т.е. из-за избежания электрического пробоя, выводящего конденсатор из строя) снижается его рабочее напряжение.
Наиболее эффективным способом увеличения емкости конденсаторов является применение в них диэлектриков с большим значением диэлектрической постоянной (например керамический).
Для
увеличения емкости конденсаторы соединяю
параллельно (рис1
б).
При этом общая емкость полученной
батареи равна суме емкостей всех входящих
в нее конденсаторов: Спар=С1+С2+С3. При последовательном соединении
конденсаторов общая емкость Спосл оказывается меньше наименьшей емкости
входящих в батарею конденсаторов и
может быть определено по формуле:
При последовательном соединении
конденсаторов общая емкость Спосл оказывается меньше наименьшей емкости
входящих в батарею конденсаторов и
может быть определено по формуле:
1/Cпосл=1/C1+1/C2+1/C3
Рис. 1
Формула цилиндрического конденсатора — GeeksforGeeks
Цилиндрический конденсатор — это устройство, которое накапливает значительное количество электрического тока на небольшой площади. Он состоит из концентрического полого сферического цилиндра, окружающего полый или сплошной цилиндрический проводник. В электродвигателях, зерновых мельницах, электрических соковыжималках и других электроприборах используются цилиндрические конденсаторы. Конденсатор предназначен для ограничения силовых линий электрического поля в ограниченном пространстве. В результате, даже если поле очень сильное, разность потенциалов между двумя проводниками конденсатора весьма мала. Хотя конденсаторы могут быть сгруппированы различными способами для достижения необходимой емкости, наиболее распространенными являются последовательные и параллельные конфигурации. Формула для расчета цилиндрической емкости представлена в этой статье.
Формула для расчета цилиндрической емкости представлена в этой статье.
Цилиндрический конденсатор
Емкость на единицу длины — это емкость для цилиндрической геометрии.
Разность потенциалов каждого конденсатора уникальна. Существует ряд электрических схем, в которых конденсаторы должны быть расположены в правильном порядке, чтобы получить желаемую емкость. Конденсаторы, соединенные последовательно, и конденсаторы, соединенные параллельно, являются двумя наиболее распространенными конфигурациями. Фарад — стандартная единица измерения емкости (Ф). Для накопления электрического заряда обычно используют цилиндрический конденсатор.
Формула для цилиндрического конденсатора
Емкость цилиндрического конденсатора можно рассчитать по следующей формуле: /а))
Где,
- C = Емкость цилиндра,
- ε 0 = Диэлектрическая проницаемость свободного пространства,
- a = Внутренний радиус цилиндра,
- b = Внешний радиус цилиндра,
- L = Длина цилиндр.

Примеры вопросов
Вопрос 1. Почему так много цилиндрических конденсаторов?
Ответ:
Две проводящие пластины разделены изолирующим зазором в общем виде конденсатора. Металлическая фольга, металлизированные полимерные пленки, электролиты и другие материалы могут использоваться для создания изолирующих и проводящих компонентов. Все вышеперечисленные элементы могут быть выполнены в виде плоской прямоугольной формы. Некоторые конденсаторы не имеют сферической формы. Их формируют укладкой слоев изоляционного и проводящего материала поочередно. Многослойные керамические чип-конденсаторы, например, являются хорошим примером.
Вопрос 2: Из каких компонентов состоит цилиндрический конденсатор? Дайте несколько применений.
Ответ:
Цилиндрический конденсатор состоит из цилиндрического проводника, окруженного полым сферическим цилиндром.
Электродвигатели, зерновые мельницы, электрические соковыжималки и другие электрические инструменты являются одними из наиболее распространенных применений цилиндрических конденсаторов.
Вопрос 3: Рассчитайте емкость цилиндрического конденсатора, упакованного в бумагу и состоящего из цилиндров с внутренним и внешним радиусами 2 см и 5 см соответственно.
Ответ:
Подставим диэлектрическую проницаемость, которая равна 3,85 для бумаги, в формулу для емкости цилиндрического конденсатора, получим:
Дано: ε 0 = 8,85 × 10 -12 , L = 3,85, b = 5 см, a = 2 см.
Так как,
C = 2πε 0 × (L/ln(b/a))
= 2 × 3,14 × 8,85 × 10 -12 × (3,85 / ln(5/2)) 9000 3
= 538,22 × 10 -12 F
Вопрос 4: Цилиндрический конденсатор состоит из двух колец с внутренним радиусом 6 см и внешним радиусом 12 см. Рассчитайте емкость конденсатора, исходя из его длины 16 см.
Рассчитайте емкость конденсатора, исходя из его длины 16 см.
Ответ:
Дано: a = 6 см, b = 12 см, L = 16 см, ε 0 = 8,85 × 10 -12
9 0002 Так как,С = 2πε 0 × (L/ln(b/a))
= 2 × 3,14 × 8,85 × 10 -12 × (16 × 10 -2 / ln(12/6))
= 2,954 × 10 -11 F
Вопрос 5. Цилиндрический конденсатор длиной 8 см состоит из двух концентрических колец с внутренним радиусом 3 см и внешним радиусом 6 см. Рассчитайте емкость конденсатора.
Ответ:
Дано: a = 3 см, b = 6 см, L = 8 см, ε 0 = 8,85 × 10 -12
900 02 Так как,С = 2πε 0 × (L/ln(b/a))
C = 2 × 3,14 × 8,85 × 10 9Вопрос 6 Длина цилиндрического конденсатора 9 см. . Он состоит из двух концентрических колец с внутренним и внешним радиусами 2 см и 7 см соответственно.
Вычислите емкость конденсатора.
Ответ:
Дано: a = 2 см, b = 7 см, L = 9 см, ε 0 = 8,85 × 10 -12
900 02 С,C = 2πε 0 × (L/ln(b/a))
C = 2 × 3,14 × 8,85 × 10 -12 × (9 × 10 -2 / ln(7/2) )
= 9,19488 × 10 -12 F
электростатика — Что представляет собой $Q$ в формуле емкости?
$\begingroup$Емкость определяется как $C = Q/V $. Таким образом, в этой формуле, какой заряд представляет $Q$,
, например, в сферическом конденсаторе с внутренним заземлением (q+q’) заряд также присутствует на внешней поверхности, поэтому мы должны это учитывать. В другом случае
в конденсаторе с параллельными пластинами заряд присутствует на 4 поверхностях, поэтому какие заряды необходимо учитывать при расчете емкости?
$\endgroup$ $\begingroup$
- электростатика
- электрические поля
- заряд
- потенциал
- емкость
Предположим, что у нас есть два проводника в непосредственной близости (это могут быть две пластины конденсатора).
Заряд в каждом проводнике сохраняется не только в взаимная емкость , связанная с двумя проводниками, но также и в (обычно непреднамеренных) емкостях между этим проводником и любым другим проводником поблизости (или «бесконечностью»). Все три емкости реального конденсатора изображены на рисунке ниже.
Вы можете визуализировать различные емкости, представляя линии электрического поля, выходящие из проводника с положительным потенциалом (скажем, проводник 1 слева): если линия поля заканчивается на проводнике 2, она (и соответствующие заряды на ней начинается или заканчивается в) связаны с взаимная емкость $C$. Если силовая линия оканчивается на другом проводнике (или бесконечности), то заряд на проводнике 1 связан с паразитной емкостью $C_1$. Общий заряд $Q_1$ на проводнике 1 равен сумме зарядов, хранящихся в $C$ и $C_1$. Мы можем математически выразить заряды двух проводников следующим образом: $$ Q_1 = C_1V_1 + C(V_1 — V_2) $$ $$ Q_2 = C_2V_2 + C(V_2 — V_1) $$ где $V_i$ — потенциал на проводнике $i$.
Если мы решим их для $V_i$, мы получим $$q = C(V_1 — V_2) = \frac{c_2 Q_1 — c_1 Q_2}{c_1 + c_2 + c_1c_2} $$ $$q_1 = C_1 V_1 = \frac{c_1 [(1 + c_2)Q_1 + Q_2]}{c_1 + c_2 + c_1c_2} $$ $$q_2 = C_2 V_2 = \frac{c_2 [(1 + c_1)Q_2 + Q_1]}{c_1 + c_2 + c_1c_2} $$ где $c_i = C_i/C$.
Ответ на ваш вопрос: $q$ (точнее, $\pm q$). Это заряд, хранящийся во взаимной емкости между проводниками. В случае практического конденсатора $C$ будет преобладать (т.е. $c_i \ll 1$), заряды $q_i$ в паразитных конденсаторах будут малы, поэтому заряды на двух пластинах обычно примерно равны в величины и противоположны по знаку. Возможны отклонения от этого, т.е. если обе пластины находятся под высоким напряжением (с одинаковым знаком), но $C$ по-прежнему является значимой емкостью, и, если необходимо, паразитные емкости включаются отдельно, т.е. в анализе цепи. Обратите внимание, что паразитные емкости характерны не только для конденсаторов: любые другие проводники в вашей цепи (например, провода) будут иметь их.
Большая взаимная емкость $C$ между его пластинами (и связанный с ней заряд $q$) делает конденсатор особенным и полезным.
Наконец, давайте посмотрим, как включение паразитных емкостей может объяснить заряды на показанных вами сферических и пластинчатых конденсаторах. Для сферического конденсатора $c_1 = 0$ (силовые линии от внутреннего проводника заканчиваются только на другом проводнике). Из приведенных выше уравнений мы получаем $q=Q_1$, $q_1 = 0$ и $q_2 = Q_1 + Q_2$, как показано на вашей диаграмме. Для плоского конденсатора можно предположить, что $c_1 = c_2 = c$, и уравнения сводятся к
$$ q = \frac{Q_1 — Q_2}{2 + c} $$ $$ q_1 = \frac{(1 + c)Q_1 + Q_2}{2 + c} $$ $$ q_2 = \frac{(1 + c)Q_2 + Q_1}{2 + c} $$
Если $c \ll 1$ (и только тогда), мы получим заряды на внутренней и внешней поверхностях, как показано на втором изображении.
$\endgroup$ $\begingroup$Сначала рассмотрим два простых случая.
Зарядите одну тарелку $+Q$, а другую $-Q$.
Это нормальный случай, который возникает, когда вы включаете конденсатор в цепь. Общая стоимость составляет $0$. $C = Q/V$, где $Q$ — размер заряда на каждой пластине.
Если вы вытянете электроны с одной пластины и переместите их на другую, электроны оттолкнутся друг от друга. Это оставляет + заряды на + плите, которые также отталкивают друг друга. Чтобы заставить заряды соединиться, требуется потенциальная энергия.
В конденсаторе две пластины расположены близко друг к другу. Заряды на противоположных пластинах притягиваются друг к другу, уменьшая эту потенциальную энергию. Разделить заряды легче, если в цепи есть конденсатор. Он по-прежнему требует энергии, и это влияет на напряжения и токи в цепи. Это может быть полезно. Это назначение конденсатора.
Вместо этого давайте поставим $+Q$ по одному на каждую тарелку. Всего у вас есть $2Q$. Этот заряд должен откуда-то поступать из-за пределов цепи. Втягивание дополнительных электронов в цепь требует энергии.
Они отталкивают друг друга и максимально расходятся. Столкновение с двумя близко расположенными плитами требует больше энергии, чем это. Это нереально. Это не то, как используются схемы, и конденсаторы не для этого.
Случай в вашем примере представляет собой комбинацию двух. На конденсатор накладывается дополнительный заряд, и к нему прикладывается напряжение, так что происходит некоторое нормальное конденсатороподобное разделение заряда. Это означает, что на обеих пластинах может быть плата $-$, но на одной она больше, чем на другой. Опять же это нереально.
В этом тоже есть смысл. Вы должны разделить два разных способа распределения заряда. Подобные разделения — обычное дело в физике.
В одном случае заряды равны и одинаковы на обеих пластинах. Другой равен и противоположен. Имея $Q_1$ на тарелке $1$ и $Q_2$ на тарелке $2$, вы можете вычислить, сколько заряда распределяется в каждом направлении.
Это запутанная вещь для конденсаторов. Это имеет больше смысла для сил и крутящих моментов.
$\endgroup$ $\begingroup$См. Опрокидывание цилиндра на блоке. Вы можете видеть, что разделяющие силы, подобные этой, могут сказать вам, как насчет сил, которые ускоряют объект и вращают объект.
Если вы подключите батарею к конденсатору, она приобретет равные и противоположные заряды на своих пластинах. Эти заряды будут располагаться на обращенных друг к другу поверхностях пластин. Трудно, не правда ли, придумать способы нанесения на пластины зарядов
, отличных от равных и противоположных . Емкость, $C$, определяется по формуле $C=Q/V$, где $Q$ — это величина одного из одинаковых и противоположных зарядов на пластинах. Уравнение неприменимо в случае зарядов, отличных от равных и противоположных.
$\endgroup$ $\begingroup$Итак, в этой формуле, какой заряд представляет $Q$,
Проще говоря, это чистый положительный или отрицательный заряд на любой пластине заряженного конденсатора.
Я думаю вы не поняли как устроен заряженный конденсатор. Надеюсь, следующее поможет вашему пониманию.
На верхнем рисунке ниже показан незаряженный конденсатор. Обратите внимание, что количество положительных и отрицательных зарядов на каждой пластине одинаково. Таким образом, чистый заряд на любой пластине равен нулю. Обратите внимание, что подвижны только электроны на каждой пластине, которые могут свободно перемещаться вокруг положительного заряда.
Нижняя диаграмма показывает тот же конденсатор после «зарядки» от какого-либо источника напряжения, например от батареи. Электроны берутся с правой пластины положительным полюсом батареи, оставляя правую пластину с чистым положительным зарядом. Обратите внимание, что положительных зарядов больше, чем отрицательных (посчитайте их). Отрицательная клемма батареи откладывает равное количество электронов на левой пластине, оставляя левую пластину с чистым отрицательным зарядом (не больше электронов, чем протонов на левой пластине.
{16}$ электронов или протонов. Надеюсь, это поможет.
$\endgroup$ 12Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью GoogleЗарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и пароль Опубликовать как гость
Электронная почтаТребуется, но не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.



 Электродвигатели, зерновые мельницы, электрические соковыжималки и другие электрические инструменты являются одними из наиболее распространенных применений цилиндрических конденсаторов.
Электродвигатели, зерновые мельницы, электрические соковыжималки и другие электрические инструменты являются одними из наиболее распространенных применений цилиндрических конденсаторов.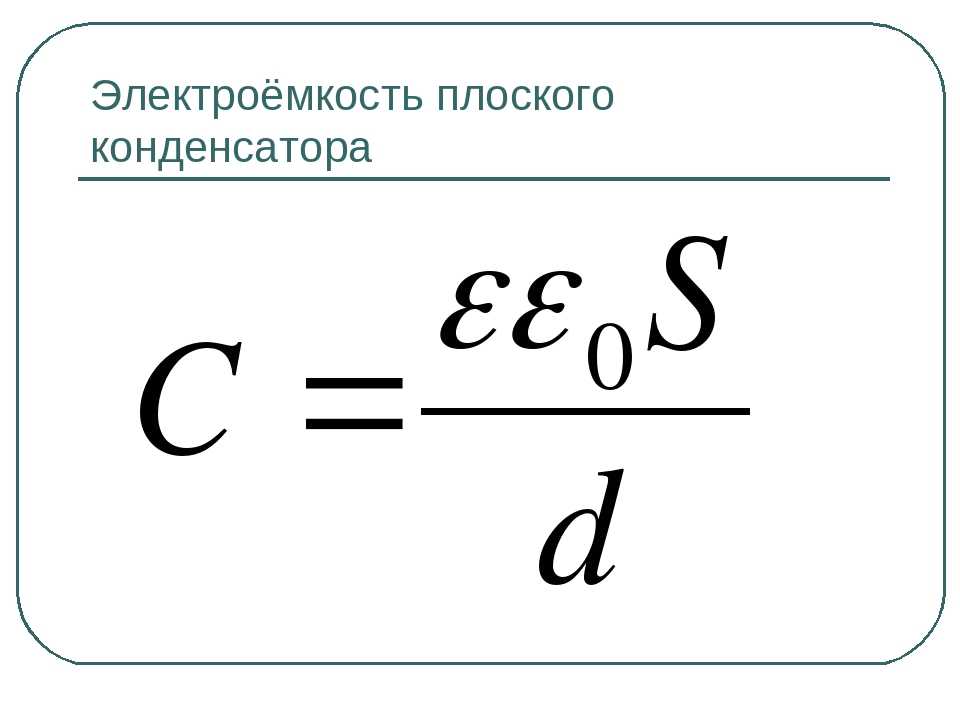 Вычислите емкость конденсатора.
Вычислите емкость конденсатора.  Заряд в каждом проводнике сохраняется не только в взаимная емкость , связанная с двумя проводниками, но также и в (обычно непреднамеренных) емкостях между этим проводником и любым другим проводником поблизости (или «бесконечностью»). Все три емкости реального конденсатора изображены на рисунке ниже.
Заряд в каждом проводнике сохраняется не только в взаимная емкость , связанная с двумя проводниками, но также и в (обычно непреднамеренных) емкостях между этим проводником и любым другим проводником поблизости (или «бесконечностью»). Все три емкости реального конденсатора изображены на рисунке ниже. Если мы решим их для $V_i$, мы получим
$$q = C(V_1 — V_2) = \frac{c_2 Q_1 — c_1 Q_2}{c_1 + c_2 + c_1c_2} $$
$$q_1 = C_1 V_1 = \frac{c_1 [(1 + c_2)Q_1 + Q_2]}{c_1 + c_2 + c_1c_2} $$
$$q_2 = C_2 V_2 = \frac{c_2 [(1 + c_1)Q_2 + Q_1]}{c_1 + c_2 + c_1c_2} $$
где $c_i = C_i/C$.
Если мы решим их для $V_i$, мы получим
$$q = C(V_1 — V_2) = \frac{c_2 Q_1 — c_1 Q_2}{c_1 + c_2 + c_1c_2} $$
$$q_1 = C_1 V_1 = \frac{c_1 [(1 + c_2)Q_1 + Q_2]}{c_1 + c_2 + c_1c_2} $$
$$q_2 = C_2 V_2 = \frac{c_2 [(1 + c_1)Q_2 + Q_1]}{c_1 + c_2 + c_1c_2} $$
где $c_i = C_i/C$. Большая взаимная емкость $C$ между его пластинами (и связанный с ней заряд $q$) делает конденсатор особенным и полезным.
Большая взаимная емкость $C$ между его пластинами (и связанный с ней заряд $q$) делает конденсатор особенным и полезным.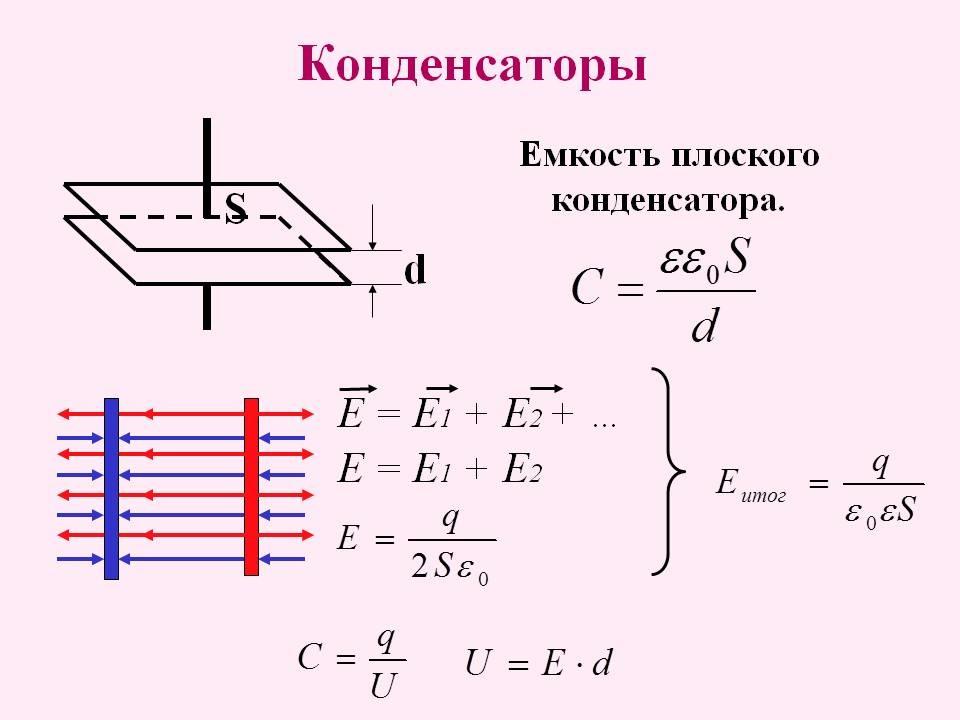 Это нормальный случай, который возникает, когда вы включаете конденсатор в цепь. Общая стоимость составляет $0$. $C = Q/V$, где $Q$ — размер заряда на каждой пластине.
Это нормальный случай, который возникает, когда вы включаете конденсатор в цепь. Общая стоимость составляет $0$. $C = Q/V$, где $Q$ — размер заряда на каждой пластине. Они отталкивают друг друга и максимально расходятся. Столкновение с двумя близко расположенными плитами требует больше энергии, чем это. Это нереально. Это не то, как используются схемы, и конденсаторы не для этого.
Они отталкивают друг друга и максимально расходятся. Столкновение с двумя близко расположенными плитами требует больше энергии, чем это. Это нереально. Это не то, как используются схемы, и конденсаторы не для этого.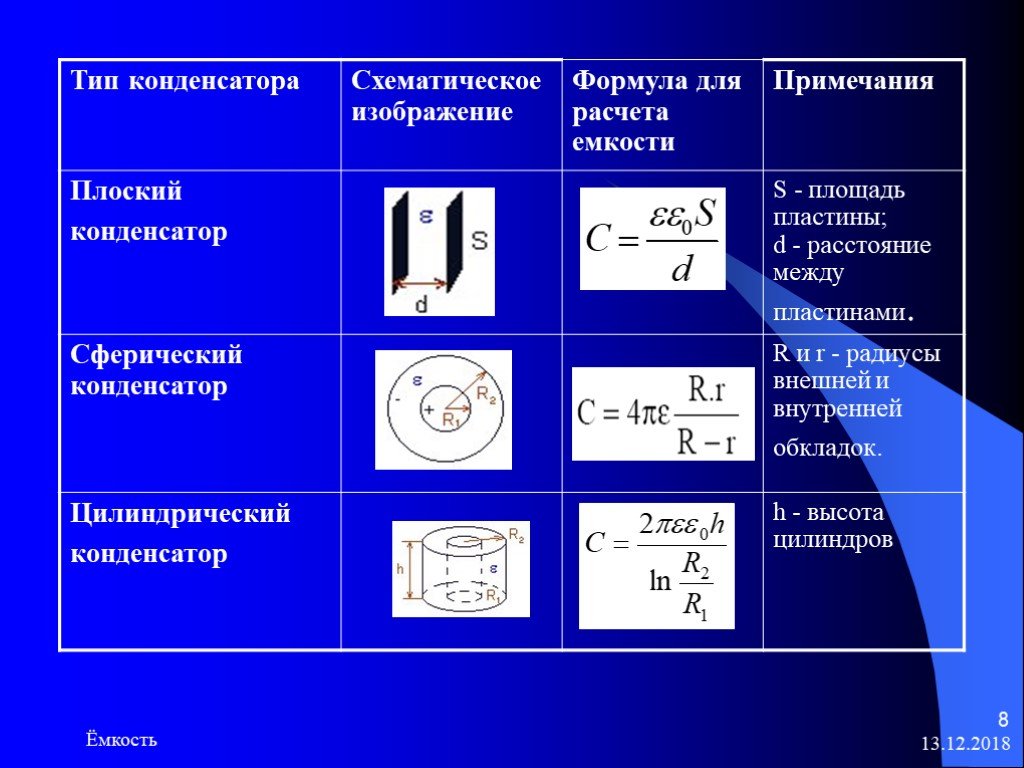 См. Опрокидывание цилиндра на блоке. Вы можете видеть, что разделяющие силы, подобные этой, могут сказать вам, как насчет сил, которые ускоряют объект и вращают объект.
См. Опрокидывание цилиндра на блоке. Вы можете видеть, что разделяющие силы, подобные этой, могут сказать вам, как насчет сил, которые ускоряют объект и вращают объект.

