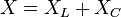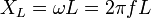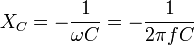Комплексное сопротивление

 

Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме — Z.

Хорошо известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то:

 

 

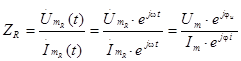
Но в предыдущей лекции было установлено, что 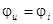. Поэтому:

 

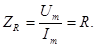(3.1)

 

Таким образом, видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между током и напряжением. Чтобы подчеркнуть этот факт такое сопротивление часто называют активным.

Комплексное сопротивление емкости определяется отношением:

 

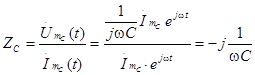. (3.2)

 

Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -j физически определяет сдвиг фаз между током и напряжением на 90^о. Это хорошо согласуется с ее математическим значением:

 

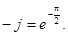
Поэтому на емкости напряжение отстает от тока на 90^о. Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.

Коэффициент 1/ определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается Х_С, т.е.:

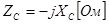. (3.3)

 

Комплексное сопротивление индуктивности определяется отношением:

 

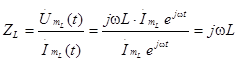. (3.4)

 

И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, то это означает, что на индуктивности напряжение опережает ток на 90

о.

Коэффициент wL определяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается Х_L, т.е.:

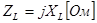. (3.5)

 

Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопротивлениями, а конденсатор и индуктивность — реактивными элементами цепи.

Определим теперь комплексное сопротивление электрической цепи, содержащей активные и реактивные элементы, например последовательно включенные R, L и С элементы (рис.3.1). Такая цепь представляет замкнутый

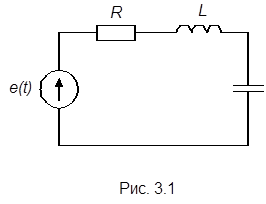
контур, поэтому для нее справедлив второй закон Кирхгофа:

 

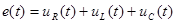. (3.6)

 

В последнем выражении проведем замену символов мгновенных напряжений и ЭДС на их комплексные изображения по правилам, определенным в лекции 1.2. Такой прием получил название символического метода. Так как ток, протекающий через все элементы последовательной цепи одинаков, то (3.6) приходит к виду:

 

 

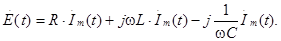
Преобразуем это выражение к виду:

 

.

 

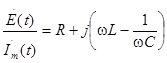По определению выражение в правой части последнего равенства есть ни что иное, как комплексное сопротивление цепи рис.3.1, т.е.:

 

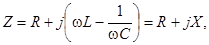(3.7)

 

где R — действительная часть или активное сопротивление цепи.

— мнимая часть или реактивное сопротивление цепи.

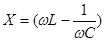
Выражение (3.7) представляет комплексное сопротивление в алгебраической форме. Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится

понятие треугольника сопротивления (рис.3.2).

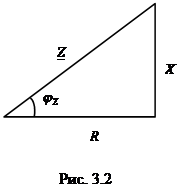В треугольнике — гипотенуза определяется модулем комплексного сопротивления Z, причем:

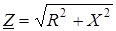. (3.8)

 

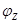Прилежащий к острому углу катет – активным сопротивлением цепи R, причем:

 

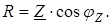(3.9)

 

 

Противолежащий катет — реактивным сопротивлением Х, причем:

 

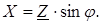(3.10)

 

Угол 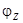определяет сдвиг фаз между током и напряжением, который вносится комплексным сопротивлением цепи, причем:

 

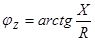. (3.11)

 

Учитывая выражения (3.8) ¸ (3.11), легко перейти от алгебраической к тригонометрической форме комплексного сопротивления:

 

Z =Z 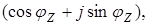(3.12)

 

a применив формулу Эйлера получить показательную форму:

 

Z =Z 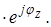(3.13)

 

Теперь можно записать закон Ома для участка цепи без источника ЭДС в комплексном изображении:

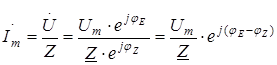(3.14)

 

Выражение (3.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение:

 

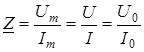. (3.15)

 

 

---

Дата добавления: 2017-03-12; просмотров: 10988;

---

Похожие статьи:

Комплексные сопротивления и проводимости

Отношение комплексного напряжения к комплексному току называют комплексным сопротивлением цепи и обозначают .

,

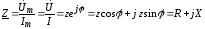где R, X и z – активное, реактивное и полное сопротивления цепи.

С другой стороны:

.

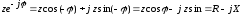
Тогда полное сопротивление z получим из соотношений:

В случае последовательного соединения элементов R,L,C комплексное сопротивление запишется в виде:

.

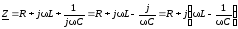Отношение комплексного тока к комплексному напряжению называют комплексной проводимостью цепи и обозначают

:

,

где –активная, реактивная и полная проводимости цепи.

Поскольку комплексная проводимость есть величина обратная комплексному сопротивлению, то:

.

Пусть: ;

.

Тогда: .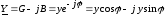

С другой стороны: .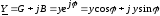

Тогда полную проводимость у получим из соотношений:

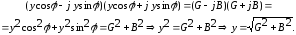
В случае параллельного соединения элементов G,L,C комплексная проводимость запишется в виде:

.

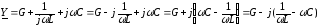Очевидно, что .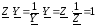

Перевод комплексных величин в показательную форму:

3 + j2

1. Находим модуль: .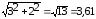

2. Находим аргумент: .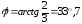

Окончательно: .

3 − j2

1. Находим модуль: .

2. Находим аргумент: .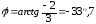

Окончательно: .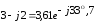

Перевод показательных величин в комплексную форму:

;

.

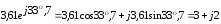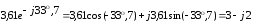Основные законы электрических цепей в комплексной форме

Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как и для цепей постоянного тока, с заменой соответствующих постоянных величин комплексными: ,,,,,.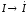

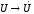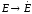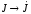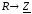Закон Ома в комплексной форме имеют вид: .

Достоинство этих выражений заключается в том, что в них учи­тывается как связь между действующими значениями тока и напряжения, так и сдвиг фаз между ними.

Первый закон Кирхгофа в применении к узлу: .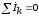

Второй закон Кирхгофа применительно к контуру: .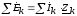

Возможность использовать соотношения для цепей постоянного тока справедлива и для эквивалентных преобразований.

При после­довательном соединении комп­лексное сопротивление всей цепи равно алгебраической сумме комплексных сопротивлений от­дельных ее участков: .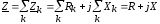

При параллельном соединении комплексная проводимость всей цепи равна алгебраической сумме комплексных проводимостей отдельных ее участков:

.

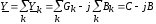При смешанном соединении:

Расчет сложных цепей переменного тока комплексным методом осуществляется с помощью тех же методов, что и цепей постоянного тока при замене соответствующих величин их комплексными аналогами.

Мощность в комплексной форме. Баланс мощностей

В качестве комплексной мощности понимают произведение комплексного напряжения на сопряженную комплексную величину тока. В ре­зультате чего, получаем комплексную мощность:

.

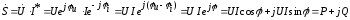Вещественная часть комплексной мощности равна активной мощности Р, а мнимая часть Q (без j) реактивной мощности. Модуль комплексной мощности равен полной мощности .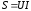

Баланс мощности:

1. Сумма комплексных мощностей для всех ветвей электрической цепи равна 0.

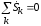, откуда .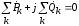

Такое равенство возможно только в том случае, есл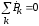и и.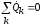

2. Поскольку в каждой цепи есть источники и приемники, то

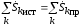
Источники ЭДС и токов можно разделить:

.

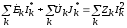Действительно, мощность, потребляемую приемником, мы можем представить как:

.

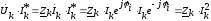С другой стороны,

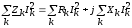
и для мощности источников

.

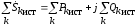Следовательно, и.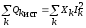

Резонансные явления в электрических цепях. Частотные характеристики.

Ранее было доказано, что действующее значение силы тока в R, L,C цепочке определяет соотношение:

.

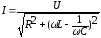Так как индуктивное и емкостное сопротивления зависят от частоты (), то сила тока вR, L,C также будет зависеть от частоты источника питания. Из приведенного выражения следует, что ток будет максимален при:

,

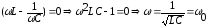где −резонансная частота контура.

В том случае, когда 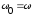в цепи наблюдаетсяявление резонанса.

На этой резонансной частоте 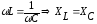, а, следовательно, в цепи действует чисто активное сопротивлениеR, поэтому напряжение и ток при резонансе совпадают по фазе.

Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.

Покажем зависимость I (ω) для фиксированных значениях напряжения U, индуктивности L и емкости С при двух различных значения R:

Резонансными называют электрические цепи, в которых могут возникать явления резонанса напряжения или тока.

Комплексные сопротивления.

При анализе и расчете цепей синусоидального тока особенный интерес представляет сопоставление по амплитуде и начальной фазе тока и напряжения одного и того же пассивного участка электрической цепи. В самом удобном и компактном виде это сопоставление осуществляется с помощью комплексных чисел.

Введем понятие комплексного сопротивления,которое определяется отношением комплексной амплитуды напряжения к комплексной амплитуде тока:

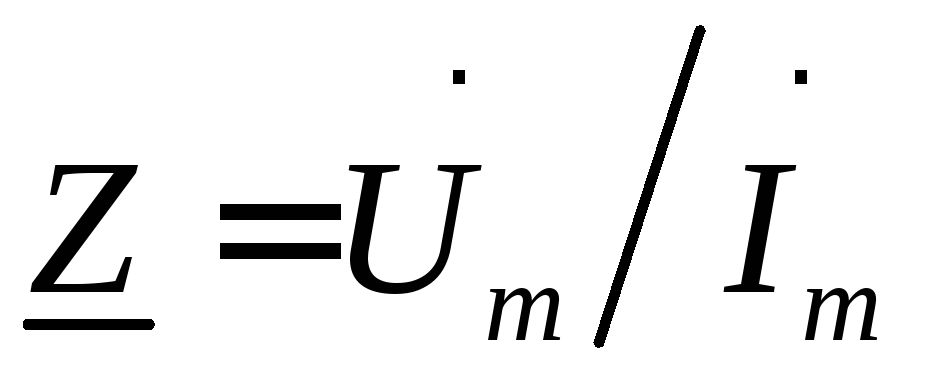. (26)

Комплексное число 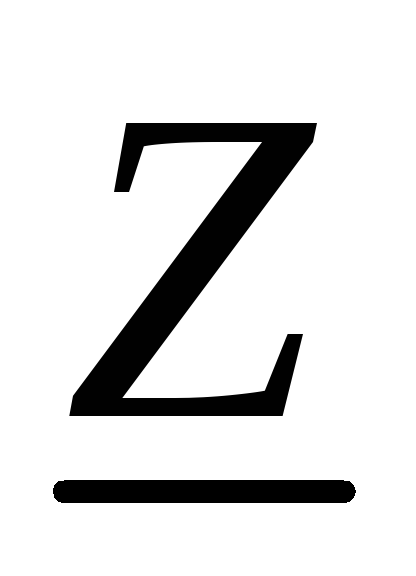дает информацию как о соотношении амплитуди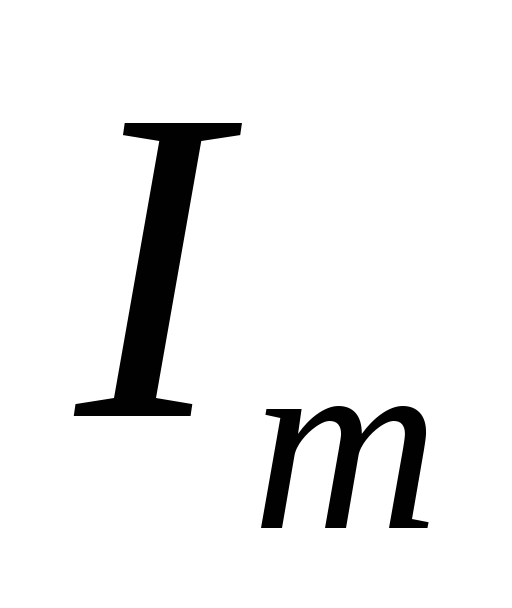, так и о сдвиге фаз между напряжением и током. Действительно,

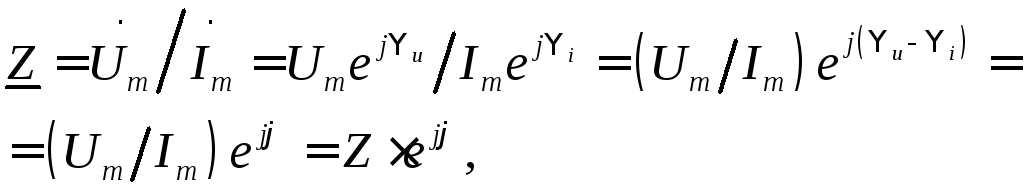
где Z – модуль, a 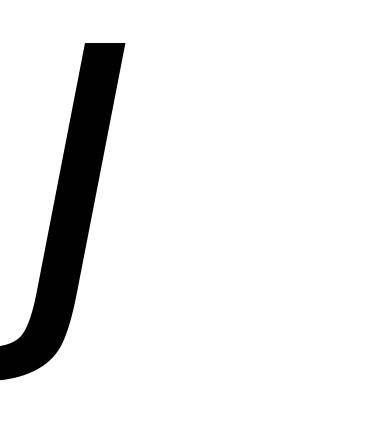– аргумент комплексного сопротивления.

Модуль комплексного сопротивления Z, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока:

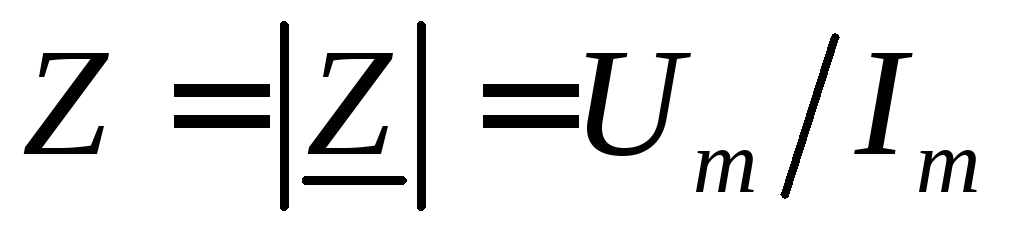. (27)

Аргумент комплексного сопротивления равен разности начальных фаз напряжения и тока:

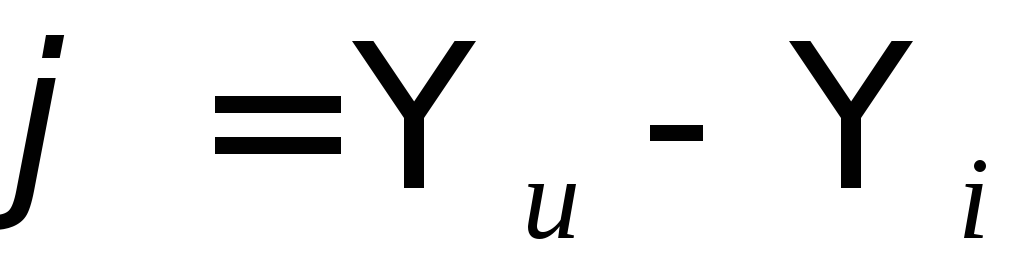. (28)

Комплексное сопротивление можно выразить также через комплексные действующие значения напряжения и тока:

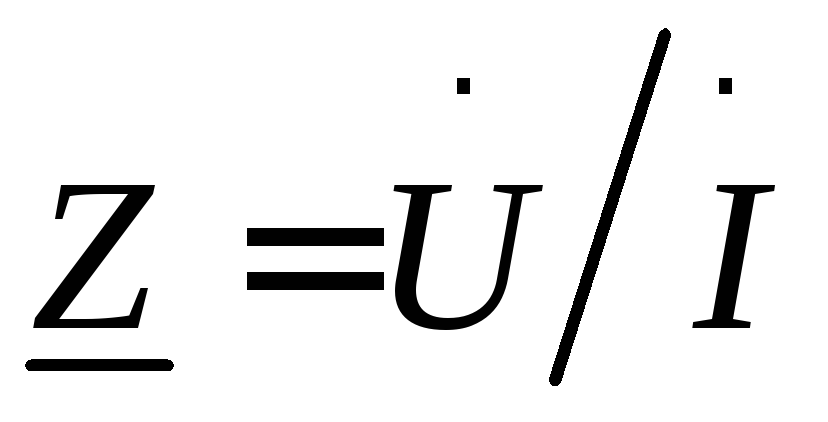. (29)

Отметим, что обозначение комплексного сопротивления отличается от обозначения комплексных токов и напряжений – вместо точки над буквой символ комплексного сопротивления имеет черту снизу. Это различие объясняется тем, что сам комплекс 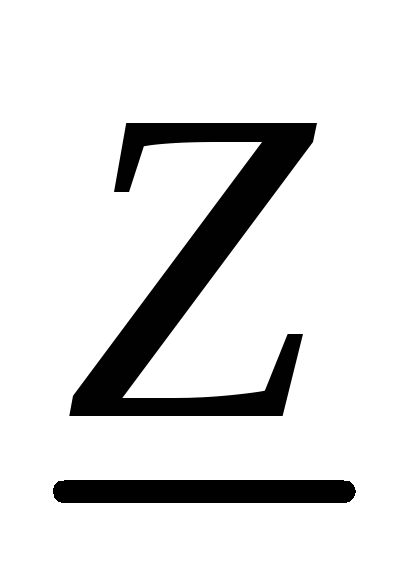не служит изображением синусоидальной функции, а является комплексным числом, с помощью которого сопоставляются комплексные изображения напряжения и тока.

Соотношения

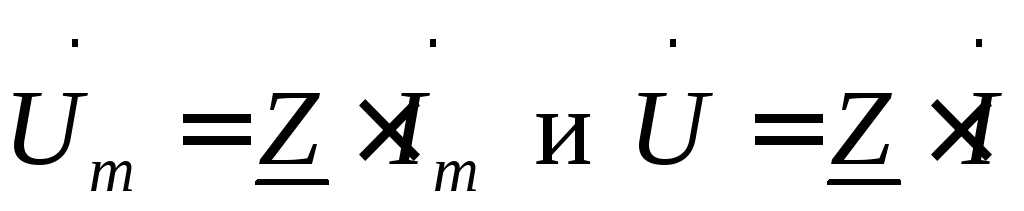, (30)

аналогичные по форме записи закону Ома для цепи постоянного тока, называют законом Ома в комплексной форме соответственно для амплитудных и действующих значений.

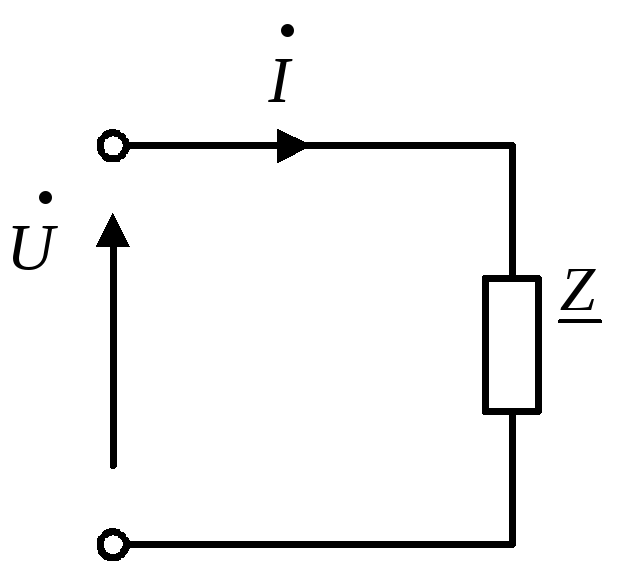
Рисунок 9 Комплексные обозначения на схеме замещения.

Обозначение комплексного сопротивления на схемах замещения приведено на рисунке 9.

5. Электрическая цепь сR- элементом.

Определим ток R- элемента, схема замещения которого показана на рисунке 10а, если он подключен к источнику синусоидального напряжения.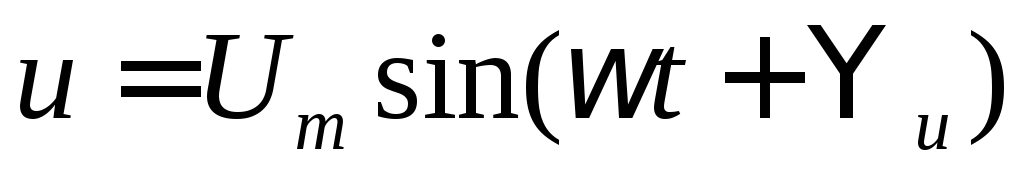

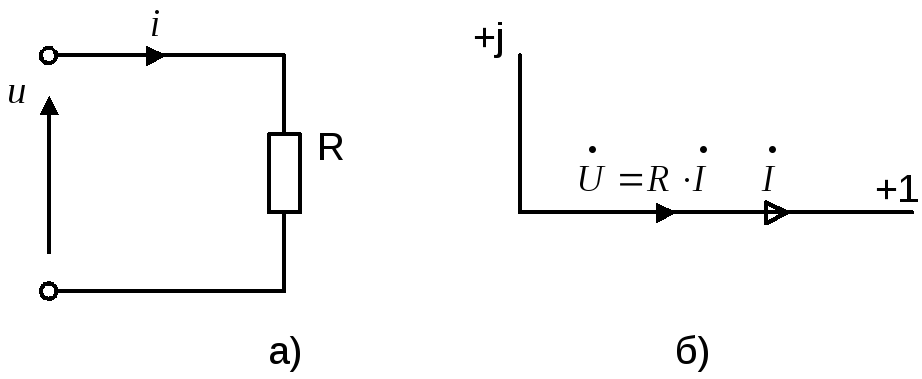
Рисунок 10

Для записи уравнения электрического состояния цепи синусоидального тока предварительно необходимо, так же как и в цепях постоянного тока, выбрать положительные направления тока и напряжения. Тот факт, что ток и напряжение в цепях синусоидального тока в течение периода изменяют свое направление на противоположное, не лишает смысла наличие стрелок положительных направлений: истинное направление тока (напряжения) совпадает со стрелкой в моменты времени, когда 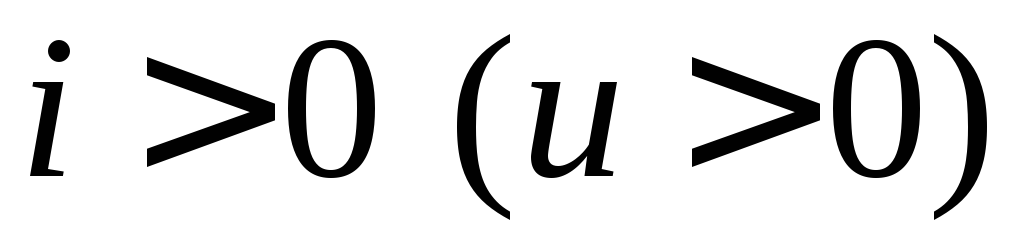, и противоположно стрелке, если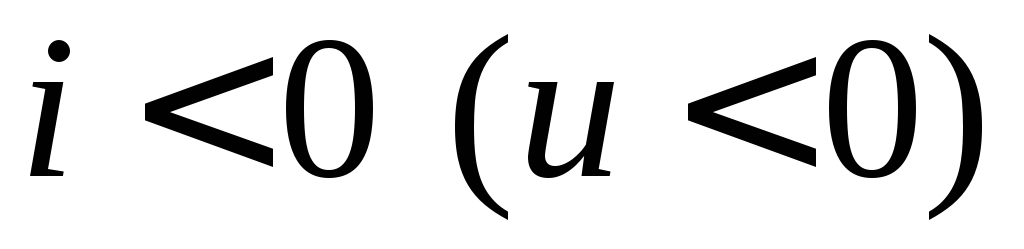. На участках электрической цепи, содержащих пассивные элементы, положительные направления тока и напряжения, так же как и в цепях постоянного тока, выбирают совпадающими.

Мгновенные значения тока и напряжения R- элемента, стрелки положительных направлений которых показаны на рисунке 10а, связаны законом Ома: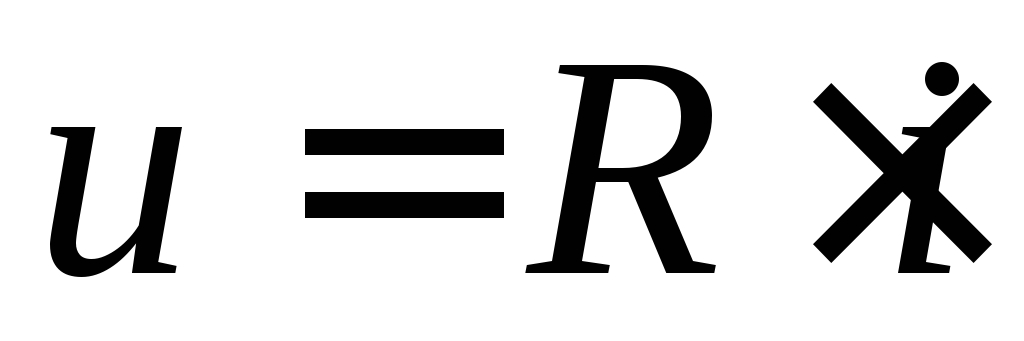. Следовательно, при заданном синусоидальном напряжении источника ток в резистивном элементе будет также синусоидальным:

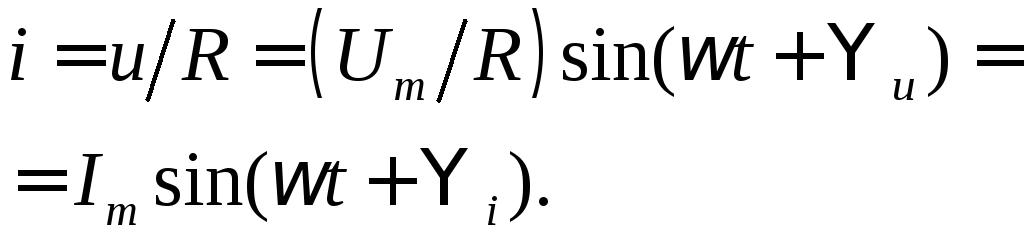(31)

Из (31) следует, что ток и напряжение в рассматриваемом случае имеют одинаковую частоту и совпадают по фазе, а соотношение между амплитудными значениями определяется законом Ома:

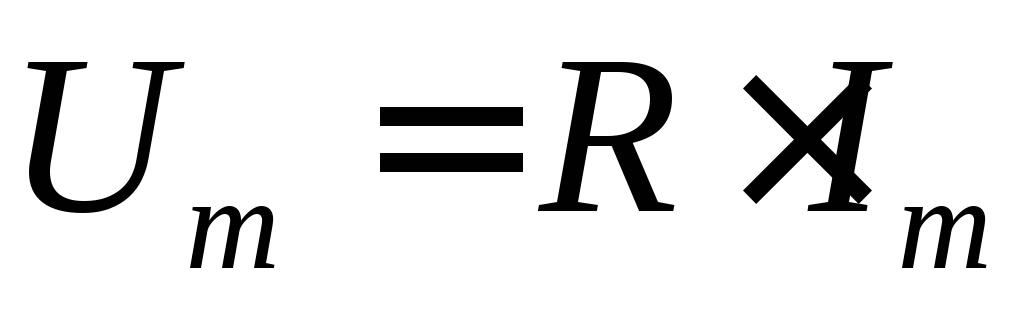; (32)

. (33)

Поделив правую и левую части (32) на , можно записать закон Ома для действующих значений напряжения и тока:

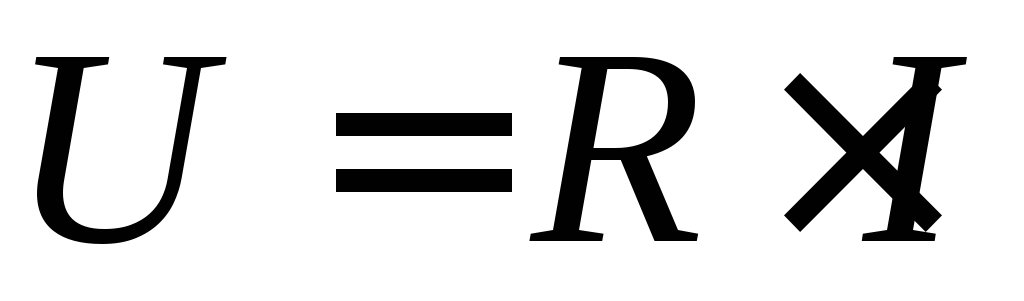. (34)

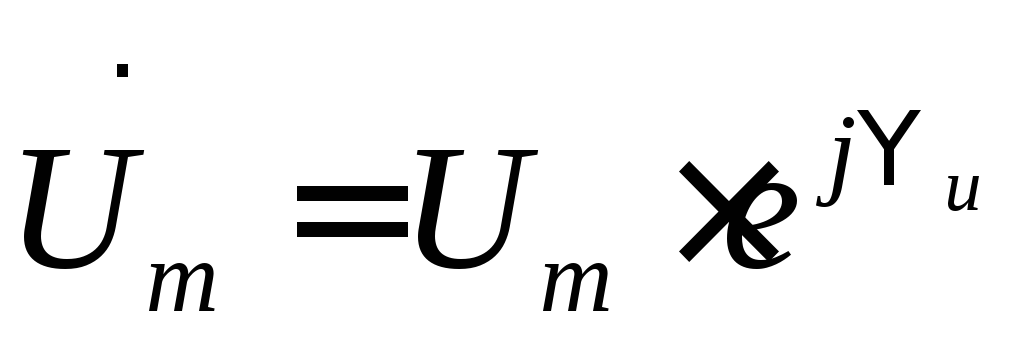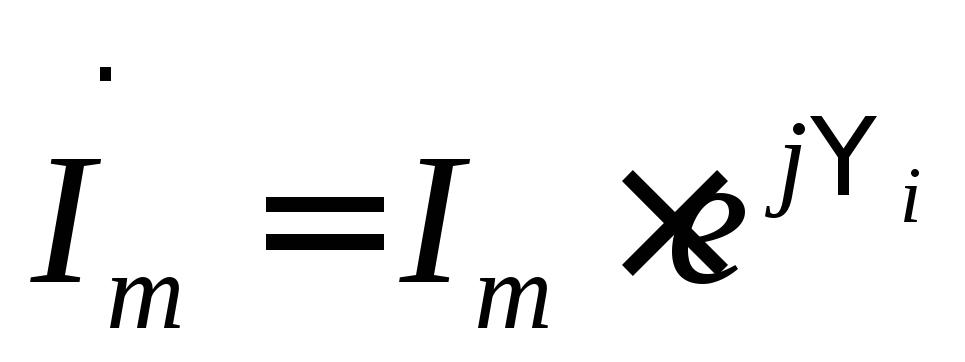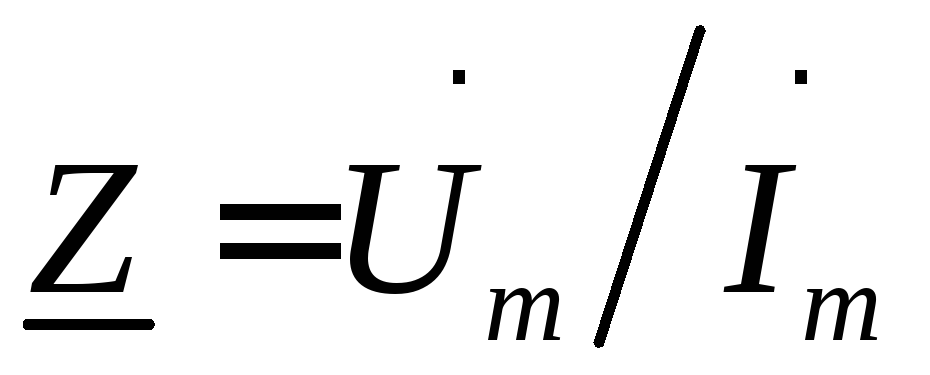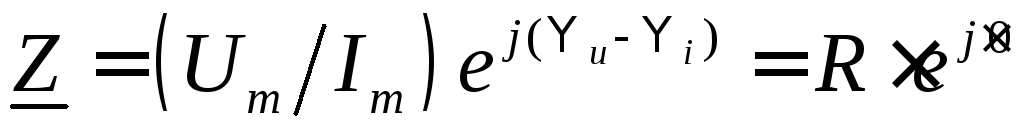Соотношение между напряжением и током R- элемента можно записать и в комплексной форме. Еслии, то комплексное сопротивлениеили, т.е.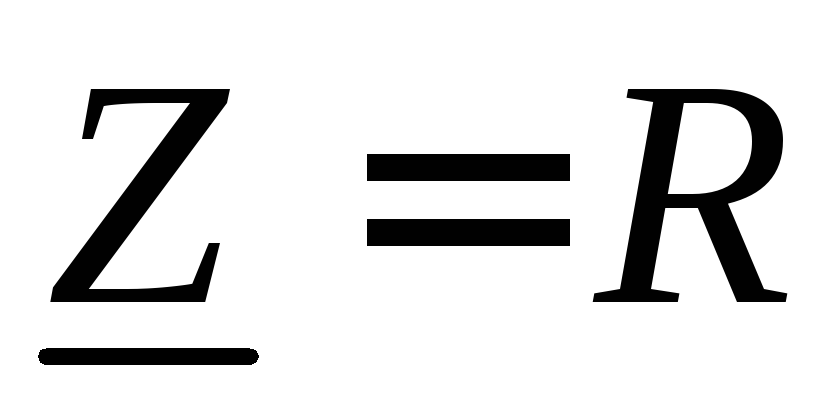, следовательно,

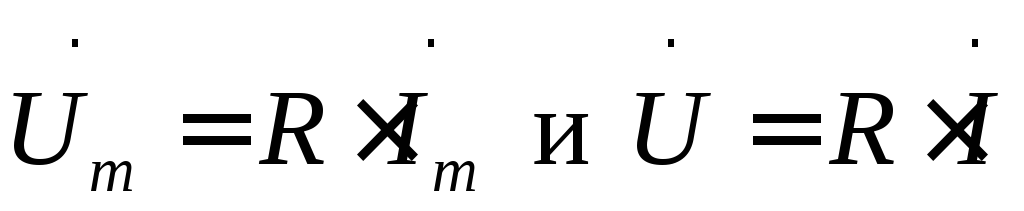. (35)

Комплексное сопротивление резистивного элемента является положительным действительным числом, равным значению активного сопротивления R. Соотношения (35) называют законом Ома соответственно для комплексных амплитуд и комплексных действующих значений напряжения и тока.

На рисунке 10б построена векторная диаграмма цепи рисунка 10а – вектор тока в R- элементе совпадает по фазе с вектором напряжения.

Рассмотрим энергетические процессы в цепи с R- элементом. Работу, совершаемую в электрической цепи, будем характеризовать скоростью поступления энергии, т.е. мгновенной мощностью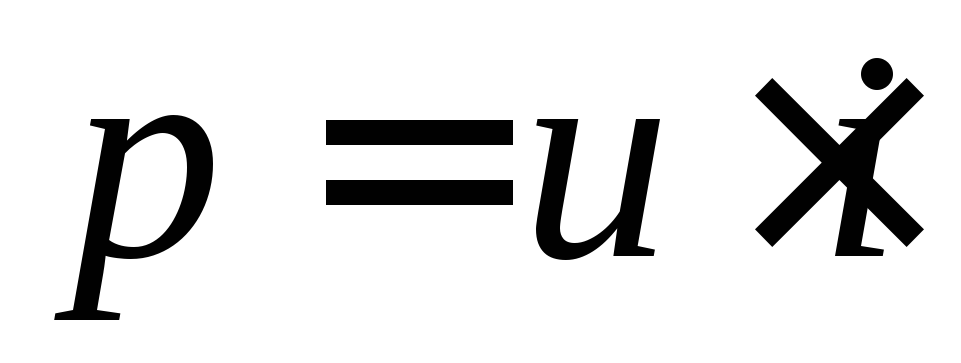. В любой момент времени истинные направления тока и напряжения совпадают и, следовательно, мгновенная мощность всегда положительна, т. е. R- элемент потребляет электрическую энергию от источника и необратимо преобразует ее в другие виды энергии. Скорость поступления энергии в течение периода не остается постоянной:

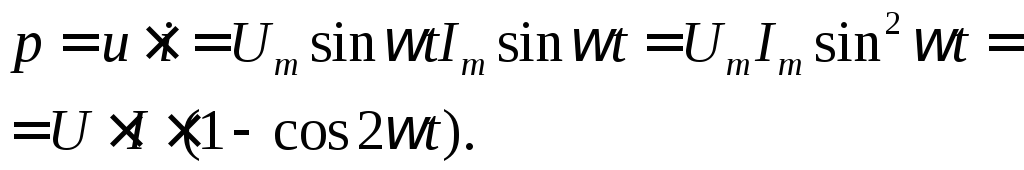(36)

Мощность колеблется с угловой частотой 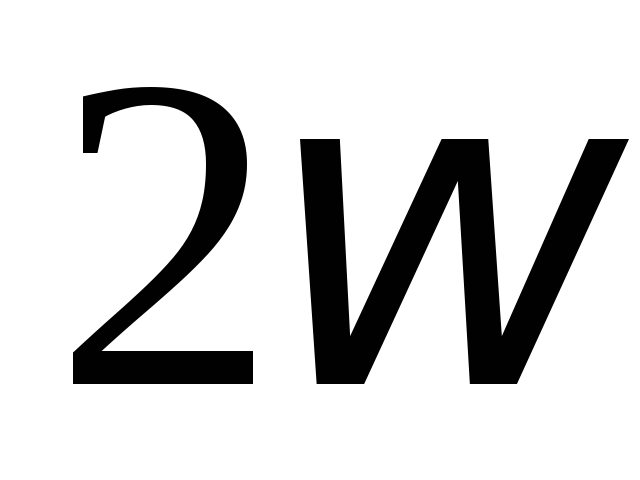в пределах от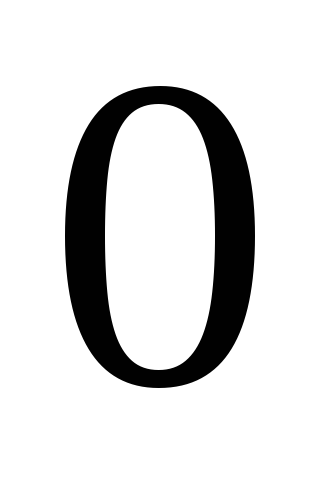до.

Энергетический процесс принято характеризовать средним значением мощности за период, которое называют активной мощностью и обозначают буквой Р:

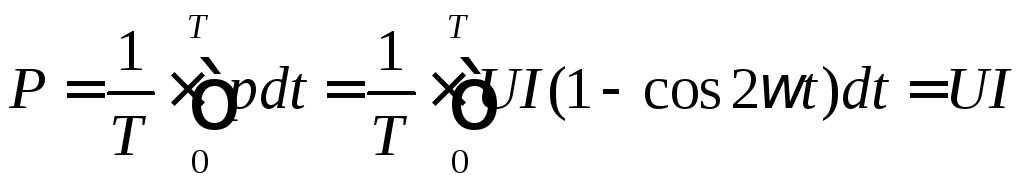. (37)

С учётом (34) полученное выражение преобразуется к виду

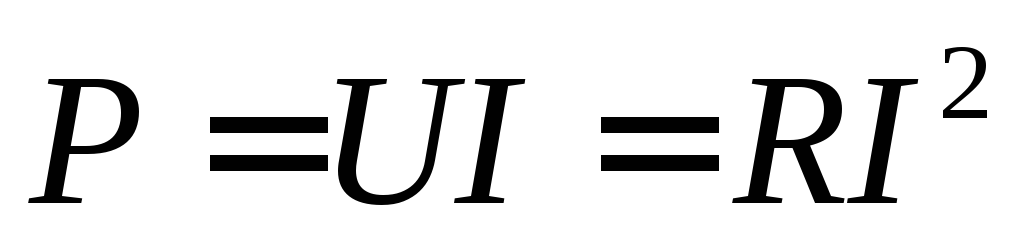. (38)

Активная мощность характеризует работу, совершаемую в электрической цепи за период, т. е. определяет электрическую энергию W, необратимо преобразовавшуюся в другие виды энергии:

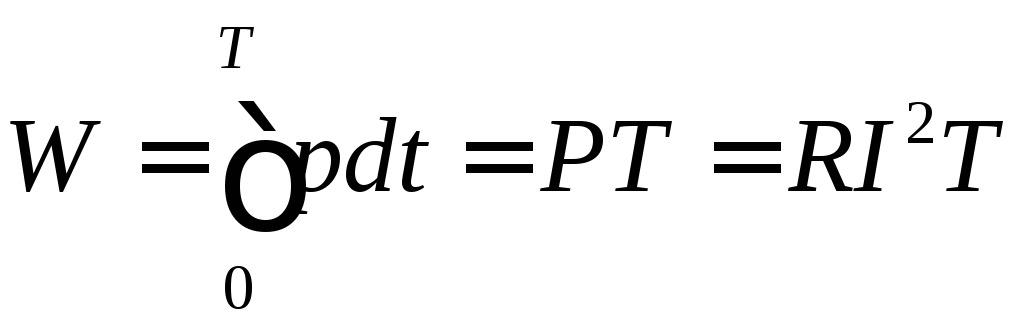. (39)

Таким образом, ток с действующим значением 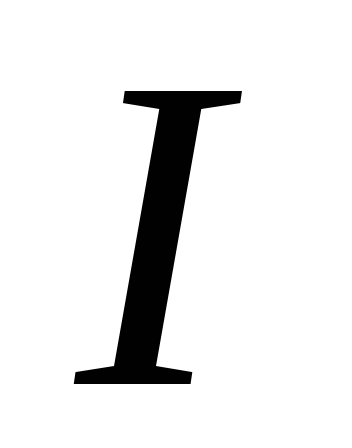по совершаемой им работе эквивалентен постоянному току, имеющему то же значение.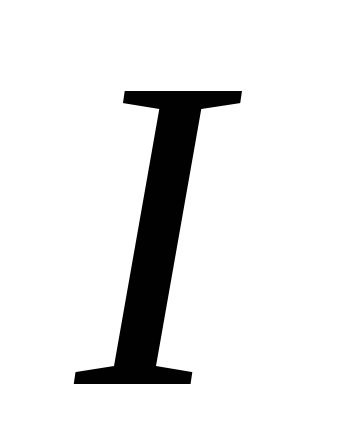

Комплексное сопротивление элемента (участка цепи)

Под комплексным сопротивлением понимают отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:

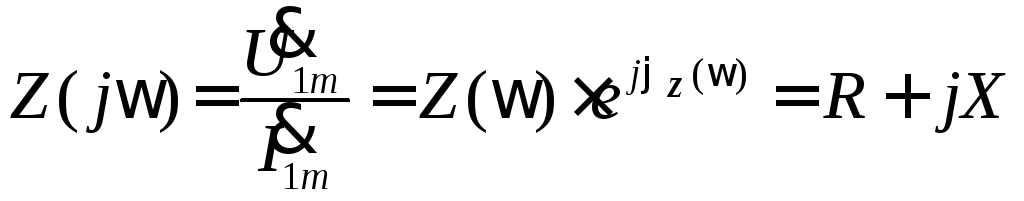. (1.6)

где Z –модуль комплексного сопротивления, φ=ψ_u — ψ_i – начальная фаза или аргумент комплексного сопротивления; R — активного сопротивления, X– реактивному сопротивлению, причем Z=(R²+X²)^1/2, а φ_z(ω)=ψ_u—ψ_i =arctg(X/R).

По виду записи комплексного сопротивления можно судить о характере участка цепи: Z=R – активное (резистивное) сопротивление; Z=R+jX — активно-индуктивное сопротивление; Z=R – j X — активно-емкостное

— комплексная проводимость, величина, обратная комплексному сопротивлению:

ПОСТРОЕНИЕ ВЕКТОРНЫХ ДИАГРАММ НА ВРАЩАЮЩЕЙСЯ КОМПЛЕКСНОЙ ПЛОСКОСТИ.

Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:

а) В цепи с активным сопротивлениемток и напряжение совпадают по фазе.

б) В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов

в) В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе на­пряжение на угол +90 градусов.

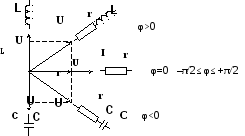
Рис.2.1.Мнемоническая схема, поясняющая возможные повороты радиусов-векторов при различном включении r-L-Cэлементов.

При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включение элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи. Возможные сдвиги фаз векторов напряжения в электрических цепях, состоящих из различных комбинаций r-L-C элементов, приведены на мнемонической схеме (см. рис.2.1.).

Радиус–вектора на схеме и ниже выделяются жирным шрифтом или точками (черточками) над ними.

Расчет цепей методом комплексных амплитуд

Метод комплексных амплитуд состоит в следующем:

1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:

а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.

б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е.х(t) =X_m cos(₀t – _x) X_m=X_m e^–jx.

R

Z_R=R

C

Z_C=1/(jC)

L

Z_L=jL

Рис. 4.27

2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождениюкомплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е.Y_m = Y_m e^–jy.

3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.

Y_m=Y_m e ^–jy  y(t) =Y_m cos(₀t – _y).

Пример 1. Алгоритм метода рассмотрим на примере анализа цепи, схема которой приведена на рис. 4.29.

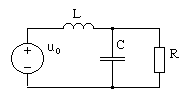
Рис. 4.29. RLC-цепь второго порядка

На вход цепи подается синусоидальное воздействие 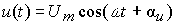. Параметры воздействия и элементов цепи известны:U_m=1 В, ω =1 с^-1 , φ _u=90⁰ , R=1 Ом, L=1 Гн, C=1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.

Решение.

1. Представим воздействие в комплексной форме:

.

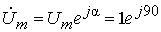2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.

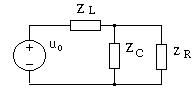
Рис. 4.30. Схема замещения цепи в частотной области

3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:

, ,,

,

, ,

,

, .

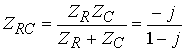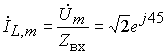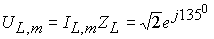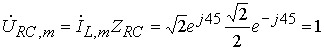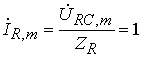3. Построим векторную диаграмму для токов и напряжений в цепи. Для этого на комплексной плоскости откладываются в соответствующем масштабе найденные токи и напряжения, как показано на рис. 4.31.

Рис. 4.31. Векторная диаграмма

 Построение векторной диаграммы, как правило, является конечным результатом решения подобных задач. Векторная диаграмма показывает амплитуду и начальную фазу любого тока или напряжения. При необходимости записать временную функцию тока или напряжения, это всегда можно сделать, имея векторную диаграмму. Например, напряжение на L-элементе имеет амплитуду 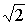, а начальную фазу 135⁰, значит, во временной области это напряжение можно записать так:

.

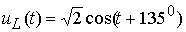Пример 2. Задана эквивалентная схема цепи синусоидального тока (рис. 10) и ее параметры.

Выполнить следующие действия:

1. Рассчитать токи в ветвях и напряжения на элементах схемы;

2. Составить и проверить баланс полных, активных и реактивных мощностей;

3. Построить векторную диаграмму токов для узла а.

Расчет проводим символическим методом в следующем порядке:

1. Рассчитываем сопротивление всех элементов схемы (учитываем, что )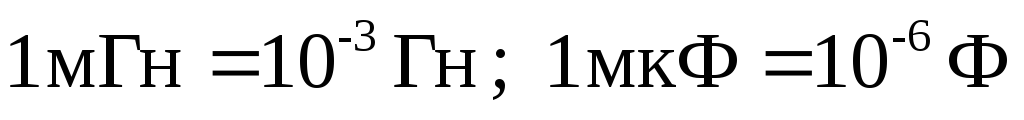

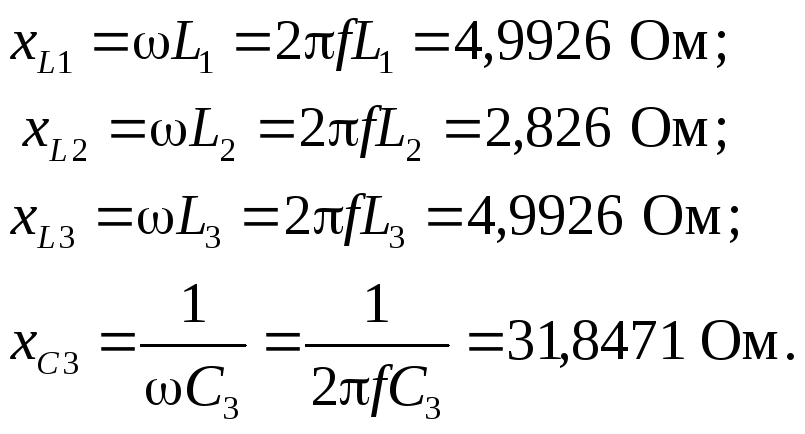
2. Представляем ЭДС источника в виде комплекса действующего значения. Определяем комплексные сопротивления и проводимости ветвей

.

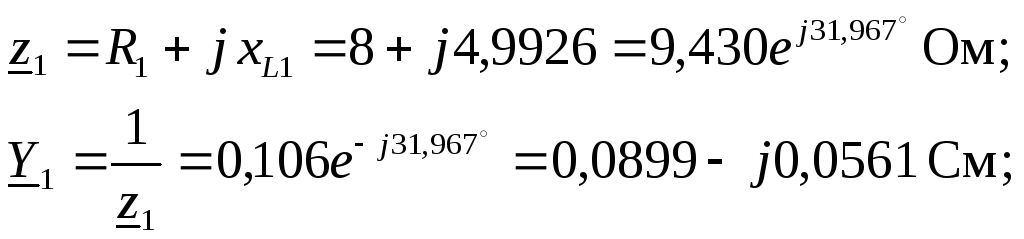
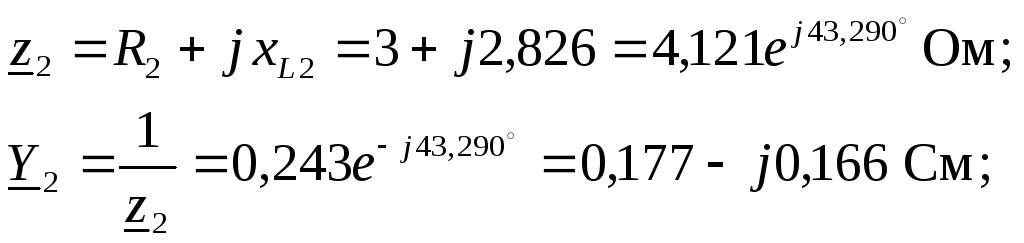
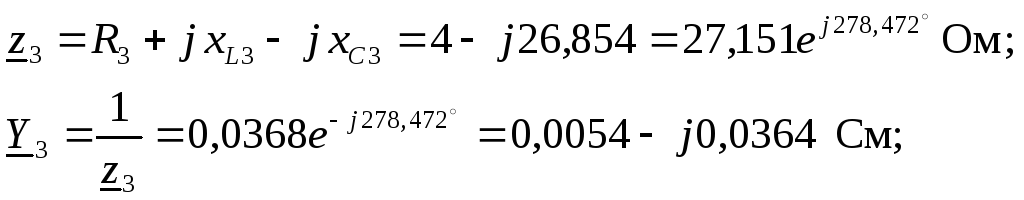
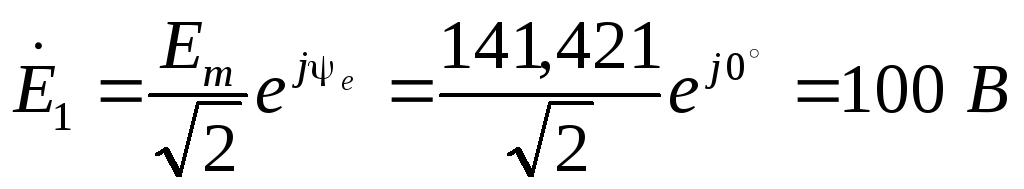3. Рассчитываем токи в ветвях методом двух узлов. Задаем произвольно положительное направление токов в ветвях и положительное направление узлового напряжения. Используя основную формулу метода, рассчитываем узловое напряжение

.

Определяем токи в ветвях, используя обобщенный закон Ома

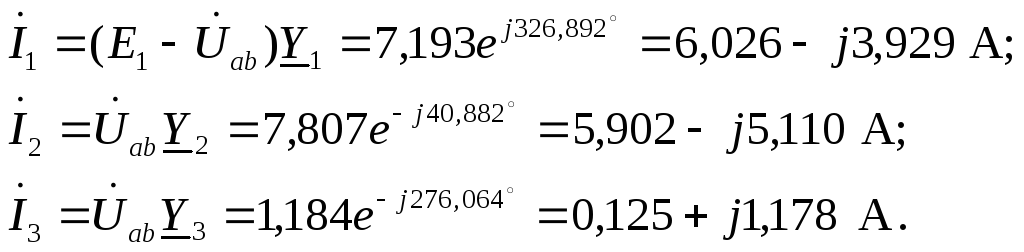
Проверяем корректность промежуточных расчетов, составив уравнение по первому закону Кирхгофа для узла а

.

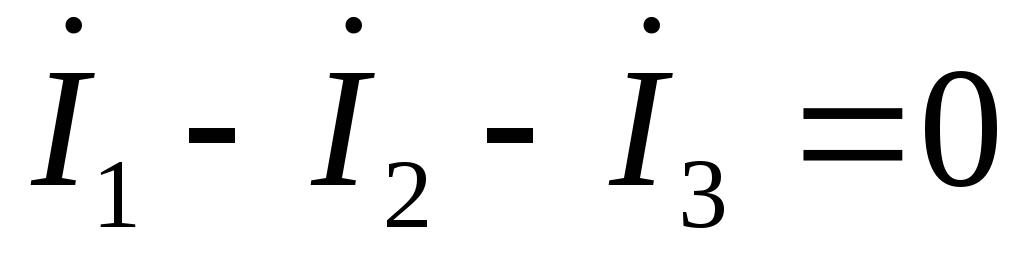Комплексная абсолютная погрешность расчета составляет

.

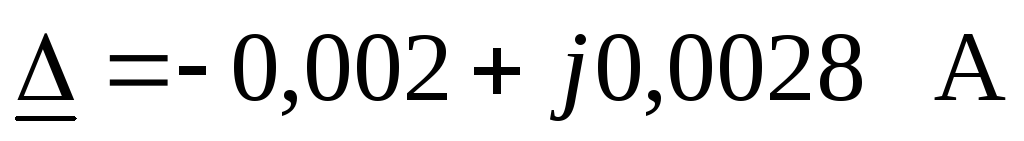Определяем ее модуль

.

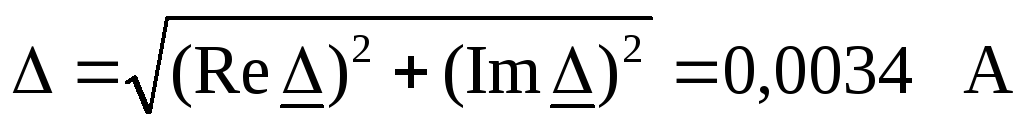Рассчитываем относительную погрешность определения токов

.

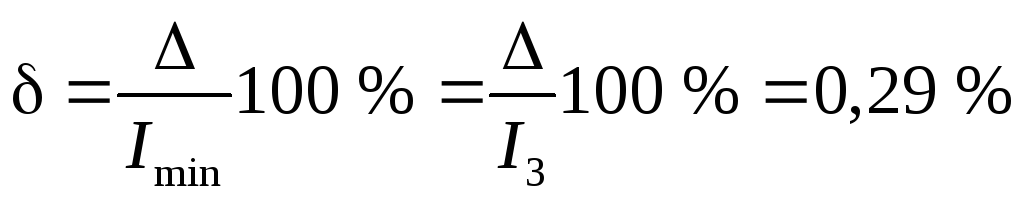Поскольку 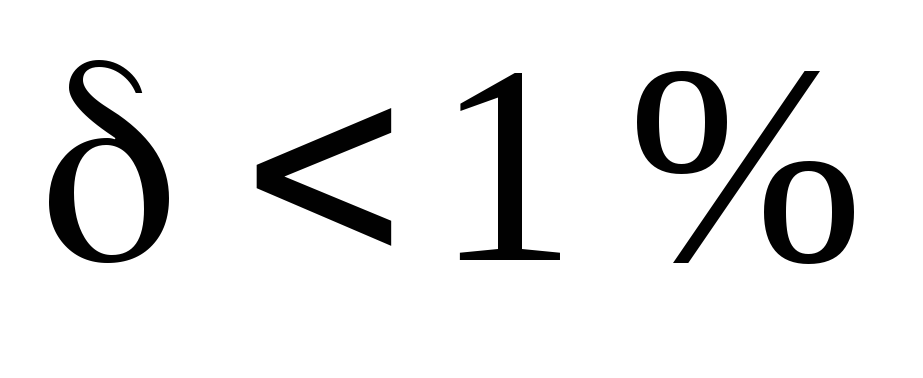, расчет токов корректен. Первый пункт задания выполнен.

4. Составляем и проверяем баланс мощностей

Рассчитываем полную комплексную мощность, развиваемую источником, а также его активную и реактивную мощность. При этом используем закон Джоуля – Ленца в комплексной форме записи

,

.

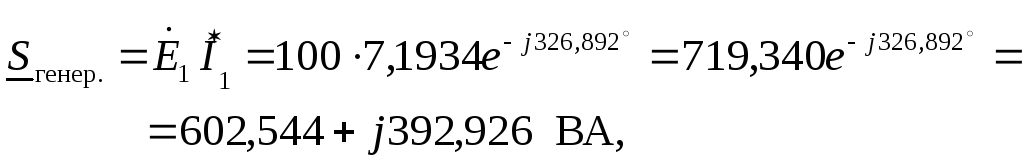Определяем суммарную активную и реактивную мощность на приемниках. При этом также используем закон Джоуля – Ленца

;

.

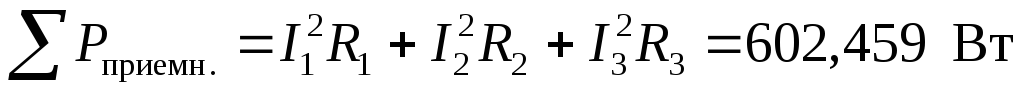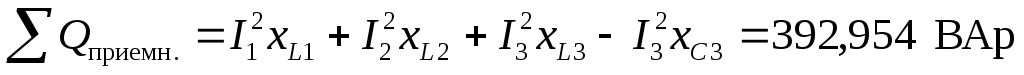Рассчитываем суммарную полную комплексную мощность на приемниках

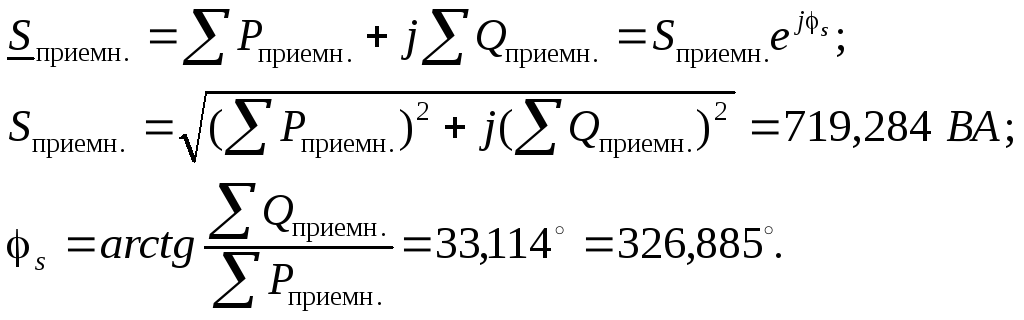
Проверяем корректность расчета, рассчитав модуль относительной погрешности определения полных мощностей

.

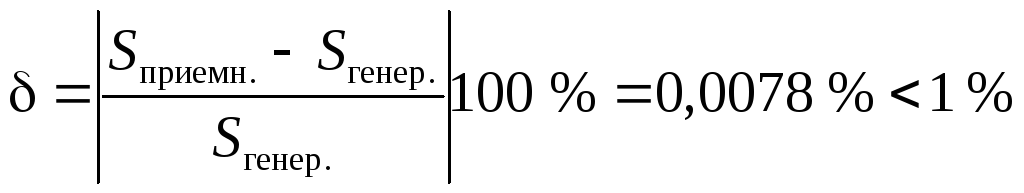Расчет проведен корректно. Второй пункт задания выполнен.

5. Строим векторную диаграмму токов на комплексной плоскости, используя их действительные () и мнимые (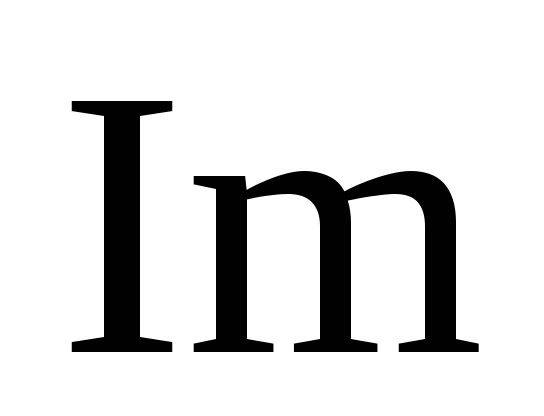) составляющие. Задаемся масштабом по току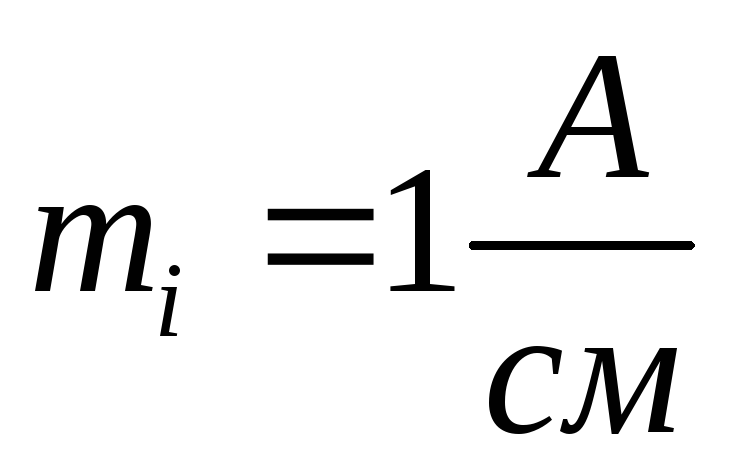, делим указанные составляющие токов на масштаб и откладываем получающиеся отрезки в сантиметрах вдоль осей комплексной плоскости (с учетом знаков составляющих).

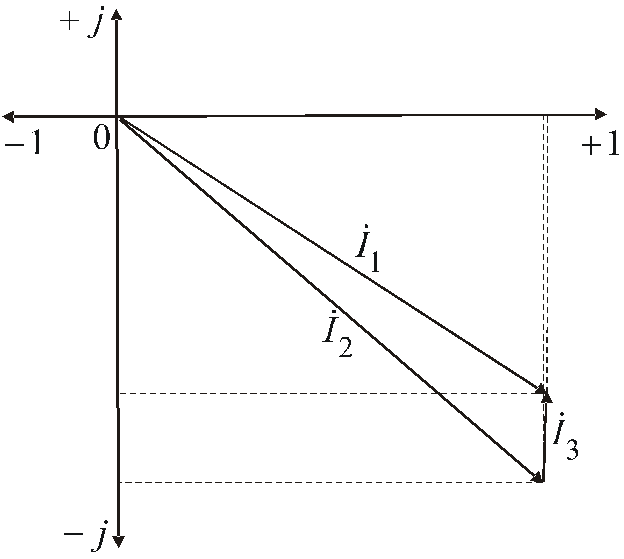
Рис. 11.

Результаты построения (рис. 11) наглядно иллюстрируют корректность проведенных расчетов. Итак, третий пункт и все задание выполнены.

При выполнении задания №2 можно также воспользоваться рекомендуемой литературой [2, 3, 4].

Пример 6. Для цепи, изображенной на рис. 1 требуется:

1. Определить комплексным методом действующие значения напряжений и токов на всех участках цепи.

2. Определить активные, реактивные и полные мощности каждого участка цепи и всей цепи.

3. Составить баланс активных и реактивных мощностей и оценить погрешность расчета.

4. Построить векторную диаграмму токов и напряжений.

Рис. 1

Исходные данные: U = 127 В , r1 = 15 Ом , C1 = 60 мкФ, r2 = 10 Ом , L2 = 80 мГн, r3 = 15 Ом , C3 = 90 мкФ. Частота питающего напряжения 50 Гц.

Комплексное сопротивление — это… Что такое Комплексное сопротивление?



Комплексное сопротивление

Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии электрическому или магнитному полю (и обратно).

Реактивное сопротивление определяет мнимую часть импеданса:

Z = R + iX, где Z — импеданс, R — величина активного сопротивления, X — величина реактивного сопротивления, i — мнимая единица.

В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

Индуктивное сопротивление (X_L) обусловлено возникновением ЭДС самоиндукции. Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:

Ёмкостное сопротивление (X_C). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока:

См. также

Активное сопротивлние

Wikimedia Foundation. 2010.

• Комплексное соединение
• Комплексные вещества

Смотреть что такое «Комплексное сопротивление» в других словарях:

• комплексное сопротивление — Комплексная величина, равная отношению комплексного действующего значения синусоидального электрического напряжения на выводах пассивной электрической цепи или ее элемента к комплексному действующему значению синусоидального электрического тока в …   Справочник технического переводчика

• КОМПЛЕКСНОЕ СОПРОТИВЛЕНИЕ — то же, что импеданс. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 …   Физическая энциклопедия

• комплексное сопротивление — kompleksinė varža statusas T sritis fizika atitikmenys: angl. complex resistance vok. komplexer Widerstand, m rus. комплексное сопротивление, n pranc. résistance complexe, f …   Fizikos terminų žodynas

• комплексное сопротивление обмотки — Импеданс измерительной обмотки, сочлененной с проводящим контролируемым изделием. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003 г.] Тематики виды… …   Справочник технического переводчика

• комплексное сопротивление электрической цепи — Комплексная величина, равная отношению комплексного напряжения на зажимах данной цепи к комплексному току в этой цепи …   Политехнический терминологический толковый словарь

• Сопротивление — Сопротивление: В Викисловаре есть статья «сопротивление» Электрическое сопротивление  физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока. Сопротивление  разговорное название резистора …   Википедия

• комплексное полное сопротивление — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN vector impedance …   Справочник технического переводчика

• сопротивление — 3.93 сопротивление (resistance): Способность конструкции или части конструкции противостоять действию нагрузок. Источник: ГОСТ Р 54382 2011: Нефтяная и газовая промышленность. Подводные трубопроводные системы. Общие технические требования …   Словарь-справочник терминов нормативно-технической документации

• комплексное (электрическое) сопротивление — 154 комплексное (электрическое) сопротивление Комплексная величина, равная отношению комплексного действующего значения синусоидального электрического напряжения на выводах пассивной электрической цепи или ее элемента к комплексному действующему… …   Словарь-справочник терминов нормативно-технической документации

• сопротивление короткого замыкания четырехполюсника — 199 сопротивление короткого замыкания четырехполюсника Комплексное или операторное сопротивление пассивного четырехполюсника со стороны одной пары выводов, когда другая пара замкнута накоротко Источник: ГОСТ Р 52002 2003: Электротехника. Термины… …   Словарь-справочник терминов нормативно-технической документации

Элементы цепи синусоидального тока. Векторные диаграммы и комплексные соотношения для них. (Лекция N 4)

1. Резистор

Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение (см. рис. 1), то ток i через него будет равен

.

(1)

Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.

Из (1) вытекает:

;

.

 

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

,

— разделим первый из них на второй:

или

.

(2)

Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.

2. Конденсатор

Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток i через него будет равен

.

(3)

Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.

Из (3) вытекает:

;

 

.

 

Введенный параметр называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при конденсатор представляет разрыв для тока, а при .

Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:

;

,

— разделим первый из них на второй:

или

.

(4)

В последнем соотношении — комплексное сопротивление конденсатора. Умножение на соответствует повороту вектора на угол по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.

3. Катушка индуктивности

Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением . Тогда для напряжения на зажимах катушки индуктивности можно записать

.

(5)

Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.

Из (5) вытекает:

.

Введенный параметр называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при катушка индуктивности не оказывает сопротивления протекающему через него току, и при .

Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:

;

,

разделим первый из них на второй:

или

.

(6)

В полученном соотношении — комплексное

сопротивление катушки индуктивности. Умножение на соответствует повороту вектора на угол против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11

 

4. Последовательное соединение резистивного и индуктивного элементов

Пусть в ветви на рис. 12 . Тогда

где

, причем пределы изменения .

Уравнению (7) можно поставить в соответствие соотношение

,

которому, в свою очередь, соответствует векторная диаграмма на рис. 13. Векторы на рис. 13 образуют фигуру, называемую треугольником напряжений. Аналогично выражение

графически может быть представлено треугольником сопротивлений (см. рис. 14), который подобен треугольнику напряжений.

 

5. Последовательное соединение резистивного и емкостного элементов

Опуская промежуточные выкладки, с использованием соотношений (2) и (4) для ветви на рис. 15 можно записать

.,

(8)

где

, причем пределы изменения .

На основании уравнения (7) могут быть построены треугольники напряжений (см. рис. 16) и сопротивлений (см. рис. 17), которые являются подобными.

6. Параллельное соединение резистивного и емкостного элементов

Для цепи на рис. 18 имеют место соотношения:

;

, где [См] – активная проводимость;

, где [См] – реактивная проводимость конденсатора.

Векторная диаграмма токов для данной цепи, называемая треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме

,

где ;

— комплексная проводимость;

.

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20.

Для комплексного сопротивления цепи на рис. 18 можно записать

.

Необходимо отметить, что полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.

7. Параллельное соединение резистивного и индуктивного элементов

Для цепи на рис. 21 можно записать

;

, где [См] – активная проводимость;

, где [См] – реактивная проводимость катушки индуктивности.

Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме

,

где ;

— комплексная проводимость;

.

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.

Выражение комплексного сопротивления цепи на рис. 21 имеет вид:

.

Литература

1.     Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2.     Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1.     В чем сущность реактивных сопротивлений?

2.     Какой из элементов: резистор, катушку индуктивности или конденсатор – можно использовать в качестве шунта для наблюдения за формой тока?

3.     Почему катушки индуктивности и конденсаторы не используются в цепях постоянного тока?

4.     В ветви на рис. 12 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

5.     В ветви на рис. 15 . Определить комплексное сопротивление ветви, если частота тока .
Ответ: .

6.     В цепи на рис. 18 . Определить комплексные проводимость и сопротивление цепи для .
Ответ: ; .

7.     Протекающий через катушку индуктивности ток изменяется по закону А. Определить комплекс действующего значения напряжения на катушке.
Ответ: .

Закон Ома в комплексной форме

Для анализа электрических цепей синусоидального тока удобнее применять закон Ома в комплексной форме. Цепи синусоидального тока – линейные цепи с установившимся режимом работы, когда после окончания в них переходных процессов, падения напряжений на участках, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В обратном случае закон в такой форме неприменим.

В отличие от обычной формы закона Ома, в комплексной форме напряжение, токи, сопротивления и ЭДС записываются как комплексные числа. Данное нововведение основано на том, что в цепях переменного тока существуют активные и реактивные значения напряжений, токов и сопротивлений, что требует определенных корректив.

Итак, вместо активного сопротивления R, которое используется в основном в цепях постоянного тока, запишем полное (комплексное) сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже становятся комплексными величинами. При практических расчетах удобнее пользоваться действующими значениями. Запишем формулу закона Ома в комплексной форме:

где

• Z – комплексное (полное) сопротивление,
• Y – комплексная (полная) проводимость.

где

• r – активное сопротивление,
• x – реактивное сопротивление,
• z – полное сопротивление,
• g – активная проводимость,
• b – реактивная проводимость,
• y – полная проводимость,
• j – комплексная единица, j=√(-1).

Решение задач

По заданной схеме определить полное сопротивление цепи, токи (I_1 ) ̇, (I_2 ) ̇, (I_3 ) ̇. U = 120 В, xC1 = 100 Ом, xL2 = 50 Ом, xC3 = 50 Ом, r1 = 25 Ом, r2 = 20 Ом.

Дано:	Решение:
U = 120 В xC1 = 100 Ом xL2 = 50 Ом xC3 = 50 Ом r1 = 25 Ом r2 = 20 Ом Z – ? I_1 – ? I_2 – ? I_3 – ?	Запишем формулу закона Ома в комплексной форме: — Найдем полное сопротивление цепи по формуле: Примем начальную фазу напряжения за нуль, тогда: По следствию из закона Ома ток распределяется обратно пропорционально сопротивлению ветвей, а значит