|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 6 из 8Следующая ⇒
Комплексной частотной характеристикой называется зависимость коэффициента передачи тока или напряжения от частоты. Иногда термин КЧХ применяется к комплексному входному или выходному сопротивлениям исследуемого элемента. Различают 4 вида передаточных функций.
Активное сопротивление не зависит от частоты, поэтому его частотная характеристика постоянна и представляет собой прямую линию. Коэффициент передачи двухполюсника, построенном на активных сопротивлениях постоянен для всех частот.
Сопротивление емкостного элемента обратно пропорционально частоте: XC = 1/ωC;
Сопротивление индуктивного элемента обратно пропорционально частоте: XL = ωL
На графике показана зависимость сопротивлений реактивных элементов от частоты, которая на комплексной плоскости является КЧХ реактивных элементов. 30. КЧХ цепей с одним реактивным элементом.
Рассмотрим цепь с одним реактивным элементом – емкостью.
Для данной схемы найдем комплексное входное сопротивление, его модуль и аргумент: (3.45) По полученным зависимостям строим соответствующие графики: а) б) а — модуль входной функции; б — аргумент входной функции Рисунок 3.13 — Частотные характеристики схемы примера 1
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме. Различают четыре вида передаточных функций: 1) передаточная функция по напряжению:
2) передаточная функция по току: 3) передаточное сопротивление:
4) передаточная проводимость: В общем виде передаточная функция: представляется в виде АЧХ — К(ω) и ФЧХ — φ(ω)
Резонансом напряженийназывают явление резонанса в участке электрической цепи, содержащей последовательно соединенные индуктивный и емкостной элементы. Резонансная частота контура находится из условия равенства нулю реактивного сопротивления: ω0 = 1/√(L∙С) Затухание– величина, обратная добротности.d = 1/Q
Абсолютная расстройка контура: Δω = |ω – ω0
Относительная расстройка контура: δω = Δω/ω0
⇐ Предыдущая12345678Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Все правила по сольфеджио
Резонансный режим работы цепи. Резонанс напряжений. Нахождение резонансной частоты контура. Добротность. Затухание. Частотные характеристики резонансного контура. Полоса пропускания контура. Обобщенная расстройка контура. Абсолютная расстройка контура. Относительная расстройка контура.
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)Частотные характеристики.
Передаточная функция выражает свойства системы через комплексную переменную, которая содержит действительную и мнимую части:
. (2.8)
Ее называют комплексная частотная характеристика, амплитудно-фазовая частотная характеристика, комплексный коэффициент усиления.
По
определению, она записывается отношением
частотных полиномов.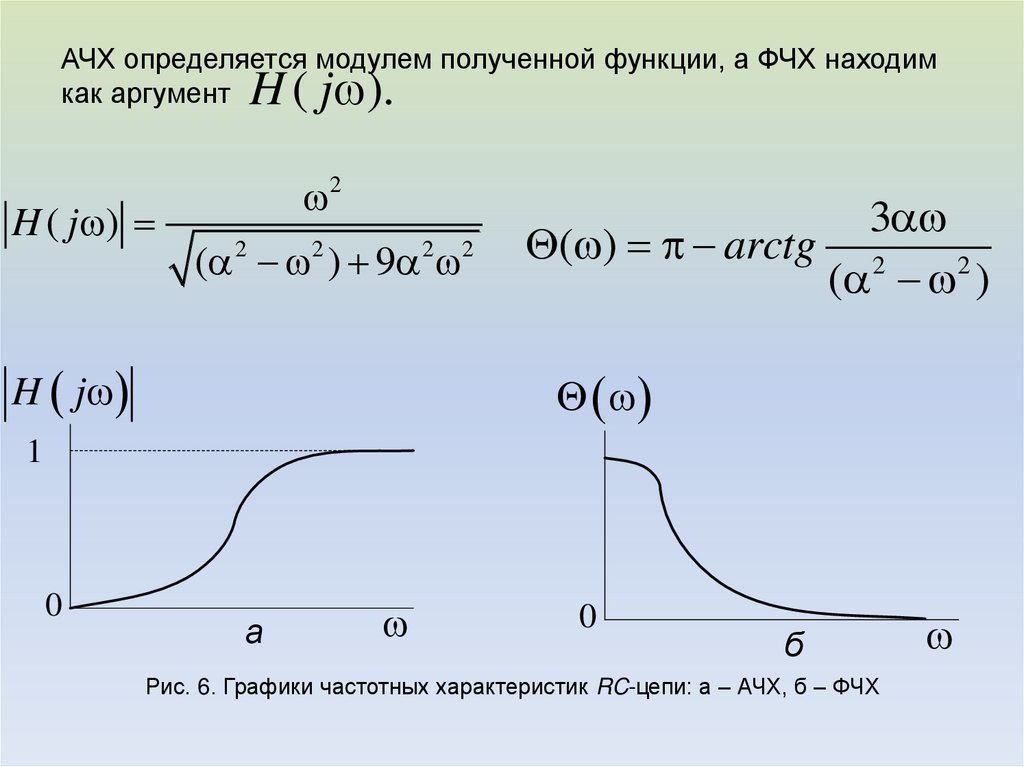
,
представляет собой сумму действительной и мнимой частей:
.
Так получается потому, что j = в четной степени будет либо –1, либо +1.
Частотный полином D(j) в развернутом виде имеет ту же структуру:
D(j) = D1() + jD2() ,
Следовательно комплексная частотная характеристика есть отношение двух комплексных чисел:
.
Умножение числителя и знаменателя на число, сопряженное знаменателю, позволяет выделить действительную и мнимую части:
.
Первое
слагаемое обозначим U(),
второе V().
U()
называют действительной
частотной характеристикой, V()
— мнимой
частотной характеристикой.
В краткой записи
W(j) = U() + jV() . (2.9)
Комплексное выражение (2.9) можно интерпретировать геометрически, отложив по оси абсцисс действительную частотную характеристику, по оси ординат – мнимую частотную характеристику, рис. 2.1.
V()
М
A V
0 U U()
Рис. 2.1.
Для заданной частоты U() и
Соединив прямой А начало
координат с точкой М , получим
прямоугольный треугольник. Для него
справедливы соотношения: , ,, . (2.10)
Все величины – функции частоты .
Комплексную частотную характеристику, следовательно, можно записать в виде
W(j) = U( ) + jV() = A ( cos () + j sin () ).
По формуле Эйлера . Поэтому
. (2.11)
А() называют амплитудной частотной характеристикой или просто амплитудой. () называют фазовой частотной характеристикой или просто фазой.
Пример 2.2.
Записать комплексную частотную характеристику, частотные характеристики, амплитуду и фазу для системы, описываемой дифференциальным уравнением
.
Преобразуя по Лапласу, получаем операторное уравнение
(p2 + 3p + 1) Y(p) = 2 X(p)
и передаточную функцию:
.
Подстановкой p = j превращаем передаточную функцию в комплексную частотную характеристику:
.
Действительная частотная характеристика
.
Мнимая частотная характеристика
.
Амплитуда
.
Фаза
.
Пример 2.3.
Найти комплексную частотную характеристику, амплитуду и фазу пропорционально-интегрального регулятора (ПИ-регу-лятора). Его уравнение
.
(T – постоянная времени, k – коэффициент усиления).
Продифференцируем исходное уравнение,
и преобразуем по Лапласу:
.
Из операторного уравнения составим передаточную функцию:
.
Полагая p = j, записываем комплексную частотную характеристику
,
находим частотные характеристики:
U() = k , V() = — ,
и амплитудную частотную характеристику:
.
Фаза в функции частоты имеет выражение
.
Пример 2.4.
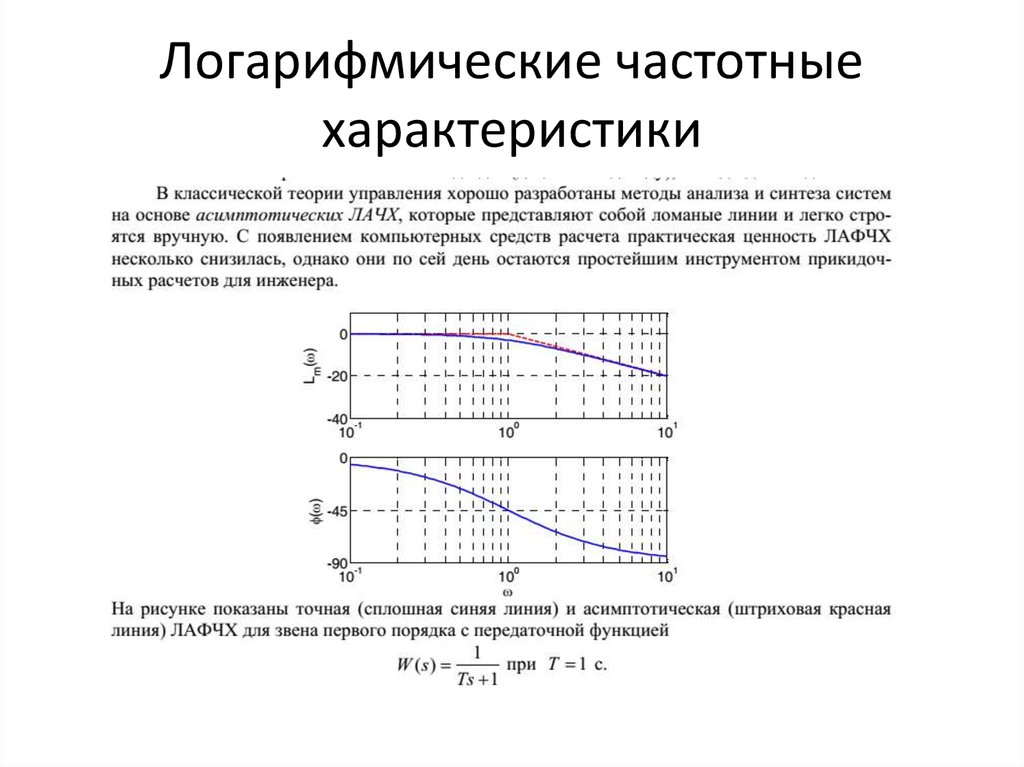
Найти логарифмическую амплитудную частотную характеристику ПИ-регулятора.
Воспользуемся выражением для амплитуды и запишем общий вид ЛАЧХ:
L() = 20 lg A() = 10 lg(k2T22 + 1) – 20 lg T .
Выделим асимптотические прямые.
В
области < 1 . С уменьшением слагаемое k2T22 становится
пренебрежимо меньше единицы.
Его можно
отбросить. Тогда первый член L()
обращается в нуль вследствие lg
1 = 0. Остается
L1 = — 20 lgT – 20 lg .
В области > 1 . В первом слагаемом следует пренебречь единицей. В таком случае
L2 = 20 lg k + 20 lg T — 20 lg T = 20 lg k.
Для построения графика надо найти точки пересечения прямой L1 c осями координат и с прямой L2 . (По ординате откладывают L1, L2, по абсциссе lg ).
Точка пересечения с осью ординат находится из условия lg = 0. Получается: L1 = -20 lg T = 20 lg (1/T).
Точка
пересечения с осью абсцисс находится
из условия L1 = 0. Получается: lg = lg
(1 / T)
.
Точка пересечения прямой L1 с прямой L2 находится из условия L1 = L2 . Получается: lg = lg (1 / kT) .
Вид графика показан на рис. 2.1.
Рис. 2.2. Асимптотическая логарифмическая
амплитудная частотная характеристика ПИ-регулятора
4.5: Вывод комплексной функции частотной характеристики — Простой вывод сложной функции частотной характеристики для стандартных стабильных систем первого порядка.
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7646
- Уильям Л.
Халлауэр мл. - Политехнический институт Вирджинии и Государственный университет через Инициативу открытого образования технических библиотек Вирджинии
Халлауэр мл.Этот раздел является примером гораздо более простого метода (чем в разделах 4.2 и 4.3) для получения функции частотной характеристики системы. Найдем АЧХ стандартных стабильных систем порядка 1 st . Из уравнения 3.4.8 стандартный устойчивый ОДУ с синусоидальным возбуждением равен
\[\dot{x}+\left(1 / \tau_{1}\right) x=b u(t)=b U \cos \omega t \nonumber \]
Мы ищем установившуюся синусоидальную характеристику \(x_{s s}(t)=X(\omega) \cos (\omega t+\phi(\omega))\), в которой \(X(\omega)\) и \(\phi(\omega)\) — функции, которые нужно найти. Первым шагом в методе является выполнение общего [для произвольного \(u(t)\)] преобразования Лапласа, установив IC равным нулю:
\[\влево.\влево(s+1 / \tau_{1}\вправо) L[x(t)]\вправо|_{x_{0}=0}=b L[u(t)] \ не число \]
Далее формируем системную общую передаточную функцию , \(T F(s)\), определяемую как отношение выходного преобразования к входному преобразованию, с нулевым IC:
\[T F(s) \equiv \frac{\left.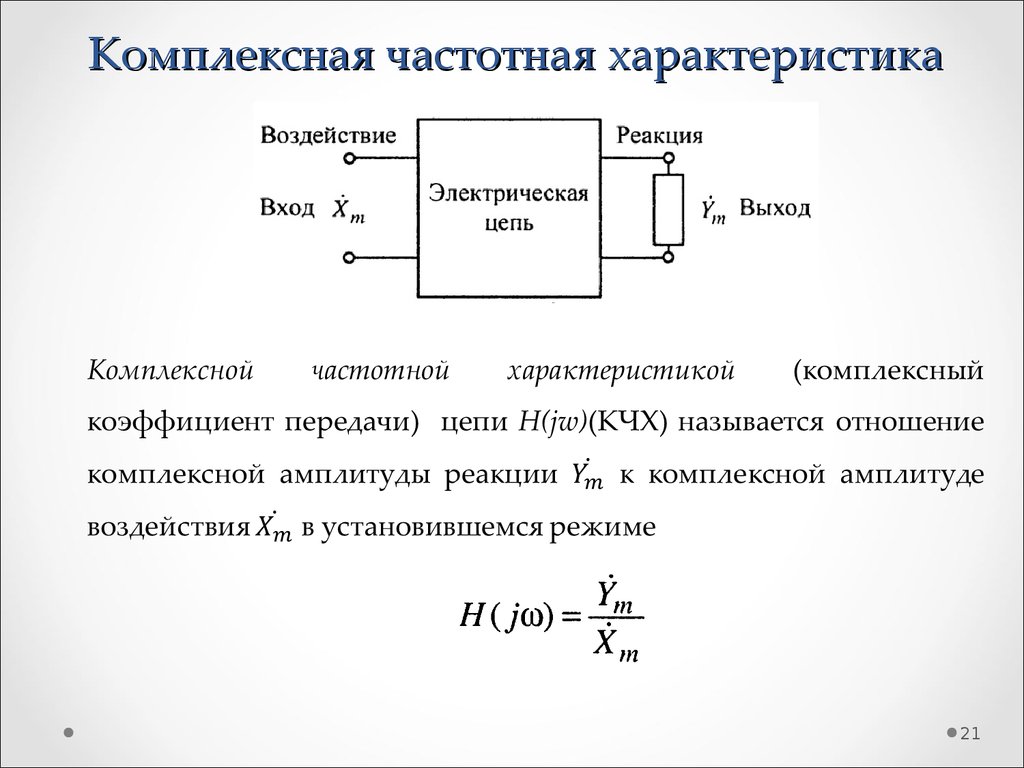
{j \phi(\omega)}\label{eqn:4.18b} \end{align} \] 9{-1}\влево(-\омега\тау_{1}\вправо)\).
Уравнения \(\ref{eqn:4.18a}\) и \(\ref{eqn:4.18b}\) определяют комплексную функцию частотной характеристики, \(FR F(\omega)\), стандартной стабильной 1 ст системы заказа. В разделах 4.6 и 4.7 доказано для систем LTI вообще , что реальная величина \(|FR F(\omega)|\) функции \(FR R F(\omega)\) есть величина отношения частоты системы отклика, а фазовый угол \(\phi(\omega)\) функции \(F R F(\omega)\) — фазовый угол частотной характеристики системы. Например, давайте адаптируем стандартное решение уравнения \(\ref{eqn:4.18b}\) к системе демпфер-пружина, для которой [из уравнения 4.2.5] \(b=1 / c\) и \(\ тау_{1}=с/к\). Таким образом, величина \(F R F(\omega)\) из уравнения \(\ref{eqn:4.18b}\) равна 9{-1}\left(-\omega\tau_{1}\right)\label{eqn:4.20} \]
, который идентичен фазе системы демпфер-пружина \(FRF\) \(\phi(\omega)\) уравнения 4.3.9.
Таким образом, с помощью \(FR F(\omega)\) уравнения \(\ref{eqn:4.18b}\) мы получили здесь те же окончательные результаты, что и раньше для системы демпфер-пружина, но гораздо проще.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Уильям Л. Халлауэр мл.
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- функция частотной характеристики (FRF)
- источник@https://vtechworks. {-j\omega t} $$. 9{j\omega t}$$
И посмотрите содержимое нашей формы волны для каждой частоты, заданной омегой, и мы переназначили нашу форму волны во временной области в область частот, где некоторые математические задачи могут быть решены намного проще (или другие причина, связанная с наблюдением или манипулированием сигналом по частоте).
Некоторые сигналы не сходятся в корреляционном интеграле и поэтому не имеют преобразования Фурье. Однако мы можем «предварительно масштабировать» эти формы волны, умножая на затухающий экспоненциал, который затем позволит сойтись решению: 9{j \omega t}$$
Результатом является преобразование Лапласа (в дискретных системах z-преобразование), где снова отображение нашей формы сигнала во временной области в s-область позволяет нам решать математические задачи намного проще (в частности, Лаплас переводит дифференциальные уравнения в простую алгебру — да!!!). Это также позволяет нам решать переходные состояния, такие как переходные характеристики и тому подобное.
И да, вы можете изобразить преобразование Лапласа как поверхность, показывающую корреляцию нашей входной функции x(t) со всеми возможными векторами вращения (как в Фурье), а также векторами вращения, которые растут или затухают со временем. (Обычно эта поверхность представлена только полюсами и нулями, показывающими, где корреляция максимальна, а где нуль, поскольку это полностью описывает остальную часть поверхности, которая не показана.)Относительно времени, частоты и сложных сигналов в целом: еще не упомянутые сложные сигналы широко используются в системах связи. Модуляция на любой несущей для линейной системы может быть смоделирована непосредственно в основной полосе частот (что приводит к гораздо более простой обработке, поскольку мы больше не занимаемся моделированием каждого цикла высокочастотной синусоидальной несущей, а можем просто моделировать относительно более низкую скорость изменения амплитуды). и фазы непосредственно этой несущей.)
Тем не менее, любая форма волны, в которой положительная половина спектра не является комплексно-сопряженной (не той же амплитуды и противоположной фазы), если смотреть в полосе модулирующих частот, как описано выше, может быть описана с использованием комплексных сигналов; который сегодня охватывает почти все современные формы сигналов связи (простые двухсторонние модуляции FM и AM — это случаи, когда в этом нет необходимости).
{j\omega t}$
). На рисунках ниже показано это соотношение при разложении Эйлера, а также то, как требуется комплексная частота, если положительная половина спектра не равна (комплексно-сопряженная) нижней половине:Сигнал во временной области отображается в виде вектора (полярная диаграмма с вектором, представляющим мгновенное время и угол, вращающимся во времени). Поскольку эти два вектора равны и вращаются в противоположных направлениях (сопряженных), получится синусоида, которая остается только на оси Real. Таким образом, мы видим тождество Эйлера, концепцию положительных и отрицательных частот и причину, по которой мы используем комплексные частоты.
Наконец, вот картинка, показывающая случай, когда сигнал модулируется. На картинке мы центрированы на 0 (постоянный ток), но мы могли бы быть в равной степени центрированы на любой несущей частоте с тем же отклонением фазы и амплитуды от несущей в зависимости от времени, как показано на диаграмме IQ (полярная диаграмма) слева.
{-j\omega t} $$. 9{j\omega t}$$
И да, вы можете изобразить преобразование Лапласа как поверхность, показывающую корреляцию нашей входной функции x(t) со всеми возможными векторами вращения (как в Фурье), а также векторами вращения, которые растут или затухают со временем. (Обычно эта поверхность представлена только полюсами и нулями, показывающими, где корреляция максимальна, а где нуль, поскольку это полностью описывает остальную часть поверхности, которая не показана.)
{j\omega t}$
). На рисунках ниже показано это соотношение при разложении Эйлера, а также то, как требуется комплексная частота, если положительная половина спектра не равна (комплексно-сопряженная) нижней половине:
