Количество теплоты, выделяемое проводником с током — урок. Физика, 8 класс.
Проходя по проводнику, ток может оказывать некоторые действия: тепловое, химическое и магнитное (подробно об этом можно почитать в \(7\) теме). Вспомним, с чем связано тепловое действие тока. Оно объясняется тем, что свободные электроны в металлах или ионы в растворах солей, кислот, щелочей, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества проводника и передают им свою энергию. В результате работы электрического тока внутренняя энергия проводника увеличивается. Например, спираль лампочки раскаляется до такой температуры, что начинает излучать свет.

Нагретый проводник отдаёт полученную энергию окружающим телам путём теплопередачи. Значит, количество теплоты, выделяемое проводником, по которому течёт ток, равно работе тока, т.е. Q = A, где \(А\) — работа тока, \(Q\) — количество теплоты.
Работу тока рассчитывают по формуле: A = U⋅I⋅t. Тогда количество теплоты будет определяться по такой же формуле: Q = U⋅I⋅t.
Пользуясь законом Ома, можно количество теплоты, выделяемое проводником с током, выразить через силу тока \(I\), сопротивление участка цепи \(R\) и время \(t\). Зная, что напряжение U = IR, получим: Q = I2⋅R⋅t.
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени.
К такому же выводу на основании опытов пришли независимо друг от друга английский учёный Джеймс Джоуль и русский учёный Эмилий Христианович Ленц. Поэтому сформулированный выше вывод называется законом Джоуля—Ленца.

Джоуль Джеймс Прескотт (\(1818—1889\)) — английский физик, член Лондонского королевского общества. Он внёс значительный вклад в исследование электромагнетизма и тепловых явлений, в создание физики низких температур, в обоснование закона сохранения и превращения энергии. Именем Джоуля назвали единицу измерения работы и энергии в системе СИ.

Эмилий Христианович Ленц (\(1804—1865\)) — российский физик и электротехник, академик Петербургской АН (\(1830\)), ректор Санкт-Петербургского университета (с \(1863\)) — один из основоположников электротехники. С его именем связано открытие закона, определяющего тепловые действия тока, и закона, определяющего направление индукционного тока.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах.
Состояние сети, когда по проводам и приборам проходит ток больше допустимого значения, называется перегрузкой. Опасность этого явления в тепловом действии тока, ведь при большой перегрузке изоляция проводников легко воспламеняется. Перегрузка может возникнуть при подключении устройств большой мощности через удлинитель (смотри рисунок и никогда так не делай!).

Для примера, перегрузка проводов на \(25\)% приводит к сокращению срока их службы где-то с \(20\) лет до \(3—5\) месяцев, а перегрузка проводов на \(50\)% — до нескольких часов.
Источники:
Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.
http://www.myshared.ru/slide/93472/
http://electricalschool.info/main/osnovy/1090-zakon-dzhoulja-lenca.html
http://class-fizika.narod.ru/10_7.htm
http://уроки.мирфизики.рф/%d0%b7%d0%b0%d0%ba%d0%be%d0%bd-%d0%b4%d0%b6%d0%be%d1%83%d0%bb%d1%8f-%d0%bb%d0%b5%d0%bd%d1%86%d0%b0/
http://www.nscience.ru/chemistry/physical/thermodynamics/what_does_thermidynamics_research/
http://energetika.in.ua/ru/books/book-2/part-2/section-1/1-2
http://to-name.ru/biography/emilij-lenc.htm
http://mistroim.ru/remont-pomesheniy/elektrichestvo/kakie-neispravnosti-v-elektroseti-mogut-vozniknut/
http://frutmrut.ru/zakon-dzhoulya-lenca
Нагревание проводников электрическим током. Закон Джоуля-Ленца (Ерюткин Е.С.)
— металлические. Электрический ток в металлических проводниках – это направленное, упорядоченное движение заряженных частиц – электронов (отрицательно заряженные частицы). Когда электроны протекают по проводнику, он нагревается, т. е. металлические проводники нагреваются при протекании тока.
— жидкие проводники (растворы и расплавы). В этих проводниках направленное движение зарядов составляют ионы. Это атомы, у которых либо избыток, либо недостаток электронов. Аналогично, если в жидких проводниках протекает электрический ток, то происходит нагревание проводников.
— газы (при определенных условиях). Электрический ток обусловлен движением ионов и электронов. Нагревается пространство, где протекает электрический ток. Все три случая, которые мы рассмотрели, подтверждают одно общее правило.
Электрический ток при протекании по проводникам увеличивает их внутреннюю энергию. В соответствие можно привести работу электрического тока, работу электрического поля и количество теплоты, которое выделяется в проводниках.
Чем больше сила тока, тем больше количество теплоты, выделившееся в проводнике.
Эксперимент состоял в том, что три одинаковых по своим геометрическим размерам, но выполненные из разных материалов проводника включены последовательно. Через проводники течет электрический ток. При последовательном соединении проводников сила тока во всех участках будет одинакова (рис. 1).
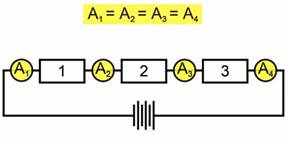
Рис. 1. Сила тока одинакова
На первый взгляд количество теплоты тоже должно было быть одинаковым, однако это не так (рис. 2). Следовательно, количество теплоты зависит не только от силы тока, а так же от еще одной характеристики проводника – электрического сопротивления.
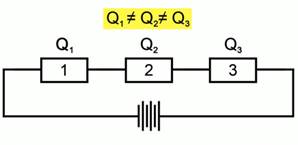
Рис. 2 Количество теплоты разное
Эти опыты независимо друг от друга провели два ученых, англичанин Джоуль (рис. 3) и русский ученый Ленц Эмиль Христианович (рис. 4). Результаты получены одинаковые, поэтому закон получил название этих двух ученых – закон Джоуля-Ленца.

Рис. 3. Д.П. Джоуль

Рис. 4. Э.Х. Ленц
В результате экспериментов было получено уравнение:
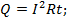
Q – количество теплоты [Дж] I – сила тока [А] R – электрическое сопротивление [Ом] t – время [c]
Формула для вычисления количество теплоты в точности соответствует формуле по вычислению работы электрического тока.
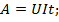
По закону Ома, сила тока определяется как отношение напряжения к сопротивлению.
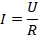
Напряжение можем выразить как произведение
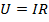
Подставив выражение для напряжения в формулу для работы электрического тока, получаем следующую зависимость:
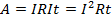
И эта формула полностью соответствует закону Джоуля-Ленца:
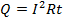 .
.
Следовательно, количество теплоты и работа соответствуют друг другу. В некотором случае работа электрического тока равна количеству теплоты, которое выделяется на проводнике.
Существуют и другие формулы для определения работы, однако только эту формулу мы можем называть законом Джоуля-Ленца. Дело все в том, что количество теплоты – это изменение внутренней энергии проводника (проводник находится в состоянии покоя). А если мы рассматриваем проводник, который не только нагревается, а еще и движется, то в этом случае работа определяет уже полное действие на этот проводник (движение, энергию, другие формы превращения энергии).
При протекании электрического тока частицы движутся в металлических, жидких и газообразных проводниках. Они взаимодействуют с окружающими частицами, у которых нет направленного и упорядоченного движения. Эти взаимодействия и превращаются в тепло.
Закон Джоуля-Ленца: количество теплоты, которое выделяется в проводнике, равно произведению квадрата силы тока в этом проводнике, умноженному на сопротивление проводника и на время, в течение которого этот ток протекает по проводнику.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Домашнее задание
- П. 53, вопросы 1–4 – стр. 125 задание 27 (1). Перышкин А.В. Физика 8. М.: Дрофа, 2010.
- В электрической печи при напряжении 220 В сила тока 30 А. какое количество теплоты выделит печь за 10 минут?
- Как изменится количество теплоты, выделяемое проводником с током, если силу тока в проводнике увеличить в 2 раза?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Ppt4web.ru (Источник).
- Физика, механика (Источник).
- Школа для Электрика (Источник).
ФИЗИКА: ЗАДАЧИ на Закон Джоуля-Ленца
Задачи на Закон Джоуля-Ленца с решениями
Формулы, используемые на уроках «Задачи на Закон Джоуля-Ленца»
Название величины | Обозначение | Единица измерения | Формула |
Сила тока | I | А | I = U / R |
Напряжение | U | В | U = IR |
Время | t | с | t = Q / I2R |
Количество теплоты | Q | Дж | Q = I2Rt |
1 мин = 60 с; 1 ч = 60 мин; 1 ч = 3600 с.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Какое количество теплоты выделит за 20 мин спираль электроплитки сопротивлением 25 Ом, если сила тока в цепи 1,2 А?

Задача № 2. Какое количество теплоты выделит за 30 мин спираль электроплитки, если сила тока в цепи 2 А, а напряжение 220 В?

Задача № 3. Сколько времени нагревалась проволока сопротивлением 20 Ом, если при силе тока 1 А в ней выделилось 6 кДж теплоты.

Задача № 4. Электрическая плитка при силе тока 5 А за 30 мин потребляет 1080 кДж энергии. Рассчитайте сопротивление плитки.

Задача № 5. Какое количество теплоты выделится за 25 мин в обмотке электродвигателя, если ее активное сопротивление равно 125 Ом, а сила тока, протекающего в ней, равна 1,2 А?

Краткая теория для решения Задачи на Закон Джоуля-Ленца.

Это конспект по теме «ЗАДАЧИ на Закон Джоуля-Ленца». Выберите дальнейшие действия:
Работа и мощность электрического тока. Закон Джоуля-Ленца – FIZI4KA

1. Электрический ток, проходя по цепи, производит разные действия: тепловое, механическое, химическое, магнитное. При этом электрическое поле совершает работу, и электрическая энергия превращается в другие виды энергии: во внутреннюю, механическую, энергию магнитного поля и пр.
Как было показано, напряжение \( (U) \) на участке цепи равно отношению работы \( (F) \), совершаемой при перемещении электрического заряда \( (q) \) на этом участке, к заряду: \( U=A/q \). Отсюда \( A=qU \). Поскольку заряд равен произведению силы тока \( (I) \) и времени \( (t) \) \( q=It \), то \( A=IUt \), т.е. работа электрического тока на участке цепи равна произведению напряжения на этом участке, силы тока и времени, в течение которого совершается работа.
Единицей работы является джоуль (1 Дж). Эту единицу можно выразить через электрические единицы:
\( [A] \)= 1 Дж = 1 В · 1 А · 1 с
Для измерения работы используют три измерительных прибора: амперметр, вольтметр и часы, однако, в реальной жизни для измерения работы электрического тока используют счётчики электрической энергии.
Если нужно найти работу тока, но при этом сила тока или напряжение неизвестны, то можно воспользоваться законом Ома, выразить неизвестные величины и рассчитать работу по формулам: \( A=\frac{U^2}{R}t \) или \( A=I^2Rt \).
2. Мощность электрического тока равна отношению работы ко времени, за которое она совершена: \( P=A/t \) или \( P=IUt/t \); \( P=IU \), т.е. мощность электрического тока равна произведению напряжения и силы тока в цепи.
Единицей мощности является ватт (1 Вт): \( [P]=[I]\cdot[U] \); \( [P] \) = 1 А · 1 В = 1 Вт.
Используя закон Ома, можно получить другие формулы для расчета мощности тока: \( P=\frac{U^2}{R};P=I^2R \).
Значение мощности электрического тока в проводнике можно определить с помощью амперметра и вольтметра, измерив соответственно силу тока и напряжение. Можно для измерения мощности использовать специальный прибор, называемый ваттметром, в котором объединены амперметр и вольтметр.
3. При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: \( Q=A \) или \( Q=IUt \). Учитывая, что \( U=IR \), \( Q=I^2Rt \).
Количество теплоты, выделяющееся при прохождении тока но проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени.
Этот закон называют законом Джоуля-Ленца.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?
1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза
2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?
1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза
3. Сопротивления резистор \( R_1 \) в четыре раза меньше сопротивления резистора \( R_2 \). Работа тока в резисторе 2


1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1
4. Сопротивление резистора \( R_1 \) в 3 раза больше сопротивления резистора \( R_2 \). Количество теплоты, которое выделится в резисторе 1
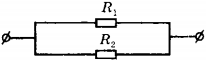

1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2
5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если
1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) и \( A_2 \) в этих проводниках за одно и то же время.
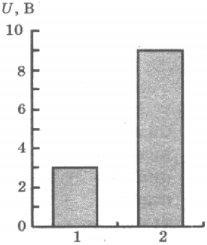

1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)
7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \) и \( A_2 \) в этих проводниках за одно и то же время.
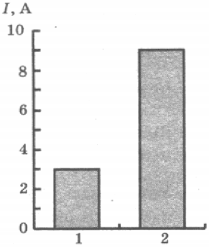

1) \( A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)
8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то
А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.
Верным(-и) является(-ются) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?
1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А
10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?
1) 10000 с
2) 2000 с
3) 10 с
4) 2 с
11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась
12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока
ФОРМУЛЫ
1) \( \frac{q}{t} \)
2) \( qU \)
3) \( \frac{RS}{L} \)
4) \( UI \)
5) \( \frac{U}{I} \)
Часть 2
13. Нагреватель включён последовательно с реостатом сопротивлением 7,5 Ом в сеть с напряжением 220 В. Каково сопротивление нагревателя, если мощность электрического тока в реостате составляет 480 Вт?
Ответы


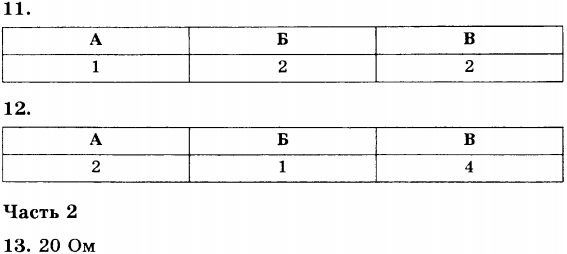

Работа и мощность электрического тока. Закон Джоуля-Ленца
5 (100%) 1 vote| 1. | Закон Джоуля—Ленца — формула | 1 вид — рецептивный | лёгкое | 1 Б. | Проверяется знание формулы, выражающей закон Джоуля—Ленца. |
| 2. | Закон Джоуля—Ленца — определение | 1 вид — рецептивный | лёгкое | 1 Б. | Проверяется знание формулировки закона Джоуля—Ленца. |
| 3. | Закон Джоуля—Ленца — физические величины | 1 вид — рецептивный | лёгкое | 1 Б. | Проверяется знание физических величин, входящих в закон Джоуля—Ленца. |
| 4. | Анализ величин, входящих в закон Джоуля—Ленца. | 2 вид — интерпретация | среднее | 2 Б. | Учащиеся анализируют изменение величины, входящей в закон Джоуля—Ленца, и делают вывод об изменении количества теплоты, которое выделяется в проводнике с током. |
| 5. | Сравнение количества теплоты, выделяемого в последовательно соединённых проводниках | 2 вид — интерпретация | среднее | 1 Б. | Учащиеся делают вывод о количестве теплоты, выделяемом в последовательно соединённых проводниках. |
| 6. | Различные схемы соединения резисторов | 3 вид — анализ | сложное | 2 Б. | Учащиеся вычисляют общее сопротивление участка цепи, а также количество теплоты, выделяющееся на этом участке за некоторое время. |
| 7. | Работа с формулой закона Джоуля—Ленца | 1 вид — рецептивный | лёгкое | 4 Б. | Учащиеся, имея формулу закона Джоуля—Ленца, вычисляют неизвестные физические величины. |
Конспект «Количество теплоты. Удельная теплоёмкость»
«Количество теплоты. Удельная теплоёмкость»
Количество теплоты
Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количествоv теплоты.
Количество теплоты – это изменение внутренней энергии тела в процессе теплопередачи без совершения работы. Количество теплоты обозначают буквой Q.
Работа, внутренняя энергия и количество теплоты измеряются в одних и тех же единицах — джоулях (Дж), как и всякий вид энергии.

В тепловых измерениях в качестве единицы количества теплоты раньше использовалась особая единица энергии — калория (кал), равная количеству теплоты, необходимому для нагревания 1 грамма воды на 1 градус Цельсия (точнее, от 19,5 до 20,5 °С). Данную единицу, в частности, используют в настоящее время при расчетах потребления тепла (тепловой энергии) в многоквартирных домах. Опытным путем установлен механический эквивалент теплоты — соотношение между калорией и джоулем: 1 кал = 4,2 Дж.

При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество тепла требуется ему для нагревания. То же самое и с охлаждением.

Количество теплоты, необходимое для нагревания тела зависит еще и от рода вещества, из которого это тело сделано. Эта зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Удельная теплоёмкость
Удельная теплоёмкость – это физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К). Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой с. Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг °К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Поскольку кол-во теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты Q, необходимое для нагревания тела массой m от температуры t1°С до температуры t2°С, равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
Q = c ∙ m (t2 — t1)
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.

Это конспект по теме «Количество теплоты. Удельная теплоёмкость». Выберите дальнейшие действия:
Закон Джоуля — Ленца — это… Что такое Закон Джоуля — Ленца?
Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1840 году независимо Джеймса Джоуля и Эмилия Ленца.
В словесной формулировке звучит следующим образом[1]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
где w — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[2]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
В математической форме этот закон имеет вид
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
Практическое значение
Снижение потерь энергии
При передаче электроэнергии тепловое действие тока является нежелательным, поскольку ведёт к потерям энергии. Поскольку передаваемая мощность линейно зависит как от напряжения, так и от силы тока, а мощность нагрева зависит от силы тока квадратично, то выгодно повышать напряжение перед передачей электроэнергии, понижая в результате силу тока. Однако, повышение напряжения снижает электробезопасность линий электропередачи.
Для применения высокого напряжения в цепи для сохранения прежней мощности на полезной нагрузке приходится увеличивать сопротивление нагрузки. Подводящие провода и нагрузка соединены последовательно. Сопротивление проводов () можно считать постоянным. А вот сопротивление нагрузки () растёт при выборе более высокого напряжения в сети. Также растёт соотношение сопротивления нагрузки и сопротивления проводов. При последовательном включении сопротивлений (провод — нагрузка — провод) распределение выделяемой мощности () пропорционально сопротивлению подключённых сопротивлений.
Ток в сети для всех сопротивлений постоянен. Следовательно, выполняются соотношение
и для в каждом конкретном случае являются константами. Следовательно, мощность, выделяемая на проводах, обратно пропорциональна сопротивлению нагрузки, то есть уменьшается с ростом напряжения, так как . Откуда следует, что . В каждом конкретном случае величина является константой, следовательно, тепло выделяемое на проводе обратно пропорционально квадрату напряжения на потребителе.
Выбор проводов для цепей
Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при сборке электрических цепей достаточно следовать принятым нормативным документам, которые регламентируют, в частности, выбор сечения проводников.
Электронагревательные приборы
Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.
За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.
Плавкие предохранители
Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

