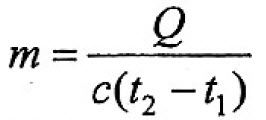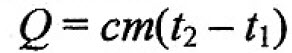Количество теплоты на резисторе формула — MOREREMONTA

В элек­три­че­ской схеме, по­ка­зан­ной на ри­сун­ке, ключ К за­мкнут.

Заряд кон­ден­са­то­ра ЭДС ба­та­рей­ки её внут­рен­нее со­про­тив­ле­ние со­про­тив­ле­ние ре­зи­сто­ра Най­ди­те ко­ли­че­ство теп­ло­ты, ко­то­рое вы­де­ля­ет­ся на ре­зи­сто­ре после раз­мы­ка­ния ключа К в ре­зуль­та­те раз­ря­да кон­ден­са­то­ра. По­те­ря­ми на из­лу­че­ние пре­не­бречь.

Ко­ли­че­ство теп­ло­ты, вы­де­ля­ю­ще­е­ся на ре­зи­сто­ре после раз­мы­ка­ния ключа:

На­пря­же­ние на кон­ден­са­то­ре равно па­де­нию на­пря­же­ния на ре­зи­сто­ре. С уче­том за­ко­на Ома для пол­ной цепи:

Ком­би­ни­руя эти фор­му­лы, на­хо­дим:

Ответ:

полностью одобряю ваш метод, но нельзя ли решить более «простым» способом? Не сочтите меня за глупца.

Смеяться не буду 🙂 Все в порядке.

А теперь о Вашем решении. Что тут могу сказать. Так решать, конечно, нельзя, и получившийся у Вас ответ, отличный от приведенного в решении, — одно из тому подтверждений. Не буду комментировать все, скажу только, что формулу

здесь использовать «в лоб» нельзя, так как через конденсатор будет течь не постоянный ток, а уменьшающийся по величине: чем больше заряд на конденсаторе, тем быстрее он стремится разрядиться. Так что закон сохранения энергии — наиболее простой и верный способ решения.

Ежели Вы настаиваете на на применении своей формулы, то тут потребуется большие знания из математического анализа: производные, интегралы, дифференциальные уравнения. Если интересно, приведу такое решение (но особого смысла в нем разбираться — нет, так как такие знания за рамками того, что проверяется на ЕГЭ). Кроме того, все равно получится, что нужно просто посчитать начальную энергию конденсатора.

Сложное решение этой задачи 🙂

Определим зависимость тока, текущего через резистор от времени. Так как конденсатор подключен к резистору параллельно, напряжения на них совпадают в любой момент времени: . По закону Ома, напряжение на резисторе пропорционально величине текущего через него тока: . Напряжение на конденсаторе связано с зарядом на нем соотношением:

. Пусть за небольшой интервал времени заряд на конденсаторе изменился на (так как конденсатор разряжается ). Тогда через резистор за это время протек заряд . Следовательно сила тока равна . Скомбинировав все равенства и переходя к бесконечно малому интервалу времени, получаем дифференциальное уравнение на величину заряда конденсатора:

.

Решая это уравнение и используя, что в начальный момент времени заряд на конденсаторе равен , имеем: . То есть, математически конденсатор разряжается бесконечно долго.

Значит ток через конденсатор равен

.

Определим теперь тепловую мощность, выделяющуюся на резисторе:

.

Мощность уменьшается со временем. Для того, чтобы найти полное тепло необходимо просуммировать по всему времени разрядки, то есть взять интеграл:

.

Вот и она, начальная энергия конденсатора 🙂

• Главная
• Обучение
• Предварительный просмотр

• Мероприятия / ВИШР
• Обучение
• Тренажер ЕГЭ
• Учебные пособия
• Игры
• 120 лет ТПУ. Викторина онлайн
• Университетские субботы
• Высшая инженерная школа России

Физика

3.2.9.1. Тепловая мощность, выделяемая на резисторе

Тепловая мощность, выделяемая на резисторе

Электрический ток, проходящий по проводнику, нагревает его. Это объясняется тем, что свободные электроны, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества и передают им свою энергию. В результате работы электрического тока внутренняя энергия вещества увеличивается, повышается его температура. Нагретый проводник передает свою энергию окружающим телам. Если проводник не движется, то вся энергия электрического тока переходит во внутреннею энергию проводника. Работа тока определяется

Количество теплоты, выделяемое на резисторе, обозначим через Q Так как Q = A, то

или используя закон Ома (U = I*R) , получим

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени.

Эта формулировка называется законом Джоуля — Ленца

Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем [1] .

Содержание

Определения [ править | править код ]

В словесной формулировке звучит следующим образом [2] :

Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.

Математически может быть выражен в следующей форме:

w = j → ⋅ E → = σ E 2 , <displaystyle w=<vec >cdot <vec >=sigma E^<2>,>

где w <displaystyle w> — мощность выделения тепла в единице объёма, j → <displaystyle <vec >> — плотность электрического тока, E → <displaystyle <vec >> — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах [3] :

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.

В интегральной форме этот закон имеет вид

d Q = I 2 R d t , <displaystyle dQ=I^<2>Rdt,> Q = ∫ t 1 t 2 I 2 R d t , <displaystyle Q=int limits _>^>I^<2>Rdt,> 2>1>

где d Q <displaystyle dQ> — количество теплоты, выделяемое за промежуток времени d t <displaystyle dt> , I <displaystyle I> — сила тока, R <displaystyle R> — сопротивление, Q <displaystyle Q> — полное количество теплоты, выделенное за промежуток времени от t 1 <displaystyle t_<1>> до t 2 <displaystyle t_<2>> . В случае постоянных силы тока и сопротивления:

Q = I 2 R t . <displaystyle Q=I^<2>Rt.>

Применяя закон Ома, можно получить следующие эквивалентные формулы:

Q = U 2 t / R = I U t . <displaystyle Q=U^<2>t/R =IUt.>

Практическое значение [ править | править код ]

Снижение потерь энергии [ править | править код ]

При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно, значит ток в сети I <displaystyle I> на проводах и нагрузке одинаков. Мощность нагрузки и сопротивление проводов не должны зависеть от выбора напряжения источника. Выделяемая на проводах и на нагрузке мощность определяется следующими формулами

Q w = R w ⋅ I 2 , <displaystyle Q_=R_cdot I^<2>,> Q c = U c ⋅ I . <displaystyle Q_=U_cdot I.>

Откуда следует, что Q w = R w ⋅ Q c 2 / U c 2 <displaystyle Q_=R_cdot Q_^<2>/U_^<2>> . Так как в каждом конкретном случае мощность нагрузки и сопротивление проводов остаются неизменными и выражение R w ⋅ Q c 2 <displaystyle R_cdot Q_^<2>> является константой, то тепло выделяемое на проводе обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.

Выбор проводов для цепей [ править | править код ]

Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.

Электронагревательные приборы [ править | править код ]

Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.

За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.

Плавкие предохранители [ править | править код ]

Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

Расчёт количества теплоты на резисторах

Задача по теме «Законы постоянного тока».  Задача может быть интересна учащимся 10-х классов и выпускникам для подготовки к ЕГЭ. Кстати, подобного рода задача была на ЕГЭ в части 1 с несколько иным вопросом (необходимо было  найти отношение количеств теплоты, выделяющихся на резисторах).

На каком из резисторов выделится наибольшее (наименьшее) количество теплоты? R1 = R4 = 4 Ом, R2 = 3 Ом, R3 = 2Ом. Дать решение. Чтобы ответить на вопрос задачи, необходимо сравнить количество теплоты, выделяющееся на каждом их резисторов. Для этого воспользуемся формулой закона Джоуля — Ленца.То есть основной задачей будет являться определение силы тока (или сравнение), протекающей через каждый резистор.

Согласно законам последовательного соединения, сила тока, протекающая через резисторы R₁ и R₂, и R₃ и R₄, одинаковая.Чтобы определить силу тока в верхней  и  в нижней ветвях, воспользуемся законом параллельного соединения, согласно которому, напряжение на этих ветвях одинаковое.Расписывая напряжение на нижней и верхней ветвях по закону Ома для участка цепи, имеем:Подставляя численные значения сопротивлений резисторов, получаем:То есть получаем соотношение между токами, протекающими в верхней и в нижней ветви:Определив силу тока через каждый из этих резисторов, определяем количество теплоты, выделяющееся на каждом из резисторов. Сравнивая числовые коэффициенты, приходим к выводу, что максимальное количество теплоты выделится на четвёртом резисторе, а минимальное количество теплоты — на втором.

Вы можете оставить комментарий, или поставить трэкбек со своего сайта.

Написать комментарий

Закон Джоуля-Ленца: история возникновения :: SYL.ru

Довольно трудно представить жизнь современного человека без электричества. Оно стало одним из главных и самых ценных атрибутов современного существования. Фактически любой человек, который когда-либо работал с электричеством, знает, что при прохождении по проводам тока у них есть свойство нагреваться. Отчего же это зависит?

Что такое ток

Ток – это упорядоченное движение заряженных частиц, которые называются электронами. И если ток протекает по проводнику, то в нём начинают происходить разные физические процессы, а именно сталкиваются электроны с молекулами.

Молекулы бывают нейтральные или те, которые потеряли свою отрицательно заряженную частицу. В результате столкновений или электроны могут становиться нейтральными молекулами, или при этом выбивается из другой такой же молекулы электрон, образовавший положительно заряженный ион. Во время этих столкновений расходуется кинетическая энергия заряженных частиц. Именно эта энергия и становится теплом.

На тепловой нагрев проводника может влиять и сопротивление. Например, можно взять определённое тело и тащить его по земле. Земля в этом случае — сопротивление. Что же с ним будет? Правильно, между телом и поверхностью будет происходить сила трения, которая, в свою очередь, нагревает тело. Ток в этом случае ведёт себя точно так же.

Зависимость

И, внимая все вышеупомянутое, учёным удалось определить эту зависимость между силой тока, сопротивлением и количеством тепла. Эта зависимость носит название закон Джоуля-Ленца, формула которого известна всем физикам. В 1832—1833 годах русским физиком Эмилием Ленцем было обнаружено, что при тепловом воздействии на металлические проводники их проводимость капитально изменялась. Это фактически усложняло работу учёного и мешало рассчитывать электрические цепи.

Тогда же молодому учёному пришла в голову мысль о том, что, возможно, существует какая-то зависимость между силой тока и температурой проводника. Но как быть? В то время отсутствовали точные электрические приборы, позволяющие измерить силу тока, сопротивление, не было даже источника стабильного ЭДС. Ленца это не остановило, он решил провести опыт.

Опыты русского физика

Суть этого опыта была настолько проста, как и все гениальное, что его может повторить даже школьник. Учёный сконструировал специальный прибор, который служил для измерения количества тепла, выделяемого проводником. Этим прибором оказался обычный сосуд, вовнутрь которого Ленц заливал раствор разбавленного спирта и ставил проводник – платиновую проволоку, на которую подавался электрический ток.

После того как прибор был создан, учёный начал проводить опыты. Он измерял точное количество времени, необходимое для того, чтобы спирт в сосуде был нагрет до 10 ^оС. На это было потрачено много не только месяцев, но и лет. И в 1843 году, спустя 10 лет, был опубликован закон, суть которого заключалась в том, что нагревание проводника током пропорционально квадрату служащего для нагревания тока.

Джоуль и Ленц

Но не тут-то было! Оказывается, несколько лет назад английский физик Джеймс Прескотт Джоуль проводил аналогичные опыты, и уже опубликовал свои наблюдения. Как быть? Ленц не сдался и внимательно изучил работу Джоуля и пришёл к выводу, что, пусть они и проводили одинаковые эксперименты, опыты Ленца были гораздо точнее. В связи с чем научное сообщество добавило к работе Джоуля поправки Ленца и этот закон стал называться как закон Джоуля-Ленца. Математическая формулировка закона выглядит таким образом:

Q = I*U*t, где:

• I – сила тока, А;
• U – напряжение, В;
• t – время, которое ток затрачивает на прохождение проводника, с.

Сам же закон звучит так: количество тепловой энергии, выделяемой в проводнике, через который течёт электрический ток, равно произведению силы тока, напряжения и времени прохождения тока через проводник.

Закон Ома

Однако будет ли всегда верным это утверждение? Можно попробовать вывести его, используя закон Ома. Судя по нему U = I*R, где R — сопротивление, Ом.

Учитывая закон Ома, можно подставить значение в формулу Q = I*U*t = I²*R*t. Из этого можно сделать вывод, что количество теплоты напрямую зависит и от сопротивления проводника. Также для закона Джоуля-Ленца будет справедливо и это утверждение: I = Q = I*U*t.

Все три формулы будут верны, однако Q = I²*R*t будет верной для любых ситуаций. Две другие тоже являются правильными, однако при определённых обстоятельствах.

Проводники

Теперь о проводниках. Изначально в своих опытах Джоуль и Ленц использовали платиновые проволоки, как и было упомянуто выше. Во всех похожих экспериментах учёные того времени использовали в основном металлические проводники, так как они были довольно недорогими и стабильными. Не удивительно, ведь до сих пор металлические проводники – основной тип проводников, в связи с чем изначально считалось, что закон Джоуля-Ленца был применим только к ним. Однако чуть позже было обнаружено, что этот закон применим не только к металлическим проводникам. Он верен для любых из них. Сами проводники по классификации можно разделить на:

• Металлические (медь, железо, серебро и т.д.). Главную роль в них играют отрицательно заряженные частицы (электроны), которые протекают по проводнику.
• Жидкие. В них же за движение зарядов отвечают ионы – это атомы, в которых или слишком много, или слишком мало электронов.
• Газообразные. В отличие от своих коллег, в таких проводниках ток определяется движением как ионов, так и электронов.

И несмотря на различия, в любом случае при увеличении силы тока или сопротивления увеличится и количество тепла.

Применение закона другими физиками

Открытие закона Джоуля-Ленца сулило огромные перспективы. Ведь, по сути, этот закон позволил создавать своего рода разные электронагревательные приборы и элементы. Например, чуть позже после открытия закона учёные заметили, что при нагревании определённых элементов они начинают светиться. Они захотели поэкспериментировать с ними, используя разные проводники, и в 1874 году русский инженер Александр Николаевич Лодыгин изобрёл современную лампу накаливания, нить которой была сделана из вольфрама.

Применяется закон Джоуля-Ленца и в электротехнике – например, при создании плавких предохранителей. Плавкий предохранитель – это некий элемент электрический цепи, конструкция которого сделана так, что при протекании по нему тока выше допустимого значения (например, при коротком замыкании) он перегревается, плавится и размыкает силовую цепь. Даже обычный электрический чайник или микроволновая печь, которая есть фактически у каждого, работает согласно этому закону.

Заключение

Довольно трудно определить вклад этих учёных в современную электронику и электротехнику, но одно можно сказать точно – появление закона Джоуля-Ленца перевернуло представление людей об электричестве и дало более конкретные знания о том, что такое электрическое поле в проводнике с током.

Без сомнения, открытый этими великими учеными-физиками закон стал определяющей ступенью во всей науке, именно благодаря этому открытию впоследствии были совершены другие более или менее грандиозные достижения других ученых. Вся наука представляет собой тесное переплетение открытий, каких-то разрешенных и неразрешенных задач. Рассмотренный в этой статье закон определенным образом повлиял на многие исследования и оставил неизгладимый и вполне отчетливый след в науке.

ФИЗИКА: Задачи на количество теплоты — Ответы и решения

Задачи на количество теплоты с решениями

Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».

Название величины	Обозначение	Единица измерения	Формула
Масса	m	кг
Температура	t	°С
Удельная теплоемкость	c	Дж/кг•°С
Количество теплоты	Q	Дж

1 г = 0,001 кг;     1 т = 1000 кг;    1 кДж = 1000 Дж;    1 МДж = 1000000 Дж

---

---

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.  В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?

При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.  Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.  Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

---

Задача № 4.  В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

---

Задача № 5.  На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

---

Задача № 6.  По графику определите удельную теплоёмкость образца, если его масса 50 г.

---

Задача № 7.  Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

---

Задача № 8.  Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?

---

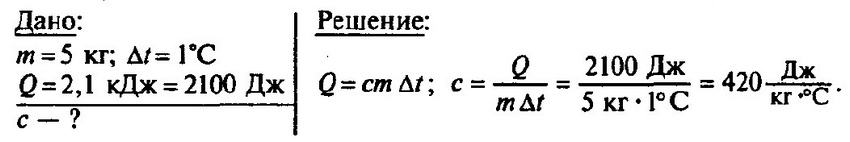
Задача № 9.  Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

---

Задача № 10.  Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

---

Задача № 11.  а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух? 
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

---

Задача № 12.   ОГЭ  Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой m_в = 300 г, а температура t_в = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды с_в = 4200 Дж/(кг К).

---

Краткая теория для решения Задачи на количество теплоты.

---

Конспект урока «Задачи на количество теплоты».

Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»

Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».

 

Количество теплоты и тепловая мощность. Расчет в Excel.

Опубликовано 13 Окт 2013
Рубрика: Теплотехника | 82 комментария

Человечеству известно немного видов энергии – механическая энергия (кинетическая и потенциальная), внутренняя энергия (тепловая), энергия полей (гравитационная, электромагнитная и ядерная), химическая. Отдельно стоит выделить энергию взрыва,…

…энергию вакуума и еще существующую только в теории – темную энергию. В этой статье, первой в рубрике «Теплотехника», я попытаюсь на простом и доступном языке, используя практический пример, рассказать о важнейшем виде энергии в жизни людей — о

тепловой энергии и о рождающей ее во времени тепловой мощности.

Несколько слов для понимания места теплотехники, как раздела науки о получении, передаче и применении тепловой энергии. Современная теплотехника выделилась из общей термодинамики, которая в свою очередь является одним из разделов физики. Термодинамика – это дословно «теплый» плюс «силовой». Таким образом, термодинамика – это наука об «изменении температуры» системы.

Воздействие на систему извне, при котором изменяется ее внутренняя энергия, может являться результатом теплообмена. Тепловая энергия, которая приобретается или теряется системой в результате такого взаимодействия с окружающей средой, называется

количеством теплоты и измеряется в системе СИ в Джоулях.

Если вы не инженер-теплотехник, и ежедневно не занимаетесь теплотехническими вопросами, то вам, столкнувшись с ними, иногда без опыта бывает очень трудно быстро в них разобраться. Трудно без наличия опыта представить даже размерность искомых значений количества теплоты и тепловой мощности. Сколько Джоулей энергии необходимо чтобы нагреть 1000 метров кубических воздуха от температуры -37˚С до +18˚С?.. Какая нужна мощность источника тепла, чтобы сделать это за 1 час?.. На эти не самые сложные вопросы способны сегодня ответить «сходу» далеко не все инженеры. Иногда специалисты даже помнят формулы, но применить их на практике могут лишь единицы!

Прочитав до конца эту статью, вы сможете легко решать реальные производственные и бытовые задачи, связанные с нагревом и охлаждением различных материалов.  Понимание физической сути процессов теплопередачи и знание простых основных формул – это главные блоки в фундаменте знаний по теплотехнике!

Количество теплоты при различных физических процессах.

Большинство известных веществ могут при разных температуре и давлении находиться в твердом, жидком, газообразном или плазменном состояниях. Переход из одного агрегатного состояния в другое происходит при постоянной температуре (при условии, что не меняются давление и другие параметры окружающей среды) и сопровождается поглощением или выделением тепловой энергии. Не смотря на то, что во Вселенной 99% вещества находится в состоянии плазмы, мы в этой статье не будем рассматривать это агрегатное состояние.

Рассмотрим график, представленный на рисунке. На нем изображена зависимость температуры вещества Т от количества теплоты Q, подведенного к некой закрытой системе, содержащей определенную массу какого-то конкретного вещества.

1. Твердое тело, имеющее температуру T1, нагреваем до температуры Tпл, затрачивая на этот процесс количество теплоты равное Q1.

2. Далее начинается процесс плавления, который происходит при постоянной температуре Тпл (температуре плавления). Для расплавления всей массы твердого тела необходимо затратить тепловой энергии в количестве Q2— Q1.

3. Далее жидкость, получившаяся в результате плавления твердого тела, нагреваем до температуры кипения (газообразования) Ткп, затрачивая на это количество теплоты равное Q3—Q2.

4. Теперь при неизменной температуре кипения Ткп жидкость кипит и испаряется, превращаясь в газ. Для перехода всей массы жидкости в газ необходимо затратить тепловую энергию в количестве Q4—Q3.

5. На последнем этапе происходит нагрев газа от температуры Ткп до некоторой температуры Т2. При этом затраты количества теплоты составят Q5—Q4. (Если нагреем газ до температуры ионизации, то газ превратится в плазму.)

Таким образом, нагревая исходное твердое тело от температуры Т1 до температуры Т2 мы затратили тепловую энергию в количестве Q5, переводя вещество через три агрегатных состояния.

Двигаясь в обратном направлении, мы отведем от вещества то же количество тепла Q5, пройдя этапы конденсации, кристаллизации и остывания от температуры Т2 до  температуры Т1. Разумеется, мы рассматриваем замкнутую систему без потерь энергии во внешнюю среду.

Заметим, что возможен переход из твердого состояния в газообразное состояние, минуя жидкую фазу. Такой процесс именуется возгонкой, а обратный ему процесс – десублимацией.

Итак, уяснили, что процессы переходов между агрегатными состояниями вещества характеризуются потреблением энергии при неизменной температуре. При нагреве вещества, находящегося в одном неизменном агрегатном состоянии, повышается температура и также расходуется тепловая энергия.

Главные формулы теплопередачи.

Формулы очень просты.

Количество теплоты Q в Дж рассчитывается по формулам:

1. Со стороны потребления тепла, то есть со стороны нагрузки:

1.1. При нагревании (охлаждении):

Q=m*c*(Т2-Т1)

Здесь и далее:

m – масса вещества в кг

с – удельная теплоемкость вещества в Дж/(кг*К)

1.2. При плавлении (замерзании):

Q=m*λ

λ – удельная теплота плавления и кристаллизации вещества в Дж/кг

1.3. При кипении, испарении (конденсации):

Q=m*r

r – удельная теплота газообразования и конденсации вещества в Дж/кг

2. Со стороны производства тепла, то есть со стороны источника:

2.1. При сгорании топлива:

Q=m*q

q – удельная теплота сгорания топлива в Дж/кг

2.2. При превращении электроэнергии в тепловую энергию (закон Джоуля — Ленца):

Q=t*I*U=t*R*I^2=(t/R)*U^2

t – время в с

I – действующее значение тока в А

U – действующее значение напряжения в В

R – сопротивление нагрузки в Ом

Делаем вывод – количество теплоты прямо пропорционально массе вещества при всех фазовых превращениях и при нагреве дополнительно прямо пропорционально разности температур. Коэффициенты пропорциональности (c, λ, r, q) для каждого вещества имеют свои значения и определены опытным путем (берутся из справочников).

Тепловая мощность N в Вт – это количество теплоты переданное системе за определенное время:

N=Q/t

Чем быстрее мы хотим нагреть тело до определенной температуры, тем большей мощности должен быть источник тепловой энергии – все логично.

Расчет в Excel прикладной задачи.

В жизни бывает часто необходимо сделать быстрый оценочный расчет, чтобы понять – имеет ли смысл продолжать изучение темы, делая проект и развернутые точные трудоемкие расчеты. Сделав за несколько минут расчет даже с точностью ±30%, можно принять важное управленческое решение, которое будет в 100 раз более дешевым и в 1000 раз более оперативным и в итоге в 100000 раз более эффективным, чем выполнение точного расчета в течение недели, а то и месяца, группой дорогостоящих специалистов…

Условия задачи:

В помещение цеха подготовки металлопроката размерами 24м х 15м х 7м завозим со склада на улице металлопрокат в количестве 3т. На металлопрокате есть лед общей массой 20кг. На улице -37˚С. Какое количество теплоты необходимо, чтобы нагреть металл до +18˚С; нагреть лед, растопить его и нагреть воду до +18˚С; нагреть весь объем воздуха в помещении, если предположить, что до этого отопление было полностью отключено? Какую мощность должна иметь система отопления, если все вышесказанное необходимо выполнить за 1час? (Очень жесткие и почти не реальные условия – особенно касающиеся воздуха!)

Расчет выполним в программе MS Excel или в программе OOo Calc.

С цветовым форматированием ячеек и шрифтов ознакомьтесь на странице «О блоге». 

Исходные данные:

1. Названия веществ пишем:

в ячейку D3: Сталь

в ячейку E3: Лед

в ячейку F3: Лед/вода

в ячейку G3: Вода

в ячейку G3: Воздух

2. Названия процессов заносим:

в ячейки D4, E4, G4, G4: нагрев

в ячейку F4: таяние

3. Удельную теплоемкость веществ c в Дж/(кг*К) пишем  для стали, льда, воды и воздуха соответственно

в ячейку D5: 460

в ячейку E5: 2110

в ячейку G5: 4190

в ячейку H5: 1005

4. Удельную теплоту плавления  льда λ в Дж/кг вписываем

в ячейку F6: 330000

5. Массу веществ m в кг вписываем соответственно для стали и льда

в ячейку D7: 3000

в ячейку E7: 20

Так как при превращении льда в воду масса не изменяется, то

в ячейках F7 и G7: =E7=20

Массу воздуха находим произведением объема помещения на удельный вес

в ячейке H7: =24*15*7*1,23=3100

6. Время процессов t в мин пишем только один раз для стали

в ячейку D8: 60

Значения времени для нагрева льда, его плавления и нагрева получившейся воды рассчитываются из условия, что все эти три процесса должны уложиться в сумме за такое же время, какое отведено на нагрев металла. Считываем соответственно

в ячейке E8: =E12/(($E$12+$F$12+$G$12)/D8)=9,7

в ячейке F8: =F12/(($E$12+$F$12+$G$12)/D8)=41,0

в ячейке G8: =G12/(($E$12+$F$12+$G$12)/D8)=9,4

Воздух также должен прогреться за это же самое отведенное время, читаем

в ячейке H8: =D8=60,0

7. Начальную температуру всех веществ T1 в ˚C заносим

в ячейку D9: -37

в ячейку E9: -37

в ячейку F9: 0

в ячейку G9: 0

в ячейку H9: -37

8. Конечную температуру всех веществ T2 в ˚C заносим

в ячейку D10: 18

в ячейку E10: 0

в ячейку F10: 0

в ячейку G10: 18

в ячейку h20: 18

Думаю, вопросов по п.7 и п.8 быть недолжно.

Результаты расчетов:

9. Количество теплоты Q в КДж, необходимое для каждого из процессов рассчитываем

для нагрева стали в ячейке D12: =D7*D5*(D10-D9)/1000=75900

для нагрева льда в ячейке E12: =E7*E5*(E10-E9)/1000= 1561

для плавления льда в ячейке F12: =F7*F6/1000= 6600

для нагрева воды в ячейке G12: =G7*G5*(G10-G9)/1000= 1508

для нагрева воздуха в ячейке h22: =H7*H5*(h20-H9)/1000= 171330

Общее количество необходимой для всех процессов тепловой энергии считываем

в объединенной ячейке D13E13F13G13h23: =СУММ(D12:h22) = 256900

В ячейках D14, E14, F14, G14, h24,  и объединенной ячейке D15E15F15G15h25 количество теплоты приведено в дугой единице измерения – в ГКал (в гигакалориях).

10. Тепловая мощность N в КВт, необходимая для каждого из процессов рассчитывается

для нагрева стали в ячейке D16: =D12/(D8*60)=21,083

для нагрева льда в ячейке E16: =E12/(E8*60)= 2,686

для плавления льда в ячейке F16: =F12/(F8*60)= 2,686

для нагрева воды в ячейке G16: =G12/(G8*60)= 2,686

для нагрева воздуха в ячейке h26: =h22/(H8*60)= 47,592

Суммарная тепловая мощность необходимая для выполнения всех процессов за время t рассчитывается

в объединенной ячейке D17E17F17G17h27: =D13/(D8*60) = 71,361

В ячейках D18, E18, F18, G18, h28,  и объединенной ячейке D19E19F19G19h29 тепловая мощность приведена в дугой единице измерения – в Гкал/час.

На этом расчет в Excel завершен.

Выводы:

Обратите внимание, что для нагрева воздуха необходимо более чем в два раза больше затратить энергии, чем для нагрева такой же массы стали.

При нагреве воды затраты энергии в два раза больше, чем при нагреве льда. Процесс плавления многократно больше потребляет энергии, чем процесс нагрева (при небольшой разности температур).

Нагрев воды в десять раз затрачивает больше тепловой энергии, чем нагрев стали и в четыре раза больше, чем нагрев воздуха.

Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.

После ввода адреса своей электронной почты и нажатия на кнопку «Получать анонсы статей» НЕ ЗАБУДЬТЕ  ПОДТВЕРДИТЬ ПОДПИСКУ кликом по ссылке в письме, которое тут же придет к вам на указанную почту (иногда — в папку «Спам»)!

Мы вспомнили понятия «количество теплоты» и «тепловая мощность», рассмотрели фундаментальные формулы теплопередачи, разобрали практический пример. Надеюсь, что мой язык был прост, понятен и интересен.

Жду вопросы и комментарии на статью!

Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.

Ссылка на скачивание файла: raschet-teplovoy-moshchnosti (xls 19,5KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Формула количества теплоты в физике

Определение и формула количества теплоты

Внутреннюю энергию термодинамической системы можно изменить двумя способами:

1. совершая над системой работу,
2. при помощи теплового взаимодействия.

Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем, что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии, которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.

Определение

Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой). Обозначается теплота, обычно буквой Q.

Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики. Говорят, что теплота – это энергия в форме молекулярного движения.

Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.

Формула расчета теплоты при изменении температуры

Элементарное количество теплоты обозначим как . Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.

Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:

где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:

где – удельная теплоемкость тела, m – масса тела, — молярная теплоемкость, – молярная масса вещества, – число молей вещества.

Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты (), которое получа

Теплота — Википедия

Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой^[1]. Теплота — это одна из основных термодинамических величин в классической феноменологической термодинамике. Количество теплоты входит в стандартные математические формулировки первого и второго начал термодинамики.

Для изменения внутренней энергии системы посредством теплообмена также необходимо совершить работу. Однако это не механическая работа, которая связана с перемещением границы макроскопической системы. На микроскопическом уровне эта работа осуществляется силами, действующими между молекулами на границе контакта более нагретого тела с менее нагретым. Фактически при теплообмене энергия передаётся посредством электромагнитного взаимодействия при столкновениях молекул. Поэтому с точки зрения молекулярно-кинетической теории различие между работой и теплотой проявляется только в том, что совершение механической работы требует упорядоченного движения молекул на макроскопических масштабах, а передача энергии от более нагретого тела менее нагретому этого не требует.

Энергия может также передаваться излучением от одного тела к другому и без их непосредственного контакта.

Количество теплоты не является функцией состояния, и количество теплоты, полученное системой в каком-либо процессе, зависит от способа, которым она была переведена из начального состояния в конечное.

Единица измерения в Международной системе единиц (СИ) — джоуль. Как единица измерения теплоты используется также калория. В Российской Федерации калория допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность»^[2].

Количество теплоты входит в математическую формулировку первого начала термодинамики, которую можно записать как Q=A+ΔU{\displaystyle Q=A+\Delta U}. Здесь ΔU{\displaystyle \Delta U} — изменение внутренней энергии системы, Q{\displaystyle Q} — количество теплоты, переданное системе, а A{\displaystyle A} — работа, совершённая системой. Однако определение теплоты должно указывать способ её измерения безотносительно к первому началу. Так как теплота — это энергия переданная в ходе теплообмена, для измерения количества теплоты необходимо пробное калориметрическое тело. По изменению внутренней энергии пробного тела можно будет судить о количестве теплоты, переданном от системы пробному телу. Без использования пробного тела первое начало теряет смысл содержательного закона и превращается в бесполезное для расчётов определение количества теплоты.

Пусть в системе, состоящей из двух тел X{\displaystyle X} и Y{\displaystyle Y}, тело Y{\displaystyle Y} (пробное) заключено в жёсткую адиабатическую оболочку. Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией (то есть теплотой) с телом X{\displaystyle X}. Предположим, что тело X{\displaystyle X} также почти полностью заключено в адиабатическую, но не жёсткую оболочку, так что оно может совершать механическую работу, но обмениваться теплотой может лишь с Y{\displaystyle Y}. Количеством теплоты, переданным телу X{\displaystyle X} в некотором процессе, называется величина QX=−ΔUY{\displaystyle Q_{X}=-\Delta U_{Y}}, где ΔUY{\displaystyle \Delta U_{Y}} — изменение внутренней энергии тела Y{\displaystyle Y}. Согласно закону сохранения энергии, полная работа, выполненная системой, равна убыли полной внутренней энергии системы двух тел: A=−ΔUx−ΔUy{\displaystyle A=-\Delta U_{x}-\Delta U_{y}}, где A{\displaystyle A} — макроскопическая работа, совершенная телом X{\displaystyle X}, что позволяет записать это соотношение в форме первого начала термодинамики:Q=A+ΔUx{\displaystyle Q=A+\Delta U_{x}}.

Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Y{\displaystyle Y} и способа теплообмена между телами. При таком определении количества теплоты первое начало становится содержательным законом, допускающим экспериментальную проверку, так как все три величины, входящие в выражение для первого начала, могут быть измерены независимо^[3].

Предположим, что рассматриваемое тело может обмениваться теплотой лишь с N{\displaystyle N} бесконечными тепловыми резервуарами, внутренняя энергия которых столь велика, что при рассматриваемом процессе температура каждого остаётся строго постоянной. Предположим, что над телом был совершён произвольный круговой процесс, то есть по окончании процесса оно находится абсолютно в том же состоянии, что и в начале. Пусть при этом за весь процесс оно заимствовало из i-го резервуара, находящегося при температуре Ti{\displaystyle T_{i}}, количество теплоты Qi{\displaystyle Q_{i}}. Тогда верно следующее неравенство Клаузиуса:

∘∑i=1NQiTi⩽0.{\displaystyle \circ \sum _{i=1}^{N}{\frac {Q_{i}}{T_{i}}}\leqslant 0.}

Здесь ∘{\displaystyle \circ } обозначает круговой процесс. В общем случае теплообмена со средой переменной температуры неравенство принимает вид

∮⁡δQ(T)T⩽0.{\displaystyle \oint {\frac {\delta Q(T)}{T}}\leqslant 0.}

Здесь δQ(T){\displaystyle \delta Q(T)} — количество теплоты, переданное участком среды с (постоянной) температурой T{\displaystyle T}. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство. Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой

S=∫δQ(T)T,{\displaystyle S=\int {\frac {\delta Q(T)}{T}},}

dS=δQT.{\displaystyle dS={\frac {\delta Q}{T}}.}

Здесь T{\displaystyle T} — это абсолютная температура внешнего теплового резервуара. В этом смысле 1T{\displaystyle {\frac {1}{T}}} является интегрирующим множителем для количества теплоты, умножением на который получается полный дифференциал функции состояния.

Для неквазистатических процессов такое определение энтропии не работает. Например, при адиабатическом расширении газа в пустоту

∫δQ(T)T=0,{\displaystyle \int {\frac {\delta Q(T)}{T}}=0,}

однако энтропия при этом возрастает, в чём легко убедиться, переведя систему в начальное состояние квазистатически и воспользовавшись неравенством Клаузиуса. Кроме того, энтропия (в указанном смысле) не определена для неравновесных состояний системы, хотя во многих случаях систему можно считать локально равновесной и обладающей некоторым распределением энтропии.

Внутренняя энергия системы, в которой возможны фазовые переходы или химические реакции, может изменяться и без изменения температуры. Например, энергия, передаваемая в систему, где жидкая вода находится в равновесии со льдом при нуле градусов Цельсия, расходуется на плавление льда, но температура при этом остаётся постоянной, пока весь лёд не превратится в воду. Такой способ передачи энергии традиционно называется «скрытой» или изотермической теплотой^[4] (англ. latent heat), в отличие от «явной», «ощущаемой» или неизотермической теплоты (англ. sensible heat), под которой подразумевается процесс передачи энергии в систему, в результате которого изменяется лишь температура системы, но не её состав.

Энергия, необходимая для фазового перехода единицы массы вещества, называется удельной теплотой фазового превращения^[5]. В соответствии с физическим процессом, имеющим место при фазовом превращении, могут выделять теплоту плавления, теплоту испарения, теплоту сублимации (возгонки), теплоту перекристаллизации и т. д. Фазовые превращения идут со скачкообразным изменением энтропии, что сопровождается выделением или поглощением тепла, несмотря на постоянство температуры.

О терминах «теплота», «количество теплоты», «тепловая энергия»[править | править код]

Многие понятия термодинамики возникли в связи с устаревшей теорией теплорода, которая сошла со сцены после выяснения молекулярно-кинетических основ термодинамики. С тех пор они используются и в научном, и в повседневном языке. Хотя в строгом смысле теплота представляет собой один из способов передачи энергии, и физический смысл имеет лишь количество энергии, переданное системе, слово «тепло-» входит в такие устоявшиеся научные понятия, как поток тепла, теплоёмкость, теплота фазового перехода, теплота химической реакции, теплопроводность и пр. Поэтому там, где такое словоупотребление не вводит в заблуждение, понятия «теплота» и «количество теплоты» синонимичны^[6]. Однако этими терминами можно пользоваться только при условии, что им дано точное определение, не связанное с представлениями теории теплорода, и ни в коем случае «количество теплоты» нельзя относить к числу первоначальных понятий, не требующих определения^[7]. Поэтому некоторые авторы уточняют, что во избежание ошибок теории теплорода под понятием «теплота» следует понимать именно способ передачи энергии, а количество переданной этим способом энергии обозначают понятием «количество теплоты»^[8]. Рекомендуется избегать такого термина, как «тепловая энергия», который по смыслу совпадает с внутренней энергией^[9].

Выработка энергопредприятиями тепловой и электрической энергии[править | править код]

В связи с зависимостью выработки электроэнергии от выработки тепла паросиловыми установками выделяют несколько видов выработки тепла и электроэнергии.

1. Раздельная выработка тепла и электроэнергии.
2. Комбинированная выработка тепла и электроэнергии.

Последний тип получения тепловой и электроэнергии является основой теплофикации, и характеризуется как совершенный метод производства энергии.^[10]

1. ↑ Сивухин, 2005, с. 57.
2. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Утверждено Постановлением Правительства РФ от 31 октября 2009 г. № 879. (неопр.) (недоступная ссылка). Дата обращения 16 февраля 2014. Архивировано 2 ноября 2013 года.
3. ↑ Сивухин, 2005, с. 58.
4. ↑ Путилов, 1971, с. 49.
5. ↑ Сивухин, 2005, с. 442.
6. ↑ Теплота / Мякишев Г. Я. // Струнино — Тихорецк. — М. : Советская энциклопедия, 1976. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 25).
7. ↑ Сивухин, 2005, с. 13.
8. ↑ Базаров, 1991, с. 25.
9. ↑ Сивухин, 2005, с. 61.
10. ↑ Энергосбережение в теплоэнергетике и теплотехнологиях: учебное пособие / Л.И. Молодежникова; Томский политехнический университет. — Томск: Изд-во Томского политехнического университета, 2011. – С.43-45.

• Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с.
• Путилов К. А. Термодинамика. — М.: Наука, 1971. — 375 с.
• Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — 5 изд., испр.. — М.: Физматлит, 2005. — 544 с. — ISBN 5-9221-0601-5.