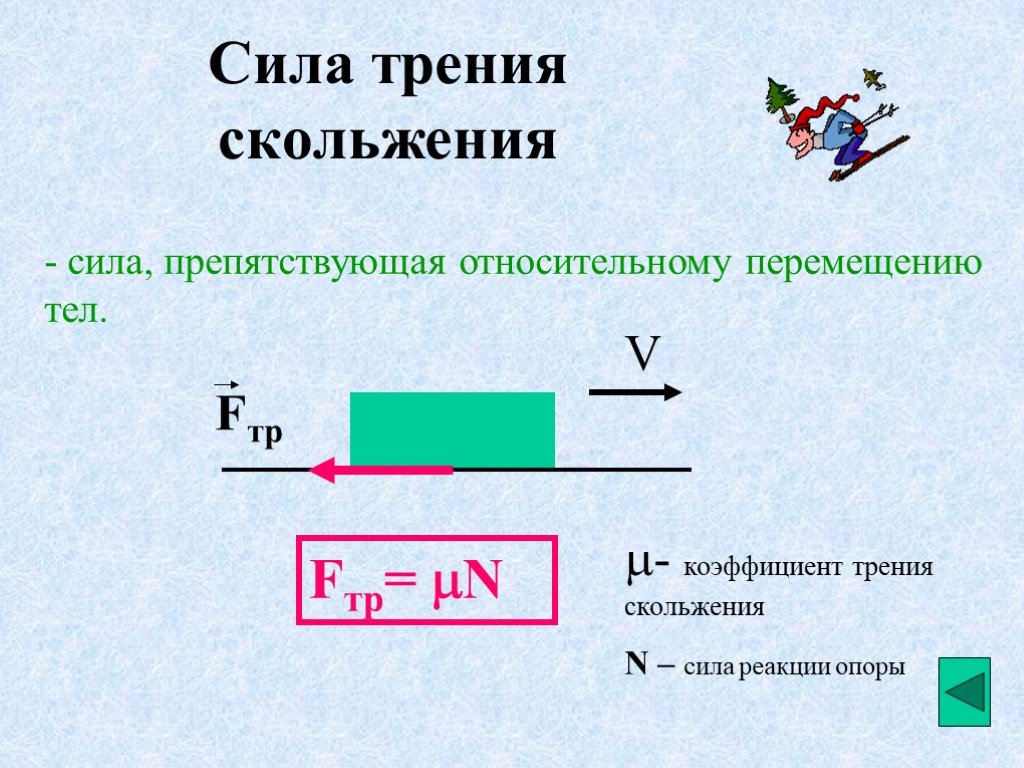
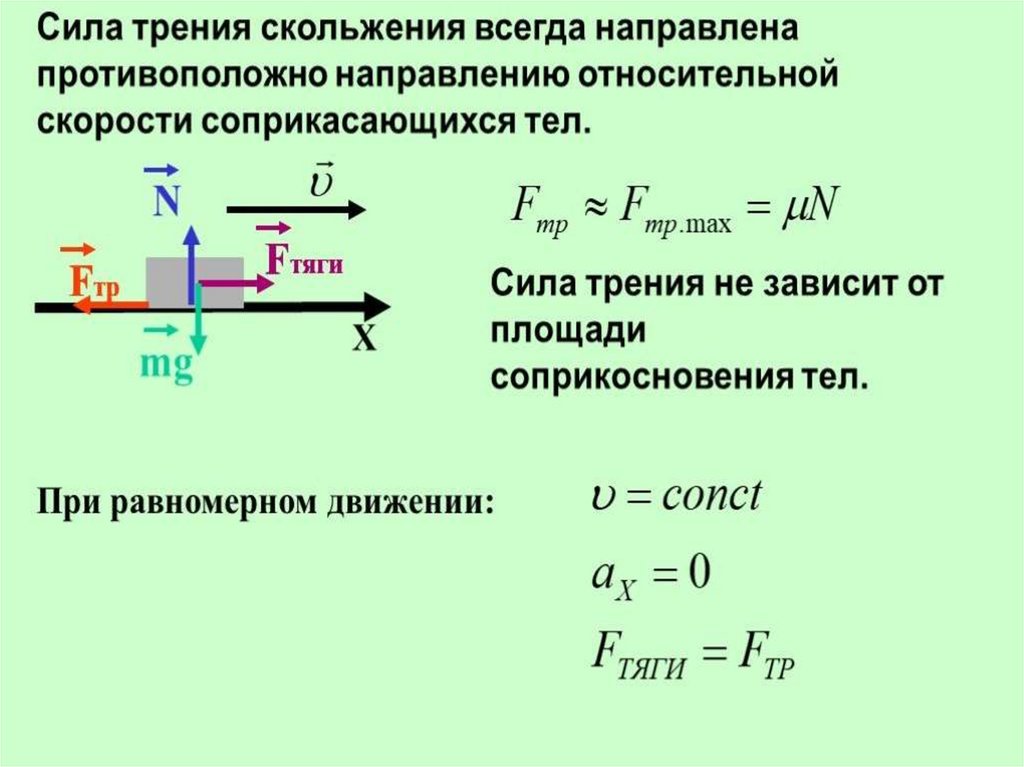
Низкий коэффициент трения — Промышленные защитные покрытия
[email protected] Понедельник-Пятница с 8-00 до 17-00 Тел.+7 (960) 522-90-00
alvirnАнтифрикционные покрытия Покрытия с низким коэффициентом трения обычно имеют коэффициенты трения, варьирующиеся от 0,05 до 0,2. Это зависит от типа используемого покрытия и нагрузки. PTFE имеет самый низкий коэффициент трения из любого твердого материала. Низкое трение не следует путать с антипригарным покрытием. Трение - это сила, противодействующая движению двух объектов, скользящих друг против друга. Эта сила приводит к износу и увеличению использования энергии для поддержания или начала движения. Мы также должны рассмотреть два различных типа трения, которые являются статическим и динамическим трением. Статическое трение - это сила, противодействующая начальному движению статического объекта.Динамическое или кинетическое трение - это сила сопротивления объектам, которые движутся друг против друга. Значения статического трения обычно выше, чем значения динамического трения. Нагрузка и скорость являются двумя очень важными факторами. Каждое значение или их комбинация могут оказать существенное влияние на выбор правильной системы. По мере увеличения трения количество энергии, необходимой для поддержания процесса, также увеличивается. Износ также увеличивается, что может привести к возможному захвату или разрушению сопряженных поверхностей. Сила трения, создаваемая между резьбами на больших гайках и шпильках, сильно варьируется из-за геометрии и технических допусков. Покрытие из PTFE, такое как Xylan® 1070, значительно уменьшит величину крутящего момента, потерянного при трении, так что может быть применена гораздо более точная и предсказуемая нагрузка при зажиме. Покрытия с низким коэффициентом трения доступны в широком спектре, в зависимости от применения. У Whitford очень широкий ассортимент покрытий с низким коэффициентом трения из серии Xylan. Соотношения фторполимера и смолы могут варьироваться для получения различных значений. Отношение смолы к фторполимеру может быть увеличено, чтобы обеспечить различные степени твердости и повышенную износостойкость, хотя будет наблюдаться незначительное увеличение коэффициента трения из-за небольшого разбавления содержания фторполимера. И наоборот, повышенное содержание PTFE и более низкое содержание смолы могут снизить значения трения, хотя износостойкость может быть снижена из-за того, что покрытие будет очень мягким. В ситуациях, когда требуется дополнительная сухая смазка, присадки, такие как MoS2 (дисульфид молибдена) или графит, добавляются для обеспечения исключительных свойств подшипников. Одно конкретное ксилановое покрытие с присадкой MoS2 может обеспечить низкоскоростную смазку при давлениях до 10 500 кг / см² (150 000 фунтов на кв. Дюйм). Длительные периоды бездействия между двумя сопряженными частями могут создавать очень высокие коэффициенты статического трения, и покрытие не только уменьшает эти силы, но и дополнительные антипригарные свойства фторполимерных покрытий предотвращают постоянное прилипание посторонних веществ к поверхностям. Также доступны покрытия с низким коэффициентом трения, специально разработанные для нанесения на материалы подложки, которые являются гибкими или чувствительными к повышенным температурам отвердевания. Значения трения могут быть значительно снижены при использовании резиновых и эластомерных подложек. Почти все автомобильные дверные и оконные уплотнители покрыты этим составом, чтобы обеспечить свободное движение окна к уплотнению, а также уменьшить эффект образования льда.
Наши поставщики:
Нам доверяют:
Силы трения в направляющих механизмов и машин
Рассмотрим определение сил трения и приведенного коэффициента трения, действующих в направляющих машин и механизмов:
На силу трения в поступательной паре влияет также форма направляющих. В технике для обеспечения точности поступательного движения часто используются клинчатые направляющие (они удобны, т.к. автоматически устраняются боковые зазоры в поступательной паре).
Рассмотрим ползун, изображенный на рисунке 23, который движется в направляющих, имеющих форму клина.
Рисунок 23
Из баланса сил, действующих на ползун, определяется результирующая нормальная реакция RN. Однако силы трения возникают на боковых поверхностях клина и зависят от нормальных реакций RN1 и RN2, перпендикулярных к этим боковым поверхностям.
Результирующая нормальная реакция является геометрической суммой реакций RN1 и RN2:
Наиболее часто в технике используется симметричное расположение боковых поверхностей клинчатых направляющих. В этом случае:
Как видно, в этом случае в значительной мере можно влиять на величину силы трения изменением угла между плоскостями направляющих (здесь β – половина угла клина).
Для дальнейших расчетов вводится понятие приведенного коэффициента трения (обозначается f‘ ):
При уменьшении угла β возрастает сила трения на боковых поверхностях клина при одной и той же результирующей нормальной реакции.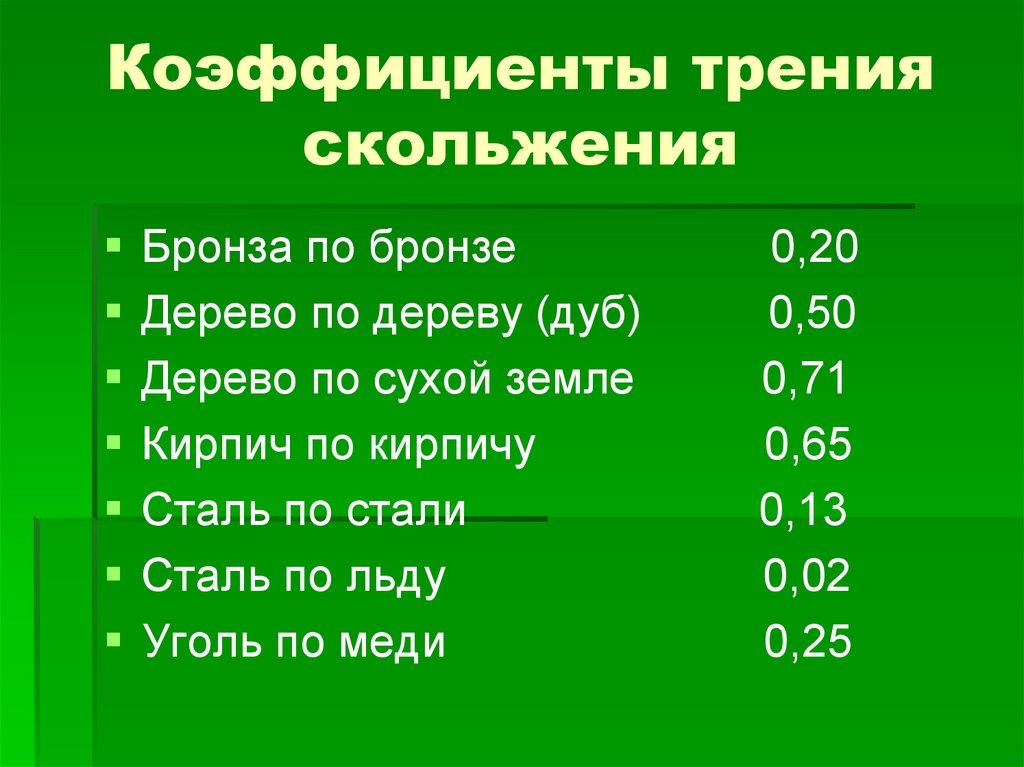 При применении малых (близких к нулю) углов сила трения увеличивается до очень больших величин (при стремлении угла клина к нулю сила трения стремится к бесконечности). Именно это явление привело к появлению термина «заклинивание».
При применении малых (близких к нулю) углов сила трения увеличивается до очень больших величин (при стремлении угла клина к нулю сила трения стремится к бесконечности). Именно это явление привело к появлению термина «заклинивание».
Этот эффект широко используется в бытовой практике и в технике (например: соединение деревянных строительных конструкций с помощью клиньев; применение для рубки дров специального топора – «колуна» с увеличенным углом заточки для предотвращения застревания при колке дров; применение клиньев для удержания бурильной колонны; применение клиноременных передач для увеличения тяговой способности; в крепежных резьбах для предотвращения самоотвинчивания и др).
Трение во вращательных парах >
Курсовой проект по ТММ >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
Поиск формул и решений задач
Коэффициент трения: уравнения и единицы измерения
Пока он качался в кресле-качалке, слушая «2 кресла-качалки» Джона Беллиона, его поразило; «Что произойдет, если этот стул никогда не перестанет качаться?». «Как насчет двигателей в машинах, представьте, что они работают бесконечно, никогда не останавливаясь. Эврика! Я нашел это», — взволнованно закричал мистер Финикки Спинс, — всему нужен тормоз, чтобы мы не сломались. разрыв, следовательно, трение». В этом увлекательном путешествии вы узнаете об уравнении, формуле, устройстве измерения, а также о единицах коэффициента трения. Давайте качаться, не ломаясь!
Давайте качаться, не ломаясь!
Что такое коэффициент трения?
Коэффициент трения \(\mu\) представляет собой отношение или частное между силой трения \((F)\) и нормальной реакцией \((R)\).
Это значение дает представление о том, с какой легкостью происходит движение, когда две поверхности соприкасаются друг с другом.
Когда коэффициент трения между материалами высок, это означает, что трение больше, следовательно, сопротивление движению между соприкасающимися поверхностями действительно велико.
Между тем, когда коэффициент трения между материалами низкий, это означает, что трение меньше, следовательно, сопротивление движению между соприкасающимися поверхностями действительно низкое.
Также коэффициент трения определяется характером поверхностей. Более гладкие поверхности обычно имеют меньшее трение, чем более шероховатые поверхности .
Прежде чем продолжить, полезно освежить в памяти информацию о силе трения и нормальной реакции.
Что такое сила трения?
Сила трения – это сила, которая стремится сопротивляться или противодействовать движению между соприкасающимися объектами или поверхностями. Прежде чем объект должен начать движение по поверхности, он должен преодолеть силу трения между двумя соприкасающимися поверхностями.
Рис. 1. Описание силы трения.
Что такое нормальная реакция?
Нормальная реакция, часто обозначаемая как \(R\), представляет собой силу, уравновешивающую вес объекта. Он равен весу \(W\) объекта, однако действует в противоположном направлении. Поскольку вес объекта представляет собой направленную вниз силу, на которую действует ускорение свободного падения, нормальная реакция представляет собой направленную вверх силу.
Без нормальной реакции вес предметов заставил бы их проваливаться сквозь поверхности, на которых они стоят.
Рис. 2. Изображение, описывающее нормальную реакцию и вес.
Формула коэффициента трения
Прежде чем определять формулу коэффициента трения, необходимо определить постулаты Шарля-Огюстена де Кулона о трении 1785 года. Этими постулатами являются:
Этими постулатами являются:
1. Сила трения всегда сопротивляется одновременное движение, происходящее между контактирующими поверхностями .
2. Сила трения действует независимо от относительной скорости соприкасающихся поверхностей, поэтому действие трения не зависит от скорости движения поверхностей.
3. Однако сила трения, существующая между соприкасающимися поверхностями, зависит от нормальной реакции между этими поверхностями, а также от уровня их шероховатости.
4. Когда между контактирующими поверхностями отсутствует скольжение, считается, что сила трения меньше или равна произведению коэффициента трения на нормальную реакцию.
5. В момент, когда должно начаться скольжение между соприкасающимися поверхностями, сила трения описывается как «ограничивающая». На этом этапе сила трения равна произведению нормальной реакции на коэффициент трения.
6. В точке скольжения сила трения равна произведению нормальной реакции на коэффициент трения.
Из предположений Кулона мы можем вывести три примера, определяющих коэффициент трения. Таких случаев:
Нет скольжения
\ [f≤µr \]
в начале скольжения
\ [f = µr \]
во время скольжения
\ Где \(F\) — сила трения, \(R\) — нормальная реакция, а \(µ\) — коэффициент трения.
Следовательно, для объекта, движущегося в контакте с поверхностью, коэффициент трения \(µ\) может быть рассчитан по формуле \[µ=\frac{F}{R}\]
Единица коэффициента трения
Зная единицы измерения силы трения и нормальной реакции, мы можем вывести единицу измерения коэффициента трения. Поскольку и трение \(F\), и нормальная реакция \(R\) измеряются в ньютонах, \(N\), а коэффициент трения есть частное трения и нормальной реакции, следовательно,
\ [µ=\frac{N}{N}\]
Таким образом,
\[µ=1\]
Это означает, что коэффициент трения не имеет единицы .
Устройство измерения коэффициента трения
Основываясь на исследованиях Кулона, он также заявил, что коэффициент трения представляет собой постоянное значение или диапазон значений между известными контактирующими поверхностями.
Теперь коэффициент трения измеряется с помощью тестеров коэффициента трения . Они измеряют статический и кинетический коэффициент трения (COF).
Ниже приведена таблица, в которой указан коэффициент трения между определенными соприкасающимися поверхностями, как в статике, так и в движении.
| Material | Material of counter-surface | Static Coefficient of Friction | Kinetic Coefficient of Friction |
| Steel | Steel | 0.74 | 0.57 |
| Copper | Steel | 0.53 | 0,36 |
| Алюминий | Сталь | 0,61 | 0,47 |
| Древесина | Древесина | 0,25 -0,50 9070108 | 0.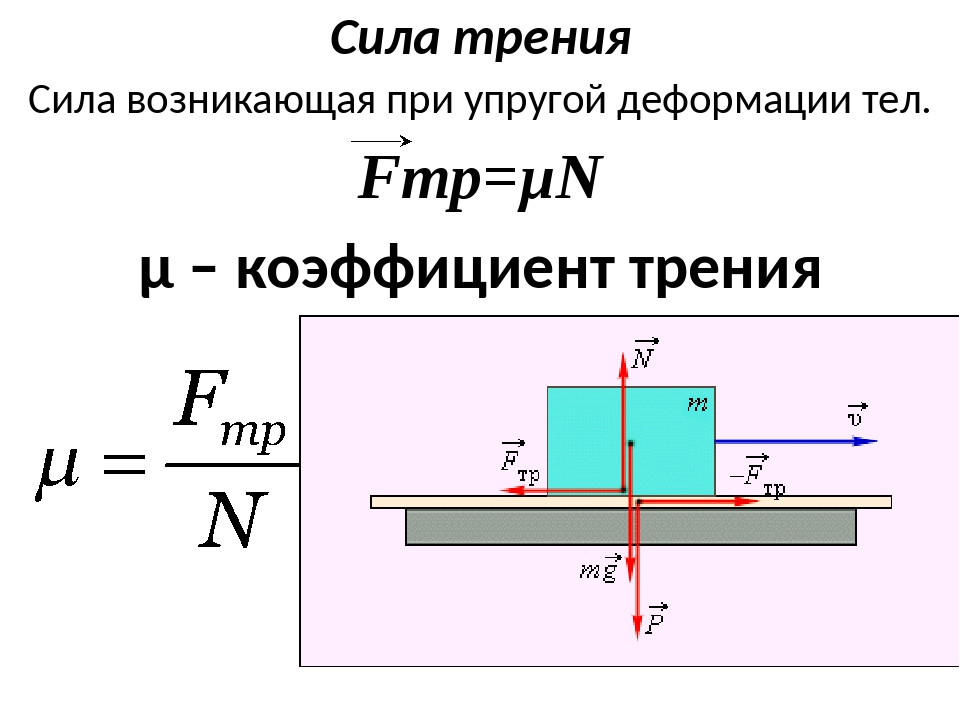 20 20 |
| Wood | Brick | 0.60 | 0.45 |
| Waxed wood | Dry snow | — | 0.040 |
| Waxed wood | Wet snow | 0.14 | 0.10 |
| Ice | Ice | 0.10 | 0.030 |
| Metal | lubricated metal | 0.15 | 0.060 |
| Rubber | Concrete | 1.0 | 0.8 |
| Glass | Glass | 0.94 | 0.40 |
| Teflon | Teflon | 0.040 | 0.040 |
| Joints | Joints with the synovial жидкости у человека | 0,010 | 0,0030 |
Таблица 1. Коэффициенты трения для различных материалов.
Отрицательный коэффициент трения
Как правило, сила трения увеличивается по мере увеличения веса объекта или груза. Однако при определенных обстоятельствах с уменьшением нагрузки возникает соответствующее увеличение трения. Это явление рассматривается как отрицательное трение . Видно, что отрицательный коэффициент трения существует для мельчайших масс объектов, подобных тем, которые измеряются на наномасштабах .
Однако при определенных обстоятельствах с уменьшением нагрузки возникает соответствующее увеличение трения. Это явление рассматривается как отрицательное трение . Видно, что отрицательный коэффициент трения существует для мельчайших масс объектов, подобных тем, которые измеряются на наномасштабах .
Уравнение коэффициента трения
Задачи, связанные с коэффициентом трения, требуют применения формулы коэффициента трения, формируя некоторые уравнения, которые используются для решения этих задач.
Всегда помните, что
\[µ=\frac{F}{R}\]
Веревка привязана к массе \(100\, \text{кг}\) прямоугольного блока, который неподвижен на плоская поверхность. Если коэффициент трения, существующий между бруском и плоскостью, равен \(0,4), определите максимальную силу, которую можно приложить, если тянуть за веревку, не заставляя брусок двигаться по плоскости.
Решение:
Сделайте набросок предоставленной информации, чтобы иметь более четкое представление.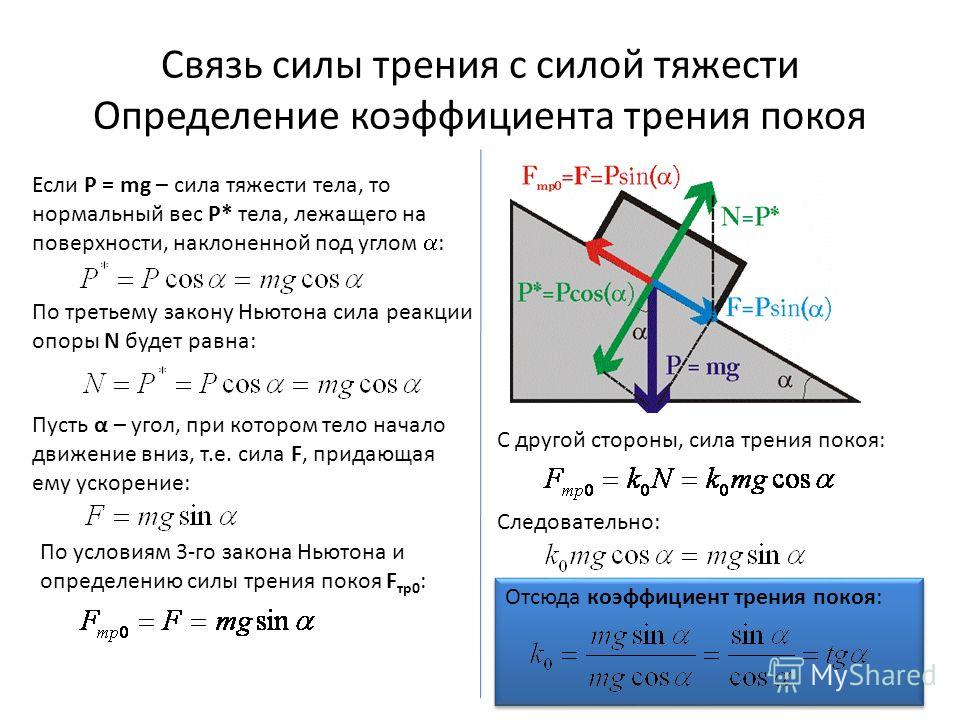
Рис. 3. Определение максимальной силы, удерживающей блок в состоянии покоя.
Напомним, что первый вывод из постулата Кулона объясняет случай покоя тела. В этом состоянии \[F≤µR\] Это означает, что на данном этапе сила трения меньше или равна произведению нормальной реакции на коэффициент трения.
Нормальная реакция эквивалентна весу блока, но действует в противоположном направлении.
Вес объекта, \(W\), равен
\[W=мг\]
что равно
\[W=100\times9.8\]
Следовательно, вес объекта равен \(980\, \text{N}\). Отсюда следует, что
\[R=W=980\, \text{N}\]
Максимальная сила, которая может быть приложена к телу, чтобы удерживать его в состоянии покоя, будет настолько близка или равна силе трения сила. Следовательно, \[F≤µR\], что равно
\[F≤0,4\times980\, \text{N}\]
, таким образом,
\[F≤392\, \text{N}\]
Это предполагает, что максимальная сила, приложенная к веревке, прикрепленной к блоку, которая все еще удерживает блок в статическом состоянии, равна \(392\, \текст{N}\).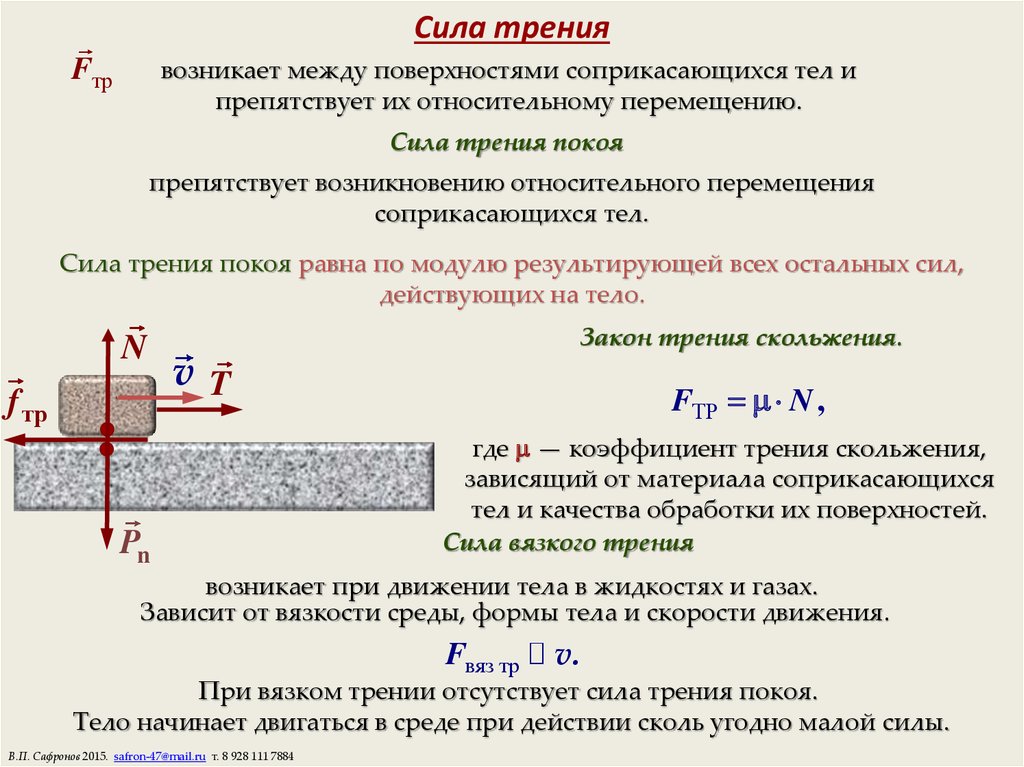
Уравнение коэффициента трения на наклонной плоскости
Представьте себе, что предмет массой \(m\) помещен на наклонную плоскость под углом \(\theta\) к горизонту. Следующие изображения ниже помогут вам.
Рис. 4. Объект на наклонной плоскости.
Из приведенного выше рисунка видно, что на блок воздействуют вес, нормальная реакция и трение, поскольку он имеет тенденцию скользить по наклонной плоскости под углом \(\theta\) к горизонтали.
Рис. 5. Определение угла на наклонной плоскости по сумме углов треугольника.
Из приведенного выше можно составить прямоугольный треугольник между весом \(мг\) и горизонталью. Следовательно, так как другой угол прямой, то третий угол равен
\[180°-(90°+θ)=90°-θ\]
Рис. 6. Определение угла наклонной плоскости с помощью противоположного углы.
Из диаграммы выше видно, что угол, образованный между силой трения \(F\) и весом, равен \(90°-0\), так как противоположные углы равны. Третий угол в исходном прямоугольном треугольнике противоположен углу, образованному силой трения и весом.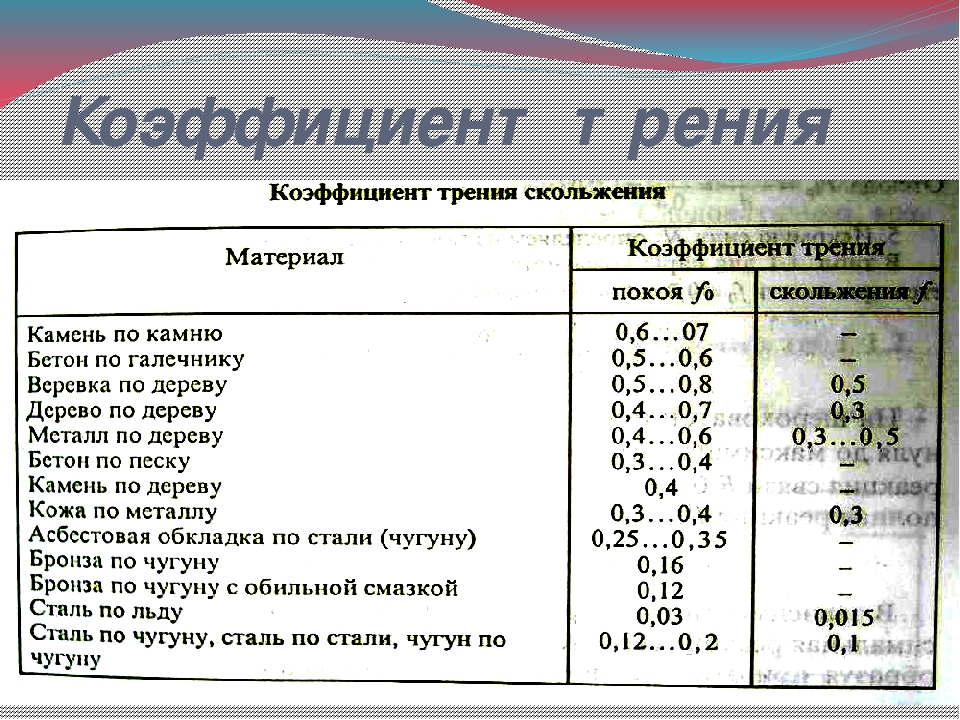
Рис. 7. Определение угла в наклонной плоскости с помощью углов на прямой.
Из рисунка выше мы можем определить угол, образованный между весом и нормальной реакцией, так как все они лежат на прямой линии наклонной плоскости как \[180°-(90°+90°-θ)=θ\ ]
Напомним, что сумма углов прямой равна \(180°\).
Рис. 8. Преобразование наклонной плоскости в прямоугольный треугольник.
Из вышеизложенного вы должны увидеть, что наклонная плоскость окончательно превратилась в прямоугольный треугольник. Это позволит вам применить SOHCTOA для определения взаимосвязи между весом, нормальной реакцией и трением. Таким образом,
\[F=mg\sin\theta\] while\[R=mg\cos\theta\]
Напомним, что \[µ=\frac{F}{R}\]
Это означает, что коэффициент трения можно получить через
\[µ=\frac{mg\sin\theta }{mg\cos\theta\ }\]
Следовательно, уравнение коэффициента трения на наклонной плоскости имеет вид
\[µ=\tan\theta \]
Учитывая, что
\[\frac{\sin\theta}{\cos\theta}=\tan\theta\]
Объект массой \(30\, \text{kg}\) равен расположен под наклоном \(38°\) к горизонтали. Найдите коэффициент трения.
Найдите коэффициент трения.
Решение:
Недолго думая, коэффициент трения на наклонной плоскости равен тангенсу угла наклона. Следовательно, \[µ=\tan38°\]
что равно \[µ=0,78\]
Дополнительные примеры по коэффициенту трения
Чтобы повысить свою компетентность в решении задач на коэффициент трения, вот еще несколько примеров.
Брусок массой \(10\, \text{кг}\) кладут на стол и закрепляют с противоположных сторон двумя пружинами, прикрепленными к \(5\, \text{кг}\) и \(12 \, \text{kg}\) массы соответственно. Если блоки и столы имеют стандартный коэффициент трения \(0,4\), найти ускорение и натяжение пружин.
Решение:
Нарисуйте диаграмму, чтобы иметь более четкое представление о том, о чем говорится в вопросе.
Рис. 9. Определение натяжения пружин по коэффициенту трения.
Теперь нужно определить силы, действующие на предмет на столе, и указать их на схеме. Здесь вам нужно быть очень осторожным, обратите внимание, что, поскольку \(12\, \text{кг}\) будет тянуть больше силы, чем масса \(5\, \text{кг}\), объект скорее всего сместится вправо.
Однако эта ваша гипотеза зависит от того, превышает ли сила силу трения, иначе объект остался бы неподвижным на столе.
Следовательно, сила трения направлена вправо, чтобы предотвратить натяжение массы \(12\, \text{кг}\).
Рис. 10. Иллюстрация сил, действующих на тело, натянутое пружинами, прикрепленными к массам.
Из диаграммы выше вы должны понять, что происходит в каждой точке.
Не волнуйтесь, просто начните с крайних концов, слева или справа, и продолжайте анализировать действие сил, пока не доберетесь до противоположного конца.
С крайнего левого угла видно, что масса \(5\, \text{кг}\) прикладывает направленную вниз силу, \(49\, Н\), но система над ней вызывает напряжение, \(T_2\ ), который стремится переместить массу вверх с ускорением \(a\). Таким образом, это можно выразить как
\[T_2-49\, \text{N}=5\, \text{kg}\times a\]
Это потому, что, в конце концов, \(5\, \text{kg}\) масса поднимается, чтобы двигаться с ускорением \(a\).
Теперь, что касается предмета на столе, вы заметите, что напряжение \(T_2\) тянет предмет влево. Кроме того, сила трения действует влево, поскольку она пытается воспрепятствовать движению вправо, вызванному натяжением \(T_1\), действующим вправо. Это выражается как
\[T_1-T_2-F=10\, \text{kg}\times a\]
Это потому, что после того, как две левые силы (т.е. \(T_2\) и \(F\)) попытались преодолеть направленную вправо силу \(T_1\) и не удалось, ожидается, что объект массой \(10\, \text{kg}\) будет двигаться вправо с ускорением \(a\).
Когда вы посмотрите на третью массу в крайнем левом положении, вы заметите, что масса прикладывает направленную вниз силу \(117,6\, \text{N}\) и сопротивляется восходящему натяжению пружины, \(Т_1\). Следовательно, это можно выразить как
\[117,6\, \text{N}-T_1=12\, \text{кг}\times a\]
В связи с ожиданием того, что направленная вниз сила, приложенная \(117,6\, \text{N }\) предназначен для преодоления напряжения \(T_1\), тогда масса \(12\, \text{kg}\) должна предположительно двигаться с ускорением, \(a\).
Теперь у нас есть три уравнения из объясненных выше.
Вот эти три уравнения:
\[T_2-49\, \text{N}=5\, \text{кг}\times a\]
\[T_1-T_2-F=10\, \text {кг}\раз в\]
\[117,6\, \text{N}-T_1=12\, \text{кг}\times a\]
Суммируйте все 3 уравнения, следовательно, \[T_2-49\, \text{N} +T_1-T_2-F+117.6\, \text{N}-T_1=5a+10a+12a\], что дает
\[68.6\, \text{N}-F=27a\]
Обратите внимание, что
\[F=µR\]
с
\[µ=0.4\]
и
\[R=W=98\, \text{N}\]
затем,
\[F =0,4\times 98\, \text{N}\]
\[F=39,2\, \text{N}\]
Следовательно, подставьте значение \(F\) в уравнение и получите 9{-2}\]
, что дает
\[T_1-93.65\, \text{N}=10.9\, \text{N}\]
Добавить \(93.65\, \text{N}\) к обеим частям уравнения, чтобы получить наше напряжение, \(T_1\), как
\[T_1=104,55\, \text{N}\]
Человек стоит неподвижно на склоне горы и коэффициент трение между подошвами его ног и поверхностью горы равно \(0,26\). Если в следующем году произошло извержение вулкана, увеличившее коэффициент трения между подошвой его ноги и горой на \(0,34\), на какой угол увеличился или уменьшился наклон горы? 9{-1}(0,26)\]
Если в следующем году произошло извержение вулкана, увеличившее коэффициент трения между подошвой его ноги и горой на \(0,34\), на какой угол увеличился или уменьшился наклон горы? 9{-1}(0,26)\]
Следовательно, нынешний склон горы имеет угол \[\theta=14,57°\]
Однако через год гора испытала извержение, которое увеличило коэффициент трения на \(0,34\). Таким образом, новый коэффициент трения равен
\[µ_{new}=0,26+0,34\]
, что дает
\[µ_{new}=0,6\]
Нам нужно определить новый угол наклона горы, используя
\[µ_{new}=\tan\theta\]
Таким образом,
9{-1}(0,6)\]Следовательно, новый склон горы имеет угол
\[\theta=30,96°\]
Склон горы имел прежний угол \(14,57°\), но при извержении он увеличился до \(30,96°\) на
\[30,96°-14,57°=16,39°\]
Следовательно, извержение увеличило угол между склонами горы на \(16,39°\).
Коэффициент трения – ключевые выводы
- Коэффициент трения, \(\mu\), представляет собой отношение или частное между силой трения \((F)\) и нормальной реакцией \((R)\).

- Сила трения – это сила, которая стремится сопротивляться или противодействовать движению между соприкасающимися объектами или поверхностями.
- Для объекта, движущегося в контакте с поверхностью, коэффициент трения \(µ\), таким образом, может быть рассчитан по формуле \[\mu=\frac{F}{R}\]
- Коэффициент трения не имеет единица.
- Отрицательное трение возникает, когда уменьшение нагрузки приводит к последующему увеличению трения.
Коэффициент трения — о трибологии
Содержание
Что такое коэффициент трения?
Трение представляет собой силу, препятствующую относительному движению, и может возникать на границе раздела тел, а также внутри тел. Понятие коэффициента трения было впервые сформулировано Леонардо да Винчи и определяется в соответствии со следующим уравнением:
(1)
где – сила трения, а – приложенная нормальная нагрузка. Величина коэффициента трения определяется свойствами поверхностей, окружающей средой, особенностями поверхности, наличием смазки и т. д.
д.
Обычно различают два вида коэффициентов трения: статический и динамический. Статический коэффициент трения определяется как отношение максимальной силы трения до относительного движения к нормальной нагрузке. Динамический (или кинетический) коэффициент трения определяется как отношение силы трения при скольжении к приложенной нормальной нагрузке. Часто статический коэффициент трения больше кинетического.
Трение также можно разделить на сухое и смазываемое. Исторически смазка использовалась для снижения общего коэффициента трения путем разделения поверхностей слоем смазки. Поскольку для обычных конструкционных материалов сухое трение значительно выше, чем трение слоев смазки, трение можно уменьшить, введя смазочную пленку. Однако классический смазочный механизм для уменьшения трения достиг своего фундаментального предела, и в настоящее время твердым смазочным материалам уделяется значительное внимание (см. пример) в попытках уменьшить потери энергии из-за трения.
Сухой коэффициент трения
Гийом Амонтон (1663-1705) и Шарль-Огюстен Кулон (1736-1806) сформулировали важные законы сухого трения:
- Сила трения пропорциональна нормальной нагрузке (первый закон Амонтона)
- Сила трения не зависит от кажущейся площади контакта (второй закон Амонтона)
- Кинетическое трение не зависит от скорости скольжения (закон Кулона)
Согласно второму закону Амонтона коэффициент трения является постоянной величиной для данной пары материалов.
Коэффициенты трения различных комбинаций материалов в атмосфере и вакууме приведены в таблице Коэффициенты трения (данные собраны из различных источников [1,2]).
Коэффициент трения со смазкой
Трение со смазкой можно разделить на три режима: граничный (BL), смешанный (ML) и эластогидродинамический (EHL). В отличие от сухого трения, трение со смазкой зависит от условий эксплуатации, таких как скорость скольжения, вязкость смазки, температура и т. д. Уровень коэффициента трения следует следующей тенденции, показанной на рис. 1.9.0003 Рис. 1. Коэффициент трения в смазанных контактах
д. Уровень коэффициента трения следует следующей тенденции, показанной на рис. 1.9.0003 Рис. 1. Коэффициент трения в смазанных контактах
Простая теория (концепция распределения нагрузки) для расчета коэффициента трения в смазанных контактах была предложена Джонсоном [3]. Эта теория рассматривает общий коэффициент трения как сумму двух составляющих, сухого и смазочного трения, взвешенных по соответствующим площадям. Было показано, что в некоторых случаях теория достаточно хорошо согласуется с экспериментальными данными. Подробнее см. [4].
Для расчета коэффициента трения в режиме смешанного смазывания можно использовать следующие коды на базе Matlab: симулятор на основе шероховатости, симулятор трибологии (автономный, в Matlab нет необходимости).
Измерение коэффициента трения
Трибометры — это устройства, которые обычно используются для измерения трения. Первый трибометр, вероятно, изобрел Леонардо да Винчи — первый триболог. Посмотрите простое устройство, разработанное на основе граммофона, на этом видео:
Манодж Раджанкунте Махадешвара
В настоящее время я работаю аспирантом в Университете Лидса.