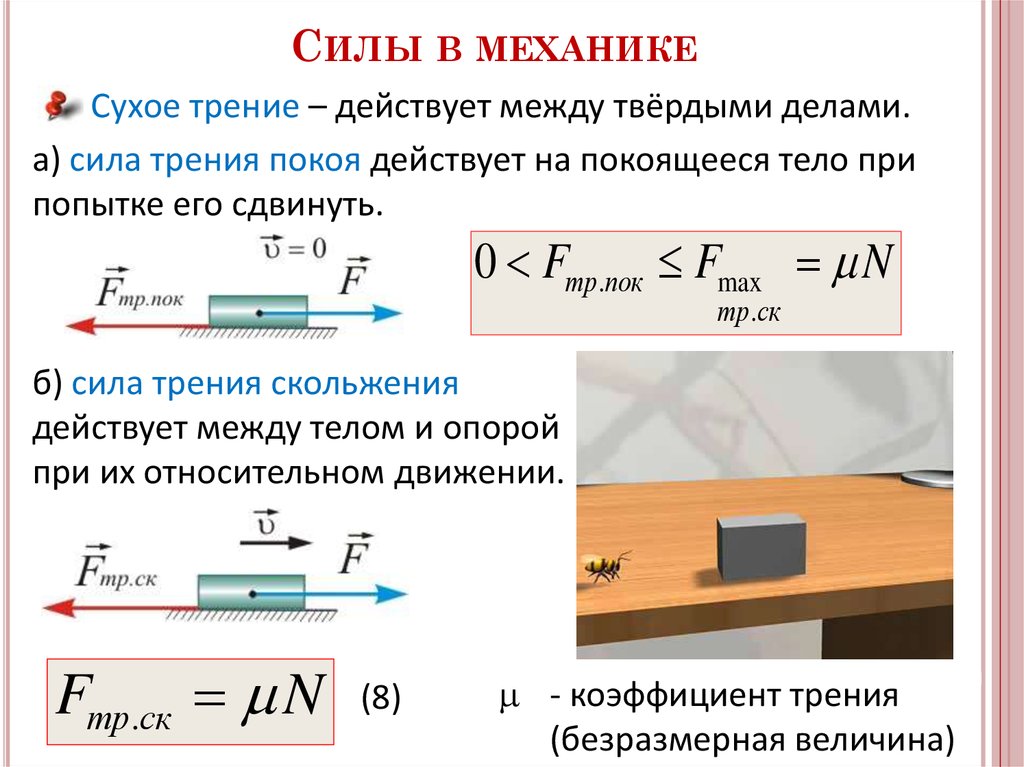
Может ли коэффициент трения скольжения быть больше единицы?
Новости
Posted on Author Admin Comment(0)
Входная дверь – лицо помещения. Именно дверь первой «встречает» входящего, а ее внешний вид способен внести солидный вклад в общее впечатление, которое останется у посетителя после визита.
Входная дверь в доме – объект совершенно уникальный. Она должна сочетать в себе массу необходимых характеристик и требований, которые соответствовали бы представлениям хозяина дома о безопасности, комфорте, эстетичном внешнем виде, смотрите Дизайнерские входные двери. Отвечать многочисленным условиям порой бывает нелегко, но все же есть мастера своего дела, продукция которых способна удовлетворить даже самый взыскательный вкус. Итальянские входные двери – яркий тому пример.
ОАО «Санкт-Петербургские электрические сети»
Входные двери из Италии обладают важным преимуществом, которое заключается в безупречном соотношении цены и качества продукции, а широкий ассортимент моделей будит интерес и вдохновляет полет фантазии.
Говоря о входной двери, безусловно, представляется традиционная металлическая дверь, надежная и прочная, способная обеспечить безопасность и сохранность. Итальянские входные двери производятся из высококачественного цельного листа стали холодного проката. Этот материал рассчитан на значительные нагрузки, связанные с перепадами температуры и влажности, а также превосходно защищает от попыток взлома.
Manual Transmission, How it works ?
Трение – это процесс взаимодействия тел между собой при движении этих тел относительно друг друга.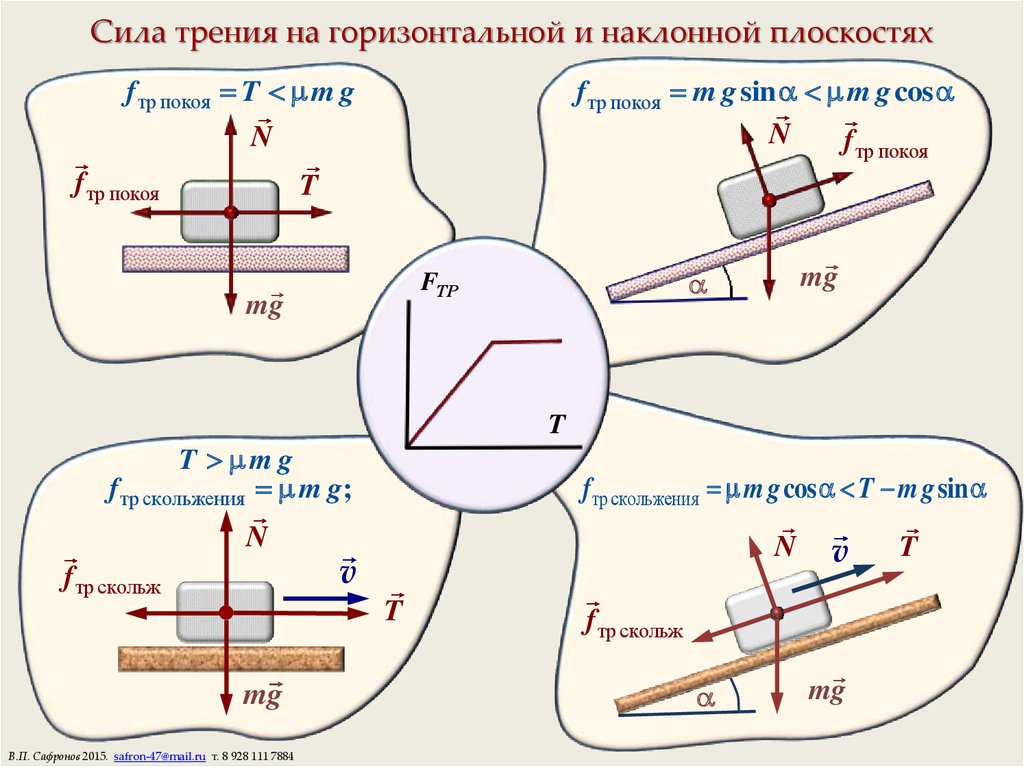 А сила трения – это та сила, которая возникает в месте соприкосновения этих тел. Почему возникают силы трения?
А сила трения – это та сила, которая возникает в месте соприкосновения этих тел. Почему возникают силы трения?
Шероховатость соприкасающихся поверхностей.
Взаимное притяжение молекул, находящихся на поверхности этих тел.
Главной характеристикой трения является коэффициент трения мю (греческая буква мю). При движении одного тела по другому сила трения F равна произведению мю на N, F=мю* N. Коэффициент трения мю – основная характеристика трения. Мю определяется материалами, из которых сделаны тела. N – сила нормального давления одного тела на другое.
Но в школьной физике не проходят так называемого закона Амонтона — Кулона с учетом адгезии. Для большинства пар материалов коэффициент трения мю не превышает 1 (обычные значения от 0,1 до 0,5). Если же мю>1, то это означает, что появляется еще и сила адгезии. Адгезия в переводе с латинского языка adhaesio — прилипание. Это сцепление поверхностей разнородных тел. Она возникает из-за взаимодействия молекул или атомов этих тел.
Это в определенной степени напоминает процессы склеивания, сварки, нанесения покрытий.
Если коэффициент трения мю>1, то это значит, что между контактирующими материалами имеется сила адгезии. Попробуйте бросить пластилин в стенку, он сразу прилипнет к стенке, то есть здесь мю>1. А почему прилипнет? Быстро возникают силы притяжения между атомами (или молекулами) пластилина и стенки. Можно и два одинаковых металлических бруска так хорошо и гладко отполировать, а потом положить один на другой, что у вас не хватит сил, чтобы не только двигать один кусок по другому, но и оторвать их друг от друга.
подробные сведения и часто задаваемые вопросы
Безразмерная физическая величина, определяющая взаимодействие двух объектов, называется коэффициентами.
Коэффициент стоимости кинетическое трение меняется в зависимости от характера используемого материала. Как правило, коэффициенты дают соотношение двух величин, участвующих в действии. В этом посте давайте обсудим, как найти коэффициент кинетического трения и его последствия.
Как найти коэффициент кинетического тренияРассмотрим две поверхности, одна из которых движется в контакте с другой. В трение всегда сопротивляется движению и, наконец, останавливает движение поверхности в направлении, противоположном движению.
Общая формула для нахождения коэффициент трения дается соотношением силы трения и нормальной реакции, действующей на поверхности в перпендикулярном направлении.
Кредиты изображения: Изображение предоставлено Pexels от Pixabay Схема свободного тела кинетической силы тренияИзменив приведенное выше выражение, мы можем узнать и кинетическое трение.
Как рассчитать неопределенность коэффициента кинетического тренияНеопределенность возникает из-за несовпадения осей координат по направлению движения.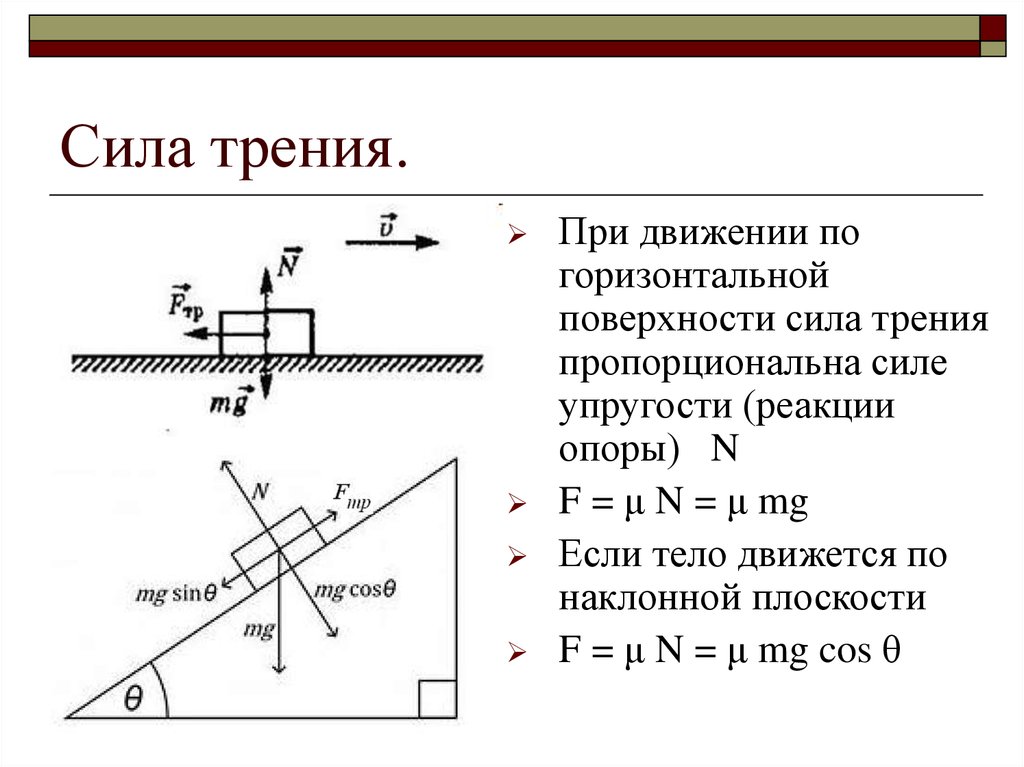 Наряду с нормальной силой на систему действует тангенциальная сила. Эта касательная сила объясняет возникновение неопределенности коэффициента кинетического трения.
Наряду с нормальной силой на систему действует тангенциальная сила. Эта касательная сила объясняет возникновение неопределенности коэффициента кинетического трения.
Значение коэффициента не измеряется непосредственно в ходе эксперимента. Он определяется путем расчета всех сил, действующих на систему, и угла наклона объекта к поверхности.
Общее выражение для коэффициента при кинетическое трение дан кем-то
Рассмотрим скольжение объекта по плоскости. Скольжение объекта принимается для различного угла объекта по плоскости для разных экземпляров. Затем рассчитайте коэффициент кинетического трения для всех углов.
Неопределенность из-за тангенциальной силы и несоосностиИз приведенного выше утверждения следует, что величина коэффициента кинетического трения изменяется с изменением угла. Это отклонение связано с неопределенностью кинетического коэффициента трения. Разберемся, как с неопределенностью найти коэффициент кинетического трения.
Наряду с нормальной силой FN, касательная сила также способствует развитию силы трения. Это приводит к ошибке при расчете коэффициента кинетического трения. Погрешность измерения компенсирует ошибку, возникшую во время расчета.
Нормальная сила действует вдоль оси Y, а угол смещения равен β. И тангенциальная сила действует вдоль оси X со смещенным углом α. Эти нормальные и касательные силы находятся в контакте, а результирующая сила по осям X и Y определяется выражением
FX = ФF коса + FN sinα
FX = мкK FN коса + FN sinα
FX = ФN (µK cosα + sinα)
Аналогично для оси Y
FY = ФN cosβ — FF грех β
FY = ФN (cosβ — µK sinβ) Путем решения результирующих сил неопределенность трения определяется как
Чтобы вычислить комбинированное измерение стандартной неопределенности, функция стандартной неопределенности должна быть стандартным значением входных значений и частных производных коэффициента трения.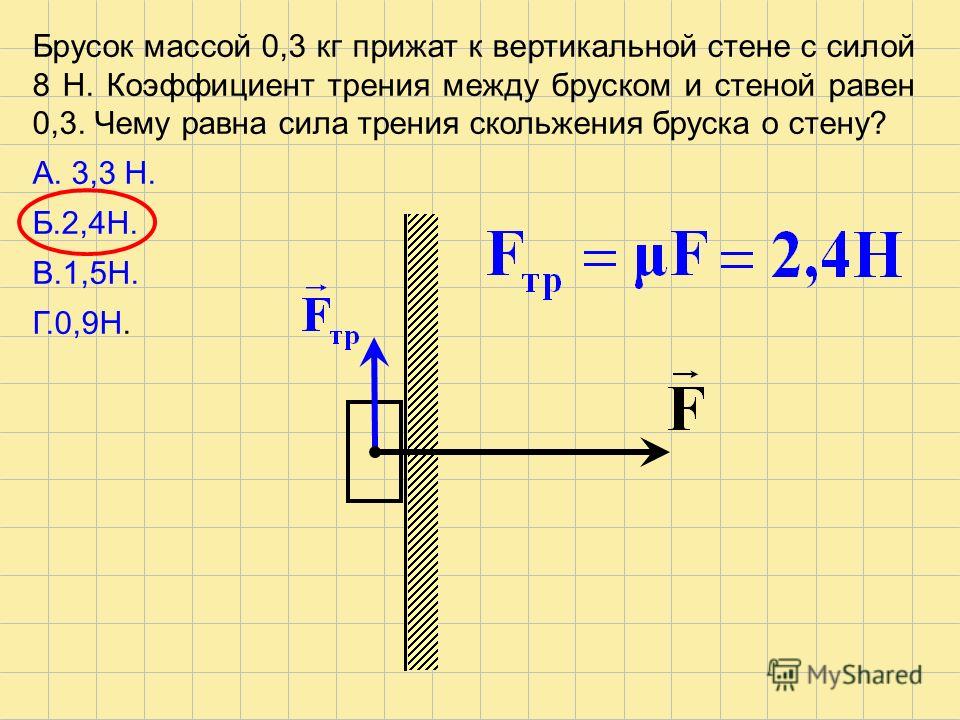 Закон «Распространение неопределенности» помогает нам дать стандартное значение неопределенности трения. Это задается уравнением.
Закон «Распространение неопределенности» помогает нам дать стандартное значение неопределенности трения. Это задается уравнением.
Где, u — неопределенность данной системы.
При дифференцировании отдельных переменных получаем стандартное значение неопределенности коэффициента кинетического трения.
Это дает стандартное значение неопределенности для входных сил, действующих на систему. Подставляя эти значения в уравнение для частных производных, мы получаем значение неопределенности.
Как рассчитать коэффициент кинетического трения без массыЧтобы рассчитать коэффициент кинетического трения без массы, рассмотрим блок, движущийся по плоской поверхности. Блок массы «m» движется с ускорением «a» в направлении приложенной силы. Нормальная сила, действующая между блоком и поверхностью, равна FN которая перпендикулярна движению блока. Мы знаем, что сила трения действие между блоком и поверхностью для замедления движения задается уравнением,
FK = мкK FN
Согласно второму закону движения Ньютона, сила, действующая на движущееся тело, равна массе, умноженной на ускорение.
F = m * a
На нормальную силу влияет сила тяжести, заданная как
FN = м * г
Подставляя в уравнение силы трения, получаем
FK = мкK м * г
Поскольку тело движется, а сила, действующая на блок, является кинетической силой трения, закон Ньютона можно изменить как
FK = м * а
Приравнивая два вышеупомянутых уравнения, мы получаем,
µK м * г = м * а
µK g = a Переставляя уравнение, мы получаем,
Это дает значение коэффициента кинетического трения.
Часто задаваемые вопросы Дает ли расчет кинетического трения без массы то же значение коэффициента, что и при учете массы?Да, значение коэффициента кинетического трения с учетом массы или без учета такое же.
Поскольку трение — это величина, не зависящая от абсолютной массы системы, масса не влияет на величину трения, участвующего в процессе. Следовательно, коэффициент кинетического трения остается неизменным с учетом массы объекта или без него.
Коэффициент кинетического трения — это числовое значение, свидетельствующее о наличии силы трения между объектами.
Поскольку на трение влияет природа материала, очевидно, что на его коэффициент также в значительной степени влияет природа материала.
Что необходимо для определения коэффициента кинетического трения движущегося объекта?Без коэффициента кинетического трения довольно сложно измерить силу, которая заставляет объект препятствовать его движению.
Трение всегда пропорционально нормальной перпендикулярной реакции между поверхностями. Это соотношение пропорциональности определяется безразмерной величиной, называемой коэффициентом. Коэффициент кинетического трения измеряет абсолютное значение силы трения, которая останавливает движущийся объект.
Может ли значение коэффициента кинетического трения быть больше 1?Обычно значение кинетического коэффициента трения колеблется от 0 до 1. Иногда это дает значение коэффициента больше 1.
Иногда это дает значение коэффициента больше 1.
Если влияние силы трения сильнее, чем перпендикулярная реакция между двумя движущимися поверхностями, значение кинетического коэффициента трения будет иметь значение больше 1. Максимальная сила трения заставляет объект ограничивать свое движение, так что автоматически увеличивается коэффициент кинетического трения. пропорционально.
Приводит ли больший коэффициент кинетического трения к рассеянию энергии?Рассеяние энергии из-за трения можно описать в терминах Закона сохранения энергии.
Более высокий коэффициент кинетического трения означает, что сила трения больше, чем приложенная сила. Сложная задача — удержать тело в движении при наличии трения. Следовательно, чтобы удерживать тело в движении, требуется большая сила. Максимальная сила, прилагаемая для удержания тела в движении, вызывает кинетическая энергия рассеивание выделяется в виде тепла.
Коэффициент трения — Sciencetopia
Коэффициент трения (COF) — это мера сопротивления между двумя поверхностями. Его также можно определить как отношение трения к нормальной реакции. Например,
Его также можно определить как отношение трения к нормальной реакции. Например,
COF = Трение / Нормальная реакция
Здесь
- Трение — когда мы толкаем объект по полу, он движется медленнее из-за противодействующей силы, называемой трением.
- Нормальная реакция – когда два тела соприкасаются друг с другом, они действуют друг на друга с силой, называемой нормальной реакцией.
Свойства коэффициента трения
- Мы используем греческий символ Mu (μ) для обозначения коэффициента трения.
- Безразмерная и безразмерная величина.
- Значение зависит от материала предметов.
- Объект может скользить, только если коэффициент трения больше 1. В противном случае он не может скользить.
Как найти коэффициент трения?
Пусть тело покоится на горизонтальном столе, как показано на рисунке ниже.
Когда к нему приложена сила F горизонтально, тело просто начинает скользить по поверхности.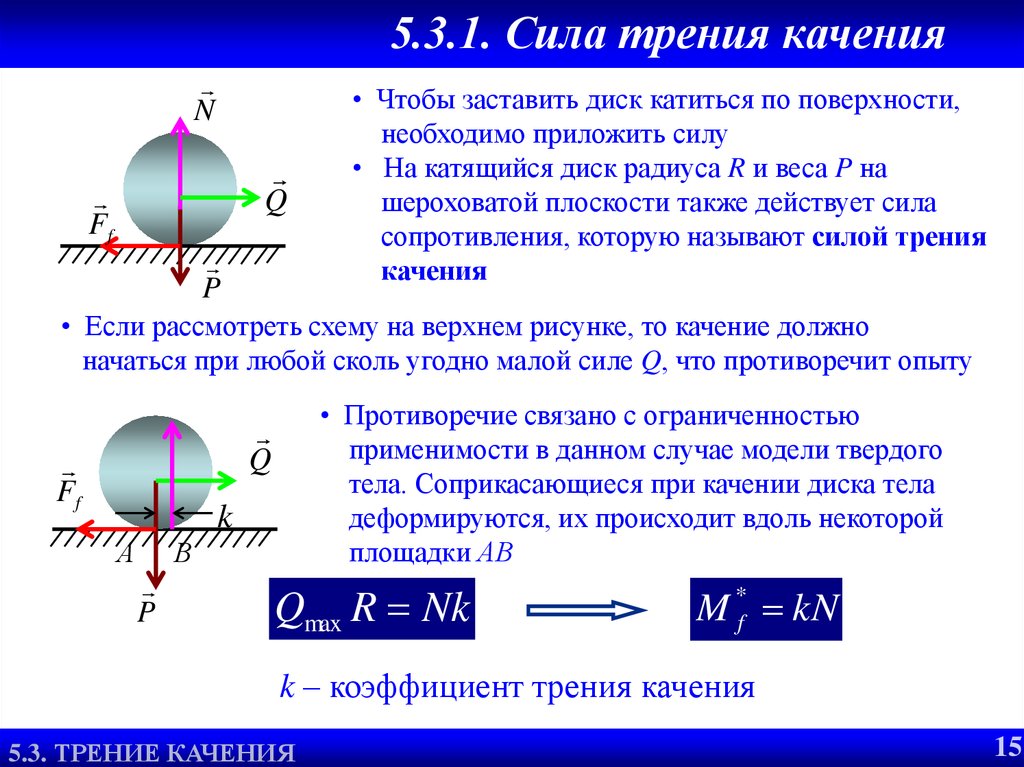 Из законов трения сила трения F пропорциональна нормальной реакции
Из законов трения сила трения F пропорциональна нормальной реакции
То есть
Трение (F) ∝ Нормальная реакция (R)
или F ∝ R или, F = мкР
, где μ — константа пропорциональности, называемая коэффициентом трения между двумя контактирующими поверхностями.
Следовательно,
μ = F / R
Какие существуют типы коэффициентов трения?
В зависимости от типа трения коэффициент трения можно разделить на два типа
- Коэффициент статического трения
- Коэффициент кинетического трения
1. Коэффициент статического трения
Мы можем определить коэффициент статического трения отношение предельного трения к нормальной реакции и его символ μ с .
Отсюда формула коэффициента трения покоя:
μ s = Предельное трение (F) / Нормальная реакция (R)
Здесь Предельное трение — это максимальное статическое трение, при котором одно тело может двигаться по другому телу.
2. Коэффициент кинетического трения
Мы можем определить коэффициент кинетического трения как отношение кинетического трения к нормальной реакции, и его символ равен μ к .
Отсюда формула коэффициента кинетического трения:
μ k = кинетическое трение (F k ) / нормальная реакция (R)
Здесь кинетическое трение — это трение между телами, когда одно тело движется или катится по другому.
Связь между коэффициентами кинетического и статического трения
Предельное трение (F) > Кинетическое трение (F k ) или, (F/R) > (F k /R) или µ s > µ k
Следовательно, коэффициент предельного трения всегда больше коэффициента кинетического трения.
1. Как найти коэффициент кинетического трения на склоне?
Предположим, у нас есть наклонная плоскость, которая составляет 60 градусов с горизонтальной плоскостью, и ящик скользит вниз с ускорением 5,62 м/с 2 .
Здесь
- Угол наклона (A) = 60 градусов
- Ускорение ящика (a) = 5,62 м/с 2
- Коэффициент трения (μ k ) = ?
На изображении выше сила, действующая на наклонную плоскость, равна
Сила = mgsinA – Сила трения
Мы знаем,
- Сила = ma
- Сила трения = μ k R (нормальная реакция)
Подставляя значение
=> ma = mgsinA - μ k R
Кроме того, на изображении значение R равно mgCosA . Итак, наше уравнение становится
=> ma = mgsinA - μ k (mgcosA)
Прием мг общий
=> ma = мг (sinA - μ k cosA)
сняв м с двух сторон, получим
=> a = g (sinA - μ k cosA)
подставив значение на , g (ускорение под действием силы тяжести) и A
=> 5,62 = 9,8 (sin60 - μ k cos60) => 5,62 / 9,8 = sin60 - мк к cos60
мы знаем значение sin60 равно 0,87 и cos60 равно 0,5
=> 0,57 = 0,87 - мк к 0,5 =>мк к 0,5 = 0,87 - 0,57 => мк к = 0,3/0,5 => μ k = 0,6
Следовательно, коэффициент кинетического трения (трения скольжения) равен 0,6 .
2. Что такое μ
k между блоком и столешницей?Предположим, что брусок массой 6 кг толкается по поверхности стола силой 9 ньютонов. Найдите коэффициент трения между бруском и поверхностью стола, если он движется с постоянной скоростью 1,8 м/с.
Здесь
- Масса блока (м) = 6 кг
- Приложенная сила (F) = 9 Ньютон
- Постоянная скорость блока (v) = 1,8 м/с
- μ k между блоком и столешницей = ?
Согласно нашей диаграмме сила, приложенная к телу, равна
Приложенная сила = ma + сила трения F = F f + мА
Из нашего вопроса мы знаем, что блок движется с постоянной скоростью, поэтому ускорение (a) становится равным 0 .
=> F = F f + м * 0 => Ф = Ф f
Мы знаем, что величина силы трения равна μ k R (сила реакции). Подстановка значения
=> F = μ k R => F = μ k (мг) => мк к = Ф/(мг)
Замена значения м , г и F

=> мк к = 9 / (6 * 9,8) => мк к = 9 / 58,8 => мк к = 0,15.
Следовательно, коэффициент трения между блоком и столешницей равен 0,15 .
Coefficient of Friction of Common Materials
| Materials | Coefficient of static friction | Coefficient of kinetic friction |
|---|---|---|
| Steel on rod | 0.74 | 0.57 |
| Aluminum on steel | 0,61 | 0,47 |
| Медь на стали | 0,53 | 0,36 |
| Латунь на стали | 0.51 | 0.44 |
| Copper on cast iron | 1.05 | 0.29 |
| Glass on glass | 0.94 | 0.40 |
| Copper on glass | 0.68 | 0.53 |
| Резина по бетону (сухая) | 1,00 | 0,80 |
| Резина по бетону (мокрая) | 0,30 | 0,25 |
Сопутствующая статья
- Типы трения
9.
 1: Сухое трение — Инженерные тексты
1: Сухое трение — Инженерные тексты- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 70274
- Дэниел У. Бейкер и Уильям Хейнс
- Университет штата Колорадо через Engineeringstatics
Ключевые вопросы
- Сравните виды трения, рассматриваемые в статике, с другими существующими типами трения
- Знайте, когда можно использовать уравнение \(F=\mu_\text{s} N\), а когда нельзя
- Графически покажите, как векторы трения и нормальной силы связаны с результирующим вектором трения и углом трения при предстоящем движении.
- Найдите и вычислите угол трения \(\phi_\text{s}\) на диаграмме свободного тела
- Объясните, как распределенная нормальная сила может быть представлена точечной силой, которая перемещается по мере изменения распределения нормальной силы.

Существует несколько типов трения, в том числе:
- Сухое трение: сила, препятствующая скольжению одной твердой поверхности по другой твердой поверхности
- Жидкостное трение: трение между слоями вязкой жидкости в движении
- Внутреннее трение: сила сопротивления внутренней деформации твердого материала
Статика фокусируется на сухом трении. Сухое трение возникает между двумя контактирующими поверхностями и всегда действует в направлении, противоположном относительному движению контактирующих поверхностей. Мы можем представить эту распределенную силу как сосредоточенную силу трения. В зависимости от деталей ситуации сухое трение может удерживать объект в равновесии или вызывать его ускорение или замедление. В Статика нас интересуют только объекты, находящиеся в равновесии; ускорение и замедление объектов будут рассмотрены в другом курсе.
Рассмотрим футбольные тренировочные сани, показанные на рис. 9.1.1. Перед использованием вес саней поддерживается нормальной силой непосредственно под центром тяжести, а трение между землей и салазками равно нулю. Когда игроки толкают сани, чтобы сдвинуть их вправо, вдоль нижней поверхности салазок возникает сухое трение, чтобы предотвратить скольжение салазок вправо. Эта сила трения представлена в виде точечной нормальной силы, смещенной от центра тяжести салазок. Это смещение требуется для поддержания вращательного равновесия с учетом толкающей силы. Если сила толкания достаточно велика, равновесие нарушится, и сани начнут скользить вправо.
9.1.1. Перед использованием вес саней поддерживается нормальной силой непосредственно под центром тяжести, а трение между землей и салазками равно нулю. Когда игроки толкают сани, чтобы сдвинуть их вправо, вдоль нижней поверхности салазок возникает сухое трение, чтобы предотвратить скольжение салазок вправо. Эта сила трения представлена в виде точечной нормальной силы, смещенной от центра тяжести салазок. Это смещение требуется для поддержания вращательного равновесия с учетом толкающей силы. Если сила толкания достаточно велика, равновесие нарушится, и сани начнут скользить вправо.
Рисунок 9.1.1. Сухое трение возникает между днищем тренировочных саней и полем, когда движение приближается или происходит.
Силы трения, действующие на мотоцикл на рис. 9.1.2, более сложны. Оба колеса вращаются по часовой стрелке, но заднее колесо приводится в движение двигателем и цепью, а переднее колесо вращается за счет трения о дорогу. Сила трения на заднем колесе действует вправо и позволяет велосипеду поддерживать скорость или ускоряться.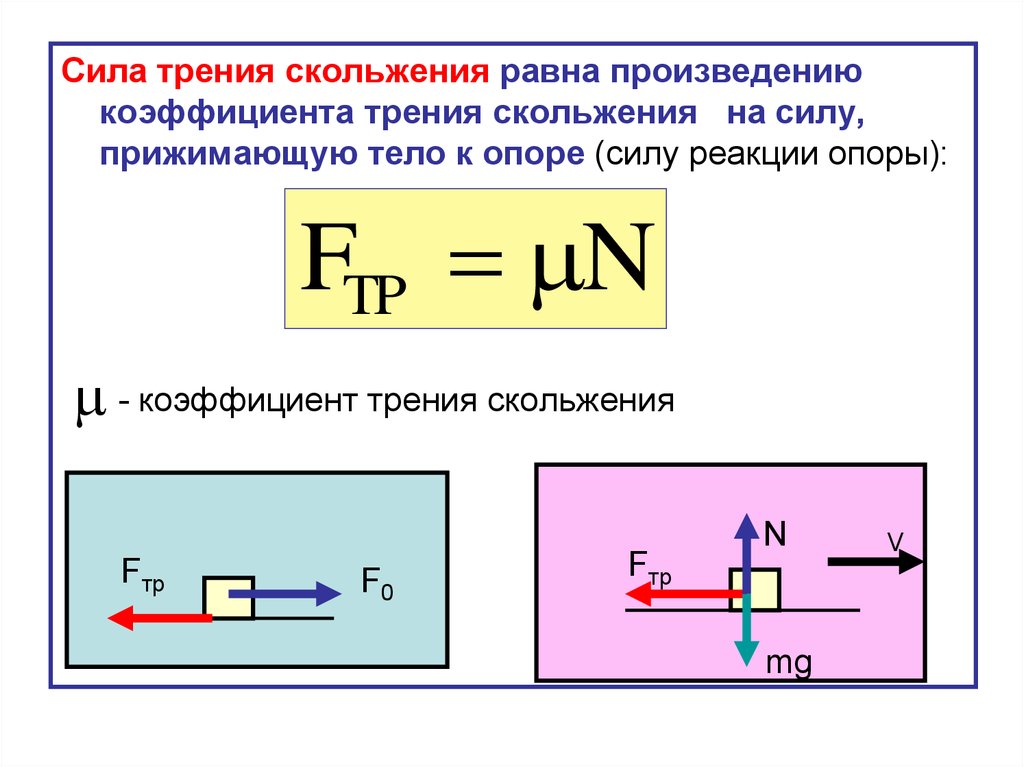 Сухое трение на передней шине действует влево и замедляет движение мотоцикла.
Сухое трение на передней шине действует влево и замедляет движение мотоцикла.
Рисунок 9.1.2. Сухое трение на мотоцикле происходит там, где шины соприкасаются с дорогой.
Как из условия задачи определить, какую фазу трения использовать?
Наиболее часто используемой моделью сухого трения является кулоновское трение, которое включает фазы (как показано на рис. 9.1.4 ниже): (1) статическое, но не предстоящее трение, (2) приближающееся движение и (3) кинетическое трение. Кулоновское трение зависит от коэффициента трения \(\mu\), который служит константой пропорциональности между нормальной силой и силой трения. Коэффициент трения \mu всегда больше 0 и обычно меньше 1. Коэффициент трения может быть больше 1 для материалов, которые проявляют положительную адгезию друг к другу (например, силиконовый каучук или склеенные поверхности).
Рисунок 9.1.4. Простая модель книги, которую толкают горизонтально, сидя на столе. FBD предназначены для системы, книги и стола. Кроме того, показан график кулоновского трения и пронумерованы различные фазы.
FBD предназначены для системы, книги и стола. Кроме того, показан график кулоновского трения и пронумерованы различные фазы.
Вот более подробное обсуждение того, что происходит на каждой фазе трения.
- В начале графика на рис. 9.1.4 существует материальное взаимодействие между книгой и столом, поэтому сила трения доступна, но не задействована \(F_f=F_\text{push}=0\text{ .}\)
- Если предположить, что толкающая сила \(F_\text{push}\) постепенно увеличивается от нуля в этой статической, но не надвигающейся фазе, сила трения увеличивается пропорционально, чтобы поддерживать равновесие сил и статическое состояние коробки \(F_f=F_\ текст{нажать}\текст{.}\)
- Затем достигается максимально возможное трение при приближающемся движении, и сила толкания соответствует максимальной силе трения \(F_{f_\text{max}}=\mu_\text{s} N\text{.}\)
- Наконец, если толкающая сила увеличивается за пределы приближающегося движения, книга начинает двигаться под действием кинетического трения \(F_{f_\text{max}}=\mu_k N\text{.
 }\)
}\)
Обратите внимание, что трение при предстоящем движении всегда больше, чем кинетическое трение, потому что коэффициент \(\mu_\text{s} \gt \mu_k\) для большинства материалов. На практике это говорит нам о том, что как только материал начинает двигаться, его легче продолжать двигаться, чем начинать движение из состояния покоя.
Если вам интересно, почему мы включаем кинетическое трение в курс статики, помните, что тело, находящееся в равновесии, может двигаться с постоянной скоростью.
Ключ к решению, какой тип трения подходит для данной проблемы, будет зависеть от специфики постановки задачи.
Таблица 9.1.5. Краткое описание трех фаз трения с ключом к распознаванию и примерами каждой из них.
Тип | Основное уравнение | Ключ к распознаванию |
Статическое, но не надвигающееся движение | Нет, \(F_f\) не зависит от \(N\text{. | Упоминание сидячего или статического, но без экстремального языка |
Пример es: К колесу, неподвижно удерживаемому тормозным рычагом, приложен момент \(\Nm{20}\). Чему равна сила трения между колесом и тормозным рычагом? Ящик стоит на наклонной поверхности, найти равнодействующую сил трения и нормальных сил, действующих на ящик. | ||
Надвигающееся движение | \(F_f = \mu_\text{s} N\) | Использование экстремального языка (связанного с максимальными или минимальными значениями) в условиях задачи |
Примеры: Какая максимальная сила приложена к ящику, прежде чем он начнет двигаться? При каком минимальном коэффициенте статического трения ящик будет оставаться неподвижным? Какой самый легкий ящик не соскользнет и не опрокинется на этом склоне? Какой наибольший момент будет удерживать тормозной рычаг в статике? | ||
Кинетическое трение | \(F_f = \mu_k N\) | Упоминание о теле, движущемся с постоянной скоростью под действием трения. |
Примеры: Коробка \(\kg{40}\) скользит вниз по склону под углом 20°, каков коэффициент трения, чтобы поддерживать постоянную скорость? Веревка скользит по дереву с известным коэффициентом трения и постоянной скоростью, чему равен контактный угол веревки? | ||
Обратите внимание, что когда вы решаете статические, но не приближающиеся задачи движения (в отличие от приближающихся или кинетических), вам потребуется один дополнительный фрагмент данных, указанный в задаче, для решения как для \(F_f \), так и для \ (N\), так как вы не сможете применить уравнение \(F_f=\mu N\text{.}\)
Угол трения и равнодействующая трения
Трение и нормальные силы могут быть представлены двумя эквивалентными способами:
Трение и нормальные силы. Использование этих перпендикулярных векторов наиболее удобно в задачах типа блоков и клиньев и одинаково хорошо применимо во всех трех фазах трения (статическое, но не надвигающееся, надвигающееся движение и кинетическое трение)
Использование этих перпендикулярных векторов наиболее удобно в задачах типа блоков и клиньев и одинаково хорошо применимо во всех трех фазах трения (статическое, но не надвигающееся, надвигающееся движение и кинетическое трение)
Результирующая сила и угол трения. Вспомним, что результанты представляют собой сумму двух или более векторов. В этом случае равнодействующая силы трения равна \(\vec{R}=\vec{F}+\vec{N}\text{.}\). Угол трения \(\phi_s \) — это угол между равнодействующей силы трения и нормальные силы, но применима только при надвигающемся движении. Результат трения и угол трения используются для задач типа винтов, гибких ремней и подшипников скольжения.
Рисунок 9.1.6. Блок веса \(W\) отталкивается в сторону под действием силы \(P\text{.}\) Совместное воздействие трения и нормальных сил можно смоделировать как отдельное трение (\(F\)) и нормальное (\(N\)) силы (слева) или результирующая сила трения (\(R\)) и угол трения \((\phi_s)\text{. }\)
}\)
Угол трения \(\phi_s\) относится непосредственно к коэффициенту трения покоя \((\mu_\text{s})\), поскольку угол трения \(\phi_s\) — это внутренний угол прямоугольного треугольника, образованный нормальной силой \(N\text{ ,}\) равнодействующая трения \(R\text{,}\) и сила трения \(F\text{.}\) Отсюда: 9{-1}\left(\frac{F}{N} \right)\tag{9.1.1} \end{equation}
Нормальные силы
Обычно в двумерных задачах нормальные силы представляются в точке контакта или в середине контактной поверхности. Однако нормальные силы редко представляют собой точечные нагрузки, а представляют собой нагрузки, распределенные по поверхности. Вектор точечной силы мы обычно представляем как нормальную силу на распределенных нагрузках (глава 7). Чтобы продемонстрировать это далее, взгляните на рисунок 9.1.7.
Рисунок 9.1.7. (A) Ящик в состоянии покоя имеет равномерно распределенную нормальную силу вдоль дна ящика. Следовательно, результирующая нормальная сила расположена непосредственно под силой веса, а сила трения (пока она доступна) не задействована.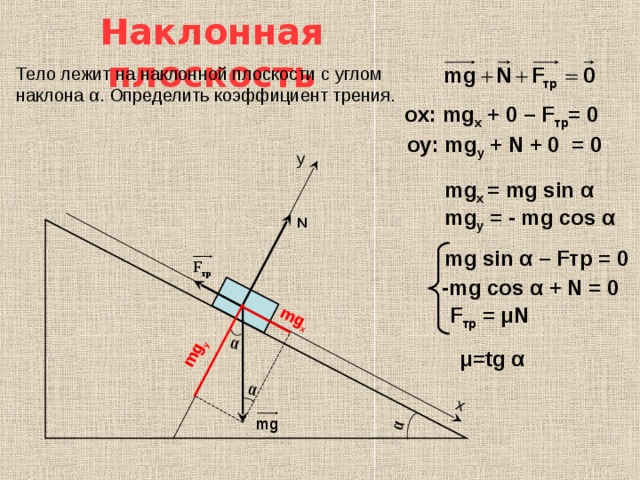 (B) При приложении толкающей силы \(F_\text{push}\) распределенная нормальная сила меняет форму, а результирующая нормальная сила \(N\) смещается вправо для поддержания равновесия. (C) Эта тенденция сохраняется по мере того, как вы сильнее нажимаете на коробку, поскольку нормальная сила продолжает смещаться вправо.
(B) При приложении толкающей силы \(F_\text{push}\) распределенная нормальная сила меняет форму, а результирующая нормальная сила \(N\) смещается вправо для поддержания равновесия. (C) Эта тенденция сохраняется по мере того, как вы сильнее нажимаете на коробку, поскольку нормальная сила продолжает смещаться вправо.
Эта страница под названием 9.1: Сухое трение распространяется под лицензией CC BY-NC-SA 4.0, автором, ремикшированием и/или курированием занимались Дэниел У. Бейкер и Уильям Хейнс (Engineeringstatics) посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Дэниел В.



 }\)
}\) }\)
}\) (Вы научитесь решать проблемы трения с непостоянной скоростью в динамике).
(Вы научитесь решать проблемы трения с непостоянной скоростью в динамике).