Site Loader
Posted on 19.07.1991

Содержание

Коэффициент сопротивления какой буквой обозначается

При замыкании электрической цепи, на зажимах которой имеется разность потенциалов, возникает электрический ток. Свободные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении свободные электроны наталкиваются на атомы проводника и отдают им запас своей кинетической энергии. Таким образом, электроны, проходя по проводнику, встречают сопротивление своему движению. При прохождении электрического тока через проводник последний нагревается.


Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

  • Графическое обозначение радиодеталей на схемах
  • СТ СЭВ 1565-79 Нормативно-техническая документация в строительстве.
    Буквенные обозначения
  • Основные обозначения в сопротивлении материалов
  • Почему необходимо корректировать коэффициент мощности?
  • I. Механика
  • Что такое терморезистор, его обозначение на схеме разновидности и применение

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Никого не слушай! Выбери насос САМ!

Графическое обозначение радиодеталей на схемах


Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах.

Для того, чтобы различать силы, их обозначают следующим образом. Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя! Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах. На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле.

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз. Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:. Сила приложена в точке соприкосновения двух поверхностей.

Направлена в сторону противоположную движению. Так как тело представляем в виде материальной точки, силу можно изображать с центра.

Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол.

То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне.

Предмет как бы деформировал привычное положение и связи молекул внутри стола , они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются». Абсолютно любое тело, даже очень легкое например,карандаш, лежащий на столе , на микроуровне деформирует опору. Поэтому возникает реакция опоры. Специальной формулы для нахождения этой силы нет.

Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как. Это сила возникает в результате деформации изменения первоначального состояния вещества.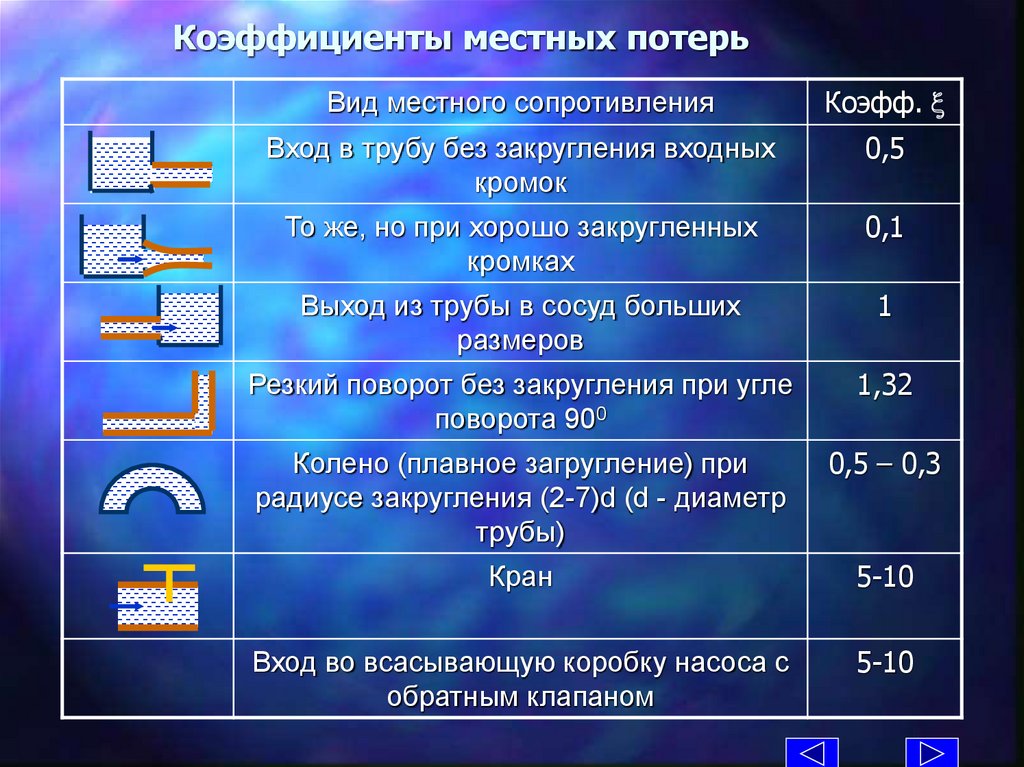 Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины.

Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости. Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия.

Значение модуля Юнга табличное. Подробнее о свойствах твердых тел здесь. Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору не на предмет!

Формулы определения веса нет. Обозначается эта силы буквой. Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление. Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело.

Сила тяжести действует на тело. Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю! Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила. Обратите внимание, вес — сила, измеряется в Ньютонах.

Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно Н! Сила возникает в результате взаимодействия тела с жидкость газом , при его погружении в жидкость или газ.

Эта сила выталкивает тело из воды газа. Поэтому направлена вертикально вверх выталкивает. Определяется по формуле:. Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет. Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона , сила Ампера , сила Лоренца , подробно рассмотрены в разделе Электричество.

Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником. Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует.

Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.

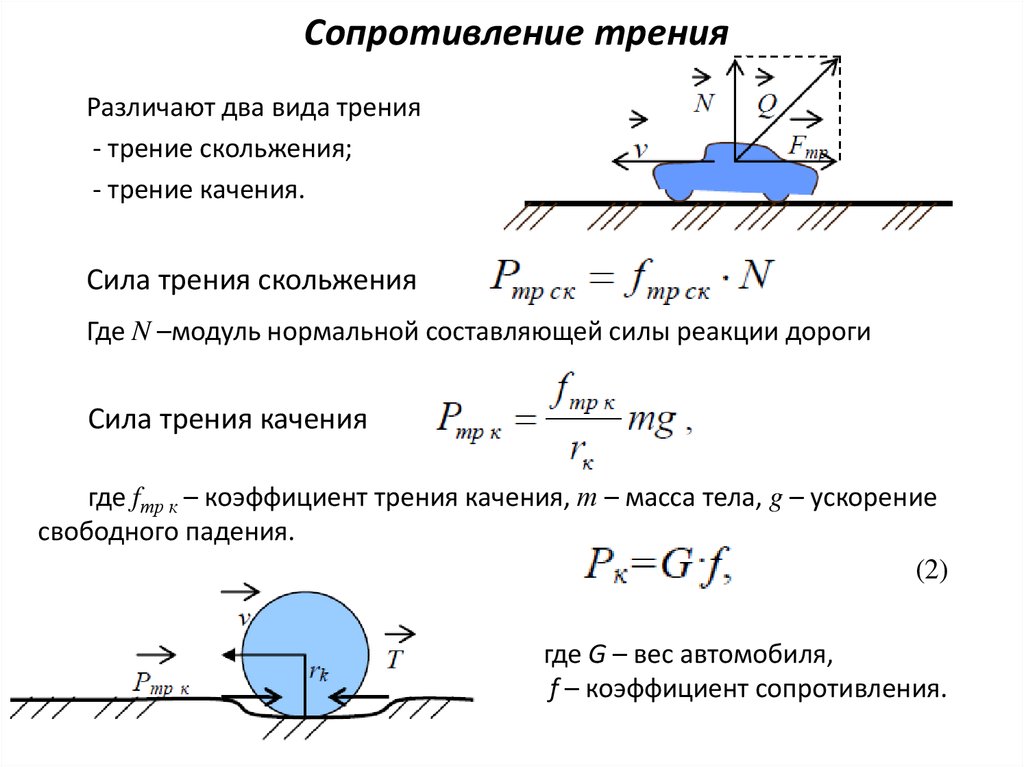
Различают внешнее сухое и внутреннее вязкое трение. Внешнее трение возникает между соприкасающимися твердыми поверхностями, внутреннее — между слоями жидкости или газа при их относительном движении. Существует три вида внешнего трения: трение покоя, трение скольжения и трение качения.

Сила сопротивления возникает при движении тела в жидкости или в газе. Величина силы сопротивления зависит от размеров и формы тела, скорости его движения и свойств жидкости или газа. При небольших скоростях движения сила сопротивления пропорциональна скорости тела. Рассмотрим взаимное притяжение предмета и Земли.

Между ними, согласно закону гравитации возникает сила А сейчас сравним закон гравитации и силу тяжести. Величина ускорения свободного падения зависит от массы Земли и ее радиуса!

Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты. Расстояние от центра Земли до полюсов меньше, чем до экватора.

Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.

При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли. Оптика Волновая оптика Геометрическая оптика V. Теория относительности Теория относительности VI. Трение качения определяется по формуле Сила сопротивления возникает при движении тела в жидкости или в газе.

При небольших скоростях движения сила сопротивления пропорциональна скорости тела При больших скоростях пропорциональна квадрату скорости.


СТ СЭВ 1565-79 Нормативно-техническая документация в строительстве. Буквенные обозначения

На потери энергии из-за низкого коэффициента мощности часто не обращают внимания. Между тем, они могут привести к снижению надёжности, проблемам с безопасностью и повышенным расходам на электроэнергию. Чем ниже коэффициент мощности, тем менее экономична система. Реальное количество используемой или рассеиваемой мощности в цепи называется активной мощностью. Реактивные нагрузки индуктивности и конденсаторы производят так называемую реактивную мощность. Линейная комбинация активной и реактивной мощностей называется полной или кажущейся мощностью.

Тип конструкции обозначается буквой радиальный (R) или диагональная RRC — коэффициент сопротивления качению (rolling resistance coefficient).

Основные обозначения в сопротивлении материалов

На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб! Коэффициент сопротивления дает возможность учитывать потери энергии при движении тела. Чаще всего рассматривают два типа движения: движение по поверхности и движение в веществе жидкости или газе. Если рассматривают движение по опоре, то обычно говорят о коэффициенте трения. В том случае, если рассматривают движение тела в жидкости или газе, то имеют в виду коэффициент сопротивления формы. Речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной.

Почему необходимо корректировать коэффициент мощности?

Главная страница Содержание Введение Основы гидростатики Основы гидродинамики Гидравлические сопротивления Истечние жидкости из отверстий, насадков и из-под затворов Гидравлический расчет простых трубопроводов Гидравлические машины Список литературы Лекция 4. Потери энергии уменьшение гидравлического напора можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются иногда равномерно по длине трубопровода — это линейные потери; в других — они сосредоточены на очень коротких участках, длиной которых можно пренебречь, — на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т. Источником потерь во всех случаях является вязкость жидкости. Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.

Наиболее распространенный элемент электрической цепи. Различают резисторы постоянные и переменные.

I. Механика

Вся информации, находящаяся на боковой части шины, называется маркировка. Как правило, это самые крупные буквы, расположенные на покрышке. Название модели располагается всегда выше страны производства. В зависимости от дизайна, наименование модели может содержать дополнительные изображения или символы. Данная информация наносится на шину с двух сторон. Последние 4 символа обозначают дату производства.

Что такое терморезистор, его обозначение на схеме разновидности и применение

Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении.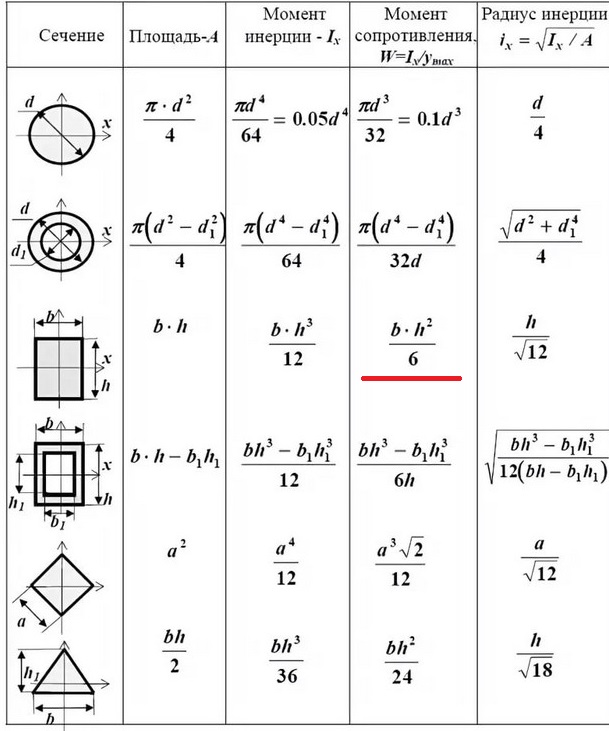 Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом. Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя! Сил в природе много.

Определенная величина обозначается буквой латинского или греческого Коэффициент объемного расширения. b Момент сопротивления сечения.

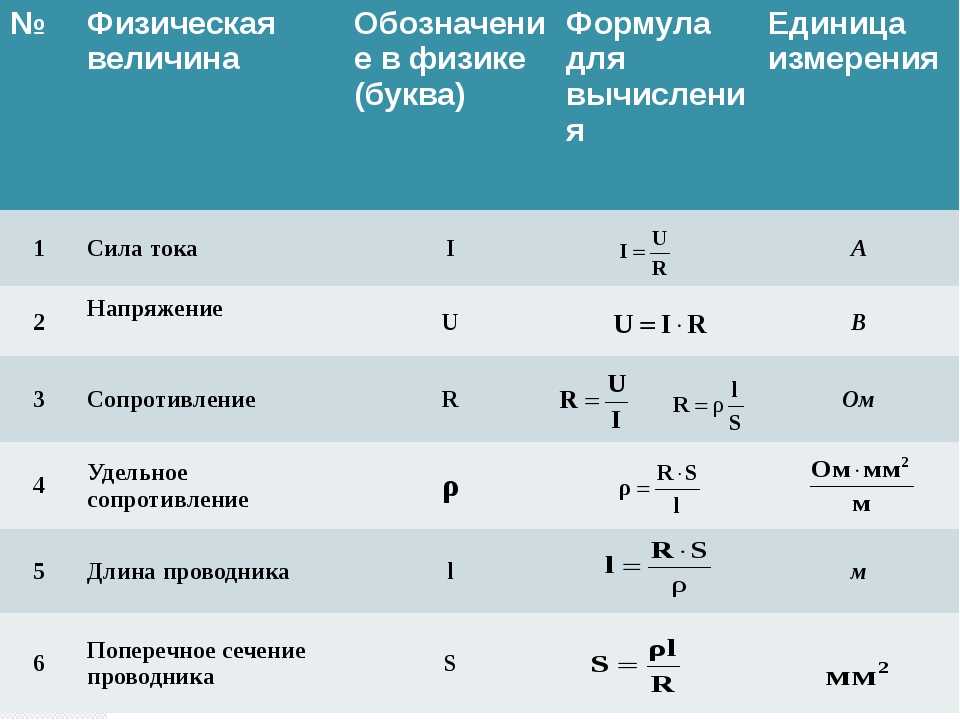
Какая связь существует между напряжением, током и сопротивлением? Это непрерывное движение свободных электронов по проводникам цепи называется током. Иногда его, по аналогии с потоком воды через трубу, называют «потоком». Напряжение — это определённая мера потенциальной энергии, которая всегда взаимосвязана с двумя точками цепи.

Вход Регистрация. Поиск по сайту. Учебные заведения. Проверочные работы. Отправить отзыв. Архив Физика Шпаргалки Буквы, используемые для обозначения величин.

Настоящий стандарт является обязательным в рамках Конвенции о применении стандартов СЭВ.

Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м 2. Имеются два проводника. У какого из них больше сопротивление, если они: а имеют одинаковую длину и площадь сечения, но один из них сделан из константана, а другой — из фехраля; б сделаны из одного и того же вещества, имеют одинаковую толщину, но один из них в 2 раза длиннее другого; в сделаны из одного и того же вещества, имеют одинаковую длину, но один из них в 2 раза тоньше другого? Электрическое сопротивление. Направленному движению электрических зарядов в любом проводнике препятствуют молекулы и атомы этого проводника. Поэтому как внешний участок цепи, так и внутренний внутри самого источника энергии оказывают препятствие прохождению тока.

Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул. Для обозначения физических величин и понятий в физике используются буквы латинского и греческого алфавитов, а также несколько специальных символов и диакритических знаков. Поскольку количество физических величин больше количества букв в латинском и греческом алфавитах, одни и те же буквы используются для обозначения различных величин.


Гидравлические сопротивления

Потери энергии (уменьшение гидравлического напора) можно наблюдать в движущейся жидкости не только на сравнительно длинных участках, но и на коротких. В одних случаях потери напора распределяются (иногда равномерно) по длине трубопровода — это линейные потери; в других — они сосредоточены на очень коротких участках, длиной которых можно пренебречь, — на так называемых местных гидравлических сопротивлениях: вентили, всевозможные закругления, сужения, расширения и т.д., короче всюду, где поток претерпевает деформацию. Источником потерь во всех случаях является вязкость жидкости.

Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.

Третья область — область больших Re и Δ/r0, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.

Итак, потери напора, определяемые по формуле Вейсбаха-Дарси, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной абсолютной шероховатости Δэ. Для удобства сводные данные по определению λ представлены в таблице 4.1.

Пользоваться приведенными в табл. 4.1 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рис.4.8), при помощи которой по известным Re и Δэ/ d весьма просто определяется λ.

Рис. 4.8. Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения

4.5. Местные гидравлические сопротивления

Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.

Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.

Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.

1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т. е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.

Рис. 4.9. Внезапное расширение трубы

При внезапном расширении русла (трубы) (рис.4.9) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:

где S1, S2 — площадь поперечных сечений 1-1 и 2-2.

Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей

Выражение ( 1 — S1/S2 )2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом

2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Рис. 4.10. Постепенное расширение трубы

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

где hтр и hрасш — потери напора на трение и расширение (вихреобразование). где n = S2/S1 = ( r2/r1 ) 2 — степень расширения диффузора. Потеря напора на расширение hрасш имеет ту же самую природу, что и при внезапном расширении русла

где k — коэффициент смягчения, при α= 5…20°, k = sinα.

Учитывая это полную потерю напора можно переписать в виде:

откуда коэффициент сопротивления диффузора можно выразить формулой

Рис. 4.11. Зависимость ζдиф от угла

Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:

При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рис. 4.11).

3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).

где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:

При выходе трубы из резервуара больших размеров, когда можно считать, что S2/S1 = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления   ζсуж = 0,5.

4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение

Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).

5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле

где ζкол — коэффициент сопротивления колена круглого сечения, который определяется по графику в зависимости от угла колена δ (рис.4.16).

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζотв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.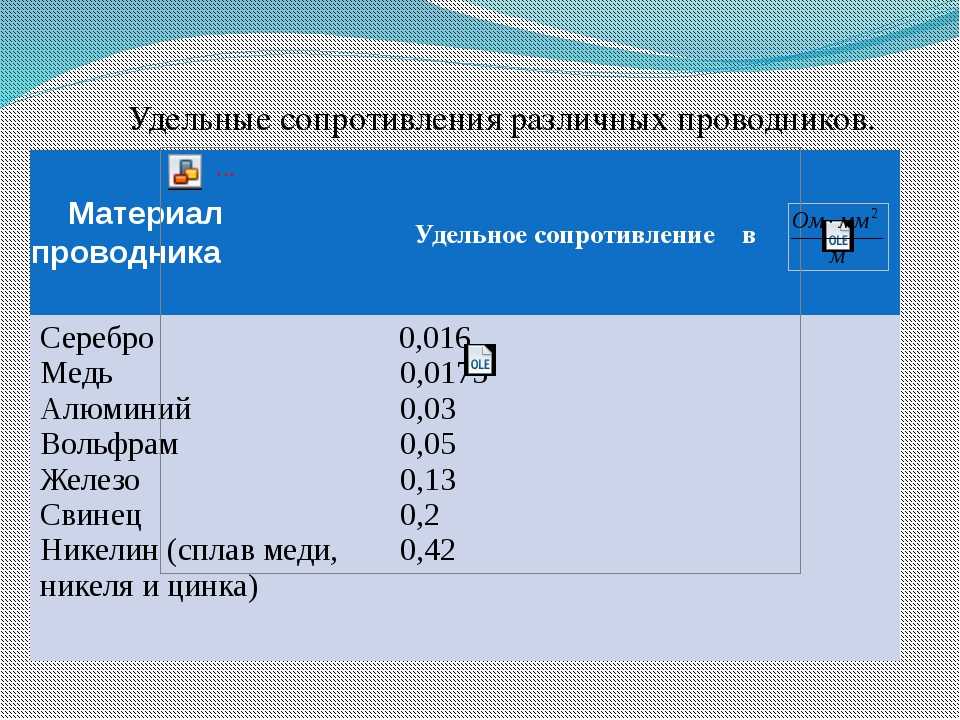

Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.

Коэффициент аэродинамического сопротивления | Автопедия | Фэндом

в: Страницы, использующие магические ссылки ISBN, Аэродинамика, Аэрокосмическая техника,

а также еще 2

Посмотреть источник File:14ilf1l.svg

В гидродинамике коэффициент сопротивления (обычно обозначаемый как: c d , c x или c w ) используется для количественной оценки безразмерной величины. сопротивление или сопротивление объекта в текучей среде, такой как воздух или вода. Он используется в уравнении сопротивления, где более низкий коэффициент сопротивления указывает на то, что объект будет иметь меньшее аэродинамическое или гидродинамическое сопротивление. Коэффициент аэродинамического сопротивления всегда связан с определенной площадью поверхности. [1]

Коэффициент аэродинамического сопротивления любого объекта включает в себя эффекты двух основных факторов гидродинамического сопротивления: поверхностного трения и сопротивления формы. Коэффициент аэродинамического сопротивления подъемной аэродинамической или подводной части также включает в себя влияние сопротивления, вызванного подъемной силой. [2] [3] Коэффициент аэродинамического сопротивления всей конструкции, такой как самолет, также включает влияние интерференционного сопротивления. [4] [5]

Содержимое

  • 1 Определение
  • 2 Фон
  • 3 Коэффициент аэродинамического сопротивления c d примеры
    • 3. 1 Общие
  • 4 Самолет
  • 5 Обтекаемые и обтекаемые потоки тела
    • 5.1 Концепция
      • 5.1.1 Практический пример
  • 6 См. также
  • 7 Примечания
  • 8 Каталожные номера

Определение

Коэффициент аэродинамического сопротивления определяется как:

где:

— сила сопротивления, которая по определению является составляющей силы в направлении скорости потока, [6]
— массовая плотность жидкости, [7]
— скорость объекта относительно жидкости, а
— эталонная область.

Эталонная площадь зависит от того, какой тип коэффициента лобового сопротивления измеряется. Для автомобилей и многих других объектов эталонной площадью является проекция передней части транспортного средства. Это не обязательно может быть площадь поперечного сечения транспортного средства, в зависимости от того, где берется поперечное сечение. Например, для сферы (обратите внимание, это не площадь поверхности = ).

Для аэродинамических профилей опорной площадью является площадь в плане. Поскольку это, как правило, довольно большая площадь по сравнению с проектируемой лобовой площадью, результирующие коэффициенты сопротивления имеют тенденцию быть низкими: намного ниже, чем для автомобиля с таким же сопротивлением и лобовой площадью и с той же скоростью.

В дирижаблях и некоторых телах вращения используется коэффициент объемного сопротивления, в котором опорной площадью является квадрат кубического корня из объема дирижабля. Погруженные обтекаемые тела используют площадь смоченной поверхности.

Два объекта с одинаковой опорной площадью, движущиеся с одинаковой скоростью в жидкости, испытывают силу сопротивления, пропорциональную их соответствующим коэффициентам сопротивления. Коэффициенты для необтекаемых объектов могут быть 1 и более, для обтекаемых гораздо меньше.

Фон

Файл:Cd flatplate. svg

Обтекание пластины с застоем.

Основная статья: Уравнение сопротивления

Уравнение сопротивления:

по сути является утверждением, что сила сопротивления любого объекта пропорциональна плотности жидкости и пропорциональна квадрату относительной скорости между объектом и жидкостью.

C d не является постоянной величиной, а изменяется в зависимости от скорости, направления потока, положения объекта, размера объекта, плотности и вязкости жидкости. Скорость, кинематическая вязкость и характерный масштаб длины объекта включены в безразмерную величину, называемую числом Рейнольдса или . таким образом, является функцией . В сжимаемом потоке важна скорость звука, которая также является функцией числа Маха.

Для определенной формы тела коэффициент сопротивления зависит только от числа Рейнольдса, числа Маха и направления потока. При малом числе Маха коэффициент лобового сопротивления не зависит от числа Маха. Кроме того, изменение числа Рейнольдса в практическом диапазоне обычно невелико, в то время как для автомобилей на скорости шоссе и самолета на крейсерской скорости направление входящего потока также более или менее одинаково. Таким образом, коэффициент лобового сопротивления часто можно рассматривать как константу. [8]

Чтобы обтекаемое тело достигло низкого коэффициента сопротивления, пограничный слой вокруг тела должен оставаться прикрепленным к поверхности тела как можно дольше, в результате чего след становится узким. Высокое сопротивление формы приводит к широкому следу. Пограничный слой будет переходить из ламинарного в турбулентный при достаточно высоком числе Рейнольдса обтекания тела. Более высокие скорости, более крупные объекты и более низкая вязкость способствуют увеличению числа Рейнольдса. [9]

File:Dragsphere nasa.svg

Коэффициент сопротивления C d для сферы как функция числа Рейнольдса Re , полученный в результате лабораторных экспериментов. Сплошная линия соответствует сфере с гладкой поверхностью, а пунктирная линия — шероховатой поверхности. Цифры вдоль линии обозначают несколько режимов течения и связанные с ними изменения коэффициента сопротивления:
• 2: присоединенное течение (стоксово течение) и стационарное отрывное течение,
• 3: отрывное нестационарное течение, имеющее ламинарный пограничный слой течения перед отрывом. , и создающий вихревую дорожку,
•4: отрывное нестационарное течение с ламинарным пограничным слоем на входной стороне, до отрыва потока, за сферой хаотический турбулентный след,
•5: закритическое отрывное течение, с турбулентным пограничным слоем.

Для других объектов, таких как мелкие частицы, уже нельзя считать коэффициент сопротивления постоянным, но, безусловно, он является функцией числа Рейнольдса. [10] [11] [12] При малом числе Рейнольдса обтекание объекта не переходит в турбулентное, а остается ламинарным вплоть до отрыва от поверхности объекта. При очень малых числах Рейнольдса, без отрыва потока, сила сопротивления пропорциональна вместо ; для сферы это известно как закон Стокса. Число Рейнольдса будет низким для небольших объектов, низких скоростей и жидкостей с высокой вязкостью. [9]

Значение, равное 1, было бы получено в том случае, когда вся жидкость, приближающаяся к объекту, останавливается, создавая застойное давление по всей передней поверхности. На верхнем рисунке показана плоская пластина с жидкостью, поступающей справа и останавливающейся на пластине. График слева от него показывает одинаковое давление по всей поверхности. В реальной плоской пластине жидкость должна вращаться по бокам, и полное стагнационное давление наблюдается только в центре, спадая к краям, как на нижнем рисунке и графике. Только с учетом лицевой стороны реальной плоской пластины будет меньше 1; за исключением того, что на задней стороне будет всасывание: отрицательное давление (относительно окружающей среды). Общая площадь реальной квадратной плоской пластины, перпендикулярной потоку, часто указывается как 1. 17.

Коэффициент аэродинамического сопротивления

c d примеры

Общее

В общем, не является абсолютной константой для данной формы тела. Она зависит от скорости воздушного потока (или, в более общем случае, от числа Рейнольдса). Гладкая сфера, например, имеет значение, которое варьируется от высоких значений для ламинарного потока до 0,47 для турбулентного потока.

Пуля
Формы
в г Предмет
8965 ламинарная плоская пластина, параллельная потоку ()
0,005 турбулентная плоская пластина, параллельная потоку ()
0,075 Пак-автомобиль
0,1 гладкая сфера ()
0,47 гладкая сфера ()
0,15 Schlörwagen 1939 [13]
0,186-0,189 Фольксваген XL1 2014
0,19 General Motors EV1 1996 [14]
0,24 Тесла Модель S
0,25 Тойота Приус (3-го поколения)
0,26 БМВ и8
0,26 Ниссан ГТ-Р (2011-2014)
0,27 Ниссан ГТ-Р (2007-2010)
0,28 Mercedes-Benz CLA-Класс Тип C 117. [15]
0,295 (не оживальная, с дозвуковой скоростью)
0,3 Ауди 100 С3 (1982)
0,48 шероховатая сфера (),
Volkswagen Beetle [16] [17]
0,75 типовая модель ракеты [18]
.8-.9 кофейный фильтр лицевой стороной вверх
1,0 дорожный велосипед плюс велосипедист, туристическое положение [19]
1,0–1,1 лыжник
1,0–1,3 провода и кабели
1,0–1,3 человек (вертикальное положение)
1,1-1,3 прыгун с трамплина [20]
1,28 плоская пластина перпендикулярно потоку (3D) [21]
1,3–1,5 Эмпайр Стейт Билдинг
1,8–2,0 Эйфелева башня
1,98–2,05 плоская пластина перпендикулярно потоку (2D)
2. 1 гладкий кирпич.

Самолет

Как отмечалось выше, для самолетов в качестве опорной площади при расчетах используется площадь крыла, в то время как для автомобилей (и многих других объектов) используется площадь лобового поперечного сечения; таким образом, коэффициенты , а не напрямую сопоставимы между этими классами транспортных средств. В аэрокосмической промышленности коэффициент лобового сопротивления иногда выражается в единицах сопротивления, где 1 единица сопротивления = 0,0001 а. [22]

Самолет [23]
в г Тип самолета
0,021 F-4 Phantom II (дозвуковой)
0,022 Лирджет 24
0,024 Боинг 787 [24]
0,027 Цессна 172/182
0,027 Цессна 310
0,031 Боинг 747
0,044 F-4 Phantom II (сверхзвуковой)
0,048 Старфайтер F-104
0,095 Х-15 (не подтверждено)

Обтекаемые и обтекаемые потоки тела

Понятие

Сопротивление в контексте гидродинамики относится к силам, которые действуют на твердый объект в направлении относительной скорости потока жидкости. Аэродинамические силы, действующие на тело, возникают в основном из-за разности давлений и вязких касательных напряжений. Таким образом, сила сопротивления тела может быть разделена на две составляющие: сопротивление трения (вязкое сопротивление) и сопротивление давления (сопротивление формы). Чистая сила сопротивления может быть представлена ​​следующим образом:

File:Aerodynamics of Airfoil.jpg

Поток через аэродинамический профиль, показывающий относительное влияние силы сопротивления на направление движения жидкости над телом. Эта сила сопротивления делится на сопротивление трения и сопротивление давления. Тот же аэродинамический профиль считается обтекаемым телом, если сопротивление трения (вязкое сопротивление) преобладает над сопротивлением давления, и считается телом с обтеканием, когда сопротивление давления (сопротивление формы) преобладает над сопротивлением трения.

где:

– коэффициент аэродинамического сопротивления,
— коэффициент сопротивления трения,
= Тангенциальное направление к поверхности площадью dA,
= нормальное направление к поверхности площадью dA,
— напряжение сдвига, действующее на поверхность, дА,
— давление вдали от поверхности, дА,
давление на поверхности дА,
— единичный вектор в направлении нормали к поверхности dA, образующий единичный вектор

Поэтому, когда в сопротивлении преобладает фрикционная составляющая, тело называется обтекаемым телом, тогда как в случае преобладающего сопротивления давлением тело называется блефовое тело. Таким образом, форма корпуса и угол атаки определяют вид сопротивления. Например, аэродинамический профиль рассматривается как тело с малым углом атаки обтекающей его жидкости. Это означает, что к нему присоединены пограничные слои, которые создают гораздо меньшее сопротивление давлению.

File:Pressure Drag and Friction Drag.png

Взаимосвязь между сопротивлением давления и сопротивлением трения

Создаваемый след очень мал, и сопротивление определяется компонентом трения. Поэтому такое тело (в данном случае профиль) называют обтекаемым, тогда как для тел с течением жидкости при больших углах атаки происходит отрыв пограничного слоя. В основном это происходит из-за неблагоприятных градиентов давления в верхней и задней частях аэродинамического профиля.

В связи с этим происходит образование следа, что, в свою очередь, приводит к образованию вихрей и падению давления из-за сопротивления давления. В таких ситуациях аэродинамический профиль останавливается и имеет более высокое сопротивление давлению, чем сопротивление трения. В этом случае тело описывается как тело блефа. Обтекаемое тело похоже на рыбу (Tuna, Oropesa и т.д.) или на профиль с малым углом атаки, тогда как обтекаемое тело похоже на кирпич, цилиндр или профиль с большим углом атаки. Для данной площади фронта и скорости обтекаемое тело будет иметь меньшее сопротивление, чем обтекаемое тело. Цилиндры и сферы принимаются в качестве тел обтекания, поскольку в сопротивлении преобладает составляющая давления в области следа при больших числах Рейнольдса.

Чтобы уменьшить это сопротивление, можно уменьшить отрыв потока или уменьшить площадь контакта с жидкостью (чтобы уменьшить сопротивление трения). Это снижение необходимо в таких устройствах, как автомобили, велосипеды и т. д., чтобы избежать вибрации и шума.

Практический пример

Аэродинамический дизайн автомобилей развивался с 1920-х до конца 20-го века. Это изменение конструкции с обтекаемого корпуса на более обтекаемый снизило коэффициент аэродинамического сопротивления примерно с 0,95 до 0,30.

Динамика аэродинамического сопротивления автомобилей по сравнению с изменением геометрии обтекаемых тел (от резкого до обтекаемого).

Динамика аэродинамического сопротивления автомобилей в сравнении с изменением геометрии обтекаемых тел (от резкого к обтекаемому).

См. также

  • Автомобильная аэродинамика
  • Коэффициент аэродинамического сопротивления автомобиля
  • Кризис перетаскивания
  • Коэффициент аэродинамического сопротивления при нулевой подъемной силе

Примечания

  1. ↑ Маккормик, Барнс В. (1979): Аэродинамика, аэронавтика и летная механика . п. 24, John Wiley & Sons, Inc., Нью-Йорк, ISBN 0-471-03032-5
  2. ↑ Клэнси, LJ: Аэродинамика . Раздел 5.18
  3. ↑ Эбботт, Айра Х., и фон Доенхофф, Альберт Э.: Теория сечений крыла . Разделы 1.2 и 1.3
  4. ↑ «Современное уравнение сопротивления НАСА». Райт.nasa.gov. 25 марта 2010 г. http://wright.nasa.gov/airplane/drageq.html. Проверено 7 декабря 2010 г. .
  5. ↑ Клэнси, LJ: Аэродинамика . Раздел 11.17
  6. ↑ См. раздел «Подъемная сила и вихревая вибрация» для возможных компонентов силы, поперечных направлению потока.
  7. ↑ Обратите внимание, что для атмосферы Земли плотность воздуха можно найти с помощью барометрической формулы. Воздух составляет 1,293 кг/м 3 при 0 °C и 1 атмосфере.
  8. ↑ Клэнси, LJ: Аэродинамика . Разделы 4.15 и 5.4
  9. ↑ 9,0 9,1 Клэнси, Л. Дж.: Аэродинамика . Раздел 4.17
  10. ↑ Клифт Р., Грейс Дж. Р., Вебер М. Э.: Пузыри, капли и частицы . Академическая пресса, Нью-Йорк (1978).
  11. ↑ Briens C.L.: Порошковая технология . 67, 1991, 87-91.
  12. ↑ Хайдер А., Левеншпиль О.: Порошковые технологии . 58, 1989, 63-70.
  13. ↑ «МБ-Экзотенфорум». http://www.nast-sonderfahrzeuge.de/MB-Exotenforum/forum_entry. php?id=25942. Проверено 7 января 2012 г. .
  14. ↑ MotorTrend: General Motors EV1 — Впечатления от вождения, 19 июня.96
  15. ↑ «Шаблон:Ошибка цитирования». http://www.mbusa.com/mercedes/vehicles/model/class-CLA/model-CLA250C#!layout=/vehicles/model/specs&class=CLA&model=CLA250C&waypoint=model-specs.
  16. ↑ «Техника VW Beetle». Maggiolinoweb.it. http://www.maggiolinoweb.it/technique.html. Проверено 24 октября 2009 г. .
  17. ↑ «Домашняя страница Мэйфилда — коэффициент аэродинамического сопротивления для выбранных транспортных средств». Mayfco.com. http://www.mayfco.com/dragcd~1.htm. Проверено 24 октября 2009 г. .
  18. ↑ «Предельная скорость». Космический центр Годдарда. http://exploration.grc.nasa.gov/education/rocket/termvr.html. Проверено 16 февраля 2012 г. .
  19. ↑ Уилсон, Дэвид Гордон (2004): Наука о велосипедах, 3-е изд. . п. 197, Массачусетский технологический институт, Кембридж, ISBN 0-262-23237-5
  20. ↑ «Коэффициент сопротивления». Engineeringtoolbox.com. http://www.engineeringtoolbox.com/drag-coefficient-d_627.html. Проверено 7 декабря 2010 г. .
  21. ↑ «Эффекты формы при перетаскивании». НАСА. http://www.grc.nasa.gov/WWW/k-12/airplane/Shaped.html. Проверено 11 марта 2013 г. .
  22. ↑ Баша, В. А. и Гали, В. С., «Прогнозирование лобового сопротивления в переходном потоке над аэродинамическими профилями», Journal of Aircraft, Vol. 44, 2007, с. 824–32.
  23. ↑ «Спросите нас — Коэффициент сопротивления и теория подъемной линии» . Aerospaceweb.org. 11 июля 2004 г. http://www.aerospaceweb.org/question/aerodynamics/q0184.shtml. Проверено 7 декабря 2010 г. .
  24. ↑ «Boeing 787 Dreamliner: анализ». Lissys.demon.co.uk. 21 июня 2006 г. http://www.lissys.demon.co.uk/samp1/index.html. Проверено 7 декабря 2010 г. .

Ссылки

  • Клэнси, Л. Дж. (1975): Аэродинамика . Pitman Publishing Limited, Лондон, ISBN 0-273-01120-0
  • Эбботт, Ира Х., и фон Доенхофф, Альберт Э. (1959): Теория сечений крыла . Dover Publications Inc., Нью-Йорк, стандартный номер книги 486-60586-8
  • Hoerner, SF (1965): Гидродинамическое сопротивление . Hoerner Fluid Dynamics, Брик Таун, Нью-Джерси, США
  • Bluff Body: http://www.engineering.uiowa.edu/~me_160/lecture…/Bluff%20Body2.pdf
  • Сопротивление тупых тел и обтекаемых тел: http://www.princeton.edu/~asmits/Bicycle_web/blunt.html
  • Hucho, WH, Janssen, LJ, Emmelmann, HJ 6 (1975): Оптимизация деталей кузова — метод снижения аэродинамического сопротивления . САЕ 760185.

Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.

Коэффициент аэродинамического сопротивления

Коэффициент аэродинамического сопротивления

./img/line01a.gif»>

По Википедия,
бесплатная энциклопедия,

http://en.wikipedia.org/wiki/Drag_coefficient

В гидродинамике коэффициент сопротивления (обычно обозначается как C d , C x или C w ) — безразмерная величина, которая используется для количественной оценки сопротивления или сопротивления объекта в текучей среде, такой как воздух или вода. Он используется в уравнении сопротивления, где более низкий коэффициент сопротивления указывает на то, что объект будет иметь меньшее аэродинамическое или гидродинамическое сопротивление. Коэффициент аэродинамического сопротивления всегда связан с определенной площадью поверхности.

Коэффициент сопротивления любого объекта включает эффекты двух основных факторов, влияющих на динамическое сопротивление жидкости: поверхностное трение и сопротивление формы. Коэффициент аэродинамического сопротивления подъемной аэродинамической или подводной части также включает влияние сопротивления, вызванного подъемной силой. Коэффициент аэродинамического сопротивления всей конструкции, такой как самолет, также включает влияние интерференционного сопротивления.

Определение

Коэффициент аэродинамического сопротивления C d определяется как:

где

F d сила сопротивления, которая по определению является составляющей силы в направлении скорости потока,
ρ — массовая плотность жидкости,
v — это скорость объекта относительно жидкости, а
A — эталонная область.

Эталонная площадь зависит от того, какой тип коэффициента лобового сопротивления измеряется. Для автомобилей и многих других объектов эталонной площадью является передняя часть транспортного средства (т. е. площадь поперечного сечения, если смотреть спереди).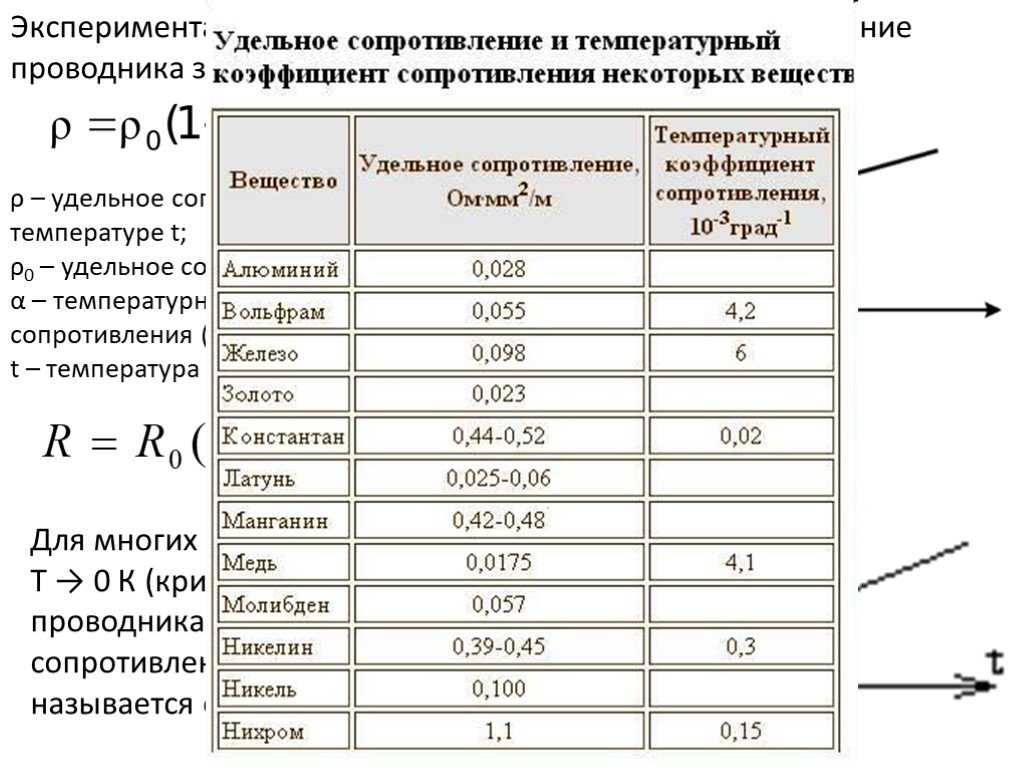 Например, для сферы A  =  π r (следовательно, , а не , площадь поверхности = 4 π r).

Для аэродинамических профилей опорная площадь представляет собой хорду аэродинамического профиля, умноженную на длину размаха, которую можно легко соотнести с площадью крыла. Поскольку это, как правило, довольно большая площадь по сравнению с проектируемой лобовой площадью, результирующие коэффициенты сопротивления имеют тенденцию быть низкими: намного ниже, чем для автомобиля с таким же сопротивлением, лобовой площадью и той же скоростью.

В дирижаблях и некоторых телах вращения используется коэффициент объемного сопротивления, в котором опорной площадью является квадрат кубического корня из объема дирижабля. Погруженные обтекаемые тела используют площадь смоченной поверхности.

Два объекта с одинаковой опорной площадью, движущиеся с одинаковой скоростью в жидкости, будут испытывать силу сопротивления, пропорциональную их соответствующим коэффициентам сопротивления. Коэффициенты для необтекаемых объектов могут быть 1 и более, для обтекаемых гораздо меньше.

Фон

Обтекание тарелки с застоем.

Уравнение сопротивления

по сути является утверждением, что сила сопротивления любого объекта пропорциональна плотности жидкости и пропорциональна квадрату относительной скорости между объектом и жидкостью.

C d не является постоянной величиной, а изменяется в зависимости от скорости, направления потока, формы объекта, плотности жидкости и жидкости. вязкость. Скорость, кинематическая вязкость и характерный масштаб длины объекта объединены в безразмерную величину, называемую числом Рейнольдса или 9.0009 Re . C d , таким образом, является функцией Re . В сжимаемом потоке важна скорость звука, и C d также является функцией числа Маха Ма .

Для определенной формы тела коэффициент сопротивления C d зависит только от числа Рейнольдса Re , числа Маха Ma и направления потока. При малом числе Маха Ma , как обычно для автомобилей и спортивных самолетов, коэффициент лобового сопротивления не зависит от числа Маха. Также вариант с числом Рейнольдса Re в практическом интересующем диапазоне обычно невелика, в то время как для автомобилей, движущихся по шоссе, и самолетов, движущихся с крейсерской скоростью, направление входящего потока также более или менее одинаково. Таким образом, коэффициент лобового сопротивления C d часто можно рассматривать как константу.

Чтобы обтекаемое тело достигло низкого коэффициента сопротивления, пограничный слой вокруг тела должен оставаться прикрепленным к поверхности тела как можно дольше, в результате чего след становится узким. Широкий след приводит к высоким из перетаскивания . Пограничный слой будет оставаться прикрепленным дольше, если он турбулентный, чем если он ламинарный. Пограничный слой будет переходить из ламинарного в турбулентный при достаточно высоком числе Рейнольдса обтекания тела. Более высокие скорости, более крупные объекты и более низкая вязкость способствуют увеличению числа Рейнольдса.

Для других объектов, таких как мелкие частицы, уже нельзя считать, что коэффициент сопротивления C d является постоянным, но, безусловно, является функцией числа Рейнольдса. При низком числе Рейнольдса обтекание объекта не переход к турбулентному, но остается ламинарным вплоть до отрыва от поверхности объекта. При очень малых числах Рейнольдса без отрыва потока сила сопротивления F d пропорционально v вместо v ; для сферы это известно как закон Стокса. Число Рейнольдса будет низким для небольших объектов, низких скоростей и жидкостей с высокой вязкостью.

A C d , равный 1, получился бы в том случае, если вся приближающаяся к объекту жидкость останавливается, создавая застойное давление по всей передней поверхности. На верхнем рисунке показана плоская пластина с жидкостью, поступающей справа и останавливающейся на пластине. График слева от него показывает одинаковое давление по всей поверхности. В реальной плоской пластине жидкость должна вращаться по бокам, и полное стагнационное давление наблюдается только в центре, спадая к краям, как на нижнем рисунке и графике. Только учитывая передний размер, C d реальной плоской пластины будет меньше 1; за исключением того, что на задней стороне будет всасывание: отрицательное давление (относительно окружающей среды). Общее значение C d реальной квадратной плоской пластины, перпендикулярной потоку, часто принимают равным 1,17. Схемы течения и, следовательно, C d для некоторых форм могут меняться в зависимости от числа Рейнольдса и шероховатости поверхностей.

Коэффициент аэродинамического сопротивления C

d примеры

Общий

В целом, C d не является абсолютной константой для данной формы тела. Он зависит от скорости воздушного потока (или, в более общем случае, от числа Рейнольдса). Гладкая сфера, например, имеет C d , которая варьируется примерно от 0,47 для ламинарного (медленного) течения до 0,1 для турбулентного (быстрого) течения.

пуля
Формы [1]
С д Товар
0,9 обычный велосипед плюс велосипедист
0,4 шероховатая сфера (Re = 10 6 )
0,1 гладкая сфера (Re = 10 6 )
0,001 ламинарная плоская пластина, параллельная потоку (Re = 10 6 )
0,005 турбулентная плоская пластина, параллельная потоку (Re = 10 6 )
0,25 современный автомобиль (например, Toyota Prius [13] )
0,295 (не оживальная, с дозвуковой скоростью)
1,0–1,3 мужчина (вертикальное положение)
1,28 плоская пластина перпендикулярно потоку
1,0–1,1 лыжник
1,0–1,3 провода и кабели
1,1-1,3 прыгун с трамплина [13]
1,3–1,5 Эмпайр Стейт Билдинг
1,8–2,0 Эйфелева башня
2.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Внимание! Внешний вид товара, комплектация и характеристики могут изменяться производителем без предварительных уведомлений. Данный интернет-сайт носит исключительно информационный характер и ни при каких условиях не является публичной офертой, определяемой положениями Статьи 437 (2) Гражданского кодекса Российской Федерации. 2024 © Все права защищены.