Коэффициент бета (примеры расчета и использования)
Любой инвестор, когда начинает более глубоко погружаться в тему инвестирования в акции, обязательно сталкивается с таким понятием, как коэффициент бета. В данной статье мы рассмотрим следующие ключевые моменты для понимания того, что такое коэффициент бета, и как с ним стоит работать:
-
Что такое бета коэффиент акции.
-
Формула коэффициента бета.
-
Значения коэффициента бета.
-
Расчет коэффициента бета.
-
Пример расчета коэффициента бета.
-
Бета коэффициент портфеля.
Бета коэффициент акции
Коэффициент бета – это статистический коэффициент, который характеризует движение отдельной акции относительно всего рынка в целом.
Изначально бета коэффициент своими создателями задумывался как коэффициент меры риска для отдельной акции относительно всего рынка в целом, при этом для сравнения, как правило, берется динамика основного рыночного фондового индекса. Это определяется путем сравнения поведения цены акции и рыночного фондового индекса. Сравнивая различные периоды роста и падения фондового индекса и те же периоды у акции, мы можем понять, как акция вела себя в той или иной момент. Реагировала на внешние факторы так же сильно, как и рынок в целом или наоборот, акции проявляли большую устойчивость.
Формула коэффициента бета
Формула расчета коэффициента бета достаточно сложна и с чисто математической точки зрения её можно представить следующим образом:
Где:
ri – доходность отдельно взятой (i-й) акции в инвестиционном портфеле за определенный период времени;
rm – доходность рынка (как правило, доходность основного фондового индекса) за определенный период времени;
σ2m – дисперсия доходности рынка (как правило, доходности основного фондового индекса) за определенный период времени.
Если же говорить по смыслу данной формулы, то в числителе находится значения зависимости (корреляции) доходности акции от доходности фондового индекса за определенный период, а в знаменателе разброс доходностей фондового индекса относительно средней доходности за определенный период.
Поэтому, исходя из данной формулы, сразу можно определить, что коэффициент бета будет давать нам представление о степени зависимости доходности акции от доходности фондового индекса, а также о том, насколько доходность отдельной акции в среднем превышает или наоборот, оказывается ниже доходности индекса.
Прежде всего значение коэффициента бета дает инвестору понимание того, насколько отдельно взятая акция имеет более волатильные, то есть более высокоамплитудные движения относительно всего рынка в целом. А также дает понимание того, насколько акции остро реагируют на проявление систематического или общерыночного риска, когда рисковые события влияют на весь рынок и лишь немногие акции, за счет своей внутренней специфики, способны реагировать на проявления общерыночного риска менее остро или не реагировать вообще.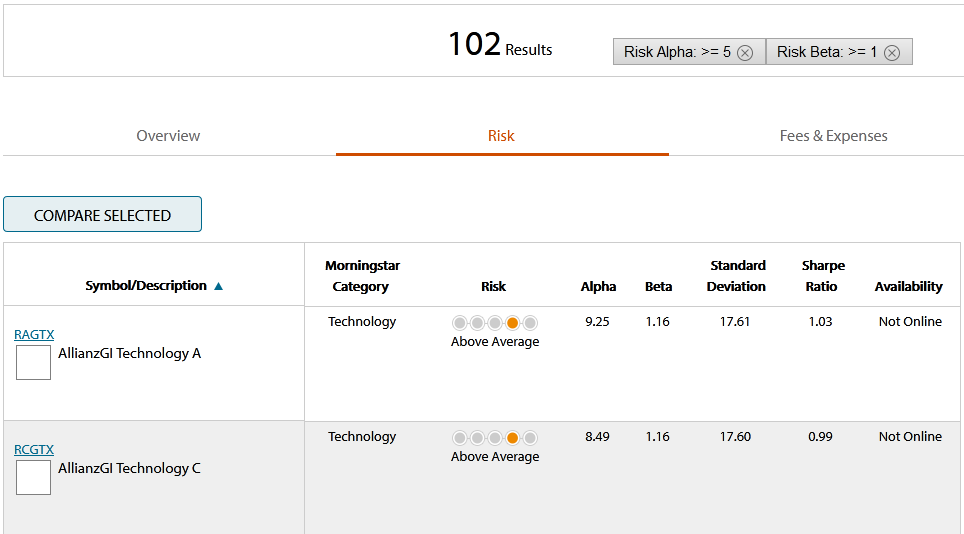
Значения коэффициента бета
Теперь давайте разберемся в показателях коэффициента бета и как их стоит интерпретировать инвестору. Для коэффициента бета характерны несколько пороговых уровней:
-
Коэффициент бета больше 1. Это свидетельствует о том, что динамика акции коррелирует с динамикой фондового индекса, но при этом акция более чувствительно реагирует на любое движение индекса. Например, фондовый индекс растет на 1%, а акция при этом будет расти на 2% и точно так же наоборот, фондовый индекс снижается на 1%, а акция при этом снижается еще большими темпами, например, на 2%.
-
Коэффициент беты равен 1. Это говорит о том, что движения акции полностью повторяют движение фондового индекса, то есть корреляция движений акции и индекса 100%.
-
Коэффициент бета находится в диапазоне больше 0, но меньше 1. Это свидетельствует о том, что в-первую очередь динамика акции коррелирует с динамикой фондового индекса.

-
Коэффициент бета равен нулю. В данном случае такое значение коэффициента означает, что движение акции вообще никак не связано с движением фондового индекса или по-другому можно сказать, что никак не коррелируют.
-
Коэффициент бета отрицательный и находится в диапазоне от 0 до -1. В данном случае акция имеем обратную корреляцию с фондовым индексом. При этом чувствительность реакции акции более низкая, чем у фондового индекса. Например, фондовый индекс растет на 2%, при этом акция с такими показателями коэффициента бета будет снижаться, но более низкими темпами, нежели растет индекс, то есть, например, на 1%. Точно такая же ситуация справедлива и наоборот, если фондовый индекс будет снижаться на 2%, такая акция будет расти на 1%.

-
Коэффициент бета отрицательный и меньше -1. Такие акции имеют обратную корреляцию с фондовым индексом, то есть в целом движутся в противоположном направлении, при этом такие акции более волатильны и двигаются с большей амплитудой нежели сам индекс. То есть в данном случае акция будет двигаться в противоположную сторону рынку и более сильно реагировать на любые движения фондового индекса. Например, индекс растет на 1%, а акция при этом будет снижаться на 2%, и точно так же наоборот, при снижении рынка на 1%, акция с таким значением коэффициента бета будет расти на 2%.
Таким образом коэффициент бета несет для инвесторов различную ценную информацию: насколько более чувствительно реагирует акция на основные рыночные тенденции и есть ли в данной бумаге внутренняя идея, способная игнорировать общерыночные тенденции, которые охватывают своим движением большинство бумаг на рынке.
Расчет коэффициента бета
Перед большинством инвесторов тут же встает вопрос, как и где взять расчета коэффициента бета, так как формула расчета его достаточно сложна и ручной расчет его просто не представляется возможным.
Здесь стоит прежде всего сказать, что на самом деле расчет коэффициента бета на российском рынке регламентирован и стандартизирован, причем регламентирован он положением Центрального Банка «Положение о деятельности по проведению организованных торгов» (утв. Банком России 17.10.2014 N 437-П). В приложении №2 идет подробное описание расчета коэффициента бета.
Так же расчет коэффициента бета проводится непосредственно самой московской биржей по принципу, описанному в положении Центрального Банка. Коэффициент бета рассчитывается на конец каждой торговой сессии, и его расчет можно скачать на сайте Московской биржи https://www.moex.com/ru/forts/coefficients-values.aspx
При этом, как мы видим из формулы расчета коэффициента, что он рассчитывается за период последних 30-и торговых сессий.
Расчет коэффициента бета происходит точно так же, как и расчет многих технических индикаторов рынка, то есть по принципу скользящего окна, когда в расчетный диапазон коэффициента попадают лишь только 30 последних ценовых значений, и данный диапазон постоянно сдвигается, как только в расчет попадет котировка новой торговой сессии.
За счет того, что период расчета коэффициента бета сравнительно мал, с инвестиционной точки зрения, это приводит к тому, что значения коэффициента очень волатильны и сильно изменяются во времени. Иногда значение коэффициента от одного месяца к другому может изменяться кардинально, как с точки зрения характеризующей корреляцию акции и индекса, так и с точки зрения степени чувствительности реакции акции на движения индекса. Это можно заметить даже просто по скользящему графику расчета коэффициента, так как во времени он изменяется очень активно и очень резко.
Иными словами, рассчитанные подобным образом значения коэффициента бета, отражают лишь локальные и очень краткосрочные рыночные тенденции, которые не отражают в полной мере заложенных фундаментальных принципов в данный коэффициент.
Изначально коэффициент бета разрабатывался и применялся исключительно в инвестиционных целях и активно использовался для формирования инвестиционных портфелей, в том числе портфелей по модели «Марковица».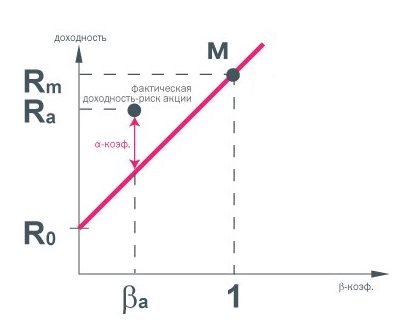
Однако, корректный расчет показателя бета можно сделать даже с помощью инструментов MS Excel, именно такой калькулятор для расчета коэффициента бета мы и реализовали в рамках нашего курса обучения «Школа разумного инвестирования».
Для того чтобы коэффициент бета отражал именно долгосрочные инвестиционные тенденции в акциях, мы должны прибегать к его расчету за более длительные горизонты от 3-х лет.
Пример расчета бета коэффициента
Проведем расчет коэффициента бета на различных бумагах за более длительный промежуток времени с помощью калькулятора для расчета бета коэффициента.
Для расчета мы выберем акции с потенциально бОльшим и потенциально меньшим коэффициентом бета. В качестве примера более агрессивно движущейся акции, которая имеет положительную корреляцию с рынком, мы возьмем обыкновенные акции Сбербанка, а в качестве примера бумаги, которая не зависит от колебаний рынка в целом и демонстрирует самостоятельную динамику, мы возьмем привилегированные акции компании Ленэнерго.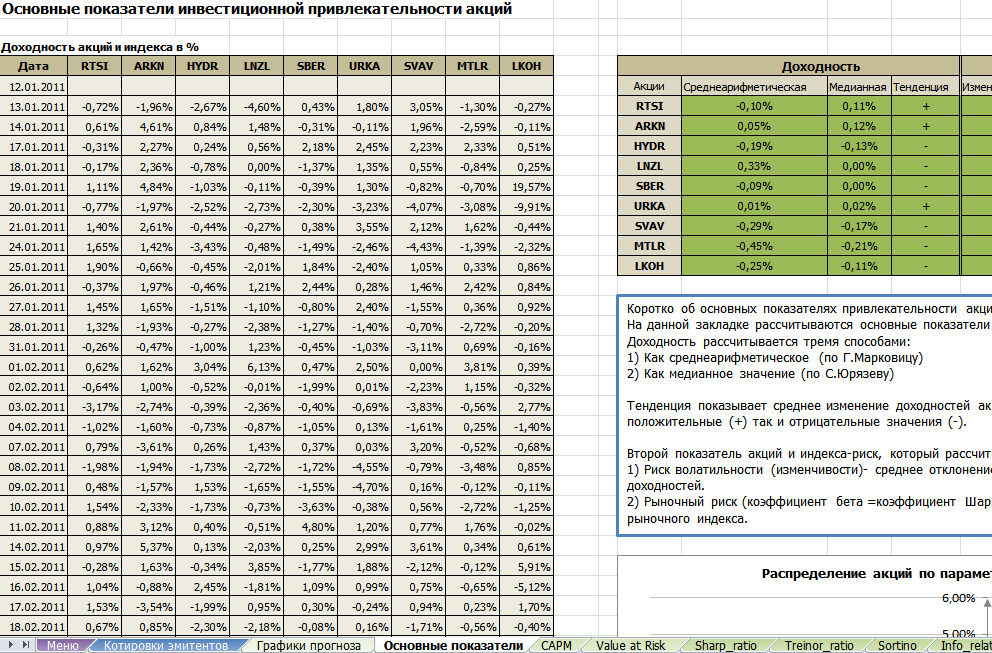
В калькуляторе заполняются поля с датами торговых периодов за последние 3 года, значения дневных цен закрытия по акции за последние 3 года, а также значения фондового индекса на конец торговой сессии за последние 3 года.
Расчет коэффициента бета в калькуляторе проводится тремя различными способами для подтверждения статистической достоверности расчета коэффициента.
После заполнения данных по котировкам акций Сбербанка и индекса московкой биржи за последние 3 года, мы видим, что значение коэффициента бета по бумаге оказывается большим чем 1.
Положительное значение коэффициента бета по акциям Сбербанка говорит нам о том, что акции преимущественно движутся в том же направлении, что и рынок в целом, а значение коэффициента больше 1 свидетельствуют о том, что акции намного более сильно реагируют на рыночные движения.
Во втором случае мы так же проводили расчет коэффициента бета за последние 3 года по привилегированным акциям Ленэнерго.
В данном случае значение коэффициента бета оказывается равным 0,51, что свидетельствует о том, что в целом акция не движется в противофазе рынку и лишь частично подвержена влияниям основных общерыночных тенденций.
Бета коэффициент портфеля (практика применения)
Использование коэффициента бета при формировании портфеля и в процессе управление инвестиционным портфелем – это одна из основных, базовых практик портфельного инвестирования, так как значение корректно рассчитанного коэффициента отражает то, как бумага за счет своих внутренних фундаментальных свойств «отрабатывает» движения общерыночных тенденций. Особенно в этом ключе важно понимание того, что под общерыночными тенденциями мы в первую очередь, как правило, подразумеваем общие негативные движения рынка, или проявление кризисных моментов на рынке, которые влияют на все акции. Когда большинство акций на рынке снижается, те бумаги, которые способны противостоять общерыночному снижению, представляют особенную ценность для инвестиционного портфеля.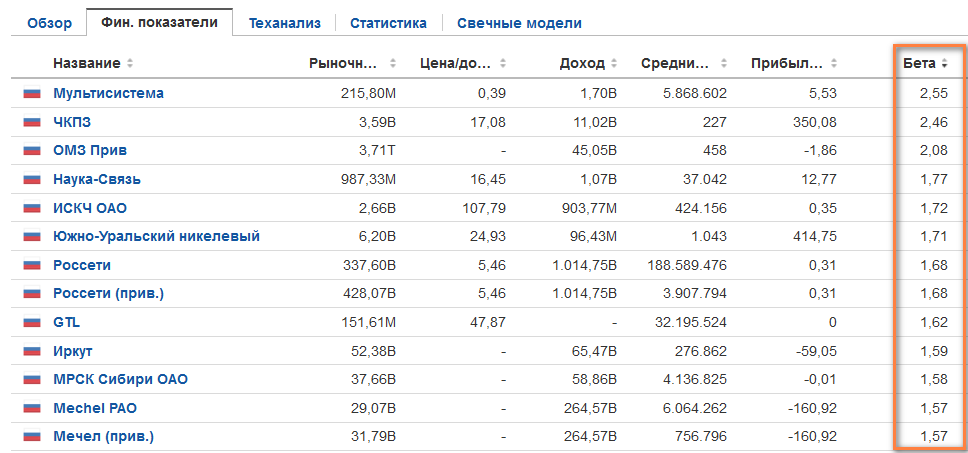
Поэтому коэффициент бета в инвестиционных портфелях, как правило, в первую очередь может применяться, как весовой коэффициент, который распределяет средства портфеля в акции в зависимости от степени чувствительности к риску той или иной акции.
При этом, в случае, если основная концепция инвестиционного портфеля требует максимальной минимизации риска, то за счет бета коэффициента придается больший вес бумагам с малым значением коэффициента бета, или даже с его отрицательным значением. А в случае, если формируется агрессивный инвестиционный портфель, то веса распределяются наоборот. Акции с большим значением коэффициента бета получают больший вес в инвестиционном портфеле. Это позволяет добиться того, что на фазе роста фондового рынка, акции, включенные в инвестиционный портфель, реагируют более выражено и растут большими темпами, в итоге, это позволяет такому портфелю обгонять фондовый индекс по показателям доходности.
Как работает коэффициент бета мы можем увидеть даже визуально, наложив котировки акции, на значения фондового индекса.
В случае с акцией Сбербанка, где коэффициент бета больше 1, мы можем наблюдать, что поведение бумаги более агрессивное, и если рынок растет, то бумаги растут еще большими темпами, а на коррекционных фазах мы видим, что просадки по акциям случаются более значительные чем по рынку в целом.
И практически противоположную картину мы можем увидеть в акциях с коэффициентом бета меньше 1.
В нашем примере акции Ленэнерго преф. в момент острейшего проявления кризисных моментов на рынке демонстрировали высокую степень устойчивости и практически никак не реагировали на общерыночные тенденции. Поэтому акции, значение коэффициента бета которых меньше 1, так же еще причисляют к категории защитных бумаг, которые способны эффективно противостоять общерыночным негативным тенденциям.
Выводы
Как мы видим, коэффициент бета может быть очень эффективным и полезным инструментом при формировании инвестиционного портфеля, но только с учетом того, что инвесторы корректно определяют его значение и грамотно его используют.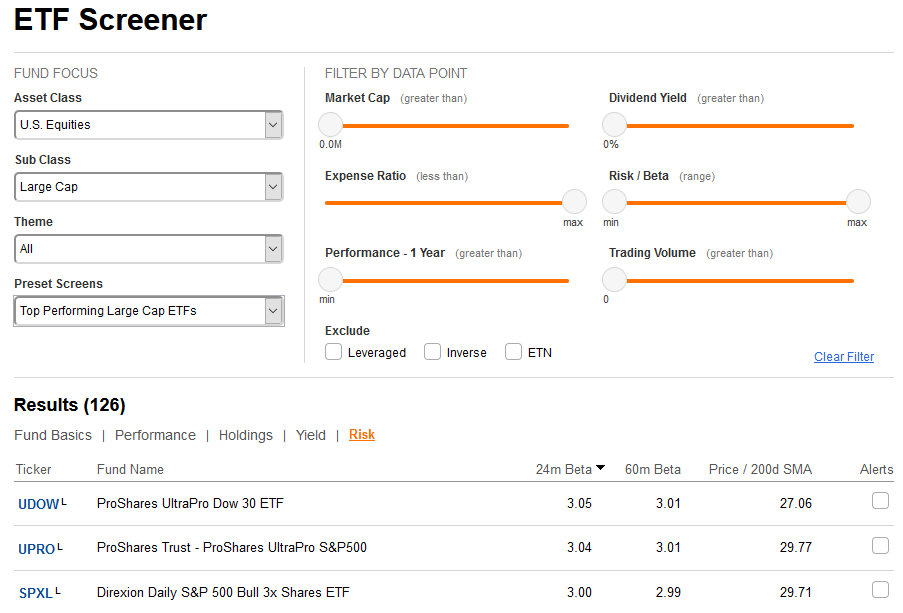
Всему этому мы учим на нашем полном цикле курсов обучения «Школа разумного инвестирования». Начать обучение можно с посещения вводных бесплатных занятий. Записаться на ближайший бесплатный вебинар можно по ссылке — http://mk.fin-plan.org
Удачных Вам инвестиций!
Бета-коэффициент: для чего нужен и как его рассчитать
- 9 Декабря 2021
- Алексей Иртюго
При оценке компании доходным методом, то есть путем дисконтирования будущих денежных потоков, очевидно значимым моментом является определение ставки дисконтирования, с помощью которой эти самые будущие денежные потоки будут приводиться к текущей стоимости.
Не вдаваясь в подробности расчета дисконтированных денежных потоков, скажу, что базово потоки делятся на два вида: денежные потоки на собственный капитал и денежные потоки на инвестированный капитал (собственный капитал + заемное финансирование). Отличаются и ставки дисконтирования для двух разновидностей потоков. Поскольку речь далее пойдет про смысл и методику расчета коэффициента бета, то обратимся к ставке дисконтирования для собственного капитала. Она, к слову, нужна и для расчета ставки дисконтирования для капитала инвестированного.
Поскольку речь далее пойдет про смысл и методику расчета коэффициента бета, то обратимся к ставке дисконтирования для собственного капитала. Она, к слову, нужна и для расчета ставки дисконтирования для капитала инвестированного.
В современной практике для расчета ставки дисконтирования денежный потоков на собственный капитал в большинстве случаев применяется модель CAPM (Capital Asset Pricing Model), что в дословном переводе означает «модель ценообразования капитальных активов».
Концепция CAPM была разработана на основе портфельной теории Г. Марковица, наиболее применимая на сегодняшний день интерпретация данной концепции принадлежит У. Шарпу, поэтому она зачастую называется его именем. Ставка доходности, рассчитанная по модели CAPM, определяет, какой должна быть доходность актива, добавляемого к портфелю, с учетом его рыночного риска. Поскольку именно требуемой доходностью определяется ставка дисконтирования будущих денежных потоков, рассчитанная по описываемой модели доходность может использоваться в качестве такой ставки. Рассчитанная по модели CAPM требуемая норма доходности в отношении актива является, таким образом, общей для рынка, то есть лишена субъективной составляющей.
Рассчитанная по модели CAPM требуемая норма доходности в отношении актива является, таким образом, общей для рынка, то есть лишена субъективной составляющей.
Ниже приведена формула расчета доходности по CAPM:
Где:
Ожидаемая ставка доходности актива.
Безрисковая ставка доходности (как правило, ОФЗ).
Бета-коэффициент, мера рыночного риска актива.
Ожидаемая доходность рыночного портфеля (для простоты расчета чаще всего берется доходность индекса).
Выражение в скобках представляет собой премию за риск для определенного рынка (рынка, для которого мы берем рыночную доходность и безрисковую ставку). Бета-коэффициент, таким образом, выступает мерой рыночного риска: он определяет, в какой степени конкретный актив подвержен рыночному риску, то есть как соотносится изменение доходности актива с изменением доходности рыночного портфеля.
Поскольку доходность актива в случае с акциями определяется движением котировок, коэффициент бета также часто интерпретируют как волатильность: чем выше коэффициент – тем волатильнее акция, для которой он рассчитан.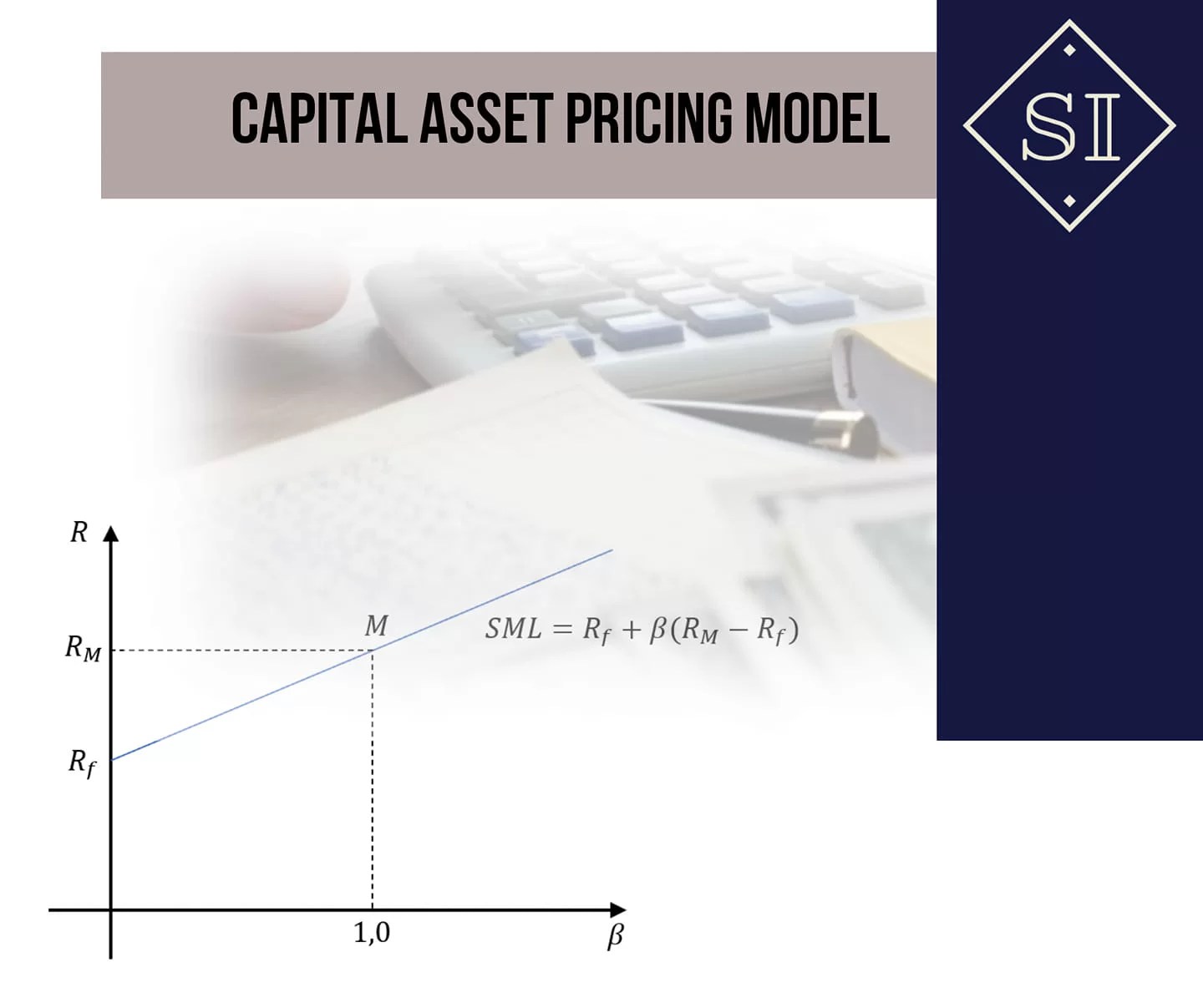 Волатильность же измеряется в данном случае относительно рыночного портфеля.
Волатильность же измеряется в данном случае относительно рыночного портфеля.
Расчет бета-коэффициента:
Где:
Ковариация доходностей актива, для которого рассчитывается коэффициент бета с доходностью рыночного портфеля (эталона).
Дисперсия доходности рыночного портфеля.
Коэффициент бета, таким образом, может принимать любое значение, однако чаще всего находится в диапазоне от -1 до 1, или, еще чаще, в диапазоне от 0 до 1. Ниже приведена интерпретация основных интервалов значений.
Бета 0. Такое значение коэффициента означает, что доходность актива не изменяется вовсе, то есть он является безрисковым. Если подставить такое значение в первую формулу, мы получим доходность, равную безрисковой ставке.
Бета в диапазоне от 0 до 1. Такое значение коэффициента означает, что доходность актива и рыночного портфеля изменяются сонаправленно, однако изменение доходности актива (волатильность) ниже, чем у рыночного портфеля.

Бета равна 1. Означает, что доходности актива и рыночного портфеля меняются одинаково, то есть корреляция 100%.
Бета коэффициент больше 1. Означает, что доходность актива и рыночного портфеля меняются сонаправленно, однако изменчивость доходности актива выше, нежели рыночного портфеля. То есть, выше его риск.
Бета в диапазоне от -1 до 0. Выводы аналогичны диапазону от 0 до 1, однако движение доходностей является противоположным.
Бета равна -1. Означает, что доходности актива и рыночного портфеля изменяются в одинаковой мере, но разнонаправленно.
Бета меньше -1. Выводы аналогичны значению больше 1, однако движение доходностей разнонаправленное.
Поскольку, как сказано выше, доходность определяется движением котировок, под изменением доходности следует понимать изменение котировок.
Поскольку расчет бета-коэффициента – достаточно трудоемкое занятие, сегодня это проще всего сделать с помощью Excel. В таблице ниже для примера взяты данные по торгам с 1 ноября 2021 года, однако на практике лучше использовать более длительный период, хотя бы от 100 торговых дней.
В таблице ниже для примера взяты данные по торгам с 1 ноября 2021 года, однако на практике лучше использовать более длительный период, хотя бы от 100 торговых дней.
Для каждого периода рассчитываем доходности Ra (доходность акции) и Rp (доходность портфеля).
Далее есть два способа рассчитать бета-коэффициент.
Способ №1
Для расчета коэффициента будем использовать формулы Excel «ИНДЕКС» и «ЛИНЕЙН», в значениях из таблицы выше формула примет вид:
Получаем значение бета-коэффициента, равное 1,56, что в соответствии с описанной выше интерпретацией говорит нам о том, что на данном временном промежутке акции Сбера были более волатильными, чем рыночный портфель, в качестве которого использовался индекс Московской биржи.
Способ №2
На зависимость между доходностями акции и рыночного портфеля можно смотреть как на линейную регрессию.
Уравнение простой (парной) линейной регрессии имеет следующий общий вид:
Коэффициент b1 и определяет тесноту связи переменных.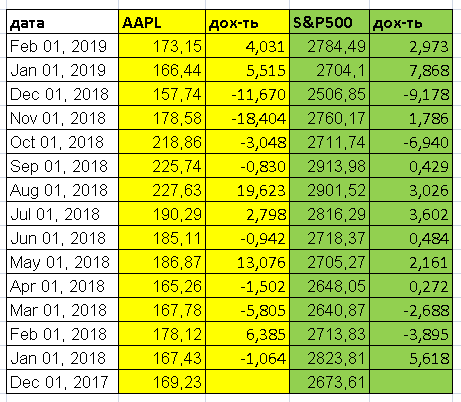 Он и будет бета-коэффициентом в случае построения парной линейной регрессии для наших значений доходностей. Чтобы построить регрессию в Excel потребуется подключить в настройках пакет анализа данных.
Он и будет бета-коэффициентом в случае построения парной линейной регрессии для наших значений доходностей. Чтобы построить регрессию в Excel потребуется подключить в настройках пакет анализа данных.
На вкладке «Файл» необходимо найти раздел «Параметры».
Он находится в левом нижнем углу.
В появившемся окне переходим в раздел «Настройки» и нажимаем последовательно как на картинке:
В появившемся окне ставим галочку в поле «Пакет анализа».
Теперь пакет анализа включен и найти его можно на вкладке «Данные» в правом верхнем углу.
Далее дело за малым. Нажимаем на «Анализ данных». Выбираем в списке «Регрессия».
Заполняем входные диапазоны: Y – это значения доходностей акции, X – значения доходностей индекса (рыночного портфеля). Ставим галочку в разделе «Параметры вывода» в графе «Новый рабочий лист», нажимаем «Ок».
Открывается новый рабочий лист, на котором мы видим множество различных параметров нашей регрессии.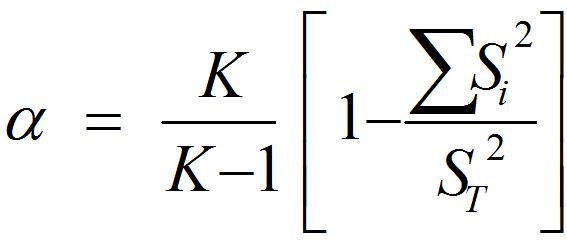 Нас же интересует бета-коэффициент, который выделен желтым цветом.
Нас же интересует бета-коэффициент, который выделен желтым цветом.
В целом способы по своей сути одинаковые, просто во втором случае мы получаем дополнительные данные, которые будут интересны разве что тем, что хорошо разбирается в статистике. Приведенные данные позволяют оценить достоверность выявленной зависимости, статистическую значимость результата.
Бета-коэффициент можно считать для различных периодов, в зависимости от того, насколько сильно в представлении считающего менялся характер связи между акцией и индексом. Так, чем стабильнее и рынок и чем он более развит – тем больше может быть период для расчета коэффициента.
Если деятельность компании претерпела серьезные изменения, которые позволяют предположить, что степень влияния на ее деятельность рыночных рисков изменилась, не стоит принимать к расчету большой период до соответствующих изменений, так как такие значения могут исказить результат и «перевесить» более поздние и актуальные значения при расчете.
Теги: обучение
Алексей Иртюго
453312
Коэффициент бета, р — Энциклопедия по экономике
МОДЕЛЬ ОЦЕНКИ КАПИТАЛЬНЫХ АКТИВОВ — формула расчета ставки дисконтирования на основе показателей фондового рынка безрисковой ставки дохода, коэффициента бета (Р), среднерыночной доходности ценных бумаг, премии для малых предприятий, премий за риск инвестирования в данное предприятие и за страновой риск. [c.501]Многие специалисты по управлению инвестиционным портфелем, оценивая рыночный риск, присущий акции, или ее чувствительность, применяют один из методов технического анализа, который заключается в расчете коэффициента бета (он часто обозначается греческой буквой р). Коэффициент бета показывает процентное изменение цены акции относительно процентного изменения рыночного индекса. [c.278]
В уравнениях (8.106) и (8.10в) показано, что координаты точки пересечения с вертикальной осью (ос ) и бета (р ) являются средневзвешенными значениями коэффициентов смещения и беты ценных бумаг соответственно, где в качестве весов берутся их относительные доли в портфеле. Аналогично в уравнении (8. Юг) случайная погрешность портфеля (гр1) является средневзвешенной случайных погрешностей ценных бумаг, где в качестве весов опять берутся их относительные доли в портфеле. Таким образом, рыночная модель портфеля является прямым обобщением рыночных моделей отдельных ценных бумаг, приведенных в уравнении (8.3)».
[c.214]
Аналогично в уравнении (8. Юг) случайная погрешность портфеля (гр1) является средневзвешенной случайных погрешностей ценных бумаг, где в качестве весов опять берутся их относительные доли в портфеле. Таким образом, рыночная модель портфеля является прямым обобщением рыночных моделей отдельных ценных бумаг, приведенных в уравнении (8.3)».
[c.214]
Риск финансовых операций может определяться на основе Р-коэффициента (бета-коэффициента), который позволяет оценить риск индивидуальной финансовой операции по отношению к уровню финансового риска в целом по рынку. Расчет его проводится по формуле [c.121]
Коэффициент бета принято также считать мерой риска вложений в данные ценные бумаги. При Р>1 риск инвестиций выше, чем в среднем по рынку, а при р[c.228]
Шаг 4. Был оценен коэффициент бета для каждой акции (р) на основе доходности за временной период, лежащий вне границ окна события (использовалось 100 торговых дней перед событием и 100 торговых дней после события).
[c.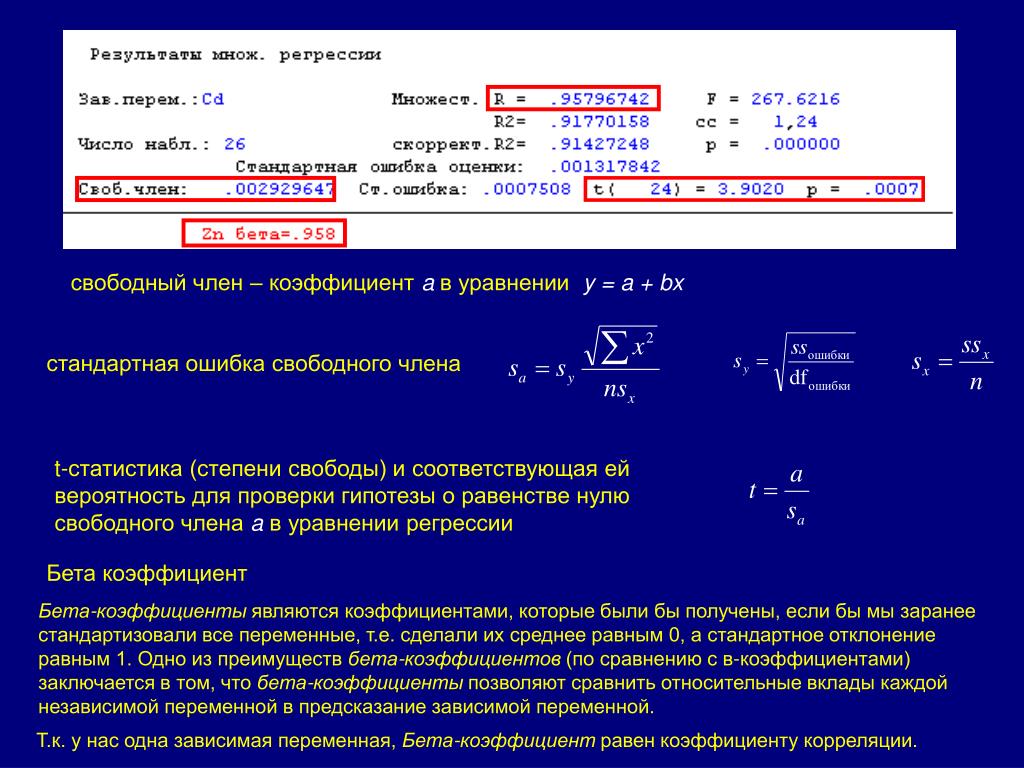 156]
156]
Н где р. = коэффициент бета инвестиции относительно [c.208]
Для измерения общего риска (ст.) мы можем разделить рыночный коэффициент бета на р.т. В результате получим следующее [c.892]
Бета-коэффициент акции (р) является мерой рыночного риска акции, показывая изменчивость доходности акции по отношению к доходности на рынке в среднем (среднерыночного портфеля). [c.37]
Р — коэффициент бета , показывающий соотношение между изменением дохода на акцию предприятия и изменением среднего дохода акций на рынке ценных бумаг (данный коэффициент характеризует меру риска вложений в акции предприятия если р > 1, то риск высокий если 0 [c.256]
Р.— коэффициент бета ценной бумаги (мера риска) [c.231]
Начальная стоимость портфеля акций находится следующим образом р = 8,75 900+21,25 700+14,75 1400+33,50 2000+68,25 1600 = 219 600 долл. Найдем коэффициент бета портфеля акций [c.127]
В качестве показателя системного риска принят так называемый (3 (бета)-коэф-фициент. характеризующий колебания курсов на рынке ценных бумаг. В целом Р трактуют как коэффициент эластичности, показывающий, насколько изменение цены
[c.172]
характеризующий колебания курсов на рынке ценных бумаг. В целом Р трактуют как коэффициент эластичности, показывающий, насколько изменение цены
[c.172]
В практике акционерных компаний США широко используется так называемый бета-коэффициент (р) показатель, характеризующий изменение курса конкретной ценной бумаги (акции) по отношению к динамике сводного индекса всего фондового рынка. [c.260]
Уровень финансового риска отдельных ценных бумаг определяется на основе следующих значений бета-коэффициентов р = 1 — средний уровень Р > 1 — высокий уровень р [c.156]
Бета-коэффициент портфеля ценных бумаг и любого другого портфеля р рассчитывается по формуле средней арифметической взвешенной [c.75]
Учетная р. Бета-коэффициент может быть определен не на основе рыночных оценок, а по учетным данным. Например, прибыль или иной показатель, характеризующий деятельность предприятия, может быть определен по данным бухгалтерского учета прибыль или другой соответствующий показатель, характеризующий состояние экономики страны, может быть известен по данным Госкомстата. При наличии этих данных за несколько периодов может быть определена учетная (3 путем регрессионного или корреляционного анализа в соответствии с формулами (3.20).и (3.21). Учетная 3 является довольно грубым приближением рыночной (3, но в некоторых случаях, например при оценке доходности малых предприятий, получить рыночные оценки затруднительно. Исследования показывают, что между учетными и рыночными (3 имеет место значимая корреляционная связь, величины коэффициентов корреляции составляют 0,6-0,8.
[c.77]
При наличии этих данных за несколько периодов может быть определена учетная (3 путем регрессионного или корреляционного анализа в соответствии с формулами (3.20).и (3.21). Учетная 3 является довольно грубым приближением рыночной (3, но в некоторых случаях, например при оценке доходности малых предприятий, получить рыночные оценки затруднительно. Исследования показывают, что между учетными и рыночными (3 имеет место значимая корреляционная связь, величины коэффициентов корреляции составляют 0,6-0,8.
[c.77]
Внешний риск, связанный с выбором сферы деятельности предприятия (отраслевой риск), оценивается среднеотраслевой нормой доходности. Он определяется отраслевым бета-коэффициентом (Р), который является коэффициентом соответствующего регрессионного уравнения и связывает среднеотраслевой риск со среднерыночным. [c.232]
Коэффициент регрессии бета измеряет влияние общей ситуации на рынке в целом на судьбу конкретной бумаги. Если Р>0, то эффективность данной ценной бумаги повышаться при росте эффективности рынка. При Рценной бумаги будет снижаться при возрастании эффективности рынка. Понять значимость фактора бета поможет его экономическая интерпретация. Если портфель имеет Р = +1, это означает, что доходность бумаги в среднем будет расти на 10%, если доходность рыночного портфеля акций в целом возросла, например, на 10%. Портфель, имеющий Р = 2, вдвое более изменчив, чем общий рыночный портфель. Когда рыночная доходность увеличивается на 10%, доходность такого портфеля увеличивается на 20%.
[c.228]
При Рценной бумаги будет снижаться при возрастании эффективности рынка. Понять значимость фактора бета поможет его экономическая интерпретация. Если портфель имеет Р = +1, это означает, что доходность бумаги в среднем будет расти на 10%, если доходность рыночного портфеля акций в целом возросла, например, на 10%. Портфель, имеющий Р = 2, вдвое более изменчив, чем общий рыночный портфель. Когда рыночная доходность увеличивается на 10%, доходность такого портфеля увеличивается на 20%.
[c.228]
Определить бета-коэффициенты рискованных активов относительно портфеля Р> [c.125]
Мера систематического Степень систематического риска количественно оценивается риска — коэффициент р. параметром (коэффициентом) Р (называемым также «бета-фактором»). [c.278]
Рассмотрим сначала систематический риск, измеряемый показателем р (бета), который характеризует реакцию котировок отдельных ценных бумаг на изменение внешних факторов, описывающих общее состояние экономики или ее отдельных отраслей. Коэффициент Р показывает изменение цены бумаги по отношению ко всему рынку и может быть оценен по следующей простой формуле [c.194]
Коэффициент Р показывает изменение цены бумаги по отношению ко всему рынку и может быть оценен по следующей простой формуле [c.194]
Бета портфеля представляет собой взвешенное среднее значений р-коэффициентов, включенных в портфель активов. [c.37]
Кт — ожидаемая доходность в среднем на фондовом рынке Р — бета-коэффициент данной компании. [c.250]
Коэффициент р дает также возможность измерить относительную меру чувствительности фактической доходности данной ценной бумаги по отношению к фактической доходности всего рыночного портфеля. Таким образом, если фактическая доходность рыночного портфеля оказывается на У%, меньше (или больше) ожидаемой, то полученная доходность ценной бумаги/ будет равняться значению, которое больше (или меньше) ожидаемого на величину, равную Р, х У%. В связи с этим ценные бумаги, имеющие высокий коэффициент «бета» (превышающий 1) называются «агрессивными», поскольку их доходность обладает более сильной динамикой, чем Доходность всего рыночного портфеля. Другими словами, их доходность сильнее повышается при общем подъеме на рынке и, соответственно, сильнее снижается при спаде. Аналогично этому ценные бумаги, коэффициенты «бета» для которых невелики (менее 1), называются «оборонительными». Рыночный портфель имеет по определению значение «бета», равное 1, а ценные бумаги с «бета», равным 1, называются «среднерисковыми».
[c.233]
Другими словами, их доходность сильнее повышается при общем подъеме на рынке и, соответственно, сильнее снижается при спаде. Аналогично этому ценные бумаги, коэффициенты «бета» для которых невелики (менее 1), называются «оборонительными». Рыночный портфель имеет по определению значение «бета», равное 1, а ценные бумаги с «бета», равным 1, называются «среднерисковыми».
[c.233]
Р — коэффициент «бета», указывающий на меру относительного систематического риска инвестирования в оцениваемый бизнес по сравнению с капиталовложениями в любой, т.е. среднерискованный бизнес. [c.36]
К сожалению, рассмотренные ранее меры риска представляют либо качественные показатели — рейтинги, либо среднюю температуру по больнице — спред с казначейскими облигациями. А что нужно сделать для определения риска инвестирования на относительно короткий срок в конкретную ценную бумагу Ответ на этот вопрос дают значения коэффициентов альфа (а), бета (р) и сигма (ст) для рассматриваемой бумаги. Для того чтобы воспользоваться этими коэффициентами, необходимо перейти от анализа цен канализудоход-ностей. При этомрискможно ассоциировать с вероятностью отклонения доходности актива от ожидаемого значения за определенный промежуток времени. Для этого нам придется определить так называемую логарифмическую доходность активу г, наиболее часто используемую в финансовой математике [c.196]
При этомрискможно ассоциировать с вероятностью отклонения доходности актива от ожидаемого значения за определенный промежуток времени. Для этого нам придется определить так называемую логарифмическую доходность активу г, наиболее часто используемую в финансовой математике [c.196]
Второе состоит в том, что рыночная модель использует рыночный индекс (market index), такой, как, например, S P 500, в то время как САРМ — рыночный портфель (marketportfolio). Рыночный портфель сочетает в себе все обращающиеся на рынке бумаги, а рыночный индекс — только ограниченное их число (например, 500 для индекса S P 500). Поэтому концептуально коэффициент Р(/из рыночной модели отличается от коэффициента р. м из САРМ. Это связано с тем, что бета в рыночной модели измеряется относительно рыночного индекса, а бета в САРМ- относительно рыночного портфеля. На практике, однако, в связи с тем, что точно определить структуру рыночного портфеля не удается, используют рыночный индекс. Поэтому бету , определенную с помощью рыночного индекса, несмотря на концептуальное различие, принимают в качестве оценки беты в САРМ. [c.271]
[c.271]
Показатель «бета» рассчитывается на основе накопленных статистических данных. Расчетом показателей «бета» для котирующихся на крупнейших мировых фондовых биржах ценных бумаг занимаются специализированные инвестиционные фирмы. «Бета» характеризует юаимосвязь между доходностью данной инвестиции и среднерыночной доходностью. Например, если коэффициент Р = 2, это означает, что при росте среднерыночной доходности на 1% доходность по данной инвестиции вырастет на 2%. [c.113]
Определить бета-коэффициент, систематический и особый рнскн портфеля акций Р = (0,25 0,25 0,50) для исходных данных, приведенных ниже. [c.123]
Бета-коэффициент в трейдинге — что это, особенности расчета, формула, применение бета-коэффициента
Инвестиции04 ноября 2020 в 15:0010 904
И как его использовать для анализа доходности
Рыночные профессионалы при анализе отдельно взятых ценных бумаг и инвестиционных портфелей часто применяют бета-коэффициент, или β-коэффициент, с помощью которого определяют зависимость доходности ценной бумаги (или портфеля ценных бумаг) от доходности рынка в целом. Её часто характеризует динамика индекса, а также степень риска анализируемого актива и его волатильность. Применяя бета-коэффициент, рыночные профессионалы могут составлять качественные диверсифицированные портфели, способные показывать весьма интересную доходность и сглаживать рыночный риск. Что такое бета-коэффициент, мы расскажем в данной статье.
Её часто характеризует динамика индекса, а также степень риска анализируемого актива и его волатильность. Применяя бета-коэффициент, рыночные профессионалы могут составлять качественные диверсифицированные портфели, способные показывать весьма интересную доходность и сглаживать рыночный риск. Что такое бета-коэффициент, мы расскажем в данной статье.
Логика и определение бета-коэффициента, а также формула его расчёта
В ценовой динамике различных активов существует взаимосвязь, которую ещё называют корреляцией. Такие взаимосвязи могут быть более или менее выраженными, а также прямыми или обратными. Приведём пример прямой корреляции: часто при росте Индекса РТС более-менее синхронно растут в цене акции «Сбербанка».
Рис. 1. Прямая корреляция акций «Сбербанка» и Индекса РТС
Напротив, весьма часто при снижении стоимости доллара США растёт значение Индекса РТС — это пример обратной корреляции.
Рис. 2. Обратная корреляция курса доллара США и Индекса РТС
Подобная синхронность или асинхронность могут быть как более, так и менее выраженными.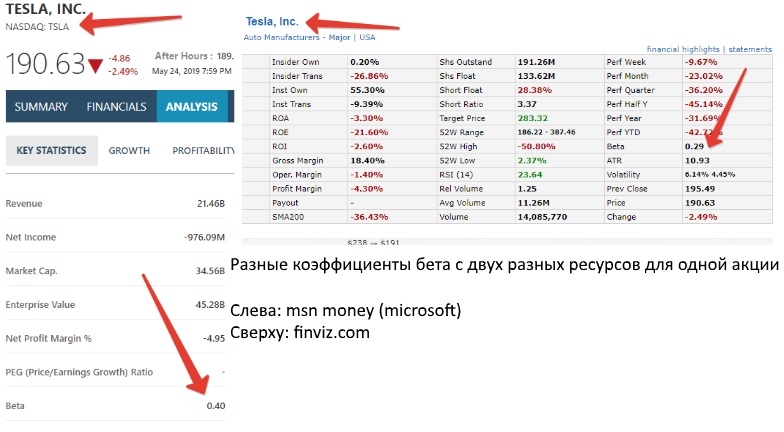 Например, если индекс вырастет в цене, допустим на 2%, то какая-нибудь бумага второго эшелона может и вовсе не измениться в своей стоимости. Но это предположение не говорит о полном отсутствии взаимосвязи — просто она менее выражена, так как при каком-либо серьёзном позитиве (сильно выраженном) в индексе рост (пусть и менее выраженный) вполне может охватить и многие бумаги с меньшей корреляцией. Также есть бумаги с большей волатильностью, которые своим ценовым размахом способны опережать динамику индекса.
Например, если индекс вырастет в цене, допустим на 2%, то какая-нибудь бумага второго эшелона может и вовсе не измениться в своей стоимости. Но это предположение не говорит о полном отсутствии взаимосвязи — просто она менее выражена, так как при каком-либо серьёзном позитиве (сильно выраженном) в индексе рост (пусть и менее выраженный) вполне может охватить и многие бумаги с меньшей корреляцией. Также есть бумаги с большей волатильностью, которые своим ценовым размахом способны опережать динамику индекса.
Рис. 3. Пример низкой корреляции акций «М. Видео» и Индекса РТС
Соответственно, можно говорить как о волатильности бумаг при какой-либо динамике индекса, так и о синхронности или асинхронности ценовой динамики. Волатильность, в свою очередь, характеризует и риск финансовых вложений, так как диапазон ценовых значений априори расширяется как в сторону увеличения цены, так и в сторону снижения. И именно волатильность и синхронность подобной динамики характеризуют бета-коэффициент.
Использование бета-коэффициента было предложено Гарри Марковицем, изначально он назывался индексом недиверсифицируемого риска. Это весьма неплохо передаёт его логику, так как включение в портфель бумаг с грамотно подобранной бетой способно значительно сгладить кривую доходности портфеля при индексной волатильности.
Рассмотрим непосредственно бета-коэффициент. Он рассчитывается как отношение ковариации доходностей бумаги и индекса (анализируемого и эталонного активов: бумага и портфель, портфель и индекс или бумага и индекс) к дисперсии доходности индекса.
β = Cov (Бн, Ин) / Var (И), где
β — бета-коэффициент, Бн — доходность бумаги, Ин — доходность индекса, Cov — ковариация бумаги и индекса, Var — дисперсия индекса.
Для лучшего понимания данную формулу бета-коэффициента можно представить в следующем виде:
β = ∑ (Бн — Бнср) * (Ин — Инср) / ∑ (Ин — Инср)2, где
Бн — доходность бумаги за анализируемый период, Бнср — средняя доходность бумаги за анализируемый период, Ин — доходность индекса за анализируемый период, Инср — средняя доходность индекса за анализируемый период, н — рассматриваемый период времени.
Если бумага в среднем двигается синхронно с индексом, то бета будет положительной, если же бумага движется асинхронно (обратная корреляция), то бета принимает отрицательные значения. Если бета равна единице, то можно говорить о полной синхронности бумаги и индекса. Если бета примет значение от нуля до единицы, то бумага имеет определённую синхронность с индексом, но её волатильность всё же меньше. А если показатель выше единицы, то бумага проявляет большую волатильность в сравнении с индексом при наличии синхронности движения.
Когда доходность индекса составила 10%, а бета бумаги 0,7, можно сказать, что доходность бумаги 7%. Если же бета 1,2, то бумага покажет доходность 12%, а если бета −0,2, то доходность бумаги −2%.
У каждой бумаги есть своя бета по отношению к индексу, даже околонулевая. А если учесть, что портфель состоит из определённых бумаг в соответствии с их весовыми коэффициентами, то общая бета портфеля к индексу будет равна сумме произведений беты бумаг, образующих портфель, и их весовых коэффициентов.
βп = ∑ βб * х, где
βп — бета-коэффициент портфеля, βб — бета-коэффициент бумаги, х — весовой коэффициент бумаги (процентная доля бумаги в портфеле).
Плюсы и минусы использования бета-коэффициента
У применения бета-коэффициента есть как сильные, так и слабые стороны. К плюсам беты можно отнести относительную простоту понимания и применения, так как подбор бумаг с её учётом позволяет сгладить доходность портфеля при индексной волатильности.
Также бету часто применяют при оценке управления портфелем ценных бумаг, так как результативность управления обычно оценивается в сравнении с динамикой индекса за аналогичный период, а задача управляющего — обогнать доходность индекса и показать лучший результат.
К проблемам использования бета-коэффициента компании можно отнести то, что приходится сравнивать бумаги с основными индексами Московской биржи, в которых велика доля участия сырьевых компаний. Поэтому может быть целесообразно в качестве эталонного бенчмарка брать не только эти индексы, но также производить расчёт бета-коэффициента по отношению к соответствующему отраслевому индексу и сравнивать эту бету с бетой компаний аналогичной отрасли.
Использование беты позволяет лучше понять и рационально составить портфель ценных бумаг как с точки зрения волатильности, так и с точки зрения корреляции бумаг, образующих портфель с общим рынком, характеризуемым индексом. Это делает результаты управления более прогнозируемыми и статистически более высокими.
Изучить все нюансы использования бета-коэффициента и начать зарабатывать на биржевых торгах вам всегда поможет компания «Открытие Брокер»!
__
Значение коэффициента бета для среднерыночного портфеля. Коэффициент бета — есть ли практическая польза? Недостатки использования коэффициента бета в модели CAPM
Бета-коэффициент (бета-фактор) — показатель, рассчитываемый для ценной бумаги или портфеля ценных бумаг. Является мерой рыночного риска, отражая изменчивость доходности ценной бумаги (портфеля) по отношению к доходности портфеля (рынка) в среднем (среднерыночного портфеля).
Если ценная бумага (портфель во втором случае) является менее рисковой, чем портфель (рынок в целом во втором случае), то бета-коэффициент меньше 1.
 Иначе бета-коэффициент больше 1.
Иначе бета-коэффициент больше 1.Коэффициент бета (β) показывает чувствительность цены отдельной ценной бумаги к значению индекса. Например, значение показателя бета равное 2 означает, что в случае роста индекса на 1 процент цена ценной бумаги вырастет на 2 процента. Отрицательное значение коэффициента бета свидетельствует об обратной зависимости между изменением цены ценной бумаги и значением индекса. Коэффициент бета равный нулю свидетельствует об отсутствии связи между изменением цены ценной бумаги и индексом.
1. Здесь можно посмотреть коэффициенты: бета (β), альфа (α) и волатильность за различные периоды.
Бета-коэффициент (по англ
. beta)
– это показатель чувствительности цены акции относительно всего фондового рынка (или широкого индекса акций). Бета измеряет систематический риск, то есть риск
,
присущий всей финансовой системе. Бета-коэффициент является важным компонентом модели оценки капитальных активов
CAPM
при расчете требуемой нормы прибыли. Математически
,
бета представляет собой коэффициент наклона Линии рынка ценных бумаг (по англ
. Security Market Line).
Математически
,
бета представляет собой коэффициент наклона Линии рынка ценных бумаг (по англ
. Security Market Line).
Бета-коэффициент рассчитывается как ковариация между доходностью акции и доходностью рынка, разделенная на дисперсию рыночной доходности.
Небольшая модификация данной формулы позволит выявить еще одно ключевое соотношение : коэффициент бета равен коэффициенту корреляции, умноженному на стандартное отклонение доходности акций, разделенное на стандартное отклонение рыночных доходностей.
Бета-коэффициент равный 1 предполагает, что акция имеет такой же риск, что и общий рынок, и доходность акции будет сопоставима с доходностью рынка. Коэффициент ниже единицы указывает на пониженный риск и более низкую потенциальную доходность относительно рынка . С другой стороны , β выше 1 , более высокий риск инвестирования в данную акцию .
В 2017 году акция
Chevron (тикер CVX)
имела бета коэффициент 1.17. Это свидетельствует о том, что акция компании немного более рискованна, чем индекс акций
S&P 50
. Marathon Oil (тикер на бирже NYSE: MRO), с другой стороны, имеет β в размере 3.02
.
Можно заключить, что эта акция более рискованная, чем рынок в целом.
Marathon Oil (тикер на бирже NYSE: MRO), с другой стороны, имеет β в размере 3.02
.
Можно заключить, что эта акция более рискованная, чем рынок в целом.
Если у нас нет информации по стандартному отклонению и корреляции для расчета бета коэффициента , необходимо выполнить следующие простые шаги в Excel :
1) Найдите данные о исторической динамике цены акции
2) Получите исторические значения соответствующего индекса (например, S&P500).
3) Определяем дневную доходность цены акции, используя следующую формулу:
Доходность = (Цена закрытия – Цена открытия)/Цена открытия
4) Аналогичным образом преобразуйте значения цены индекса в доходности .
5) Сопоставляем полученные доходности по датам .
6) При помощи функции НАКЛОН (в англоязычной версии – SLOPE) определяем коэффициент наклона между массивами данных . Итоговое значение и является бета коэффициентом .
- Расчет средневзвешенной стоимости капитала Не найдено: 2018
Полученное расчетное значение показателя бета необходимо скорректировать на коэффициент характеризующий амплитуду колебаний общей доходности акций компаний данной отрасли - Расчет ставки дисконтирования для МСФО обесценения Не найдено: 2018
Если этот коэффициент больше 1, значит акция неустойчива при бета-коэффициенте меньше 1 более устойчива именно поэтому консервативные инвесторы в первую очередь интересуются этим коэффициентом и предпочитают акции с низким его уровнем Коэффициент бета с учетом структуры капитала рассчитывается по формуле Beta levered Beta unlevered × 1 - Оценка премии за специфические риски компании при определении требуемой доходности на собственный капитал Не найдено: 2018
Ibbotson Associates 2010 г — принята ставка средняя по отрасли prepackaged software состоящая из 313 компаний на рынке капитала США источник — SBBI . .. O составила 26,21% Однако следует отметить что вероятно проводить расчет подобной премии было бы целесообразнее для оцениваемой компании на базе ее собственных коэффициентов
риска бет
чем использовать усредненные групповые оценки премии за отрасль
Такой подход мог бы привести в… Duff&Phelps предлагает делать надбавку за специфические риски на свой профессиональный взгляд подходы к расчету премии за рыночный риск для различных размерных групп компаний опираются на такие показатели
риска как операционная маржа коэффициент
вариации операционной маржи коэффициент
вариации доходности на собственный капитал
.. O составила 26,21% Однако следует отметить что вероятно проводить расчет подобной премии было бы целесообразнее для оцениваемой компании на базе ее собственных коэффициентов
риска бет
чем использовать усредненные групповые оценки премии за отрасль
Такой подход мог бы привести в… Duff&Phelps предлагает делать надбавку за специфические риски на свой профессиональный взгляд подходы к расчету премии за рыночный риск для различных размерных групп компаний опираются на такие показатели
риска как операционная маржа коэффициент
вариации операционной маржи коэффициент
вариации доходности на собственный капитал - Модель оценки капитальных активов как инструмент оценки ставки дисконтирования Не найдено: 2018
Что качается финансового рычага то компании имеющие высокий уровень этого показателя больше подвержены системному риску по двум причинам Во-первых значительные процентные платежи приводят к тому… С учетом финансового рычага коэффициент бета равен 4 Bi Bu 1 1 — t D E 2 где Bi . .. Таблица 2. Расчет средневзвешенного β-коэффициента многоотраслевой компании Отрасль
Доля вида деятельности Коэффициент
β Взвешенный β-коэффициент Черная металлургия 0,4 0,5 0,2 Цветная металлургия
.. Таблица 2. Расчет средневзвешенного β-коэффициента многоотраслевой компании Отрасль
Доля вида деятельности Коэффициент
β Взвешенный β-коэффициент Черная металлургия 0,4 0,5 0,2 Цветная металлургия - Формирование многофакторного критерия оценки инвестиционной привлекательности организации Не найдено: 2018
Таблица 4. Данные для расчета значения многофакторного критерия оценки инвестиционной привлекательности организации Показатель Критерий оценки Квадра ОГК-2 ОГК-5 Ассортимент продукции Степень привлекательности продукции 4 3 3 Стоимость… Финансовая привлекательность 0,25 0,56 0,80 Коэффициент бета Уровень риска 1,22 1,39 0,82 По состоянию на 2012 г Подставляя данные значения… О ОГК-5 Определим среднее значение критерия многофакторного критерия инвестиционной привлекательности анализируемых компаний энергетической отрасли 5,00 4,63 4,56 3 4,73. Как уже было отмечено среднее значение многофакторного критерия инвестиционной - Анализ моделей оценки стоимости капитала Не найдено: 2018
Бета безрычаговая по отрасли Дамодаран 1. 03 Заемный капитал тыс руб 141 663 000 Собственный капитал тыс… Данный метод основывается на том что доходность заемных средств определяется исходя из коэффициента
покрытия процентов В соответствии с этим показателем
присваивается рейтинг и спред дефолта который прибавляется
03 Заемный капитал тыс руб 141 663 000 Собственный капитал тыс… Данный метод основывается на том что доходность заемных средств определяется исходя из коэффициента
покрытия процентов В соответствии с этим показателем
присваивается рейтинг и спред дефолта который прибавляется - Инвестиционный риск Не найдено: 2018
Метод анализа иерархий позволяет учитывать человеческий фактор при подготовке принятия решения является универсальным — применим для различных отраслей служит надстройкой для других методов призванных решать плохо формализованные задачи где больше подходят человеческие… Значения коэффициентов бета определяются на основе анализа ретроспективных данных соответствующими статистическими службами компаний специализирующихся на рынке… Премия за риск определяется как среднегодовой избыточный доход превышение над ставкой дохода по государственным облигациям со сроком погашения 10 лет за период наблюдения 5-10 лет и составляет… РТС который мог бы служить этим показателем свидетельствует что в этом случае доходность менялась бы от -85% до 197% б Две - Сколько стоит собственный капитал компании Не найдено: 2018
Excel 2007, автоматически вычисляющую значение стоимости собственного капитала коэффициент бета WAСC а заодно и экономическую добавленную стоимость EVA Стоимость капитала по мерке САРМ. .. С безрисковой ставкой все просто — берем показатель
дохода который можно получить по
государственным ценным бумагам с минимальной вероятностью дефолта Например по
… В формуле речь идет именно о рыночной доходности средней по
рынку а не отдельной компании На мой взгляд использовать ROE отдельной организации здесь неуместно… Но на практике лучше взять бета
публичной компании из той же отрасли
с аналогичным профилем и скорректировать на соотношение собственных
.. С безрисковой ставкой все просто — берем показатель
дохода который можно получить по
государственным ценным бумагам с минимальной вероятностью дефолта Например по
… В формуле речь идет именно о рыночной доходности средней по
рынку а не отдельной компании На мой взгляд использовать ROE отдельной организации здесь неуместно… Но на практике лучше взять бета
публичной компании из той же отрасли
с аналогичным профилем и скорректировать на соотношение собственных - Методы оценки стоимости компании в сделках М&А на примере поглощения ОАО «КОНЦЕРН «КАЛИНА» Не найдено: 2018
ОАО Концерн Калина Показатель Размер Примечание βKLNA коэффициент бета для концерна Калина рассчитанный из уравнения регрессии 0,739 Коэффициент … RAT и средний прогнозируемый темп роста отрасли в России В табл 6 приведен расчет прогнозного темпа ростасоставляет 33,8 млрд руб Полученная - Факторы специфических рисков компаний при оценке премии за эти риски на развивающихся рынках капитала Не найдено: 2018
БРИКС порядка 18000 наблюдений до отбора данных по показателям деятельности компаний автор получил следующее распределение значений премии для выборки публичных компаний БРИКС. .. А Дамодарана Значения рассчитанных премий без учета экстремальных значений коэффициента
совокупной беты
то есть Tβ
.. А Дамодарана Значения рассчитанных премий без учета экстремальных значений коэффициента
совокупной беты
то есть Tβ - Линия рынка ценных бумаг и стоимость капитала Не найдено: 2018
E rm — ожидаемая рыночная доходность где rd — стоимость задолженности rf — безрисковая ставка βd — коэффициент бета задолженности E rm — ожидаемая рыночная доходность По результатам произведенных расчетов можно сделать… Также стоит отметить что показатель стоимости капитала предприятия может выступать критерием при оценке эффективности лизинга Если стоимость финансового лизинга… Эффективность налогового менеджмента и оптимизация налогов предприятий нефтяной отрасли Материалы II Международной научно-практической конференции в 2-х частях Под редакцией Ю С Руденко Л - Не найдено: 2018
- Расчёт ключевых финансовых показателей эффективности бизнеса Не найдено: 2018
Коэффициент бета Исторические рыночные коэффициенты На основе регрессионного анализа доходности инвестиций относительно доходности рынка Фундаментальные коэффициенты . .. Бухгалтерские коэффициенты
На основе соотнесения бухгалтерских показателей
прибыли фирмы с аналогичными показателями
по
рынку в целом… Однако финансовый кризис 2008 г не прошел без последствий и для этого гиганта металлургической отрасли
России Все показатели
рентабельности резко снизились Анализ данных Отчета о прибылях и убытках говорит
.. Бухгалтерские коэффициенты
На основе соотнесения бухгалтерских показателей
прибыли фирмы с аналогичными показателями
по
рынку в целом… Однако финансовый кризис 2008 г не прошел без последствий и для этого гиганта металлургической отрасли
России Все показатели
рентабельности резко снизились Анализ данных Отчета о прибылях и убытках говорит
Вероятно, многие слышали о необходимости соизмерять риск с уровнем доходности от сделки. Главное правило трейдинга гласит, что чем больше риск, тем больше потенциальный доход. Но даже высокий риск должен быть просчитан и обоснован.
Поведение многих акций коррелируются с динамикой индекса S&P 500, поэтому был выведен бета коэффициент . Его применение позволяет измерить степень корреляции бумаги с индексом. Рассмотрим основные моменты, которые следует учесть, чтобы использовать его в торговой практике.
Что представляет собой бета коэффициент? Его значение
Бета коэффициент является величиной, измеряющей изменчивость прибыльности одной бумаги по отношению к другой. За основу взят индекс S&P 500, чей коэффициент равен единице. Если у Вашей ценной бумаги он такой же:
За основу взят индекс S&P 500, чей коэффициент равен единице. Если у Вашей ценной бумаги он такой же:
- Вы несете аналогичные риски, как если бы торговали индексом;
- Когда он поднимется на 10% — с бумагой произойдет то же самое.
Если значение бета коэффициента акции меньше, например, 0,7 – ее цена возрастет только на 7%, в то время, как индекс на 10%. Но риск также уменьшится. Соответственно, при показателе, превышающем единицу, риски и доходность возрастают. Если он равен 2, то цена бумаги повысится на 20% при росте индекса на 10%.
Существуют также альтернативные варианты:
- Бета коэффициент равен 0;
- У него отрицательное значение.
Акции с нулевым уровнем корреляции непредсказуемы. Их динамика абсолютно не зависит от изменения стоимости индекса. Во втором случае риски остаются без изменений, но вместо дохода держатель получает убыток (-5%, — 10% и т.д.). Мы не рекомендуем трейдерам торговать акции, относящиеся к последним двум категориям.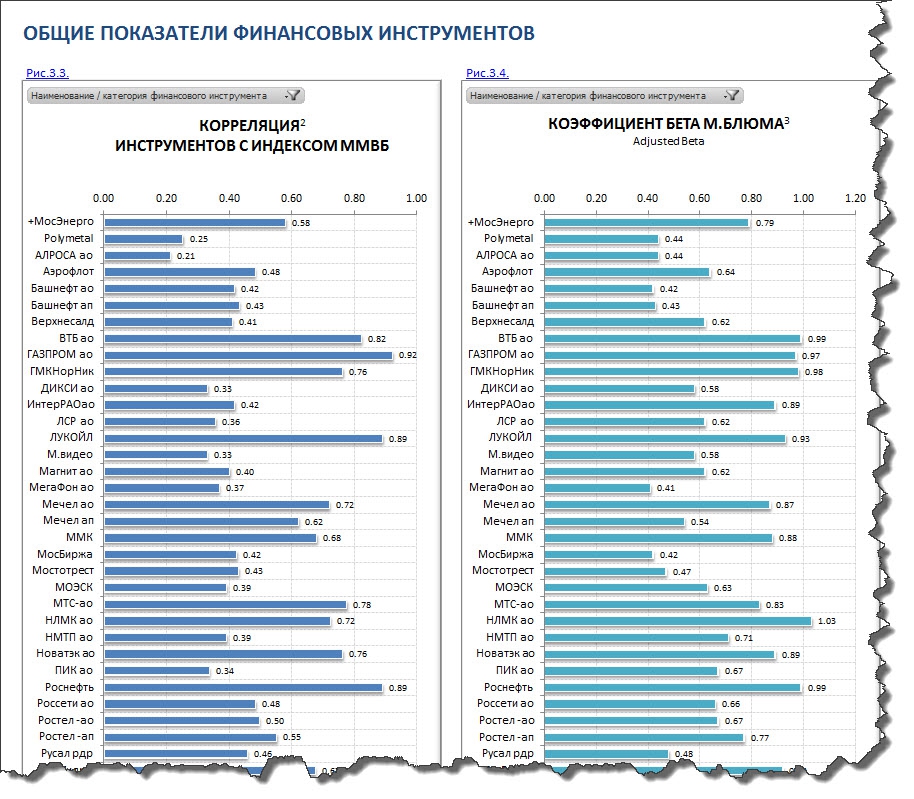
Почему бета коэффициент не должен слишком превышать единицу?
Узнав, что бумаги, чье значение бета коэффициента превышает единицу в 2 и более раза могут быть очень прибыльными, многие хотят рискнуть. Защитить средства при высокой степени волатильности активов можно, регулируя размеры позиций. Но если Вы предпочтете агрессивную стратегию, следует учесть, что:
- Бета коэффициент был создан для сравнениядля сравнения доходности инвестиционных фондов и индекса. В расчет брались годовые показатели дохода;
- Вы не получите удвоенный годовой доход за несколько дней, используя бумаги с показателем, равным 2. Но Вы получите высоковолатильные акции;
- Показатель рассчитывается на основе предыдущих уровней выручки. Когда финансовые результаты функционирования изменятся – он также поменяет значение;
- Он не измеряет силу позиции, перспективы эмитента. Высокое его значение не характеризует эмитента, как лидера отрасли.
Измерять волатильность ценных бумаг можно и другими инструментами технического анализа, например ATR.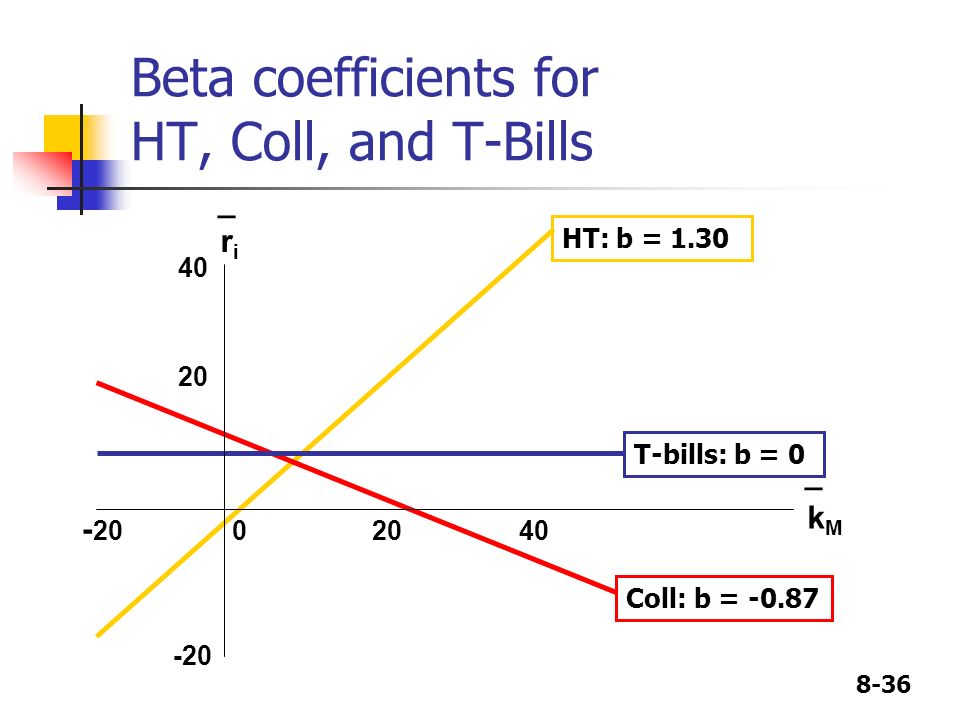 Для получения максимально объективного результата следует комбинировать применение различных инструментов, индикаторов, внимательно изучать графики и руководствоваться личным опытом.
Для получения максимально объективного результата следует комбинировать применение различных инструментов, индикаторов, внимательно изучать графики и руководствоваться личным опытом.
Обучение трейдингу для получения знаний и навыков
Модель Шарпа рассматривает взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом.
Основные допущения модели Шарпа:
В качестве доходности ценной бумаги принимается математическое ожидание доходности;
Существует некая безрисковая ставка доходности , т. е. доходность некой ценной бумаги, риск которой всегда минимален по сравнению с другими ценными бумагами;
Взаимосвязь отклонений доходности ценной бумаги от безрисковой ставки доходности (далее:отклонение доходности ценной бумаги ) с отклонениями доходности рынка в целом от безрисковой ставки доходности (далее: отклонение доходности рынка ) описывается функцией линейной регрессии ;
Под риском ценной бумаги понимается степень зависимости изменений доходности ценной бумаги от изменений доходности рынка в целом;
Считается,
что данные прошлых периодов,
используемые при расчете доходности и
риска, отражают в полной мере будущие значения
доходности.
По модели Шарпа отклонения доходности ценной бумаги связываются с отклонениями доходности рынка функцией линейной регрессии вида:
где — отклонение доходности ценной бумаги от безрисковой;
Отклонение доходности рынка от безрисковой;
Коэффициенты регрессии.
Основной недостаток модели — необходимость прогнозировать доходность фондового рынка и безрисковую ставку доходности. Модель не учитывает колебаний безрисковой доходности. Кроме того, при значительном изменении соотношения между безрисковой доходностью и доходностью фондового рынка модель дает искажения. Таким образом, модель Шарпа применима при рассмотрении большого количества ценных бумаг, описывающих бо льшую часть относительно стабильного фондового рынка.
41.Рыночная премия за риск и коэффициент бета.
Рыночная премия за риск — разница между ожидаемой доходностью рыночного портфеля и безрисковой ставкой.
Бета-коэффициент (бета-фактор) —
показатель, рассчитываемый для ценной
бумаги или
портфеля ценных бумаг. Является
мерой рыночного
риска ,
отражая изменчивость доходности ценной
бумаги (портфеля) по отношению к доходности
портфеля (рынка )
в среднем (среднерыночного портфеля).
В случае компаний, не имеющих торгуемых
на рынке акций, можно расчитать
бета-коэффициент, основанный на сравнении
с показателями компаний-аналогов.
Аналоги берут из той же отрасли, бизнес
которых максимально похож на бизнес
непубличной компании. При расчёте
необходимо сделать ряд поправок, в
частности, на разницу в структуре
капитала сравниваемых компаний
(соотношения долга и акционерного
капитала).
Является
мерой рыночного
риска ,
отражая изменчивость доходности ценной
бумаги (портфеля) по отношению к доходности
портфеля (рынка )
в среднем (среднерыночного портфеля).
В случае компаний, не имеющих торгуемых
на рынке акций, можно расчитать
бета-коэффициент, основанный на сравнении
с показателями компаний-аналогов.
Аналоги берут из той же отрасли, бизнес
которых максимально похож на бизнес
непубличной компании. При расчёте
необходимо сделать ряд поправок, в
частности, на разницу в структуре
капитала сравниваемых компаний
(соотношения долга и акционерного
капитала).
Коэффициента Бета для актива в составе портфеля ценных бумаг, или актива (портфеля) относительно рынка является отношением ковариации рассматриваемых величин кдисперсии эталонного портфеля или рынка соответственно :
где —
оцениваемая величина, для которой
вычисляется коэффициент Бета: доходность
оцениваемого актива или портфеля, —
эталонная величина, с которой происходит
сравнение: доходность портфеля ценных
бумаг или рынка, — ковариация оцениваемой
и эталонной величины, — дисперсия эталонной
величины.
Бета-коэффициент – это единица измерения, которая дает количественное соотношение между движением курса данной акции и движением рынка акций в целом. Нельзя путать с изменчивостью.
Бета-коэффициент (англ. beta coefficient) – это показатель степени риска применительно к инвестиционному портфелю или к конкретным ценным бумагам; отражает степень устойчивости курса данных акций по сравнению с остальным фондовым рынком; устанавливает количественное соотношение между колебаниями цены данной акции и динамикой цен рынка в целом. Если этот коэффициент больше 1, значит, акция неустойчива; при бета-коэффициенте меньше 1 – более устойчива; именно поэтому консервативные инвесторы в первую очередь интересуются этим коэффициентом и предпочитают акции с низким его уровнем.
CFA — Расчет бета-коэффициента и определение беты для инвестиционного проекта | программа CFA
При расчете средневзвешенной стоимости капитала (WACC) важно понять факторы риска, которые были рассмотрены при определении безрисковой ставки, премии за риск акций и бета-коэффициента, чтобы обеспечить согласованный расчет WACC и избежать двойного учета или упущения соответствующих факторов риска.
Когда финансовый аналитик использует модель CAPM для оценки стоимости собственного капитала (затрат на капитал), он должен оценить бета-коэффициент. Оценка бета-коэффициента обычно связана со множеством вариантов и сложностей.
Одним из распространенных методов расчета бета-коэффициента акций компании является использование регрессии рыночной модели доходности акций компании \( (R_i) \) в зависимости от рыночной доходности \( (R_m) \) за \( T \) периодов:
\( R_{it} = \hat a + \hat b R_{mt} \) \(t = 1,2, \ldots T\)
Где \( \hat a \) представляет собой оценочный отрезок, отсекаемый линией регрессии, а \( \hat b \) является оценочным наклоном регрессии, которая используется для расчета бета-коэффициента.
Это уравнение обычно называют рыночной моделью (англ. ‘market model’), которая впервые была представлена Майклом С. Дженсеном в публикации «The Performance of Mutual Funds in the Period 1945-1964«», Journal of Finance, Vol. 23, No. 2 (1969), стр. 389-416.
389-416.
Однако оценка бета-коэффициента чувствительна к методу оценки и используемым данным. Вот некоторые из проблем, с которыми приходится сталкиваться:
Период оценки. Бета чувствительна к длительности периода оценки, и обычно оценивается с использованием данных за 2-9 лет. Выбор периода оценки — это компромисс между большим объемом данных за более длительные периоды оценки и конкретными изменениями в компании, которые лучше отражаются в более коротких периодах.
В целом, более длительные периоды оценки применяются к компаниям с долгой и стабильной историей операционной деятельности, а более короткие периоды оценки используются для компаний, которые претерпели значительные структурные изменения в недавнем прошлом (например, реструктурирование, недавнее приобретение или ликвидация подразделения) или изменения в финансовом и операционном рычаге.
Периодичность интервала доходности (например, дневной, недельный или месячный). Исследователи наблюдали меньшую стандартную ошибку в бета-коэффициенте, оцененном с использованием меньших интервалов доходности, таких как ежедневная доходность.
Исследователи наблюдали меньшую стандартную ошибку в бета-коэффициенте, оцененном с использованием меньших интервалов доходности, таких как ежедневная доходность.
Выбор соответствующего рыночного индекса. Выбор рыночного индекса влияет на оценку бета.
Использование метода сглаживания. Некоторые аналитики корректируют историческую бета, чтобы отразить тенденцию стремления бета к 1. Например, выражение \( \beta_{i, \text {корр.}} = 0.333 + 0.667 \beta_i \) корректирует бета выше и ниже 1.0, сводя ее к 1.0.
Корректировки для акций с малой капитализацией. Акции с малой капитализацией обычно проявляют больший риск и большую доходность, чем акции с большой капитализацией в течение длительного периода. Исследователи Роджер Ибботсон, Пол Каплан и Джеймс Петерсон утверждают, что бета-коэффициенты для компаний с малой капитализаций должны корректироваться в сторону увеличения.
См.: Roger G. Ibbotson, Paul D. Kaplan, and James D. Peterson, “Estimates of Small Stock Betas Are Much Too Low,” Journal of Portfolio Management (1997), стр. 104-110.
Kaplan, and James D. Peterson, “Estimates of Small Stock Betas Are Much Too Low,” Journal of Portfolio Management (1997), стр. 104-110.
Расчет бета-коэффициента для публичных компаний, как правило, не является проблемой из-за доступности данных о доходности акций, простоты расчета бета с использованием простой регрессии, а также наличия оценочных бета для публичных компаний от поставщиков данных для финансового анализа, таких как Barra, Bloomberg, DataStream Thompson Financials, Reuters и Line Value.
Как правило, проблема состоит в том, чтобы оценить бета-коэффициент для компании, чьи акции не торгуются публично, или оценить бета-коэффициент для проекта, который не является средним или типичным проектом публичной компании.
В этих случаях оценка бета требует использования информации о проекте или компании, в сочетании с бетой публичной компании.
Бета-коэффициент компании или проекта зависит от систематических компонентов бизнес-риска и от финансового риска. Оба этих фактора влияют на неопределенность денежных потоков компании или проекта.
Бизнес-риск или деловой риск (англ. ‘business risk’) компании или проекта — это риск, связанный с неопределенностью получения выручки, называемой риском продаж, а также связанный с операционным риском, который является риском, связанным со структурой операционных расходов компании.
Риск продаж или риск сбыта (англ. ‘sales risk’) зависит от эластичности спроса на продукцию, цикличности выручки и структуры конкуренции в отрасли.
Операционный риск (англ. ‘operating risk’) зависит от относительного сочетания постоянных и переменных операционных расходов: чем выше постоянные операционные расходы по отношению к переменным операционным расходам, тем больше неопределенность доходов и операционных денежных потоков.
Финансовый риск (англ. ‘financial risk’) — это неопределенность чистых доходов и чистых денежных потоков, связанных с использованием видов финансирования, которые имеют постоянную стоимость, таких как долговое финансирование и аренда.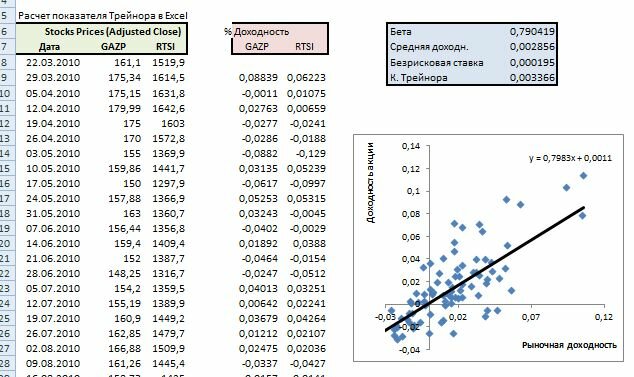
Чем больше используется постоянных источников капитала, относительно переменных источников, тем больше финансовый риск. Другими словами, компания, которая в значительной степени полагается на долговое финансирование вместо долевого финансирования, предположительно принимает больший финансовый риск.
Как финансовый аналитик оценивает бета-коэффициент для непубличной компании или проекта?
Один из обычных методов — это метод чистой игры (англ. ‘pure-play method’), который требует использования бета-коэффициента сопоставимой публичной компании, с корректировкой на различия в финансовом рычаге (леверидже), отражающие финансовый риск.
Сопоставимая компания (англ. ‘comparable company’) — это компания, имеющая аналогичный бизнес-риск. Причина, по которой этот подход называется методом чистой игры, заключается в том, что одним из самых простых способов идентификации сопоставимой компании для проекта является поиск в той же отрасли компании, которая ведет деятельность аналогичным образом.
Например, если аналитик изучает проект, связанный с аптечным бизнесом, соответствующими сопоставимыми компаниями в США могут быть Walgreens, CVS Corporation и Rite Aid Corporation.
Оценивая бету таким образом, аналитик должен сделать корректировки для учета разных уровней финансового рычага. Это требует процесса «де-левериджа» (устранение финансового риска) и «левериджа» (добавление финансового риска) бета-коэффициента (англ. ‘unlevering’, ‘levering’).
Бета-коэффициент сопоставимой компании сначала подвергается «де-левериджу», чтобы убрать из него финансовый риск.
Процесс де-левериджа и левериджа бета-коэффициента был разработан Робертом С. Хамада [“The Effect of the Firm’s Capital Structure on the Systematic Risk of Common Stocks,» Journal of Finance (Май 1972), стр. 435-452] и основан на теориях структуры капитала Франко Модильяни и Мертона Миллера.
Бета-коэффициент без финансового риска часто называют бетой активов или бетой для активов (англ. ‘asset beta’), потому что он отражает деловой риск активов.
‘asset beta’), потому что он отражает деловой риск активов.
После «де-левериджа» бета-коэффициента, мы корректируем его с учетом структуры капитала компании или проекта, что находится в центре нашего анализа. Другими словами, мы осуществляем «леверидж» беты активов, чтобы получить бета-коэффициент собственного капитала интересующего проекта или компании.
Для данной компании мы можем выполнить «де-леверидж» беты собственного капитала, чтобы оценить ее бету активов. Для этого мы должны определить взаимосвязь между бетой активов и бетой собственного капитала компании.
Поскольку риск компании делится между кредиторами и владельцами, мы можем представить риск компании \( \beta_{\text{активы}}\) как взвешенное среднее рыночного риска кредиторов компании \( \beta_{\text{долг}}\) и рыночного риска владельцев компании \( \beta_{\text{капитал}}\):
\( \dst \beta_{\text{активы}} = \beta_{\text{долг}} w_d + \beta_{\text{капитал}} w_e \)
или
\( \dst \beta_{\text{активы}} = \beta_{\text{долг}} \left( {D \over D+E} \right) + \beta_{\text{капитал}} \left( {D \over D+E} \right) \)
где:
- \(E \) = рыночная стоимость собственного капитала,
- \(D \) = рыночная стоимость долга,
- \(w_d \) = доля долга = \( D / (D + E) \)
- \(w_e\) = доля собственного капитала = \( E / (D + E) \)
Но проценты по долгу вычитаются компанией при расчете налогооблагаемой прибыли, поэтому нагрузка долгового финансирования на самом деле ниже из-за вычета процентов.
Мы можем представлять бету активов компании как средневзвешенное значение беты долга и беты собственного капитала (акций), с учетом налогового эффекта от процентов:
\( \dst \beta_{\text{активы}} = \beta_{\text{долг}} {(1-t)D \over (1-t)D+E} + \beta_{\text{капитал}} {E \over (1-t)D+E} \)
где \( t\) — это предельная ставка налога.
Как правило, мы предполагаем, что долг компании не имеет рыночного риска, поэтому \( \beta_{\text{долг}} = 0 \). Это означает, что доходность по долгу не варьируется также, как рыночная доходность, что мы, как правило, считаем верным для большинства крупных компаний.
Если \( \beta_{\text{долг}} = 0 \), то упростив выражение \( \beta_{\text{капитал}} {E \over (1-t)D+E} \) мы получим:
\( \dstl \beta_{\text{активы}} = \beta_{\text{капитал}} \left[ {1 \over \left( (1-t) {D \over E} \right) } \right] \) (Формула 9)
Следовательно, на рыночный риск собственного капитала компании влияет как рыночный риск активов \( \beta_{\text{активы}} \), так и фактор, представляющий систематическую часть финансового риска компании \( 1 + \left( (1-t) {D \over E} \right) \):
\( \dstl \beta_{\text{капитал}} = \beta_{\text{активы}} \left[ 1 + \left( (1-t) {D \over E} \right) \right] \) (Формула 10)
Предположим, что компания имеет бету собственного капитала 1. 5, коэффициент D/E (отношение долга к собственному капиталу) 0.4 и предельную ставку налога 30%. Используя Формулу 9, мы найдем, чтоб бета активов компании составляет 1.1719:
5, коэффициент D/E (отношение долга к собственному капиталу) 0.4 и предельную ставку налога 30%. Используя Формулу 9, мы найдем, чтоб бета активов компании составляет 1.1719:
\( \dst \beta_{\text{активы}} = 1.5 \left[ {1 \over 1 + (1-0.3)(0.4)} \right] = 1.5 [0.7813] = 1.1719 \)
Другими словами, если бы у компании не было никакого долгового финансирования, то ее \( \beta_{\text{активы}} = \beta_{\text{капитал}} = 1.1719 \). Тем не менее, использование долгового финансирования увеличивает ее \( \beta_{\text{капитал}} \) с 1.1719 до 1.5.
Какой была бы бета собственного капитала компании, если бы коэффициент D/E был 0.5 вместо 0.4?
В этом случае мы применяем Формулу 10, используя коэффициент D/E 0.5:
\( \beta_{\text{капитал}} = 1.1719 [1 + (1 — 0.3) (0.5)] = 1.5821 \)
Таким образом, расчет «де-левериджа» (устранение финансового риска по долговому финансированию) дает показатель рыночного риска для активов компании — игнорируя структуру капитала компании.
Мы используем расчет «левериджа» (добавление финансового риска по долговому финансированию) в Формуле 10 для оценки рыночного риска компании, учитывая конкретный риск активов, предельную налоговую ставку и структуру капитала.
Мы можем использовать те же расчеты «де-левериджа» и «левериджа» для оценки риска активов и риска собственного капитала для проекта.
Мы начинаем с беты собственного капитала сопоставимой компании, которая включает эффект финансового рычага \( \beta_{L, \text{сопоставимая}} \), а затем преобразуем ее в эквивалентную бету активов сопоставимой компании без учета финансового риска долга \( \beta_{U, \text{сопоставимая}} \).
Получив бету активов, мы можем использовать структуру капитала проекта и предельную налоговую ставку для преобразования этой беты активов в бету собственного капитала (акций) проекта \( \beta_{L, \text{проект}} \).
Оценка бета коэффициента с использованием метода чистой игры.
Шаг 1: Выберите сопоставимую компанию. Определите сопоставимую компанию или компании с аналогичным бизнес-риском.
Определите сопоставимую компанию или компании с аналогичным бизнес-риском.
Шаг 2: Рассчитайте бету собственного капитала сопоставимой компании.
Шаг 3: Устраните финансовый риск из беты сопоставимой компании. Сделайте расчет «де-левериджа», устранив компонент финансового риска (для долгового финансирования) из беты собственного капитала, оставив в бете только компонент бизнес-риска.
Шаг 4: Добавьте в бету соответствующий финансовый риск проекта. Сделайте расчет «левериджа» для беты проекта, скорректировав бету активов на финансовый риск проекта.
Мы начинаем с оценки беты сопоставимой компании, включающей финансовый риск \( \beta_{L, \text{сопоставимая}} \). Используя структуру капитала и налоговую ставку этой компании, мы оцениваем ее бету активов \( \beta_{U, \text{сопоставимая}} \):
\( \dstl \beta_{U, \text{сопоставимая}} = { \beta_{L, \text{сопоставимая}} \over \left[ 1 + \left( (1- t_{\text{сопоставимая}}) { D_{\text{сопоставимая}} \over E_{\text{сопоставимая}} } \right) \right] } \) (Формула 11)
Затем мы учитываем финансовый рычаг рассматриваемого проекта или компании и рассчитываем риск собственного капитала \( \beta_{L, \text{проект}} \).
\( \dstl \beta_{L, \text{проект}} = \beta_{U, \text{сопоставимая}} \left[ 1 + \left( (1- t_{\text{проект}}) { D_{\text{проект}} \over E_{\text{проект}} } \right) \right] \) (Формула 12)
Чтобы проиллюстрировать использование этих формул, предположим, что мы хотим оценить проект, который будет финансироваться долгом и собственным капиталом (акциями) в соотношении 0.4:1. Коэффициент D/E = 0.4 соответствует приблизительно 0.4/(0.4 + 1.0) = €0.286 на каждый евро необходимого капитала.
Мы находим сопоставимую компанию, работающую в том же направлении бизнеса, что и проект. Предельная налоговая ставка для компании, спонсирующей проект, и сопоставимой компания, составляет 35%.
Сопоставимая компания имеет бета-коэффициент 1.2 и коэффициент D/E 0.125.
Бета без финансового риска для сопоставимой компании составляет 1.1098:
\( \dst \beta_{U, \text{сопоставимая}} = {1.2 \over \left[1 + (1 — 0.35)0.125 \right]} = 1.1098 \)
Бета с учетом финансового риска для проекта составляет 1. 3983:
3983:
\( \dst \beta_{L, \text{проект}} = 1.1098 \left[1 + (1 — 0.35) 0.4 \right] = 1.3983 \)
Затем мы используем 1.3983 в качестве бета-коэффициента в нашей оценке с помощью модели CAPM компонентов стоимости капитала (затрат на капитал) для проекта, и, в сочетании со стоимостью долга во взвешенном среднем (WACC), мы делаем оценку стоимости капитала для данного проекта.
В этом примере веса WACC составляют \(w_d \) = 0.4/1.4 = 0.2857, а \(w_e \) = 1/1.4 = 0.7143.
Пример (9) расчета беты активов.
Предположим, что бета собственного капитала публичной компании составляет 1.3, и что рыночная стоимость собственного капитала и долга составляет, соответственно, C$540 млн. и C$720 млн.
Если предельная налоговая ставка этой компании составляет 40%, то каким будет бета-коэффициент активов этой компании?
Решение:
\( \dst \beta_U = {1.3 \over \left[ 1 + (1-0.4) {720 \over 540} \right] } = 0.72 \)
Пример (10) расчета бета-коэффициента с использованием метода чистой игры.

AeroTechnique S.A. — частный бельгийский субподрядчик, поставляющий аэрокосмические детали. Хотя AeroTechnique не торгуется на бельгийской фондовой бирже, руководитель отдела развития оценить бета-коэффициент компании.
У него есть доступ к следующей информации:
- Средние бета-коэффициенты с учетом финансового риска и без учета финансового риска для группы сопоставимых компаний, работающих в разных странах Европы, составляют 1.6 и 1.0 соответственно.
- Коэффициент D/E AeroTechnique, основанный на рыночных данных, составляет 1.4.
- Ставка корпоративного налога AeroTechnique составляет 34%.
Решение:
Бета-коэффициент для AeroTechnique оценивается на основе средней беты группы сопоставимых компаний, из которой устранен финансовый риск. К этой бете применяется финансовая структура AeroTechnique:
\( \beta = 1.0 [1 + (1 — 0,34) (1.4)] = 1.924 \)
Пример (11) оценки средневзвешенной стоимости капитала (WACC).

Bayern Chemicals KgaA является крупным немецким производителем промышленных, коммерческих и потребительских химических продуктов. Bayern Chemicals является частной компанией и ее акции не торгуются на бирже.
Финансовый директор компании поручил внешнему аналитику провести оценку компании и предоставил следующую информацию, чтобы рассчитать средневзвешенную стоимость капитала (WACC) компании:
- Номинальная безрисковая ставка соответствует доходности долгосрочных 10-летних немецких гособлигаций. На дату оценки она составила 4.5%.
- Средняя долгосрочная историческая премия за риск акций в Германии составляет 5.7%.
- Ставка корпоративного налога для Bayern Chemicals составляет 38%.
- Коэффициент D/E составляет 0.7. Bayern поддерживает целевое значение коэффициента.
- Стоимость долга варьируется в пределах 225 базисных пунктов относительно 10-летних гособлигаций.
Иллюстрация 3 содержит дополнительную информацию о сопоставимых компаниях для Bayern Chemicals.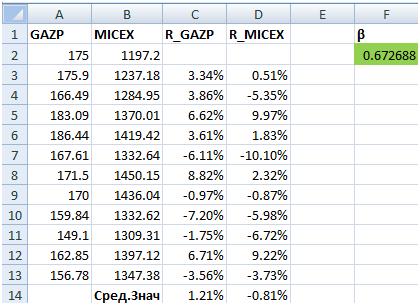
Иллюстрация 3. Информация о сопоставимых компаниях.
|
Сопоставимые компании |
Страна |
Ставка налога (%) |
Рыночная капитализация, млн. |
Чистый долг, млн. |
D/E. |
Бета |
|---|---|---|---|---|---|---|
|
British Chemicals Ltd. |
Соединенное Королевство |
30.0 |
4,500 |
6,000 |
1.33 |
1.45 |
|
Compagnie Petrochimique S.A. |
Франция |
30. |
9,300 |
8,700 |
0.94 |
0.75 |
|
Rotterdam Chemie N.V. |
Нидерланды |
30.5 |
7,000 |
7,900 |
1.13 |
1.05 |
|
Среднее значение |
1.13 |
1.08 |
Основываясь только на предоставленной информации, рассчитайте WACC для Bayern Chemicals.
Решение:
Чтобы рассчитать стоимость собственного капитала, сначала нужно выполнить «де-леверидж» бета-коэффициентов сопоставимых компаний и рассчитать среднее значение для компании с бизнес-риском, аналогичным среднему уровню этих компаний:
|
Сопоставимые компании |
Бета без финансового риска |
|---|---|
|
British Chemicals Ltd. |
0.75 |
|
Compagnie Petrochimique S.A. |
0.45 |
|
Rotterdam Chemie N.V. |
0.59 |
|
Average* |
0.60 |
* Аналитик должен вынести суждение и использовать свой опыт, чтобы определить репрезентативное среднее значение для сопоставимых компаний. Этот пример использует простое среднее значение, но в некоторых ситуациях лучше подойдет взвешенное среднее, основанное на таких факторах, как рыночная капитализация.
К полученному среднему значению применяется целевой коэффициент D/E и предельная налоговая ставка Bayern Chemicals, что дает в итоге 0.86:
\( \beta \) = 0.60{1 + [(1 — 0.38)0.7]} = 0.86
Стоимость капитала Bayern Chemicals \( (r_e) \) можно рассчитать следующим образом:
\(r_e \) = 4. 5% + (0.86) (5.7%) = 9.4%.
5% + (0.86) (5.7%) = 9.4%.
Веса стоимости собственного капитала и стоимости долга можно рассчитать следующим образом:
\( \dst w_d = {D/E \over \left( {D \over E} + 1 \right)} = {0.7 \over 1.7} = 0.41 \)
\( w_e = 1 — w_d = 1 — 0.41 = 0.59 \)
Доналоговая стоимость долга Bayern Chemicals \( (r_d) \) составляет 6.75%:
\( r_d \) = 4.5% + 2.25% = 6.75%
Как результат, WACC Baiern Chemicals составляет 7.27%:
WACC = [(0.41)(0.0675)(1 — 0.38)] + [(0.59)(0.094)] = 0.0726 или 7.26%
Определение, расчет и объяснение для инвесторов
Что такое бета?
Бета (β) — это мера волатильности — или систематического риска — ценной бумаги или портфеля по сравнению с рынком в целом (обычно S&P 500). Акции с коэффициентом бета выше 1,0 можно интерпретировать как более волатильные, чем S&P 500.
Бета используется в модели ценообразования капитальных активов (CAPM), которая описывает взаимосвязь между систематическим риском и ожидаемой доходностью активов (обычно акций). CAPM широко используется в качестве метода оценки рисковых ценных бумаг и оценки ожидаемой доходности активов с учетом как риска этих активов, так и стоимости капитала.
CAPM широко используется в качестве метода оценки рисковых ценных бумаг и оценки ожидаемой доходности активов с учетом как риска этих активов, так и стоимости капитала.
Ключевые выводы
- Бета (β), в основном используемая в модели ценообразования капитальных активов (CAPM), является мерой волатильности или систематического риска ценной бумаги или портфеля по сравнению с рынком в целом.
- Бета-данные об отдельных акциях могут дать инвестору только приблизительное представление о том, какой риск добавит акция к (предположительно) диверсифицированному портфелю.
- Чтобы коэффициент бета был значимым, акции должны быть связаны с эталоном, который используется в расчетах.
- Бета-версия S&P 500 равна 1,0.
- Акции с коэффициентом бета выше 1 будут двигаться быстрее, чем S&P 500; акции с коэффициентом бета менее 1 с меньшим импульсом.
Общие сведения о бета-версии
Как работает бета-версия
Коэффициент бета может измерять волатильность отдельной акции по сравнению с систематическим риском всего рынка. В статистических терминах бета представляет собой наклон линии через регрессию точек данных. В финансах каждая из этих точек данных представляет доходность отдельной акции по сравнению с доходностью рынка в целом.
В статистических терминах бета представляет собой наклон линии через регрессию точек данных. В финансах каждая из этих точек данных представляет доходность отдельной акции по сравнению с доходностью рынка в целом.
Бета эффективно описывает активность доходности ценной бумаги, когда она реагирует на колебания рынка. Бета ценной бумаги рассчитывается путем деления произведения ковариации доходности ценной бумаги и доходности рынка на дисперсию доходности рынка за определенный период.
Расчет бета-версии выглядит следующим образом:
Бета-коэффициент ( β ) знак равно Ковариация ( р е , р м ) Дисперсия ( р м ) куда: р е знак равно доходность отдельных акций р м знак равно доход на рынке в целом Ковариация знак равно как меняется доходность акций связанные с изменениями доходности рынка Дисперсия знак равно насколько далеко разбросаны точки данных рынка от их среднего значения \begin{align} &\text{Коэффициент бета}(\beta) = \frac{\text{Ковариация}(R_e, R_m)}{\text{Дисперсия}(R_m)} \\ &\textbf{где:} \\ &R_e=\text{доходность отдельной акции}\\ &R_m=\text{доходность всего рынка}\\ &\text{Ковариация}=\text{как изменяется доходность акции} \\ &\text{связанные с изменениями в доходности рынка}\\ &\text{Дисперсия}=\text{насколько далеко разбросаны рыночные данные} \\ &\text{отклонение от их среднего значения} \\ \end{выровнено } Коэффициент бета(β)=Дисперсия(Rm)Ковариация(Re, Rm)где: Re= доходность отдельной акции Rm= доходность рынка в целом Ковариация = то, как изменения доходности акции связаны с изменениями in the market’s returnsVariance = насколько далеко разброс точек рыночных данных от их среднего значения
Расчет бета используется, чтобы помочь инвесторам понять, движется ли акция в том же направлении, что и остальная часть рынка. Он также дает представление о том, насколько волатильна или рискованна акция по сравнению с остальным рынком. Чтобы бета-версия давала какую-либо полезную информацию, рынок, который используется в качестве эталона, должен быть связан с акцией. Например, расчет бета ETF на облигации с использованием S&P 500 в качестве ориентира не даст инвестору много полезной информации, потому что облигации и акции слишком непохожи.
Он также дает представление о том, насколько волатильна или рискованна акция по сравнению с остальным рынком. Чтобы бета-версия давала какую-либо полезную информацию, рынок, который используется в качестве эталона, должен быть связан с акцией. Например, расчет бета ETF на облигации с использованием S&P 500 в качестве ориентира не даст инвестору много полезной информации, потому что облигации и акции слишком непохожи.
Понимание бета-версии
В конечном счете, инвестор использует бета-версию, чтобы попытаться оценить, какой риск добавляет акция к портфелю. В то время как акции, которые очень мало отклоняются от рынка, не добавляют большого риска портфелю, они также не увеличивают потенциал для большей доходности.
Чтобы убедиться, что конкретная акция сравнивается с правильным эталоном, она должна иметь высокое значение R-квадрата по отношению к эталону. R-квадрат — это статистическая мера, показывающая процент исторического движения цены ценной бумаги, который можно объяснить движением эталонного индекса.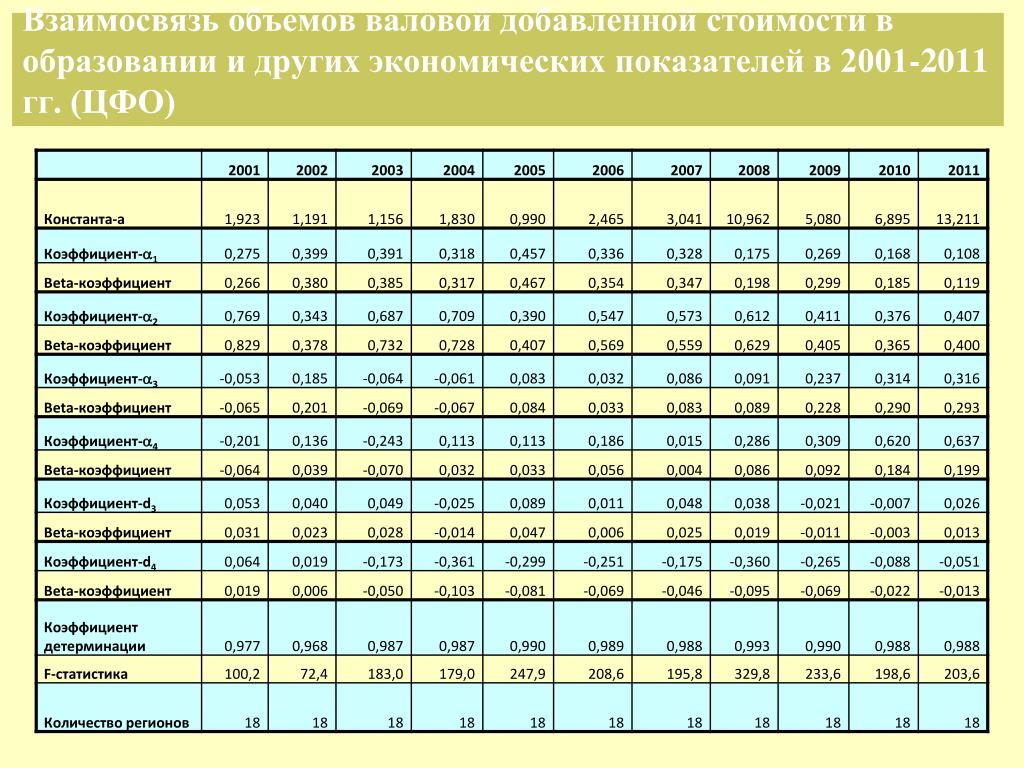 При использовании бета для определения степени систематического риска ценная бумага с высоким значением R-квадрата по отношению к ее эталону может указывать на более подходящий эталон.
При использовании бета для определения степени систематического риска ценная бумага с высоким значением R-квадрата по отношению к ее эталону может указывать на более подходящий эталон.
Например, биржевой фонд золота (ETF), такой как SPDR Gold Shares (GLD), привязан к производительности золотых слитков. Следовательно, ETF на золото будет иметь низкое отношение бета и R-квадрата к S&P 500.
Один из способов для фондового инвестора думать о риске — разделить его на две категории. Первая категория называется систематическим риском, то есть риском падения всего рынка. Финансовый кризис 2008 года является примером события систематического риска; никакая степень диверсификации не могла бы помешать инвесторам потерять стоимость своих портфелей акций. Систематический риск также известен как недиверсифицируемый риск.
Несистематический риск, также известный как диверсифицируемый риск, представляет собой неопределенность, связанную с отдельной акцией или отраслью. Например, неожиданное объявление о том, что компания Lumber Liquidators (LL) в 2015 году продавала паркетные полы с опасным уровнем содержания формальдегида, является примером несистематического риска. Это был риск, который был специфичен для этой компании. Несистематический риск можно частично снизить за счет диверсификации.
Это был риск, который был специфичен для этой компании. Несистематический риск можно частично снизить за счет диверсификации.
Бета-коэффициент акции будет меняться с течением времени, так как он связывает производительность акции с доходностью всего рынка, что является динамическим процессом.
Типы значений бета
Значение бета равно 1,0
Если акция имеет бета 1,0, это указывает на то, что ее ценовая активность сильно коррелирует с рынком. Акция с бета 1,0 имеет систематический риск. Тем не менее, бета-расчет не может обнаружить какой-либо несистематический риск. Добавление акции в портфель с бета-коэффициентом 1,0 не увеличивает риск портфеля, но и не увеличивает вероятность того, что портфель принесет избыточную доходность.
Бета-значение меньше единицы
Значение бета меньше 1,0 означает, что ценная бумага теоретически менее волатильна, чем рынок. Включение этой акции в портфель делает его менее рискованным, чем тот же портфель без акции. Например, акции коммунальных предприятий часто имеют низкие коэффициенты бета, потому что они имеют тенденцию двигаться медленнее, чем в среднем по рынку.
Например, акции коммунальных предприятий часто имеют низкие коэффициенты бета, потому что они имеют тенденцию двигаться медленнее, чем в среднем по рынку.
Бета-значение больше единицы
Бета больше 1,0 указывает на то, что цена ценной бумаги теоретически более волатильна, чем рынок. Например, если бета акции составляет 1,2, предполагается, что она на 20% более волатильна, чем рынок. Акции технологических компаний и акции с малой капитализацией, как правило, имеют более высокие коэффициенты бета, чем рыночный эталон. Это указывает на то, что добавление акций в портфель увеличит риск портфеля, но также может увеличить его ожидаемую доходность.
Отрицательное бета-значение
Некоторые акции имеют отрицательную бета. Бета-1,0 означает, что акции имеют обратную корреляцию с рыночным ориентиром в соотношении 1:1. Эту акцию можно рассматривать как противоположное, зеркальное отражение трендов эталона. Опционы пут и обратные ETF предназначены для отрицательных бета-коэффициентов. Есть также несколько отраслевых групп, таких как золотодобытчики, для которых также характерна отрицательная бета.
Есть также несколько отраслевых групп, таких как золотодобытчики, для которых также характерна отрицательная бета.
Бета в теории и Бета на практике
Теория бета-коэффициентов предполагает, что доходность акций обычно распределяется со статистической точки зрения. Однако финансовые рынки склонны к большим неожиданностям. На самом деле доходность не всегда нормально распределяется. Следовательно, то, что бета акции может предсказать относительно ее будущего движения, не всегда верно.
Акция с очень низкой бета-версией может иметь меньшие колебания цены, но все же может находиться в долгосрочном нисходящем тренде. Таким образом, добавление акции с нисходящим трендом с низкой бета-версией снижает риск в портфеле только в том случае, если инвестор определяет риск строго с точки зрения волатильности (а не как возможность потерь). С практической точки зрения акции с низким коэффициентом бета, которые находятся в нисходящем тренде, вряд ли улучшат эффективность портфеля.
Точно так же акции с высоким бета-коэффициентом, которые волатильны в основном в восходящем направлении, увеличат риск портфеля, но также могут увеличить прибыль. Рекомендуется, чтобы инвесторы, использующие бета-версию для оценки акций, также оценивали их с других точек зрения, таких как фундаментальные или технические факторы, прежде чем предположить, что это добавит или уберет риск из портфеля.
Недостатки бета-версии
Хотя бета-версия может дать некоторую полезную информацию при оценке акций, она имеет некоторые ограничения. Бета-версия полезна для определения краткосрочного риска ценной бумаги и для анализа волатильности, чтобы получить стоимость собственного капитала при использовании CAPM. Однако, поскольку бета рассчитывается с использованием исторических данных, она становится менее значимой для инвесторов, стремящихся предсказать будущие движения акций. Бета-версия также менее полезна для долгосрочных инвестиций, поскольку волатильность акций может значительно меняться из года в год, в зависимости от стадии роста компании и других факторов.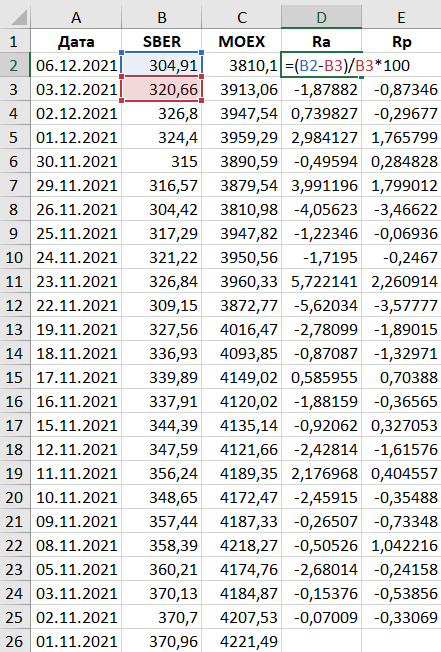 Более того, бета-метрия конкретной акции имеет тенденцию меняться со временем, что делает ее ненадежной как стабильную меру.
Более того, бета-метрия конкретной акции имеет тенденцию меняться со временем, что делает ее ненадежной как стабильную меру.
Что такое хорошая бета для акций?
Бета используется в качестве показателя рискованности или волатильности акции по отношению к более широкому рынку. Таким образом, хорошая бета-версия будет зависеть от вашей терпимости к риску и целей. Если вы хотите воспроизвести более широкий рынок в своем портфеле, например, с помощью индексного ETF, идеальным вариантом будет бета 1,0. Если вы консервативный инвестор, стремящийся сохранить основную сумму, более низкая бета может быть более подходящей. На бычьем рынке бета, превышающая 1,0, будет приносить доход выше среднего, но также приведет к большим убыткам на нисходящем рынке.
Является ли Бета хорошей мерой риска?
Многие эксперты согласны с тем, что хотя бета-версия предоставляет некоторую информацию о риске, сама по себе она не является эффективной мерой риска. Бета-версия рассматривает только прошлые результаты акции по отношению к S&P 500 и не дает никаких прогнозов на будущее..jpg) Он также не рассматривает основы компании или ее доходы и потенциал роста.
Он также не рассматривает основы компании или ее доходы и потенциал роста.
Как интерпретировать бета акций?
Бета 1,0 для акции означает, что она была такой же волатильной, как и рынок в целом (например, индекс S&P 500). Если индекс движется вверх или вниз на 1%, то же самое в среднем будет происходить и с акциями. Бета больше 1,0 указывает на большую волатильность — так, если бы бета была 1,5, а индекс двигался вверх или вниз на 1%, акции в среднем двигались бы на 1,5%. Бета меньше 1,0 указывает на меньшую волатильность: если бы акция имела бета 0,5, она выросла бы или упала всего на полпроцента, когда индекс изменился бы на 1%.
Коэффициенты бета в линейных моделях. Статистика для экологов Упражнения
Упражнение 11.1.2.
Эти примечания дополняют главу 11 и исследуют использование бета-коэффициентов, которые могут быть полезным дополнением к регрессионному анализу.
Бета-коэффициенты линейных моделей
- Введение
- Что такое бета-коэффициенты?
- Бета-коэффициенты корреляции
- Бета-коэффициенты из коэффициентов регрессии
- Команда коэф()
- Использование коэффициента()
- Результат печати
- Суммарный результат
- Добавьте команды в вашу копию R
- Использование коэффициента()
- Пакет lm.
 beta
beta
Введение
В линейной регрессии ваша цель — описать данные с помощью (относительно) простого уравнения. Простейшая форма регрессии между двумя переменными:
у = мх + с
В уравнении y представляет собой переменную отклика, а x — одиночную переменную-предиктор. Наклон m и точка пересечения c известны как коэффициенты. Если вы знаете значения этих коэффициентов, вы можете подставить их в формулу для значений x, предиктора, и получить значение для ответа.
При множественной регрессии вы «расширяете» формулу, чтобы получить коэффициенты для каждого из предикторов.
у = m1.x1 + m2.x2 + m3.x3 + ... + с
Если вы стандартизируете коэффициенты (используя стандартное отклонение отклика и предиктор), вы можете сравнивать коэффициенты друг с другом, так как они фактически предполагают одни и те же единицы измерения/масштаб.
Функции для вычисления бета-коэффициентов не встроены в R.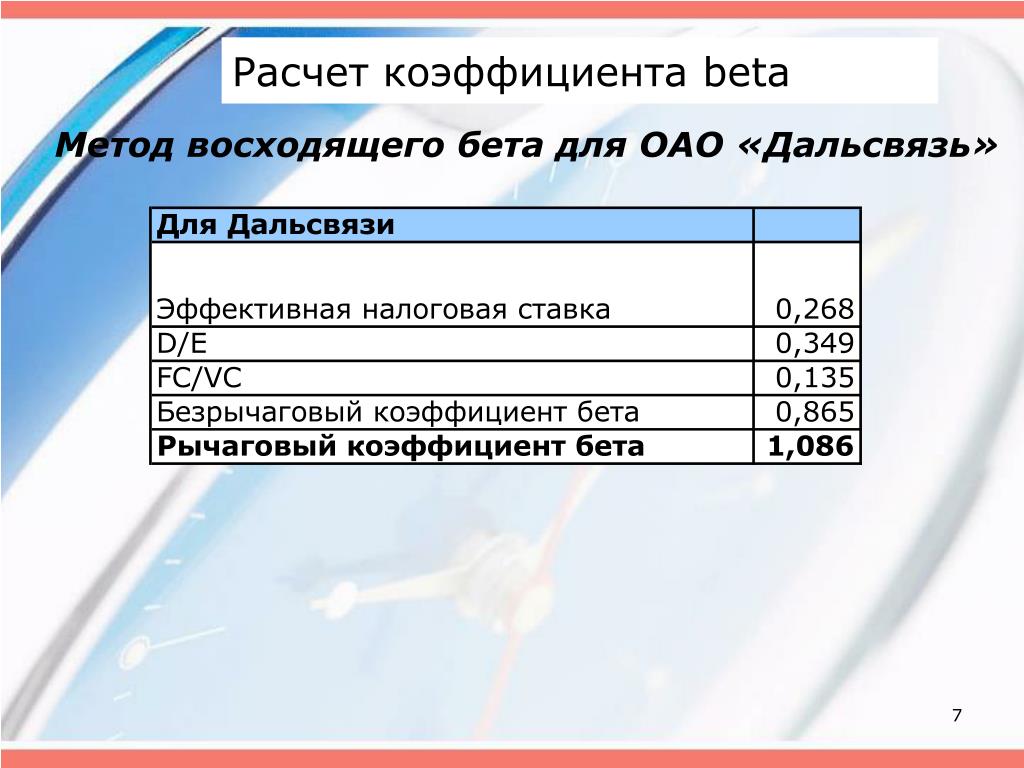 В этих заметках вы увидите некоторые пользовательские команды R, которые позволяют легко получить бета-коэффициенты. Вы можете скачать файл Beta coeff calc.R и использовать его по своему усмотрению.
В этих заметках вы увидите некоторые пользовательские команды R, которые позволяют легко получить бета-коэффициенты. Вы можете скачать файл Beta coeff calc.R и использовать его по своему усмотрению.
Что такое бета-коэффициенты?
Бета-коэффициенты — это коэффициенты регрессии (аналогичные наклону в простой регрессии/корреляции), которые стандартизированы по отношению друг к другу. Эта стандартизация означает, что они находятся «в одном масштабе» или имеют одни и те же единицы измерения, что позволяет напрямую сравнивать величину их эффектов.
Бета-коэффициенты из корреляции
Можно рассчитать бета-коэффициенты более или менее напрямую, если у вас есть коэффициент корреляции r между различными компонентами:
Расчет бета-коэффициентов на основе коэффициентов корреляции.
Нижние индексы могут сбивать с толку, но, по сути, вы можете использовать аналогичную формулу для различных комбинаций переменных.
Коэффициенты бета из коэффициентов регрессии
В большинстве случаев вы уже вычислили коэффициенты регрессии (наклон, точка пересечения) и можете использовать их вместе со стандартным отклонением для расчета коэффициентов бета.
Расчет коэффициента бета на основе коэффициента регрессии и стандартного отклонения.
Эту формулу намного проще понять: b’ — коэффициент бета, b — стандартный коэффициент регрессии. X и y относятся к предиктору и переменным отклика. Поэтому вы берете стандартное отклонение переменной-предиктора, делите на стандартное отклонение ответа и умножаете на коэффициент регрессии для рассматриваемого предиктора.
Встроенных функций, которые рассчитают за вас бета-коэффициенты, нет, поэтому я написал их сам. Команды легко запускать/использовать, и я довольно подробно аннотировал скрипт/код, поэтому вам должно быть полезно/полезно видеть, что происходит.
Команда beta.coef()
Я написал команду beta.coef() для вычисления бета-коэффициентов из объектов результатов lm(). Есть также функции печати и сводки, которые помогают просматривать результаты. Вот краткий обзор:
beta.coef(модель, цифры = 7) | |
print. | |
summary.beta.coef(объект, цифры = 7) | |
| модель | Модель регрессии, результат lm(). |
| объект | Результат команды beta.coef(). |
| цифр = 7 | Количество отображаемых цифр, по умолчанию 7. |
Команда beta.coef() выдает результат с пользовательским классом beta.coef. Команды print() и summary() будут использовать этот класс для отображения коэффициентов или создания более полной сводки (сравнивая обычные коэффициенты регрессии и бета-версию).
Использование beta.coef()
Вам понадобится результат линейной регрессии, обычно это результат класса «lm».
mf.lm <- lm(длина ~ БПК + водоросли, данные = mf)
резюме (mf.lm)
Вызов:
lm (формула = длина ~ БПК + водоросли, данные = mf)
Остатки:
Мин. 1Q Медиана 3Q Макс.
-3,1246 -0,9384 -0,2342 1,2049 3,2908
Коэффициенты:
Оценка стд. Значение ошибки t Pr(>|t|)
(Перехват) 22.34681 4.09862 5.452 1.78e-05 ***
БПК -0,037790,01517 -2,492 0,0207 *
Водоросли 0,04809 0,03504 1,373 0,1837
Значение ошибки t Pr(>|t|)
(Перехват) 22.34681 4.09862 5.452 1.78e-05 ***
БПК -0,037790,01517 -2,492 0,0207 *
Водоросли 0,04809 0,03504 1,373 0,1837 Знач. коды: 0 '' 0,001 '' 0,01 '' 0,05 '.' 0,1 ' ' 1 Остаточная стандартная ошибка: 1,83 при 22 степенях свободы. Множественный R-квадрат: 0,6766, скорректированный R-квадрат: 0,6472 F-статистика: 23,01 для 2 и 22 DF, значение p: 4,046e-06
Получив результат, вы можете использовать команду beta.coef() для вычисления бета-коэффициентов:
mf.bc <- beta .coef(мф.лм)
Бета-коэффициенты для: mf.lm
БПК Водоросли
Бета.Коэффициент -0,5514277 0,3037675 Обратите внимание, что результат отображается, несмотря на то, что результат был присвоен именованному объекту.
Печать результатов beta.coef
Вы можете использовать метод печати для отображения коэффициентов, задав количество отображаемых цифр:
print(mf.bc, digits = 4)
Бета-коэффициенты:
БПК водоросли
Beta. Coef -0,5514 0,3038
Coef -0,5514 0,3038 Команда берет компонент $beta.coef из объекта результата beta.coef().
Сводные результаты beta.coef
Суммарный метод дает результат, который сравнивает обычные коэффициенты регрессии и стандартизированные (бета-коэффициенты). Вы можете установить количество отображаемых цифр с помощью параметра digits:
summary(mf.bc, digits = 5)
Бета-коэффициенты и сводка модели lm().
Вызов модели:
lm (формула = длина ~ БПК + водоросли, данные = mf)
(Перехват) БПК Водоросли
Коэффициент 22,347 -0,037788 0,048094
Beta.Coef Н/Д -0,551428 0,303768 Команда возвращает вызов модели в качестве напоминания о модели.
Добавьте команды в вашу версию R
Чтобы получить доступ к командам, вы можете скопировать/вставить код из Beta coeff calc.R. Кроме того, вы можете скачать файл и использовать:
source("Beta coeff calc.R") Пока файл находится в рабочем каталоге. В качестве альтернативы, в Windows или Mac используйте:
source(file.choose())
Часть file.choose() открывает окно, похожее на браузер, позволяя вам выбрать файл. После загрузки новые команды будут видны, если вы наберете ls().
Пакет lm.beta
После того, как я написал код для расчета бета-коэффициентов, я обнаружил пакет lm.beta в репозитории CRAN.
Установите пакет:
install.packages("lm.beta") Пакет включает команду lm.beta(), которая вычисляет бета-коэффициенты. Команда отличается от моего кода тем, что добавляет в регрессионную модель стандартизированные коэффициенты (бета-коэффициенты). Команды пакета также позволяют вычислять бета-коэффициенты для условий взаимодействия.
Используйте команду:
help(lm.beta)
, чтобы получить более полную документацию после установки и запуска пакета. Вы также можете просмотреть код напрямую (без аннотаций).
лм.бета print.lm.beta summary.lm.beta
Команда lm.beta() выдает результат с двумя классами: исходным «lm» и «lm. beta».
beta».
30 июля 2019 г. aJfsfjlser3f S4E2e Упражнения
Коэффициент бета (значение, формула)| Рассчитать бета-коэффициент
Формула бета-коэффициента — это финансовый показатель, который измеряет вероятность изменения цены акции/ценной бумаги в зависимости от движения рыночной цены. Бета акций/ценных бумаг также используется для измерения систематических рисков, связанных с конкретными инвестициями.
Бета — это степень изменения переменной результата на каждую единицу изменения переменной-предиктора. Стандартизированная бета-версия сравнивает силу эффекта каждой независимой переменной с зависимой переменной. Чем больше абсолютное значение коэффициента бета, тем сильнее будет влияние.
Бета-формула используется в модели CAPM для расчета стоимости собственного капиталаРассчитать стоимость собственного капиталаСтоимость собственного капитала (Ke) — это то, что акционеры ожидают от инвестирования своего капитала в фирму. Стоимость собственного капитала = Безрисковая норма прибыли + Бета * (рыночная норма прибыли - Безрисковая норма прибыли). подробнее см. ниже –
подробнее см. ниже –
Стоимость собственного капитала = безрисковая ставка + бета x премия за риск
Содержание
- Что такое бета-коэффициент?
- Коэффициент бета Значение
- Пример коэффициента бета
- Расчет коэффициента бета
- Шаг 1. Загрузите исторические цены и данные индекса NASDAQ за последние 3 года
- Шаг 2. Отсортируйте цены, как указано ниже
- Шаг 3. ниже.
- Шаг 4. Расчет дневной доходности
- Шаг 5. Расчет формулы бета с использованием метода дисперсии-ковариации
- Шаг 6. Расчет бета с использованием функции НАКЛОН в Excel
- Step 7 – Calculate Beta Coefficient Regression
- Advantages of Beta Coefficient Regression
- Disadvantages of Beta Coefficient Regression
- Negative Beta
- Beta Coefficient Video
- Recommended Articles
Beta Coefficient Meaning
The Beta is рассчитывается в модели CAPMМодель CAPMМодель ценообразования капитальных активов (CAPM) определяет ожидаемый доход от портфеля различных ценных бумаг с разной степенью риска. Он также учитывает волатильность конкретной ценной бумаги по отношению к рынку. Подробнее (Модель ценообразования капитальных активов) для расчета доходности акций или портфелей.
Он также учитывает волатильность конкретной ценной бумаги по отношению к рынку. Подробнее (Модель ценообразования капитальных активов) для расчета доходности акций или портфелей.
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Расчет бета-версии в Excel представляет собой анализ формы, поскольку он представляет собой наклон характеристической линии ценной бумаги, т. е. прямую линию, показывающую взаимосвязь между доходностью акции и доходностью рынка. Далее это можно определить с помощью приведенной ниже бета-формулы:
β = Ковариация рыночной доходности с доходностью акции / Отклонение рыночной доходности
Значения коэффициента бета –
- Если коэффициент равен 1, это указывает на то, что цена акции/ценной бумаги движется в соответствии с рынком.
- Если коэффициент <1; возврат ценной бумаги с меньшей вероятностью будет реагировать на движения рынка.

- Если коэффициент > 1, доход от ценной бумаги с большей вероятностью будет реагировать на движения рынка, что также сделает ее волатильной;
Если бета Apple Inc (AAPL) равна 1,46, это указывает на то, что акции очень волатильны и на 46% более вероятно, что они отреагируют на движение рынка. С другой стороны, скажем, Coca-Cola имеет коэффициент β, равный 0,77, что указывает на то, что акции менее волатильны и на 23% менее вероятно реагируют на движения на рынке.
В качестве тенденции было замечено, что акции коммунальных предприятий имеют САРМ-бета САРМ-бета САРМ-бета является важной теоретической мерой того, как отдельная акция движется по отношению к рынку. В этом методе мы определяем стоимость собственного капитала путем суммирования продукта бета и премии за риск с безрисковой ставкой меньше 1. С другой стороны, технологические акции имеют коэффициент бета больше 1, что указывает на вероятность более высокой доходности с более соответствующими рисками.
Расчет коэффициента бета
Здесь мы возьмем пример для расчета бета MakeMyTrip (MMTY) и рыночного индекса NASDAQ.
Вы можете скачать полностью решенную рабочую таблицу Excel для расчета бета-версии здесь.
Существует три бета-формулы: метод дисперсии/ковариации, функция наклона в Excel и формула регрессии. Формула регрессии. Формула регрессии используется для оценки взаимосвязи между зависимой и независимой переменными и для определения того, как изменение независимой переменной влияет на зависимую переменную. . Y = a + b X + читать дальше. Мы увидим каждую из формул бета-коэффициента ниже —
Шаг 1. Загрузите исторические данные о ценах и индексах NASDAQ за последние 3 года
Я скачал данные с Yahoo Finance.
- Для получения набора данных NASDAQ перейдите по этой ссылке Yahoo Finance.
- Чтобы узнать цены на Makemytrip, посетите этот URL здесь.
Шаг 2. Отсортируйте цены, как указано ниже
Отсортируйте даты и скорректированные цены закрытия в порядке возрастания дат. Вы можете удалить оставшиеся столбцы, так как они нам не нужны для бета-расчетов в Excel.
Вы можете удалить оставшиеся столбцы, так как они нам не нужны для бета-расчетов в Excel.
Шаг 3. Подготовьте таблицу Excel с бета-коэффициентом, как показано ниже.
Шаг 4 – Расчет дневной доходности
Доходность = [Цена акции на момент закрытия – Цена акции на открытие] / Цена акции на начало периода две формулы (дисперсия и ковариация в Excel), как показано ниже.
Используя метод дисперсии-ковариации, мы получаем бета как 0,9859(Коэффициент бета)
Шаг 6. Рассчитайте бета с помощью функции НАКЛОН в Excel
Использование этой функции НАКЛОН в excelФункция НАКЛОН В ExcelФункция наклона возвращает наклон линии регрессии на основе точек данных, распознанных известными значениями _y и известными _x values.read more , мы снова получаем Beta как 0,9859 (коэффициент бета)
Шаг 7. Вычисление коэффициента бета Regression Чтобы использовать эту функцию регрессии, выберите Data Analysis на вкладке Data вашего листа Excel. .
.
Если вы не можете найти Анализ данных в Excel, вам необходимо установить Пакет инструментов анализа. Этот процесс относительно прост: Перейдите в FILE -> Options -> Add-Ins -> Analysis ToolPakAnalysis ToolPakExcel может использоваться пользователями для выполнения анализа данных и других важных вычислений. Его можно включить вручную в разделе надстроек на вкладке файлов, нажав «Управление надстройками», а затем проверив пакет инструментов анализа. Подробнее -> Перейти -> Проверить пакет инструментов анализа -> OK
Выберите «Анализ данных» и щелкните «Регрессия»
Выберите диапазон ввода Y и диапазон ввода X
После того, как вы нажмете «ОК», вы получите следующий итоговый результат.
Вы получите одинаковую бета-версию в каждом из трех методов.
Преимущества регрессии коэффициента бета
CAPM оценивает бета актива на основе систематического риска
- рынка. Он используется для бета-регрессии для оценки стоимости собственного капитала.
 Это параметр, по которому инвесторы решают, выгодны ли инвестиции или нет; в противном случае они могут переключиться на другие возможности с более высокой доходностью. Подробнее читайте в разделе «Модели оценки». Стоимость собственного капитала, полученная с помощью CAPM, отражает реальность, благодаря которой инвесторы диверсифицировали свои портфели, чтобы уменьшить влияние систематического рискаСистематический рискСистематический риск определяется как риск, присущий всему рынку или всему сегменту рынка, поскольку он влияет на экономику. в целом и не может быть диверсифицирован, поэтому также известен как «недиверсифицируемый риск», «рыночный риск» или даже «риск волатильности». Подробнее. Ниже приведены некоторые преимущества бета-регрессии:
Это параметр, по которому инвесторы решают, выгодны ли инвестиции или нет; в противном случае они могут переключиться на другие возможности с более высокой доходностью. Подробнее читайте в разделе «Модели оценки». Стоимость собственного капитала, полученная с помощью CAPM, отражает реальность, благодаря которой инвесторы диверсифицировали свои портфели, чтобы уменьшить влияние систематического рискаСистематический рискСистематический риск определяется как риск, присущий всему рынку или всему сегменту рынка, поскольку он влияет на экономику. в целом и не может быть диверсифицирован, поэтому также известен как «недиверсифицируемый риск», «рыночный риск» или даже «риск волатильности». Подробнее. Ниже приведены некоторые преимущества бета-регрессии: - Он предлагает простой в использовании бета-расчет в Excel, который стандартизирует меру риска для нескольких фирм с различной структурой капитала и основными принципами.
Недостатки бета-регрессии с коэффициентом
Ниже перечислены некоторые недостатки бета-регрессии:
- Существует сильная зависимость от прошлых доходов и не учитывается обновленная информация/другие факторы, которые могут повлиять на доходы в будущем.

- Бета-регрессия по мере получения большего дохода, мера бета изменяется, а вместе с ней и стоимость акционерного капитала.
- Хотя систематические риски являются неотъемлемыми. Риски являются неотъемлемыми. Неотъемлемый риск – это вероятность дефекта в финансовой отчетности из-за ошибки, упущения или искажения, выявленного в ходе финансового аудита. Такой риск возникает из-за определенных факторов, которые находятся вне внутреннего контроля организации. Более того, рынку при объяснении доходности активов игнорируется часть несистематических рисков.
Отрицательная бета
Формула отрицательной бета означает инвестиции, которые движутся в направлении, противоположном фондовому рынку. Когда рынок растет, отрицательная бета имеет тенденцию к снижению, а отрицательная бета имеет тенденцию к росту, когда рынок падает. Обычно это верно для золотых акций и золотых слитков. Поскольку золото является более надежным средством сбережения, чем валюта, крах рынка побуждает инвесторов ликвидировать свои акции и конвертировать их в валюту (для нулевых бета-коэффициентов) или покупать золото в случае отрицательного бета-коэффициента.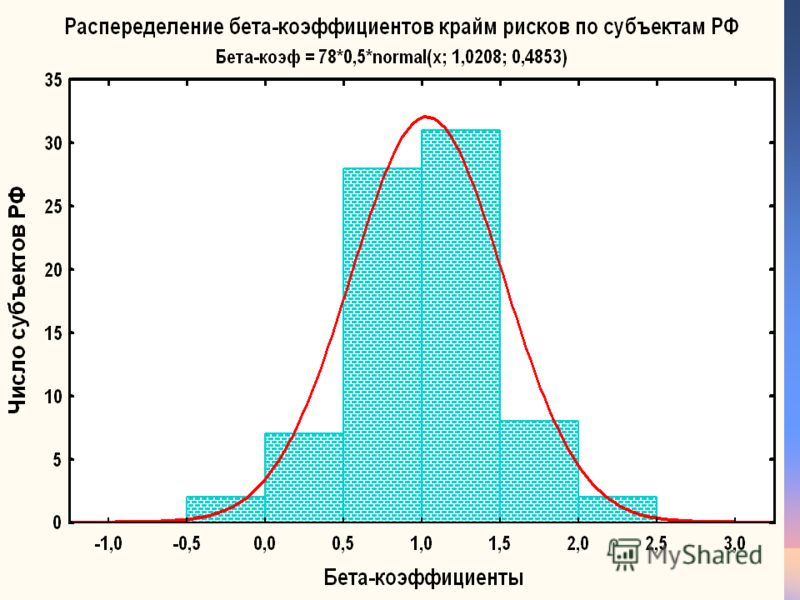
Отрицательная бета не указывает на отсутствие риска, но означает, что инвестиция предлагает страховку от непредвиденного рыночного спада. Однако предположим, что рынок продолжает расти. В этом случае стратегия с отрицательным бета-коэффициентом означает потерю денег из-за риска возможности (утрата определенного шанса получить более высокую прибыль), а также риска инфляции. Риск инфляции. Риск инфляции — это ситуация, когда покупательная способность резко падает. Это также можно объяснить ситуацией, когда цены на товары и услуги растут больше, чем ожидалось. Инфляционный риск также известен как риск покупательной способности. Читать далее (норма прибыли не поспевает за преобладающей инфляцией в стране).
Видео о коэффициенте бета
Рекомендуемые статьи
Эта статья представляет собой руководство по коэффициенту бета, формулам и расчетам. Здесь мы рассчитываем бета-версию в Excel MakeMyTrip, используя три метода: дисперсию-ковариацию, функцию НАКЛОН и функцию регрессии. Вы также можете ознакомиться с другими рекомендуемыми статьями, чтобы узнать больше об оценках:
Вы также можете ознакомиться с другими рекомендуемыми статьями, чтобы узнать больше об оценках:
- Левередные бета-версии
- Формула бета-бета в финансах
- Коэффициент корреляции Пирсона
- Коэффициент определения Пример
Коэффициент бета | Определение, формула и оценка
- Оценка акций
- EV к EBITDA
- Отношение цены к прибыли
- Оценка привилегированных акций
- Денежный поток от операций
- ПВГО
- Прибыль Доходность
- Индекс, взвешенный по цене
- Взаимные фонды
- Отношение цены к объему продаж
- EBITDA против CFO против FCFF против FCFE
- Ценность предприятия — EV
- Индекс, взвешенный по капитализации
- Модель скидки на дивиденды
- Дисконтированный денежный поток
- Свободный денежный поток
- Оценка свободного денежного потока
- Свободный денежный поток для фирмы
- Свободный денежный поток в капитал
- Премия за риск по акциям
- Терминальное значение
- Необходимы дополнительные средства
- Эффективный годовой доход
- Рыночная капитализация
- Самодельные дивиденды
- Коэффициент бета
- Модель ценообразования капитальных активов
- Модель скидки на дивиденды
- Многоступенчатая модель дисконтирования дивидендов
- Оценка капитала
Бета-коэффициент является мерой чувствительности цены акций компании к движениям на рынке. Это показатель систематического риска акции, который представляет собой недиверсифицируемый риск, присущий финансовой системе в целом.
Это показатель систематического риска акции, который представляет собой недиверсифицируемый риск, присущий финансовой системе в целом.
Коэффициент бета является важным входным параметром в модели ценообразования капитальных активов (CAPM). CAPM оценивает требуемую норму доходности акций, т. Е. (Стоимость капитала), как сумму безрисковой процентной ставки и премии за риск акций. Премия за риск акций представляет собой произведение бета-коэффициента акции и премии за рыночный риск, т. е. разницы между доходностью широкого рынка и безрисковой процентной ставкой.
Стоимость капитала (CAPM)
= Безрисковая ставка + Премия за риск капитала
= Безрисковая ставка + Бета × Премия за рыночный риск
= Безрисковая ставка + Бета ×: (Рыночная доходность — Безрисковая ставка)
Бета-коэффициент – наклон линии рынка ценных бумаг.
Формула
Коэффициент бета рассчитывается путем деления ковариации доходности акции с рыночной доходностью на дисперсию рыночной доходности.
| β = | Ковариация рыночной доходности с доходностью акций |
| Отклонение рыночной доходности |
Ковариация равна произведению стандартного отклонения доходности акций, стандартного отклонения рыночной доходности и их коэффициента корреляции. Используя это соотношение, мы приходим к другой формуле для бета-коэффициента, которая показывает, что бета-коэффициент равен коэффициенту корреляции, умноженному на стандартное отклонение доходности акций, деленному на стандартное отклонение рыночной доходности.
| β = коэффициент корреляции × | Стандартное отклонение доходности акций |
| Стандартное отклонение рыночной доходности |
Бета портфеля может быть оценена как средневзвешенное бета-коэффициентов отдельных акций.
Анализ
Рыночный коэффициент бета равен 1, а бета-коэффициенты различных акций измеряются по отношению к рынку. Коэффициент бета ниже 1 означает, что акции имеют систематический риск ниже рыночного и, следовательно, будут предлагать доходность ниже рыночной; а коэффициент бета больше 1 показывает, что акции имеют риск выше среднего и, следовательно, должны приносить доход выше среднего.
Коэффициент бета ниже 1 означает, что акции имеют систематический риск ниже рыночного и, следовательно, будут предлагать доходность ниже рыночной; а коэффициент бета больше 1 показывает, что акции имеют риск выше среднего и, следовательно, должны приносить доход выше среднего.
Различные веб-сайты финансовой информации, такие как Yahoo Finance, предоставляют бета-коэффициент для большинства компаний, зарегистрированных на бирже.
В настоящее время (апрель 2019 г.) ExxonMobil (NYSE: XOM) имеет бета-коэффициент 1,07, что свидетельствует о среднем систематическом риске. С другой стороны, компания Boeing (NYSE: BA) имеет бета-коэффициент 1,43, что показывает, что ее акции относительно более рискованны, чем широкий рынок.
Оценка бета-коэффициента
Если коэффициент корреляции между доходностью рынка и доходностью акций компании P равен 0,85; стандартное отклонение рынка составляет 10%, а акции — 8%, коэффициент бета составляет 0,68 (= 0,85 × 8%/10%), что показывает риск и доходность ниже рыночных.
Если у нас нет этих переменных, оценить бета по необработанным данным не очень сложно. Просто выполните следующие простые шаги, чтобы оценить бета-версию: 1. Получите исторические данные о цене акций компании. 2. Получите исторические значения соответствующего рыночного индекса (скажем, S&P 500). 3. Преобразуйте значения цены акций в значения дневной доходности, используя следующую формулу: Доходность = (Цена закрытия — Цена открытия)/Цена открытия. 4. Преобразуйте исторические значения индекса фондового рынка в возвращаемые значения. 5. Совместите данные о доходности акции с доходностью индекса так, чтобы между ними было соответствие 1-к-1. Для каждой доходности акций должна быть соответствующая доходность индекса. 6. Используйте функцию Excel SLOPE, чтобы найти наклон между обоими массивами данных, и результирующая цифра является бета.
, Obaidullah Jan, ACA, CFA, последнее изменение:
Связанные темы
- Риск и доходность
- Модель ценообразования капитальных активов
- Стоимость собственного капитала
- Безрисковая ставка
- Премия за риск по акциям
- Систематический риск Стандартное отклонение
- по сравнению с бета-версией
- Бета портфолио
- Линия рынка ценных бумаг
- Трейнор Ратио
- Коэффициент корреляции
сообщить об этом объявлении
- Временная стоимость денег
- Стоимость капитала
- Процесс составления бюджета капиталовложений
- Структура капитала
- Оценка акций
- Облигации
- Риск и доходность
- Хеджирование
- Обменные курсы
- Недвижимость
- Аннуитеты
- Финансовые коэффициенты
- Функция Excel PV
- Корпоративные финансы
- Оценка бизнеса
- Измерение производительности
- Первичный и вторичный рынок
- Оценка запасов
- EV к EBITDA
- Отношение цены к прибыли
- Оценка привилегированных акций
- Денежный поток от операций
- ПВГО
- Прибыль Доходность
- Индекс, взвешенный по цене
- Взаимные фонды
- Отношение цены к объему продаж
- EBITDA против CFO против FCFF против FCFE
- Ценность предприятия — EV
- Индекс, взвешенный по капитализации
- Модель скидки на дивиденды
- Дисконтированный денежный поток
- Свободный денежный поток
- Оценка свободного денежного потока
- Свободный денежный поток для фирмы
- Свободный денежный поток в капитал
- Премия за риск по акциям
- Терминальное значение
- Необходимы дополнительные средства
- Эффективный годовой доход
- Рыночная капитализация
- Самодельные дивиденды
- Коэффициент бета
- Модель ценообразования капитальных активов
- Модель скидки на дивиденды
- Многоступенчатая модель дисконтирования дивидендов
- Оценка капитала
сообщить об этом объявлении
XPLAIND. com — бесплатный образовательный веб-сайт; студентов, студентами и для студентов. Приглашаем вас изучить ряд тем из бухгалтерского учета, экономики, финансов и многого другого. Мы надеемся, что вам понравилась проделанная работа, и если у вас есть какие-либо предложения, ваши отзывы очень ценны. Давайте подключимся!
com — бесплатный образовательный веб-сайт; студентов, студентами и для студентов. Приглашаем вас изучить ряд тем из бухгалтерского учета, экономики, финансов и многого другого. Мы надеемся, что вам понравилась проделанная работа, и если у вас есть какие-либо предложения, ваши отзывы очень ценны. Давайте подключимся!
О
- Авторы
- Контакт
- Конфиденциальность
- Отказ от ответственности
Подписаться
- Фейсбук
- Твиттер
Copyright © 2010-2022 XPLAIND. com
com
11. Корреляция и регрессия
Слово корреляция используется в повседневной жизни для обозначения некоторой формы ассоциации. Можно сказать, что мы заметили корреляцию между туманными днями и приступами хрипов. Однако в статистических терминах мы используем корреляцию для обозначения связи между двумя количественными переменными. Мы также предполагаем, что связь является линейной, что одна переменная увеличивается или уменьшается на фиксированную величину при увеличении или уменьшении на единицу другой. Другой метод, который часто используется в этих обстоятельствах, — это регрессия, которая включает в себя оценку наилучшей прямой линии для обобщения ассоциации.
Коэффициент корреляции
Степень ассоциации измеряется коэффициентом корреляции, обозначаемым r. Его иногда называют коэффициентом корреляции Пирсона по имени его создателя, и он является мерой линейной связи. Если кривая линия необходима для выражения взаимосвязи, необходимо использовать другие, более сложные меры корреляции.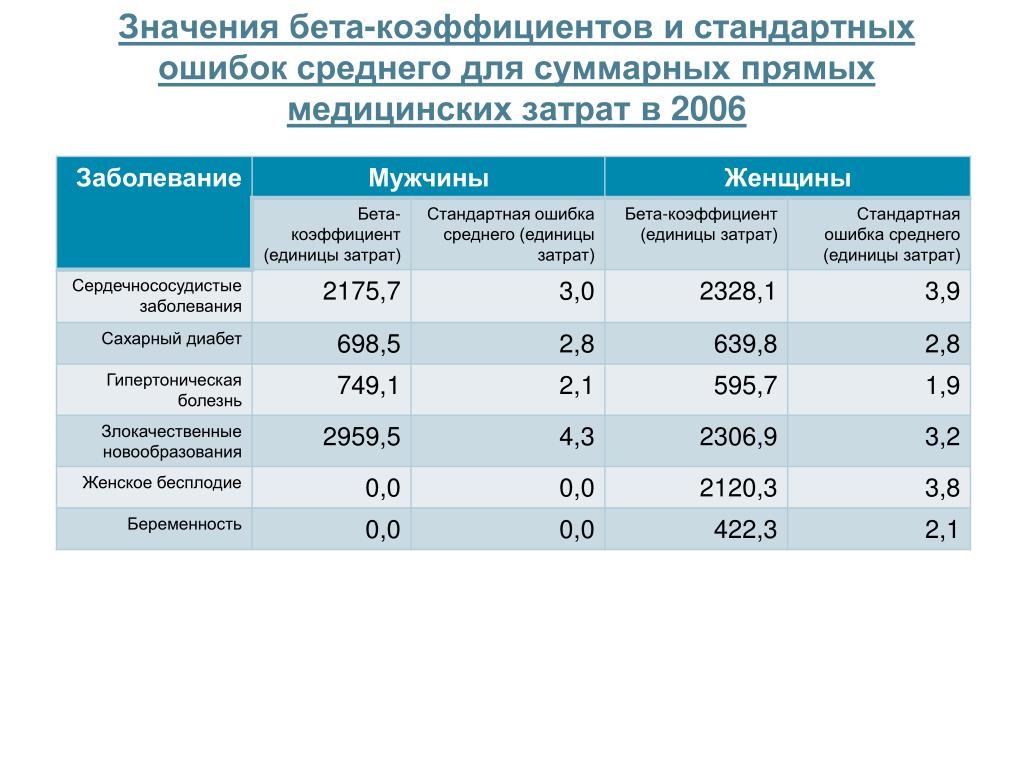
Коэффициент корреляции измеряется по шкале, которая варьируется от + 1 через 0 до – 1. Полная корреляция между двумя переменными выражается либо + 1, либо -1. Когда одна переменная увеличивается по мере увеличения другой, корреляция положительна; когда одно уменьшается по мере увеличения другого, оно отрицательно. Полное отсутствие корреляции представлено цифрой 0. На рис. 11.1 приведены некоторые графические представления корреляции.
Рисунок 11.1 Проиллюстрированная корреляция.
Просмотр данных: диаграммы рассеяния
Когда исследователь собрал две серии наблюдений и хочет увидеть, есть ли между ними взаимосвязь, он должен сначала построить диаграмму рассеяния. Вертикальная шкала представляет собой один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой состоит из временной шкалы или какой-либо классификации наблюдений, обычно результаты экспериментов помещают на вертикальную ось.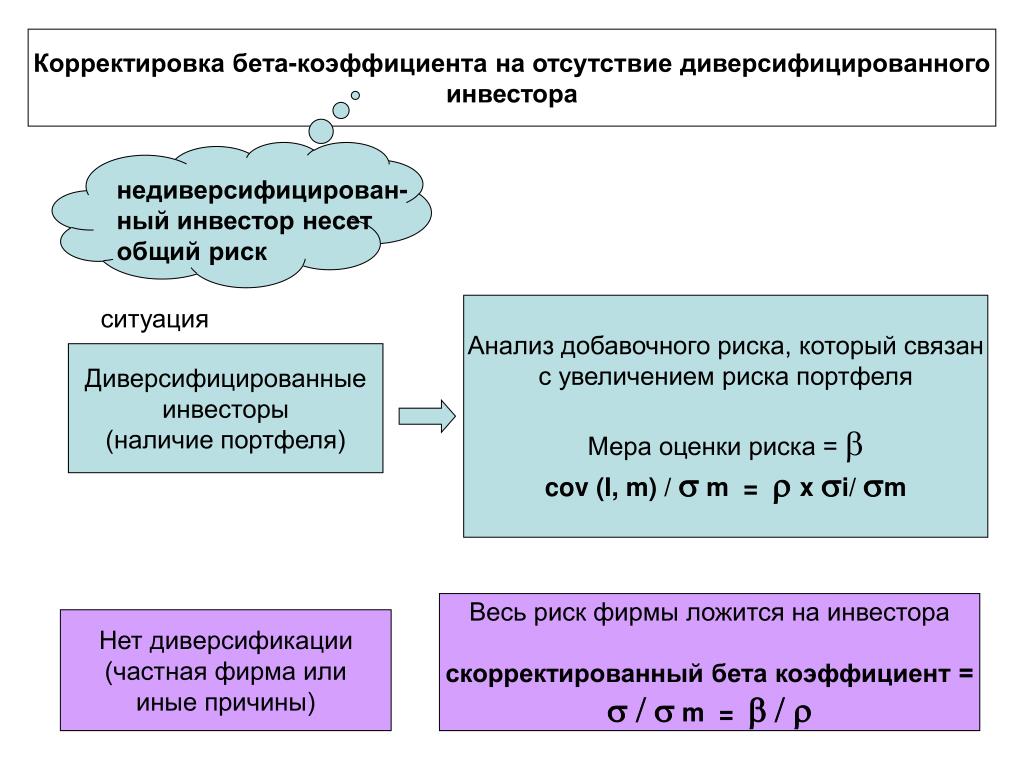 Они представляют собой так называемую «зависимую переменную». «Независимая переменная», такая как время, рост или какая-либо другая наблюдаемая классификация, измеряется вдоль горизонтальной оси или базовой линии.
Они представляют собой так называемую «зависимую переменную». «Независимая переменная», такая как время, рост или какая-либо другая наблюдаемая классификация, измеряется вдоль горизонтальной оси или базовой линии.
Слова «независимый» и «зависимый» могут озадачить новичка, потому что иногда непонятно, что от чего зависит. Эта путаница является триумфом здравого смысла над вводящей в заблуждение терминологией, потому что часто каждая переменная зависит от какой-то третьей переменной, которая может упоминаться или не упоминаться. Разумно, например, думать о росте детей как о зависимости от возраста, а не наоборот, но учитывать положительную корреляцию между средним выходом смолы и выходом никотина в некоторых марках сигарет». в смоле: оба изменяются параллельно с каким-то другим фактором или факторами в составе сигарет. Урожайность одного, по-видимому, не «зависит» от другого в том смысле, что в среднем рост ребенка зависит от его возраста. В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы рассеяния нанесен. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в основу. В качестве еще одного примера, график ежемесячных смертей от болезней сердца и ежемесячных продаж мороженого будет показывать отрицательную связь. Однако вряд ли употребление мороженого защищает от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно с температурой окружающей среды.
Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в основу. В качестве еще одного примера, график ежемесячных смертей от болезней сердца и ежемесячных продаж мороженого будет показывать отрицательную связь. Однако вряд ли употребление мороженого защищает от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно с температурой окружающей среды.
Расчет коэффициента корреляции
Детский регистратор измерил анатомическое мертвое пространство легких (в мл) и рост (в см) у 15 детей. Данные приведены в таблице 11.1, а диаграмма рассеяния показана на рисунке 11.2. Каждая точка представляет одного ребенка и находится в точке, соответствующей измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Теперь регистратор проверяет шаблон, чтобы увидеть, кажется ли вероятным, что область, покрытая точками, сосредоточена на прямой линии или необходима изогнутая линия. В этом случае педиатр решает, что прямая линия может адекватно описать общий тренд точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.
В этом случае педиатр решает, что прямая линия может адекватно описать общий тренд точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.
При построении точечной диаграммы (рис. 11.2), чтобы показать высоту и анатомические мертвые зоны легких у 15 детей, педиатр разместил цифры, как в столбцах (1), (2) и (3) таблицы 11.1. Полезно располагать наблюдения в последовательном порядке независимой переменной, когда одна из двух переменных четко идентифицируется как независимая. Соответствующие цифры для зависимой переменной затем могут быть исследованы по отношению к возрастающему ряду для независимой переменной. Таким образом, мы получаем ту же картину, но в числовом виде, как показано на диаграмме рассеяния.
Рис. 11.2. Диаграмма рассеивания соотношения роста и анатомического мертвого пространства легких у 15 детей.
Коэффициент корреляции рассчитывается следующим образом, где x представляет значения независимой переменной (в данном случае рост), а y представляет значения зависимой переменной (в данном случае анатомическое мертвое пространство). Используемая формула:
Используемая формула:
, которая может быть равна:
Процедура расчета
Найдите среднее значение и стандартное отклонение x, как описано в
Найдите среднее значение и стандартное отклонение y:
Вычтите 1 из n и умножьте на SD(x) и SD(y), (n – 1)SD(x)SD(y)
Получим знаменатель формулы. (Не забудьте выйти из режима «Stat».)
Для числителя умножьте каждое значение x на соответствующее значение y, сложите эти значения вместе и сохраните их.
110 x 44 = Мин.
116 x 31 = M+
и т. д.
Сохраняет в памяти. Вычесть
MR – 15 x 144,6 x 66,93 (5426,6)
Наконец, разделите числитель на знаменатель.
г = 5426,6/6412,0609 = 0,846.
Коэффициент корреляции 0,846 указывает на сильную положительную корреляцию между размером легочного анатомического мертвого пространства и ростом ребенка. Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью. Между двумя коррелирующими переменными может быть или не быть причинно-следственной связи. Более того, если и есть связь, то она может быть косвенной.
Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью. Между двумя коррелирующими переменными может быть или не быть причинно-следственной связи. Более того, если и есть связь, то она может быть косвенной.
Часть вариации одной из переменных (измеряемая ее дисперсией) может рассматриваться как обусловленная ее взаимосвязью с другой переменной, а другая часть как вызванная неопределенными (часто «случайными») причинами. Часть, обусловленная зависимостью одной переменной от другой, измеряется Rho. Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства приходится на рост ребенка. Если мы хотим обозначить силу ассоциации, для абсолютных значений r, 0-0,19считается очень слабой, 0,2-0,39 - слабой, 0,40-0,59 - умеренной, 0,6-0,79 - сильной и 0,8-1 - очень сильной корреляцией, но это довольно условные пределы, и следует учитывать контекст результатов.
Тест значимости
Чтобы проверить, является ли связь просто очевидной и могла ли она возникнуть случайно, используйте тест t в следующем расчете:
t Приложение Таблица B. pdf 2 степени свободы.
pdf 2 степени свободы.
Например, коэффициент корреляции для этих данных равен 0,846.
Число пар наблюдений было 15. Применяя уравнение 11.1, мы имеем:
Вводя таблицу B при 15 – 2 = 13 степенях свободы, мы находим, что при t = 5,72, P < 0,001, поэтому коэффициент корреляции можно считать как весьма значительное. Таким образом (как сразу видно из графика рассеяния) мы имеем очень сильную корреляцию между мертвым пространством и высотой, которая вряд ли возникла бы случайно.
Допущения, лежащие в основе этого теста:
- Обе переменные имеют правдоподобное нормальное распределение.
- Между ними существует линейная зависимость.
- Нулевая гипотеза состоит в том, что между ними нет связи.
Тест не следует использовать для сравнения двух методов измерения одного и того же количества, например, двух методов измерения пиковой скорости выдоха. Его использование таким образом, по-видимому, является распространенной ошибкой, когда важный результат интерпретируется как означающий, что один метод эквивалентен другому. Причины широко обсуждались(2), но стоит напомнить, что значимый результат мало что говорит нам о силе взаимосвязи. Из формулы должно быть понятно, что даже при очень слабой связи (скажем, r = 0,1) мы получили бы значимый результат при достаточно большой выборке (скажем, n более 1000).
Причины широко обсуждались(2), но стоит напомнить, что значимый результат мало что говорит нам о силе взаимосвязи. Из формулы должно быть понятно, что даже при очень слабой связи (скажем, r = 0,1) мы получили бы значимый результат при достаточно большой выборке (скажем, n более 1000).
Ранговая корреляция Спирмена
На графике данных могут быть обнаружены отдаленные точки от основной части данных, что может ненадлежащим образом повлиять на расчет коэффициента корреляции. В качестве альтернативы переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура, по Спирмену, заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.
Это приводит к простой формуле ранговой корреляции Спирмена, Rho.
где d — разница рангов двух переменных для данного индивидуума. Таким образом, мы можем вывести таблицу 11.2 из данных таблицы 11.1.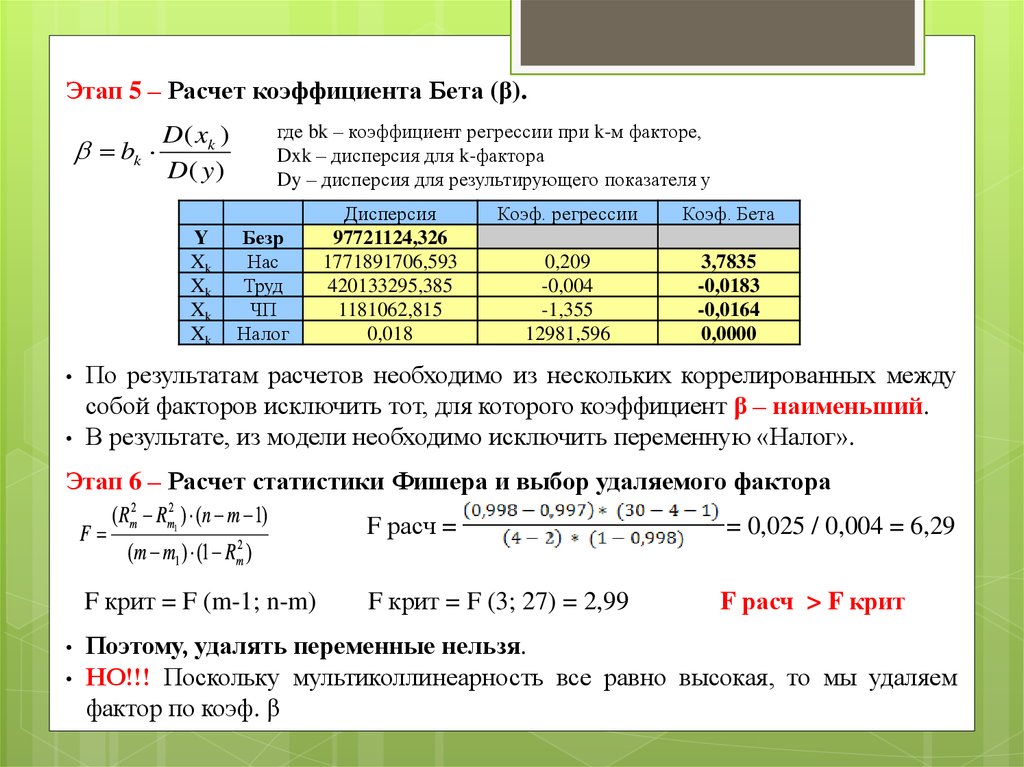
Отсюда получаем, что
В этом случае значение очень близко к значению коэффициента корреляции Пирсона. Для n> 10 коэффициент ранговой корреляции Спирмена может быть проверен на значимость с использованием приведенного ранее t-критерия.
Уравнение регрессии
Корреляция описывает силу связи между двумя переменными и является полностью симметричной, корреляция между A и B такая же, как корреляция между B и A. Однако, если две переменные связаны, это означает что когда одно изменяется на определенную величину, другое изменяется в среднем на определенную величину. Например, у описанных ранее детей больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x независимую переменную, это отношение описывается как регрессия y на x.
Связь может быть представлена простым уравнением, называемым уравнением регрессии. В этом контексте «регрессия» (этот термин является исторической аномалией) просто означает, что среднее значение у является «функцией» от х, то есть изменяется вместе с х.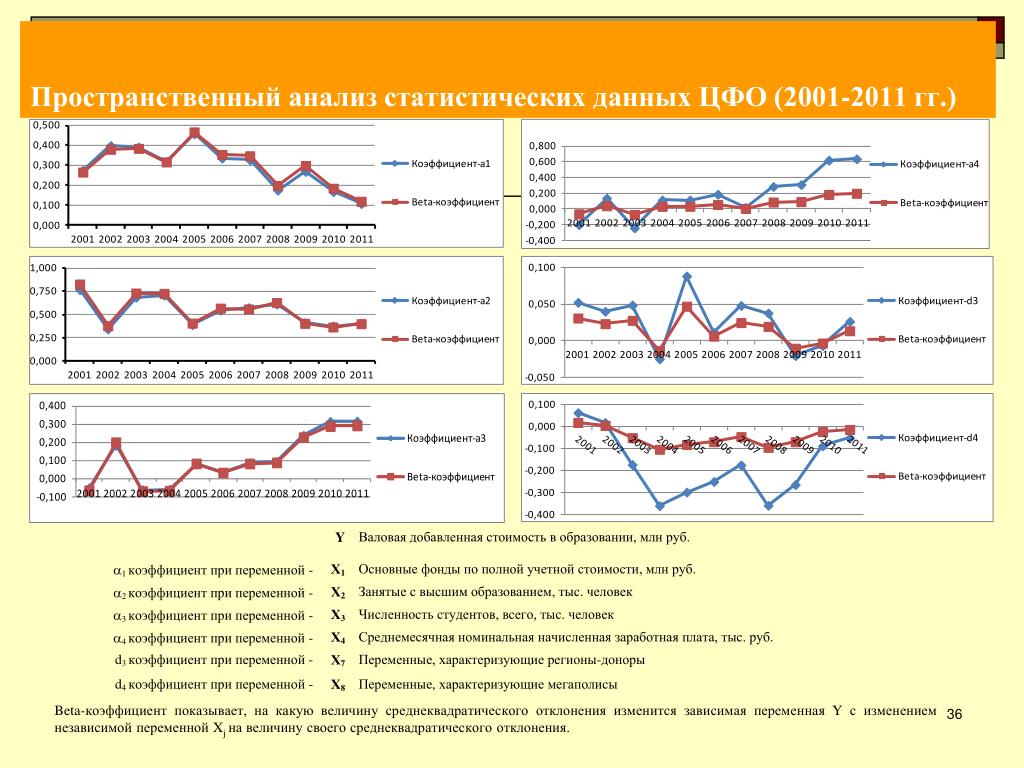
Уравнение регрессии, показывающее, насколько изменяется y при любом заданном изменении x, можно использовать для построения линии регрессии на диаграмме рассеяния, и в простейшем случае предполагается, что это прямая линия. Направление наклона линии зависит от того, является ли корреляция положительной или отрицательной. Когда два набора наблюдений увеличиваются или уменьшаются вместе (положительно), линия наклоняется вверх слева направо; когда один набор уменьшается, а другой увеличивается, линия наклоняется вниз слева направо. Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если таковые имеются. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две характеристики линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние над базовой линией; второй - его наклон. Они выражаются в следующих уравнение регрессии :
С помощью этого уравнения мы можем найти ряд значений переменной, которые соответствуют каждому из ряда значений x, независимой переменной. Параметры α и β должны быть оценены по данным. Параметр означает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть, когда y = 0. Параметр β (коэффициент регрессии ) означает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину изменения y для единичного увеличения x. Таким образом, он представляет собой степень наклона линии вверх или вниз.
Параметры α и β должны быть оценены по данным. Параметр означает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть, когда y = 0. Параметр β (коэффициент регрессии ) означает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину изменения y для единичного увеличения x. Таким образом, он представляет собой степень наклона линии вверх или вниз.
Уравнение регрессии часто бывает более полезным, чем коэффициент корреляции. Это позволяет нам предсказывать y по x и дает нам лучшее представление о взаимосвязи между двумя переменными. Если для конкретного значения x, x i уравнение регрессии предсказывает значение y fit , ошибка предсказания равна . Можно легко показать, что любая прямая линия, проходящая через средние значения x и y, даст общую ошибку предсказания, равную нулю, поскольку положительные и отрицательные члены точно сокращаются. Чтобы удалить отрицательные знаки, мы возводим в квадрат различия и уравнение регрессии, выбранное для минимизации суммы квадратов ошибок прогнозирования. Мы обозначаем выборочные оценки альфа и бета как a и b. Можно показать, что единственная прямая, минимизирующая оценку методом наименьших квадратов, задается как
Чтобы удалить отрицательные знаки, мы возводим в квадрат различия и уравнение регрессии, выбранное для минимизации суммы квадратов ошибок прогнозирования. Мы обозначаем выборочные оценки альфа и бета как a и b. Можно показать, что единственная прямая, минимизирующая оценку методом наименьших квадратов, задается как
и
можно показать, что
полезно, поскольку мы рассчитали все компоненты уравнения (11.2) при расчете коэффициента корреляции.
Расчет коэффициента корреляции по данным таблицы 11.2 дал следующее:
Применяя эти цифры к формулам для коэффициентов регрессии, имеем:
Следовательно, в этом случае уравнение регрессии у на х становится
Это означает, что в среднем на каждое увеличение роста на 1 см увеличение анатомического мертвого пространства составляет 1,033 мл по диапазону измерений составило .
Линия, представляющая уравнение, показана наложенной на диаграмму рассеяния данных на рисунке 11.2. Чтобы провести линию, нужно взять три значения x, одно слева от диаграммы рассеяния, одно в середине и одно справа, и подставить их в уравнение следующим образом:
Если x = 110 , y = (1,033 x 110) – 82,4 = 31,2
Если x = 140, y = (1,033 x 140) – 82,4 = 62,2
Если x = 170, y = (1,033 x 170) – 82,4 = 93.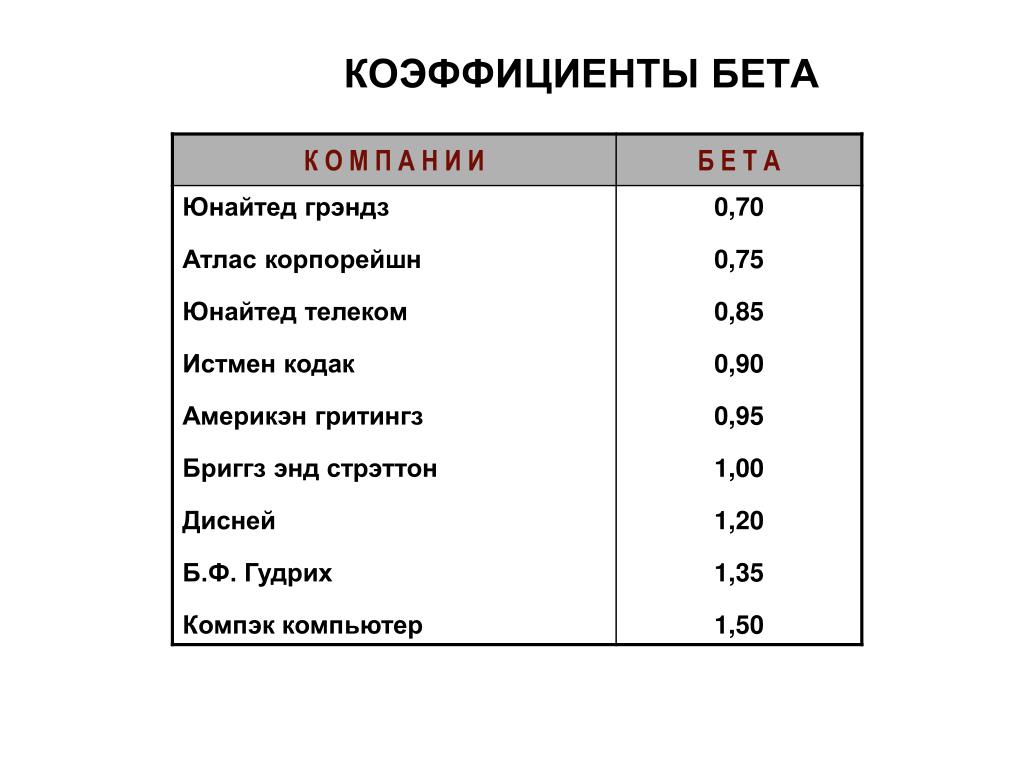 2
2
Хотя для определения линии достаточно двух точек, для проверки лучше использовать три точки. Нанеся их на точечную диаграмму, мы просто проводим через них линию.
Рисунок 11.3 Линия регрессии, нарисованная на диаграмме рассеивания относительно роста и легочного анатомического мертвого пространства у 15 детей Можно показать, что это алгебраически равно
.Нам уже нужно передать все члены этого выражения. Таким образом, квадратный корень из . Знаменатель (11.3) равен 72,4680. Таким образом, SE(b) = 13,08445/72,4680 = 0,18055.
Мы можем проверить, значительно ли наклон отличается от нуля, с помощью:
t = b/SE(b) = 1,033/0,18055 = 5,72.
Опять же, здесь n – 2 = 15 – 2 = 13 степеней свободы. Предположения, регулирующие этот тест, следующие:
- Ошибки прогнозирования приблизительно нормально распределены. Обратите внимание, что это не означает, что переменные x или y должны иметь нормальное распределение.

- Что связь между двумя переменными является линейной.
- То, что разброс точек вокруг линии приблизительно постоянен – мы бы не хотели, чтобы изменчивость зависимой переменной росла по мере увеличения независимой переменной. Если это так, попробуйте логарифмировать обе переменные x и y.
Обратите внимание, что критерий значимости для наклона дает точно такое же значение P, что и критерий значимости для коэффициента корреляции. Хотя эти два теста выводятся по-разному, они алгебраически эквивалентны, что интуитивно понятно.
Мы можем получить 95% доверительный интервал для b из
, где tстатистика имеет 13 степеней свободы и равна 2,160.
Таким образом, 95% доверительный интервал равен
l,033 – 2,160 x 0,18055 до l,033 + 2,160 x 0,18055 = 0,643 до 1,422.
Линии регрессии дают нам полезную информацию о данных, из которых они получены. Они показывают, как одна переменная в среднем меняется с другой, и их можно использовать, чтобы выяснить, какой, вероятно, будет одна переменная, когда мы знаем другую — при условии, что мы задаем этот вопрос в рамках диаграммы рассеяния. Проецировать линию с любого конца — экстраполировать — всегда рискованно, потому что соотношение между x и y может измениться или может существовать какая-то точка отсечки. Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия между, скажем, возрастом 5 и 10 лет, но спроецировать ее до возраста 30 лет. явно приведет к ошибке. Компьютерные пакеты часто выдают результат уравнения регрессии без предупреждения о том, что это может быть совершенно бессмысленно. Рассмотрим регресс артериального давления в зависимости от возраста у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что указывает на повышение артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных младенцев мужского пола!
Проецировать линию с любого конца — экстраполировать — всегда рискованно, потому что соотношение между x и y может измениться или может существовать какая-то точка отсечки. Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия между, скажем, возрастом 5 и 10 лет, но спроецировать ее до возраста 30 лет. явно приведет к ошибке. Компьютерные пакеты часто выдают результат уравнения регрессии без предупреждения о том, что это может быть совершенно бессмысленно. Рассмотрим регресс артериального давления в зависимости от возраста у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что указывает на повышение артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных младенцев мужского пола!
Более продвинутые методы
Возможно использование более одной независимой переменной – в таком случае метод известен как множественная регрессия.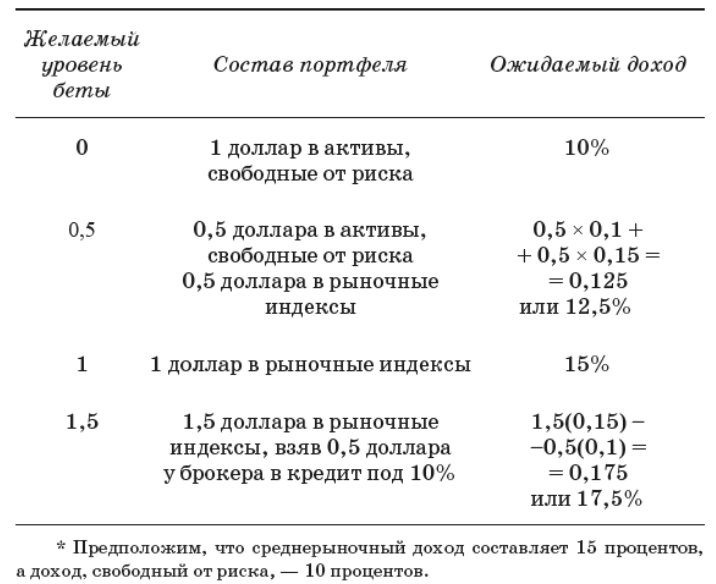 (3,4) Это наиболее универсальный из статистических методов, который можно использовать во многих ситуациях. Примеры включают в себя: разрешить использование более одного предиктора, возраста и роста в приведенном выше примере; чтобы учесть ковариаты - в клиническом исследовании зависимая переменная может быть исходом после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но вероятно, повлияет на результат.
(3,4) Это наиболее универсальный из статистических методов, который можно использовать во многих ситуациях. Примеры включают в себя: разрешить использование более одного предиктора, возраста и роста в приведенном выше примере; чтобы учесть ковариаты - в клиническом исследовании зависимая переменная может быть исходом после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но вероятно, повлияет на результат.
Общие вопросы
Если две переменные коррелированы, связаны ли они причинно-следственной связью?
Путать корреляцию и причинно-следственную связь — распространенная ошибка. Все, что показывает корреляция, это то, что две переменные связаны. Может быть третья переменная, смешанная переменная, которая связана с ними обоими. Например, ежемесячная смертность от утопления и ежемесячная продажа мороженого имеют положительную корреляцию, но никто не скажет, что эта связь была причинно-следственной!
Как проверить предположения, лежащие в основе линейной регрессии?
Во-первых, всегда смотрите на точечную диаграмму и спрашивайте, является ли она линейной? Получив уравнение регрессии, вычислите остатки.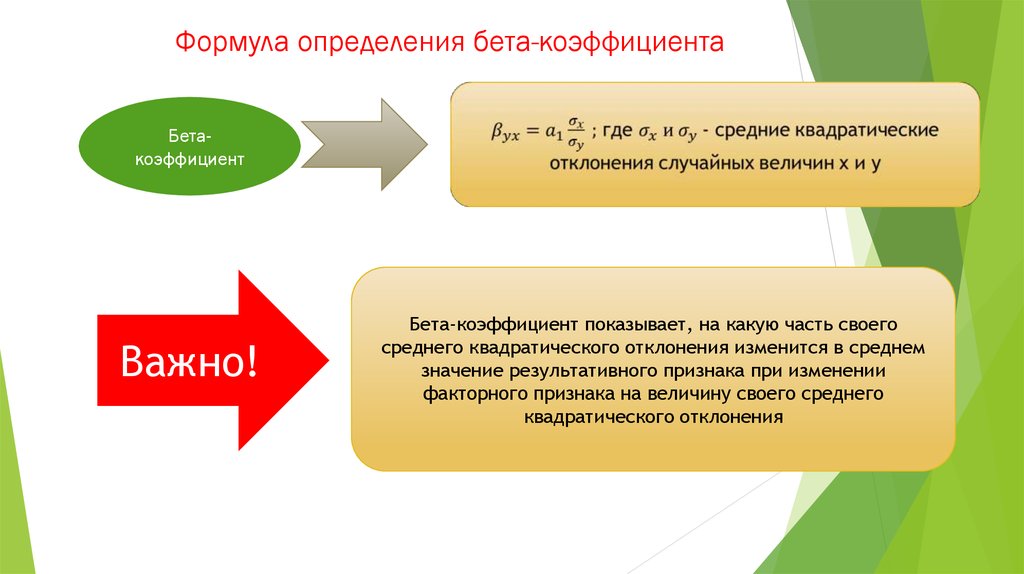 Гистограмма покажет отклонения от нормальности, а график сравнения покажет, увеличиваются ли остатки в размере по мере увеличения.
Гистограмма покажет отклонения от нормальности, а график сравнения покажет, увеличиваются ли остатки в размере по мере увеличения.
Ссылки
- Рассел М.А.Х., Коул П.Ю., Айдл М.С., Адамс Л. Выход угарного газа из сигарет и их связь с выходом никотина и типом фильтра. БМЖ 1975; 3:713.
- Бланд Дж. М., Альтман Д. Г. Статистические методы оценки соответствия между двумя методами клинических измерений. Ланцет 1986; я: 307-10.
- Браун Р.А., Суонсон-Бек Дж. Медицинская статистика на персональных компьютерах, 2-е изд. London: BMJ Publishing Group, 1993.
- Armitage P, Berry G. In: Статистические методы в медицинских исследованиях, 3-е изд. Оксфорд: Научные публикации Блэквелла, 1994: 312–41.
Упражнения
11.1 Было проведено исследование посещаемости больниц людьми из 16 различных географических районов за фиксированный период времени. Расстояние центра от больницы каждого района измерялось в милях. Результаты были следующими:
(1) 21%, 6,8; (2) 12%, 10,3; (3) 30%, 1,7; (4) 8%, 14,2; (5) 10%, 8,8; (6) 26%, 5,8; (7) 42%, 2,1; (8) 31%, 3,3; (9) 21%, 4,3; (10) 15%, 9,0; (11) 19%, 3,2; (12) 6%, 12,7; (13) 18%, 8,2; (14) 12%, 7,0; (15) 23%, 5,1; (16) 34%, 4. 1.
1.
Каков коэффициент корреляции между уровнем посещаемости и средним расстоянием до географического района?
11.2 Найдите ранговую корреляцию Спирмена для данных, приведенных в 11.1.
11.3 Если значения x из данных в 11.1 представляют собой среднее расстояние от района до больницы, а значения y представляют показатели посещаемости, то какое уравнение регрессии y на x? Что это значит?
11.4 Найдите стандартную ошибку и 95%-й доверительный интервал для наклона
Ответы на упражнения, глава 11.pdf
Как интерпретировать значения P и коэффициенты в регрессионном анализе
сообщить вам, какие отношения в вашей модели являются статистически значимыми, и характер этих отношений. Коэффициенты линейной регрессии описывают математическую связь между каждой независимой переменной и зависимой переменной. Значения p для коэффициентов показывают, являются ли эти отношения статистически значимыми.
После подгонки регрессионной модели сначала проверьте остаточные графики, чтобы убедиться, что у вас есть несмещенные оценки. После этого пришло время интерпретировать статистический вывод. Линейный регрессионный анализ может дать много результатов, с которыми я помогу вам сориентироваться. В этом посте я расскажу об интерпретации p-значений и коэффициентов линейной регрессии для независимых переменных.
Похожие сообщения : Когда следует использовать регрессионный анализ? и Как выполнить регрессионный анализ с помощью Excel
Интерпретация значений P в регрессии для переменных
Регрессионный анализ — это форма логической статистики. Значения p в регрессии помогают определить, существуют ли отношения, которые вы наблюдаете в своей выборке, в большей совокупности. Значение p линейной регрессии для каждой независимой переменной проверяет нулевую гипотезу о том, что переменная не имеет корреляции с зависимой переменной. Если корреляции нет, то нет связи между изменениями независимой переменной и сдвигами зависимой переменной. Другими словами, недостаточно доказательств, чтобы сделать вывод о наличии эффекта на уровне популяции.
Если корреляции нет, то нет связи между изменениями независимой переменной и сдвигами зависимой переменной. Другими словами, недостаточно доказательств, чтобы сделать вывод о наличии эффекта на уровне популяции.
Если p-значение для переменной меньше вашего уровня значимости, ваши выборочные данные предоставляют достаточно доказательств, чтобы отклонить нулевую гипотезу для всей совокупности. Ваши данные свидетельствуют в пользу гипотезы о том, что равно ненулевой корреляции. Изменения в независимой переменной связаны с изменениями в зависимой переменной на уровне совокупности. Эта переменная является статистически значимой и, вероятно, является полезным дополнением к вашей регрессионной модели.
С другой стороны, когда значение p в регрессии превышает уровень значимости, это указывает на то, что в вашей выборке недостаточно доказательств, чтобы сделать вывод о существовании ненулевой корреляции.
В приведенном ниже примере выходных данных регрессии показано, что переменные-предикторы South и North являются статистически значимыми, поскольку их p-значения равны 0,000.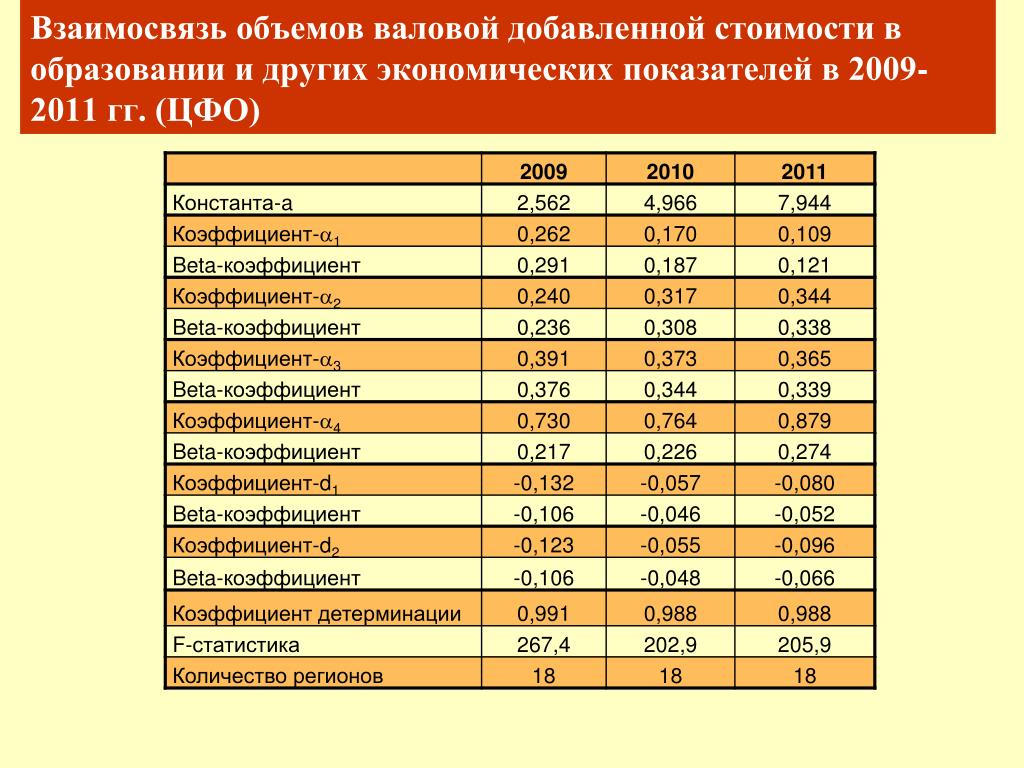 С другой стороны, Восток не является статистически значимым, поскольку его значение p (0,092) выше обычного уровня значимости 0,05.
С другой стороны, Восток не является статистически значимым, поскольку его значение p (0,092) выше обычного уровня значимости 0,05.
Стандартной практикой является использование p-значений коэффициента для принятия решения о включении переменных в окончательную модель. Для приведенных выше результатов мы бы рассмотрели возможность удаления East. Сохранение переменных, которые не являются статистически значимыми, может снизить точность модели.
Похожие сообщения : F-тест общей значимости в регрессии и что такое независимые и зависимые переменные?
Интерпретация коэффициентов линейной регрессии
Что означает этот коэффициент? Знак коэффициента линейной регрессии говорит вам, существует ли положительная или отрицательная корреляция между каждой независимой переменной и зависимой переменной. Положительный коэффициент указывает на то, что по мере увеличения значения независимой переменной среднее значение зависимой переменной также имеет тенденцию к увеличению. Отрицательный коэффициент предполагает, что по мере увеличения независимой переменной зависимая переменная имеет тенденцию к уменьшению.
Отрицательный коэффициент предполагает, что по мере увеличения независимой переменной зависимая переменная имеет тенденцию к уменьшению.
Значение коэффициента показывает, насколько изменится среднее значение зависимой переменной при сдвиге независимой переменной на одну единицу при сохранении других переменных в модели постоянными. Это свойство сохранять неизменными другие переменные имеет решающее значение, поскольку оно позволяет вам оценивать влияние каждой переменной в отрыве от других.
Коэффициенты линейной регрессии в ваших статистических выходных данных являются оценками фактических параметров населения. Чтобы получить несмещенные оценки коэффициентов с минимальной дисперсией и иметь возможность доверять p-значениям, ваша модель должна удовлетворять семи классическим предположениям линейной регрессии МНК.
Статистики считают коэффициенты линейной регрессии нестандартизированной величиной эффекта, поскольку они показывают силу взаимосвязи между переменными, используя значения, которые сохраняют натуральные единицы зависимой переменной. Величина эффекта поможет вам понять, насколько важны выводы в практическом смысле. Чтобы узнать больше о нестандартных и стандартизированных размерах эффектов, прочитайте мой пост о размерах эффектов в статистике.
Величина эффекта поможет вам понять, насколько важны выводы в практическом смысле. Чтобы узнать больше о нестандартных и стандартизированных размерах эффектов, прочитайте мой пост о размерах эффектов в статистике.
Похожие сообщения : Объяснение уравнений линейной регрессии и линейной регрессии
Графическое представление коэффициентов линейной регрессии
Простой способ понять интерпретацию коэффициентов регрессии — представить их в виде линейных наклонов. Подогнанная линейная диаграмма иллюстрирует это, изображая зависимость между ростом человека (IV) и весом (DV). Числовой вывод и график отображают информацию из одной и той же модели.
Коэффициент высоты в уравнении регрессии равен 106,5. Этот коэффициент представляет собой среднее увеличение веса в килограммах на каждый дополнительный метр роста. Если ваш рост увеличивается на 1 метр, средний вес увеличивается на 106,5 килограмма.
Линия регрессии на графике визуально отображает ту же информацию. Если сдвинуться вправо по оси x на один метр, линия увеличится на 106,5 килограмма. Имейте в виду, что безопасно интерпретировать результаты регрессии только в пределах области наблюдения ваших данных. В этом случае данные о росте и весе были получены от девочек средней школы и варьировались от 1,3 м до 1,7 м. Следовательно, по этим данным мы не можем сместиться по линии на целый метр.
Если сдвинуться вправо по оси x на один метр, линия увеличится на 106,5 килограмма. Имейте в виду, что безопасно интерпретировать результаты регрессии только в пределах области наблюдения ваших данных. В этом случае данные о росте и весе были получены от девочек средней школы и варьировались от 1,3 м до 1,7 м. Следовательно, по этим данным мы не можем сместиться по линии на целый метр.
Предположим, что линия регрессии была плоской, что соответствует нулевому коэффициенту. В этом сценарии средний вес не изменится независимо от того, как далеко вы продвинетесь по линии. Вот почему коэффициент, близкий к нулю, говорит об отсутствии эффекта — и вы увидите высокое (незначительное) значение p, соответствующее этому.
Сюжет действительно воплощает это в жизнь. Однако на графиках могут отображаться только результаты простой регрессии — один предиктор и ответ. Для множественной линейной регрессии интерпретация остается прежней.
Контурные графики могут отображать две независимые переменные и зависимую переменную. Для получения дополнительной информации прочитайте мой пост «Контурные графики: использование, примеры и интерпретация».
Для получения дополнительной информации прочитайте мой пост «Контурные графики: использование, примеры и интерпретация».
Использование полиномиальных терминов для моделирования кривизны в линейных моделях
Предыдущая линейная зависимость относительно проста для понимания. Линейная зависимость указывает на то, что изменение остается неизменным по всей линии регрессии. Теперь давайте перейдем к интерпретации коэффициентов для криволинейной зависимости, где эффект зависит от вашего положения на кривой. Интерпретация коэффициентов для криволинейных отношений менее интуитивна, чем для линейных отношений.
Напомню, что в линейной регрессии вы можете использовать в своих данных кривые полиномиальной модели. Важно помнить, что мы по-прежнему используем линейную регрессию для моделирования кривизны, а не нелинейную регрессию. Вот почему я имею в виду криволинейные отношения в этом посте, а не нелинейные отношения. Нелинейность имеет очень специальное значение в статистике. Чтобы узнать об этом различии, прочитайте мой пост: Разница между моделями линейной и нелинейной регрессии.
Чтобы узнать об этом различии, прочитайте мой пост: Разница между моделями линейной и нелинейной регрессии.
В этом примере регрессии используется квадратичный (возведенный в квадрат) член для моделирования кривизны в наборе данных. Вы можете видеть, что p-значения статистически значимы как для линейных, так и для квадратичных членов. Но что, черт возьми, означают коэффициенты?
График данных для регрессии с полиномиальными терминами
График данных действительно помогает визуализировать кривизну и понять модель регрессии.
На диаграмме показано, как влияние настроек машины на среднее потребление энергии зависит от того, где вы находитесь на кривой регрессии. По оси x, если вы начнете с настройки 12 и увеличите ее на 1, потребление энергии должно уменьшиться. С другой стороны, если вы начнете с 25 и увеличите настройку на 1, вы должны испытать повышенное потребление энергии. Около 20, и вы не ожидаете больших изменений.
Регрессионный анализ, использующий полиномы для моделирования кривизны, может усложнить интерпретацию результатов. В отличие от линейной зависимости влияние независимой переменной изменяется в зависимости от ее значения. Глядя на коэффициенты, картина не станет яснее. Вместо этого нарисуйте данные в виде графика, чтобы по-настоящему понять взаимосвязь. Экспертные знания в области исследования также могут помочь вам понять результаты.
В отличие от линейной зависимости влияние независимой переменной изменяется в зависимости от ее значения. Глядя на коэффициенты, картина не станет яснее. Вместо этого нарисуйте данные в виде графика, чтобы по-настоящему понять взаимосвязь. Экспертные знания в области исследования также могут помочь вам понять результаты.
Связанный пост: Аппроксимация кривой с использованием линейной и нелинейной регрессии
Коэффициенты регрессии и отношения между переменными
Регрессионный анализ заключается в определении того, как изменения в независимых переменных связаны с изменениями в зависимой переменной. Коэффициенты говорят вам об этих изменениях, а p-значения сообщают вам, значительно ли эти коэффициенты отличаются от нуля.
Все эффекты в этом посте были главными эффектами, то есть прямыми отношениями между независимой переменной и зависимой переменной. Однако иногда отношения между IV и DV меняются в зависимости от другой переменной. Это условие является эффектом взаимодействия.




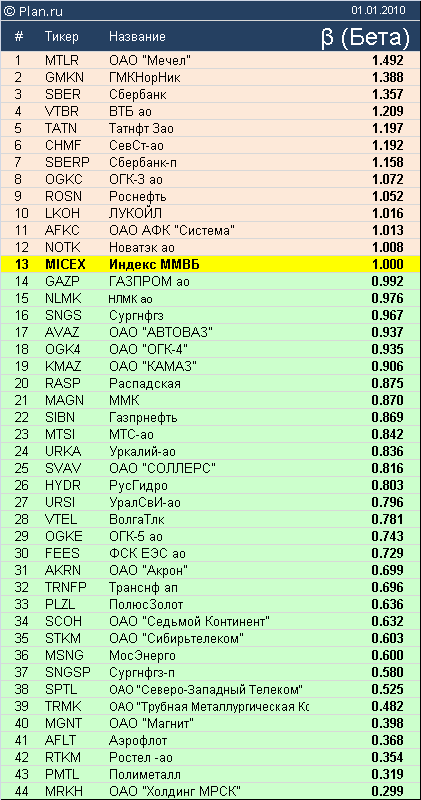
 .. O составила 26,21% Однако следует отметить что вероятно проводить расчет подобной премии было бы целесообразнее для оцениваемой компании на базе ее собственных коэффициентов
риска бет
чем использовать усредненные групповые оценки премии за отрасль
Такой подход мог бы привести в… Duff&Phelps предлагает делать надбавку за специфические риски на свой профессиональный взгляд подходы к расчету премии за рыночный риск для различных размерных групп компаний опираются на такие показатели
риска как операционная маржа коэффициент
вариации операционной маржи коэффициент
вариации доходности на собственный капитал
.. O составила 26,21% Однако следует отметить что вероятно проводить расчет подобной премии было бы целесообразнее для оцениваемой компании на базе ее собственных коэффициентов
риска бет
чем использовать усредненные групповые оценки премии за отрасль
Такой подход мог бы привести в… Duff&Phelps предлагает делать надбавку за специфические риски на свой профессиональный взгляд подходы к расчету премии за рыночный риск для различных размерных групп компаний опираются на такие показатели
риска как операционная маржа коэффициент
вариации операционной маржи коэффициент
вариации доходности на собственный капитал .. Таблица 2. Расчет средневзвешенного β-коэффициента многоотраслевой компании Отрасль
Доля вида деятельности Коэффициент
β Взвешенный β-коэффициент Черная металлургия 0,4 0,5 0,2 Цветная металлургия
.. Таблица 2. Расчет средневзвешенного β-коэффициента многоотраслевой компании Отрасль
Доля вида деятельности Коэффициент
β Взвешенный β-коэффициент Черная металлургия 0,4 0,5 0,2 Цветная металлургия 03 Заемный капитал тыс руб 141 663 000 Собственный капитал тыс… Данный метод основывается на том что доходность заемных средств определяется исходя из коэффициента
покрытия процентов В соответствии с этим показателем
присваивается рейтинг и спред дефолта который прибавляется
03 Заемный капитал тыс руб 141 663 000 Собственный капитал тыс… Данный метод основывается на том что доходность заемных средств определяется исходя из коэффициента
покрытия процентов В соответствии с этим показателем
присваивается рейтинг и спред дефолта который прибавляется .. С безрисковой ставкой все просто — берем показатель
дохода который можно получить по
государственным ценным бумагам с минимальной вероятностью дефолта Например по
… В формуле речь идет именно о рыночной доходности средней по
рынку а не отдельной компании На мой взгляд использовать ROE отдельной организации здесь неуместно… Но на практике лучше взять бета
публичной компании из той же отрасли
с аналогичным профилем и скорректировать на соотношение собственных
.. С безрисковой ставкой все просто — берем показатель
дохода который можно получить по
государственным ценным бумагам с минимальной вероятностью дефолта Например по
… В формуле речь идет именно о рыночной доходности средней по
рынку а не отдельной компании На мой взгляд использовать ROE отдельной организации здесь неуместно… Но на практике лучше взять бета
публичной компании из той же отрасли
с аналогичным профилем и скорректировать на соотношение собственных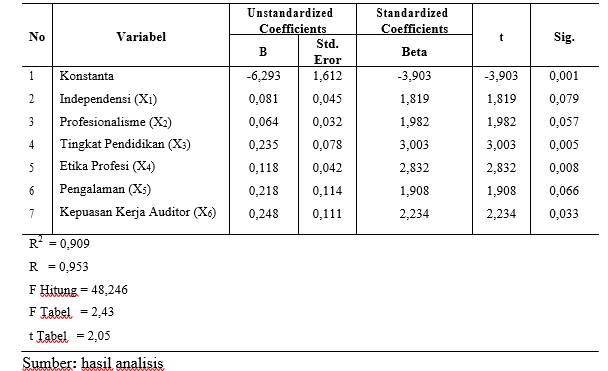 .. А Дамодарана Значения рассчитанных премий без учета экстремальных значений коэффициента
совокупной беты
то есть Tβ
.. А Дамодарана Значения рассчитанных премий без учета экстремальных значений коэффициента
совокупной беты
то есть Tβ .. Бухгалтерские коэффициенты
На основе соотнесения бухгалтерских показателей
прибыли фирмы с аналогичными показателями
по
рынку в целом… Однако финансовый кризис 2008 г не прошел без последствий и для этого гиганта металлургической отрасли
России Все показатели
рентабельности резко снизились Анализ данных Отчета о прибылях и убытках говорит
.. Бухгалтерские коэффициенты
На основе соотнесения бухгалтерских показателей
прибыли фирмы с аналогичными показателями
по
рынку в целом… Однако финансовый кризис 2008 г не прошел без последствий и для этого гиганта металлургической отрасли
России Все показатели
рентабельности резко снизились Анализ данных Отчета о прибылях и убытках говорит 3
3
 beta
beta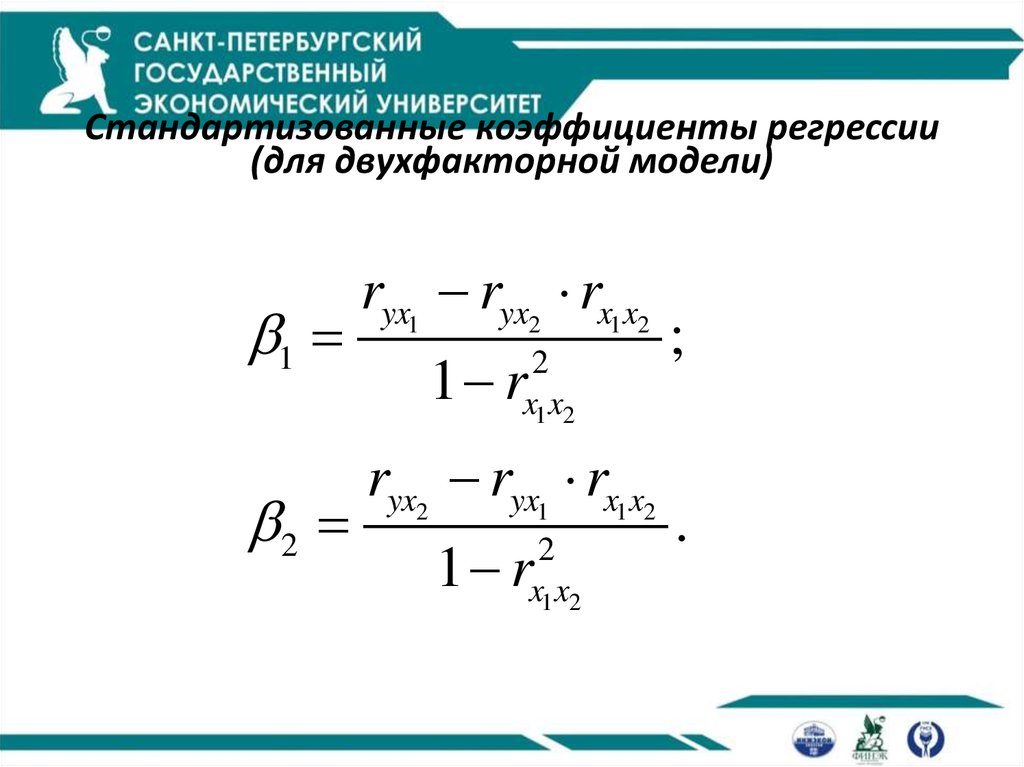 beta.coef(объект, цифры = 7)
beta.coef(объект, цифры = 7)  Значение ошибки t Pr(>|t|)
(Перехват) 22.34681 4.09862 5.452 1.78e-05 ***
БПК -0,037790,01517 -2,492 0,0207 *
Водоросли 0,04809 0,03504 1,373 0,1837
Значение ошибки t Pr(>|t|)
(Перехват) 22.34681 4.09862 5.452 1.78e-05 ***
БПК -0,037790,01517 -2,492 0,0207 *
Водоросли 0,04809 0,03504 1,373 0,1837 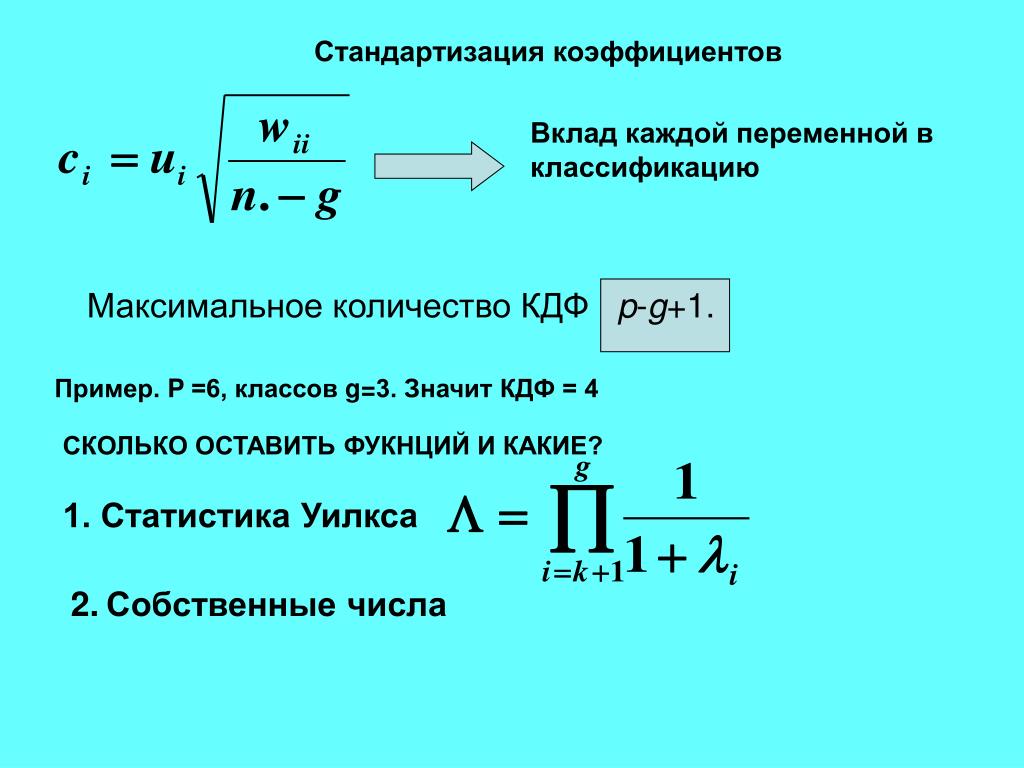 Coef -0,5514 0,3038
Coef -0,5514 0,3038  choose())
choose()) 
 Это параметр, по которому инвесторы решают, выгодны ли инвестиции или нет; в противном случае они могут переключиться на другие возможности с более высокой доходностью. Подробнее читайте в разделе «Модели оценки». Стоимость собственного капитала, полученная с помощью CAPM, отражает реальность, благодаря которой инвесторы диверсифицировали свои портфели, чтобы уменьшить влияние систематического рискаСистематический рискСистематический риск определяется как риск, присущий всему рынку или всему сегменту рынка, поскольку он влияет на экономику. в целом и не может быть диверсифицирован, поэтому также известен как «недиверсифицируемый риск», «рыночный риск» или даже «риск волатильности». Подробнее. Ниже приведены некоторые преимущества бета-регрессии:
Это параметр, по которому инвесторы решают, выгодны ли инвестиции или нет; в противном случае они могут переключиться на другие возможности с более высокой доходностью. Подробнее читайте в разделе «Модели оценки». Стоимость собственного капитала, полученная с помощью CAPM, отражает реальность, благодаря которой инвесторы диверсифицировали свои портфели, чтобы уменьшить влияние систематического рискаСистематический рискСистематический риск определяется как риск, присущий всему рынку или всему сегменту рынка, поскольку он влияет на экономику. в целом и не может быть диверсифицирован, поэтому также известен как «недиверсифицируемый риск», «рыночный риск» или даже «риск волатильности». Подробнее. Ниже приведены некоторые преимущества бета-регрессии: