Формула Кирхгофа — Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.

Формула Кирхгофа — Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

Примечания

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.

Ссылки

Формула Кирхгофа — Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

Примечания

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.

Ссылки

Формула Кирхгофа — это… Что такое Формула Кирхгофа?

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

, где функции и определены на , а  — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью в моменты времени .

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени :

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

где поверхностные интегралы берутся по сфере .

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени на некотором компакте M есть локальное возмущение ( и/или ). Если мы находимся в некоторой точке , то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время .

Вне отрезка времени , где , функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в , уже не будет компактным в , а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).

[1]

Решение уравнения колебаний мембраны (двумерного пространства)

(функция соответствует вынуждающей внешней силе)

с начальными условиями

задаётся формулой:

.

Решение одномерного волнового уравнения

(функция соответствует вынуждающей внешней силе)

с начальными условиями

имеет вид^[2]

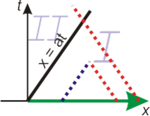В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области . Решение волнового уравнения представляется в виде суммы двух функций: , то есть оно определяется двумя семействами характеристик: . Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения с начальными условиями и искать решение в виде суммы трех функций: , которые удовлетворяют следующим условиям:

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путем замены переменных. Например, пусть . Тогда, сделав замену , уравнение для задачи «С» примет вид:

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

В силу четности начального условия, решение сохранит свой вид во всей области .

Примечания

1. ↑ КИРХГОФА ФОРМУЛА // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.
2. ↑ Формула Д’Аламбера в Физической энциклопедии

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6

Ссылки

Формула Кирхгофа — Википедия. Что такое Формула Кирхгофа

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\quad \left.{\frac {\partial u}{\partial t}}\right|_{t=0}=\varphi _{1}({\bar {x}})}

Тогда обобщённая формула Кирхгофа даёт решение этой задачи в трёхмерном случае:

u(x,t)=∂∂t[14πa2t∬Sφ0(y)d2Sn]+14πa2t∬Sφ1(y)d2Sn+14πa2∭|x−y|⩽atf(y,t−|x−y|a)|x−y|d3y{\displaystyle u(\mathbf {x} ,t)={\frac {\partial }{\partial t}}\left[{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{0}(\mathbf {y} )d^{2}S_{n}\right]+{\frac {1}{4\pi a^{2}t}}\iint \limits _{S}\varphi _{1}(\mathbf {y} )d^{2}S_{n}+{\frac {1}{4\pi a^{2}}}\iiint \limits _{\left|\mathbf {x} -\mathbf {y} \right|\leqslant at}{\frac {f\left(\mathbf {y} ,t-{\frac {\left|\mathbf {x} -\mathbf {y} \right|}{a}}\right)}{\left|\mathbf {x} -\mathbf {y} \right|}}d^{3}\mathbf {y} }

где поверхностные интегралы берутся по сфере S:|x−y|=at{\displaystyle S\colon \left|\mathbf {x} -\mathbf {y} \right|=at}.

Сам Кирхгоф рассматривал только трёхмерный случай.

Простой вывод решения основной задачи использует преобразование Фурье.

Физические следствия

Передний и задний волновые фронты от локализованного в пространстве возмущения действуют на наблюдателя в течение ограниченного отрезка времени

Пусть в начальный момент времени t=0{\displaystyle t=0} на некотором компакте M есть локальное возмущение (φ0≠0{\displaystyle \varphi _{0}\neq 0} и/или φ1≠0{\displaystyle \varphi _{1}\neq 0}). Если мы находимся в некоторой точке x¯0∈R3{\displaystyle {\bar {x}}_{0}\in \mathbb {R} ^{3}}, то, как видно из формулы (область интегрирования), возмущение мы почувствуем через время t1=1ainfy¯∈M|y¯−x¯0|{\displaystyle t_{1}={\frac {1}{a}}\inf _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}.

Вне отрезка времени [t1;t2]{\displaystyle \left[t_{1};t_{2}\right]}, где t2=1asupy¯∈M|y¯−x¯0|{\displaystyle t_{2}={\frac {1}{a}}\sup _{{\bar {y}}\in M}\left|{\bar {y}}-{\bar {x}}_{0}\right|}, функция u(x ₀, t) равна нулю.

Таким образом, начальное возмущение, локализованное в пространстве, вызывает в каждой точке пространства действие, локализованное во времени, то есть возмущение распространяется в виде волны, имеющей передний и задний фронты, что выражает принцип Гюйгенса). На плоскости же этот принцип нарушается. Обоснованием этого является тот факт, что носитель возмущения, компактный в R2{\displaystyle \mathbb {R} ^{2}}, уже не будет компактным в R3{\displaystyle \mathbb {R} ^{3}}, а будет образовывать бесконечный цилиндр, и, следовательно, возмущение будет неограниченно во времени (у цилиндрических волн отсутствует задний фронт).^[1]

Решение уравнения колебаний мембраны (двумерного пространства)

utt=a2△u+f{\displaystyle u_{tt}=a^{2}\triangle u+f}

(функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

задаётся формулой:

u(x¯,t)=u(x1,x2,t)=12πa∫0t∬r<a(t−τ)f(y1,y2,τ)dy1dy2dτa2(t−τ)2−(y1−x1)2−(y2−x2)2+∂∂t12πa∬r<atφ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2+12πa∬r<atψ(y1,y2)dy1dy2a2t2−(y1−x1)2−(y2−x2)2{\displaystyle u({\bar {x}},t)=u(x_{1},x_{2},t)={\frac {1}{2\pi a}}\int \limits _{0}^{t}\iint \limits _{r<a(t-\tau )}{\frac {f(y_{1},y_{2},\tau )dy_{1}dy_{2}d\tau }{\sqrt {a^{2}(t-\tau )^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {\partial }{\partial t}}{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\varphi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}+{\frac {1}{2\pi a}}\iint \limits _{r<at}{\frac {\psi (y_{1},y_{2})dy_{1}dy_{2}}{\sqrt {a^{2}t^{2}-(y_{1}-x_{1})^{2}-(y_{2}-x_{2})^{2}}}}}.

Решение одномерного волнового уравнения

utt=a2uxx+f{\displaystyle u_{tt}=a^{2}u_{xx}+f\quad } (функция f(x,t){\displaystyle f(x,t)} соответствует вынуждающей внешней силе)

с начальными условиями

u(x,0)=φ(x),ut(x,0)=ψ(x){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x)}

имеет вид^[2]

u(x,t)=φ(x+at)+φ(x−at)2+12a∫x−atx+atψ(α)dα+12a∫0t∫x−a(t−τ)x+a(t−τ)f(s,τ)dsdτ{\displaystyle u(x,t)={\frac {\varphi (x+at)+\varphi (x-at)}{2}}+{\frac {1}{2a}}\int \limits _{x-at}^{x+at}{\psi (\alpha )d\alpha }+{\frac {1}{2a}}\int \limits _{0}^{t}\int \limits _{x-a(t-\tau )}^{x+a(t-\tau )}f(s,\tau )dsd\tau }

В область II приходят характеристики только из одного семейства

При пользовании формулой Д’Аламбера следует учесть, что иногда решение может не быть единственным во всей рассматриваемой области R1×[0,T]{\displaystyle \mathbb {R} ^{1}\times [0,T]}. Решение волнового уравнения представляется в виде суммы двух функций: u(x,t)=f(x+at)+g(x−at){\displaystyle u(x,t)=f(x+at)+g(x-at)}, то есть оно определяется двумя семействами характеристик: x+at=ξ, x−at=η{\displaystyle x+at=\xi ,\ x-at=\eta }. Пример, показанный на рисунке справа, иллюстрирует волновое уравнение для полубесконечной струны, и начальные условия в нём заданы только на зеленой линии x≥0. Видно, что в область I приходят как ξ-характеристики, так и η-характеристики, в то время как в области II есть только ξ-характеристики. То есть, в области II формула Д’Аламбера не работает.

Применение формул

В общем виде формула Кирхгофа довольно громоздка, а потому решение задач математической физики с её помощью обычно является затруднительным. Однако, можно воспользоваться линейностью волнового уравнения ∂2u∂t2=a2△u+f(x¯,t){\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=a^{2}\triangle u+f({\bar {x}},t)} с начальными условиями u(x¯,0)=φ0(x¯), ut(x¯,0)=φ1(x¯){\displaystyle u({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ u_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}})} и искать решение в виде суммы трех функций: u(x,t)=A(x,t)+B(x,t)+C(x,t){\displaystyle u(x,t)=A(x,t)+B(x,t)+C(x,t)}, которые удовлетворяют следующим условиям:

∂2A∂t2=a2△A+f(x¯,t),A(x¯,0)=0, At(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}A}{\partial t^{2}}}=a^{2}\triangle A+f({\bar {x}},t),\qquad A({\bar {x}},0)=0,\ A_{t}({\bar {x}},0)=0;}

∂2B∂t2=a2△B,B(x¯,0)=φ0(x¯), Bt(x¯,0)=0;{\displaystyle {\frac {\partial ^{2}B}{\partial t^{2}}}=a^{2}\triangle B,\qquad B({\bar {x}},0)=\varphi _{0}({\bar {x}}),\ B_{t}({\bar {x}},0)=0;}

∂2C∂t2=a2△C,C(x¯,0)=0, Ct(x¯,0)=φ1(x¯).{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=a^{2}\triangle C,\qquad C({\bar {x}},0)=0,\ {\mathit {C}}_{t}({\bar {x}},0)=\varphi _{1}({\bar {x}}).}

Сама по себе такая операция не упрощает пользование формулой Кирхгофа, но для некоторых задач оказывается возможным подбор решения, либо сведение многомерной задачи к одномерной путём замены переменных. Например, пусть φ1(x,y,z)=11+(x+3y−2z)2{\displaystyle \varphi _{1}(x,y,z)={\frac {1}{1+(x+3y-2z)^{2}}}}. Тогда после замены ξ=x+3y−2z{\displaystyle \xi =x+3y-2z} уравнение для задачи «С» примет вид:

∂2C∂t2=14a2∂2C∂ξ2,C(ξ,0)=0, Ct(ξ,0)=11+ξ2.{\displaystyle {\frac {\partial ^{2}C}{\partial t^{2}}}=14a^{2}{\frac {\partial ^{2}C}{\partial \xi ^{2}}},\qquad {\mathit {C}}(\xi ,0)=0,\ C_{t}(\xi ,0)={\frac {1}{1+\xi ^{2}}}.}

Таким образом, пришли к одномерному уравнению, а, значит, можно воспользоваться формулой Д’Аламбера:

C(ξ,t)=1214a∫ξ−14atξ+14atdη1+η2=1214a(arctg⁡(ξ+14at)−arctg⁡(ξ−14at)).{\displaystyle C(\xi ,t)={\frac {1}{2{\sqrt {14}}a}}\int \limits _{\xi -{\sqrt {14}}at}^{\xi +{\sqrt {14}}at}{\frac {d\eta }{1+\eta ^{2}}}={\frac {1}{2{\sqrt {14}}a}}\left(\operatorname {arctg} (\xi +{\sqrt {14}}at)-\operatorname {arctg} (\xi -{\sqrt {14}}at)\right).}

В силу четности начального условия, решение сохранит свой вид во всей области t>0{\displaystyle t>0}.

Примечания

Литература

• Михайлов В.П., Михайлова Т.В., Шабунин М.И. Сборник типовых задач по курсу Уравнения математической физики. — М.: МФТИ, 2007. — ISBN 5-7417-0206-6.

Ссылки

Формула Кирхгофа Википедия

Фо́рмула Кирхго́фа — аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного (Формула Пуассона) и одномерного (Формула Д’Аламбера) уравнения.

Полная формулировка задачи и ответа[ | ]

Рассмотрим уравнение

∂2u∂t2−a2△u=f{\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-a^{2}\triangle u=f}, где функции u=u(x,t){\displaystyle u=u(\mathbf {x} ,t)} и f=f(x,t){\displaystyle f=f(\mathbf {x} ,t)} определены на (x,t)∈Rn×R+{\displaystyle (\mathbf {x} ,t)\in \mathbb {R} ^{n}\times \mathbb {R} ^{+}}, а △{\displaystyle \triangle } — оператор Лапласа.

Это уравнение определяет распространение бегущей волны в n-мерной однородной среде со скоростью a{\displaystyle a} в моменты времени t>0{\displaystyle t>0}.

Для того, чтобы решение было однозначным, необходимо определить начальные условия. Начальные условия определяют состояние пространства (или, говорят, «начальное возмущение») в момент времени t=0{\displaystyle t=0}:

u|t=0=φ0(x¯),∂u∂t|t=0=φ1(x¯){\displaystyle u|_{t=0}=\varphi _{0}({\bar {x}}),\q

Закон Кирхгофа (химия) — Википедия

У этого термина существуют и другие значения, см. Закон Кирхгофа.

Закон Кирхгофа гласит, что температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции. Уравнение Кирхгофа, являющееся следствием этого закона, используется для расчёта тепловых эффектов при разных температурах.

Дифференциальная форма закона:

(d(ΔrH)dT)p=Δrcp{\displaystyle \left({\frac {d(\Delta _{r}H)}{dT}}\right)_{p}=\Delta _{r}c_{p}}

(d(ΔrU)dT)V=ΔrcV{\displaystyle \left({\frac {d(\Delta _{r}U)}{dT}}\right)_{V}=\Delta _{r}c_{V}}

Интегральная форма закона:

ΔrHT2=ΔHT1+∫T1T2Δrcp(T)dT{\displaystyle \Delta _{r}H_{T_{2}}=\Delta H_{T_{1}}+\int \limits _{T_{1}}^{T_{2}}\Delta _{r}c_{p}(T)dT}

ΔrUT2=ΔUT1+∫T1T2ΔrcV(T)dT{\displaystyle \Delta _{r}U_{T_{2}}=\Delta U_{T_{1}}+\int \limits _{T_{1}}^{T_{2}}\Delta _{r}c_{V}(T)dT}

где Cp{\displaystyle C_{p}} и CV{\displaystyle C_{V}} — изобарная и изохорная теплоёмкости, Δrcp{\displaystyle \Delta _{r}c_{p}} — разность изобарных теплоёмкостей продуктов реакции и исходных веществ, ΔrcV{\displaystyle \Delta _{r}c_{V}} — разность изохорных теплоёмкостей продуктов реакции и исходных веществ, а ΔrH{\displaystyle \Delta _{r}H} и ΔrU{\displaystyle \Delta _{r}U} — соответствующие тепловые эффекты.

Если разница (T2−T1){\displaystyle (T_{2}-T_{1})} невелика, то можно принять Δrcp=const{\displaystyle \Delta _{r}c_{p}=const} и ΔrcV=const{\displaystyle \Delta _{r}c_{V}=const}, соответственно интегральная форма уравнений примет следующий вид:

ΔrHT2=ΔHT1+ΔrCp(T2−T1){\displaystyle \Delta _{r}H_{T_{2}}=\Delta H_{T_{1}}+\Delta _{r}C_{p}(T_{2}-T_{1})}

ΔrUT2=ΔUT1+ΔrCV(T2−T1){\displaystyle \Delta _{r}U_{T_{2}}=\Delta U_{T_{1}}+\Delta _{r}C_{V}(T_{2}-T_{1})}

При большой разнице температур необходимо учитывать температурные зависимости теплоёмкостей: Δrcp=f(T){\displaystyle \Delta _{r}c_{p}=f(T)} и ΔrcV=f(T){\displaystyle \Delta _{r}c_{V}=f(T)}

• Химическая энциклопедия / Редкол.: Кнунянц И.Л. и др.. — М.: Советская энциклопедия, 1990. — Т. 2 (Даф-Мед). — 671 с. — ISBN 5-82270-035-5.

• Закон Кирхгофа — конспект лекций