6.5. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений
6.5.1. Общие сведения
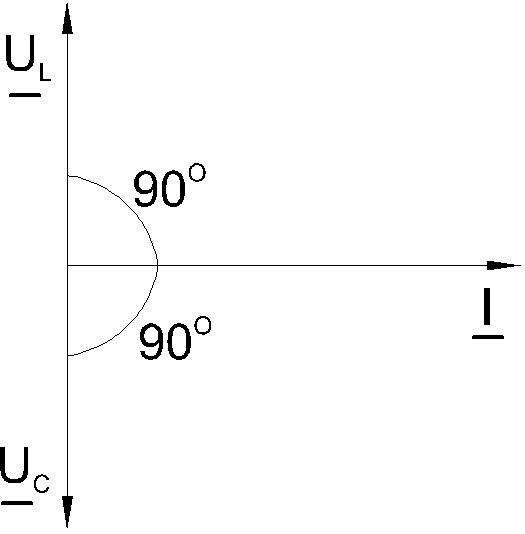
Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсатореUCотстает от токаIна 900, а напряжение на катушке индуктивностиULопережает ток на 900. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 1800).
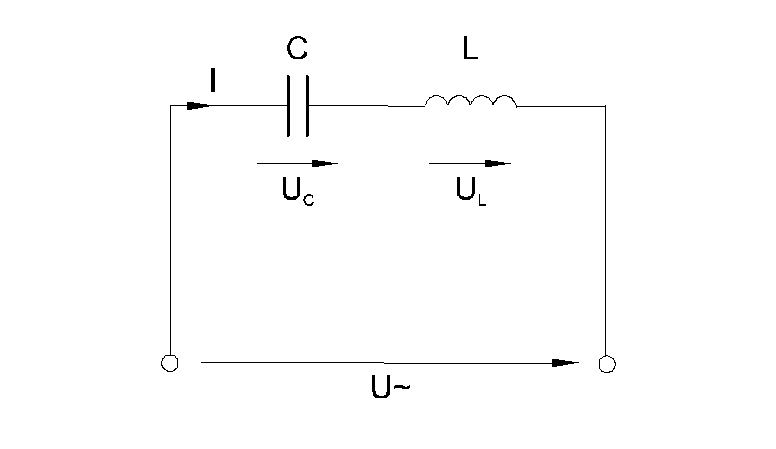
Рис. 6.5.1
Когда одно из напряжений больше другого,
цепь оказывается либо преимущественно
индуктивной (рис. 6.5.2), либо преимущественно
емкостной (рис. 6.5.3). Если напряжения U
|
|
|
Рис. 6.5.2 | Рис. 6.5.3 | Рис. 6.5.4 |
При резонансе напряжений реактивное сопротивление цепи
X = XL – XC
оказывается равным нулю. При заданных значениях LиCрезонанс может быть получен путем изменения частоты.
Поскольку XL=L, аXC= 1 /C, то резонансная частота
0L – 1 / 0C = 0,
откуда
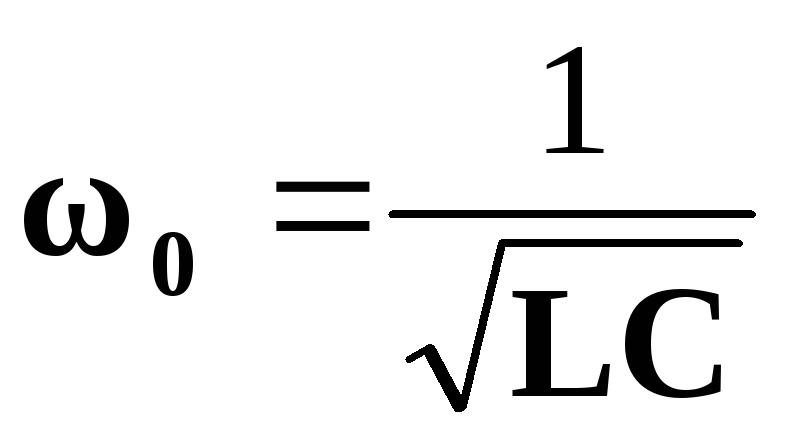 и
и .
.
Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения U
6.5.2. Экспериментальная часть Задание
Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока Iи напряженийU,UC,UL при = 0, <0 и >0. Постройте векторные диаграммы.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.5.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
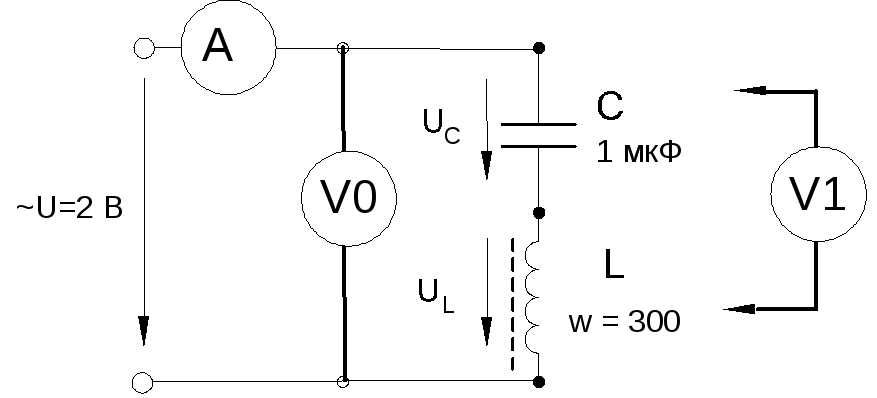
Рис. 6.5.5
Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному току. Для точной настройки по максимуму тока необходимо поддерживать неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входными напряжением и током. Тогда нет необходимости поддерживать входное напряжение неизменным.
Произведите измерения и запишите в табл. 6.5.1 результаты измерений при резонансе f=f0 при f1 0,75f0 и f2 1,25f0.
Таблица 6.5.1
f, Гц
I, мА
U, B
UC, B
f0 =
f1 =
f2 =
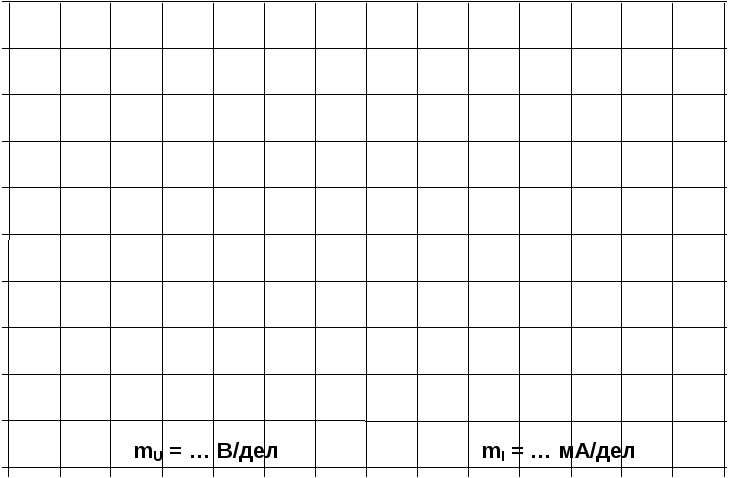
Рис. 6.5.6
Задачи для схемы с последовательным соединением катушки и конденсатором с решением
Пример решения
Теоретический материал для решения задач.
Задача 14,1
Конденсатор емкостью С = 3,4 мкФ и катушка с активным сопротивлением R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к генератору с напряжением U = 200 В (рис. 14.6).

Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и трех значениях частоты: f=fp;
f<fp; f>fр. где fр — резонансная частота.
Решение.
Для примера далее приведен расчет при частоте f = 250 Гц.
Реактивное сопротивление индуктивности





Сделать аналогичный подсчет для f=fp; f<fp; f>fр
Задача решается легко оставляйте свои ответы в комментариях.
Задача 14,2
В сеть переменного тока частотой 50 Гц включены последовательно катушка с активным R = 30 Ом и индуктивным XL = 50 Ом сопротивлениями и конденсатор с емкостью С = 318 мкФ. Напряжение на конденсаторе Uc = 100 В.
Определить ток в цепи, напряжение на катушке и в сети, активную и реактивную мощности цепи. Построить векторную диаграмму.
Оставляем свои ответы в комментариях

 Загрузка …
Загрузка …6.7. Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока
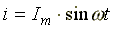 .
.
Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа,
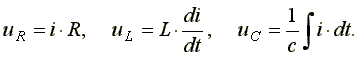 (7.15)
(7.15)
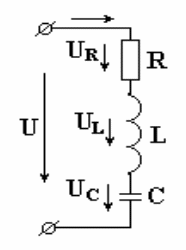
Рис. 7.8
Подставим эти формулы в уравнение (7.15). Получим:
 (7.16)
(7.16)
Из выражения (7.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение (7.16) в комплексной форме:
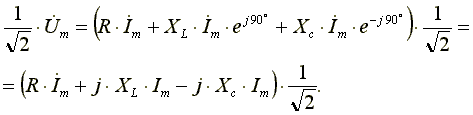 (7.17)
(7.17)
Поделим левую и правую части уравнения (7.17) на √2. Получим уравнение для комплексов действующих значений токов и напряжений
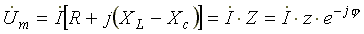 ,
(7.18)
,
(7.18)
Где 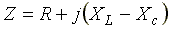 — комплексное сопротивление цепи;
— комплексное сопротивление цепи;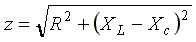 — модуль комплексного сопротивления,
или полное сопротивление цепи;
— модуль комплексного сопротивления,
или полное сопротивление цепи;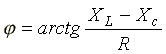 —
начальная фаза комплексного сопротивления.
—
начальная фаза комплексного сопротивления.
При построении векторных диаграмм цепи рассмотрим три случая.
XL> XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока(рис.7.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.7.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.7.11).
Ток в резонансном режиме достигает максимума, так как полное сопротивление
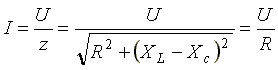
Условие возникновения резонанса:
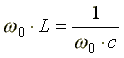 ,
,
отсюда резонансная частота равна
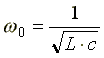 .
.
Из формулы следует, что режима резонанса можно добиться следующими способами:
— изменением частоты;
— изменением индуктивности;
— изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0(а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
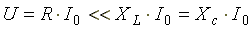 .
.
 Рис. 7.9
Рис. 7.10 Рис. 7.11
Рис. 7.9
Рис. 7.10 Рис. 7.11
7.8. Параллельно соединенные индуктивность, емкость и активное сопротивление в цепи синусоидального тока
К схеме на рис. 7.12 подключено синусоидальное
напряжение 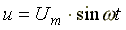 .
Схема состоит из параллельно включенных
индуктивности, емкости и активного
сопротивления.
Определим ток на входе
схемы.
.
Схема состоит из параллельно включенных
индуктивности, емкости и активного
сопротивления.
Определим ток на входе
схемы.
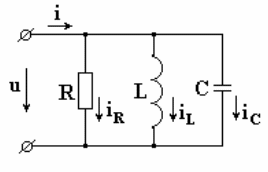
Рис. 7.12
В соответствии с первым законом Кирхгофа:
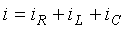 ,
(7.19)
,
(7.19)
где 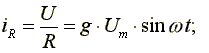
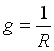 — активная проводимость.
— активная проводимость.
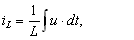
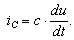
Подставим эти формулы в уравнение (7.19). Получим:
 ,
(7.20)
,
(7.20)
Где 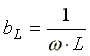 — индуктивная проводимость;
— индуктивная проводимость; — емкостная проводимость.
— емкостная проводимость.
Из уравнения (7.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90o. Запишем уравнение (6.20) в комплексной форме.
 ,
(7.21)
,
(7.21)
где 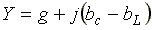 — комплексная проводимость;
— комплексная проводимость; — полная проводимость;
— полная проводимость; — начальная фаза комплексной
проводимости.
— начальная фаза комплексной
проводимости.
Построим векторные диаграммы, соответствующие комплексному уравнению (7.21).
 Рис. 7.13
Рис. 7.14 Рис. 7.15
Рис. 7.13
Рис. 7.14 Рис. 7.15
В схеме на рис.
7.12может возникнуть режим
резонанса токов. Резонанс токов возникает
тогда, когда индуктивная и емкостная
проводимости одинаковы. При этом
индуктивный и емкостный токи, направленные
в противоположные стороны, полностью
компенсируют друг друга. Ток в
неразветвленной части схемы совпадает
по фазе с напряжением.
Из условия
возникновения резонанса тока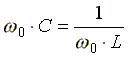 получим
формулу для резонансной частоты тока
получим
формулу для резонансной частоты тока
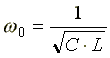 .
.
В режиме резонанса тока полная проводимость
цепи 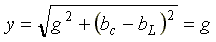 —
минимальна, а полное сопротивление
—
минимальна, а полное сопротивление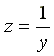 —
максимально. Ток в неразветвленной
части схемы
—
максимально. Ток в неразветвленной
части схемы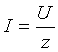 в
резонансном режиме имеет минимальное
значение. В идеализированном случае R
= 0,
в
резонансном режиме имеет минимальное
значение. В идеализированном случае R
= 0,
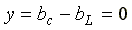 и
и .
.
Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.
Последовательное соединение резистора, конденсатора и катушки индуктивности
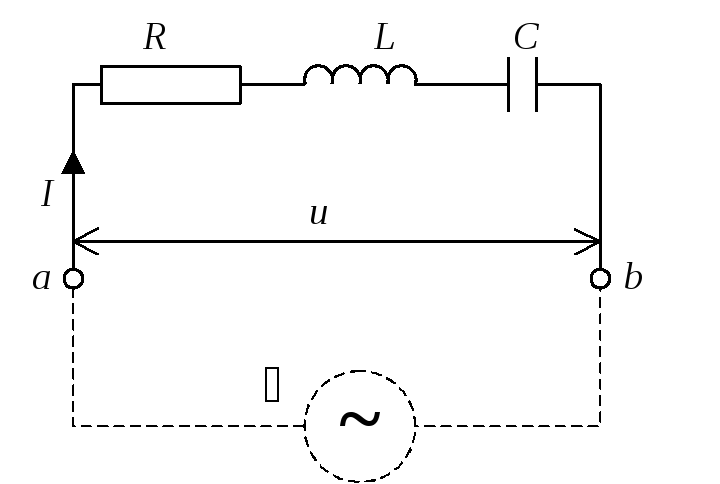
Пользуясь полученными выше результатами, можно найти соотношения между колебаниями тока и напряжения в любой цепи. Рассмотрим последовательное соединение резистора, конденсатора и катушки индуктивности (рис. 8.).
Рис.8. Последовательное соединение резистора, конденсатора и катушки индуктивности |
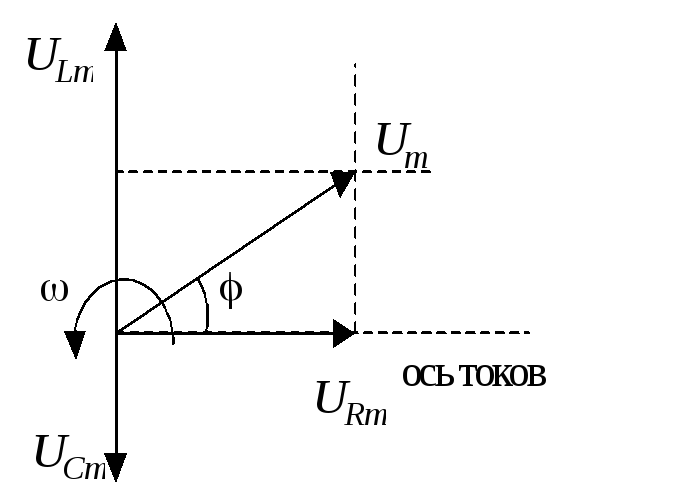
Рис.9. Векторная диаграмма |
Положим по-прежнему, что ток в цепи изменяется по закону
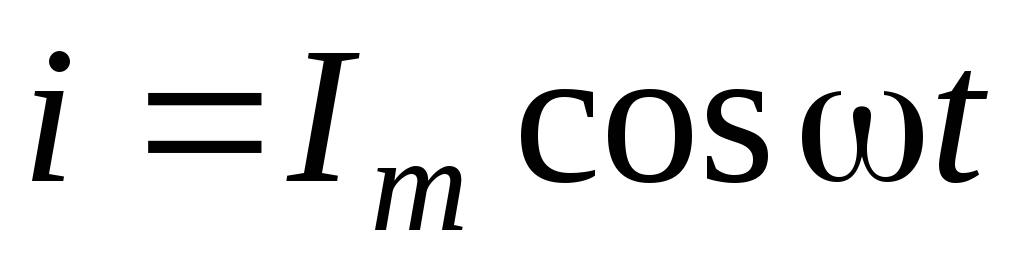 ,
,
и
вычислим напряжение между концами цепи u.
Так как при последовательном соединении
проводников складываются напряжения,
то искомое напряжение u есть сумма
трех напряжений: на сопротивлении 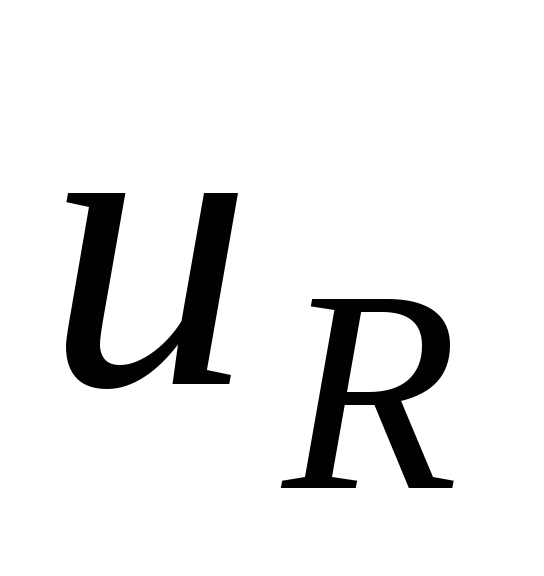 ,
на емкости
,
на емкости 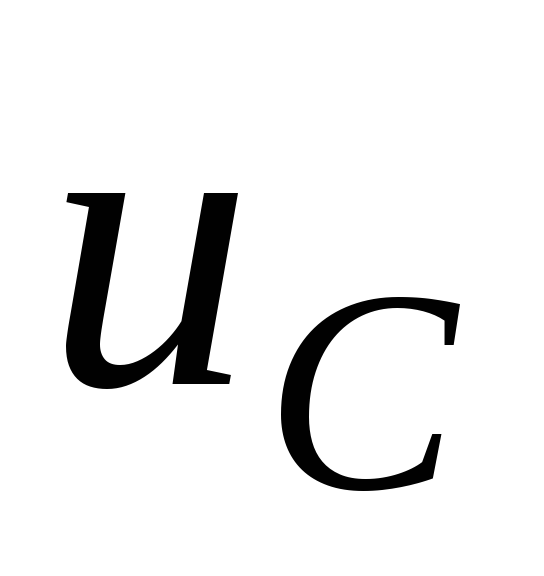 и на
индуктивности
и на
индуктивности 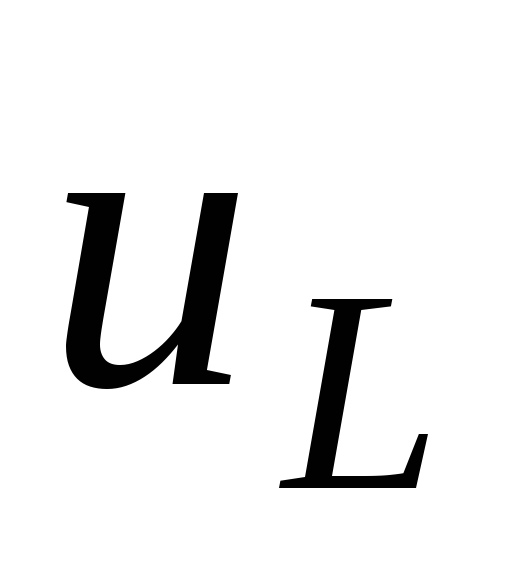 ,
причем каждое из этих напряжений, как
мы видели, изменяется со временем по
закону косинуса:
,
причем каждое из этих напряжений, как
мы видели, изменяется со временем по
закону косинуса:
 ,
(5)
,
(5)
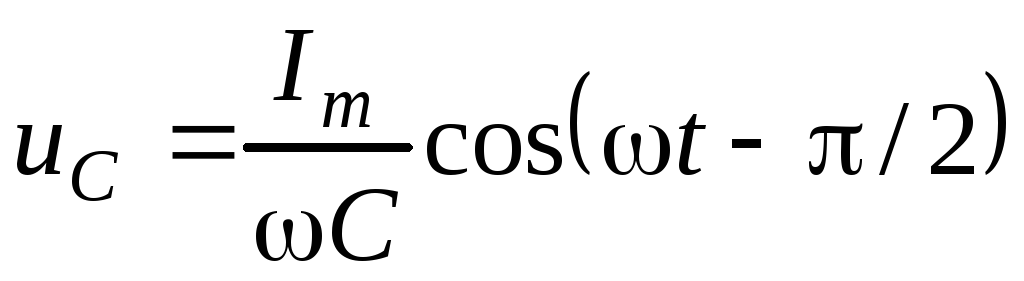 ,
(6)
,
(6)
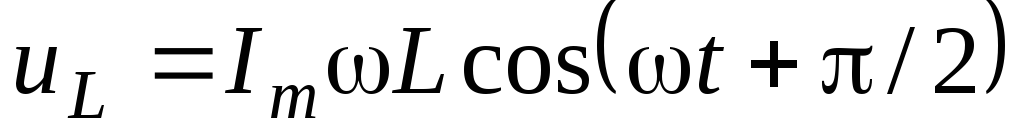 .
(7)
.
(7)
Для
сложения этих трех колебаний воспользуемся
векторной диаграммой напряжений.
Колебания напряжения на сопротивлении
изображаются на ней вектором 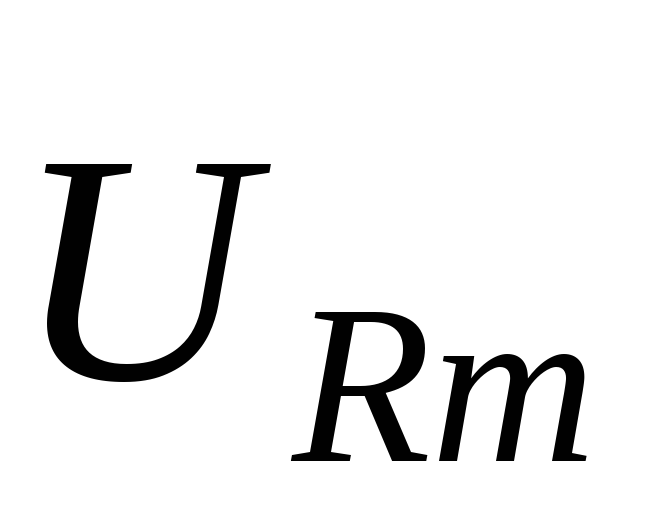 ,
направленным вдоль оси токов и имеющим
длину
,
направленным вдоль оси токов и имеющим
длину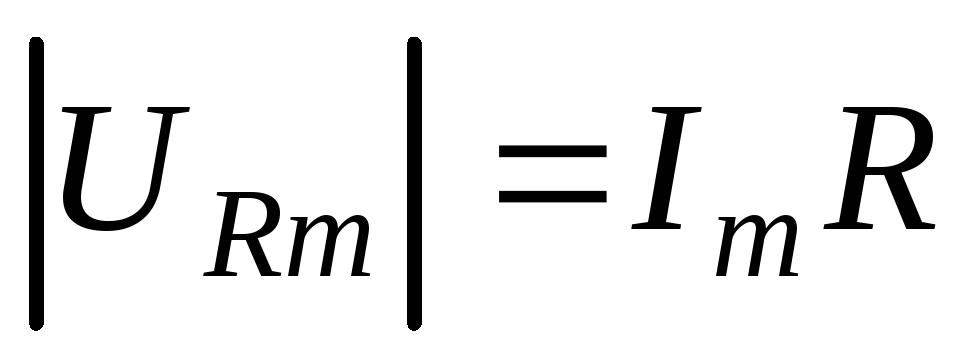 ,
колебания же напряжений на емкости и
индуктивности — векторами
,
колебания же напряжений на емкости и
индуктивности — векторами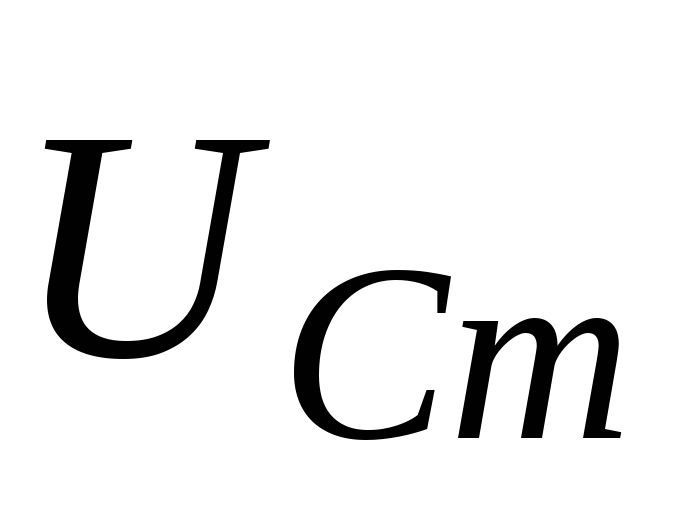 и
и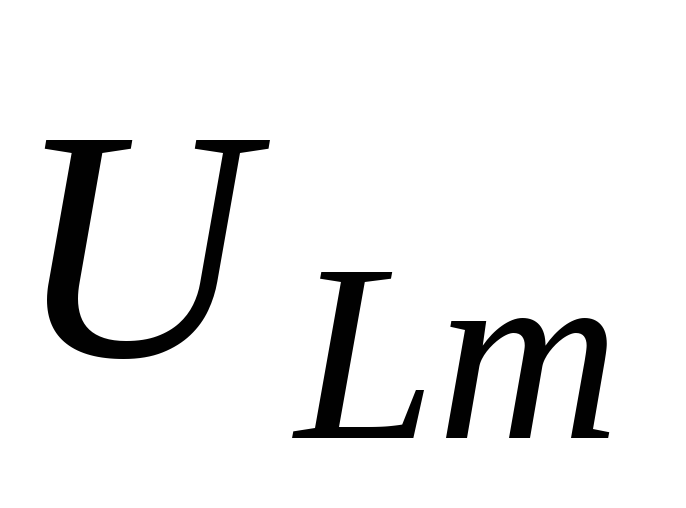 ,
перпендикулярными к оси токов, с длинами
(Im/C)
и (ImL)
(рис.9.).
Представим себе, что эти векторы вращаются
против часовой стрелки вокруг общего
начала с угловой скоростью .
Тогда проекции на ось токов векторов
,
перпендикулярными к оси токов, с длинами
(Im/C)
и (ImL)
(рис.9.).
Представим себе, что эти векторы вращаются
против часовой стрелки вокруг общего
начала с угловой скоростью .
Тогда проекции на ось токов векторов  ,
,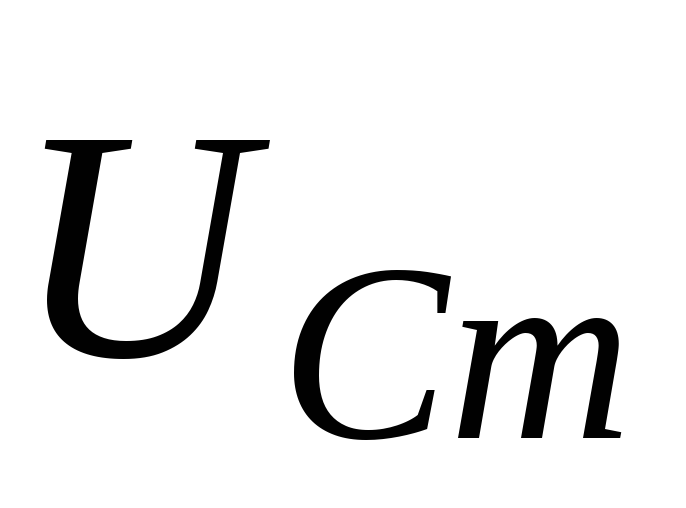 и
и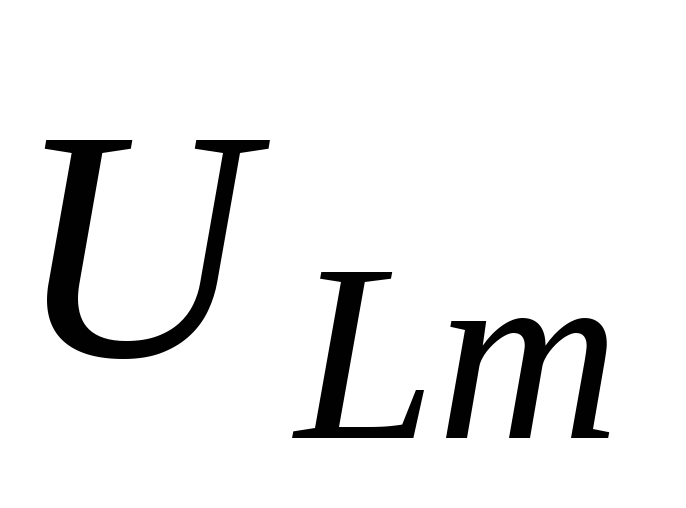 ,
будут описываться соответственно
формулами (5)-(7). Очевидно, что проекция
на ось токов суммарного вектора
,
будут описываться соответственно
формулами (5)-(7). Очевидно, что проекция
на ось токов суммарного вектора
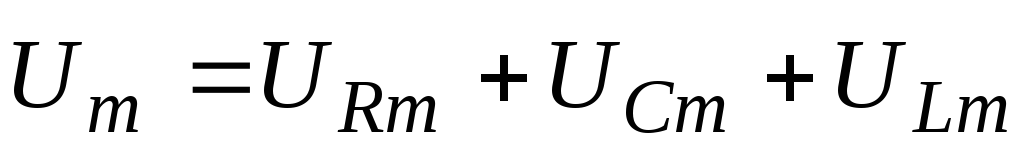
равна
сумме 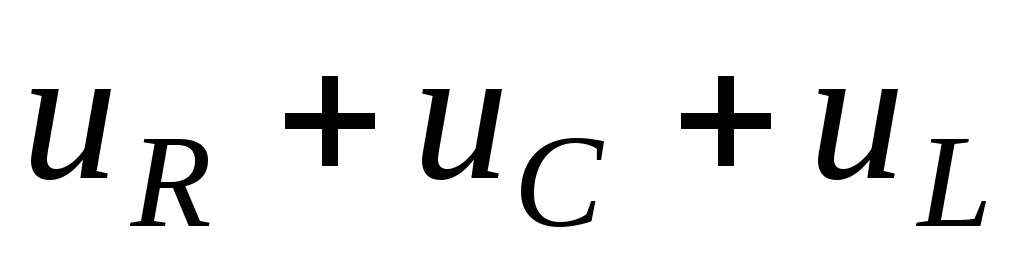 , то
есть равна общему напряжению на участке
цепи. Максимальное значение этого
напряжения равно модулю вектора
, то
есть равна общему напряжению на участке
цепи. Максимальное значение этого
напряжения равно модулю вектора 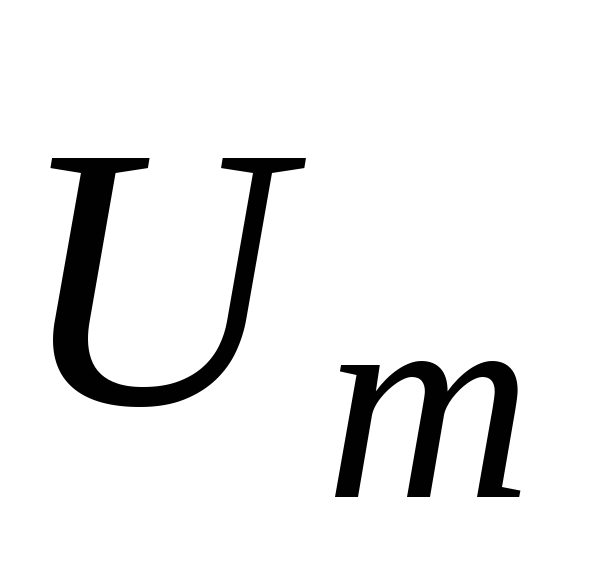 .
Эта величина легко определяется
геометрически. Сначала целесообразно
найти модуль вектора
.
Эта величина легко определяется
геометрически. Сначала целесообразно
найти модуль вектора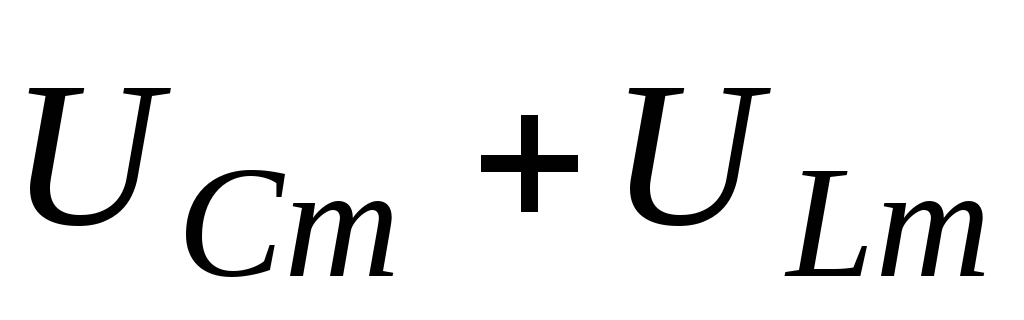 :
:
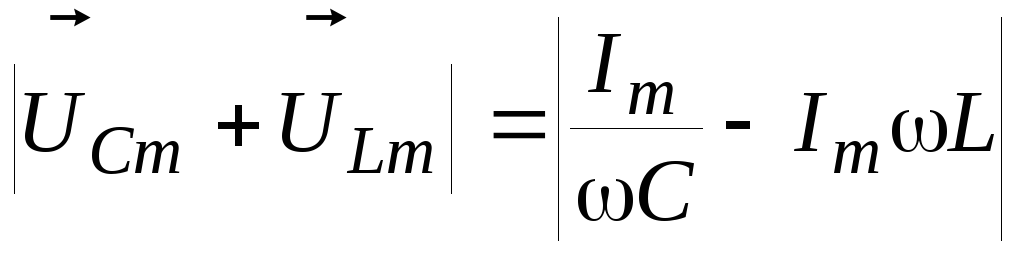 ,
,
а затем по теореме Пифагора:
 .
(8)
.
(8)
Из рисунка также видно, что
 .
(9)
.
(9)
Для напряжения на участке цепи можно записать
 ,
,
где
амплитуда напряжения и фазовый сдвиг
между током и напряжением определяются
формулами (8), (9). Если 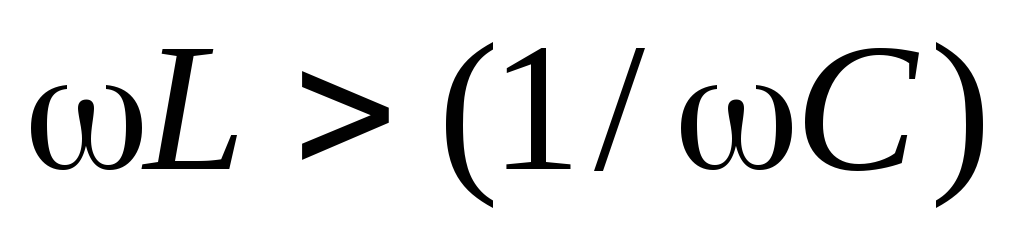 ,
то напряжение по фазе опережает ток, в
противном случае — напряжение отстает
по фазе.
,
то напряжение по фазе опережает ток, в
противном случае — напряжение отстает
по фазе.
Формула
(8) имеет сходство с законом Ома в том
смысле, что амплитуда напряжения
пропорциональна амплитуде тока. Поэтому
ее иногда называют законом Ома для
переменного тока. Однако нужно помнить,
что эта формула относится только к
амплитудам, но не к мгновенным значениям 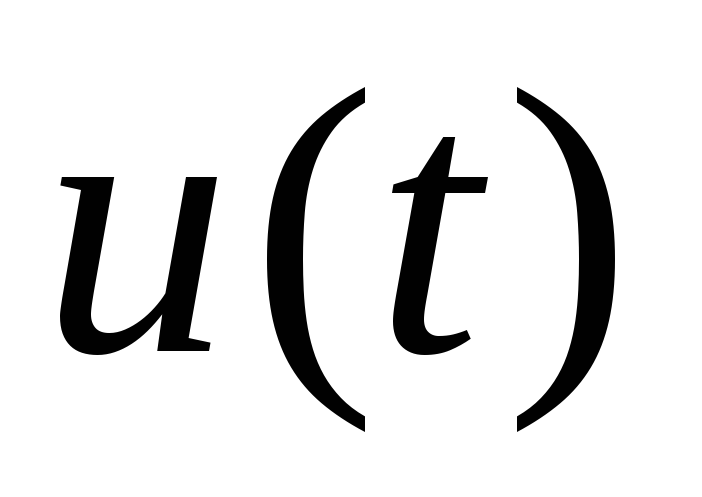 и
и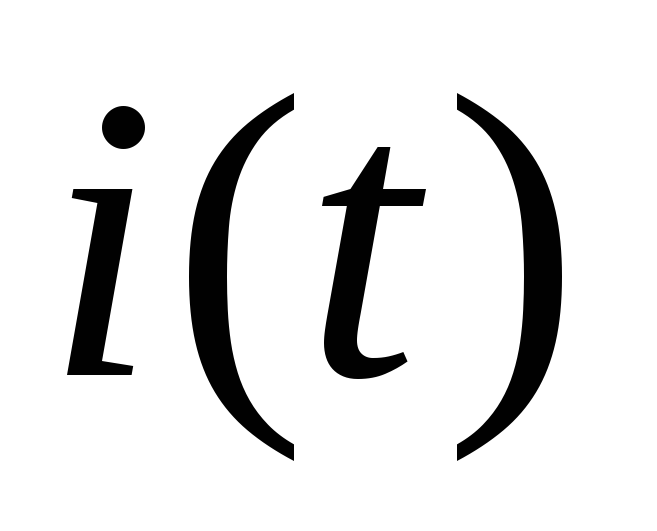 .
Величину
.
Величину

называют сопротивлением цепи для переменного тока, величину
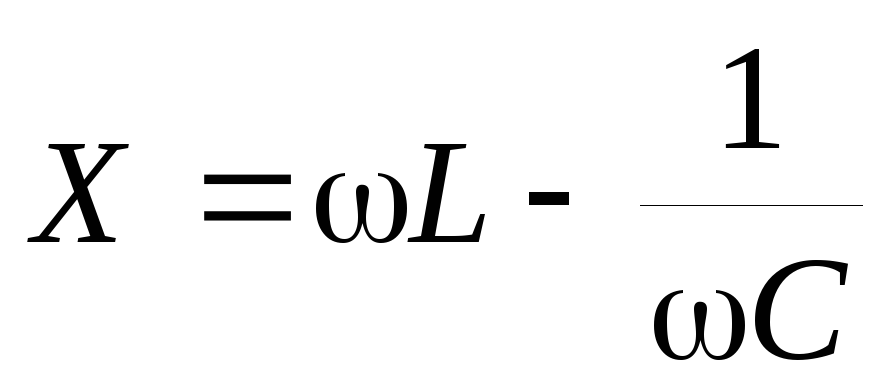
называют реактивным сопротивлением цепи, а величину R — активным сопротивлением.
Полученные
формулы справедливы и для замкнутой
цепи, включающей в себя генератор
переменного напряжения, если под R, C и L понимать их значения для всей цепи
(например R представляет собой суммарное активное
сопротивление цепи, включая и внутреннее
сопротивление генератора). В этом случае
во всех формулах следует заменить u на ЭДС генератора.
Действительно,
для всех наших рассуждений было
безразлично, в каком именно месте
сосредоточены емкость, индуктивность
и сопротивление, поэтому в замкнутой
цепи (рис.8) мы можем считать, что  представляет собой суммарное активное
сопротивление цепи, включая и внутреннее
сопротивление генератора, а
представляет собой суммарное активное
сопротивление цепи, включая и внутреннее
сопротивление генератора, а и
и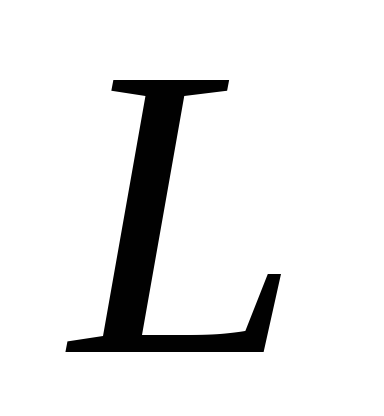 — емкость и индуктивность цепи, и заменить
реальный генератор воображаемым, у
которого внутреннее сопротивление
равно нулю. При этом напряжениеu между точками a и b будет равно ЭДС генератора
— емкость и индуктивность цепи, и заменить
реальный генератор воображаемым, у
которого внутреннее сопротивление
равно нулю. При этом напряжениеu между точками a и b будет равно ЭДС генератора  .
Отсюда следует, что формулы (8), (9)
справедливы и для замкнутой цепи
переменного тока, если под
.
Отсюда следует, что формулы (8), (9)
справедливы и для замкнутой цепи
переменного тока, если под ,
, ,
и
,
и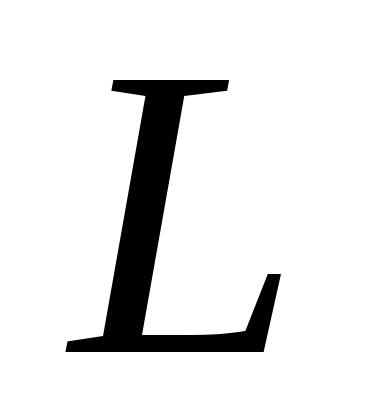 понимать их значения для всей цепи и
заменить во всех формулахu на ЭДС генератора
понимать их значения для всей цепи и
заменить во всех формулахu на ЭДС генератора  .
.
6.7. Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока
Катушка с активным сопротивлением Rи индуктивностьюLи конденсатор емкостьюСвключены последовательно(рис.7.8). В схеме протекает синусоидальный ток
 .
.
Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа,
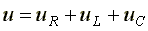
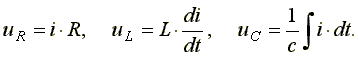 (7.15)
(7.15)
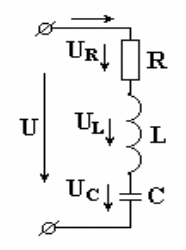
Рис. 7.8
Подставим эти формулы в уравнение (7.15). Получим:
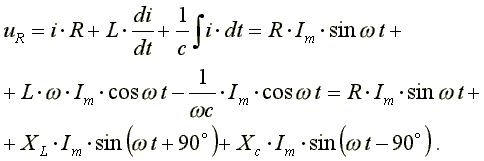 (7.16)
(7.16)
Из выражения (7.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o. Запишем уравнение (7.16) в комплексной форме:
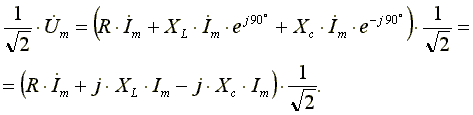 (7.17)
(7.17)
Поделим левую и правую части уравнения (7.17) на √2. Получим уравнение для комплексов действующих значений токов и напряжений
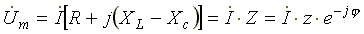 ,
(7.18)
,
(7.18)
Где 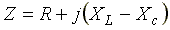 — комплексное сопротивление цепи;
— комплексное сопротивление цепи;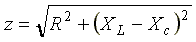 — модуль комплексного сопротивления,
или полное сопротивление цепи;
— модуль комплексного сопротивления,
или полное сопротивление цепи;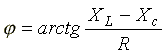 —
начальная фаза комплексного сопротивления.
—
начальная фаза комплексного сопротивления.
При построении векторных диаграмм цепи рассмотрим три случая.
XL> XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока(рис.7.9).
Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.7.10).
Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.7.11).
Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

Условие возникновения резонанса:
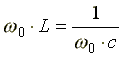 ,
,
отсюда резонансная частота равна
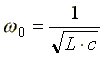 .
.
Из формулы следует, что режима резонанса можно добиться следующими способами:
— изменением частоты;
— изменением индуктивности;
— изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0(а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
 .
.
 Рис. 7.9
Рис. 7.10 Рис. 7.11
Рис. 7.9
Рис. 7.10 Рис. 7.11
7.8. Параллельно соединенные индуктивность, емкость и активное сопротивление в цепи синусоидального тока
К схеме на рис. 7.12 подключено синусоидальное
напряжение 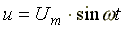 .
Схема состоит из параллельно включенных
индуктивности, емкости и активного
сопротивления.
Определим ток на входе
схемы.
.
Схема состоит из параллельно включенных
индуктивности, емкости и активного
сопротивления.
Определим ток на входе
схемы.
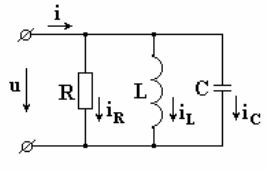
Рис. 7.12
В соответствии с первым законом Кирхгофа:
 ,
(7.19)
,
(7.19)
где 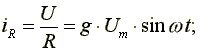
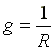 — активная проводимость.
— активная проводимость.

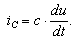
Подставим эти формулы в уравнение (7.19). Получим:
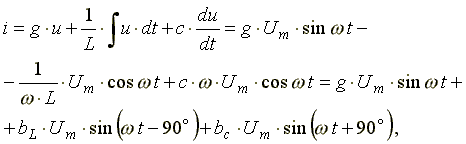 ,
(7.20)
,
(7.20)
Где 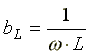 — индуктивная проводимость;
— индуктивная проводимость;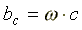 — емкостная проводимость.
— емкостная проводимость.
Из уравнения (7.20) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90o. Запишем уравнение (6.20) в комплексной форме.
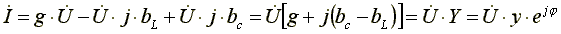 ,
(7.21)
,
(7.21)
где 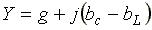 — комплексная проводимость;
— комплексная проводимость;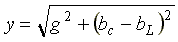 — полная проводимость;
— полная проводимость;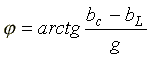 — начальная фаза комплексной
проводимости.
— начальная фаза комплексной
проводимости.
Построим векторные диаграммы, соответствующие комплексному уравнению (7.21).
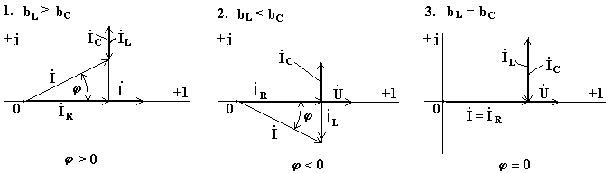 Рис. 7.13
Рис. 7.14 Рис. 7.15
Рис. 7.13
Рис. 7.14 Рис. 7.15
В схеме на рис. 7.12может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. Из условия возникновения резонанса токаполучим формулу для резонансной частоты тока
 .
.
В режиме резонанса тока полная проводимость
цепи 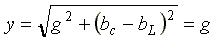 —
минимальна, а полное сопротивление
—
минимальна, а полное сопротивление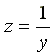 —
максимально. Ток в неразветвленной
части схемы
—
максимально. Ток в неразветвленной
части схемы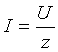 в
резонансном режиме имеет минимальное
значение. В идеализированном случае R
= 0,
в
резонансном режиме имеет минимальное
значение. В идеализированном случае R
= 0,
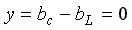 и
и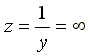 .
.
Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр — пробкой.
Параллельное включение конденсатора и катушки индуктивности в цепь переменного тока
Параллельное включение конденсатора и катушки индуктивности в цепь переменного тока
Рассмотрим явления в цепи переменного тока, содержащей генератор, конденсатор и катушку индуктивности, соединенные параллельно. Предположим при этом, что активным сопротивлением цепь не обладает.
Очевидно, в такой цепи напряжение как на катушке, так и на конденсаторе в любой момент времени равно напряжению, развиваемому генератором.
Общий же ток в цепи слагается из токов в ее разветвлениях. Ток в индуктивной ветви отстает по фазе от напряжения на четверть периода, а ток в емкостной ветви опережает его на те же четверть периода. Поэтому токи в ветвях в любой момент времени оказываются сдвинутыми по фазе один относительно другого на полупериода, т. е. находятся в противофазе. Таким образом токи в ветвях в любой момент времени направлены навстречу один другому, а общий ток в неразветвленной части цепи равен разности их.
Это дает нам право написать равенство I = IL -IC
где I — действующее значение общего тока в цепи, IL и IC — действующие значения токов в.ветвях.
Пользуясь законом Ома для определения действующих значений тока в ветвях, получим:
Il = U / XL и IC = U / XC
Если в цепи преобладает индуктивное сопротивление, т. е. XL больше XC, ток в катушке меньше тока в конденсаторе; следовательно, ток в неразветвленном участке цепи носит емкостный характер, и цепь в целом для генератора будет емкостной. И, наоборот, при ХC большем XL, ток в конденсаторе меньше тока в катушке; следовательно, ток в неразветвленном участке цепи имеет индуктивный характер, и цепь в целом для генератора будет индуктивной.
При этом не следует забывать, что в том и другом случае нагрузка реактивная, т. е. цепь не потребляет энергии генератора.
Резонанс токов
Рассмотрим теперь случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC.
Если мы, как и прежде, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов.
При резонансе токов действующие значения токов в каждом разветвлении, определяемые отношениями IL = U / XL и IC= U / XC будут равны между собой, так XL = ХC.
Вывод, к которому мы пришли, может показаться на первый взгляд довольно странным. Действительно, генератор нагружен двумя сопротивлениями, а тока в неразветвленной части цепи нет, тогда как в самих сопротивлениях протекают равные и притом наибольшие по величине токи.
Объясняется это поведением магнитного поля катушки и электрического поля конденсатора. При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор.
Таким образом, и при параллельном соединении катушки индуктивности и конденсатора мы получили колебательный контур, отличающийся от описанного выше только тем, что генератор, создающий колебания, не включен непосредственно в контур и контур получается замкнутым.
Графики токов, напряжения и мощности в цепи при резонансе токов: а — активное сопротивление равно нулю, цепь мощности не потребляет; б — цепь обладает активным сопротивлением, в неразветвленной части цепи появился ток, цепь потребляет мощность
Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства:
ωL = 1 / ωC
Следовательно:
fрез = 1 / 2π√LC
Lрез = 1 / ω2С
Срез = 1 / ω2L
Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. е. превратить цепь в колебательный контур.
Итак, мы получили замкнутый колебательный контур, в котором можно вызвать электрические колебания, т. е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии — генератор переменного тока.
В цепях несинусоидального тока резонансные режимы возможны для различных гармоничных состовляющих.
Резонанс токов широко используется в практике.Явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту. Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции. Колебательный контур, работающий в режиме резонанса токов, является одним из основных узловэлектронных генераторов.
Если в цепь переменного тока включены последовательно катушка индуктивности иконденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением.
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Применив к этой цепи закон Ома, получим:
Формулу эту можно преобразовать следующим образом:
В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать:
Резонанс напряжений
Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой последовательно, то резонанс в такой цепи называется последовательным резонансом или резонансом напряжений. Характерная черта резонанса напряжений — значительные напряжения на емкости и на индуктивности, по сравнению с ЭДС источника.
Причина появления такой картины очевидна. На активном сопротивлении по закону Ома будет напряжение Ur, на емкости Uc, на индуктивности Ul, и составив отношение Uc к Ur можно найти величину добротности Q. Напряжение на емкости будет в Q раз больше ЭДС источника, такое же напряжение окажется приложенным к индуктивности.
То есть резонанс напряжений приводит к возрастанию напряжения на реактивных элементах в Q раз, а резонансный ток будет ограничен ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, сопротивление последовательного контура на резонансной частоте минимально.
Резонанс токов
Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой параллельно, то резонанс в такой цепи называется параллельным резонансом или резонансом токов. Характерная черта резонанса токов — значительные токи через емкость и индуктивность, по сравнению с током источника.
Причина появления такой картины очевидна. Ток через активное сопротивление по закону Ома будет равен U/R, через емкость U/XC, через индуктивность U/XL, и составив отношение IL к I можно найти величину добротности Q. Ток через индуктивность будет в Q раз больше тока источника, такой же ток будет течь каждые пол периода в конденсатор и из него.
То есть резонанс токов приводит к возрастанию тока через реактивные элементы в Q раз, а резонансная ЭДС будет ограничена ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, на резонансной частоте сопротивление параллельного колебательного контура максимально.
Применение резонанса токов
Аналогично резонансу напряжений, резонанс токов применяется в различных фильтрах. Но включенный в цепь, параллельный контур действует наоборот, чем в случае с последовательным: установленный параллельно нагрузке, параллельный колебательный контур позволит току резонансной частоты контура пройти в нагрузку, поскольку сопротивление самого контура на собственной резонансной частоте максимально.
Установленный последовательно с нагрузкой, параллельный колебательный контур не пропустит сигнал резонансной частоты, поскольку все напряжение упадет на контуре, а на нагрузку придется мизерная доля сигнала резонансной частоты.
Так, основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты.
В электротехнике резонанс токов используется с целью достижения высокого коэффициента мощности нагрузок, обладающих значительными индуктивными и емкостными составляющими.
Например, установки компенсации реактивной мощности (КРМ) представляют собой конденсаторы, подключаемые параллельно обмоткам асинхронных двигателей и трансформаторов, работающих под нагрузкой ниже номинальной.
К таким решениям прибегают как раз с целью достижения резонанса токов (параллельного резонанса), когда индуктивное сопротивление оборудования делается равным емкостному сопротивлению подключаемых конденсаторов на частоте сети, чтобы реактивная энергия циркулировала между конденсаторами и оборудованием, а не между оборудованием и сетью; чтобы сеть отдавала энергию только тогда, когда оборудование нагружено и потребляет активную мощность.
Когда же оборудование работает в холостую, сеть оказывается подключена параллельно резонансному контуру (внешние конденсаторы и индуктивность оборудования), который представляет для сети очень большое комплексное сопротивление и позволяет снизитьсякоэффициенту мощности.
ЛитератураПравить
§ Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 928.
§ Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Параллельное включение конденсатора и катушки индуктивности в цепь переменного тока
Рассмотрим явления в цепи переменного тока, содержащей генератор, конденсатор и катушку индуктивности, соединенные параллельно. Предположим при этом, что активным сопротивлением цепь не обладает.
Очевидно, в такой цепи напряжение как на катушке, так и на конденсаторе в любой момент времени равно напряжению, развиваемому генератором.
Общий же ток в цепи слагается из токов в ее разветвлениях. Ток в индуктивной ветви отстает по фазе от напряжения на четверть периода, а ток в емкостной ветви опережает его на те же четверть периода. Поэтому токи в ветвях в любой момент времени оказываются сдвинутыми по фазе один относительно другого на полупериода, т. е. находятся в противофазе. Таким образом токи в ветвях в любой момент времени направлены навстречу один другому, а общий ток в неразветвленной части цепи равен разности их.
Это дает нам право написать равенство I = IL -IC
где I — действующее значение общего тока в цепи, IL и IC — действующие значения токов в.ветвях.
Пользуясь законом Ома для определения действующих значений тока в ветвях, получим:
Il = U / XL и IC = U / XC
Если в цепи преобладает индуктивное сопротивление, т. е. XL больше XC, ток в катушке меньше тока в конденсаторе; следовательно, ток в неразветвленном участке цепи носит емкостный характер, и цепь в целом для генератора будет емкостной. И, наоборот, при ХC большем XL, ток в конденсаторе меньше тока в катушке; следовательно, ток в неразветвленном участке цепи имеет индуктивный характер, и цепь в целом для генератора будет индуктивной.
При этом не следует забывать, что в том и другом случае нагрузка реактивная, т. е. цепь не потребляет энергии генератора.
Резонанс токов
Рассмотрим теперь случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC.
Если мы, как и прежде, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов.
При резонансе токов действующие значения токов в каждом разветвлении, определяемые отношениями IL = U / XL и IC= U / XC будут равны между собой, так XL = ХC.
Вывод, к которому мы пришли, может показаться на первый взгляд довольно странным. Действительно, генератор нагружен двумя сопротивлениями, а тока в неразветвленной части цепи нет, тогда как в самих сопротивлениях протекают равные и притом наибольшие по величине токи.
Объясняется это поведением магнитного поля катушки и электрического поля конденсатора. При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор.
Таким образом, и при параллельном соединении катушки индуктивности и конденсатора мы получили колебательный контур, отличающийся от описанного выше только тем, что генератор, создающий колебания, не включен непосредственно в контур и контур получается замкнутым.
Графики токов, напряжения и мощности в цепи при резонансе токов: а — активное сопротивление равно нулю, цепь мощности не потребляет; б — цепь обладает активным сопротивлением, в неразветвленной части цепи появился ток, цепь потребляет мощность
Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства:
ωL = 1 / ωC
Следовательно:
fрез = 1 / 2π√LC
Lрез = 1 / ω2С
Срез = 1 / ω2L
Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. е. превратить цепь в колебательный контур.
Итак, мы получили замкнутый колебательный контур, в котором можно вызвать электрические колебания, т. е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии — генератор переменного тока.
В цепях несинусоидального тока резонансные режимы возможны для различных гармоничных состовляющих.
Резонанс токов широко используется в практике.Явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту. Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции. Колебательный контур, работающий в режиме резонанса токов, является одним из основных узловэлектронных генераторов.
Если в цепь переменного тока включены последовательно катушка индуктивности иконденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением.
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Применив к этой цепи закон Ома, получим:
Формулу эту можно преобразовать следующим образом:
В полученном равенстве IXL —действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХС—действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать: