Калькулятор сопротивления конденсатора переменному току — MOREREMONTA
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора.
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения
Отсюда выразим соотношение среднеквадратичных значений .
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.
Онлайн-калькулятор расчёта реактивного сопротивления
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчитать ёмкость или индуктивность для реактивного сопротивления:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Прежде, чем мы приступим к расчётам разнообразных пассивных и активных фильтров, не плохо было бы сориентироваться в пространстве и задуматься — а за счёт чего происходит процесс частотной фильтрации сигналов, какой неведомый зверь должен выбежать на свист царевича после преобразования частотно-зависимыми цепями, и что это за цепи такие — частотно-зависимые?
Большая Энциклопедия Нефти и Газа учит нас, что частотно-зависимыми цепями называются электрические цепи с использованием емкостных и резистивных элементов. Спасибо, господа нефтяники и газовики — будем знать. От себя добавлю, что индуктивные элементы в частотно-зависимом хозяйстве также иногда пригождаются.
Для постоянного тока ни конденсаторы, ни катушки индуктивности никакого интереса не представляют. Сопротивление идеального конденсатора — бесконечность, индуктивности — ноль. Другое дело — переменный ток, тут наши частотно-зависимые элементы, начинают приобретать определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от частоты протекающего тока. Для особо продвинутых, вымучаю из себя умную фразу — «Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах».
Другое дело — переменный ток, тут наши частотно-зависимые элементы, начинают приобретать определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от частоты протекающего тока. Для особо продвинутых, вымучаю из себя умную фразу — «Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах».
Графики, фазовые сдвиги, интегралы и прочие атрибуты студенческих знаний, как правило, мало кого интересуют. Если я не прав, пусть первыми бросят в меня камень и с лёгкостью найдут необходимую информацию на других сайтах. А мы ребята весёлые, поэтому сразу перейдём к делу и напишем всего пару формул:
Xс = 1 / 2πƒС, Xl = 2πƒL, где
Xc — сопротивление конденсатора переменному току, а Xl — сопротивление индуктивности переменному току.
РИСУЕМ ТАБЛИЧКУ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ КОНДЕНСАТОРА
ТО ЖЕ САМОЕ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ ИНДУКТИВНОСТИ
В реальной жизни конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлениями и индуктивностью, а катушки индуктивности — омическим сопротивлением провода обмотки и межвитковой паразитной ёмкостью.
Нужно Вам вооружаться этими знаниями, или нет, судить не возьмусь, а вот то, что электролитические конденсаторы имеют обыкновение иногда взрываться при превышении допустимых уровней напряжений, либо перегреве, вызванным утечками вследствие старения — знать надо обязательно.
Так что, если не хотите превратиться в одноглазого шахматиста из Васюков, соблюдайте технику безопасности, покупайте электролиты приличных производителей.
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Калькулятор | ColorAndCode
| LCD1602/2004 — HD44780 | |
Параллельное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Последовательное соединение резисторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Параллельное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
Последовательное соединение конденсаторов
Двойное нажатие на введенное значение в списке позволяет его отредактировать. | |
| Реактивное сопротивление конденсатора | |
| Реактивное сопротивление конденсатора (+) | |
| Реактивное сопротивление катушки индуктивности | |
| Реактивное сопротивление катушки индуктивности (+) | |
| Обратное определение при параллельном соединении резисторов и последовательном конденсаторов | |
| Определение индуктивности из частоты и реактивного сопротивления | |
| Определение емкости из частоты и реактивного сопротивления | |
| Проводники | |
| Цилиндрические однослойные катушки | |
| Цилиндрические однослойные катушки (+) | |
Тороидальные катушки на ферритовых кольцах
Дополнительно: — Возможность использовать данные из справочника. | |
| Программирование ДПКД (делитель с переменным коэффициентом деления) | |
Сопротивление резистора для светодиода
Дополнительно: — Возможность использовать данные из справочника; — Вывод номинала в 4-х цветной маркировке для ряда E24 +/- 5 %. | |
| Расчёт схемы на основе NE555 | |
| Расчёт схем на основе LM317, LM338, LM350 | |
| Расчёт схем на основе LM2596 | |
| Расчет катушек на ферритовых кольцах фирмы Amidon |
|
| Расчёт индуктивности квадратной плоской катушки |
|
| Индуктивность прямого провода над проводящей подложкой |
Дополнительный материал в статье:
— Полупроводниковая светотехника № 4 за 2019 год
— Радиолюбитель № 3 за 2010 год
— Компоненты и технологии № 6 за 2010 год
Конденсаторный импеданс — электротехнические и электронные инструменты
Калькулятор импеданса конденсатора
Этот инструмент вычисляет реактивное сопротивление конденсатора для заданного значения емкости и частоты сигнала.
Вывод
Сопротивление конденсатора
Ω
обзор
Наш калькулятор емкостного реактивного сопротивления позволяет определить импеданс конденсатора, если дано его значение емкости (C) и частота сигнала, проходящего через него (f). Вы можете ввести емкость в фарады, микрофарады, нанофарады или пикофарады. Для частоты параметры устройства — Гц, кГц, МГц и ГГц.
Уравнение
$$ X_ {C} = \ frac {1} {\ omega C} = \ frac {1} {2 \ pi fC} $$
Где:
$$ X_ {C} $$ = реактивное сопротивление конденсатора в омах (Ω)
$$ \ omega $$ = угловая частота в rad / s = $$ 2 \ pi f $$, где $$ f $$ — частота в Гц
$$ C $$ = емкость в фарадах
Реакция (X) передает сопротивление компонента переменному току. Импеданс (Z) передает сопротивление компонента как постоянному току, так и переменному току; он выражается как комплексное число, т. е. Z = R + jX. Сопротивление идеального резистора равно его сопротивлению; в этом случае действительной частью импеданса является сопротивление, а мнимая часть равна нулю. Импеданс идеального конденсатора равен величине его реактивности, но эти две величины не идентичны. Реакция выражается как обычное число с единичными омами, тогда как импеданс конденсатора представляет собой реактивное сопротивление, умноженное на -j, т. Е. Z = -jX. Термин -j учитывает 90-градусный сдвиг фазы между напряжением и током, который возникает в чисто емкостной схеме.
Импеданс идеального конденсатора равен величине его реактивности, но эти две величины не идентичны. Реакция выражается как обычное число с единичными омами, тогда как импеданс конденсатора представляет собой реактивное сопротивление, умноженное на -j, т. Е. Z = -jX. Термин -j учитывает 90-градусный сдвиг фазы между напряжением и током, который возникает в чисто емкостной схеме.
Вышеприведенное уравнение дает вам реактивное сопротивление конденсатора. Чтобы преобразовать это в импеданс конденсатора, просто используйте формулу Z = -jX. Реакция является более простой ценностью; он говорит вам, сколько сопротивления конденсатор будет иметь на определенной частоте. Импеданс, однако, необходим для всестороннего анализа цепи переменного тока.
Как видно из приведенного выше уравнения, реактивное сопротивление конденсатора обратно пропорционально как частоте, так и емкости: более высокая частота и более высокая емкость приводят к снижению реактивности. Обратная зависимость между реактивным сопротивлением и частотой объясняет, почему мы используем конденсаторы для блокировки низкочастотных составляющих сигнала, позволяя передавать высокочастотные компоненты.
Дальнейшее чтение
Учебник — Конденсаторы переменного тока
Учебник — Резисторные конденсаторные схемы
Рабочий лист — Емкостный реактив
Чистая мощность для каждой ИС: понимание байпасных конденсаторов
Электрическая емкость
Электрической емкостью называется способность проводника накапливать электрический заряд. Электронные элементы с такими свойствами называются конденсаторами. Единицей эл ёмкости является Фарада, а также применяются микрофарада, нанофарада, пикофарада. Активным сопротивлением емкости является сопротивление её постоянному электрическому току, который возникает вследствие несовершенства конструкции конденсатора,(идеальный конденсатор не пропускает постоянный ток вообще). Реактивное сопротивление конденсатора — то сопротивление, которое он оказывает прохождению переменного тока. Вычисляется по формуле: Xc=1/(2р*f*С), где:
Xc-реактивное емкостное сопротивление, Ом;
f — частота, Герц;
С — емкость, фарад.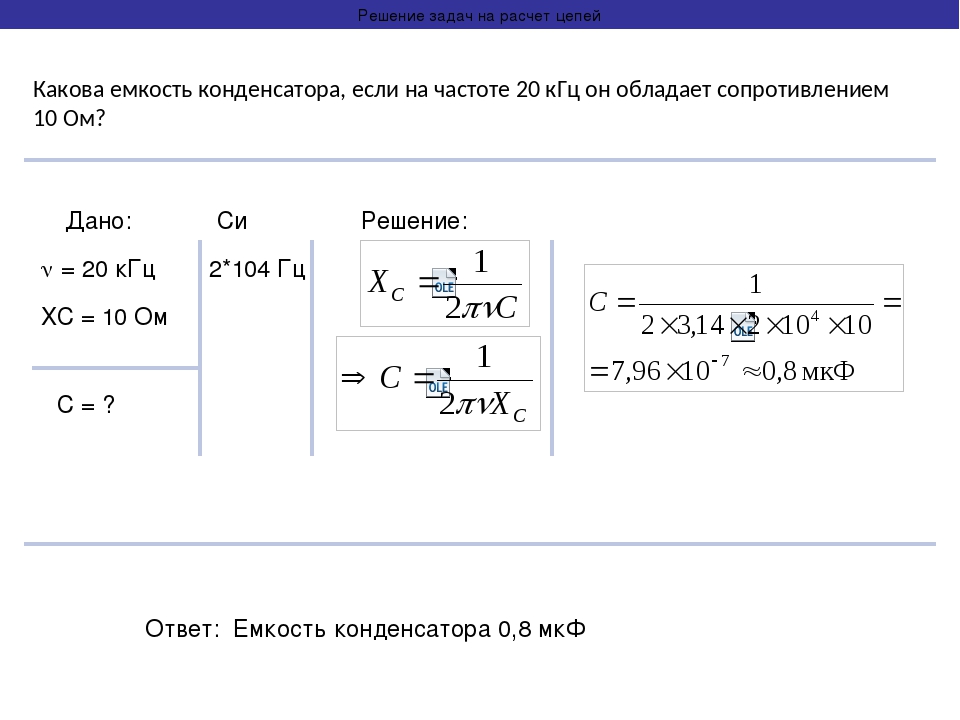
ТКЕ — температурный коэффициент емкости — определяет зависимость величины электрической емкости конденсатора от его температуры.
Калькулятор расчета емкости конденсатора
Конденсаторы бывают бумажные, металлобумажные, слюдяные, керамические, воздушные, электролитические и т д. Они широко применяются в электронных схемах в качестве фильтров и накопителей заряда.
Основные параметры:
- Номинальная емкость
- %
- Тангенс угла потерь или добротность
- ТКЕ — температурный коэфициент емкости(изменение емкости при изменении температуры).Характеризует температурную стабильность конденсаторов
- Стабильность во времени-коэфициент старения
- Сопротивление изоляции и ток утечки
При длительном воздействии «U» на обкладках конденсатора возможен пробой диэлектрика. Поэтому величина «U» нормируется. Материал диэлектрика (д/э) между обкладками определяет свойства конденсатора и область его использования.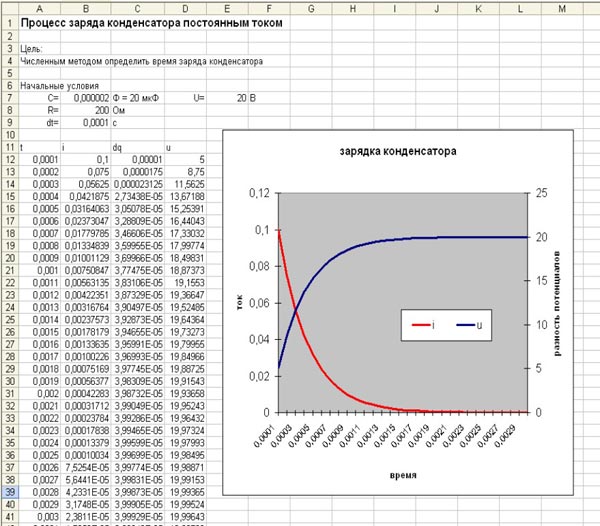
По данному классификационному признаку кон-ры бывают:
- C газообразным д/э(воздушные,газонаполненные,ваккумные)
- C жидким д/э(некоторые виды солей)
- C твердым органическим д/э(слюдяные,керамические,стелокерамические,стеклоэмалевые,пленочные,стеклопленочные)
- C твердым органическим д/э (бумажные,металлобумажные,фторопластовые,полиэтиленфлатантные)
- C оксидным д/э(электролитические,оксиднополупроводниковые,оксиднометаллические).В этом случае оксидная д/э пленка образуется на обкладках из тантала,титана,алюминия,ниобия и в названии присутствует материал обкладок.
Радио для всех — Лаборатория
В разделе представлены on-line калькуляторы
Цветовая маркировка резисторов
Расчет индуктивности
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки L
Расчёт параллельного соединения резисторов и последовательного конденсаторов
Расчёт резистивного и ёмкостного делителей
Расчёт частоты колебательного контура и цепочки RC.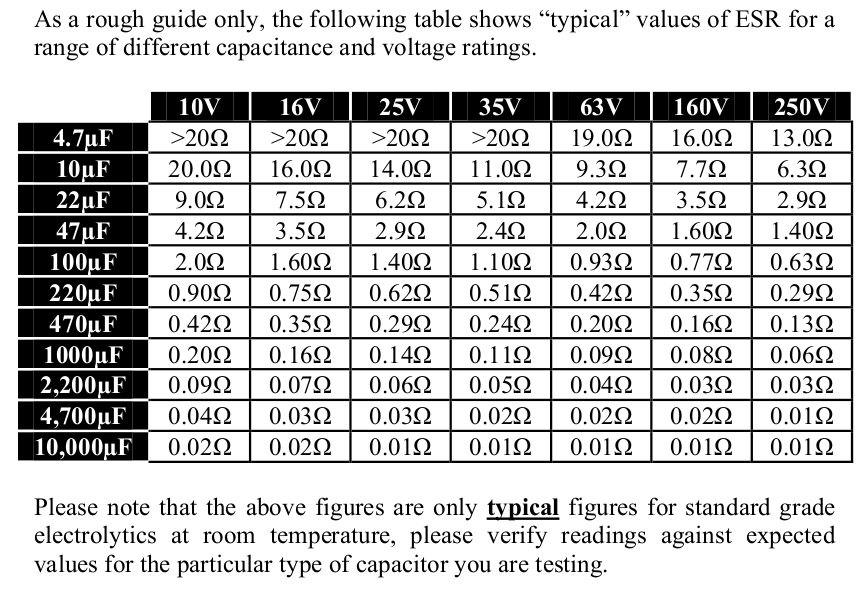 Частота среза фильтра ФНЧ и ФВЧ
Частота среза фильтра ФНЧ и ФВЧ
Компенсация реактивной мощности
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
Расчет элементов J антенны
Расчет резонансной частоты LC-контура
Расчет резистивного Пи аттенюатора
Делитель напряжения
Цветовой код конденсаторов
Стабилизация напряжения
Дроссели, намотанные на резисторах МЛТ
Реактивное сопротивление конденсатора
Реактивное сопротивление катушки индуктивности
Калькулятор определения номинала SMD-резистора
Расчет значения резистора для LM317
Онлайн калькулятор таймер 555
Расчет «Cantenna» (баночной антенны) для Wi Fi
Расчет усилителя на биполярном транзисторе
Калькулятор расчета компактных монолитных усилителей
Расчет силового трансформатора
Расчет дискоконусной антенны
Сопротивления для согласующего трансформатора
Расчет для тороидальных (ферритовых) сердечников Amidon
Расчет петлевого вибратора
Калькулятор DC-DC преобразователя MC34063A
Расчет выпрямителя для блока питания
Расчет гасящего конденсатора в блоке питания
Расчет резистора для подключения светодиода
Цветовая маркировка резисторов
Расчет индуктивности
Расчёты электронных цепей.
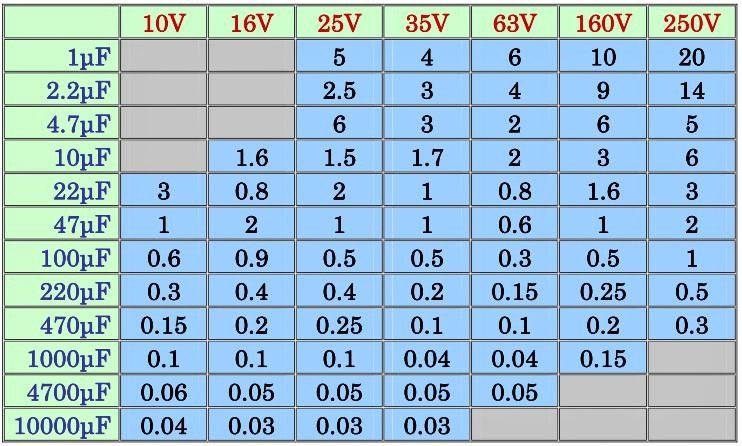
Вписываем значения и кликаем мышкой в таблице
Расчёт реактивного сопротивления конденсатора C и реактивного сопротивления катушки LРеактивное сопротивление ёмкости | Реактивное сопротивление индуктивности |
Параллельное соединение двух сопротивлений | Последовательное соединение двух ёмкостей |
Расчёт резистивного и ёмкостного делителей
Расчёт резистивного делителя напряжения | Расчёт ёмкостного делителя напряжения |
Расчёт частоты колебательного контура и цепочки RC.
 Частота среза фильтра ФНЧ и ФВЧ
Частота среза фильтра ФНЧ и ФВЧЧастота резонанса колебательного контура LC | Пост. времени τ RC и частота среза RC-фильтра |
Компенсация реактивной мощности
Реактивная мощность Q = √((UI)²-P²) |
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности
После сброса ввести два любых известных параметра I=U/R; U=IR; R=U/I; P=UI P=U²/R; P=I²R; R=U²/P; R=P/I² U=√(PR) I= √(P/R) |
Расчет элементов J антенны
Дополнение: Арифметические калькуляторы и конвертеры величин
Цветовая маркировка резисторов, конденсаторов, индуктивностей, калькулятор определения номинала.
В раздел: Советы → Цветная маркировкаЦветная маркировка резисторов, конденсаторов и индуктивностей
Он-лайн калькулятор дает возможность рассчитать номинальное значение радиоэлементов таких как резистор, конденсатор и индуктивность, имеющие на своем корпусе вместо цифрового обозначения цветные полоски на корпусе. Для правильного определения номинала расположите элемент таким образом, чтобы цветовые кольца были как-бы сдвинуты к левому краю, или широкая полоска находилась с левой стороны.
Для пользования калькулятором определения номинала резистора по цветным полоскам, расположите его перед собой как указано на рисунке, поочередно, начиная с левого столбца, выберите нажатием нужный цвет, старайтесь не ошибиться в правильном определении цвета полоски, в правом окошке увидите полученный результат.
Маркировка конденсаторов
Обычно на конденсаторах наносится цифровая маркировка, обозначающий номинал.
Рядом с этим цифровым кодом маркируется наибольшее рабочее напряжение, а иногда класс (точность), температурный коэффициент и другие значения. Но на самых миниатюрных конденсаторах (например, для поверхностного монтажа) нет таких полных обозначений, и вы не должны удалять полоски до тех пор, пока они будут вам необходимы.
В зависимости от производителя имеются различия в обозначении, касается материала диэлектрика и др. Обозначение конденсаторов на схеме 4n7/40V означает, что емкость конденсатора 4,700pF, его максимальное рабочее напряжение 40В. Имеется и другое обозначение 4n7.
Конденсаторы идентифицируются и по нанесенным цветным полосам, обозначение подобное резисторам по 4-полосный системе. Первые два цвета (A и B) обозначают первые две цифры, третий цвет (C) — множитель, четвертый цвет (D) допуск, и пятый цвет (E) рабочее напряжение.
На корпусе дисковых керамических конденсаторов (рис. 2.2b) и трубчатых конденсаторов (рис. 2.2) рабочее напряжение не указывается, так как они используются в цепях с низким напряжением постоянного тока. Если трубчатый конденсатор имеет пять цветных полос, первый цвет представляет температурный коэффициент, в то время как другие четыре обозначают емкость.
|
Цветная маркировка танталовых электролитических конденсаторов
Первые два цвета определяют две первые цифры и имеют такое же назначение как и при определении резисторов. Третий цвет множитель в мкф, четвертый максимальное рабочее напряжение.
|
Как быть с цифровой маркировкой SMD резисторов? Сопротивление резистора обозначается в Омах и равно первым цифрам, последние указывают количество нулей после них. К примеру, обозначение 472 =4700 Ом или 4,7 кОм.
Таблица маркировки резисторов, калькулятор цветовой маркировки резисторов, обозначение резистора, конденсатора. Программа расчета.
Размеры резисторов в зависимости от мощности
В зависимости от рассеивания мощности резисторов зависят и размеры корпуса (самого элемента) резистора. Корпус зависит от материала из которого изготовлен резистор и типа резистора.
Реактивное сопротивление конденсатора + Калькулятор
Реактивным называется сопротивление, препятствующее прохождению переменного электротока в цепи под действием конденсатора или катушки индуктивности, включенных в эту цепь. Это связано со свойствами индуктивности, которая выступает в качестве обычного проводника для постоянного тока с бесконечно малым сопротивлением. В тех же условиях конденсатор уже становится диэлектриком с возрастающим сопротивлением.
Свойства реактивного сопротивления конденсатора
При переменном токе реактивное сопротивление конденсатора оказывает влияние на такие параметры, как частота самого тока, индуктивность катушки или емкость. Из-за этого свойства конденсатор получил наименование реактивного элемента или реактивного электронного компонента.
В каждом заряженном конденсаторе присутствует электрический ток. В этих условиях он является составной частью процесса зарядки и разрядки, когда электрическое поле, образующееся между обкладками, накапливает или отдает энергию.
Установленный в цепь переменного тока, конденсатор будет накапливать энергию, то есть заряжаться, до определенного максимума, пока направление тока не изменится на противоположное. Поэтому при амплитудном значении напряжения, ток в конденсаторе будет иметь нулевое значение. В результате, ток и напряжение конденсатора будут постоянно расходиться во времени на четверть периода. Таким образом, падение напряжения на конденсаторе ограничивает ток во всей цепи, создавая реактивное сопротивление. Его значение обратно пропорционально частоте тока и емкости конденсатора.
Если к конденсатору подвести напряжение U, в этом случае начнется уменьшение тока от максимума до нуля. Одновременно, напряжение на его выводах будет возрастать от нулевого до максимального значения. В этом случае напряжение на обкладках конденсатора отстает по фазе от тока на угол, равный 90 градусам. Данное явление получило название отрицательного сдвига фаз.
Практическое использование реактивного сопротивления
С помощью конденсаторных установок осуществляется компенсация реактивной мощности. Через электрические сети высоковольтная электроэнергия передается на большие расстояния. В большинстве случаев она потребляется электродвигателями с резистивными элементами и значительным индуктивным сопротивлением.
Полная мощность, поступающая к потребителям, включает в себя активную составляющую Р, с помощью которой совершается полезная работа, и реактивную составляющую Q, приводящую к нагреву обмоток электродвигателей и трансформаторов. Качество электроэнергии существенно снижается под действием реактивной составляющей, возникающей на индуктивных сопротивлениях. Для того чтобы ликвидировать ее негативное воздействие, была разработана специальная схема компенсации. С этой целью подключались конденсаторные батареи, емкостное сопротивление которых способствовало понижению косинуса угла ф.
Установка таких конденсаторных батарей практиковалась в основном на подстанциях, осуществляющих непосредственную поставку электроэнергии проблемным потребителям. Данное мероприятие позволяло эффективно регулировать качество поставляемой энергии.
Снижение уровня реактивной компоненты способствует существенному уменьшению нагрузки на установленное оборудование, хотя активная мощность остается на одном и том же уровне. Используя реактивное сопротивление конденсатора, удалось добиться экономии электроэнергии на предприятиях промышленного производства и объектах жилищно-коммунального хозяйства, повысить надежность работы энергетических систем.
Расчет онлайн
Калькулятор емкостного реактивного сопротивления
Это калькулятор емкостного реактивного сопротивления — отличный инструмент, который поможет вам оценить так называемое сопротивление конденсатора в электрической цепи. Вы можете найти формулу емкостного реактивного сопротивления в тексте ниже, и мы объясним, почему реактивное сопротивление возникает для переменного тока, а не постоянного. Если вы хотите узнать, как рассчитать емкостное реактивное сопротивление, вы попали в нужное место — поехали!
Что такое емкостное реактивное сопротивление?
Реактивное сопротивление — это свойство элемента электрической цепи противодействовать прохождению тока .Используя это определение, мы можем сказать, что емкостное реактивное сопротивление аналогично сопротивлению конденсатора . Даже единица реактивного сопротивления такая же, как и сопротивление — Ом ( Ом, ). Обычно мы обозначаем реактивное сопротивление как X .
Хотя и реактивное сопротивление ( X ), и сопротивление ( R ) имеют тенденцию быть одним и тем же в цепи, между ними существует определенное различие. Реактивное сопротивление влияет на переменный ток (AC), а сопротивление влияет на постоянный ток (DC) .Как правило, они являются составляющими полного сопротивления Z , комплексной величины, определяющей полное сопротивление цепи протеканию тока:
Z = R ± j * X ,, где j = √-1 — мнимое число (квадратный корень из отрицательного числа).
Емкостное реактивное сопротивление — это свойство конденсатора . Точно так же индуктивное реактивное сопротивление — это свойство катушки индуктивности. Идеальный резистор имеет нулевое реактивное сопротивление, в то время как это чисто резистивный элемент.Напротив, идеальные конденсаторы и катушки индуктивности имеют нулевое сопротивление .
Итак, строго говоря, сопротивления конденсатора не существует. Обычно мы рассматриваем эту фразу как сокращение для определения емкостного реактивного сопротивления.
Как рассчитать емкостное реактивное сопротивление? Формула емкостного реактивного сопротивления
Как мы упоминали в предыдущем разделе, емкостное реактивное сопротивление — это свойство конденсатора, которое противодействует переменному току. То же самое верно для любого набора конденсаторов, который мы можем расположить последовательно или параллельно.
Одним из важнейших свойств переменного тока является его частота f . Мы можем рассчитать емкостное реактивное сопротивление X конденсатора C , используя следующее уравнение:
X = 1 / (2 * π * f * C) .В качестве альтернативы мы можем записать формулу емкостного реактивного сопротивления как:
X = 1 / (ω * C) ,, где ω = 2 * π * f — угловая частота тока.
Как видите, , чем выше частота , , емкость , , тем ниже реактивное сопротивление .Имеет ли это смысл?
Совершенно верно! Помните, что конденсатор хранит электрическую энергию. Во время зарядки похоже, что конденсатор почти беспрепятственно пропускает ток. Чем больше он может поглотить (чем выше емкость), тем меньше он сопротивляется пропусканию тока. Кроме того, чем выше частота переменного тока, тем меньше времени остается для полной зарядки конденсатора. В случае постоянного тока ( f = 0 ) конденсатор сначала заряжается, но затем (в состоянии равновесия) он действует как разомкнутая цепь.
Как пользоваться калькулятором емкостного реактивного сопротивления?
Нет ничего сложного в оценке емкостного реактивного сопротивления любого конденсатора. Попрактикуемся в вычислениях на примере.
Допустим, у нас есть схема со сферическим конденсатором емкостью С = 30 нФ . Применяем источник напряжения, которое чередуется с частотой f = 60 Гц . Какое емкостное сопротивление в этой цепи?
Перевести единицы емкости в Фарады.Мы можем использовать научную нотацию, чтобы записать значения компактно:
C = 30 нФ = 3 · 10⁻⁸ F.Найдите произведение всех значений в знаменателе формулы емкостного реактивного сопротивления:
2 * π * f * C = 2 * π * 60 * 3 · 10⁻⁸ = 1,131 · 10⁻⁵.Найдите его обратную мультипликативную величину, которая является отношением
1и нашего произведения:1 / 1,131 · 10⁻⁵ = 88 419,41 Ом. Не забывайте про единицу реактивного сопротивления!Запишите результат, используя соответствующий префикс:
X = 88.41941 кОм.Округлим результат до четырех значащих цифр:
X = 88,42 кОм.Проверьте результат с помощью нашего калькулятора емкостного реактивного сопротивления! Вау, относительно безболезненно, не так ли?
Калькулятор импеданса конденсатора • Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц
Обратите внимание, что величина импеданса идеального конденсатора равна его реактивному сопротивлению. Однако они не идентичны из-за фазового сдвига между напряжением и током в емкостной цепи.Для расчета используется следующая формула:
где:
X C — реактивное сопротивление конденсатора в Ом (Ом),
Z C — реактивное сопротивление конденсатора в Ом (Ом). ),
ω = 2πf — угловая частота в рад / с,
j — мнимая единица,
f — частота в герцах (Гц), а
C — емкость в фарадах (Ф).
Для расчета введите емкость и частоту, выберите единицы измерения, и результат будет показан в омах.
График зависимости реактивного сопротивления идеального конденсатора X C от частоты f для данной емкости показывает обратную пропорциональность частоте
Конденсатор представляет собой пассивный обычно двухконтактный электрический компонент, состоящий в основном из двух электрических проводников, часто в форма тонких металлических пластин, разделенных диэлектриком, например пластиковой пленкой, керамикой, бумагой или даже воздухом.Конденсаторы используются для хранения энергии в виде электрического заряда.
Когда первоначально незаряженный конденсатор подключен к источнику постоянного напряжения постоянного тока, он заряжается до приложенного напряжения, а его зарядный ток экспоненциально спадает от максимального значения в начальной точке зарядки до нуля. При этом напряжение на конденсаторе увеличится до напряжения источника постоянного тока.
Итак, когда напряжение достигает своего максимума, ток достигает своего минимума.Скорость зарядки определяется постоянной времени цепи, к которой подключен конденсатор. Полностью заряженный конденсатор блокирует ток и действует как временное запоминающее устройство.
Идеальный конденсатор будет поддерживать этот заряд бесконечно, даже если напряжение зарядки постоянного тока будет снято. Однако в реальной жизни конденсаторы, особенно электролитические, не могут действовать как постоянные накопители из-за их относительно низкого сопротивления утечке и, следовательно, высокого тока утечки.
Если на конденсатор подается переменное синусоидальное напряжение, он заряжается то в одном направлении, то в противоположном. Его полярность изменяется с той же скоростью, что и напряжение переменного тока. Как мы упоминали выше, когда напряжение достигает своего максимума, ток достигает своего минимума, а когда напряжение достигает своего минимума, ток достигает своего максимума. Ток пропорционален скорости изменения напряжения , и ток является наибольшим, когда изменение напряжения является самым быстрым, то есть когда синусоидальное напряжение пересекает нулевую точку.На рисунке показан график напряжения V на конденсаторе, его заряда Q и тока в нем I.
В чисто емкостной схеме протекание тока зависит от скорости изменения напряжения. Ток заряжает конденсатор, и когда ток медленно приближается к нулю, конденсатор полностью заряжен и напряжение на нем достигает максимума. В C — напряжение, Q C — заряд, I C — ток, φ = –90 ° = — π /2 — фазовый сдвиг.1 — конденсатор начинает заряжаться, ток достигает своего положительного максимума, скорость его изменения равна нулю, а напряжение и заряд конденсатора равны нулю; 2 — конденсатор полностью заряжен, ток равен нулю, скорость его изменения максимальная, а напряжение и заряд конденсатора находятся на своих положительных максимумах; 3 — конденсатор заряжается в обратном направлении, ток имеет отрицательный максимум, скорость его изменения равна нулю, а напряжение и заряд конденсатора равны нулю; 4 — конденсатор полностью заряжен, ток равен нулю, скорость его изменения максимальная, а напряжение и заряд конденсатора имеют отрицательный максимум
Как мы видим, напряжение отстает от тока по времени и фазе (90 °), потому что в конденсаторе должен течь ток, чтобы на нем повышалось напряжение.Или мы можем сказать, что ток опережает напряжение. Насколько это отставание или опережение зависит от значения реактивного сопротивления цепи по отношению к ее сопротивлению? Если в цепи вообще нет сопротивления, запаздывание или опережение могут достигать 90 ° (ток равен нулю, когда напряжение максимально). Этот угол называется разностью фаз.
Рассмотрим следующую аналогию: Солнце (солнечный свет — ток) наиболее мощно в астрономический полдень, но самая жаркая часть дня (температура — напряжение) обычно наступает на несколько часов позже.Или зимнее солнцестояние в северном полушарии (самый короткий день) приходится на конец декабря, но самые холодные месяцы еще впереди — в зависимости от того, где вы живете, это январь или даже февраль. Причина этого «сезонного запаздывания» или «фазового сдвига» заключается в поглощении энергии Солнца массивными океанами Земли. Позже они выпускают его медленно — точно так же, как это делают конденсаторы.
День зимнего солнцестояния
Расчетное сопротивление — это мера сопротивления конденсатора сигналу на определенной частоте , который проходит через него.Емкостное реактивное сопротивление обратно пропорционально изменению частоты приложенного переменного напряжения. Формула показывает, что реактивное сопротивление конденсатора X C велико на низких частотах и мало на высоких частотах. При нулевой частоте (постоянное напряжение) емкостное сопротивление становится бесконечным или полностью противоположным току. Конденсатор блокирует постоянное напряжение и ток. С другой стороны, на очень высоких частотах конденсатор проводит очень хорошо — отсюда правило, которое мы усвоили в средней школе: конденсаторы пропускают переменный ток и блокируют постоянный ток.Если частота очень высокая, конденсаторы очень хорошо пропускают сигналы.
Импеданс измеряется в омах, как и сопротивление. Так же, как сопротивление, импеданс показывает величину сопротивления компонента потоку электрического тока. Но чем импеданс отличается от простого сопротивления? Разница заключается в зависимости импеданса от частоты сигнала. Сопротивление не зависит от частоты и от нее зависит полное сопротивление конденсаторов. Импеданс конденсаторов увеличивается с уменьшением частоты.Емкость конденсатора оказывает такое же влияние на импеданс, как и частота. Чем выше емкость, тем ниже сопротивление и наоборот.
Этот калькулятор разработан для идеальных конденсаторов. Настоящие конденсаторы всегда имеют некоторую индуктивность и сопротивление. Используйте наш калькулятор импеданса RLC, чтобы рассчитать импеданс реальных конденсаторов.
Винтажные конденсаторы, произведенные в СССР в конце 1960-х
Резисторный конденсаторный калькулятор — дюймовый калькулятор
Рассчитайте время заряда, энергию и характеристическую частоту или импеданс, реактивное сопротивление и угловую частоту цепи резистор-конденсатор.
Расчет энергии и времени зарядки
Расчет импеданса и реактивного сопротивления
Цепь резистор-конденсатор, или RC-цепь, представляет собой цепь с последовательно соединенными резистором и конденсатором. Конденсатор в цепи накапливает энергию, а резистор изменяет скорость заряда и разряда конденсатора. Эти схемы чаще всего используются для фильтрации формы волны и используются для создания фильтров нижних, верхних и полосовых частот.
Схема, показывающая цепь резисторного конденсатора.Формулы RC-цепей
RC-цепи имеют несколько характеристик, включая постоянную времени, накопление энергии, заряд, импеданс, емкостное реактивное сопротивление, характеристическую частоту и угловую частоту. Расчет каждой из этих характеристик схемы можно выполнить по следующим формулам.
Формула постоянной времени
Постоянная времени, выраженная как tau (τ), — это время в секундах, в течение которого конденсатор в RC-цепи достигает 63.2% заряда. Формула для расчета постоянной времени:
τ = RC
Постоянная времени τ равна сопротивлению R в омах, умноженному на емкость C в фарадах. Конденсатор достигнет заряда 63,2% за τ, 86,5% за 2τ и 99,3% за 5τ.
Энергетическая формула
Энергия, запасенная в полностью заряженном конденсаторе RC-цепи, может быть найдена по формуле:
E = CV 2 2
Энергия E в джоулях равна емкости C в фарадах, умноженной на квадрат напряжения V, деленной на два.
Формула заряда
Максимальный заряд в цепи конденсатора резистора можно найти по формуле:
Q = CV
Заряд Q в кулонах равен емкости C в фарадах, умноженной на напряжение V.
Текущая формула
Максимальный ток RC-цепи можно найти с помощью закона Ома. Формула:
I = VR
Ток I в амперах равен напряжению V, деленному на сопротивление R в омах.
Формула характеристической частоты
Характеристическая частота цепи, часто называемая обычной или циклической частотой, может быть найдена по следующей формуле:
f = 12πRC
Частота f в герцах равна 1, деленному на 2, умноженное на π, умноженное на сопротивление R в омах, умноженное на емкость C в фарадах.
Формула угловой частоты
Угловую частоту контура можно найти по формуле:
ω = 2πf
Угловая частота ω в радианах в секунду равна удвоенной π-кратной характеристической частоте f в герцах.
Формула импеданса
Импеданс RC-цепи можно найти с помощью нескольких формул:
Z = R + 1jωC
| Z | = √ (R 2 + 1 (ωC) 2 )
Где j — мнимая единица, Z — импеданс в омах, R — сопротивление в омах, C — емкость в фарадах, а ω — угловая частота в рад / с.
Формула емкостного реактивного сопротивления
Емкостное реактивное сопротивление RC-цепи можно найти по формуле:
X = 1ωC
Емкостное реактивное сопротивление X равно 1, деленному на угловую частоту ω, умноженную на емкость C.
Формула разности фаз
Эта формула выражает разность фаз между полным напряжением и полным током.
φ = загар -1 (-1ωCR)
φ — разность фаз, ω — угловая частота, C — емкость, R — сопротивление.
Импеданс R и C параллельно Калькулятор
- Цель использования
- разработка навигации на основе емкости система
[1] 2020/11/19 22:30 — / 60 лет или старше / Другое / Не совсем /
- Цель использования
- Проверка домашнего задания
[2] 2020/08/27 09:11 Мужской / 20-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- При обратном, т.е.е. известны разные значения угла и импеданса, каковы значения сопротивления и емкости?
- Комментарий / запрос
- При обратном, т.е. известны разные значения угла и импеданса, каковы значения сопротивления и емкости?
[3] 2020/08/22 22:25 Мужской / Уровень 50 лет / Учитель / Исследователь / Полезно /
- Цель использования
- Сравните результаты с индивидуальной конструкцией анализатора импеданса.
[4] 2020/04/17 00:06 Мужчина / Уровень 20 лет / Инженер / Очень /
- Цель использования
- Убедитесь, что я правильно рассчитываю полное сопротивление для параллельная цепь переменного тока для класса электроники.
[5] 2020/04/13 06:49 Женский / 50-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Определите значения R, C для желаемого гистерезиса, используемого с ОУ (Horowitz & Hill стр. 134-5)
[6] 2020/03/14 09:14 Мужчина / Уровень 40 лет / Инженер / Очень /
- Цель использования
- bangin ur mom
[7] 2019/12/13 05:07 Мужчина / Уровень 30 лет / Инженер / Очень /
- Цель использования
- Проверь мою интуицию в задаче домашнего задания
[8] 2019/10/04 01:42 Мужской / Уровень 20 лет / Средняя школа / Университет / Аспирант / Очень /
- Цель использования
- Проверка прибора Fluke RCL, чтобы убедиться, что он все еще функционирует нормально
действительно оценил вашу точную программу
[9] 2019/09 / 10 05:36 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /
- Назначение o f используйте регулятор вентилятора
- Комментарий / запрос
- дайте мне принципиальную схему с номинальными характеристиками конденсаторного регулятора вентилятора
[10] 2018/03/21 16:15 Женщина / Уровень 30 лет / Инженер / — /
Импеданс R и C последовательно Калькулятор
- Цель использования
- Мы не видели теории сложных схем, поэтому используем u. 2
[1] Женщина / 60 лет и старше / Частные предприниматели / Немного /
- Цель использования
- ухудшает ли мой осциллограф 20pf результаты измерения при 50 Ом, 14 МГц?
[5] 21.03.2019 02:23 Мужчина / 60 лет и старше / A пенсионер person / Useful /
- Цель использования
- Радиолюбитель
- Комментарий / Запрос
- Просто нужна была формула, но калькулятор — хорошее дополнение для предотвращения ошибок
[6] 2018/02/24 01:50 Женский / До 20 лет / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- Быстрые вычисления, когда я не хочу делать их вручную
[7] 23.01.2018 10:58 Мужчина / Моложе 20 лет / Старшая школа / Университет / аспирант / Очень /
- Цель используйте
- Расчет R & C для защиты реле, активирующего индуктивное оборудование (насос)
[8] 2017/12/03 17:59 Мужчина / 60 лет и старше / Пенсионеры / Очень /
- Назначение
- Светодиодные лампы в доме 3-х ходовые цепи накаливания после отключения.Проверка демпфера для включения параллельно осветительной арматуре.
[9] 2017/11/24 00:51 Мужчина / 50-летний уровень / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Программные алгоритмы Verify серии RC.
- Комментарий / запрос
- Метод для генерации значений амплитуды и фазы в указанном диапазоне частот.
[10] 2017/11/13 08:53 Мужчина / 30 лет / Инженер / Очень /
Постоянная времени, сопротивление, конденсатор онлайн-калькулятор
Онлайн-калькулятор и формулы для расчета постоянной времени τ (тау) резистора и конденсатора
На этой странице вы можете рассчитать постоянную времени, сопротивление или конденсатор резистора и цепи конденсатора.
Формула для расчета постоянной времени
Постоянная времени RC-элемента (нижних частот) является произведением R * C. Единица измерения — секунды. Символ — греческая буква Τ (тау).
Постоянная времени требуется для расчета состояния заряда в определенный момент времени. при зарядке или разрядке конденсатора.
После периода 3 постоянных времени выходной сигнал имеет прибл. 95% размера входного сигнала. Через 5 Τ заряд ок. 99,3%.
\ (\ Displaystyle Τ = р · С \) \ (\ Displaystyle R = \ гидроразрыва {Τ} {C} \) \ (\ Displaystyle С = \ гидроразрыва {Τ} {R} \)
Легенда
\ (\ Displaystyle R \)
Резистор
\ (\ Displaystyle С \)
Конденсатор
Τ
Постоянные времени
|
Реактивное сопротивление, индуктивное и емкостное | Физика II
Цели обучения
К концу этого раздела вы сможете:
- Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Рассчитайте индуктивное и емкостное сопротивление.
- Рассчитайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.
Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное сопротивление
Предположим, индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке 1.Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на схему. Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
График на Рисунке 1 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и повышается до своего пика после напряжения, которое им управляет, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе.Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c и начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Кратко это поведение можно описать следующим образом:
Напряжение переменного тока в индуктореКогда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. При изменении тока возникает обратная ЭДС В = — L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I через катушку индуктивности L определяется версией закона Ома:
[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на катушке индуктивности, а X L определяется как
.[латекс] {X} _ {L} = 2 \ pi {fL} \\ [/ латекс],
с f частота источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение). X L называется индуктивным реактивным сопротивлением , потому что катушка индуктивности препятствует прохождению тока. X L имеет единицы измерения Ом (1 Гн = 1 Ом с, так что частота, умноженная на индуктивность, имеет единицы (циклов / с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше его сопротивление изменениям.Также разумно, что X L пропорционально частоте f , поскольку большая частота означает большее изменение тока. То есть Δ I / Δ t является большим для больших частот (большие f , маленькие Δ t ). Чем больше изменение, тем больше сопротивление катушки индуктивности.
Пример 1. Расчет индуктивного сопротивления, а затем тока
(a) Рассчитайте индуктивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?
СтратегияИндуктивное реактивное сопротивление находится непосредственно из выражения X L = 2πf L . Как только X L найден на каждой частоте, закон Ома, как указано в уравнении I = V / X L , можно использовать для определения тока на каждой частоте.
Решение для (a)Ввод частоты и индуктивности в уравнение X L = 2πf L дает
X L = 2πf L = 6,28 (60,0 / с) (3,00 мГн) = 1,13 Ом при 60 Гц.
Аналогично, на 10 кГц,
X L = 2πf L = 6,28 (1,00 × 10 4 / с) (3,00 мГн) = 188 Ом при 10 кГц.
Решение для (b)Среднеквадратичный ток теперь определяется с использованием версии закона Ома в уравнении I = В / X L , при условии, что приложенное действующее напряжение составляет 120 В.Для первой частоты это дает
[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {1.13 \ text {} \ Omega} = 106 \ text {A at} 60 \ текст {Hz} \\ [/ latex].
Аналогично, на 10 кГц,
[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {188 \ text {} \ Omega} = 0,637 \ text {A at} 10 \ текст {кГц} \\ [/ latex].
ОбсуждениеКатушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению.Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.
Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, поскольку индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.
Конденсаторы и емкостное сопротивление
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.
Рисунок 2.(а) Источник переменного напряжения, включенный последовательно с конденсатором С, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.
График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем Q = 0 ) и напряжение на нем равно нулю.Ток остается отрицательным между точками a и b, вызывая обратное напряжение на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и доводя напряжение до нуля в точке c, что позволяет току достичь своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение соответствует тому, что делает ток, на четверть цикла:
Напряжение переменного тока в конденсатореКогда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º.
Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I в цепи, содержащей только конденсатор C , определяется другой версией закона Ома равным
.[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],
, где В — среднеквадратичное напряжение, а X C определено (Как и в случае с X L , это выражение для X C является результатом анализа цепи используя правила и исчисление Кирхгофа) равным
[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex],
, где X C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует прохождению тока. X C имеет единицы измерения Ом (проверка оставлена в качестве упражнения для читателя). X C обратно пропорционален емкости C ; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Она также обратно пропорциональна частоте f ; чем выше частота, тем меньше времени остается для полной зарядки конденсатора и, следовательно, меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?
СтратегияЕмкостное реактивное сопротивление находится непосредственно из выражения в [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]. После того, как X C найден на каждой частоте, закон Ома сформулирован как I = V / X C может использоваться для определения тока на каждой частоте.
Решение для (a)Ввод частоты и емкости в [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex] дает
[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} \\ & = & \ frac {1} {6.28 \ left (60.0 / \ text {s} \ right) \ left (5.00 \ text {} \ mu \ text {F} \ right)} = 531 \ text {} \ Omega \ text {at} 60 \ text {Hz} \ end {массив }\\[/латекс].
Аналогично, на 10 кГц,
[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} = \ frac {1} {6.{4} / \ text {s} \ right) \ left (5,00 \ mu \ text {F} \ right)} \\ & = & 3,18 \ text {} \ Omega \ text {at} 10 \ text {кГц} \ end {array} \\ [/ latex].
Решение для (b)Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в I = В / X C , учитывая приложенное действующее напряжение 120 В. Для первой частоты это дает
[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {531 \ text {} \ Omega} = 0,226 \ text {A at} 60 \ текст {Hz} \\ [/ latex].
Аналогично, на 10 кГц,
[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {3.18 \ text {} \ Omega} = 3.37 \ text {A at} 10 \ текст {Hz} \\ [/ latex].
ОбсуждениеКонденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, а индукторы — противодействуют. Конденсаторы больше всего препятствуют низким частотам, так как низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, и ток равен нулю после зарядки конденсатора.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (он действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока, чем индукторы .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны точно в фазах в резисторе.Отсутствует частотная зависимость поведения простого сопротивления в цепи:
Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Напряжение переменного тока на резистореКогда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0 °.
Сводка раздела
- Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на катушку подается синусоидальное напряжение, напряжение опережает ток на одну четверть цикла или на фазовый угол 90 °.
- Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.
- Закон Ома для катушки индуктивности
[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на катушке индуктивности.
- X L определяется как индуктивное реактивное сопротивление, определяемое по формуле
[латекс] {X} _ {L} = 2 \ pi fL \\ [/ латекс],
с f частота источника переменного напряжения в герцах.
- Индуктивное реактивное сопротивление X L выражается в единицах Ом и имеет наибольшее значение на высоких частотах.
- Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла или на фазовый угол 90º.
- Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора
[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],
, где В, — среднеквадратичное значение напряжения на конденсаторе.
- X C определяется как емкостное реактивное сопротивление, определяемое по формуле
[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex].
- X C имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.
Концептуальные вопросы
1. Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.
2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.
3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.
4. Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?
5. Объясните, почему конденсатор на рисунке 4 (a) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на рисунке 4 (b) действует как фильтр высоких частот.
Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.
6. Если конденсаторы на Рисунке 4 заменить катушками индуктивности, какой фильтр действует как фильтр низких частот, а какой — как фильтр высоких частот?
Задачи и упражнения
1. На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление 100 Ом?
2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм при частоте 500 Гц?
3.Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц?
4. На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?
5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?
6. (a) Какой ток течет, когда источник переменного тока 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? (b) Каким будет ток на частоте 25,0 кГц?
7. А 20.Источник 0 кГц, 16,0 В, подключенный к катушке индуктивности, вырабатывает ток 2,00 А. Что такое индуктивность?
8. Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?
9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от источника питания, подаваемого на персональный компьютер, включается последовательно с компьютером. Какая минимальная индуктивность должна обеспечивать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60?0 Гц?
10. Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм при частоте 120 Гц? (б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).
11. Конденсатор на рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекса] \ text {10.0 м \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).
12. Необоснованные результаты При регистрации напряжений, связанных с мозговой активностью (ЭЭГ), на конденсатор подается сигнал 10,0 мВ с частотой 0,500 Гц, производящий ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?
13. Создайте свою проблему Рассмотрите возможность использования индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.
Глоссарий
- индуктивное реактивное сопротивление:
- противодействие катушки индуктивности изменению тока; рассчитывается по X L = 2π fL
- емкостное реактивное сопротивление:
- сопротивление конденсатора изменению тока; рассчитывается по [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]
Избранные решения проблем и упражнения
1.



