Расчёт реактивного сопротивления

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал

dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U_amp

sin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U_ampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

---

Онлайн-калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Реактивное сопротивление ёмкости XC = 1 /(2πƒC)

Реактивное сопротивление индуктивности XL = 2πƒL

Расчитать ёмкость или индуктивность для реактивного сопротивления:

Расчёт ёмкости: C = 1 /(2πƒXC)

Расчёт индуктивности: L = XL /(2πƒ)

---

Похожие страницы с расчётами:

Расcчитать импеданс.
Расcчитать частоту резонанса колебательного контура LC.
Расcчитать реактивную мощность и компенсацию.

Расчёт реактивного сопротивления конденсатора и индуктивности. Он-лайн калькулятор сопротивлений ёмкости Xc и индуктивности Xl переменному току.

Прежде, чем мы приступим к расчётам разнообразных пассивных и активных фильтров, не плохо было бы сориентироваться в пространстве и задуматься — а за счёт чего происходит процесс частотной фильтрации сигналов, какой неведомый зверь должен выбежать на свист царевича после преобразования частотно-зависимыми цепями, и что это за цепи такие — частотно-зависимые?

Большая Энциклопедия Нефти и Газа учит нас, что частотно-зависимыми цепями называются электрические цепи с использованием емкостных и резистивных элементов. Спасибо, господа нефтяники и газовики — будем знать. От себя добавлю, что индуктивные элементы в частотно-зависимом хозяйстве также иногда пригождаются.

Для постоянного тока ни конденсаторы, ни катушки индуктивности никакого интереса не представляют. Сопротивление идеального конденсатора — бесконечность, индуктивности — ноль. Другое дело — переменный ток, тут наши частотно-зависимые элементы, начинают приобретать определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от частоты протекающего тока. Для особо продвинутых, вымучаю из себя умную фразу — «Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах».

Графики, фазовые сдвиги, интегралы и прочие атрибуты студенческих знаний, как правило, мало кого интересуют. Если я не прав, пусть первыми бросят в меня камень и с лёгкостью найдут необходимую информацию на других сайтах. А мы ребята весёлые, поэтому сразу перейдём к делу и напишем всего пару формул:

Xс = 1 / 2πƒС,   Xl = 2πƒL, где
Xc — сопротивление конденсатора переменному току, а Xl — сопротивление индуктивности переменному току.

РИСУЕМ ТАБЛИЧКУ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ КОНДЕНСАТОРА

ТО ЖЕ САМОЕ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ ИНДУКТИВНОСТИ

В реальной жизни конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлениями и индуктивностью, а катушки индуктивности — омическим сопротивлением провода обмотки и межвитковой паразитной ёмкостью.

Нужно Вам вооружаться этими знаниями, или нет, судить не возьмусь, а вот то, что электролитические конденсаторы имеют обыкновение иногда взрываться при превышении допустимых уровней напряжений, либо перегреве, вызванным утечками вследствие старения — знать надо обязательно.
Делают они это, ни кем не посоветовавшись, эффектно, громко, с выделение токсичных паров электролита в виде облака из дыма, и с лёкгостью могут выбить глаз пытливому радиолюбителю.
Так что, если не хотите превратиться в одноглазого шахматиста из Васюков, соблюдайте технику безопасности, покупайте электролиты приличных производителей.

 

Онлайн расчет сопротивления конденсатора Xc и индуктивности Xl переменному току | hardware

Удобные методы онлайн-расчета сопротивления емкости C и индуктивности L переменному току с частотой F.

[Xc — сопротивление конденсатора переменному току]

Формула для расчета: Xc = 1/(2*pi*F*C), где Xc — сопротивление конденсатора переменному току в

Омах, F — частота в Герцах, C — емкость в Фарадах. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкФ, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).

[Xl — сопротивление индуктивности переменному току]

Формула для расчета: Xl = 2*pi*F*L, где Xl — сопротивление индуктивности переменному току в Омах, F — частота в Герцах, L — индуктивность в Генри. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкГн, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки). 

[Общие замечания по использованию калькуляторов]

1. 1 микрофарад (мкф) = 1000000 пикофарад (пФ). 1 фарад (Ф) = 1000000 микрофарад (мкФ) = 10¹² пикофарад (пФ).

2. Десятичные значения с точкой нужно вводить с точкой, а не с запятой, иначе скрипт будет выдавать «infinity». Например, емкость 50 пФ следует ввести как 0.00005.

[Ссылки]

1. Микрофарад, Электрическая ёмкость site:convertworld.com. Очень удобный калькулятор для преобразования физических величин.
2. Расчёт резонансной частоты колебательного контура.
3. Расчет начальной магнитной проницаемости ферритовых колец по пробной обмотке.
4. Расчет дросселей на резисторах МЛТ.

Калькулятор сопротивления конденсатора переменному току — MOREREMONTA

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

Онлайн-калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Расчитать ёмкость или индуктивность для реактивного сопротивления:

Похожие страницы с расчётами:

Замечания и предложения принимаются и приветствуются!

Прежде, чем мы приступим к расчётам разнообразных пассивных и активных фильтров, не плохо было бы сориентироваться в пространстве и задуматься — а за счёт чего происходит процесс частотной фильтрации сигналов, какой неведомый зверь должен выбежать на свист царевича после преобразования частотно-зависимыми цепями, и что это за цепи такие — частотно-зависимые?

Большая Энциклопедия Нефти и Газа учит нас, что частотно-зависимыми цепями называются электрические цепи с использованием емкостных и резистивных элементов. Спасибо, господа нефтяники и газовики — будем знать. От себя добавлю, что индуктивные элементы в частотно-зависимом хозяйстве также иногда пригождаются.

Для постоянного тока ни конденсаторы, ни катушки индуктивности никакого интереса не представляют. Сопротивление идеального конденсатора — бесконечность, индуктивности — ноль. Другое дело — переменный ток, тут наши частотно-зависимые элементы, начинают приобретать определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от частоты протекающего тока. Для особо продвинутых, вымучаю из себя умную фразу — «Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах».

Графики, фазовые сдвиги, интегралы и прочие атрибуты студенческих знаний, как правило, мало кого интересуют. Если я не прав, пусть первыми бросят в меня камень и с лёгкостью найдут необходимую информацию на других сайтах. А мы ребята весёлые, поэтому сразу перейдём к делу и напишем всего пару формул:

Xс = 1 / 2πƒС, Xl = 2πƒL, где
Xc — сопротивление конденсатора переменному току, а Xl — сопротивление индуктивности переменному току.

РИСУЕМ ТАБЛИЧКУ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ КОНДЕНСАТОРА

ТО ЖЕ САМОЕ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ ИНДУКТИВНОСТИ

В реальной жизни конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлениями и индуктивностью, а катушки индуктивности — омическим сопротивлением провода обмотки и межвитковой паразитной ёмкостью.

Нужно Вам вооружаться этими знаниями, или нет, судить не возьмусь, а вот то, что электролитические конденсаторы имеют обыкновение иногда взрываться при превышении допустимых уровней напряжений, либо перегреве, вызванным утечками вследствие старения — знать надо обязательно.
Делают они это, ни кем не посоветовавшись, эффектно, громко, с выделение токсичных паров электролита в виде облака из дыма, и с лёкгостью могут выбить глаз пытливому радиолюбителю.
Так что, если не хотите превратиться в одноглазого шахматиста из Васюков, соблюдайте технику безопасности, покупайте электролиты приличных производителей.

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.

Конденсатор в цепи постоянного тока

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Заряд конденсатора от источника постоянной ЭДС

Точность вычисления

Знаков после запятой: 2

Постоянная времени RC-цепи, миллисекунд

 

Время зарядки конденсатора до 99.2%, миллисекунд

 

Начальный ток, Ампер

 

Максимальная рассеиваемая мощность, Ватт

 

Напряжение на конденсаторе, Вольт

 

Заряд на конденсаторе, микроКулон

 

Энергия конденсатора, миллиДжоуль

 

Работа, совершенная источником, миллиДжоуль

 

save Сохранить share Поделиться extension Виджет

Разряд конденсатора через сопротивление

Начальное напряжение на конденсаторе, Вольт

Точность вычисления

Знаков после запятой: 2

Начальная энергия конденсатора, миллиДжоуль

 

Начальный заряд конденсатора, микроКулон

 

Постоянная времени RC-цепи, миллисекунд

 

Начальный ток, Ампер

 

Максимальная рассеиваемая мощность, Ватт

 

Конечный заряд конденсатора, микроКулон

 

Конечная энергия конденсатора, миллиДжоуль

 

Конечное напряжение конденсатора, Вольт

 

save Сохранить share Поделиться extension Виджет

Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):

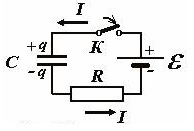
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:

При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.

Во время зарядки конденсатора, напряжение на нем изменяется по закону

где величину

называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:

Энергия, запасенная в конденсаторе:

Работа, выполненная источником ЭДС:

Онлайн калькулятор расчета запасаемой энергии в конденсаторе

Конструктивно конденсатор представляет собой емкостной элемент, состоящий из двух параллельно расположенных пластин, пространство между которыми заполнено диэлектриком.

Устройство конденсатора

Принцип работы конденсатора заключается в способности накапливать определенную величину заряда на пластинах и отдавать их обратно в сеть при прохождении через него переменного тока. Для цепи постоянного тока конденсатор представляет собой разрыв, но пластины все равно способны накапливать заряд. Основным параметром конденсатора является емкость, выражающаяся в Фарадах и способность накапливать заряд, выражаемая величиной энергии в Джоулях.

Если емкость конденсатора указывается на корпусе элемента и является его паспортным значением, то количество запасаемой энергии можно определить путем вычислений. Наиболее простым способом вычисления является использования онлайн калькулятора.

Для этого выполните такую последовательность действий:

• Внесите в первую графу калькулятора значение напряжения на конденсаторе в Вольтах;
• Укажите во втором поле величину емкости элемента в микрофарадах;
• Внесите значения сопротивления конденсатора и нажмите кнопку «Рассчитать».

В результате онлайн калькулятор расчета запасаемой энергии в конденсаторе выдаст значение заряда и времени, расходуемого на полный заряд емкостного элемента, подключенного к цепи.

Расчет величины заряда, накапливаемого в конденсаторе, и времени, необходимого для накопления этого заряда производится по таким формулам:

Где,

• W – это количество запасаемой энергии в конденсаторе;
• U – величина напряжения, приложенного к конденсатору;
• C – емкость конденсатора.

Для определения времени, затрачиваемого на накопление этого количества запасаемой энергии, в калькуляторе используется формула: T_зар = R*C

Где

• T_зар  — период времени, необходимый для накопления заряда, зависящий от параметров элемента;
• R – величина омического сопротивления конденсатора;
• C – емкость конденсатора.

 

Расчёт блока питания с гасящим конденсатором + онлайн-калькулятор — radiohlam.ru

Осторожно, текст под спойлером перегружен физикой!

Итак, процессы в этой схеме будут достаточно нелинейны, поэтому при рассчётах придётся делать различные упрощения и допущения.

Для начала давайте будем считать, что ёмкость конденсатора C₂ достаточна для полного сглаживания пульсаций напряжения после моста, то есть напряжение на конденсаторе C₂ = const. Далее попробуем нарисовать пару графиков, — напряжение на входе моста (U_M) и ток через конденсатор C₁ (I_C1), опираясь на график сетевого напряжения U_С(t). Будем считать, что сетевое напряжение у нас изменяется по синусоидальному закону и имеет амплитуду Uca (вообще-то рисовать мы будем косинусоиду, нам так будет удобнее, но это по сути одно и то же, только косинусоида сдвинута относительно синусоиды на π/2).

Рассуждаем следующим образом: в каждый момент времени полное напряжение и полный ток в этой цепи можно описать следующими уравнениями:

U_C=U_C1+U_М (1), i_C=i_C1+i_М (2)

В момент времени t₀ уравнение напряжения примет вид: Uca=U_C1+U_М. Поскольку Uca — это максимальное значение сетевого напряжения, то U_C1 и U_М также в этот момент должны иметь максимальные значения (здесь в логике есть небольшой провал, максимум суммы — это не всегда сумма максимумов, функции могут быть сдвинуты по фазе, но… в общем, мы потом всё экспериментально проверим).

Максимальное значение U_М равно Uвых, поскольку если бы напряжение на мосту поднималось выше, то и конденсатор C₂ заряжался бы до большего напряжения (мост бы открылся и к конденсатору C₂ потёк бы зарядный ток, увеличивая напряжение на нём).

Токи через конденсатор и мост в момент t₀ равны нулю. Про мост я выше уже написал (если бы через него тек ток, то конденсатор C₂ заряжался бы дальше), а через C₁ ток не течёт, поскольку ток через конденсатор — это первая производная от напряжения, которая в точках экстремума обращается в ноль (значит когда напряжение на конденсаторе максимально — ток равен нулю).

Далее сетевое напряжение (U_C) начинает уменьшаться. При этом напряжение на C₁ не меняется (тока-то через мост нет, заряд на C₁ не меняется), следовательно вместе с падением U_C уменьшается напряжение на входе моста.

В момент, когда сетевое напряжение упадёт до значения Uca-2Uвых (момент времени t₁) — напряжение на входе моста достигнет значения -Uвых (находим с помощью формулы 1), диоды моста откроются и в первичной цепи (через мост и конденсатор C₁) потечёт ток. При этом напряжение на входе моста перестанет меняться (помните, мы договорились, что ёмкость C₂ достаточно большая для того, чтобы полностью сгладить пульсации).

Обратите внимание, что напряжение на входе моста в этот момент равно -Uм, так что ток потечёт в обратную сторону от того направления, в котором он тёк до момента времени t₀. Этот ток, поскольку он течёт в обратную сторону, начнёт перезаряжать конденсатор C₁.

К моменту времени t₃ напряжение в сети достигнет максимума, только с противоположной относительно момента t₀ полярностью. Соответственно, для этого момента экстремума сетевого напряжения будут справедливы все те же рассуждения касательно напряжений и токов, которые мы использовали для момента t₀. То есть, к этому моменту конденсатор C₁ полностью перезарядится (напряжение на нём достигнет максимального значения отрицательной полярности), а ток через C₁ и мост упадёт до нуля.

Далее, по мере роста сетевого напряжения, напряжение на конденсаторе C₁ будет оставаться неизменным, а напряжение на входе моста будет расти.

В момент времени t₄, когда сетевое напряжение вырастет до значения -(Uca-2Uвых), напряжение на входе моста достигнет значения Uвых, диоды моста откроются и в первичной цепи (через мост и конденсатор C₁) снова потечёт ток. Этот ток снова будет перезаряжать конденсатор C₁, но уже напряжением положительной полярности.

В момент t₆ напряжение на конденсаторе C₁ достигнет максимального значения положительной полярности, а ток через C₁ и мост упадёт до нуля.

Далее весь цикл повторится с самого начала.

Теперь давайте вспомним закон сохранения заряда. В соответствии с этим законом за один полный цикл через конденсатор C₁, мост и нагрузку должно протекать одинаковое количество заряда. Поскольку ток нагрузки у нас постоянный, то количество заряда, протекающего через нагрузку за один цикл, можно найти по формуле Q=Iн*tцикла=Iн/fc, где fc — частота питающего сетевого напряжения. Количество заряда, протекающего через конденсатор C₁, будет равно площади под графиком тока (заштрихованная площадь графика I_C1(t)). Остаётся только найти эту площадь, приравнять её к заряду, протекающему за один цикл через нагрузку, и выразить из полученного выражения необходимую ёмкость конденсатора C₁ в зависимости от тока нагрузки.

Подробные математические расчёты можно найти под вторым спойлером.

[свернуть]