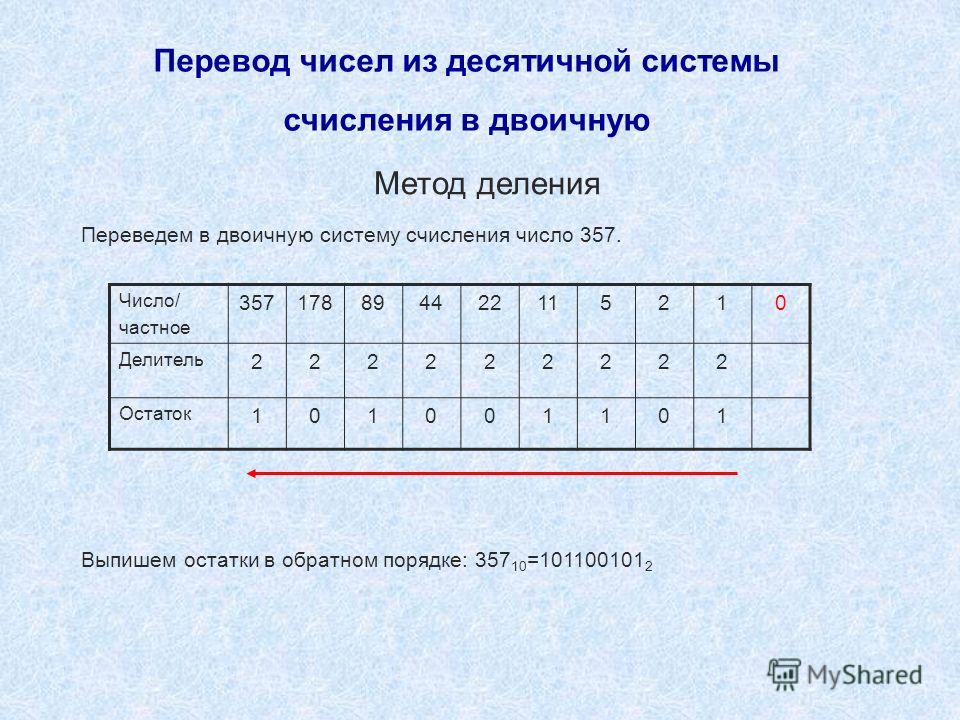
Перевод чисел из одной системы счисления в другую с использованием программных сред «Калькулятор» и «MS Excel»
Тип урока: урок с применением современных компьютерных технологий.
Вид урока: комбинированный.
Технология: личностно-ориентированная, развивающая.
Пояснение: при хорошей подготовке учащихся можно провести как один урок. При слабой подготовке можно разделить на два урока.
Цель урока.
Повторить и закрепить знания учащихся по способам представления чисел в позиционных системах счисления, переводу целых чисел из десятичной системы счисления в любую другую и обратно с помощью программных сред обработки числовой информации Калькулятор и MS Excel.
Задачи урока.
- Образовательная – закрепить знания
учащихся по способам представления чисел в
позиционных системах счисления, переводу
десятичных чисел в любую другую и обратно,
повторение операций копирования, ввода формул и
данных в ячейки электронной таблицы, построение
точечных диаграмм.

- Развивающая – развитие логического мышления, формирование информационной культуры, компьютерной грамотности и потребности в приобретении знаний, умения обобщать, систематизировать полученные знания.
- Воспитательная – воспитание познавательного интереса учащихся, чувства товарищества, умения слушать.
Изучаемые вопросы:
- Система счисления: позиционная и непозиционная.
- Развернутая форма записи числа.
- Перевод чисел из любой системы счисления в десятичную.
- Перевод чисел из десятичной системы счисления в любую другую.
Практика. Перевод целых чисел из одной системы счисления в другую с помощью приложения “Калькулятор” и программы “MS Excel”.
Приобретаемые умения и навыки:
- Перевод чисел из десятичной системы счисления в
двоичную, восьмеричную, шестнадцатеричную и
обратно с помощью приложения Калькулятор.

- Перевод чисел из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно с помощью ЭТ (Excel).
- Построение точечных диаграмм.
- Использование стандартных функций “ОКРУГЛВНИЗ” и “ОСТАТОК”.
Межпредметные связи: математика – координатная плоскость, округление чисел, деление с остатком.
Домашнее задание: § 45, вопрос № 4 (учебник И. Г. Семакин 7–9).
Ход урока
Мы переходим к изучению темы “Теоретические основы компьютера”. Она включает следующие темы:
- Представление чисел
- Машинная арифметика
- Представление команд
В теме “Представление чисел” рассматриваются следующие темы: “Системы счисления”, “Коды чисел”.
Цель. Повторить и углубить знания о
системах счисления, перевод чисел из десятичной
системы счисления в любую другую и обратно с
помощью программных сред обработки числовой
информации Калькулятор и MS Excel.
Презентация “Система счисления”
План изложения темы.
Системы счисления. Виды систем счисления
Перевод десятичных чисел из десятичной системы счисления в любую другую и обратно. (Слайды 7–10)
Перевод целых чисел из десятичной системы счисления с помощью приложения Калькулятор в двоичную, восьмеричную, шестнадцатеричную системы счисления. (Слайд 11)
Перевод целых чисел из десятичной системы счисления с помощью приложения Excel в двоичную, восьмеричную, шестнадцатеричную системы счисления, используя общий метод перевода.
Теория
I. Основные понятия темы
Цифра – это символ, используемый в записи числа.
Система счисления – это способ записи (изображения) чисел.
Алфавит системы счисления – это множество всех
символов (знаков), используемых для записи чисел
в данной системе счисления.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – алфавит десятичной позиционной системы счисления
I, V, X, L, C, D, M – алфавит римской непозиционной системы счисления
Системы счисления: непозиционные системы счисления, позиционные системы счисления.
Любое десятичное число можно представить в виде суммы произведений значащих цифр числа на степени десятки. Такое представление называется развернутой формой записи числа.
15525510 = 1 ·105 + 5 ·104 + 5 ·103 + 2 ·102 + 5 ·101 + 5 ·100
2534,6510 = 2 ·103 + 5 ·102 + 3 ·101 + 4 ·100 + 6 ·10-1 + 5 ·10-2
Эти примеры показывают, что в развернутой форме
показатель степени десяти зависит от позиции соответствующей
цифры в записи числа. Позиция цифры в записи
числа называется разрядом числа. Цифра в
разряде единиц умножается на 100 = 1; цифра в
разряде десятков умножается на 10
Цифра в
разряде единиц умножается на 100 = 1; цифра в
разряде десятков умножается на 10
Степень десятки равна номеру соответствующего разряда в числе.
Формула представления числа
Хb = an? · bп + … + a0 · b0 + a-1 · b-1 + …
Число можно представить в виде суммы произведений составляющих его цифр на соответствующие степени основания системы. На этом принципе основан перевод чисел из любой СС в десятичную СС.
111101
3D16 = 3 ·161 + 13 ·160 = 48 + 13 =6110
Закрепление
- Какое количество цифр используется для записи чисел в восьмеричной СС?
- Назовите наибольшее однозначное число в десятичной СС? В шестнадцатеричной СС?
- Назовите числа соответствующее данному
разложению в А8, А10.

1*8
II. Перевод в десятичную СС
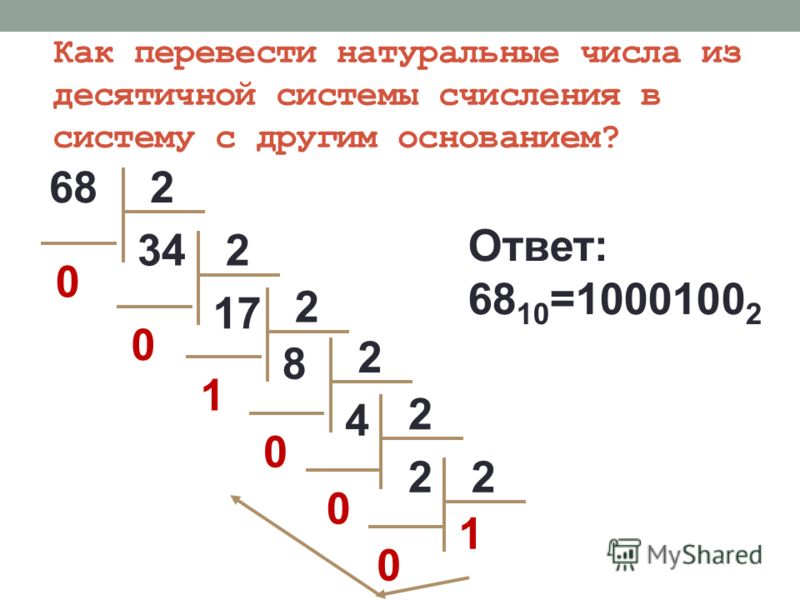
Данное десятичное число делится с остатком на основание системы. Полученный остаток – это младший разряд искомого числа, а полученное частное снова делится с остатком на основание системы и т.д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное – старшая цифра искомого числа.
Перевод дробного десятичного числа в другую систему счисления производится путем последовательных умножений на основание новой системы с выделением цифр целой части произведений в качестве искомых.
Вертикальная черта отделяет целые части от
дробных частей. Подчеркиванием отмечены искомые
значения цифры дробного числа. Умножение
повторяется до тех пор, пока в дробной части
очередного произведения не получится ноль или не
будет обнаружен период повторяющихся цифр.
Фронтальная работа.
Перевести число из А2 в А10: 1010112 43
Перевести число из А16 в А10: 4А16 74
Перевести число из А10 в А2: 17, 2510 10001, 01
III. Перевод целых чисел из одной системы
счисления в другую с помощью приложения
“Калькулятор”.
Практическая работа.
I. Перевести число 849 с помощью приложения Калькулятор в двоичную, восьмеричную, шестнадцатеричную системы счисления.
- Открыть приложение Калькулятор (Вид Инженерный)
- Ввести целое десятичное число 849.
- Перевести это число в двоичную, восьмеричную, шестнадцатеричную системы счисления. Полученные данные скопировать и вставить в электронную таблицу Excel (Практика.xls):
| A10 | A10 | A2 | A10 | A8 | ||
| 849 | 849 | 849 |
II. Перевести с помощью Калькулятора
данные из таблицы в десятичную систему
счисления, занести их в таблицу Excel и построить
точечную диаграмму. Файл сохранить в личной
папке под именем praktika.xls
Перевести с помощью Калькулятора
данные из таблицы в десятичную систему
счисления, занести их в таблицу Excel и построить
точечную диаграмму. Файл сохранить в личной
папке под именем praktika.xls
(Раздаточный материал с таблицами). <Приложение 4>
III. Используя метод перевода целого десятичного числа в другие системы счисления переведите число 849 в двоичную, восьмеричную, шестнадцатеричную системы счисления, используя функции ЭТ:
= ОКРУГЛВНИЗ ()
= ОСТАТ ()
Теория.
Стандартные функции округления числа ОКРУГЛВНИЗ, ОКРУГЛВВЕРХ
= ОКРУГЛВНИЗ ( <АРИФМ ВЫРАЖЕНИЕ>; <КОЛ-ВО ДЕСЯТ. РАЗРЯДОВ>)
= ОКРУГЛВНИЗ (157,856; 0) 157
= ОКРУГЛВВЕРХ (157,856; 0) 158
= ОКРУГЛВНИЗ (157,856; 2) 157, 85
= ОКРУГЛВНИЗ (С4/2; 0) 78
- Какой объект является аргументом этой функции? (Числовое
значение ячейки С4 разделить на 2.
 )
) - Что означает, что второй аргумент имеет значение 0? (Полученное частное округлено с точностью до единицы.)
| 157, 856 |
| 78, 928 |
| 157 |
| 158 |
| 157,85 |
| 78 |
2. Стандартная функция ОСТАТОК
= ОСТАТОК (12, 6) 0
= ОСТАТОК (45, 2) 1
= ОСТАТОК (F4, 2)
= ОСТАТОК (<АРИФМ.ВЫРАЖ>, <НАТУРАЛЬНОЕ ЧИСЛО>)
| 61 | 1 |
| 30 | 0 |
| 15 | 1 |
| 7 | 1 |
| 3 | 1 |
| 1 | 1 |
6110 = 1111012
Итог урока.
Сегодня на уроке мы повторили и систематизировали ранее полученные знания, но и использовали различные программные среды для решения одной и той же задачи.
Мы сегодня познакомились с новыми возможностями приложения Калькулятор, и с новыми функциями и возможностями Excel.
Приложение 1
(презентация)
Приложение 2 (практическая
работа для учителя)
Приложение 3 (практическая
работа для учащихся)
Приложение 4 (таблицы)
Приложение 5 (текст
практической работы)
App Store: калькулятор — Calc Pro +
Снимки экрана (iPhone)
Описание
10 в 1 Калькулятор!
10 в 1 Калькулятор!
Лучший мобильный калькулятор, теперь доступен и на Вашем iPhone. Он единственный, кто действительно может заменить Ваш карманный калькулятор. Calc Pro предлагает больше возможностей, функции и большую точность, чем любой другой мобильный калькулятор. Calc Pro на сегодняшний день является лучшим выбором для учёбы, бизнеса и дома. Проверяете ли Вы последний курс валюты или делаете простые преобразования величин для приготовления вашего любимого торта, Calc Pro позволяет легко произвести даже самые сложные расчеты.
Calc Pro на сегодняшний день является лучшим выбором для учёбы, бизнеса и дома. Проверяете ли Вы последний курс валюты или делаете простые преобразования величин для приготовления вашего любимого торта, Calc Pro позволяет легко произвести даже самые сложные расчеты.
10 мощных калькуляторов:
• Обычный калькулятор.
• Научный (с ОПЗ(RPN) — Обратная Польская Запись).
• Построение графиков функций: Введите до 8 уравнений. Дополнительные функции при построении графиков функции: построение нескольких графиков одновременно, нахождение точек на графике и показ касательных к графику.
• Базовые преобразование: Преобразование между десятичной, шестнадцатеричной, восьмеричной и двоичной системами исчислениями.
• Преобразование единиц измерения: Более 3000 преобразования в 19 различных категориях.
• Константы: Более 1500 констант в 4 категориях: Математика, Физика, Солнечная система, и Периодическая Таблица Элементов.
• Калькулятор статистики: Вводите и сохраняйте свой данные для регрессионных вычислений.
• Финансовый калькулятор: 10 рабочих листов, Ипотека, Совет, Кредит, Временная стоимость денег, Финансовые даты, Процентное изменение, Безубыточность, Прибыль, Амортизация, Сложных проценты.
• Мировые валюты: 150 + валют обновляется ежедневно.
• Дата и время: Расчет точной даты и времени. Лунные фазы включены.
Пять вариантов отображения: обычный, научный, фракции, инженерный и фиксированный (2-10 десятичных знаков).
Пять режимов калькулятора: простой, алгебраический, прямой алгебраический, выражения и ОПЗ(RPN) — Обратная Польская Запись.
Пять видов шкурок каждая с десять цветовыми схемами.
Дополнительные функции при построении графиков функции: построение нескольких графиков одновременно, нахождение точек на графике и показ касательных к графику.
Лента отображает Ваши последние уравнения и позволяет копировать или отправлять друзьям.
======================================
См. информацию на Twitter — @Panoramicsoft
000Z» aria-label=»1 сентября 2021 г.»>1 сент. 2021 г.
Версия 6.8.6
Устранение небольших багов.
Оценки и отзывы
Оценок: 417
Щ
Защити дудлблиущ не бббд билайн не дл
Пользователь
После обновления 18 мая программа 6.7.0, не запускается на iOS 10.3. До обновления работало без всяких нареканий.
.
Мусор
Разработчик Panoramic Software Inc. указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
- Идентификаторы
- Данные об использовании
- Диагностика
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Подробнее
Информация
- Провайдер
- Panoramic Software Inc.
- Размер
- 83 МБ
- Категория
- Утилиты
- Возраст
- 4+
- Copyright
- © 2007-2021 Panoramic Software Inc.
- Цена
- Бесплатно
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Двоичный калькулятор из бусин и палок — Журнал «Код»
Можно ли создать автоматическую счётную машину, если у вас есть только бусины и палки? Да, можно.
На наш друг Эван из YouTube провёл такой опыт и получил интересный результат: он создал механическую счётную машину, которая работает как обычный цифровой калькулятор, но при этом не требуют ни электричества, ни микрочипов. Всё работает благодаря гравитации и двоичной логике.
Если вы понимаете по-английски, смотрите видео. Если нет — читайте наш разбор.
В чём идея
Существуют электронные калькуляторы: они используют алгоритмы преобразования двоичного кода, чтобы складывать, умножать, вычитать и делить.
Все алгоритмы основаны на логических операциях: И, ИЛИ, НЕ и др. Если взять два числа в двоичном коде и прогнать каждый их бит через последовательность логических операций, то на выходе получится, например, сумма. Соль в том, чтобы правильно соединить между собой логические операции.
В обычной жизни логические операции исполняют транзисторные полупроводники. Представьте, что это трубы и краны, только не для воды, а для электричества. И электричество, которое «вытекает» из одного крана, может управлять открытием или закрытием другого крана.
Если много-много раз правильным образом соединить эти полупроводниковые «краны», получится калькулятор.
Мы об этом подробно рассказывали в цикле статей про сумматоры →
Что новенького
Эван решил сделать калькулятор на той же логической базе, что и настоящие калькуляторы, но с одним отличием: вместо тока и полупроводников он использует бусины и силу гравитации. Бусинки падают вниз, катятся, задевают какие-то стены, отодвигают что-то на своём пути и так далее. При этом такой калькулятор работает как нужно: числа считаются и все логически элементы работают правильно.
🤔 Зачем это нужно? Да просто так.
Двоичная логика
Самые простые состояния в логике — ДА и НЕТ. Их два, поэтому такая логика, где используются только два состояния, называется двоичной. Мы уже разбирали, как устроена двоичная логика и почему она используется для всех вычислений в компьютере.
Мы уже разбирали, как устроена двоичная логика и почему она используется для всех вычислений в компьютере.
В транзисторах ДА обозначается единицей и наличием тока в проводнике, а НЕТ — нулём и отсутствием тока. Так как у нас вместо тока бусинки, то правила будут такие:
1 = есть бусинка
0 = нет бусинки
Этого нам хватит, чтобы сделать логические элементы. Чтобы работать с числами, мы просто будем переводить их в двоичную систему счисления и смотреть, в каком порядке ставить бусинки и пустоту между ними.
Например, вот как в двоичном представлении будет выглядеть число 5:
Колонны — это трубы, в которые будут падать бусинки.А вот как запишется число 12:
🤔 Если не понимаете, почему цифры стоят именно в этих местах, — прочитайте статью про двоичное счисление, там всё хорошо объяснено.
Логическое И
Первое, что делаем, — реализуем логическое И. Если забыли, что это такое, — почитайте в статье про транзисторы, а пока вот короткая справка:
На вход поступает два сигнала. Логическое И выдаёт в результате единицу, только если на вход поступило сразу две единицы. Если хотя бы один из них ноль — будет ноль.
Логическое И выдаёт в результате единицу, только если на вход поступило сразу две единицы. Если хотя бы один из них ноль — будет ноль.
Так как у нас бусинки, то на входе и выходе тоже будут бусинки. Первая версия элемента, которую сделал Эван, выглядела так:
Логика была такая: падают две бусинки, одна закрывает ямку, вторая перекатывается и передаёт сигнал дальше. Если бусинка будет одна, то она застрянет в лунке и сигнал дальше не пойдёт.
Но такая реализация оказалась ненадёжной:
Эван модернизировал элемент, добавив в него розовые подвижные части — в зависимости от положения бусинок они сдвигались, освобождая итоговую бусинку:
Отлично, попробуем так же реализовать остальные элементы.
Логическое ИЛИ
ИЛИ отличается от И тем, что на входе достаточно хотя бы одной единицы, чтобы на выходе тоже получилась единица. Ноль в логическом ИЛИ возвращается только тогда, когда на входе всё по нулям.
Это оказалось проще, чем И, — достаточно, чтобы в трубу попала хотя бы одна бусинка, которая вытолкнет итоговую:
Логическое НЕ
А вот этот элемент придумать было сложнее: нужно, чтобы он запускал бусинку, когда на вход не попадало ничего. Но как это сделать на практике, как отследить отсутствие бусинки с точки зрения физики?
Но как это сделать на практике, как отследить отсутствие бусинки с точки зрения физики?
Выход Эван придумал такой: он сильно заранее запускает итоговую бусинку, которая медленно скатывается вниз. За это время по соседней трубе пролетит или не пролетит бусинка, которая закроет выход для итоговой. Если пролетит (на входе будет единица), то на выходе будет ноль, потому что выход будет закрыт. А если по трубе ничего не пролетит, то выход не закроется, и итоговая бусинка в конце концов доедет до выхода:
Удвоитель
Иногда нужно распараллелить сигнал, чтобы он пошёл сразу в обе точки. В электронике это сделать просто: делаем два провода в нужном месте, и электроны разбегаются в обоих направлениях. Но в механической логике так не получится, нужно идти на хитрость. Например, сделать развилку с дополнительной бусинкой:
Перенос бусинки наверх
Так как у нас всё завязано на гравитации и бусинках, то может понадобиться такое: итоговая бусинка вышла из какой-то части механизма, и её нужно отправить наверх, для запуска новых вычислений. Для этого Эван придумал виртуальный перенос бусинки — та, которая внизу, запускает ту, которая наверху:
Для этого Эван придумал виртуальный перенос бусинки — та, которая внизу, запускает ту, которая наверху:
Собираем калькулятор для двух бусинок
Чтобы проверить в деле всю предыдущую теорию, Эван собирает простой сумматор: он складывает два сигнала. Забегая чуть вперёд, Эван сразу предусматривает перенос разряда (carry).
Простой калькулятор на JavaScript
Вот какая схема нужна для сложения двух сигналов на бусинках:
Отлично, у нас работает сложение двух сигналов, поэтому можно переходить к чему посложнее. Но сначала поговорим про перенос разряда.
Обрабатываем перенос разряда
Когда мы складываем обычные числа, например 19 и 7, то у нас иногда получается перенос единицы в новый разряд:
В двоичной системе счисления всё то же самое — разряды переносятся налево и складываются с теми числами, которые уже там стоят:
Чтобы сделать такой же перенос разряда и получить ноль после сложения двух единиц, добавим элемент XOR. Он возвращает ноль, если на входе было сразу две единицы или оба нуля, в противном случае он возвращает единицу. Именно так работает сложение с переносом в двоичной системе, а вот как это работает на бусинках:
Именно так работает сложение с переносом в двоичной системе, а вот как это работает на бусинках:
Чтобы проверить работу элемента в деле и убедиться, что 1+1+1 будет давать 1 в сумме и 1 в новом разряде, Эван собирает основную схему сумматора:
Видно, что на выходе получилось 11: одна бусинка вышла в первом разряде, а вторая — в переносе (carry).
Если собрать три таких сумматора подряд, можно складывать трёхразрядные числа, например, 7 (111) и 5 (101):
Чтобы посмотреть на результат работы, посмотрите видео с отметки 7:35. Мы специально не будем портить интригу, чтобы вы сами оценили весь масштаб движения бусинок 🙂
Текст:
Михаил Полянин
Редактор:
Максим Ильяхов
Художник:
Алексей Сухов
Корректор:
Ирина Михеева
Вёрстка:
Кирилл Климентьев
Соцсети:
Виталий Вебер
Средство преобразования с основанием 16 в число с основанием 10
Базовый номер
База 10
База 10 эквивалентна десятичной дроби.
База-11
Десятичная (база-11) позиционная система счисления основана на числе одиннадцать. Для десятичной дроби требуется одиннадцать символов от 0 до 9 и A.
Основание-12
Двенадцатеричная система (также известная как основание-12 или дюжина) представляет собой позиционную систему счисления с основанием двенадцать. Для двенадцатеричной системы требуется двенадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A и B.
Основание-13
Трехдесятичная, треугольная, трискадичная или основание-13 — это позиционная система счисления, основанная на тринадцати. Он использует 13 различных цифр для представления чисел. Цифры для основания 13 могут быть 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B и C. основано на числе четырнадцать. Для тетрадесятичного числа требуется четырнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D.
База-15
Пятидесятеричная (база-15) позиционная система счисления основана на числе пятнадцать. Для пятидесятичного числа требуется пятнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E.
Для пятидесятичного числа требуется пятнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E.
Base-16
Base-16 эквивалентно в шестнадцатеричный.
База-17
База 17 или семеричная система счисления — это позиционная система счисления с основанием 17. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, C, D, E, F и G.
Base-18
Основание 18 или восьмидесятеричное число основано на восемнадцати и требует 18 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G и H).
База-19
База 19 или недесятичная система основана на девятнадцати и требует 19 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H и I.
Основание 2
Основание 2 эквивалентно двоичному коду
Основание 20
Система счисления с основанием 20 основана на двадцати. , 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I и J.
Основание-21
Основание 21 или недесятичная система счисления основана на двадцати одном. Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K.
Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K.
Основание-22
Основание 22 или двенадцатеричная система счисления основана на двадцати двух. Используются двадцать два символа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K и L.
Основание-23
Основание 23 или десятичная система счисления основана на двадцати трех. Используются двадцать три символа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L и M.
Основание-24
Система с основанием 24 — это система счисления, основанная на 24. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M и N.
Основание-25
Система счисления с основанием-25 — это система счисления, основанная на 25. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N и O.
Основание-26
Шестнадцатеричная система счисления имеет основание двадцать шесть. В этой системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L, M, N, O и P.
В этой системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L, M, N, O и P.
Base-27
Семидесятичная система счисления имеет основание двадцать- Семь. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N, O, P и Q.
Base-28
Система счисления с основанием 28 основана на двадцати восьми и использует 28 различных символов ( 0, 1, 2, 3, 4, 5, 6, 7 , 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q и R.)
Base-29
Система счисления с основанием 29 основана на двадцати девяти и использует 29 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R и S.)
Base-3
Ternay или тринарная система счисления с основанием 3. Для троичной системы счисления требуется только три символа: 0, 1 и 2.
Основание-30
Тройная система счисления или основание 30 — это позиционная система счисления, использующая 30 в качестве основания. Цифры в этом основании могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-T.
Цифры в этом основании могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-T.
Основание-31
Нетроичная система счисления или основание 31 — это позиционная система счисления, использующая 31 в качестве основания. Цифры в этом основании могут быть представлены с помощью арабских цифр 0-9 и латинских букв A-U.
Основание-32
Двенадцатикратная или основание-32 — это система счисления с основанием 32. Цифры в этой базе могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-V.
Base-33
Система счисления с основанием 33 основана на 33 различных символах (числа 0-9и букву A-W).
Base-34
Система счисления с основанием 34 основана на 34 различных символах (числа 0-9 и буквы A-X).
База-35
Система счисления с основанием 35 основана на 35 различных символах (числа 0-9 и буквы A-Y).
Основание-36
Основание 36 или шестнадцатеричная система счисления — это позиционная система счисления, использующая 36 в качестве основания. Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9 и латинских букв A-Z.
Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9 и латинских букв A-Z.
Основание-4
Четверка — это система счисления с основанием 4. Он использует цифры 0, 1, 2 и 3 для представления любого действительного числа.
Основание-5
Квинарий (основание-5) — это система счисления, основанная на пятерке. Базовая пятерка начинается с 0-4.
Основание-6
Сенарий (основание-6) — это система счисления с секс-символами (0, 1, 2, 3, 4, 5).
Base-7
Семеричная система счисления является системой счисления с основанием 7 и использует цифры 0-6.
Основание-8
Base-8 эквивалентен восьмеричной системе.
Base-9
Nonary — это система счисления с основанием 9, обычно использующая цифры 0-8.
Двоичная система счисления
Двоичная система счисления, или система счисления с основанием 2, представляет числовые значения с помощью двух символов: 0 и 1.
Десятичная система счисления
база.
Шестнадцатеричная
Шестнадцатеричная (также с основанием 16 или шестнадцатеричная) — это позиционная система счисления с основанием 16. В ней используется шестнадцать различных символов, чаще всего символы 0–9.для представления значений от нуля до девяти и A, B, C, D, E, F.
Восьмеричная система счисления
Восьмеричная система счисления, или сокращенно восьмеричная, представляет собой систему счисления с основанием 8 и использует цифры от 0 до 7
Преобразование в другие системы счисления — онлайн-калькулятор
десятичных знаков) от данной системы счисления (основания) до другой базы (двоичной, десятичной, шестнадцатеричной, восьмеричной и всех оснований от 2 до 62).
Как пользоваться этим калькулятором?
Используемые цифры
Для оснований от 2 до 10 мы используем арабские цифры 0123…789.
для оснований от 10 до 36 мы используем символы ABCD…XYZ (прописные буквы) для представления чисел 11,12,13. ..34,35,36. Для этих баз (от 10 до 36), если вы вводите числа строчными буквами, мы автоматически преобразуем их в прописные буквы.
..34,35,36. Для этих баз (от 10 до 36), если вы вводите числа строчными буквами, мы автоматически преобразуем их в прописные буквы.
Для оснований от 36 до 62 мы используем строчные буквы (abcdef…xyz). Например, в базе 62 используются цифры: 0123456789 ABCDEFGHIJKLMNOPQRSTUVWXYZ abcdefghijklmnopqrstuvwxyz, что в сумме составляет 62 символа. Обратите внимание, что для этих баз важны регистры букв. Например, А=11, но а=37. 90 = 71`
Повторим тот же процесс, 71 ÷ 9 = 7 остается 8, выводим, `a_1` = 7 и `a_0` = 8
Последовательно доказано,
`a_3 = 1`
`a_2 = 5`
`a_1 = 7`
` a_0 = 8`
1205 по основанию 9 записывается как 1578 по основанию 9.
Подводя итог этому методу,
Чтобы преобразовать число P из основания 10 в основание n
— Запись степеней n (целевое основание)
— Фрейм P на 2 последовательных степени n (кстати, это определяет количество цифр P в базе n)
— Выполните евклидово деление P на степень n, определенную на предыдущем шаге (наименьшее значение из двух степеней)
— Частное этого деления равно первой цифре P (начиная слева) в основании n
— Повторяйте последовательно эти деления, используя остаток в качестве нового делимого и непосредственно меньшую степень в качестве делителя, пока не достигнете степени 1 числа n.
Преобразовать число по основанию n в основание m?
Самый простой способ — пройти по основанию 10:9.0170 — Сначала преобразуйте число из базы n в базу 10, следуя первому методу, описанному выше.
— Затем преобразуйте полученное число в базе 10 в базу m, следуя второму методу выше.
Пример: преобразовать 1526 из 7 по основанию 2
1526 в 7 = 608 в 10
608 в 10 = 1001100000 в 2 десятичное число с дробной частью по основанию n
Чтобы упростить задачу, возьмем n = 16 и P = 220,412, где P — десятичное число для преобразования в основание 16. Приведенный ниже метод можно легко обобщить на любое основание n.
У нас есть,
`P = (220,412)_10`
Мы пытаемся переписать P с точностью до 3 знаков после запятой по основанию 16.
Итак, мы ищем `c_2, c_1, c_0, c _ (- 1) , c _ (- 2), c _ (- 3)`, 16 цифр с основанием, например
`P = (c_2c_1c_0.c_(-1)c_(-2)c_(-3))_16`
Примечание: целая часть P по основанию 16 (часть P до десятичной точки) состоит из 3 или менее цифр, потому что в системе счисления 10 целая часть (= 220) состоит из трех цифр. Следовательно, мы ищем три цифры `c_2, c_1, c_0` для всей части, не больше! 9k*P` и сохранить его целую часть
Следовательно, мы ищем три цифры `c_2, c_1, c_0` для всей части, не больше! 9k*P` и сохранить его целую часть
— Преобразовать последнее в основание 16, используя метод последовательного деления на степени 16 (см. подробности вышеприведенного метода, применимого к целым числам)
— Вставить десятичную точку после k-я цифра справа
Программирование
Python
Эта программа на Python преобразует число из десятичной системы счисления в другую базу.
строка импорта
digs = строка.цифры + строка.ascii_letters
def int2base (x, база):
если х < 0:
знак = -1
Элиф х == 0:
вернуть раскопки [0]
еще:
знак = 1
х * = знак
цифры = []
в то время как х:
digits.append (копает [int (x% base)])
х = целое число (х/основание)
если знак < 0:
digits.append ('-')
цифры.реверс ()
вернуть ''.join(цифры)
См. также
Евклидово деление
Случайный преобразователь | Преобразование шестнадцатеричной системы счисления в шестнадцатеричную Конвертер длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Откуда: двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base-23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 Как улучшить прием сотового телефона?Используйте контрольный список, чтобы улучшить его! Обзор Различные способы представления чисел Индуистские цифры Roman Системы в других культурах Unary позиционная система Бинарный0007 Negative Numbers Rational Numbers Natural Numbers Integers Complex Numbers Prime Numbers Interesting Facts about Numbers Anti-Fraud Numerals Modern Counting in Commerce Numeral Grouping Unlucky Numbers Изучайте технический английский с помощью этого видео! ОбзорПриложение-калькулятор для iPhone Число — это абстрактное математическое понятие, представляющее количество. Различные способы представления чиселНекоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания. Индуистско-арабские цифры Индо-арабская система счисления сегодня является одной из наиболее широко используемых в мире. Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. Десять — обычное число для счета, потому что у людей десять пальцев, а части тела исторически часто использовались для счета. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках. Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне. Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910). РимскиеРимские цифры использовались в Римской империи и Европе до 14 века. Они до сих пор используются в некоторых контекстах, например, на часах, для обозначения часов. Roman numerals are based on seven numbers written with the letters of the Latin alphabet:
. Заказ важен в виде римской системы, но и малы, но и малы, но и малы, но и малы, но и малы, но не знает, что больше, но и малы, но и малы, но не знает, что больше, но и малы, но и малы, но не знает, что больше, но и малы, но не знает, что больше, но и малы, но не знает, что больше, но и малы, но не знает, что больше, но и малы, но не знает, что больше. меньшее число перед большим означает, что меньшее число вычитается из большего. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, в которой есть только два клинописных символа: один (немного напоминающий букву «Т») и десять (немного похожий на букву «С»). Унарная система счисления. Метки счета в различных культурах Унарная Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему. Позиционная система Позиционная система работает с основанием.
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ Двоичная система счисления Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например: 11111 (31) В этом случае, работая справа налево:
Итак, складывая это вместе, мы получаем 101010. Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» единицы. Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например: 101 (5) Деление и расчет квадратных корней также очень похожи на основание-10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — это отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число. Рациональные числа Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают нули, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательной единицы. Простые числа Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге. Интересные факты о числахКитайские цифры для защиты от мошенничества Числительные для защиты от мошенничестваДля предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив дополнительные штрихи. Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи. Современный счет в торговле Некоторые языки в странах, где в настоящее время используется десятичная система счисления, по-прежнему свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов. Группировка чиселИ в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году. В России и многих странах бывшего СССР все четные числа считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае номер 7 тоже неудачный, потому что он представляет духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов. В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». Это подразумевает, что жизнь окончена, и относится к смерти. 666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или позорным номером, связанным с проституцией. Ссылки Эта статья была написана Катериной Юрием Преобразование шестнадцатеричной системы счисления в десятичную Преобразование 24-й системы счисления в десятичную Преобразование десятичной системы в 20-ю Преобразование 3-й системы в десятичную 7 90Преобразование двоичного числа в шестнадцатеричное Преобразование двоичного числа в десятичное Вам могут быть интересны другие преобразователи из группы «Общие преобразователи единиц измерения»:Преобразователь длины и расстояния массовый преобразователь сухой объем и общие измерения приготовления приготовления Преобразователь площади Объем и общий преобразователь измерения приготовления ТЕМПРЕССОВЫЙ ПЕРЕДАЧНЫЙ Преобразователь времени Преобразователь линейной скорости и скорости Преобразователь угла Преобразователь эффективности использования топлива, расхода топлива и экономии топлива Преобразователь единиц информации и хранения данных Конвертер метрических префиксов Передача данных Скорости обмена валюты Мужская одежда и размеры обуви Женская одежда и размеры обуви Компактный калькулятор. |
Другой метод преобразования между основаниями
Результаты обучения
- Ознакомьтесь с историей позиционных систем счисления
- Определение оснований, которые исторически использовались в системах счисления
- Преобразование чисел между основанием
- Использовать два разных метода преобразования чисел между основаниями
Другой метод преобразования десятичной системы счисления в другую систему счисления
Когда вы читали решение этого последнего примера и пытались решить задачи «Попробуйте», вам, возможно, приходилось несколько раз останавливаться и думать о том, что происходит. Тот факт, что вы, вероятно, изо всех сил пытаетесь следовать объяснению и воспроизвести процесс самостоятельно, в основном связан с тем, что недесятичные системы вам настолько незнакомы. На самом деле, единственная система, с которой вам, вероятно, удобно, — это десятичная система.
На самом деле, единственная система, с которой вам, вероятно, удобно, — это десятичная система.
Как подающие надежды математики, вы всегда должны задавать вопросы вроде «Как я могу упростить этот процесс?» В общем, это одно из основных занятий математиков: они ищут способы взять сложные ситуации и сделать их более простыми или более знакомыми. В этом разделе мы попытаемся это сделать.
Для этого начнем с нашей собственной десятичной системы. То, что мы делаем, может показаться очевидным и, может быть, даже интуитивным, но в этом суть. Мы хотим найти процесс, который, как мы легко распознаем, работает и имеет для нас смысл в знакомой системе, а затем использовать его для распространения наших результатов на другую, незнакомую систему.
Начнем с десятичного числа, 4863 10 . Мы преобразуем это число в десятичную систему счисления. Да, я знаю, что оно уже находится в десятичной системе счисления, но если вы внимательно проследите за тем, что мы делаем, вы увидите, что позже это очень хорошо работает с другими системами счисления. Прежде всего отметим, что наивысшая степень числа 10, при которой число 4863 делится хотя бы один раз, равна 10 90 623 3 90 624 = 1000. 90 844 В общем, это первый шаг в нашем новом процессе; мы находим наивысшую степень, которую данное основание будет делить хотя бы один раз на наше заданное число.
Прежде всего отметим, что наивысшая степень числа 10, при которой число 4863 делится хотя бы один раз, равна 10 90 623 3 90 624 = 1000. 90 844 В общем, это первый шаг в нашем новом процессе; мы находим наивысшую степень, которую данное основание будет делить хотя бы один раз на наше заданное число.
Теперь 1000 делим на 4863:
4863 ÷ 1000 = 4,863
Это говорит о том, что в 4863 четыре тысячи (очевидно). Однако там также говорится, что в числе 4863 0,863 тысячи. Эта дробная часть является нашим остатком и будет преобразована в меньшие степени нашего основания (10). Если мы возьмем это десятичное число и умножим на 10 (поскольку это основание, в котором мы находимся), мы получим следующее:
0,863 × 10 = 8,63
Зачем умножать на 10 в этот момент? Здесь нужно признать, что 0,863 тысячи — это то же самое, что 8,63 сотни. Думайте об этом, пока это не впитается.
(0,863)(1000) = 863
(8,63)(100) = 863
Эти два оператора эквивалентны. Итак, то, что мы на самом деле делаем здесь, умножая на 10, — это перефразирование или преобразование из одного разряда (тысячи) в следующий разряд вниз (сотни).
Итак, то, что мы на самом деле делаем здесь, умножая на 10, — это перефразирование или преобразование из одного разряда (тысячи) в следующий разряд вниз (сотни).
0,863 × 10 ⇒ 8,63
(части тысяч) × 10 ⇒ сотни
Теперь у нас есть 8 сотен и остаток 0,63 сотни, что равно 6,3 десятка. Мы можем сделать это снова с 0,63, оставшимися после этого первого шага.
0,63 × 10 ⇒ 6,3
Сотни × 10 ⇒ Десятки
Итак, у нас есть шесть десятков и 0,3 десятка, что равно 3 единицам, нашему последнему разряду.
А теперь кульминация. Давайте соберем все вместе в одном месте:
Преобразование из базы 10 в базу b : Другой метод Обратите внимание, что на каждом шаге остаток переносится на следующий шаг и умножается на 10, основание. Также на каждом шаге целая часть числа, обведенная кружком, дает цифру, которая принадлежит этому конкретному месту. Что удивительно, так это то, что это работает для любой базы! Итак, чтобы преобразовать число с основанием 10 в какое-либо другое основание, b , у нас есть следующие шаги, которые мы можем выполнить:
Преобразование из базы 10 в базу
b : Другой метод- Найдите наибольшую степень базы b , которая будет делиться на заданное число хотя бы один раз а потом разделить.

- Сохранить целую часть числа и умножить дробную часть на основание b .
- Повторите второй шаг, сохраняя целую часть числа (включая 0), перенося дробную часть на следующий шаг, пока не будет получен результат только целого числа.
- Соберите все части целого числа, чтобы получить число в системе счисления b .
Мы проиллюстрируем эту процедуру несколькими примерами.
Пример
Преобразовать число с основанием 10, 348 10 , в число с основанием 5.
Показать решение
Мы можем сравнить наш результат с тем, что видели ранее, или просто проверить с помощью нашего калькулятора и обнаружить, что эти два числа действительно эквивалентны друг другу.
Пример
Преобразование числа с основанием 10, 3007 10 , на базу 5.
Показать решение
Этот последний пример показывает важность использования калькулятора в определенных ситуациях и осторожность, чтобы не очистить память калькулятора или дисплей, пока вы не дойдете до самого конца процесса.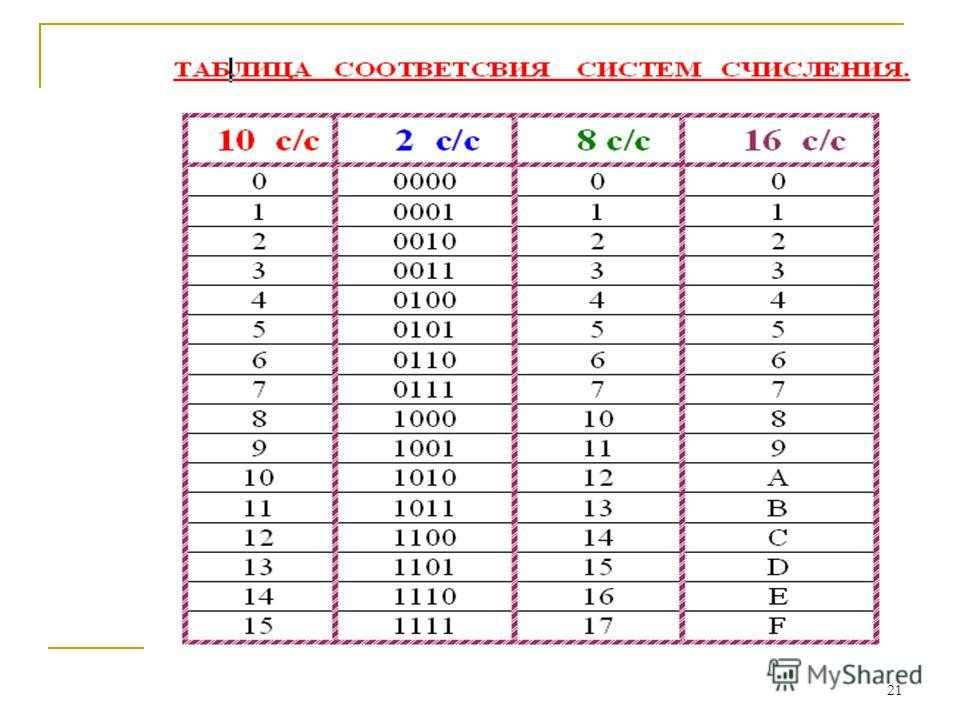
Пример
Преобразовать число с основанием 10, 63201 10 , в число с основанием 7.
Показать решение
Если мы будем округлять даже до двух знаков после запятой на каждом шаге, очищая наш калькулятор на каждом шаге по пути, мы получим ряд чисел, которые не заканчиваются, а начинают бесконечно повторяться. (Попробуйте!) В итоге мы получим что-то, что не имеет никакого смысла, по крайней мере, не в этом контексте. Так что будьте осторожны, чтобы использовать ваш калькулятор с осторожностью для этих проблем преобразования.
Также помните, что если ваше первое деление на 7 5 , то вы ожидаете, что в окончательном ответе будет 6 цифр, соответствующих местам для 7 5 , 7 4 и так далее до 7 0 . Если вы обнаружите, что у вас более 6 цифр из-за ошибок округления, вы знаете, что что-то пошло не так.
Попробуйте
Преобразуйте число с основанием 10, 9352 10 , в число с основанием 5.
Показать решение
Преобразовать число с основанием 10, 1500, в число с основанием 3.
Будьте осторожны, чтобы не очистить свой калькулятор на этом. Кроме того, если вы не будете осторожны на каждом шаге, вы можете не получить все цифры, которые ищете, поэтому двигайтесь медленно и осторожно.
Показать решение
В следующем видеоролике показано, как использовать калькулятор для преобразования чисел с основанием 10 в другие числа с основанием.
Преобразователь двоичных чисел в десятичные, шестнадцатеричные и ASCII
Преобразование двоичных - в десятичные, шестнадцатеричные и ASCII
Щелкайте на кнопках двоичных чисел для переключения между 0 и 1 для каждого бита:
| unsigned binary number (8 bits, one byte) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 | |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| decimal number | 0 | |||||||
| hexadecimal number | 0 | |||||||
| ASCII | ||||||||
A binary number is a number выражается в двоичной системе счисления или в системе счисления с основанием 2 . Двоичное число может выражать любое число, используя только две цифры: 0 и 1. Приведенный выше калькулятор преобразует двоичные числа с от 1 до 8 бит ( один байт ) в десятичном или шестнадцатеричном эквиваленте.
Двоичное число может выражать любое число, используя только две цифры: 0 и 1. Приведенный выше калькулятор преобразует двоичные числа с от 1 до 8 бит ( один байт ) в десятичном или шестнадцатеричном эквиваленте.
- Типы данных
. Двоичное число по умолчанию (один байт). + 1 2 5 + 0 2 4 + 0 2 3 + 1 2 2 + 0 2 1 + 0 2 0
= 128 + 0 + 32 + 0 + 0 + 4 + 0 + 0
= 164
8 бит или байт могут использоваться для представления буквенного символа ASCII (Американский стандартный код для обмена информацией), например, двоичного числа 01000001 или десятичного числа 45 , 90 A.
Decimal - to Binary, Hexadecimal and ASCII Converter
| decimal number | |
|---|---|
| binary number | |
| hexadecimal number | |
| ASCII |
Стандартная система счисления называется десятичной с основанием 10 и использует 10 символов: 0,1,2,3,4,5,6,7,8,9.
Преобразователь шестнадцатеричных чисел в двоичные, десятичные и ASCII
| hexadecimal number | |
|---|---|
| binary number | |
| decimal number | |
| ASCII |
The hexadecimal (also base 16, or hex) is a positional система счисления с основанием 16 .
Шестнадцатеричная система использует шестнадцать различных символов, где 0–9 представляют значения от нуля до девяти, а A, B, C, D, E, F (или a, b, c, d, e, f) , представляющий значения от десяти до пятнадцати.
The default hexadecimal number a4 from the calculator above can be converted to its decimal equivalent:
a4
= a 16 16 1 + 4 16 16 0
= 10 16 1 + 4 16 0
= 160 + 4
= 164
7 4шестнадцатеричное число0845 from the calculator above can be converted to its decimal equivalent:
a4b3
= a 16 16 3 + 4 16 16 2 + b 16 16 1 + 3 16 16 0
= 10 16 3 + 4 16 2 + 11 16 1 + 3 16 0 9 + 3 16 0 1 + 3 16 0 + 1 + 3 16 0 + 11 16 1 + 3 16 0844 + 11 16 1 + 3 16 0845 + 11 16 1 + 3 16 0845 + 11 16 1 . 3
3
= 42163
Шестнадцатеричные и десятичные и двоичные числа
Для полной таблицы - поверните экран!
| Hexadecimal Number | |||||||||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | в | г | д | е | ||||||||
| Decimal Number | |||||||||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||||||
| Двоичное число | |||||||||||||||||||||||
| 0000 | 0001 | 0010 | 0001 | 0010 | 00019 | 0010 | 000 | 0010 | 000 | 0010 | 000 | 0010 | 000 | 0010 | .0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Each hexadecimal digit represents four binary bits - a nibble. Четыре цифровых бита могут представлять до 16 различных значений. Два полубайта по 8 бит — это байт. Компьютеры используют в своих операциях в основном байты или умножения байтов (16, 32, 64 .. бит).
Двоичное представление шестнадцатеричного числа
A4
= 1010 0100
Двоичное представление шестнадцатеричного числа
A4B3
= 1010 01100 1011 0011 0079007 9008 9007 9008 9008 9008 9008 007
79595900007
007
007 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008
9007 9007 9008
9007 9007
9007
9007. систематический способ представления чисел с помощью символьных символов и использует базовое значение для удобной группировки чисел в компактной форме. Наиболее распространенной системой счисления является десятичная, имеющая базовое значение 10 и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Однако существуют и другие системы счисления, и они могут быть более эффективными для использования в определенных целях. Например, поскольку компьютеры используют логическую логику для выполнения вычислений и операций, они используют двоичную систему счисления, базовое значение которой равно 2.
Наиболее распространенной системой счисления является десятичная, имеющая базовое значение 10 и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Однако существуют и другие системы счисления, и они могут быть более эффективными для использования в определенных целях. Например, поскольку компьютеры используют логическую логику для выполнения вычислений и операций, они используют двоичную систему счисления, базовое значение которой равно 2.
Microsoft Office Excel имеет несколько функций, которые можно использовать для преобразования чисел в следующие системы счисления и из них:
Система счисления | Базовое значение | Набор символов |
Двоичный | 2 | 0,1 |
Восьмеричный | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Десятичный | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 |
Шестнадцатеричный | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, Б, В, Г, Д, Ф |
Для выполнения этой задачи используйте функцию BIN2DEC.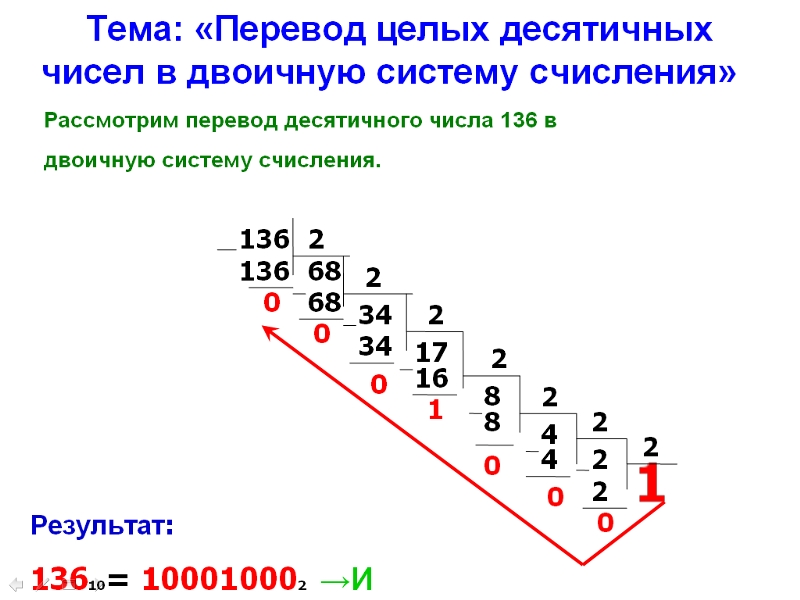
|
Для выполнения этой задачи используйте функцию BIN2HEX.
|
|
Для выполнения этой задачи используйте функцию BIN2OCT.
|
|
Для выполнения этой задачи используйте функцию DEC2BIN.
|
Для выполнения этой задачи используйте функцию DEC2HEX.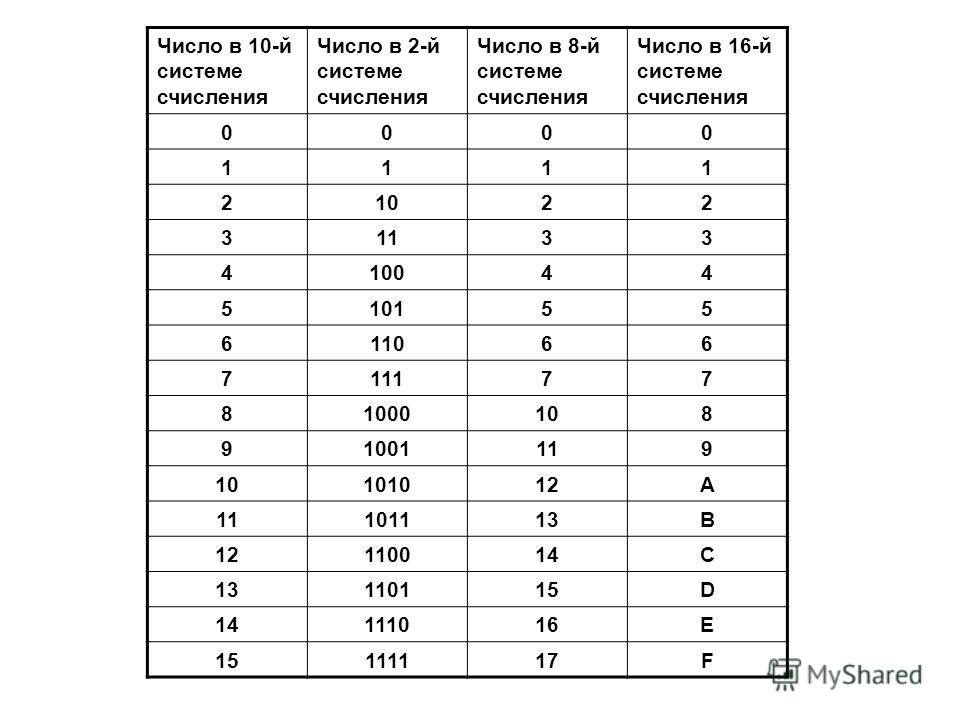
|
Для выполнения этой задачи используйте функцию DEC2OCT.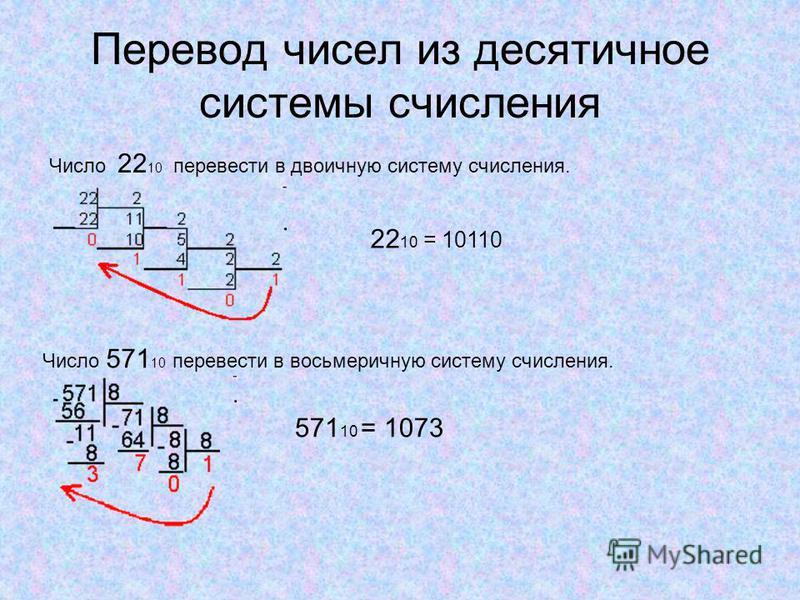
|
Для выполнения этой задачи используйте функцию HEX2BIN.
|
|
Для выполнения этой задачи используйте функцию HEX2DEC.
|
|
Для выполнения этой задачи используйте функцию HEX2OCT.
|
|
Для выполнения этой задачи используйте функцию OCT2BIN.
|
Для выполнения этой задачи используйте функцию OCT2DEC.
|
Для выполнения этой задачи используйте функцию OCT2HEX.





 )
) Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.
Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
 Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.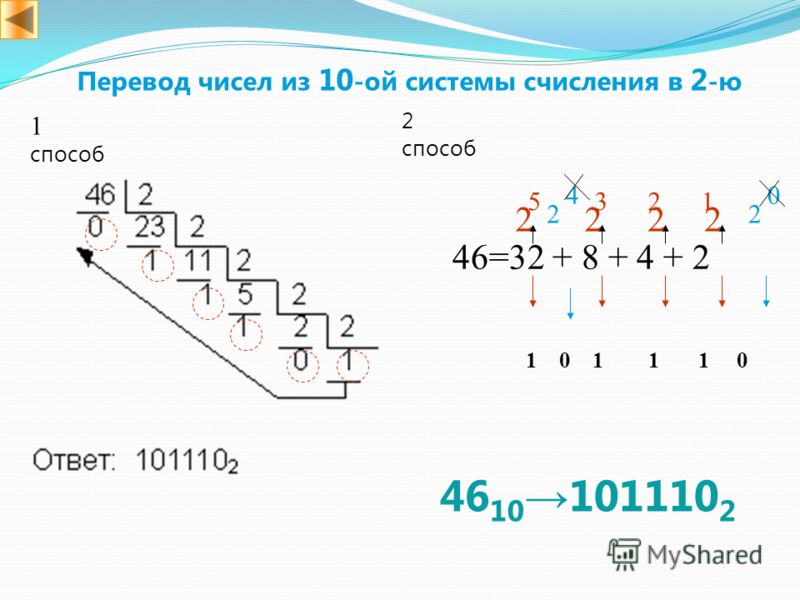 Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике. Например, в базе 10 у нас есть следующее:
Например, в базе 10 у нас есть следующее: Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
 Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
 В Японии другое несчастливое число — 9.0168 9 , что имеет то же произношение, что и «страдание».
В Японии другое несчастливое число — 9.0168 9 , что имеет то же произношение, что и «страдание». Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят. у вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков.
у вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков.
 Это числовая база, наиболее широко используемая современными цивилизациями.
Это числовая база, наиболее широко используемая современными цивилизациями.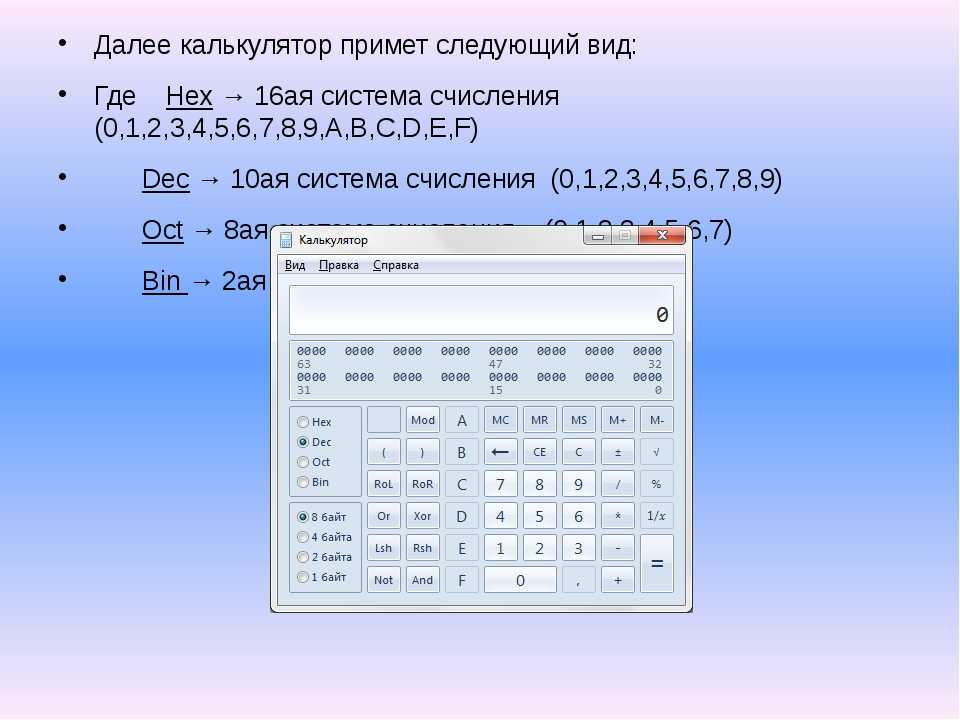 9», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
9», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.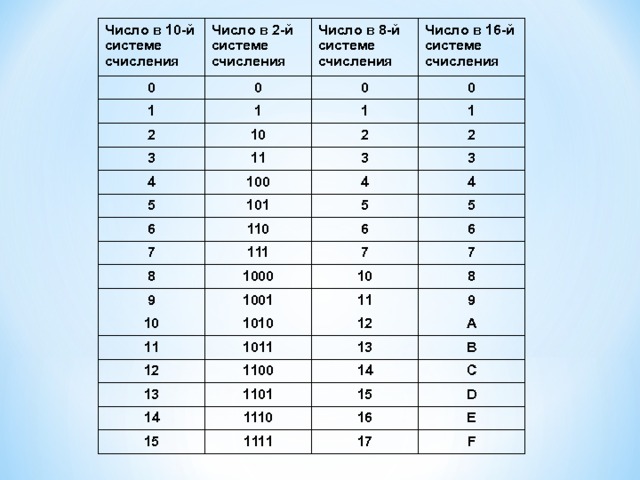 Условия и положения.
Условия и положения.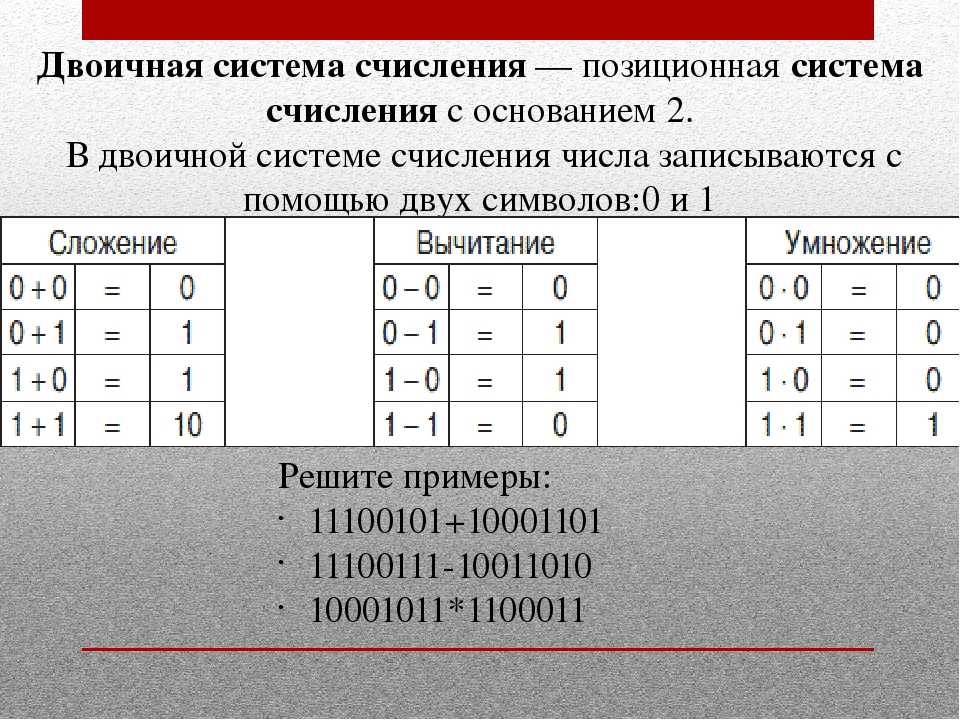
 0381
0381 2ШЕСТ.(11111011, 4)
2ШЕСТ.(11111011, 4)