Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Радиогоризонт и дальность прямой видимости РЛС.
hr высота антенны РЛС,
ht высота цели,
dh радиогоризонт,
dt расстояние от точки касания луча РЛС поверхности Земли до цели,
D=dh + dt дальность прямой видимости,
R0 средний радиус Земли
Этот калькулятор определяет геометрическую дальность прямой видимости цели (без учета рефракции радиоволн в атмосфере) и дальность прямой радиовидимости цели по известным высоте антенны РЛС и высоте цели. Если высота цели равна нулю (наземная цель), то речь идет о геометрическом горизонте (без учета рефракции) и радиогоризонте (с учетом рефракции). Отметим, что в морском судовождении и в авиации дальность измеряется в морских милях. Морские мили удобно использовать в связи с тем, что они прямо связаны с географическими координатами — одна морская миля соответствует одной минуте географической широты. Этот и другие калькуляторы на TranslatorsCafe.com пригодятся не только инженерам и студентам технических специальностей, но и всем, кто хочет изучить технический английский, так как все они есть и в английской версии.
Морские мили удобно использовать в связи с тем, что они прямо связаны с географическими координатами — одна морская миля соответствует одной минуте географической широты. Этот и другие калькуляторы на TranslatorsCafe.com пригодятся не только инженерам и студентам технических специальностей, но и всем, кто хочет изучить технический английский, так как все они есть и в английской версии.
Пример: Рассчитать радиогоризонт радиолокационной станции (РЛС) и дальность прямой радиовидимости, если ее антенна поднята на высоту 10 м, а цель находится на высоте 15 м.
Входные данные
Высота цели
htметр (м)километр (км)фут
Высота антенны РЛС
hr км
Поделиться
Поделиться ссылкой на этот калькулятор, включая входные параметры
Twitter Facebook Google+ VK
Закрыть
Выходные данные
Геометрический горизонт
dg м миля морская миля (международная)
Радиогоризонт
dr м миля морская миля (международная)
Геометрическая дальность прямой видимости цели
Dg м миля морская миля (международная)
Дальность прямой радиовидимости цели
Dr м миля морская миля (международная)
Для расчета введите величины в соответствующие поля, выберите британские или метрические единицы и нажмите на кнопку Рассчитать.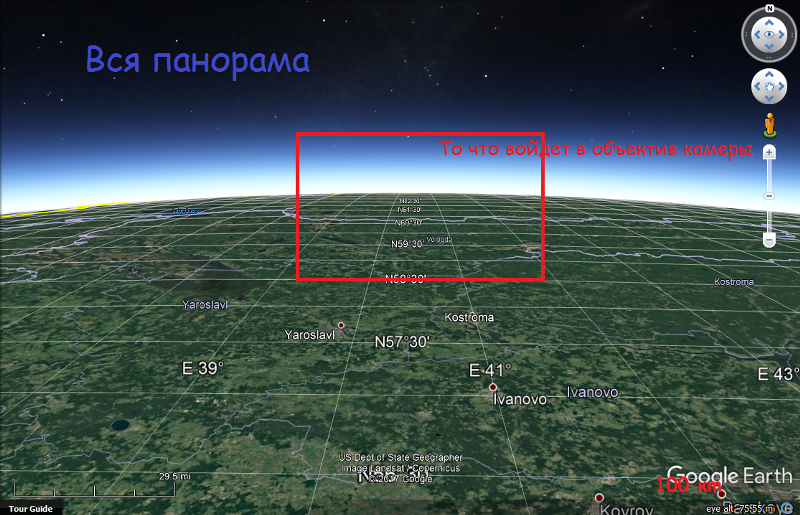
Радиогоризонт РЛС определяется как расстояние от антенны до места, в котором луч РЛС «касается» земной поверхности. При этом цели, находящиеся ниже линии, соединяющей точку касания и антенну РЛС, обнаружить невозможно. Для облегчения расчетов предположим, что Земля представляет собой идеальную сферу с радиусом R0=6 371.009 км. Предположим также (пока), что в атмосфере отсутствует рефракция, которую мы рассмотрим позднее. На рисунке выше коричневая окружность представляет собой поверхность Земли. Антенна РЛС поднята на высоту hr, а цель летит на высоте h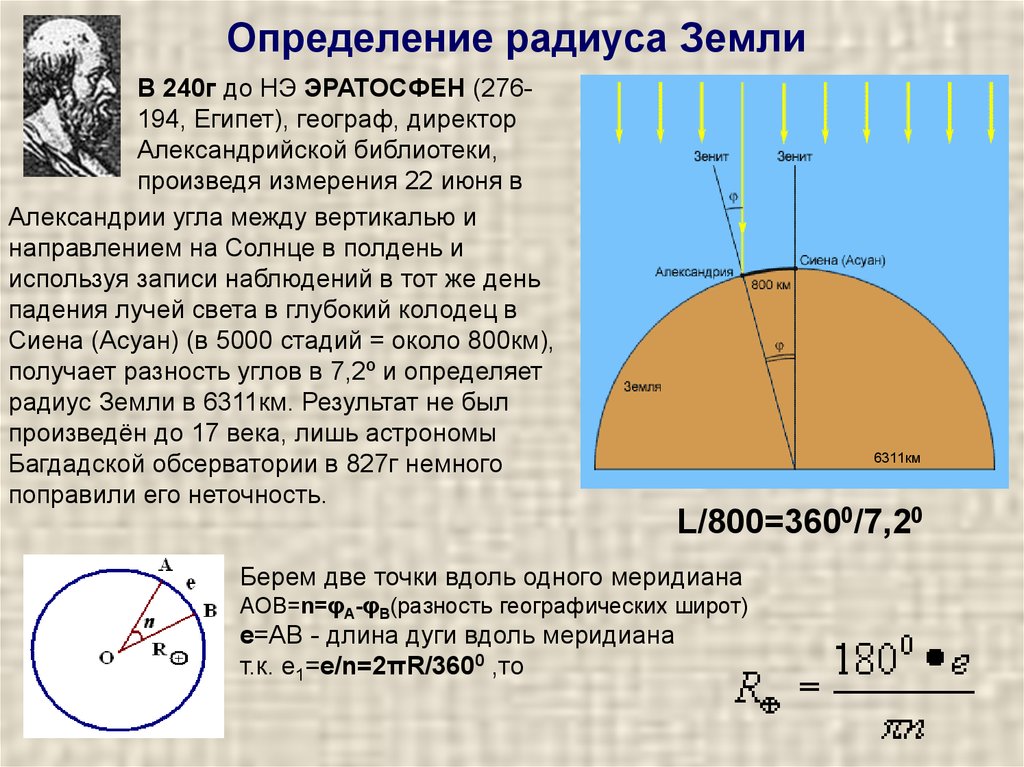 По теореме Пифагора имеем:
По теореме Пифагора имеем:
и
Если величины hr и ht малы по сравнению с радиусом Земли, эти выражения можно упростить:
и
Для значений hr<250 км и ht<250 км ошибка составляет менее 1%. То есть, используя полученные формулы, мы можем рассчитывать радиогоризонт для спутников и космических станций на околоземной орбите.
Геометрическая дальность прямой видимости цели Dg определяется по формуле:
Эта формула используется в нашем калькуляторе для расчета геометрической дальности прямой видимости. Например, по этой формуле геометрический (визуальный) горизонт до РЛС на 30-метровой мачте или вышке будет приблизительно равен 20 000 м. Отметим, что в приведенных выше формулах все величины должны быть в одних и тех же единицах длины и расстояния.
Показатель преломления атмосферы n уменьшается с высотой и из-за этого радиоволны изгибаются вниз, к поверхности Земли; n1 — рефракция меньше, n2 — рефракция больше
Теперь попробуем учесть рефракцию электромагнитных волн, распространяющихся в атмосфере. В стандартной атмосфере (что такое стандартная — обсудим позже) температура и давление воздуха понижаются с увеличением высоты, так как воздух в верхних слоях атмосферы более разреженный. В результате показатель преломления атмосферы с высотой уменьшается. В связи с атмосферной рефракцией, электромагнитные волны изгибаются вниз и, таким образом, могут распространяться за геометрический горизонт. Это изгибание уменьшает зону тени РЛС и в то же время приводит к ошибкам при измерении расстояния и высоты цели.
В стандартной атмосфере (что такое стандартная — обсудим позже) температура и давление воздуха понижаются с увеличением высоты, так как воздух в верхних слоях атмосферы более разреженный. В результате показатель преломления атмосферы с высотой уменьшается. В связи с атмосферной рефракцией, электромагнитные волны изгибаются вниз и, таким образом, могут распространяться за геометрический горизонт. Это изгибание уменьшает зону тени РЛС и в то же время приводит к ошибкам при измерении расстояния и высоты цели.
Наша модель распространения радиоволн будет проще, если мы предположим, что радиоволны распространяются по прямым линиям в стандартной атмосфере. Для этого нужно предположить, что радиус Земли больше, чем на самом деле. Расчеты показывают, что если увеличить радиус Земли в 4/3 раза, рефракцией можно будет пренебречь. Таким образом, приведенная выше формула для дальности прямой радиовидимости цели с учетом рефракции Dr будет такой:
Эта формула и используется в нашем калькуляторе для определения радиогоризонта и дальности прямой радиовидимости цели.
Антенна бортовой метеонавигационной радиолокационной станции, установленная под обтекателем в носовой части самолета Боинг-747, и дисплей этой станции в кабине пилотов. На дисплее можно наблюдать изображения опасной грозовой и кучево-дождевой облачности. Если самолет летит на высоте 33 000 футов или 10 000 метров, то радиогоризонт будет равен 412 км или 222 морских мили
Атмосфера считается «стандартной», если отсутствует инверсия температуры и влажности, которые обычно приводят к аномальному распространению радиоволн и образованию атмосферных волноводов. Атмосферные волноводы могут образовываться в тех случаях, когда температура необычно быстро увеличивается с высотой. При этом концентрация водяного пара в воздухе быстро уменьшается с высотой. Например, в ясную летнюю ночь поверхность земли может быстро охладиться, что приведет к охлаждению слоя воздуха возле нее. Таким образом, получается, что сразу над землей имеется слой холодного воздуха, а над ним более теплый воздух. Такое явление называется температурной инверсией, то есть температура с высотой не уменьшается, как обычно, а, наоборот, увеличивается.
Автор статьи: Анатолий Золотков
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Физический справочник/ / Длина, расстояние, линейный размер / / Таблица расстояния до горизонта (удаления горизонта) в зависимости от высоты глаз наблюдателя.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Кривизна земли и ее учет при измерении горизонтальных расстояний
R- радиус Земли
α- центральный угол в радианной мере ( )
d- горизонтальное проложение
(кратчайшее расстояние по горизонтальной поверхности)
S-
длина линии с учётом кривизны Земли.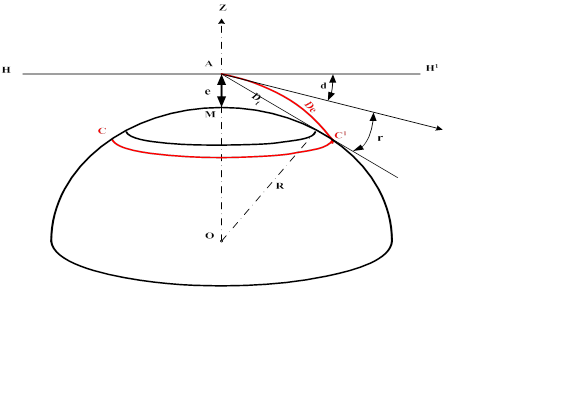
Задача определить разность Δd длин d и S
т.к.
Анализ R=6371км. S=10км. Δd=1см.
На участке земной поверхности при радиусе 10км., кривизну Земли можно не учитывать.
2. При измерении превышений (высот).
Задача определить Δh.
Анализ: R=6371км.
S=1км.
Δh=8см.
Допустимая разность Δh на 1км. не более 5см.
Уменьшим значение S до 0,3км. S=0,3км.
К ривизну Земли на участке длиной до 300 при измерении высот можно не учитывать.
Кривизна Земли не влияет на условие измерения (т.к. проекция равноугольная) и её при измерениях не учитывают.
3.Системы координат
.Положение точек поверхности земли определяется координатами.
Координаты — величины, определяющие положение точки на поверхности, в пространстве, на плоскости.
Системы координат
— составляют
исходные плоскости, линии, точки.
Все системы координат, применяемые в геодезии, можно разделить на две группы:
— пространственные,
— плоские.
Пространственные системы координат:
1 . Географическая система координат (обще название), которая объединяет астрономическую и геодезическую системы координат. Будем рассматривать геодезическую систему координат.
2.Пространственная полярная система координат.
Плоские системы координат:
1. Зональная система плоских прямоугольных координат.
2. Плоская условная система прямоугольных координат.
3. Система плоских полярных координат.
Плоская прямоугольная система координат.
А)
зональная система плоских прямоугольных
координат В
соответствии с принятой равноугольной
поперечно-цилиндрической проекцией
Гаусса, в геодезии принята зональная
система плоских прямоугольных координат.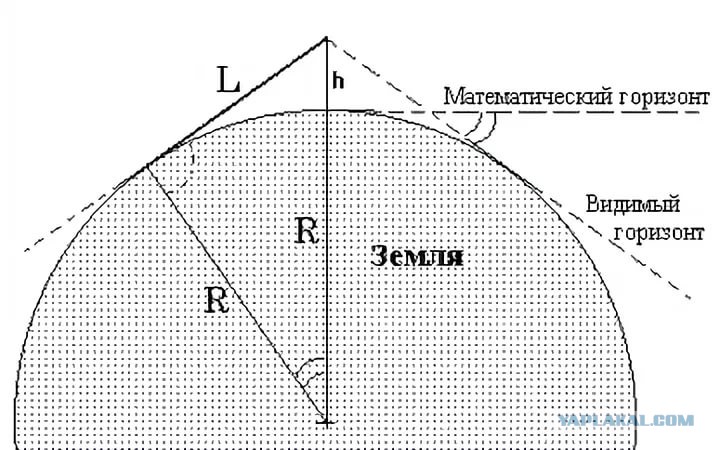
Положение точек земной поверхности определяется прямоугольными координатами Х и У. Оси координат в геодезии развернуты на 90 градусов по сравнению с декартовой системой координат.
Счет абсцисс ведется от экватора к северу со знаком плюс. К югу — со знаком минус. Для территории нашей страны абсциссы положительны, поэтому знак перед значением абсциссы не ставится (опускается).
Ординаты к востоку от осевого меридиана положительны, а к западу отрицательны.
Для того, чтобы все значения ординат были со знаком плюс, счет их ведется от условного меридиана, вынесенного на запад на 500 км, т.е. осевому меридиану придается значение 500 000 м. при этом впереди значения ординаты пишут номер зоны.
Исправленную таким
образом ординату называют приведенной или условной, а координаты
называют условными или действительными.
Связь между условными координатами и их
действительным значением.
Х’=Х
У’ = У — 500 000
Х’, У’ — действительные значения координат
Х, У — условные значения координат.
Пример:
Хм = 5 650 450, где 5 650 км, 450 м
Ум = 3 250 550, где 3 — номер зоны, 250 км, 550 м.
Это полные условные прямоугольные координаты точки.
Полные действительные координаты:
Х’ = 5 650450
У’ = 3 -249 450
Точка М расположена в третьей зоне в 249 км 550 м к западу от осевого меридиана (250 550 — 500 000) и к северу от экватора на удалении 5 650 км 450 м.
Для измерения
прямых координат на карты наносится координатная
сетка. Координаты,
в которых указываются только десятки
и единицы километров и метров, называются сокращенными.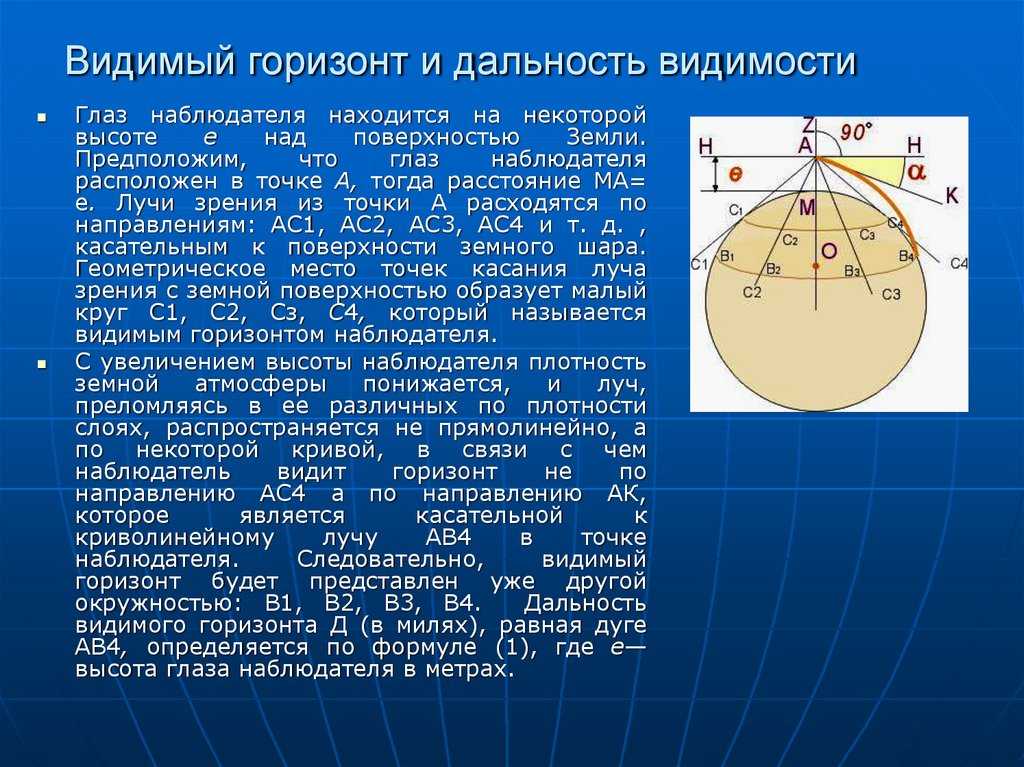
Хм= 05450 Ум =50550
Они применяются при работе в пределах границ карты, плана. Система применяется при составлении планов, карт.
Б) Система плоских полярных координат.
Элемент системы:
— полярная ось
— начало координатной системы (полюс)
Возможные варианты элементов системы координат: Полярная ось — любое ориентирное направление (А, Ам, а, сторона теодолитного хода и т.д.)
Начало координат: — точка стояния
— точка теодолитного хода
Координаты, определяющие положение точки:
— горизонтальный угол между полярной осью и направлением на определяемую точку
— горизонтальное расстояние от полюса до определяемой точки (d).
Применение системы:
— при теодолитной съемке
— при выполнении
разбивочных работ (вынос точки в натуру).
В) Плоская условная система прямоугольных координат
Элементы системы:
-начало — произвольная точка
-ось абсцисс (произвольно)
— ось ординат (перпендикулярна к оси абсцисс)
Обобщенный анализ плоской системы координат
1. Осями координат горизонтальная плоскость делится на 4 четверти.
2. В геодезии принята правая система прямоугольных координат (в отличие от принятой в математике левой декартовой системы)
3. Нумерация четвертей ведется по ходу стрелки часов, начиная с северо-восточной четверти, что позволяет использовать в геодезических вычислениях формулы тригонометрии без каких-либо изменений. Ось абсцисс 1 четверти ориентирована на север (0градусов).
4
.
Координаты точек равны кратчайшим
расстояниям от начала координат до
проекции этих точек на оси Х и У.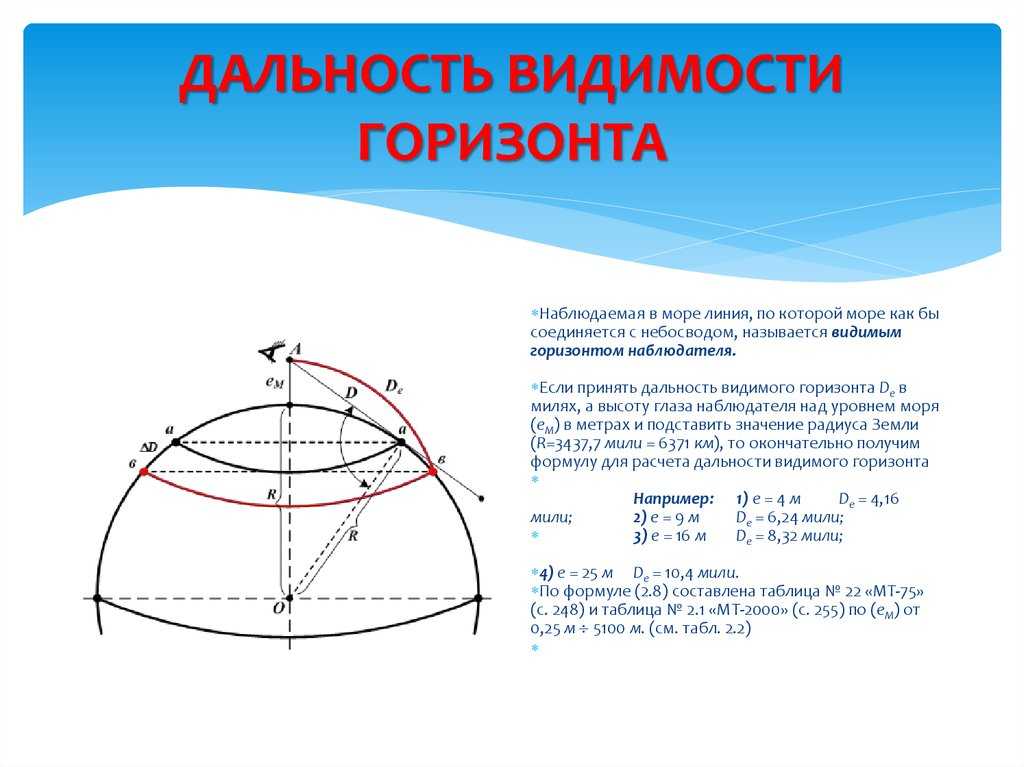
5. Разность между проекциями двух точек на оси Х и У принято называть приращением координат и обозначать ( х, у) (разность между координатами двух точек)
6. Приращения координат имеют знаки (+), значение которых определяется координатными осями четвертей.
7. Если известны координаты одной точки, то координаты другой можно найти
Хв =Ха + ( )
Yв = Yа + ( )
8. 8. Система плоских координат имеет широкое применение в инженерной геодезии.
Калькулятор кривизны Земли
Создано Bogna Szyk
Отзыв Стивена Вудинга и Джека Боуотера
Последнее обновление: 29 сентября 2022 г.
Содержание:- Что такое кривизна Земли?
- Кривизна Земли на милю
- Как далеко я могу видеть до того, как Земля искривится?
- Расчет высоты объекта с препятствиями
- Является ли этот калькулятор кривизны Земли точным?
- Часто задаваемые вопросы
Этот калькулятор кривизны Земли позволяет вам определить, какая часть удаленного объекта скрыта из-за кривизны Земли . Итак, если вы когда-нибудь хотели оценить общую высоту цели, которая частично скрыта за горизонтом, теперь вы можете это сделать. Вы также сможете узнать , как далеко вы можете видеть до кривизны Земли — то есть, каково ваше расстояние до горизонта.
Итак, если вы когда-нибудь хотели оценить общую высоту цели, которая частично скрыта за горизонтом, теперь вы можете это сделать. Вы также сможете узнать , как далеко вы можете видеть до кривизны Земли — то есть, каково ваше расстояние до горизонта.
Не волнуйтесь, если вы еще не знаете, какова кривизна Земли – просто продолжайте читать, чтобы узнать всю необходимую информацию!
Какова кривизна Земли?
Представьте, что вы смотрите на море. Земли не видно, только бескрайние голубые воды, мерцающие в лучах послеполуденного солнца. Вы можете разглядеть линию, которая разделяет море и небо. Эта линия называется горизонтом .
Внезапно вы начинаете видеть точку, которая становится все больше и больше. Во-первых, это вершина белого паруса; когда он приближается, вы также можете заметить форму корабля. Где был этот корабль раньше? Оно было скрыто за горизонтом.
Причина этого очевидна: поскольку форма Земли очень похожа на шар, поверхность между вами и кораблем не совсем плоская, а немного «выпучена».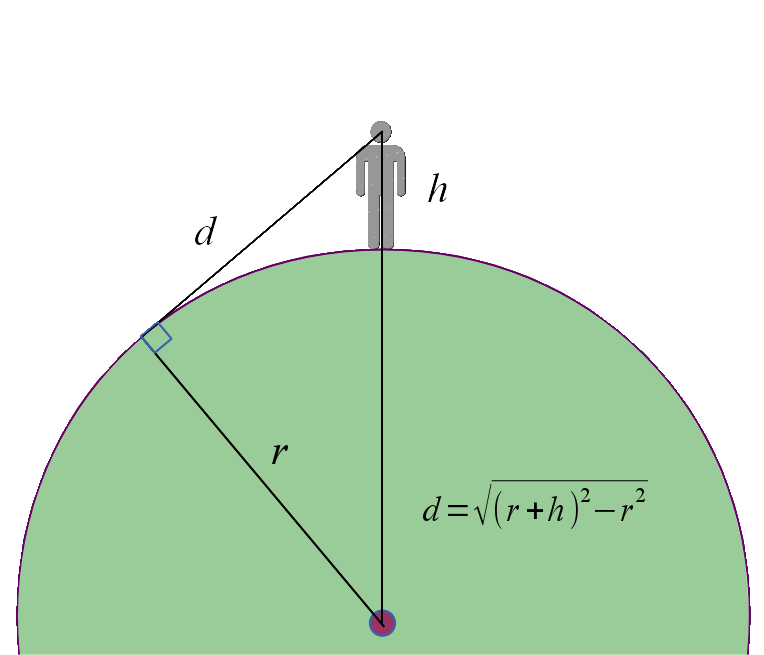 Вот почему он загораживает вам обзор. Кривизна Земли — это просто мера этой «выпуклости». Он выражается как высота «выпуклости» на километр или милю.
Вот почему он загораживает вам обзор. Кривизна Земли — это просто мера этой «выпуклости». Он выражается как высота «выпуклости» на километр или милю.
💡 Обратите внимание, что , если бы Земля была плоской, вы бы увидели весь корабль , ожидайте, что сначала он был бы очень маленьким (точка), а затем увеличивался бы по мере приближения. Наблюдая только за верхней частью паруса, вы сами убедились, что Земля не плоская. Однако, если вы заинтересованы в дальнейшем изучении этого вопроса, вам следует воспользоваться нашим калькулятором плоской и круглой земли.
Кривизна Земли на милю
Тогда насколько велика кривизна Земли? Поскольку мы не замечаем его в повседневной жизни, он должен быть относительно небольшим. Большинство источников считают 8 дюймов на милю как наиболее точная оценка. Это означает, что на каждую милю между вами и объектом кривизна будет препятствовать 8 дюймам высоты объекта.
Как далеко я могу видеть до того, как Земля искривится?
Первое, что вы можете найти с помощью нашего калькулятора кривизны Земли, это точное ** расстояние между вами и горизонтом **. Вам нужно знать только два значения: ваш уровень зрения (другими словами, расстояние между вашими глазами и средним уровнем моря — при условии, что вы смотрите на море) и радиус Земли . Введите эти числа в следующее уравнение:
Вам нужно знать только два значения: ваш уровень зрения (другими словами, расстояние между вашими глазами и средним уровнем моря — при условии, что вы смотрите на море) и радиус Земли . Введите эти числа в следующее уравнение:
a = √[(r + h)² - r²]
где:
-
a— расстояние до горизонта; -
h— Уровень зрения выше среднего уровня моря; и -
r— радиус Земли, равный 3959 миль или 6371 км.
Это уравнение можно вывести с помощью теоремы Пифагора. Вы можете попробовать вывести его самостоятельно – это не так уж и сложно!
Расчет высоты объекта с препятствиями
Посмотрите на изображение выше. Это представляет собой ситуацию, аналогичную ситуации с кораблем сверху. Вы можете видеть часть объекта, но остальная его часть скрыта за горизонтом . Если вы хотите узнать высоту препятствия, просто введите все необходимые значения в калькулятор кривизны Земли. Вы также можете рассчитать высоту вручную:
Вы также можете рассчитать высоту вручную:
Определить расстояние между вами (наблюдателем) и самой нижней точкой объекта, которую вы действительно можете видеть. Назовем это значение
dи предположим, что оно равно 25 милям.Измерьте свой уровень зрения — то есть высоту, на которой ваши глаза находятся над морем. Обозначим его буквой
h. Можно предположить, что она равна 6 футам, что примерно равно 0,0011 мили.Рассчитайте расстояние между вами и горизонт ,
a, используя приведенную выше формулу:a = √[(r + h)² - r²] = √[(3959 + 0,0011364)² - 3959²] = 3 милиТеперь вы можете ввести эти значения во вторую формулу, чтобы найти высоту загороженной части объекта
x:х = √(a² - 2ad + d² + r²) - rх = √(3² - 2*3*25 + 25² + 3959²) - 3959х = 0,0611 мили = 322,76 футаЕсли у вас возникли проблемы с преобразованием единиц , просто используйте наш конвертер длины.

Является ли этот калькулятор кривизны Земли точным?
Вы можете обнаружить, что если бы вы сравнили наш калькулятор с реальным сценарием, наш калькулятор мог бы в некоторых случаях ошибаться. Почему это происходит? Означает ли это, что Земля плоская и совсем не кривая?
Конечно нет! Это просто означает, что наш калькулятор не учитывает феномен преломление . Когда свет проходит через среду, которая не является идеально однородной, например воздух, он преломляется или преломляется . Например, преломление может произойти, когда свет попадает в карман с холодным воздухом или в горячий поток восходящего воздуха.
Когда луч света слегка изгибается, он меняет направление. Это означает, что некоторые фотоны от объекта, которые обычно попадают на землю, могут огибать поверхность Земли и достигать вашего глаза, поэтому высоты и расстояния, как показано на рисунке выше, могут показаться другими.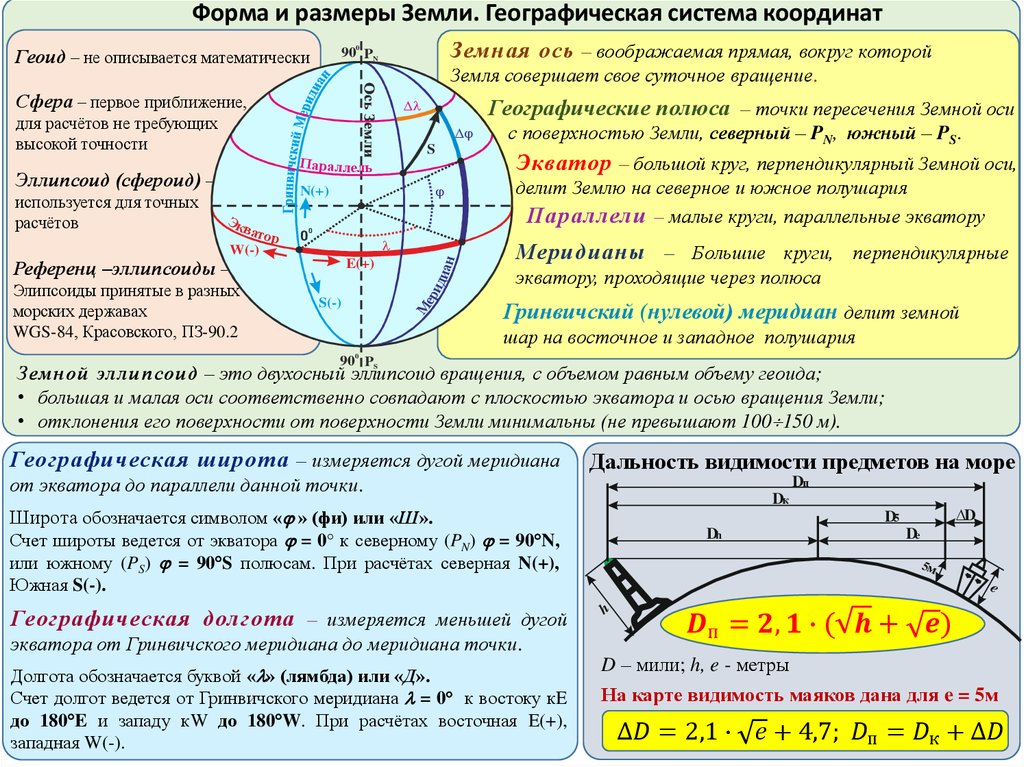 Вот почему, когда вы вычисляете высоту объекта с препятствиями, расстояния, которые вы видите, могут немного отличаться от наблюдаемых!
Вот почему, когда вы вычисляете высоту объекта с препятствиями, расстояния, которые вы видите, могут немного отличаться от наблюдаемых!
Если вам интересно узнать больше о законе преломления Снелла, вам следует воспользоваться нашим калькулятором закона Снелла здесь.
Часто задаваемые вопросы
Как далеко находится горизонт на уровне моря?
Горизонт на уровне моря примерно 4,5 км . Чтобы вычислить его, выполните следующие действия:
- Предположим, что высота ваших глаз равна
h = 1,6 м. - Постройте прямоугольный треугольник с гипотенузой
r + h(гдеr— радиус Земли) и катетомр. - Рассчитайте последний катет по теореме Пифагора: результатом будет расстояние до горизонта:
a = √[(r + h)² - r²] - Подставьте значения в формулу выше:
a = √[(6 371 000 + 1,6)² - 6 371 000²] = 4 520 м
Как рассчитать расстояние до горизонта?
Чтобы рассчитать теоретическое расстояние до горизонта с вашей точки зрения, представьте, что вы строите прямоугольный треугольник со сторонами, равными:
- Радиус Земли плюс высота ваших глаз над уровнем моря,
r + h; - Радиус Земли
r; и - Линия, касательная к поверхности Земли, начинается у вас перед глазами.
 Это расстояние до горизонта.
Это расстояние до горизонта.
Рассчитываем расстояние до горизонта по формуле a = √[(r + h)² - r²] .
Видишь ли ты Францию из Англии?
Да, но только в отличном состоянии. Со скал Дувра, высотой около 100 м , ваш горизонт будет на 35,7 км . Вы можете рассчитать это расстояние по этой формуле, где h — высота над уровнем моря, а r — радиус Земли:
a = √[(r + h)² — r²]
Поскольку самая узкая часть Ла-Манша едва достигает 33 км , Францию можно увидеть, но точь-в-точь точь-в-точь.
Как далеко можно увидеть гору Эверест?
Вы можете увидеть Эверест (теоретически) с расстояния 340 км .
Если предположить, что вы находитесь на уровне моря, а ваши глаза находятся на высоте 1,6 м над землей, ваш горизонт (на расстоянии около 4,5 км ) покрывает всю самую высокую гору на Земле, только если вы находитесь на высоте более чем 340 км от него.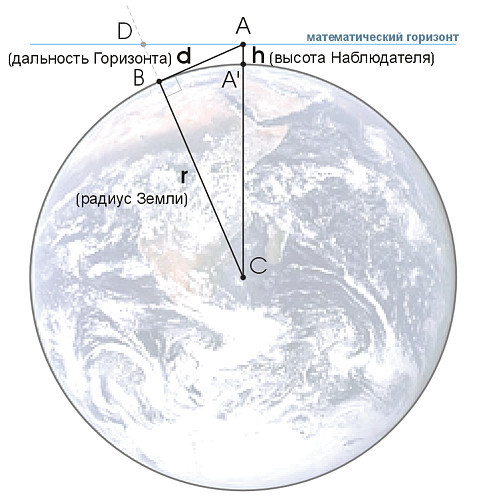 Теоретически увидеть вершину Эвереста можно из Бангладеш; однако другие вершины покрывают его!
Теоретически увидеть вершину Эвереста можно из Бангладеш; однако другие вершины покрывают его!
Bogna Szyk
Расстояние до объекта
Уровень зрения
Расстояние до горизонта
Часть скрытого объекта
Ознакомьтесь с 435 подобными физическими калькуляторами
Размер провода 100 ампер Размер провода 12 вольт Размер провода 220 вольт… Еще 432
Калькулятор кривизны + формула кривизны Земли — [100% бесплатно] связанных с кривизной Земли. Используя формулы и геодезические инструменты, они могут определить часть удаленного объекта, которая затемняется этой кривизной. Это позволяет им получить точную оценку общей высоты объекта, который частично скрыт горизонтом. В таком случае этот калькулятор кривизны пригодится для быстрых расчетов.
Загрузка калькулятора…
Содержание
Как пользоваться калькулятором кривизны?
Этот калькулятор кривизны предельно прост. Если у вас есть необходимые значения, вы можете использовать этот онлайн-инструмент без необходимости вычислять вручную, используя формулу кривизны Земли. Вот шаги, которые необходимо выполнить:
Вот шаги, которые необходимо выполнить:
- Сначала введите значение расстояния до объекта и выберите единицу измерения из раскрывающегося меню.
- Затем введите значение уровня зрения и выберите единицу измерения в раскрывающемся меню.
- После ввода обоих значений калькулятор кривизны Земли автоматически сгенерирует для вас значение расстояния до горизонта и значение скрытой части объекта.
Какова кривизна Земли?
Представьте, что вы смотрите далеко в открытое море, где вы не видите земли, только бескрайнюю голубую воду. В ясные дни можно увидеть горизонт, разделяющий небо и море. Возможно, вы также случайно увидите определенную точку на горизонте, которая начинает становиться все больше и больше.
Когда он приближается, вы обнаруживаете, что это корабль, и первое, что вы заметите, это его парус. Чем ближе он подходит, тем более четкой становится форма корабля. Прежде чем вы сможете сделать такое наблюдение, вы можете задать себе вопросы: «Где был корабль до того, как он постепенно появился?» и «Было ли оно скрыто за горизонтом?»
К этому моменту мы уже знаем, что Земля сферическая, а не плоская.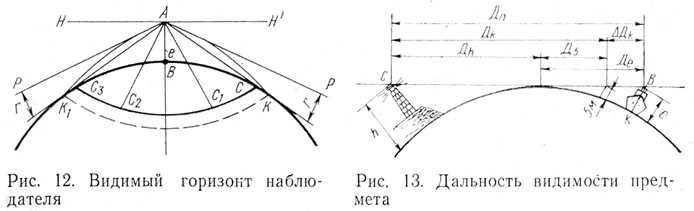 Поэтому между кораблем и вами он довольно сильно выпирает. Вот почему это мешало вам видеть. Эта «выпуклость» и есть то, что известно как кривизна Земли. Вы измеряете это значение как высоту «выпуклости» на милю или километр.
Поэтому между кораблем и вами он довольно сильно выпирает. Вот почему это мешало вам видеть. Эта «выпуклость» и есть то, что известно как кривизна Земли. Вы измеряете это значение как высоту «выпуклости» на милю или километр.
Как рассчитать кривизну Земли?
Степень препятствия удаленному объекту, вызванная кривизной Земли, зависит от нескольких факторов, а именно:
- Расстояние до объекта.
- Высота наблюдателя.
- Высота объекта.
- Величина атмосферной рефракции.
«Плоскоземельцы» или те люди, которые до сих пор верят, что Земля плоская, предпочитают использовать видимость далеких объектов, чтобы доказать, что кривизна Земли — всего лишь миф. Конечно, как и следовало ожидать, их теории терпят неудачу, потому что они не учитывают высоту наблюдателя и атмосферную рефракцию.
Помимо этих факторов, они также делают еще несколько ошибок, таких как ошибки в преобразовании единиц измерения, ошибки в вычислении расстояния и так далее. Если бы только эти плоскоземельцы отнеслись к этим соображениям должным образом и попытались исправить свои ошибки, все должно было бы сложиться иначе. Затем они обнаружат, что у нас есть сферическая Земля.
Если бы только эти плоскоземельцы отнеслись к этим соображениям должным образом и попытались исправить свои ошибки, все должно было бы сложиться иначе. Затем они обнаружат, что у нас есть сферическая Земля.
Неучет высоты наблюдателя является наиболее распространенной ошибкой при расчете кривизны Земли, независимо от того, используете ли вы калькулятор кривизны или формулу кривизны Земли. Все, что обычно делают, это рассчитывают падение с горизонтальной плоскости.
Даже если вы используете профессиональное программное обеспечение AutoCAD, обладающее высокой точностью, полученные числа все равно окажутся неверными, если вы изначально допустили ошибку в геометрии.
Неучет атмосферной рефракции — еще одна очень распространенная ошибка. Атмосферная рефракция относится к отклонению света от прямой линии при прохождении через атмосферу из-за изменения плотности воздуха в зависимости от высоты.
Проще говоря, атмосферная рефракция обычно изгибает свет, чтобы следовать за кривизной Земли в определенную точку.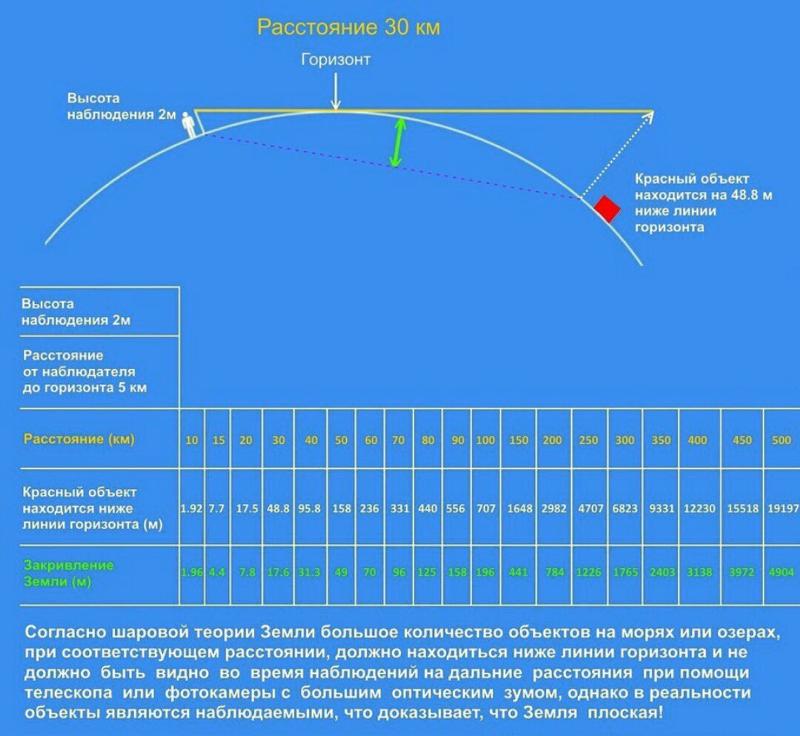 Это заставляет объект казаться выше над горизонтом, чем он есть на самом деле. Также важно отметить, что атмосферная рефракция никогда не бывает постоянной, поскольку она зависит от погодных условий и от того, насколько рефракция может меняться в течение одного дня.
Это заставляет объект казаться выше над горизонтом, чем он есть на самом деле. Также важно отметить, что атмосферная рефракция никогда не бывает постоянной, поскольку она зависит от погодных условий и от того, насколько рефракция может меняться в течение одного дня.
Если вы приняли во внимание всю эту информацию и исправили все ошибки, вы сможете найти нужные вам значения с помощью простого процесса. Вот как рассчитать кривизну Земли без использования калькулятора кривизны:
Для этого примера предположим, что Земля имеет сферическую форму с радиусом 3963 мили. Если вы находитесь в точке P на поверхности Земли, то переместите касательную к поверхности на расстояние в одну милю, чтобы образовался прямоугольный треугольник. Then using the Pythagorean theorem:
c² = a² + b²
c² = (3963)² + (1)²
c² = 15705370
Then take the square root of both sides of the equation:
c = 3963.
000126 miles
You should also solve for your position above the Earth’s surface:
P = 3963.000126 – 3963
P = 0.000126 miles
P = 7,98 дюйма
Этот результат означает, что поверхность Земли изгибается примерно на 8 дюймов на каждую милю.
Насколько изгибается Земля на милю?
У Земли есть кривизна, но почти никто этого не замечает, потому что величина очень мала. Для тех, кто в курсе, наиболее точное значение кривизны составляет около 8 дюймов на милю. Это означает, что на каждую милю расстояния между вами и другим объектом кривизна закрывает примерно 8 дюймов высоты объекта.
Как далеко вы можете видеть кривизну Земли?
Калькулятор кривизны Земли вычисляет расстояние между вами и горизонтом. Для решения этой задачи необходимы только два значения, а именно уровень вашего зрения или расстояние между землей и вашими глазами и радиус Земли. Введите эти значения в уравнение кривизны:
Введите эти значения в уравнение кривизны:
a = √[(r + h)² – r²]
где
a 9 относится к расстоянию до горизонта0180 h относится к уровню вашего зрения
r относится к радиусу Земли, который составляет 3963 мили
Само уравнение происходит из теоремы Пифагора. Вы даже можете попробовать вывести уравнение самостоятельно, это не так сложно!
5 Веб-сайты онлайн-калькулятора кривизны Земли Бесплатные
Рейтинги редактора:
Рейтинги пользователей:
[Всего: 0 Среднее: 0]
Эта статья охватывает 5 бесплатных онлайн-калькуляторов кривизны Земли веб-сайты. Используя эти веб-сайты, вы можете вычислить скрытую часть удаленного объекта. Вы можете просто ввести расстояние до этого объекта вместе с высотой точки обзора и получить результаты. Эти калькуляторы также показывают вам расстояние до горизонта с точки обзора.
Все эти программы предполагают, что Земля имеет сферическую форму с радиусом 3959 миль, а затем используют теорему Пифагора для расчета расстояния до горизонта. Затем они используют это расстояние для расчета кривизны Земли. Если вы не знаете точного расстояния до объекта, вы можете получить его с помощью карт и навигационных сервисов.
Когда у вас есть расстояние и кривизна Земли, вы можете использовать их для расчета скрытой высоты отдельного объекта. Итак, давайте начнем и обсудим эти сайты-калькуляторы один за другим.
Читайте также: Узнайте, насколько велика Солнечная система на интерактивной карте Солнечной системы веб-сайт немецкого инженера и педагога, предлагающий бесплатный образовательный контент и инструменты. На этом сайте Усовершенствованный калькулятор кривизны Земли , который дает подробные результаты вместе с другими соответствующими терминами и графиками. Версия Основы имеет 6 следующих полей ввода: Высота наблюдателя , Расстояние до цели , Размер цели , Отражение , Масштаб и 2 Угол обзора 7 . Вы можете просто ввести Наблюдатель Высота и Цель Расстояние до вычислить кривизну Земли и расстояние до горизонта вместе с закрытой высотой цели .
Вы можете просто ввести Наблюдатель Высота и Цель Расстояние до вычислить кривизну Земли и расстояние до горизонта вместе с закрытой высотой цели .
Если вы хотите копнуть глубже, вы можете настроить значения всех этих полей ввода и получить подробные данные цели и данные горизонта . Этот калькулятор имеет отдельные разделы для View , Targets и Refraction , где он дает вам аналогичные подробные данные для этих объектов. Кроме того, вы можете изменить цель камеры/зрителя вместе с моделью земного шара, а также переключить 9Система единиц измерения 0023 в метрическую или имперскую .
Наряду с подробными данными, этот калькулятор также показывает графики всех углов с преломлением и без него . Он использует цветовые коды для отображения соответствующих данных на графике, что облегчает понимание.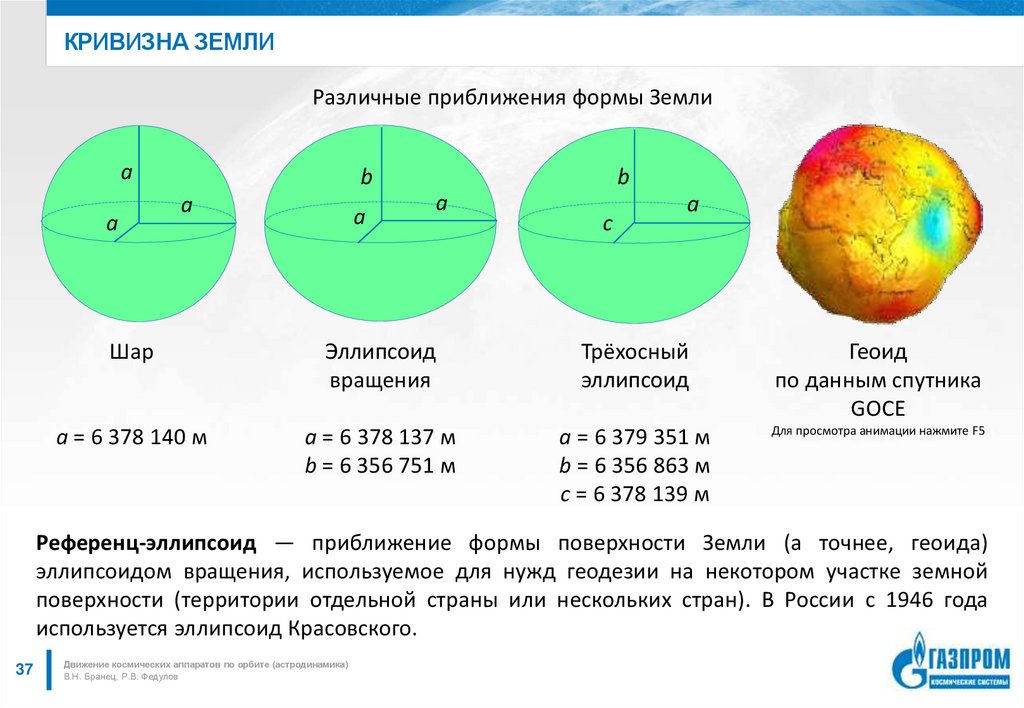
Попробуйте этот расширенный калькулятор кривизны Земли здесь .
MetaBunk.org
MetaBunk.org это интернет-сообщество, где вы можете найти научное объяснение и (несколько раз) правду о реальных событиях, явлениях, заговорах и многом другом. Этот веб-сайт также предлагает онлайн-инструменты и образовательный контент по различным темам. У него есть бесплатный онлайн-инструмент, с помощью которого вы можете рассчитать Кривизна Земли , горизонт , выпуклость , падение и скрытая высота .
Этот инструмент имеет базовый режим, в котором вы получаете два поля ввода; один для ввода целевого расстояния, а другой для ввода высоты зрителя. Когда вы вводите обе эти сущности, это дает вам расстояние между зрителем и целью. Результаты сопровождаются другой дополнительной информацией, показывающей вам расстояние до горизонта , выпуклость , падение , скрытая высота и падение горизонта .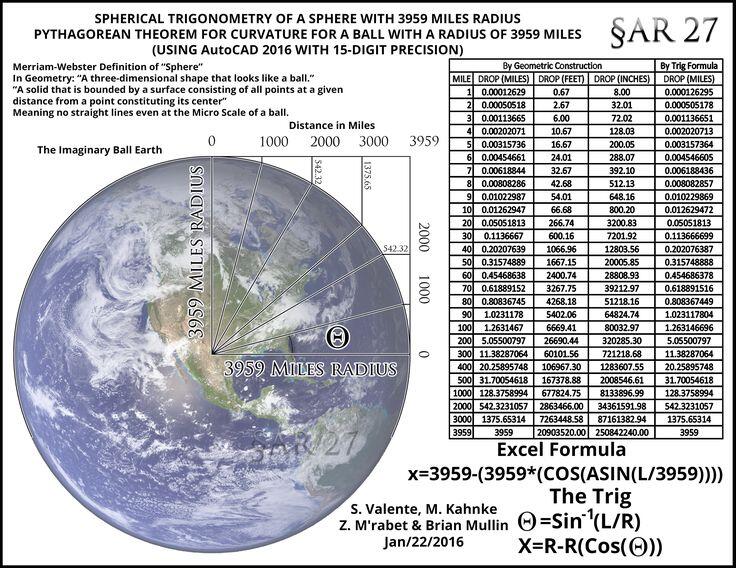 Он показывает вам всю эту информацию для обоих случаев; один раз без учета преломления и один раз со стандартным значением преломления.
Он показывает вам всю эту информацию для обоих случаев; один раз без учета преломления и один раз со стандартным значением преломления.
Кроме того, в расширенном режиме он дает вам возможность ввести пользовательские значения для радиуса Земли , горизонтального FOV и ширины изображения . И вы также получаете возможность изменить систему единиц.
Дайте это онлайн Калькулятор кривизны Земли попробуйте здесь .
Horizzn.com
Следующий веб-сайт калькулятора кривизны Земли в этом списке — Horizzn . Это простой калькулятор с аккуратным и элегантным дизайном. Этот калькулятор имеет четыре информационных поля; Уровень зрения , Расстояние до объекта , Расстояние до горизонта , и Часть скрытого объекта (скрытая высота) . Из этих четырех полей первые два принимают пользовательский ввод, а последние два обеспечивают вывод.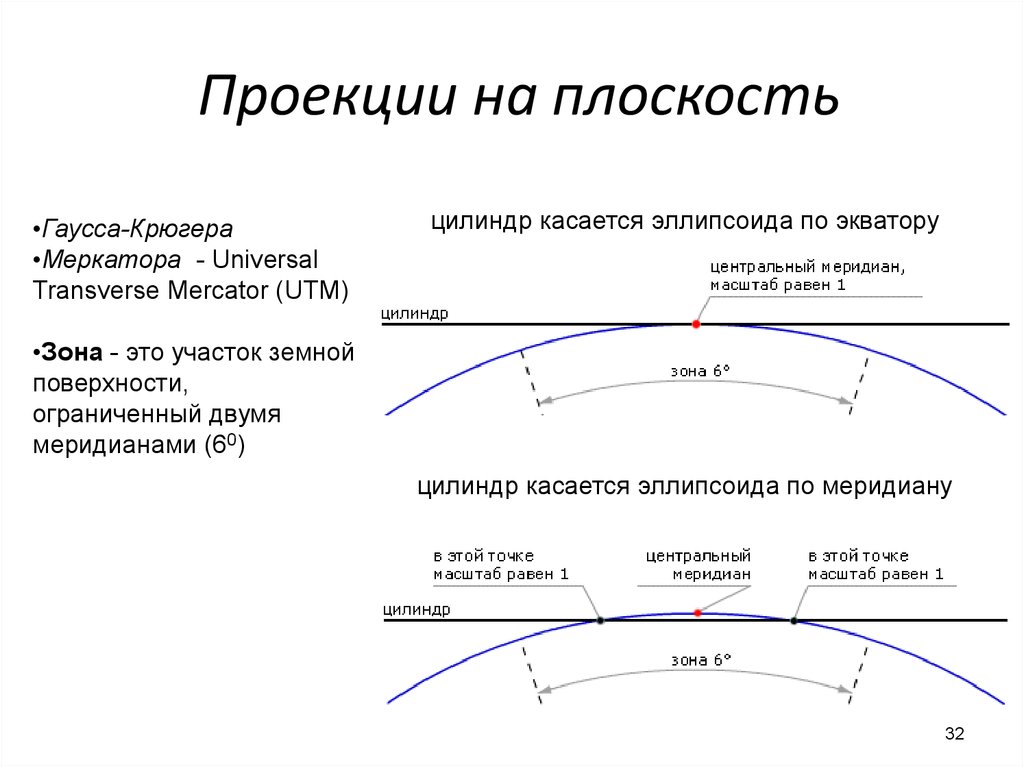
Как только вы введете Уровень зрения и Расстояние до объекта в этот калькулятор, он сразу же рассчитает расстояние до горизонта, используя теорему Пифагора. С этим значением он определяет скорость, с которой Земля изгибается, и вычисляет скрытую высоту объекта. Этот калькулятор поддерживает как метрическую, так и имперскую системы единиц измерения, которые вы можете переключать, щелкая единицу измерения рядом с любым полем значений.
Вы можете попробовать этот бесплатный калькулятор кривизны Земли здесь .
OnmiCalculator.com
Как следует из названия, OmniCalculator.com – это бесплатный веб-сайт, который предлагает в общей сложности 682 калькулятора для математики, физики, химии, конверсии, финансов, экологии, здравоохранения, и многого другого. В разделе «Физика» есть Калькулятор кривизны Земли , который можно использовать для расчета затемненной части удаленного объекта.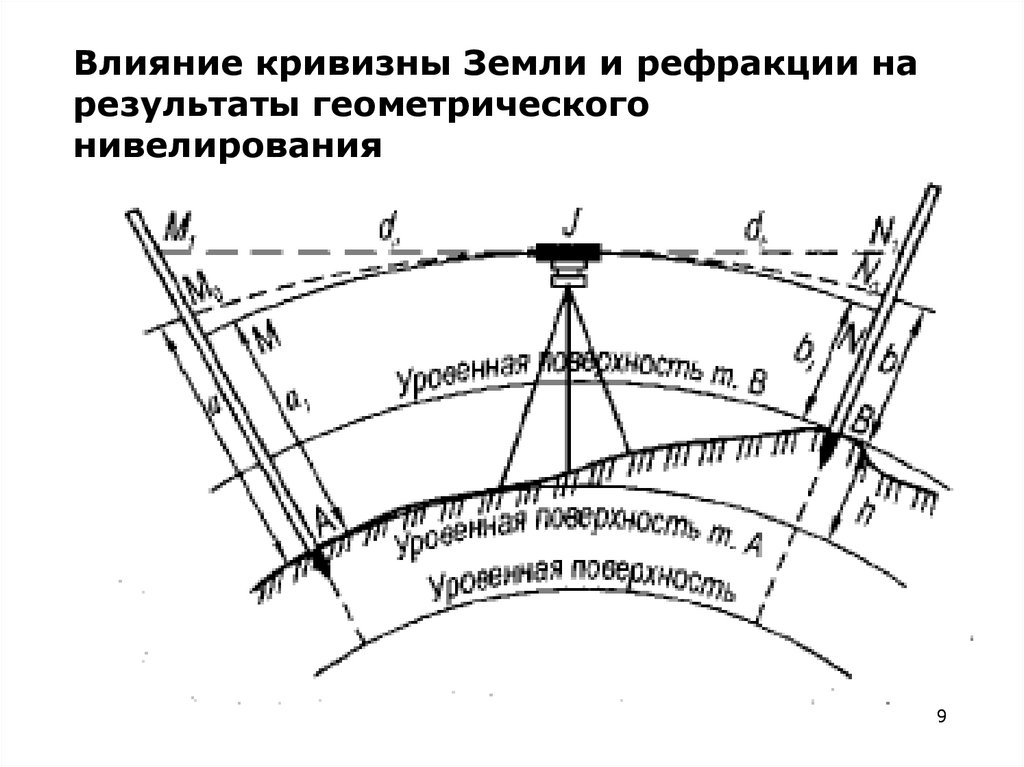
Этот калькулятор имеет три поля ввода; Расстояние до объекта , Уровень зрения , Расстояние до горизонта . Вы можете ввести значение для любых двух полей, чтобы рассчитать высоту скрытого объекта вместе с оставшимся полем. Это также дает вам возможность поделиться результатами с другими по электронной почте, в социальных сетях или по URL-адресу.
Рассчитайте кривизну Земли онлайн с помощью OmniCalculator здесь .
Dizzib.GitHub.io
Dizzib.GitHub.io — один из самых простых калькуляторов кривизны Земли в этом списке. Он имеет простой, но удобный дизайн, где вы можете вводить свои данные и получать результаты. Вверху есть возможность выбрать систему единиц для расчета. Затем есть два варианта ввода; один для Высота обзора и другой для Расстояние до цели . Вы можете просто ввести эти два значения здесь и нажать кнопку Calculate , чтобы получить скрытую высоту цели вместе с Горизонтальное расстояние .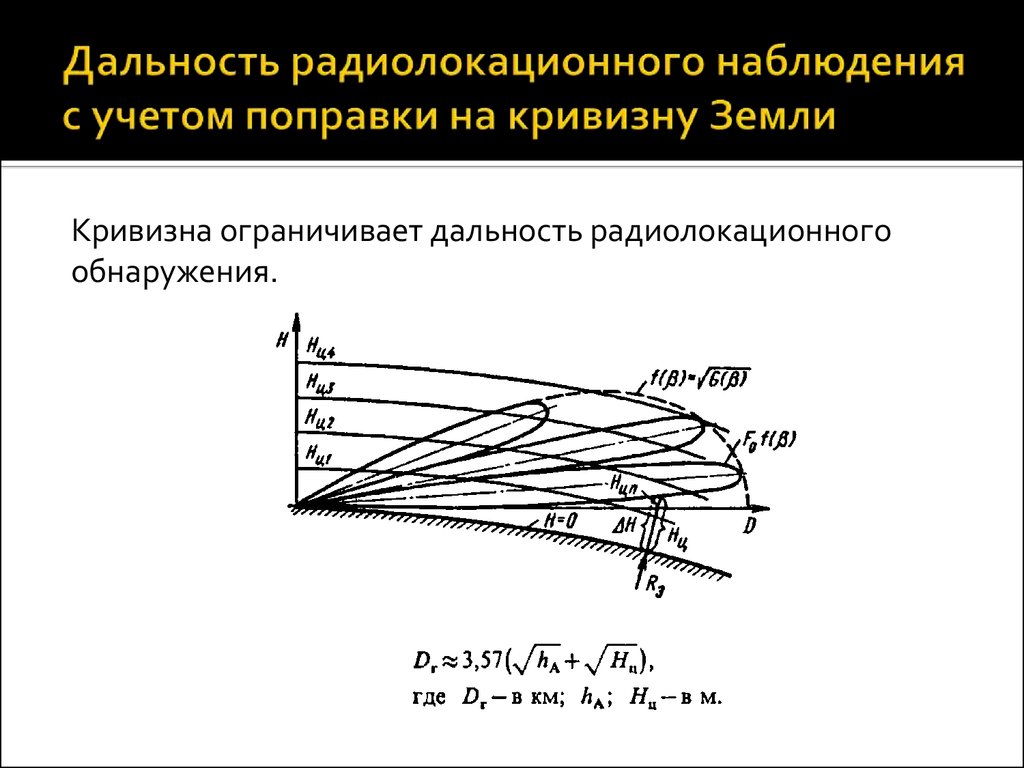


 0
0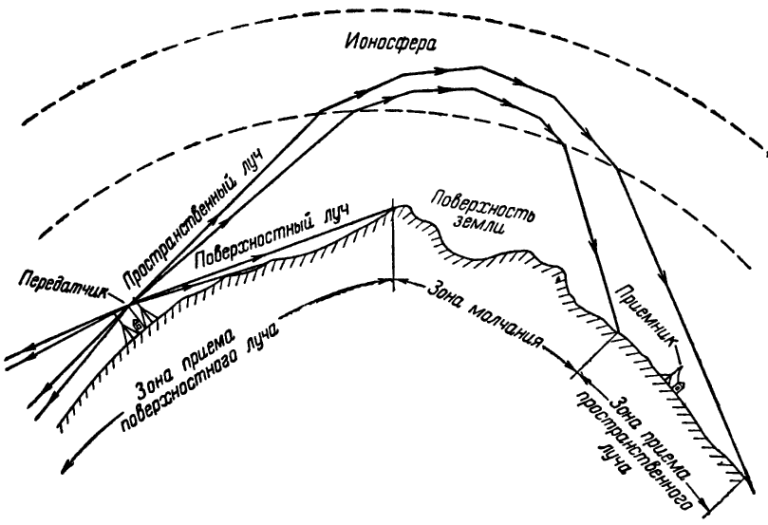 0
0 1
1 9
9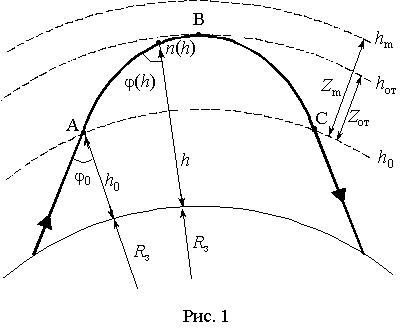 5
5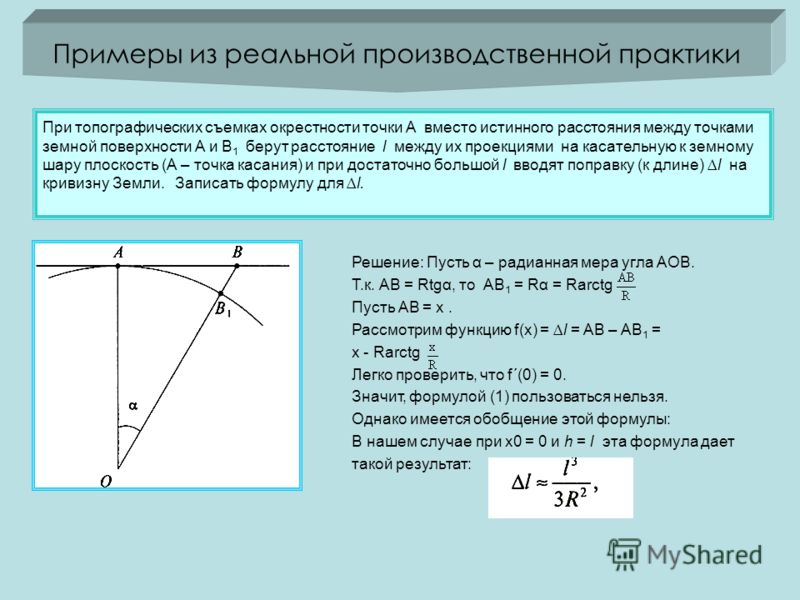 1
1 3
3 5
5 0
0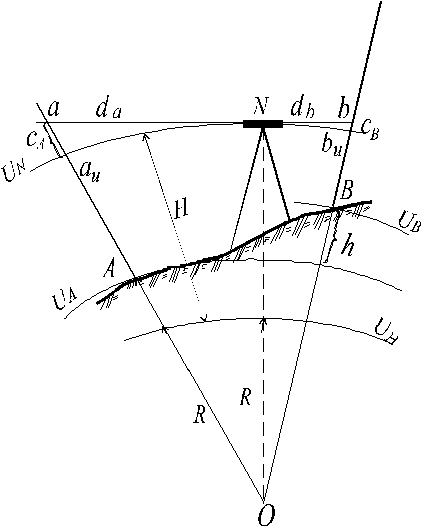 ru:
ru:
 Это расстояние до горизонта.
Это расстояние до горизонта. 000126 miles
000126 miles