Видимый горизонт и дальность видимости
РаботаНавигация
Расчет видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта.
Калькулятор ниже предназначен для расчета видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта. Под ним, как водится, немного теории.
Видимый горизонт и дальность видимости
Высота наблюдателя (м.)Высота наблюдателя (метры)
Высота объекта (м.)Высота наблюдаемого объекта (метры)
ОтображениеКилометрыМорские милиТочность вычисленияЗнаков после запятой: 3
Видимый горизонт
Дальность видимости
Видимый горизонт
Так как земля изогнута, наблюдателю, находящемуся, например, в море, представляется, что он находится в центре круга, по краям которого небо как бы смыкается с морской поверхностью. Эта окружность и называется видимым горизонтом наблюдателя. На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).
На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).
Говоря о видимом горизонте чаще всего имеют в виду длину d отрезка BC. Длину d легко вывести из теоремы Пифагора.
где R — радиус Земли, который обычно принимают за 6378 километров.
В реальной жизни на стороне человека выступает атмосфера. Она, благодаря явлению рефракции, то есть преломлению лучей в верхних слоях атмосферы, расширяет его горизонты примерно на 6% 🙂
Формула, таким образом, принимает вид
В принципе, везде (по крайней мере, насколько я находил в Интернете) для расчетов используют упрощенную формулу, из которой исключен радиус Земли. Она, кстати, вполне выводится из верхней.
, для результата в морских милях или
, для результата в километрах
Дальность видимости
Дальность видимости предметов определяется наибольшим расстоянием, на котором наблюдатель увидит вершину наблюдаемого объекта на линии горизонта. Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.
Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.
В калькуляторе я ее вычисляю, а на практике, насколько я понимаю, дальности видимости береговых ориентиров указываются во всяческих лоциях, мореходных таблицах и тому подобном для высоты наблюдателя, равной пяти метрам. Для поправки на фактическую высоту наблюдателя используется «номограмма для расчета дальности видимости предметов в море в дневное время при среднем состоянии атмосферы».
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Положение Солнца на заданную дату. Таблица азимута и высоты над горизонтом
- • Азимут и высота солнца над горизонтом
- • Расстояние по поверхности Земли и расстояние сквозь Землю
- • Угловой размер, линейный размер и расстояние
- • Расстояние между двумя координатами
- • Раздел: Навигация ( 9 калькуляторов )
видимый горизонт горизонт дальность видимости Навигация расстояние
PLANETCALC, Видимый горизонт и дальность видимостиTimur2020-11-03 14:19:28
Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Радиогоризонт и дальность прямой видимости РЛС.
hr высота антенны РЛС,
ht высота цели,
dh радиогоризонт,
dt расстояние от точки касания луча РЛС поверхности Земли до цели,
D=dh + dt дальность прямой видимости,
R0 средний радиус Земли
Этот калькулятор определяет геометрическую дальность прямой видимости цели (без учета рефракции радиоволн в атмосфере) и дальность прямой радиовидимости цели по известным высоте антенны РЛС и высоте цели. Если высота цели равна нулю (наземная цель), то речь идет о геометрическом горизонте (без учета рефракции) и радиогоризонте (с учетом рефракции). Отметим, что в морском судовождении и в авиации дальность измеряется в морских милях. Морские мили удобно использовать в связи с тем, что они прямо связаны с географическими координатами — одна морская миля соответствует одной минуте географической широты.
Пример: Рассчитать радиогоризонт радиолокационной станции (РЛС) и дальность прямой радиовидимости, если ее антенна поднята на высоту 10 м, а цель находится на высоте 15 м.
Входные данные
Высота цели
ht
Высота антенны РЛС
hr км
Поделиться
Поделиться ссылкой на этот калькулятор, включая входные параметры
Twitter Facebook Google+ VK
Закрыть
Выходные данные
Геометрический горизонт
dg м миля морская миля (международная)
Радиогоризонт
dr м миля морская миля (международная)
Геометрическая дальность прямой видимости цели
Dg м миля морская миля (международная)
Дальность прямой радиовидимости цели
Dr м миля морская миля (международная)
Для расчета введите величины в соответствующие поля, выберите британские или метрические единицы и нажмите на кнопку

Радиогоризонт РЛС определяется как расстояние от антенны до места, в котором луч РЛС «касается» земной поверхности. При этом цели, находящиеся ниже линии, соединяющей точку касания и антенну РЛС, обнаружить невозможно. Для облегчения расчетов предположим, что Земля представляет собой идеальную сферу с радиусом R0=6 371.009 км. Предположим также (пока), что в атмосфере отсутствует рефракция, которую мы рассмотрим позднее. На рисунке выше коричневая окружность представляет собой поверхность Земли. Антенна РЛС поднята на высоту
 По теореме Пифагора имеем:
По теореме Пифагора имеем:и
Если величины hr и ht малы по сравнению с радиусом Земли, эти выражения можно упростить:
и
Для значений hr<250 км и ht<250 км ошибка составляет менее 1%. То есть, используя полученные формулы, мы можем рассчитывать радиогоризонт для спутников и космических станций на околоземной орбите.
Геометрическая дальность прямой видимости цели Dg определяется по формуле:
Эта формула используется в нашем калькуляторе для расчета геометрической дальности прямой видимости. Например, по этой формуле геометрический (визуальный) горизонт до РЛС на 30-метровой мачте или вышке будет приблизительно равен 20 000 м. Отметим, что в приведенных выше формулах все величины должны быть в одних и тех же единицах длины и расстояния.
Показатель преломления атмосферы n уменьшается с высотой и из-за этого радиоволны изгибаются вниз, к поверхности Земли; n1 — рефракция меньше, n2 — рефракция больше
Теперь попробуем учесть рефракцию электромагнитных волн, распространяющихся в атмосфере. В стандартной атмосфере (что такое стандартная — обсудим позже) температура и давление воздуха понижаются с увеличением высоты, так как воздух в верхних слоях атмосферы более разреженный. В результате показатель преломления атмосферы с высотой уменьшается. В связи с атмосферной рефракцией, электромагнитные волны изгибаются вниз и, таким образом, могут распространяться за геометрический горизонт. Это изгибание уменьшает зону тени РЛС и в то же время приводит к ошибкам при измерении расстояния и высоты цели.
В стандартной атмосфере (что такое стандартная — обсудим позже) температура и давление воздуха понижаются с увеличением высоты, так как воздух в верхних слоях атмосферы более разреженный. В результате показатель преломления атмосферы с высотой уменьшается. В связи с атмосферной рефракцией, электромагнитные волны изгибаются вниз и, таким образом, могут распространяться за геометрический горизонт. Это изгибание уменьшает зону тени РЛС и в то же время приводит к ошибкам при измерении расстояния и высоты цели.
Наша модель распространения радиоволн будет проще, если мы предположим, что радиоволны распространяются по прямым линиям в стандартной атмосфере. Для этого нужно предположить, что радиус Земли больше, чем на самом деле. Расчеты показывают, что если увеличить радиус Земли в 4/3 раза, рефракцией можно будет пренебречь. Таким образом, приведенная выше формула для дальности прямой радиовидимости цели с учетом рефракции
Эта формула и используется в нашем калькуляторе для определения радиогоризонта и дальности прямой радиовидимости цели.
Антенна бортовой метеонавигационной радиолокационной станции, установленная под обтекателем в носовой части самолета Боинг-747, и дисплей этой станции в кабине пилотов. На дисплее можно наблюдать изображения опасной грозовой и кучево-дождевой облачности. Если самолет летит на высоте 33 000 футов или 10 000 метров, то радиогоризонт будет равен 412 км или 222 морских мили
Атмосфера считается «стандартной», если отсутствует инверсия температуры и влажности, которые обычно приводят к аномальному распространению радиоволн и образованию атмосферных волноводов. Атмосферные волноводы могут образовываться в тех случаях, когда температура необычно быстро увеличивается с высотой. При этом концентрация водяного пара в воздухе быстро уменьшается с высотой. Например, в ясную летнюю ночь поверхность земли может быстро охладиться, что приведет к охлаждению слоя воздуха возле нее. Таким образом, получается, что сразу над землей имеется слой холодного воздуха, а над ним более теплый воздух. Такое явление называется температурной инверсией, то есть температура с высотой не уменьшается, как обычно, а, наоборот, увеличивается.
Автор статьи: Анатолий Золотков
Калькулятор кривизны Земли
Создано Bogna Szyk
Отзыв Стивена Вудинга и Джека Боуотера
Последнее обновление: 01 февраля 2023 г.
Содержание:- Что такое кривизна Земли?
- Кривизна Земли на милю
- Как далеко я могу видеть до того, как Земля искривится?
- Расчет высоты объекта с препятствиями
- Является ли этот калькулятор кривизны Земли точным?
- Часто задаваемые вопросы
Этот калькулятор кривизны Земли позволяет вам определить, какая часть удаленного объекта скрыта из-за кривизны Земли . Итак, если вы когда-нибудь хотели оценить общую высоту цели, которая частично скрыта за горизонтом, теперь вы можете это сделать. Вы также сможете узнать , как далеко вы можете видеть до кривых Земли — то есть, каково ваше расстояние до горизонта.
Не волнуйтесь, если вы еще не знаете, какова кривизна Земли – просто продолжайте читать, чтобы узнать всю необходимую информацию!
Какова кривизна Земли?
Представьте, что вы смотрите на море.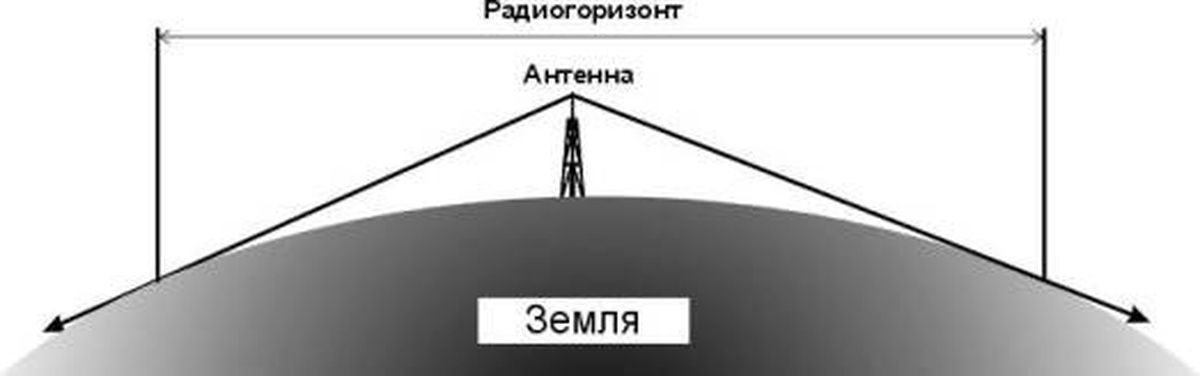 Земли не видно, только бескрайние голубые воды, мерцающие в лучах послеполуденного солнца. Вы можете разглядеть линию, которая разделяет море и небо. Эта линия называется горизонтом .
Земли не видно, только бескрайние голубые воды, мерцающие в лучах послеполуденного солнца. Вы можете разглядеть линию, которая разделяет море и небо. Эта линия называется горизонтом .
Внезапно вы начинаете видеть точку, которая становится все больше и больше. Во-первых, это вершина белого паруса; когда он приближается, вы также можете заметить форму корабля. Где был этот корабль раньше? Оно было скрыто за горизонтом.
Причина этого очевидна: поскольку форма Земли очень похожа на шар, поверхность между вами и кораблем не совсем плоская, а немного «выпуклая». Вот почему он загораживает вам обзор. Кривизна Земли — это просто мера этой «выпуклости». Он выражается как высота «выпуклости» на километр или милю.
💡 Обратите внимание, что , если бы Земля была плоской, вы бы видели весь корабль даже издалека. Ожидайте, что сначала он будет очень маленьким целым кораблем (точкой), а затем станет больше по мере приближения. Однако, наблюдая сначала издалека только верхнюю часть паруса, вы сами убедились, что Земля не плоская. Если вы заинтересованы в дальнейшем изучении этого вопроса, вам следует воспользоваться нашим калькулятором плоской и круглой земли.
Если вы заинтересованы в дальнейшем изучении этого вопроса, вам следует воспользоваться нашим калькулятором плоской и круглой земли.
Кривизна Земли на милю
Тогда насколько велика кривизна Земли? Поскольку мы не замечаем его в повседневной жизни, он должен быть относительно небольшим. Большинство источников считают 8 дюймов на милю как наиболее точная оценка. Это означает, что на каждую милю между вами и объектом кривизна будет препятствовать 8 дюймам высоты объекта.
Как далеко я могу видеть до того, как Земля искривится?
Первое, что вы можете найти с помощью нашего калькулятора кривизны Земли, это точное расстояние между вами и горизонтом . Вам нужно знать только два значения: ваш уровень зрения (другими словами, расстояние между вашими глазами и средним уровнем моря — при условии, что вы смотрите на море) и 92}a=(r+h)2−r2
где:
- ааа — расстояние до горизонта;
- hhh — уровень зрения выше среднего уровня моря; и
- ррр — радиус Земли, равный 3959 миль или 6371 км.

Это уравнение можно вывести с помощью теоремы Пифагора. Вы можете попробовать вывести его самостоятельно – это не так уж и сложно!
Расчет высоты объекта с препятствиями
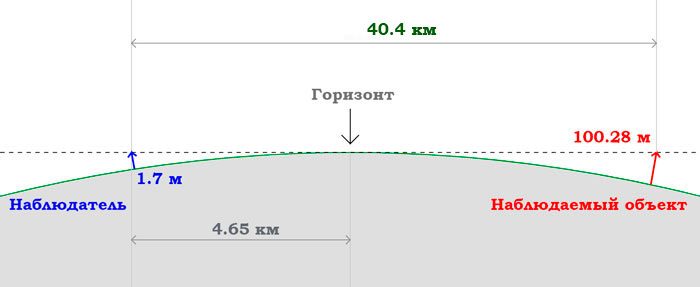
Посмотрите на изображение выше. Это представляет собой ситуацию, аналогичную ситуации с кораблем сверху. Вы можете видеть часть объекта, но остальная часть скрыт за горизонтом . Если вы хотите узнать высоту препятствия, просто введите все необходимые значения в калькулятор кривизны Земли. Вы также можете вычислить высоту вручную:
- Определите расстояние между вами (наблюдателем) и самой нижней точкой объекта, которую вы реально видите. Назовем это значение ddd и предположим, что оно равно 25 милям.
- Измерьте свой уровень зрения — то есть высоту, на которой ваши глаза находятся над морем. Мы будем обозначать его буквой ххх. Можно считать, что она равна 6 футам, что примерно равно 0,0011364 мили. 92} \\[0,5см]
\qquad — 3959 \\[1em]
Икс \! = 0,0611 \mathrm{ \ миль} = 322,76 \mathrm{\ ft}x=a2−2ad+d2+r2 −rx=32−2×3×25+252+39592 −3959x=0,0611 мили =322,76 фута
- Если у вас возникли проблемы с преобразованием единиц , просто используйте наш конвертер длины.

Является ли этот калькулятор кривизны Земли точным?
Вы можете обнаружить, что если бы вы сравнивали наш калькулятор с реальным сценарием, наш калькулятор мог бы в некоторых случаях ошибаться. Почему это происходит? Означает ли это, что Земля плоская и совсем не кривая?
Конечно нет! Это просто означает, что наш калькулятор не учитывает феномен преломления . Когда свет проходит через среду, которая не является идеально однородной, например воздух, он преломляется или преломляется . Например, преломление может произойти, когда свет попадает в карман с холодным воздухом или в горячий поток восходящего воздуха.
Когда луч света слегка изгибается, он меняет направление. Это означает, что некоторые фотоны от объекта, которые обычно попадают на землю, могут огибать поверхность Земли и достигать вашего глаза, поэтому высоты и расстояния, как показано на рисунке выше, могут показаться другими. Вот почему, когда вы вычисляете высоту объекта с препятствиями, расстояния, которые вы видите, могут немного отличаться от наблюдаемых!
Если вам интересно узнать больше о законе преломления Снелла, вам следует воспользоваться нашим калькулятором закона Снелла здесь.

Часто задаваемые вопросы
Как далеко находится горизонт на уровне моря?
Горизонт на уровне моря примерно
4,5 км. Чтобы вычислить его, выполните следующие действия:- Предположим, что высота ваших глаз равна
h = 1,6 м. - Постройте прямоугольный треугольник с гипотенузой
r + h(гдеr— радиус Земли) и катетомр. - Рассчитайте последний катет по теореме Пифагора: результатом будет расстояние до горизонта:
a = √[(r + h)² - r²] - Подставьте значения в формулу выше:
a = √[(6 371 000 + 1,6)² - 6 371 000²] = 4 520 м
Как рассчитать расстояние до горизонта?
Чтобы рассчитать теоретическое расстояние до горизонта с вашей точки зрения, представьте, что вы строите прямоугольный треугольник со сторонами, равными:
- Радиус Земли плюс высота ваших глаз над уровнем моря,
r + h; - Радиус Земли
r; и - Линия, касательная к поверхности Земли, начинается у вас перед глазами.
 Это расстояние до горизонта.
Это расстояние до горизонта.
Рассчитываем расстояние до горизонта по формуле
a = √[(r + h)² - r²].Можно ли увидеть Францию из Англии?
Да, но только в отличном состоянии. Со скал Дувра, высотой около
100 м, ваш горизонт будет на35,7 км. Вы можете рассчитать это расстояние по этой формуле, гдеh— высота над уровнем моря, аr— радиус Земли:
a = √[(r + h)² — r²]
Поскольку самая узкая часть Ла-Манша едва достигает33 км, можно увидеть Францию, но точь-в-точь точь-в-точь.Как далеко можно увидеть гору Эверест?
Вы можете увидеть Эверест (теоретически) с расстояния
340 км.Если предположить, что вы находитесь на уровне моря, а ваши глаза находятся на высоте
1,6 мнад землей, ваш горизонт (на расстоянии около4,5 км) покрывает всю самую высокую гору на Земле, только если вы находитесь на высоте более чем340 кмот него. Теоретически вершину Эвереста можно увидеть из Бангладеш; однако другие вершины покрывают его!
Теоретически вершину Эвереста можно увидеть из Бангладеш; однако другие вершины покрывают его!Bogna Szyk
Расстояние до объекта
Уровень зрения
Расстояние до горизонта
Часть скрытого объекта
Посмотрите 24 похожих калькулятора оптики и света 🔍
Угловое разрешениеПлощадь апертуры Дальность бинокля… Еще 21
Калькулятор плоской и круглой Земли
Created by Steven Wooding
Отзыв от Bogna Szyk
Последнее обновление: май 10, 2023
Содержание:- Вера в плоскую Землю
- Модель плоской Земли
- Дважды закат эксперимент
- Как увидеть закат дважды
- Эксперимент с исчезающим объектом
- Инструкции по сокрытию объекта за кривизной Земли
- Эксперимент с тенью от палочки
- Инструкции по измерению размера Земли с использованием теней от палочки
- Пример расчета эксперимента с тенью от палочки
- Что происходит в провести эксперимент с тенью, если Земля плоская?
Как лучше всего познавать мир? Предложить теорию и вознамериться доказать ее наблюдениями (наукой)? Или просто выдумываете и игнорируете очевидные факты (ерунда)? Здесь, в Omni, мы склонны думать, что первый вариант работает довольно хорошо.
 Это привело нас на Луну, не так ли? – Между прочим, это действительно так.
Это привело нас на Луну, не так ли? – Между прочим, это действительно так. Чтобы отпраздновать Всемирный день науки за мир и развитие , который проводится 10 ноября, мы создали калькулятор, который поможет вам бороться с чушью, полуправдой и чепухой, а также за науку, наблюдательность и непредубежденность. .
Калькулятор плоской и круглой Земли Omni включает эксперименты, которые помогают доказать, что Земля действительно круглая. Не волнуйся; вы не будете строить свою собственную ракету, чтобы отправиться в открытый космос, чтобы проверить (или рассчитать ее импульс и импульс или ее кинетическую энергию).
У нас есть три относительно простых эксперимента, которые вы можете попробовать:
- Тени палочки – Используйте длины теней, отбрасываемых палкой в разных местах, чтобы оценить окружность Земли.
- Закат дважды – Изменив точку обзора над землей, вы сможете увидеть закат дважды.
 Наш калькулятор подскажет, сколько второго заката вы увидите.
Наш калькулятор подскажет, сколько второго заката вы увидите. - Исчезающие объекты – Скройте объекты за кривизной Земли, изменив высоту точки обзора. Этот калькулятор покажет вам, какой высоты объект вы можете заставить исчезнуть.
Прежде чем мы перейдем к экспериментам, давайте кратко рассмотрим, почему люди верят в плоскую Землю и в модель мира, которую они выдвигают.
Вера в плоскую Землю
Удивительно, но в самой богатой, самой технологически развитой стране мира каждый шестой житель не уверен, что Земля круглая 🤔. Конечно, страна — это США , и вера в плоскую Землю может проистекать из ее крайне индивидуалистической культуры и недоверия к властям, институтам и экспертам.
Пост Общества Плоской Земли в FacebookПлоскоземельцы, кажется, смотрят на мир самостоятельно, не обращая внимания на колодец за 2000 лет человеческих открытий . Вау, они упускают. Они также крайне недоверчивы к любым фактам, которые не проверили на себе лично.
 Поговорите о проблемах с доверием.
Поговорите о проблемах с доверием. Затем они берутся за невероятные испытания, чтобы доказать, что Земля плоская, когда есть простые вещи, которые они могут сделать, чтобы доказать, что Земля круглая. Вот несколько примеров:
- «Безумный» Майк Хьюз построил свои собственные паровые ракеты, чтобы летать на высоту 1800 футов (550 м), чтобы сфотографировать отсутствие кривизны пустыни Мохаве. К сожалению, вам нужно подняться на высоту не менее 35 000 футов (11 000 м), чтобы увидеть кривизну Земли. К сожалению, он скончался в феврале 2020 года в результате неудачного полета ракеты.
- Звезда YouTube Логан Пол собирается посетить Антарктиду, чтобы найти край плоской Земли. Ему лучше упаковать много припасов, так как до другой стороны Антарктиды около 3000 миль (5000 км).
- Рэпер B.o.B пытался собрать средства на запуск собственного спутника, чтобы проверить плоскость Земли. Ему удалось собрать только 6 883 доллара из своей цели в 1 миллион долларов.
 Ну да ладно. Может быть, вместо этого он мог бы попробовать наши простые, недорогие эксперименты.
Ну да ладно. Может быть, вместо этого он мог бы попробовать наши простые, недорогие эксперименты.
Этот мультфильм Тома Фондера очень хорошо описывает сторонников плоской Земли.
Мультфильм Тома Фондера.Модель плоской Земли
В модели плоской Земли мир представляет собой диск (похожий на шестерни, используемые для редукторов) с северным полюсом в центре. По краю диска лед и снег «южного полюса». Затем он образует ледяной барьер, по-видимому, для того, чтобы вода океанов не падала с диска в космос.
Карта физического мира в трехосной бореальной проекции Хеллерик, которую сторонники плоской Земли используют в качестве модели плоской Земли.Толщина плоского земного диска не ясна. Однако задействованная масса должна быть намного меньше круглой Земли, поэтому Земля не сможет удержать свою атмосферу. Может быть, над Землей есть прозрачный купол , не дающий ей сбежать.
Традиционная модель плоской Земли имеет солнце, расположенное над диском, кружащимся по небу, как мобильник ребенка, и на гораздо более близком расстоянии.
 Тогда это не объясняет закаты и рассветы. Для здравого смысла представим, что диск вращается, как монета, относительно солнца. Это, по крайней мере, вернуло бы наш восход и закат (то, что могли бы наблюдать даже простейшие животные). Однако не было бы часовых поясов, поскольку восход и закат были бы в одно и то же время по всему миру.
Тогда это не объясняет закаты и рассветы. Для здравого смысла представим, что диск вращается, как монета, относительно солнца. Это, по крайней мере, вернуло бы наш восход и закат (то, что могли бы наблюдать даже простейшие животные). Однако не было бы часовых поясов, поскольку восход и закат были бы в одно и то же время по всему миру.🔎 💻 Вы можете испытать, каково это жить на плоской Земле, используя компьютерную модель, созданную Брюсом Шервудом. Он показывает, что солнце никогда не садится и его видимый размер меняется в течение дня, а также многие другие вещи, которые мы просто не наблюдаем в реальности.
Это основная проблема модели плоской Земли. Он полон несоответствий и необъяснимых наблюдений. Например, почему холодно и в центре, и на краю диска?
Вернемся к более научному мышлению и представим первый эксперимент.
Двойной эксперимент «Закат»
Этот первый эксперимент может быть очень простым. Двигайтесь вверх достаточно быстро, чтобы опередить тень, отбрасываемую горизонтом.
 После этого вы сможете дважды увидеть часть заката! Если вы заметите это, то Земля действительно круглая. Этот эксперимент подсчитает, сколько секунд вы могли бы видеть закат и как долго вы могли бы продлить закат.
После этого вы сможете дважды увидеть часть заката! Если вы заметите это, то Земля действительно круглая. Этот эксперимент подсчитает, сколько секунд вы могли бы видеть закат и как долго вы могли бы продлить закат.Что бы вы увидели, если бы Земля была плоской? Нет второго заката 😭. Неважно, как высоко или быстро вы поднялись с поверхности плоской Земли; ты не увидишь солнца снова до рассвета.
Для круглой Земли, когда солнце садится, представьте тень, отбрасываемую земным горизонтом, приближающуюся к вам и движущуюся вверх по вашему телу. Если вы сможете опередить эту тень, двигаясь вверх достаточно быстро, вы снова сможете увидеть закат. Давайте посмотрим на математику.
В этой статье дается уравнение, связывающее время с высотой тени:
t = 8 × √h,где
t— время, за которое тень поднимается вверх на величинуч. Мы можем связатьчс разницей высот между двумя высотами, аtсо временем, которое требуется для движения вверх. Поскольку мы не можем мгновенно переместиться с более низкой высоты на более высокую, нам необходимо учитывать время в пути. Наконец, чтобы найти количество секунд заката, которое мы можем увидеть снова, нам нужно знать продолжительность заката. Затем у нас есть это уравнение для процента заката два, который вы будете наблюдать снова:
Поскольку мы не можем мгновенно переместиться с более низкой высоты на более высокую, нам необходимо учитывать время в пути. Наконец, чтобы найти количество секунд заката, которое мы можем увидеть снова, нам нужно знать продолжительность заката. Затем у нас есть это уравнение для процента заката два, который вы будете наблюдать снова:процент заката два = 100 × (1 - ((продолжительность заката - t - время в пути) / продолжительность заката)))Как дважды увидеть закат
Есть несколько способов снова увидеть солнце сразу после его захода, в разной степени. Калькулятор плоской и круглой Земли Omni подскажет, сколько секунд заката вы сможете наблюдать. Давайте рассмотрим три идеи, которые мы придумали.
1. Лечь, встать
Эта идея самая простая с точки зрения оборудования. Вам просто нужно место, где вы можете видеть закат солнца в море или на очень плоской земле (например, в пустыне). Поможет и красивое безоблачное небо.
 Все, что вам нужно сделать, это смотреть на закат лежа. Как только вы больше не сможете видеть Солнце, немедленно встаньте так быстро, как только сможете. Вы должны снова увидеть небольшую часть верхней части солнца.
Все, что вам нужно сделать, это смотреть на закат лежа. Как только вы больше не сможете видеть Солнце, немедленно встаньте так быстро, как только сможете. Вы должны снова увидеть небольшую часть верхней части солнца.Вот как использовать калькулятор для точного подсчета.
- Выберите ближайшее к вам место или вручную введите продолжительность заката там, где вы находитесь.
- Введите нижнюю начальную высоту вашего уровня глаз. В данном случае лежа. Мы рекомендуем около 8 дюймов (20 см).
- Введите, сколько времени вам понадобится, чтобы подняться на большую высоту. Мы рассчитываем примерно на полсекунды, но давайте перепроверим время.
- Введите окончательную высоту вашего уровня глаз, когда вы стоите. Вы можете измерить это, вычтя расстояние от макушки головы до глаз из вашего роста.
- Затем вы увидите процент солнца, которое вы снова сможете увидеть заходящим. Хочу увидеть больше? Попробуйте изменить значения в калькуляторе или перейдите к более сложным вариантам эксперимента ниже.

С помощью этого метода вы сможете увидеть около 5% второго заката.
2. Быстро подняться на небоскреб
Чтобы увидеть больше второго заката, вам придется подниматься выше и быстрее, чтобы опередить тень горизонта. Небоскреб с быстрым лифтом — один из вариантов. Это явление наблюдалось в отеле Buri Khalifa в Дубае.
Чтобы выбрать входные значения для этого небоскреба, выберите «Небесный подъемник — отель Buri Khalifa» из списка идей. Если вы хотите попробовать это в другом здании, измените входные значения соответствующим образом.
Вы снова сможете увидеть массивный 88% закат, и таким образом продолжительность почти удвоится. Если вы любитель заката, это то, что нужно сделать.
3. Дрон с камерой
Еще одна идея — использовать качественный дрон с камерой для прямой трансляции. Мы нашли один беспилотник, который может подняться на высоту 3300 футов (1000 м) за 200 секунд.
 Если вы выберете «Дрон» из списка идей, вы увидите, что должны снова увидеть около трети заката этим методом.
Если вы выберете «Дрон» из списка идей, вы увидите, что должны снова увидеть около трети заката этим методом.Проверьте, насколько быстро и высоко может летать ваш дрон, и соответствующим образом скорректируйте значения в калькуляторе.
Эксперимент с исчезающим объектом
В этом эксперименте мы скроем часть объекта за кривизной Земли. Вам нужно будет найти водоем, где дальний берег находится на расстоянии не менее мили с четвертью (2 км), и это должен быть хороший безветренный день.
Кроме того, чтобы избежать светового эффекта миража [преломление]), проведите эксперимент утром, когда прохладно. Вот почему мы не рекомендуем использовать пустыню — эффект миража будет означать, что вы не сможете достаточно четко видеть объекты на дальнем берегу.
В этом видео на YouTube парень заставил грузовик в 4 милях (7 км) исчезнуть на дальнем берегу озера, опустив камеру ближе к земле.
com/embed/JTfhYyTuT44?rel=0&showinfo=0&start=655″ loading=»lazy»> Посмотреть это на YouTubeВ качестве альтернативы, морская ветряная электростанция также является хорошим вариантом, как показано на этой фотографии:
Морские ветряные мельницы исчезают за кривизной Земли, у берегов Бельгии. Оффшорные ветряные мельницы, исчезающие за кривизной Земли у берегов Бельгии (Атрибуция: Lieven, CC BY-SA 4.0, через Wikimedia Commons).Обратите внимание, чем дальше ветряная мельница, тем больше она скрыта. Вот о чем этот эксперимент — вычисление того, какую часть удаленного объекта вы можете скрыть за кривизной Земли.
💡 Кривизна Земли была измерена как 8 дюймов на милю (12 см на километр). Это означает, что на каждую милю, которую вы удаляете от объекта, 8 дюймов нижней части объекта скрыты кривизной Земли. Однако это предполагает, что вы смотрите на объект с нулевой высотой, что не очень практично.
Как кривизна Земли скрывает часть удаленного объекта.
В этом эксперименте мы начнем с высокой точки обзора, а затем спустимся на более низкую точку обзора, чтобы скрыть удаленный объект . Говоря математическим языком, мы находим, сколько скрыто при высоких и низких просмотрах, и вычисляем разницу.
Чтобы рассчитать скрытую высоту, нам сначала нужно знать расстояние до горизонта. Это определяется следующим уравнением:
a = √[(r + h)² - r²], где:
- a это расстояние до горизонта,
- h — уровень точки обзора над землей, а
- r — радиус Земли, равный 3959 миль или 6371 км.
Затем мы вводим результат во второе уравнение, которое вычисляет, какая часть объекта затемнена,
x, если смотреть с нулевой высоты:x = √(a² - 2ad + d² + r²) - rРазница между двумя значениями
x— это высота объекта, который мы можем заставить исчезнуть, изменив точку обзора.
Инструкции по сокрытию объекта за кривизной Земли
Итак, вы нашли отличное место, например, озеро с берегом в нескольких милях от вас. Чтобы увидеть какие-либо предметы на дальнем берегу, вам понадобится хороший бинокль . А еще лучше видеокамера с мощным зум-объективом. Это также позволит вам записать эксперимент, как на видео выше.
Чтобы получить четкий обзор через бинокль или камеру, установите их на штатив рекомендуется. Использование штатива также позволяет точно измерить две высоты.
Вот как с помощью калькулятора вычислить объект какого размера вы могли бы скрыться за кривизной Земли.
- Измерить расстояние до дальнего берега озера. Для этого вы можете использовать бумажную карту или функцию измерения на Google Maps. Введите расстояние в переменную «Расстояние до объекта» в калькуляторе.
- Измерьте высоту над землей на уровне ваших глаз, когда вы стоите, или камеры, когда она находится в верхнем положении.
 Введите эту высоту в следующее поле ввода.
Введите эту высоту в следующее поле ввода. - Сделайте то же самое, когда вы лежите или ваша камера находится в низком положении. Чтобы добиться максимального эффекта, постарайтесь опуститься как можно ниже до уровня воды.
- Затем вы увидите, что высота объекта, скрытого из-за кривизны Земли, рассчитывается для вас. Если он кажется слишком маленьким, чтобы его можно было увидеть, попробуйте увеличить большую высоту и уменьшить нижнюю.
Если бы Земля была плоской, вы не увидели бы никакой разницы в объектах на дальнем берегу озера, как бы низко вы ни смотрели на них.
Эксперимент с тенью палки
Этот эксперимент не только доказывает, что Земля круглая, вы также можете оценить окружность Земли. Именно это и сделал греческий математик Эратосфен в Александрии примерно в 240 году до н. э. года. Он знал, что в Асуане, примерно в 500 милях к югу, есть колодец, где солнечный свет достигает дна в полдень летнего солнцестояния.
 В то же время он измерил тень, отбрасываемую палкой в Александрии.
В то же время он измерил тень, отбрасываемую палкой в Александрии.Предполагая, что Земля круглая, а Солнце находится далеко, и используя математику, которую мы рассмотрим ниже, он пришел к выводу, что окружность Земли примерно в 50 раз превышает расстояние между Александрией и Асуаном. это в пределах 10% от правильного ответа . Фантастический результат для такого простого эксперимента, проведенного более 2000 лет назад.
💡 Окружность Земли — это расстояние вокруг Земли. Измеряя вокруг полюсов, это 24 860 миль (40 008 км). По экватору это 24 901 миля (40 075 км). Небольшая разница между двумя измерениями связана с тем, что Земля вращается.
Палки на разных широтах отбрасывают тени разной длины.Глядя на треугольник, образованный палкой и тенью, мы можем использовать тригонометрическую функцию арктангенса, чтобы вычислить угол между палкой и солнечным лучом, используя уравнение:
θ = арктангенс (длина тени / высота палочки)
Итак, мы делаем это для двух мест.
Показывает, как углы тени палочки соотносятся с углом в центре Земли между двумя точками А и В. Как эти два угла связаны с окружностью Земли? Рисунок ниже поможет нам ответить на этот вопрос.
Как эти два угла связаны с окружностью Земли? Рисунок ниже поможет нам ответить на этот вопрос.Используя некоторую геометрию, мы можем показать, что угол α между линиями, проходящими через точки А и В, и центром Земли, разница углов тени от палочки:
α = θ₂ — θ₁
Теперь мы знаем длину дуги (расстояние по поверхности Земли) между A и B и угол α. Это позволяет нам просто увеличить расстояние до полной окружности Земли, используя уравнение:
Окружность Земли = Расстояние A → B × (360° / α)
Важно отметить, что расстояние от A до B должно быть расстояние, если бы вы могли путешествовать только на север или юг (расстояние север-юг). Нам нужно это расстояние, так как только когда вы движетесь на север, тень, отбрасываемая палкой, становится длиннее.
Карта США, показывающая расстояние с севера на юг между точками A и B.
Предполагая, что точка A находится к югу от точки B, начертите на карте линию строго на север от точки A. Затем проведите линию строго на восток от точки B. Расстояние с севера на юг — это длина от точки А до пересечения двух начерченных вами линий.
Инструкции по измерению размеров Земли с помощью теней от палочек
Есть два основных способа провести этот эксперимент. Вы можете либо путешествовать на значительное расстояние на север или юг (более 100 миль, но чем дальше, тем лучше), либо сотрудничать с кем-то, кто живет далеко, чтобы помочь вам.
Начнем с путешествия. Лучше всего делать это в самый короткий или самый длинный день в году, так как продолжительность дня относительно стабильна. Это уменьшит ошибки измерения угла тени в двух точках. Вот пошаговые инструкции:
- Измерьте длину вашей палки . Вам нужно будет ввести это в первое поле ввода калькулятора. Если часть палки находится в земле, укажите только длину над землей.

- Измерьте длину тени в точке A в полдень по местному времени. Если это не солнечный день, подождите, пока он не появится. Введите длину тени в калькулятор, и угол тени будет рассчитан для вас.
- Отправляйтесь в локацию B и сделайте то же самое, что и в шаге 2.
- Используя карту, измерьте расстояние с севера на юг между двумя точками и введите это значение в калькулятор (см. инструкции выше).
- Затем вы получите ответ с измеренной оценкой окружности Земли и тем, насколько близко вы подошли к реальному ответу.
Если у вас есть друг в другом месте, чтобы помочь вам, шаги в основном такие же. Убедитесь, что две палочки имеют одинаковую длину и что вы измеряете тень в полдень по местному времени того же дня. Этот вариант намного проще и может выполняться в любой солнечный день в году.
Пример расчета эксперимента с тенью от палки
Например, давайте отправимся на север из Флориды в Пенсильванию (от А до Б), преодолев расстояние с севера на юг около 1000 миль (1609км).
 Палка имеет длину 3 фута (0,91 м), и мы измеряем длину тени 3 фута в точке A. Это означает угол тени 45°. Затем мы отправляемся в точку B и измеряем тень длиной 5,2 фута, что означает, что угол тени здесь составляет около 60°.
Палка имеет длину 3 фута (0,91 м), и мы измеряем длину тени 3 фута в точке A. Это означает угол тени 45°. Затем мы отправляемся в точку B и измеряем тень длиной 5,2 фута, что означает, что угол тени здесь составляет около 60°.Введите все эти цифры в калькулятор, и мы получим результат 24 000 миль (38 624 км) . Это в пределах 4% от реальной окружности, измеренной между полюсами на расстоянии 24 860 миль (40 008 км).
Что происходит в эксперименте с тенью палки, если Земля плоская?
Давайте на мгновение представим, что плоскоземельцы правы. Как приведенный выше пример работает в модели плоской Земли?
Диаграмма показывает, что происходит без эксперимента с тенью палки в модели плоской Земли.В модели плоской Земли палочки по-прежнему будут отбрасывать тени разной длины. Однако результат выполнения некоторой тригонометрии приводит к странному результату. Ссылаясь на приведенную выше диаграмму и применяя указанную тригонометрию, мы можем сказать, что:
d = h × (tan θ₂ — tan θ₁)
Используя углы 45° и 60° и 1000 миль для d, мы видим, что расстояние до Солнца h равно
h = 1000 / (1,73 — 1) = 1370 миль
Это делает кажутся очень близкими.
 Однако модель плоской Земли может сказать, что Солнце намного меньше, чем считает наука.
Однако модель плоской Земли может сказать, что Солнце намного меньше, чем считает наука.Теперь мы можем вычислить два других расстояния до Солнца из двух точек:
R₁ = h / cos θ₁ = 1370 / cos(45°) = 1937 миль
R₂ = h / cos θ₂ = 1370 / cos(60°) = 2740 миль
Этот результат означает, что, пройдя на юг 1000 миль, солнце должно было стать меньше примерно на 40% . На самом деле, как вы можете убедиться сами, солнце не становится меньше по мере вашего продвижения на юг.
Следовательно, можно сделать вывод, что модель плоской Земли неверна. Это не согласуется с наблюдением. Это важнейшее свойство любой научной модели. Он должен согласовываться с экспериментальными результатами.
Стивен Вудинг
Выберите эксперимент
Если Земля круглая 🌎, вы сможете дважды увидеть часть заходящего солнца! Вы делаете это, двигаясь вверх быстрее, чем тень, отбрасываемая горизонтом. Давайте подсчитаем, сколько секунд вы должны увидеть закат.
Инструкции:
- Выберите свое местоположение или введите продолжительность заката, где вы находитесь.
- Выберите способ набора высоты или введите начальную высоту, время и конечную высоту.
- Если калькулятор говорит, что вы снова можете увидеть часть второго заката, а вы это сделали, вы только что доказали, что Земля круглая!
Закат
Местоположение 📍
Продолжительность заката 🌅
Продолжительность заката зависит от того, насколько севернее или южнее находится место.
Набрать высоту, чтобы поймать второй закат
Метод
Начальная высота
Время в пути ⏱️
Конечная высота
2-й закат
Количество, которое вы сможете увидеть снова
Дополнительное время заката 🌞
Общая продолжительность
Вы сможете увидеть 4,8% заката снова и снова! Этот результат означает, что Земля действительно кажется круглой 🌎 .
- Если у вас возникли проблемы с преобразованием единиц , просто используйте наш конвертер длины.





 Это расстояние до горизонта.
Это расстояние до горизонта. Теоретически вершину Эвереста можно увидеть из Бангладеш; однако другие вершины покрывают его!
Теоретически вершину Эвереста можно увидеть из Бангладеш; однако другие вершины покрывают его! Это привело нас на Луну, не так ли? – Между прочим, это действительно так.
Это привело нас на Луну, не так ли? – Между прочим, это действительно так.  Наш калькулятор подскажет, сколько второго заката вы увидите.
Наш калькулятор подскажет, сколько второго заката вы увидите.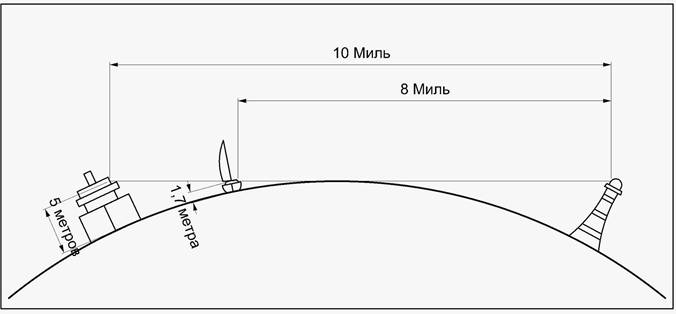 Поговорите о проблемах с доверием.
Поговорите о проблемах с доверием.  Ну да ладно. Может быть, вместо этого он мог бы попробовать наши простые, недорогие эксперименты.
Ну да ладно. Может быть, вместо этого он мог бы попробовать наши простые, недорогие эксперименты. Тогда это не объясняет закаты и рассветы. Для здравого смысла представим, что диск вращается, как монета, относительно солнца. Это, по крайней мере, вернуло бы наш восход и закат (то, что могли бы наблюдать даже простейшие животные). Однако не было бы часовых поясов, поскольку восход и закат были бы в одно и то же время по всему миру.
Тогда это не объясняет закаты и рассветы. Для здравого смысла представим, что диск вращается, как монета, относительно солнца. Это, по крайней мере, вернуло бы наш восход и закат (то, что могли бы наблюдать даже простейшие животные). Однако не было бы часовых поясов, поскольку восход и закат были бы в одно и то же время по всему миру. После этого вы сможете дважды увидеть часть заката! Если вы заметите это, то Земля действительно круглая. Этот эксперимент подсчитает, сколько секунд вы могли бы видеть закат и как долго вы могли бы продлить закат.
После этого вы сможете дважды увидеть часть заката! Если вы заметите это, то Земля действительно круглая. Этот эксперимент подсчитает, сколько секунд вы могли бы видеть закат и как долго вы могли бы продлить закат. Поскольку мы не можем мгновенно переместиться с более низкой высоты на более высокую, нам необходимо учитывать время в пути. Наконец, чтобы найти количество секунд заката, которое мы можем увидеть снова, нам нужно знать продолжительность заката. Затем у нас есть это уравнение для процента заката два, который вы будете наблюдать снова:
Поскольку мы не можем мгновенно переместиться с более низкой высоты на более высокую, нам необходимо учитывать время в пути. Наконец, чтобы найти количество секунд заката, которое мы можем увидеть снова, нам нужно знать продолжительность заката. Затем у нас есть это уравнение для процента заката два, который вы будете наблюдать снова: Все, что вам нужно сделать, это смотреть на закат лежа. Как только вы больше не сможете видеть Солнце, немедленно встаньте так быстро, как только сможете. Вы должны снова увидеть небольшую часть верхней части солнца.
Все, что вам нужно сделать, это смотреть на закат лежа. Как только вы больше не сможете видеть Солнце, немедленно встаньте так быстро, как только сможете. Вы должны снова увидеть небольшую часть верхней части солнца.
 Если вы выберете «Дрон» из списка идей, вы увидите, что должны снова увидеть около трети заката этим методом.
Если вы выберете «Дрон» из списка идей, вы увидите, что должны снова увидеть около трети заката этим методом.

 Введите эту высоту в следующее поле ввода.
Введите эту высоту в следующее поле ввода. В то же время он измерил тень, отбрасываемую палкой в Александрии.
В то же время он измерил тень, отбрасываемую палкой в Александрии. Как эти два угла связаны с окружностью Земли? Рисунок ниже поможет нам ответить на этот вопрос.
Как эти два угла связаны с окружностью Земли? Рисунок ниже поможет нам ответить на этот вопрос.

 Палка имеет длину 3 фута (0,91 м), и мы измеряем длину тени 3 фута в точке A. Это означает угол тени 45°. Затем мы отправляемся в точку B и измеряем тень длиной 5,2 фута, что означает, что угол тени здесь составляет около 60°.
Палка имеет длину 3 фута (0,91 м), и мы измеряем длину тени 3 фута в точке A. Это означает угол тени 45°. Затем мы отправляемся в точку B и измеряем тень длиной 5,2 фута, что означает, что угол тени здесь составляет около 60°. Однако модель плоской Земли может сказать, что Солнце намного меньше, чем считает наука.
Однако модель плоской Земли может сказать, что Солнце намного меньше, чем считает наука.
