Калькуляторы | Практическая информатика | Рецепты Linux
такое
Как уже было сказано выше, программы, имитирующие функции и внешний вид обыкновенных карманных калькуляторов, существуют во всех операционных системах. Все они содержат ряд кнопок для ввода цифр и основных арифметических действий, а также панель, отображающую получаемые результаты. Большинство из них в дополнение к стандартному набору арифметических операций предлагает возможность вычисления элементарных математических функций, таких как логарифмические, степенные и тригонометрические (аргументы последних могут быть выражены как в радианах, так и градусах). Многие позволяют работать с числами в различных системах счисления.
Следующий рисунок дает представление о внешнем виде типичного представителя программ данного класса — калькуляторе KCalc, хорошо знакомого пользователям ОС Linux.
Процесс работы на калькуляторе прост и понятен практически без объяснений: после ввода выражения нажатие на кнопку со знаком = (равно) или на клавишу Enter приводит к вычислению результата.
Использование дополнительных возможностей, предоставляемых конкретным программным средством, позволяет сделать процесс вычислений более легким и удобным. Далее мы подробнее остановимся на работе с калькулятором KCalc. Отметим, что пользователь может легко настроить внешний вид (шрифты и цвет панелей), а также задать точность вычислений.
KCalc в своей работе использует стек результатов, что дает возможность обращаться к результатам предыдущих вычислений. Каждый раз, когда пользователь нажимает на клавишу Enter или на клавишу =, результат, отображаемый калькулятором, записывается в стек результатов. Для просмотра этого стека используются клавиатурные клавиши с изображением стрелок вверх и вниз.
Нажатие на кнопку AC приводит к аннулированию текущего ввода, а кнопка C отменяет последнюю из введенных операций. Кнопки MR, M+- и
KCalc позволяет проводить вычисления в следующих системах счисления: шестнадцатеричная (Hex), десятичная (Dec), восьмеричная (Oct) и двоичная (Bin). Для ввода чисел в шестнадцатеричной системе используется дополнительная панель, содержащая буквы латинского алфавита от A до F (обозначающие шестнадцатеричные цифры от 10 до 15). Перевод чисел из одной системы счисления в другую выполняется так: введя число в одной системе, следует изменить основание системы — число отобразится в новой системе счисления.
Пример
Пусть требуется перевести число 17 в двоичную систему счисления. Введем указанное число, для чего можно использовать как клавиатуру, так и кнопки на панели калькулятора. Изменив освование системы счисления с помощью переключателя, получим отображение числа в новой системе. Рисунок демонстрирует полученное представление числа в двоичной системе счисления (включена опция Bin).
Введем указанное число, для чего можно использовать как клавиатуру, так и кнопки на панели калькулятора. Изменив освование системы счисления с помощью переключателя, получим отображение числа в новой системе. Рисунок демонстрирует полученное представление числа в двоичной системе счисления (включена опция Bin).
Перевод чисел из одной системы счисления в другую с использованием программных сред «Калькулятор» и «MS Excel»
Тип урока: урок с применением современных компьютерных технологий.
Вид урока: комбинированный.
Технология: личностно-ориентированная, развивающая.
Пояснение: при хорошей подготовке учащихся можно провести как один урок. При слабой подготовке можно разделить на два урока.
Цель урока.
Повторить и закрепить знания учащихся по
способам представления чисел в позиционных
системах счисления, переводу целых чисел из
десятичной системы счисления в любую другую и
обратно с помощью программных сред обработки
числовой информации Калькулятор и MS Excel.
Задачи урока.
- Образовательная – закрепить знания учащихся по способам представления чисел в позиционных системах счисления, переводу десятичных чисел в любую другую и обратно, повторение операций копирования, ввода формул и данных в ячейки электронной таблицы, построение точечных диаграмм.
- Развивающая – развитие логического мышления, формирование информационной культуры, компьютерной грамотности и потребности в приобретении знаний, умения обобщать, систематизировать полученные знания.
- Воспитательная
Изучаемые вопросы:
- Система счисления: позиционная и непозиционная.
- Развернутая форма записи числа.

- Перевод чисел из любой системы счисления в десятичную.
- Перевод чисел из десятичной системы счисления в любую другую.
Практика. Перевод целых чисел из одной системы счисления в другую с помощью приложения “Калькулятор” и программы “MS Excel”.
Приобретаемые умения и навыки:
- Перевод чисел из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно с помощью приложения Калькулятор.
- Перевод чисел из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно с помощью ЭТ (Excel).
- Построение точечных диаграмм.
- Использование стандартных функций “ОКРУГЛВНИЗ” и “ОСТАТОК”.
Межпредметные связи: математика – координатная плоскость, округление чисел, деление с остатком.
Домашнее задание: § 45, вопрос № 4 (учебник И. Г.
Семакин 7–9).
Г.
Семакин 7–9).
Ход урока
Мы переходим к изучению темы “Теоретические основы компьютера”. Она включает следующие темы:
- Представление чисел
- Машинная арифметика
- Представление команд
В теме “Представление чисел” рассматриваются следующие темы: “Системы счисления”, “Коды чисел”.
Цель. Повторить и углубить знания о системах счисления, перевод чисел из десятичной системы счисления в любую другую и обратно с помощью программных сред обработки числовой информации Калькулятор и MS Excel.
Презентация “Система счисления”
План изложения темы.
Системы счисления. Виды систем счисления (слайды 3–6). <Приложение 1>
Перевод десятичных чисел из десятичной системы
счисления в любую другую и обратно. (Слайды 7–10)
(Слайды 7–10)
Перевод целых чисел из десятичной системы
счисления с помощью приложения Калькулятор в
двоичную, восьмеричную, шестнадцатеричную
системы счисления.
Перевод целых чисел из десятичной системы счисления с помощью приложения Excel в двоичную, восьмеричную, шестнадцатеричную системы счисления, используя общий метод перевода.
Теория
I. Основные понятия темы
Цифра – это символ, используемый в записи числа.
Система счисления – это способ записи (изображения) чисел.
Алфавит системы счисления – это множество всех символов (знаков), используемых для записи чисел в данной системе счисления.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – алфавит десятичной позиционной системы счисления
I, V, X, L, C, D, M –
Системы счисления: непозиционные системы
счисления, позиционные системы счисления.
Любое десятичное число можно представить в виде суммы произведений значащих цифр числа на степени десятки. Такое представление называется развернутой формой записи числа.
15525510 = 1 ·105 + 5 ·104 + 5 ·103 + 2 ·102 + 5 ·101 + 5 ·100
2534,6510 = 2 ·103 + 5 ·102 + 3 ·10
Эти примеры показывают, что в развернутой форме показатель степени десяти зависит от позиции соответствующей цифры в записи числа. Позиция цифры в записи числа называется разрядом числа. Цифра в разряде единиц умножается на 100 = 1; цифра в разряде десятков умножается на 101 и т.д. Дробные разряды умножаются на отрицательные степени десяти: 10-1, 10-2, 10-3 и т.д.
Степень десятки равна номеру соответствующего
разряда в числе.
Формула представления числа
Хb = an? · bп + … + a0 · b0 + a-1 · b-1 + …
Число можно представить в виде суммы произведений составляющих его цифр на соответствующие степени основания системы. На этом принципе основан перевод чисел из любой СС в десятичную СС.
1111012 = 1 ·25 + 1 ·24 + 1 ·23 + 1 ·22 + 0 ·21 + 1 ·20 = 32 + 16 + 8 + 4 + 1 = 6110
3D16 = 3 ·161 + 13 ·160 = 48 + 13 =6110
Закрепление
- Какое количество цифр используется для записи чисел в восьмеричной СС?
- Назовите наибольшее однозначное число в десятичной СС? В шестнадцатеричной СС?
- Назовите числа соответствующее данному
разложению в А8, А10.

1*82 + 3*81 + 5*80 (1358, 9310)
II. Перевод в десятичную СС
Данное десятичное число делится с остатком на основание системы. Полученный остаток – это младший разряд искомого числа, а полученное частное снова делится с остатком на основание системы и т.д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное – старшая цифра искомого числа.
Перевод дробного десятичного числа в другую систему счисления производится путем последовательных умножений на основание новой системы с выделением цифр целой части произведений в качестве искомых.
Вертикальная черта отделяет целые части от
дробных частей. Подчеркиванием отмечены искомые
значения цифры дробного числа. Умножение
повторяется до тех пор, пока в дробной части
очередного произведения не получится ноль или не
будет обнаружен период повторяющихся цифр.
Фронтальная работа.
Перевести число из А2 в А10: 1010112 43
Перевести число из А16 в А10: 4А16 74
Перевести число из А10 в А2: 17, 2510 10001, 01
III. Перевод целых чисел из одной системы счисления в другую с помощью приложения “Калькулятор”. (Слайд)
Практическая работа.
I. Перевести число 849 с помощью приложения Калькулятор в двоичную, восьмеричную, шестнадцатеричную системы счисления.
- Открыть приложение Калькулятор (Вид Инженерный)
- Ввести целое десятичное число 849.
- Перевести это число в двоичную, восьмеричную, шестнадцатеричную системы счисления. Полученные данные скопировать и вставить в электронную таблицу Excel (Практика.xls):
| A10 | A10 | A2 | A10 | A8 | ||
| 849 | 849 | 849 |
II. Перевести с помощью Калькулятора
данные из таблицы в десятичную систему
счисления, занести их в таблицу Excel и построить
точечную диаграмму. Файл сохранить в личной
папке под именем praktika.xls
Перевести с помощью Калькулятора
данные из таблицы в десятичную систему
счисления, занести их в таблицу Excel и построить
точечную диаграмму. Файл сохранить в личной
папке под именем praktika.xls
(Раздаточный материал с таблицами). <Приложение 4>
III. Используя метод перевода целого десятичного числа в другие системы счисления переведите число 849 в двоичную, восьмеричную, шестнадцатеричную системы счисления, используя функции ЭТ:
= ОКРУГЛВНИЗ ()
= ОСТАТ ()
Теория.
Стандартные функции округления числа ОКРУГЛВНИЗ, ОКРУГЛВВЕРХ
= ОКРУГЛВНИЗ ( <АРИФМ ВЫРАЖЕНИЕ>; <КОЛ-ВО ДЕСЯТ. РАЗРЯДОВ>)
= ОКРУГЛВНИЗ (157,856; 0) 157
= ОКРУГЛВВЕРХ (157,856; 0) 158
= ОКРУГЛВНИЗ (157,856; 2) 157, 85
= ОКРУГЛВНИЗ (С4/2; 0) 78
- Какой объект является аргументом этой функции? (Числовое
значение ячейки С4 разделить на 2.
 )
) - Что означает, что второй аргумент имеет значение 0? (Полученное частное округлено с точностью до единицы.)
| 157, 856 |
| 78, 928 |
| 157 |
| 158 |
| 157,85 |
| 78 |
2. Стандартная функция ОСТАТОК
= ОСТАТОК (12, 6) 0
= ОСТАТОК (45, 2) 1
= ОСТАТОК (F4, 2)
= ОСТАТОК (<АРИФМ.ВЫРАЖ>, <НАТУРАЛЬНОЕ ЧИСЛО>)
| 61 | 1 |
| 30 | 0 |
| 15 | 1 |
| 7 | 1 |
| 3 | 1 |
| 1 | 1 |
6110 = 1111012
Итог урока.
Сегодня на уроке мы повторили и систематизировали ранее полученные знания, но и использовали различные программные среды для решения одной и той же задачи.
Мы сегодня познакомились с новыми возможностями приложения Калькулятор, и с новыми функциями и возможностями Excel.
Приложение 1
(презентация)
Приложение 2 (практическая
работа для учителя)
Приложение 3 (практическая
работа для учащихся)
Приложение 4 (таблицы)
Приложение 5 (текст
практической работы)
Hex to Binary — Конвертер шестнадцатеричных чисел в двоичные
РЕКЛАМАСодержание:
- Шестнадцатеричный код в двоичный
- Этот преобразователь имеет простой набор опций
- Входы и выходы этого преобразователя
- Бесплатный инструмент, обеспечивающий точность
- Много усилий не требуется
Полезен ли этот инструмент?
Да Нет Возможно
Как мы можем это улучшить? Минимальное ограничение символов 10
Шестнадцатеричный в двоичный
Существуют различные форматы хранения данных, включая шестнадцатеричный и двоичный. Данные преобразуются из одной формы в другую, для чего необходимо соблюдать надлежащий процесс. Учитывая, что у вас есть число 10А и его нужно преобразовать в двоичную форму. Чтобы выполнить преобразование, вы можете выполнить ручной процесс, который очень длительный. Для выполнения этого преобразования требуется длительный период времени, и большинство людей не предпочитают тратить так много времени. Если необходимо выполнить несколько преобразований, требуется более длительный промежуток времени. Студенты должны работать над конверсионными заданиями, когда они изучают основы информатики. Если вам нужно преобразовать десять чисел из шестнадцатеричного формата в двоичный формат, будет довольно сложно выполнить каждое преобразование за ограниченное время. Следовательно, использование правильного калькулятора является лучшей альтернативой для пользователей.
Данные преобразуются из одной формы в другую, для чего необходимо соблюдать надлежащий процесс. Учитывая, что у вас есть число 10А и его нужно преобразовать в двоичную форму. Чтобы выполнить преобразование, вы можете выполнить ручной процесс, который очень длительный. Для выполнения этого преобразования требуется длительный период времени, и большинство людей не предпочитают тратить так много времени. Если необходимо выполнить несколько преобразований, требуется более длительный промежуток времени. Студенты должны работать над конверсионными заданиями, когда они изучают основы информатики. Если вам нужно преобразовать десять чисел из шестнадцатеричного формата в двоичный формат, будет довольно сложно выполнить каждое преобразование за ограниченное время. Следовательно, использование правильного калькулятора является лучшей альтернативой для пользователей.
Этот преобразователь имеет простой набор опций
Этот преобразователь прост в использовании и имеет простые функции. Иногда инструменты довольно продвинуты, и пользователям необходимо иметь много технических знаний. Такие инструменты используются только определенными пользователями, обладающими обширными техническими знаниями. С этим преобразователем вам не нужно быть технически подкованным, а его адаптируемость проста.
Иногда инструменты довольно продвинуты, и пользователям необходимо иметь много технических знаний. Такие инструменты используются только определенными пользователями, обладающими обширными техническими знаниями. С этим преобразователем вам не нужно быть технически подкованным, а его адаптируемость проста.
Прежде чем приступить к выполнению преобразований с помощью этого инструмента, важно знать о входах и выходах. Это поможет вам в развитии понимания.
- В качестве входных данных необходимо ввести данные в шестнадцатеричном формате. Для этого предусмотрено текстовое поле. Это первый шаг для предоставления входных данных. Вам просто нужно ввести данные в шестнадцатеричном формате, а затем перейти к следующему шагу.
- Под полем ввода вы увидите две кнопки для преобразования и сброса. Если вы считаете, что ввод в шестнадцатеричном формате был введен неправильно. Точно так же, если вы считаете, что входные данные были введены правильно, вы можете нажать кнопку преобразования.
 Когда вы нажимаете кнопку, вывод будет производиться в двоичном и десятичном форматах. В целом этот процесс преобразования шестнадцатеричного формата в двоичный прост и удобен в исполнении.
Когда вы нажимаете кнопку, вывод будет производиться в двоичном и десятичном форматах. В целом этот процесс преобразования шестнадцатеричного формата в двоичный прост и удобен в исполнении.
Бесплатный инструмент, обеспечивающий точность
Поиск бесплатного инструмента не означает, что вы можете выбрать любое случайное приложение из Интернета, загрузить его и использовать. Если он не дает 100% безошибочных результатов, его не следует использовать, даже если он бесплатный. Надежность – очень важный фактор. Во-вторых, многие инструменты, которые утверждают, что они бесплатные, имеют множество ограничений. Обычно пользователи не проверяют этот аспект. Они доверяют почти каждому бесплатному конвертеру шестнадцатеричных чисел в двоичные. Это не интеллектуальное мышление.
- Одним из основных преимуществ этого инструмента является надежность. Вы можете рассчитывать на вывод, произведенный в двоичной форме. Когда вы говорите о том, как преобразовать шестнадцатеричный формат в двоичный, важно сэкономить время и получить 100% правильный результат.
 Это два самых важных фактора. Нет смысла использовать инструмент, если полученные результаты неверны. Этот конвертер работает быстро, поэтому пользователи могут сэкономить время. Вы также можете выполнить более одного преобразования, не тратя долгие часы.
Это два самых важных фактора. Нет смысла использовать инструмент, если полученные результаты неверны. Этот конвертер работает быстро, поэтому пользователи могут сэкономить время. Вы также можете выполнить более одного преобразования, не тратя долгие часы.
- Этот инструмент на самом деле бесплатный, и ни к одному из пользователей не применяются никакие условия. Проблема работы с ограниченными возможностями действительно существует, когда вы используете некоторые бесплатные инструменты. Только несколько вариантов бесплатны, и это тоже в течение ограниченного периода времени. Когда этот промежуток времени истекает, пользователь должен потратить деньги и выбрать платную версию. Это, очевидно, проблема для пользователей, потому что они должны либо выбрать платную опцию, либо прекратить использование инструмента. С нашим конвертером шестнадцатеричных данных в двоичные такой проблемы не существует. Это полностью бесплатный инструмент, и к людям, которые его используют, не применяются никакие условия.
 Кроме этого, все функции инструмента бесплатны.
Кроме этого, все функции инструмента бесплатны.
Много усилий не требуется
В конце концов, выполнение этих расчетов вручную — непростая задача. Это связано с тем, что процесс не является простым. Вы должны иметь современные математические навыки, чтобы выполнить эти шаги и выполнить преобразование. Большинство людей не имеют достаточных навыков для выполнения этих шагов. Следовательно, использование этого инструмента является гораздо более простым вариантом. Лучше всего то, что вы можете использовать этот инструмент, даже если у вас нет больших математических знаний. Варианты просты, и каждый может их использовать.
- Экономится много времени, когда вам нужно выполнить несколько преобразований, а время начинает истекать. Это происходит, когда вы не используете инструмент и выполняете преобразование без какой-либо технической помощи. Если вы хотите выполнять точные преобразования шестнадцатеричных чисел в двоичные, не утомляя себя, использование этого инструмента поможет вам.

- Когда мы выполняем преобразования из одного формата в другой, у нас возникают сомнения относительно того, правильные ответы или нет. Этих сомнений нет, если вы используете технологический инструмент для выполнения преобразований. Этот преобразователь разработан с использованием лучших технологических платформ и не имеет проблем с надежностью. Другими словами, вам не нужно проверять ни один из ответов после завершения вычислений. Как только результаты будут получены, вы можете рассчитывать на них во всех отношениях. Эта гарантия отсутствует, когда вы используете ручные методы преобразования шестнадцатеричного формата в двоичный. С помощью этого инструмента вы можете получить необходимый уровень точности и сэкономить время.
Использование этого инструмента, несомненно, решит множество проблем для студентов, желающих выполнить преобразование из шестнадцатеричной формы в двоичную. Нет необходимости платить что-либо, чтобы использовать этот конвертер. Кроме того, не нужно беспокоиться о выполнении нескольких преобразований, даже если у вас меньше свободного времени.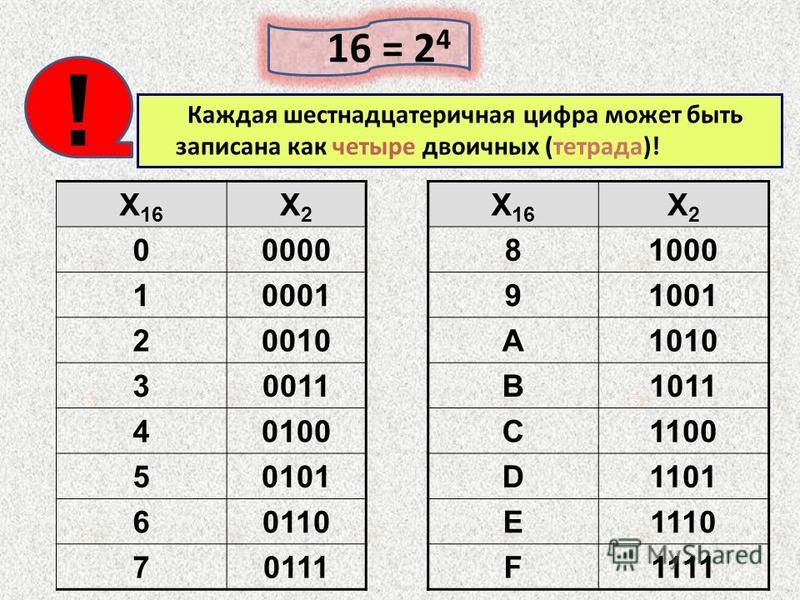
Другие бесплатные инструменты, связанные с Hex
Prepostseo не ограничивается только несколькими инструментами, связанными с Hex. Мы предлагаем широкий спектр шестнадцатеричных инструментов, чтобы внести изменения в образование, решить современные компьютерные проблемы и сыграть ключевую роль в формировании будущего в мире технологий. Получите информацию о других наших бесплатных инструментах Hex здесь: Binary to Hex. Шестнадцатеричный в десятичный, десятичный в шестнадцатеричный, шестнадцатеричный в RGB, RGB в шестнадцатеричный, шестнадцатеричный в восьмеричный, восьмеричный в шестнадцатеричный, шестнадцатеричный калькулятор, ASCII в шестнадцатеричный, шестнадцатеричный в ASCII, шестнадцатеричный в текст, текст в шестнадцатеричный.
Онлайн-инструмент Hex to Binary Converter
- Инструменты
- Шестнадцатеричный код в двоичный
Преобразуйте шестнадцатеричные данные в двоичный формат.
Настройки
Номер строки
Перенос строки
Темный режим
Преобразование шестнадцатеричных чисел в двоичные числа
Простой в использовании интерфейс
Шестнадцатеричные числа используются во многих компьютерных приложениях, но с ними может быть сложно работать. Наш инструмент для преобразования шестнадцатеричных чисел в двоичные позволяет легко преобразовывать шестнадцатеричные числа в двоичные с лучшим удобным интерфейсом.
Наш инструмент для преобразования шестнадцатеричных чисел в двоичные позволяет легко преобразовывать шестнадцатеричные числа в двоичные с лучшим удобным интерфейсом.
Мгновенное создание двоичного числа
Вам нужно мгновенно сгенерировать двоичное число? Не смотрите дальше! Наш бесплатный онлайн-инструмент позволяет преобразовывать шестнадцатеричные числа в двоичные числа, что занимает менее минуты для преобразования числа в двоичную систему счисления.
Доступен бесплатно
Когда дело доходит до преобразования шестнадцатеричных чисел в двоичные, нет необходимости тратить деньги на конвертер. Этот бесплатный онлайн-инструмент поможет быстро и легко выполнить работу бесплатно.
Безопасное использование
Если вы ищете безопасный инструмент для преобразования двоичного кода в восьмеричный, обратите внимание на наш. Мы серьезно относимся к безопасности и внедрили новейшие меры безопасности, чтобы гарантировать безопасность использования нашего инструмента.
Часто задаваемые вопросы об онлайн-конвертере шестнадцатеричных чисел в двоичные
Что такое двоичная система счисления?
Двоичная система счисления — это система счисления с основанием 2, в которой используются две различные цифры, 0 и 1. Эта система счисления является наиболее распространенной системой счисления, используемой в компьютерном программировании, поскольку ее проще всего понять компьютерам.
Двоичная система счисления также используется в цифровой электронике, такой как компьютерная память и микропроцессоры.
Что такое шестнадцатеричная система счисления?
Шестнадцатеричные числа представляют собой числа с основанием 16. Это означает, что число может быть представлено 16 различными цифрами. Наиболее распространенный способ представления шестнадцатеричного числа — использование букв A-F. Шестнадцатеричная система счисления часто используется в компьютерном программировании, потому что это более эффективный способ представления двоичных чисел. При представлении числа в двоичной форме каждая цифра может быть только 0 или 1. Это может быть громоздко при представлении больших чисел. Однако в шестнадцатеричной форме каждая цифра может быть от 0 до 9.или А-Ф. Это значительно упрощает работу с большими числами.
При представлении числа в двоичной форме каждая цифра может быть только 0 или 1. Это может быть громоздко при представлении больших чисел. Однако в шестнадцатеричной форме каждая цифра может быть от 0 до 9.или А-Ф. Это значительно упрощает работу с большими числами.
Для чего нужен онлайн-инструмент для преобразования шестнадцатеричных чисел в двоичные?
Онлайн-инструмент для преобразования шестнадцатеричных чисел в двоичные — отличный инструмент для всех, кому необходимо преобразовать шестнадцатеричное число в двоичное. Этот инструмент прост в использовании, и его можно найти в Интернете бесплатно.
Как преобразовать шестнадцатеричную систему счисления в двоичную?
Чтобы преобразовать шестнадцатеричное число в двоичное:
- Введите шестнадцатеричное число для преобразования.
- Нажмите кнопку «Преобразовать», чтобы преобразовать его в двоичное число.
- Ваш результат будет в текстовом поле вывода, которое вы можете скопировать или загрузить для дальнейшего использования.





 )
) Когда вы нажимаете кнопку, вывод будет производиться в двоичном и десятичном форматах. В целом этот процесс преобразования шестнадцатеричного формата в двоичный прост и удобен в исполнении.
Когда вы нажимаете кнопку, вывод будет производиться в двоичном и десятичном форматах. В целом этот процесс преобразования шестнадцатеричного формата в двоичный прост и удобен в исполнении. Это два самых важных фактора. Нет смысла использовать инструмент, если полученные результаты неверны. Этот конвертер работает быстро, поэтому пользователи могут сэкономить время. Вы также можете выполнить более одного преобразования, не тратя долгие часы.
Это два самых важных фактора. Нет смысла использовать инструмент, если полученные результаты неверны. Этот конвертер работает быстро, поэтому пользователи могут сэкономить время. Вы также можете выполнить более одного преобразования, не тратя долгие часы.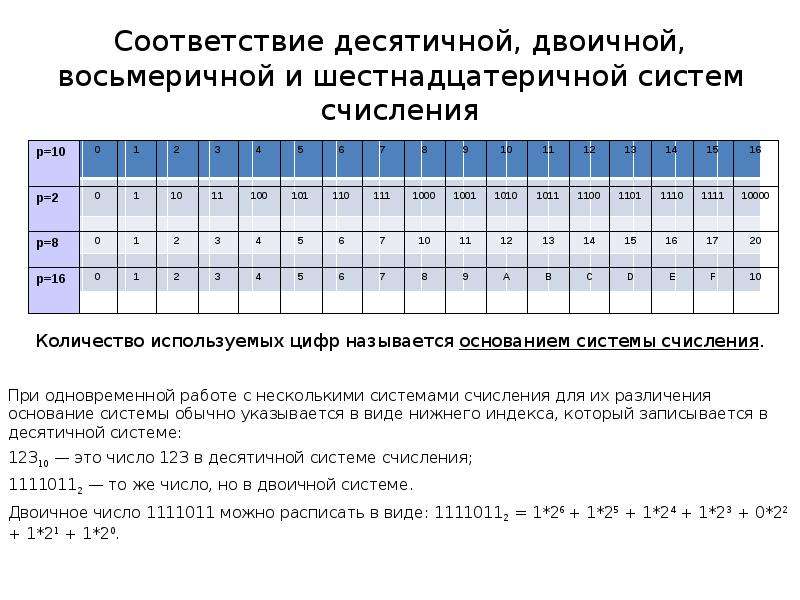 Кроме этого, все функции инструмента бесплатны.
Кроме этого, все функции инструмента бесплатны.
