Умножение двоичных чисел онлайн
Примеры решенийПеревод дробных чисел Формат с плавающей точкой Перевести в 2 систему Перевод в 8 систему Перевод в 10 систему Дополнительный код Сложение двоичных чиселУмножение двоичных чисел
- Решение онлайн
- Видеоинструкция
Число №1
Число №2
Пример №1. Умножить двоичные числа
111 и 101.
Решение.
| 1 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| = | = | = | = | = |
| 1 | 1 | 1 | ||
| 0 | 0 | 0 | ||
| 1 | 1 | 1 | ||
| = | = | = | = | = |
| 0 | 0 | 0 | 1 | 1 |
При суммировании в разрядах 2, 3, 4 возникло переполнение.
 Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100011
Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100011
В десятичной системе счисления данное число имеет следующий вид:
Для перевода необходимо умножить разряд числа на соответствующую ему степень разряда.
100011 = 25*1 + 24*0 + 23*0 + 22*0 + 21*1 + 20*1 = 32 + 0 + 0 + 0 + 2 + 1 = 35
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 111 и 101 в десятичное представление.
1012 = 22*1 + 21*0 + 20*1 = 4 + 0 + 1 = 5
7 x 5 = 35
Пример №2. Найти двоичное произведение 11011*1100. Перевести ответ в десятичную систему.
Решение. Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 — то переписываем первое число.
| 1 | 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 0 | ||||
| = | = | = | = | = | = | = | = |
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 1 | |||
| = | = | = | = | = | = | = | = |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
При суммировании в разрядах 3, 4, 5, 6, 7 возникло переполнение.
 Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 101000100
Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 101000100101000100 = 28*1 + 27*0 + 26*1 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*0 = 256 + 0 + 64 + 0 + 0 + 0 + 4 + 0 + 0 = 324
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 11011 и 1100 в десятичное представление.
11011 = 24*1 + 23*1 + 22*0 + 21*1 + 20*1 = 16 + 8 + 0 + 2 + 1 = 27
1100 = 23*1 + 22*1 + 2
27 x 12 = 324
Пример №3. 1101.11*101
Будем умножать числа без учета плавающей точки: 110111 x 101
Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 — то переписываем первое число.
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | |||||
| = | = | = | = | = | = | = | = |
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| = | = | = | = | = | = | = | = |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
При суммировании в разрядах 2, 3, 4, 5, 6, 7 возникло переполнение.
 Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100010011
Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100010011Поскольку умножали без учета плавающей запятой, то окончательный результат запишем как: 1000100.11
В десятичной системе счисления данное число имеет следующий вид:
1000100 = 26*1 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*0 = 64 + 0 + 0 + 0 + 4 + 0 + 0 = 68
11 = 2-1*1 + 2-2*1 = 0.75
В итоге получаем число 68.75
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 1101.11 и 101 в десятичное представление.
1101 = 23*1 + 22*1 + 21*0 + 20*1 = 8 + 4 + 0 + 1 = 13
11 = 2-1*1 + 2-2*1 = 0.75
В итоге получаем число 13.75
Переводим число: 1012 = 22*1 + 21*0 + 20*1 = 4 + 0 + 1 = 5
13.
75 x 5 = 68.75
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
8.Свойства операций над множествами, свойства элементарных булевых функций (доказать два свойства). Приоритет операций над множествами.
Свойства операций над множествами:
Сначала выполняются операции дополнения, затем пересечения, объединения и разности, которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками.
10.Многочлен Жегалкина. Теорема Жегалкина. Алгоритмы построения многочлена Жегалкина.
По
теореме Жегалкина каждая булева
функция единственным образом
представляется в виде полинома Жегалкина.
Теорема доказывается следующим образом.
Заметим, что различных булевых функций
от n переменных
штук.
При этом конъюнкций вида
существует
ровно 2n, так как из n возможных
сомножителей каждый или входит в
конъюнкцию, или нет.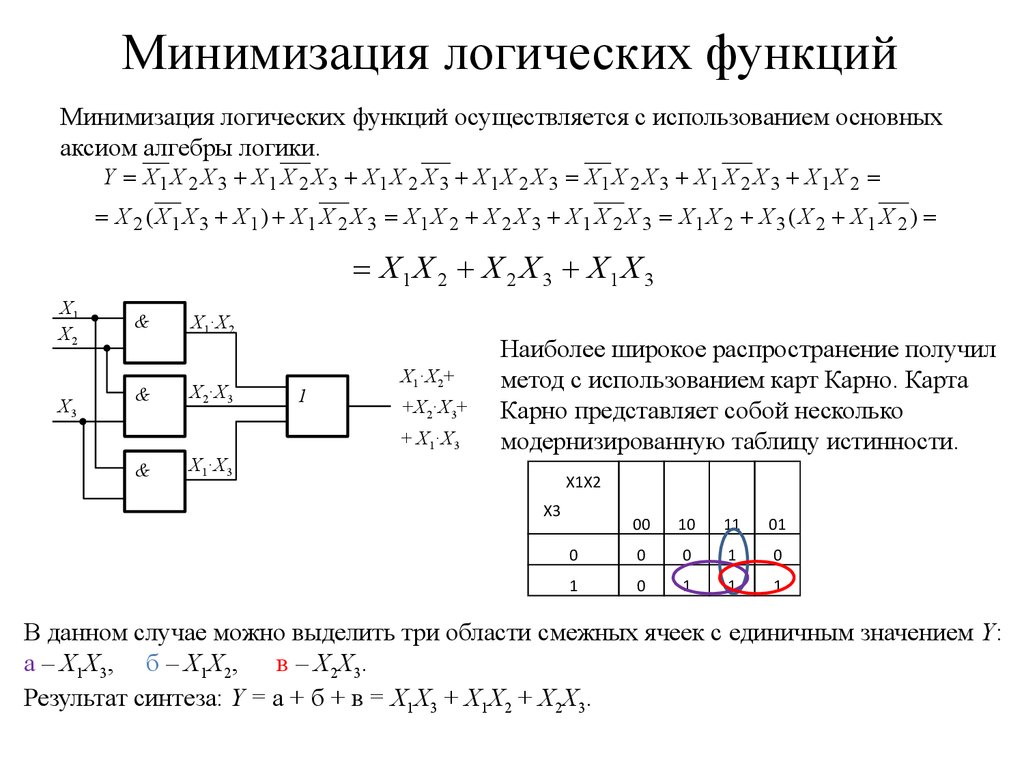 В полиноме у каждой
такой конъюнкции стоит 0 или 1, то есть
существует
различных
полиномов Жегалкина от n переменных.
Теперь достаточно лишь доказать, что
различные полиномы реализуют различные
функции. Предположим противное. Тогда
приравняв два различных полинома и
перенеся один из них в другую часть
равенства, получим полином, тождественно
равный нулю и имеющий ненулевые
коэффициенты. Тогда рассмотрим слагаемое
с единичным коэффициентом наименьшей
длины, то есть с наименьшим числом
переменных, входящих в него (любой один,
если таких несколько). Подставив единицы
на места этих переменных, и нули на
места остальных, получим, что на этом
наборе только одно это слагаемое
принимает единичное значение, то есть
нулевая
функция
на одном из наборов
принимает
значение 1. Противоречие. Значит, каждая
булева функция реализуется полиномом
Жегалкина единственным образом.
В полиноме у каждой
такой конъюнкции стоит 0 или 1, то есть
существует
различных
полиномов Жегалкина от n переменных.
Теперь достаточно лишь доказать, что
различные полиномы реализуют различные
функции. Предположим противное. Тогда
приравняв два различных полинома и
перенеся один из них в другую часть
равенства, получим полином, тождественно
равный нулю и имеющий ненулевые
коэффициенты. Тогда рассмотрим слагаемое
с единичным коэффициентом наименьшей
длины, то есть с наименьшим числом
переменных, входящих в него (любой один,
если таких несколько). Подставив единицы
на места этих переменных, и нули на
места остальных, получим, что на этом
наборе только одно это слагаемое
принимает единичное значение, то есть
нулевая
функция
на одном из наборов
принимает
значение 1. Противоречие. Значит, каждая
булева функция реализуется полиномом
Жегалкина единственным образом.
По
сравнению с ДНФ в
полиноме Жегалкина отсутствуют операции
ИЛИ и НЕ. Таким образом, полином Жегалкина
можно получить из ДНФ, выразив операции
ИЛИ и НЕ через операции Исключающее
ИЛИ, И и константу 1. Для этого применяются
следующие соотношения:
Для этого применяются
следующие соотношения:
Ниже приведён пример преобразования ДНФ в полином Жегалкина:
При преобразованиях использованы соотношения:
Полином Жегалкина это форма представления логической функции с помощью Функции Жегалкина (Исключающее ИЛИ). Для получения полинома Жегалкина следует выполнить следующие действия:
Получить ДНФ функции
Все ИЛИ заменить на Исключающее ИЛИ
Во всех термах заменить элементы с отрицанием на конструкцию: («элемент» «исключающее ИЛИ» 1)
Раскрыть скобки по правилам алгебры Жегалкина и привести попарно одинаковые термы
11.Линейные и нелинейные булевы функции. Алгоритм определения линейности (или нелинейности) булевой функции.
Необходимое
условие линейности.
Если
функция линейна и не равна некоторой
постоянной, то на половине своих наборов
она равна 1.
Если
в векторе значений функции число 0 и 1
различно, то функция обязательно
нелинейна, а если число нулей совпадает
с числом единиц, то эта функция может
быть линейной, а может быть и нелинейной. В таком случае, чтобы это проверить,
нужно выписать для нее многочлен
Жегалкина.
Функция
называется самодвойственной, если
двойственная к ней функция является
самой этой функцией. F* = F.
В таком случае, чтобы это проверить,
нужно выписать для нее многочлен
Жегалкина.
Функция
называется самодвойственной, если
двойственная к ней функция является
самой этой функцией. F* = F.
Совершенной дизъюнктивной нормальной формой или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: .Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».
Онлайн-минимизация булевых функций
Онлайн-минимизация булевых функцийГлавная японский английский Калькулятор дробей Твит
9 октября 2011 г. B (циркумфлекс)
B (циркумфлекс)
Введите таблицу истинности
Введите «0», «1» или «x».
| Выход | ||
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
| Выход | |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
| Выход | ||||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 |
| Выход | |||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
| Выход | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 9№Калькулятор упрощения логической алгебрыКалькулятор упрощения логических выражений Программа предназначена для получения таблиц истинности логических функций с количеством переменных от одной до пяти. А Б С Д 0 1 · + ¬ ⊕ ⇒ ⇔ ↓ | ( ) Вперёд! Решение для перехода Основные функции логики Переменные, которые могут принимать только два значения 0 и 1, называются логическими переменными (или просто переменными). Из определения логической функции следует, что функция n переменных есть отображение Bn в B, которое может быть определено непосредственно таблицей, называемой таблицей истинности этой функции. Основные функции логики — это функции двух переменных z = f(x,y). Число этих функций 24 = 16. Перенумеруем их и расположим в естественном порядке. Рассмотрим эти функции подробнее. Два из них f0 = 0 и f15 = 1 являются константами. Функции f3, f5, f10 и f12 по существу являются функциями одной переменной. Наиболее важные функции двух переменных имеют специальные имена и обозначения. 1) f1 – соединение (функция И) 2) f7 — дизъюнкция (или функция). 3) f13 — импликация (следующая). Обозначается ->. 4) f6 – сложение по модулю 2. Обозначается знаком «+» или знаком «+» в кружке. 5) f9 эквивалентность или подобие. Это f9 = 1 тогда и только тогда, когда x = y. Обозначается x ~ y. 6) f14 — черточка Шеффера. Эту функцию иногда называют «не и» (поскольку она равна отрицанию союза). Обозначается x|y. 7) f8 — стрелка Пирса (иногда эту функцию называют штрихом Лукасевича). Остальные три функции (f2 , f4 и f11) не имеют специального обозначения.
|



 Логическая (булева) функция от n переменных y = f(x1, x2, …, xn) — это функция со всеми переменными, причем сама функция может принимать только два значения: 0 и 1.
Логическая (булева) функция от n переменных y = f(x1, x2, …, xn) — это функция со всеми переменными, причем сама функция может принимать только два значения: 0 и 1.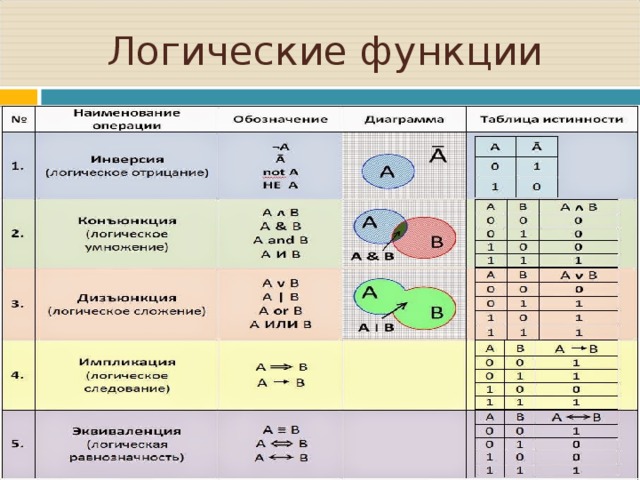 Обратите внимание, что логическая переменная x может подразумевать под номером 0 некоторое утверждение, которое является ложным, и под номером 1 какое-то утверждение, которое является истинным.
Обратите внимание, что логическая переменная x может подразумевать под номером 0 некоторое утверждение, которое является ложным, и под номером 1 какое-то утверждение, которое является истинным. Обозначается V.
Обозначается V.