| ||
| ||
Преобразователь случайных чисел | Преобразование десятичного числа в основание 16 Конвертер длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Откуда: двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base-23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 Угловая скоростьЗнаете ли вы, что у спутников есть загробная жизнь на орбита кладбища? Обзор Различные способы представления чисел Индо-арабские цифры Римские Системы в других культурах Унарная Позиционная система
Орден важен в римской системе, потому что большее число, за которым следует меньшее значение, которое нужно добавить, но меньшее число перед большим означает, что меньшее число вычитается из большего. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, которая имеет только два клинописных символа: один (немного напоминающий букву «Т») и десять (немного похожий на букву «С»). Унарная система счисления. Метки подсчета в различных культурах Унарная Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему. Позиционная система Позиционная система работает с основанием.
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ Двоичная система счисления Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например: 11111 (31) В этом случае, работая справа налево:
Итак, складывая это вместе, мы получаем 101010. Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» их. Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например: 101 (5) Деление и расчет квадратных корней также очень похожи на основание-10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число. Рациональные числа Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают нули, отрицательные и положительные числа, которые не являются дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательного числа. Простые числа Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге. Интересные факты о числахКитайские цифры для защиты от мошенничества Числительные для защиты от мошенничестваДля предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив дополнительные штрихи. Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи. Современный счет в торговлеНекоторые языки в странах, где в настоящее время используется 10-кратная система счисления, свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов. Группировка чисел И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году. В России и многих странах бывшего СССР все четных чисел считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае число 7 также является несчастливым, потому что оно представляет собой духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов. В Японии другое несчастливое число — 9.0016 9 , что имеет то же произношение, что и «страдание». В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». 666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией. Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Список литературы Эта статья была написана Kateryna Yuri Преобразовать базу-24 в десятичное значение Преобразовать базу-20 в десятичное значение Преобразование десятичного числа в восьмеричное Преобразование с основанием 4 в десятичное Преобразование числа с основанием 36 в двоичное Преобразование десятичного числа в представление с основанием 36 Вам могут быть интересны другие преобразователи в группе Общие преобразователи единиц:Длина и преобразователь расстояний массовый преобразователь Сухой объем и общие измерения приготовления Площадь преобразователя площади Объем и общий преобразователь измерения приготовления ТЕМПЕРАТУРА Давление, напряжение, модульный преобразователь модуля и рабочий преобразователь . Преобразователь мощности Преобразователь силы Преобразователь времени Преобразователь линейной скорости и скорости Преобразователь угла Конвертер топливной экономичности, расхода топлива и экономии топлива Конвертер единиц хранения информации и данных Конвертер метрических префиксов Конвертер передачи данных Курсы обмена валют Размеры мужской одежды и обуви 4 Размеры Компактный калькулятор Полный калькулятор Определения единиц измерения У вас возникли трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms Общие конвертеры единиц измеренияДлина, масса, объем, площадь, температура, давление, энергия, мощность, скорость и другие популярные конвертеры единиц измерения. Преобразователь чисел Позиционное обозначение или разрядное обозначение — это метод представления или кодирования чисел. Основание 1 — Унарная система счисления. Это простейшая система счисления для представления натуральных чисел: для представления числа N произвольно выбранный символ, представляющий 1, повторяется N раз. Основание 2 — Двоичная система счисления. Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1. Основание 3 — Троичная (иногда называемая троичной) система счисления. Троичная цифра — это трит (троичная цифра). Он использует цифры 0, 1 и 2 для представления любого действительного числа. Эта система иногда используется в логике и вычислениях для подсчета трех состояний (низкое, высокое, неизвестное или открытое состояние). Основание 8 — восьмеричная система счисления — это система счисления с основанием 8, в которой используются цифры от 0 до 7. Она используется в цифровом оборудовании. Основание 10 — Десятичная система счисления (также называемая системой с основанием десять) представляет собой позиционную систему счисления, в основе которой лежит 10. Это числовая база, наиболее широко используемая современными цивилизациями. Основание 12 — двенадцатеричная система (также известная как основание 12 или дюжина) представляет собой позиционную систему счисления с основанием двенадцать. Основание 16 — Шестнадцатеричная система счисления (также называемая основанием 16 или шестнадцатеричной) — это позиционная система счисления с основанием 16. Она используется в современном цифровом оборудовании, информатике и математике. В системах с основанием менее 36 чаще всего символы 0–9 представляют значения от нуля до девяти, а латинские буквы от A до Z и альтернативно от a до z представляют значения от 10 до 36. Использование конвертера чиселЭтот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовать множество единиц измерения из одной системы в другую. Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах. 9», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
Библиотека JavaScript BigInteger Мы усердно работаем над тем, чтобы результаты, представленные конвертерами и калькуляторами TranslatorsCafe.com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения. Если вы заметили ошибку в тексте или расчетах, или вам нужен другой конвертер, которого вы здесь не нашли, сообщите нам об этом! TranslatorsCafe.com Канал Unit Converter YouTube КАЛЬКУЛЯТОР ШЕСТНАДЦАТЕРИЧНОГО ВЫЧИТАНИЯ С ШАГАМИВведите положительные шестнадцатеричные числа. 5BA23FC2CD1 ШАГИ РЕШЕНИЯ ⟲ Повтор 5BA23FC2CD11B9119163s Место101 Последний шаг: 16 3 разряд s: Вычтите числа в разряде 16 3 s. 1 16 — 0 16 = 1 16 Напишите 1 до 16 3 SO. Все шаги: 16 0 s разряд: Вычесть числа в 16 0 место. 5 16 — 3 16 = 2 16 Напишите 2 до 16 0 с. 16 1 s место: B < F Занять 1 из 16 2 s место 16 2 s Место: После заимствования из 16 2 s поместите число в 16 2 s place reduces by 1 and and becomes 9 A 16 – 1 16 = 9 16 16 1 s place: Добавьте 10 16 на место 16 1 s. B 16 + 10 16 = 1B 16 16 1 S Place: 16 1 S Place: 16 1 S Place: 16 1 S Place: 16 1 S Place: 16 1 S Place: 16 1 S Place: 16 1 . 1B 16 — F 16 = C 16 Напишите C до 16 1 S. 16 2 s место: 9 < C Занять 1 из 16 3 s место 16 3 Место: После заимствования из 16 3 S Поместите номер в 16 3 S Place уменьшается на 1, а и становится 1 2 16 — 1 16 = 1 16 = 1 9844844844844844844844844844844844844844844844844844844844844844844844844844844849н 16 2 место: Добавьте 10 16 к месту 16 2 . 9 16 + 10 16 = 19 16 16 2 разряд: Вычтите числа в разряде 16 2 . 19 16 — C 16 = D 16 Напишите D . 16 3 разряд s: Вычтите числа в разряде 16 3 s. 1 16 – 0 16 = 1 16 Запишите 1 на место 16 3 s. Скачать решение Скопировано в буфер обмена Копировать текст © Madformath См. Решение Hexadecimal вычитание, чтобы вычесть несвидецкое число с других шагов ниже.
Калькулятор шестнадцатеричного вычитания,
Калькулятор шестнадцатеричного вычитания можно использовать двумя способами.
|





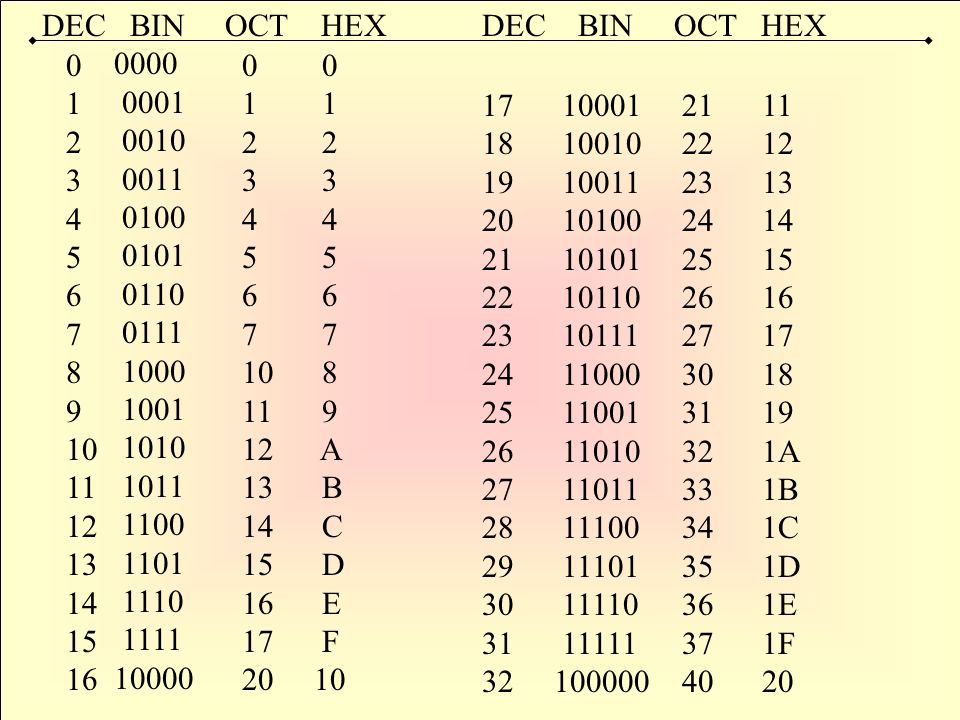 Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел. Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910).
Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910). Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.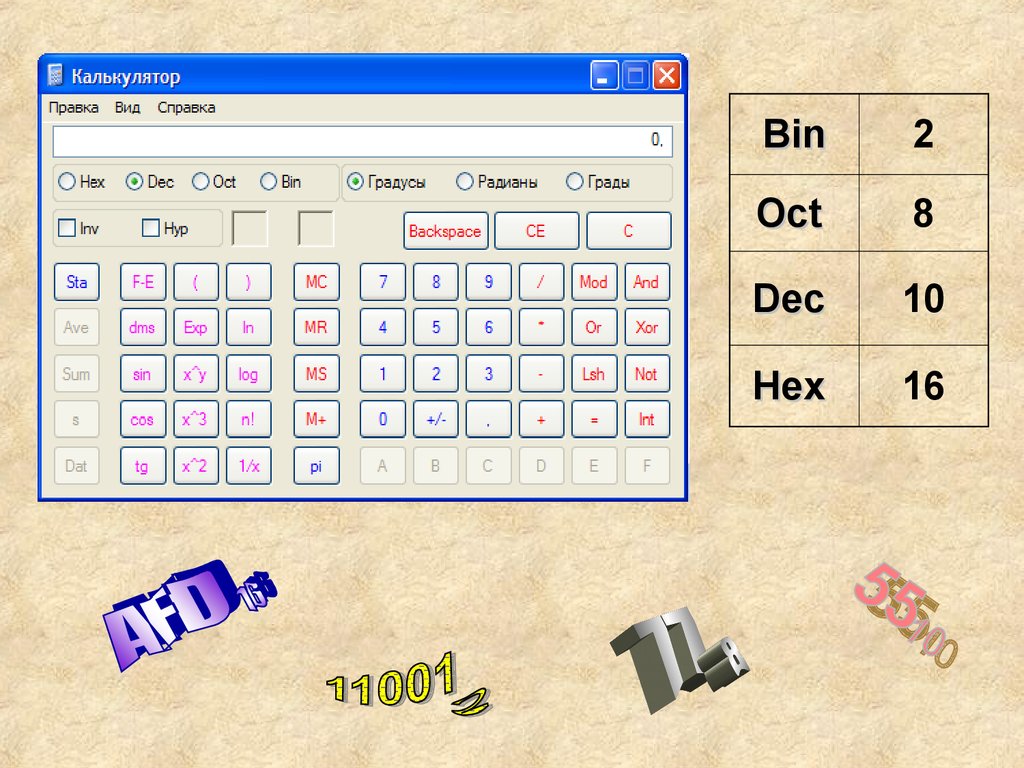 Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике. Например, в базе 10 у нас есть следующее:
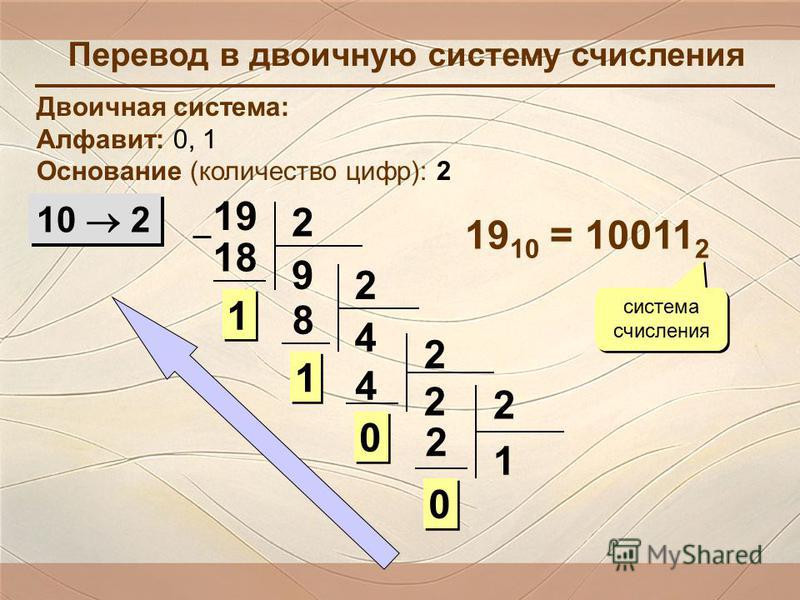
Например, в базе 10 у нас есть следующее: Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
 Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
 В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны. Это подразумевает, что жизнь окончена, и относится к смерти.
Это подразумевает, что жизнь окончена, и относится к смерти. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
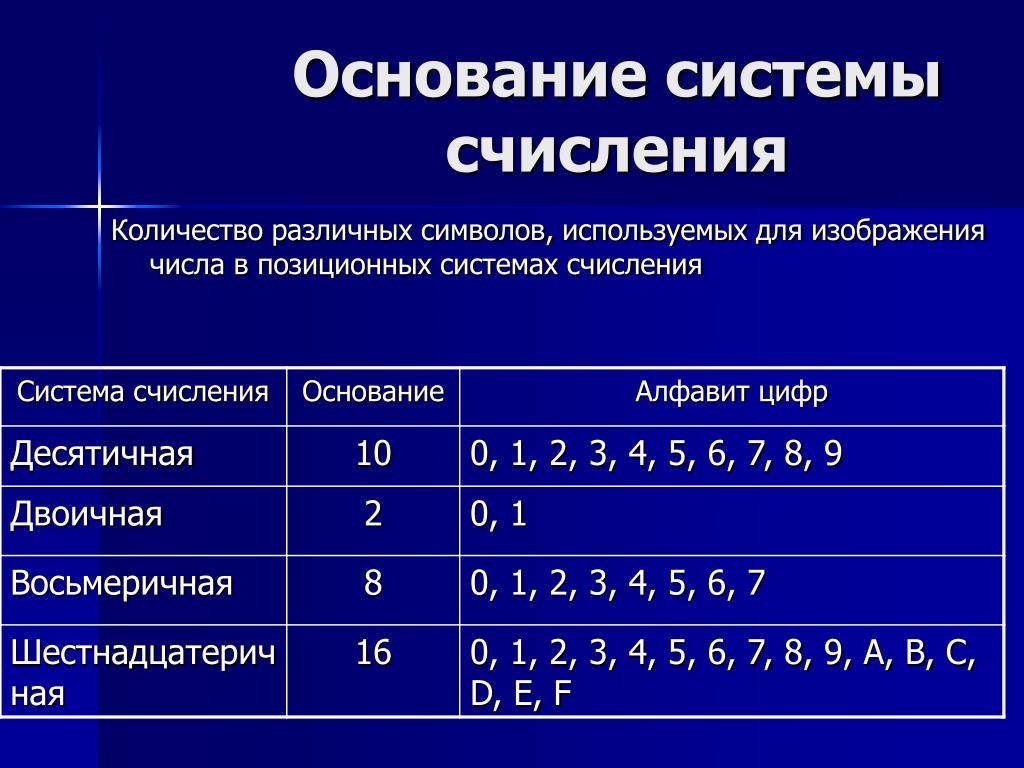
Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят. Позиционное обозначение отличается от других обозначений (таких как римские цифры) использованием одного и того же символа для разных порядков величины (например, «разряд единиц», «разряд десятков», «разряд сотен»). В математических системах счисления основание или основание обычно представляет собой количество уникальных цифр, включая ноль, которые позиционная система счисления использует для представления чисел.
Позиционное обозначение отличается от других обозначений (таких как римские цифры) использованием одного и того же символа для разных порядков величины (например, «разряд единиц», «разряд десятков», «разряд сотен»). В математических системах счисления основание или основание обычно представляет собой количество уникальных цифр, включая ноль, которые позиционная система счисления использует для представления чисел.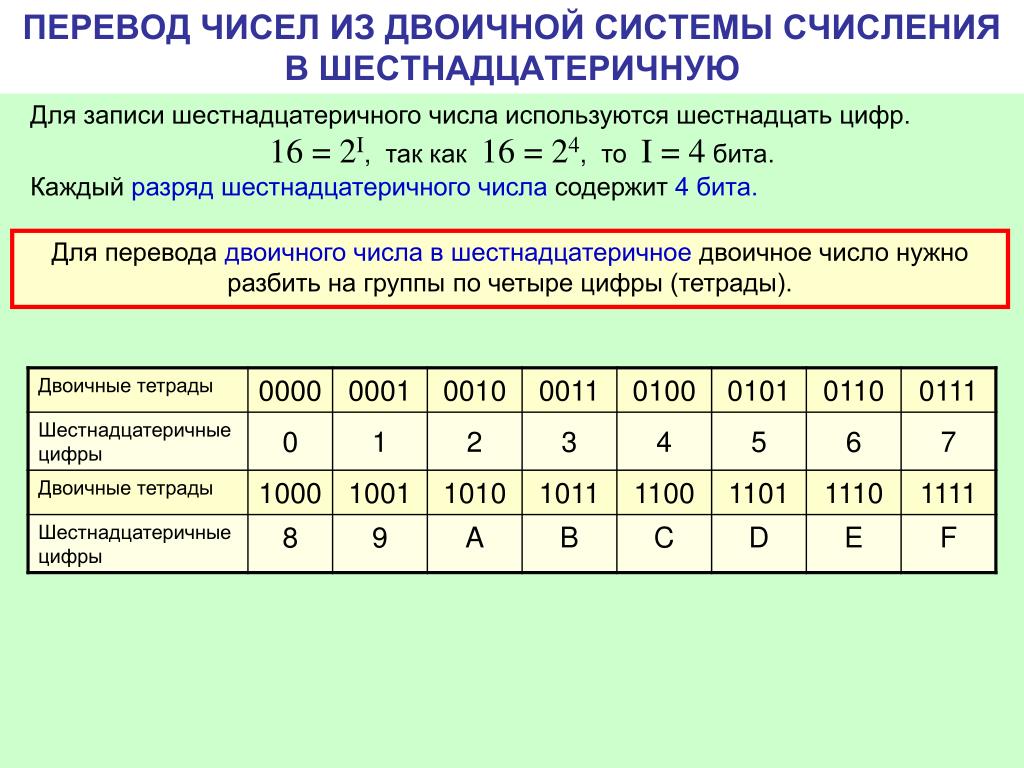

 0007 Вычесть числа в разряде 16 1 s.
0007 Вычесть числа в разряде 16 1 s.