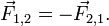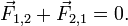§ 12. Силы в механике
Силы тяготения (гравитационные силы).
В
системе отсчета связанной с Землей, на
всякое тело массой m
действует сила:  ,
называемая силой тяжести – сила, с
которой тело притягивается с Землей.
Под действием силы притяжения к Земле
все тела падают с одинаковым ускорением
,
называемая силой тяжести – сила, с
которой тело притягивается с Землей.
Под действием силы притяжения к Земле
все тела падают с одинаковым ускорением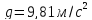 ,
называемым ускорением свободного
падения.
,
называемым ускорением свободного
падения.
Весом тела – называется сила, с которой тело вследствие тяготения к Земле действует на опору или натягивает нить подвеса.
Сила
тяжести действует всегда, а вес проявляется
лишь тогда, когда на тело кроме силы
тяжести действуют другие силы. Сила
тяжести равна весу тела только в том
случае, когда ускорение тела относительно
Земли равно нулю. В противном случае 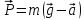
 — ускорение тела с опорой относительно
Земли. Если тело свободно движется в
поле силы тяготения, то
— ускорение тела с опорой относительно
Земли. Если тело свободно движется в
поле силы тяготения, то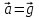 и вес равен нулю, т.е. тело будет невесомым.
и вес равен нулю, т.е. тело будет невесомым.Невесомость — это состояние тела, при котором оно движется только под действием силы тяжести.
Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией.
Упругая сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия:
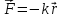 ,
,
где 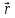 –
радиус-вектор, характеризующий смещение
частицы из положения равновесия,
–
радиус-вектор, характеризующий смещение
частицы из положения равновесия, —
упругость. Примером такой силы является
сила упругости деформации пружины при
растяжении или сжатии.
—
упругость. Примером такой силы является
сила упругости деформации пружины при
растяжении или сжатии.
Сила трения скольжения возникает при скольжении данного тела по поверхности другого:
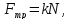
где k – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей; N — сила нормального давления, прижимающая трущиеся поверхности друг другу.
Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.
§ 13. Энергия. Работа и мощность
Энергия –это универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и т.д.
Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.

Рисунок 13.1
Если
рассматриваемая сила 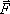 постоянна,
а тело, к которому она приложена, движется
поступательно и прямолинейно, то работой,
совершаемой силой
постоянна,
а тело, к которому она приложена, движется
поступательно и прямолинейно, то работой,
совершаемой силой
 ,
называют величину
,
называют величину  ,
,
где а
— угол
между силой 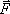 и
направлением движения тела.
и
направлением движения тела.

Рисунок 13.2
Работа —
скалярная величина. Если вектор силы и
вектор перемещений образуют острый
угол, т.е. 
 ,
если
,
если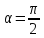 ,
то
,
то ,
т.е. сила, действующая перпендикулярно
к перемещению тела, работы не совершает.
,
т.е. сила, действующая перпендикулярно
к перемещению тела, работы не совершает.В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.13.2). Выделим элементарный участок пути dS, на котором силу можно считать постоянной, и перемещение прямолинейным. Элементарная работа на этом участке равна

Полная
работа на пути  определяется
интегралом
определяется
интегралом

Единица работы – джоуль (Дж) – работа совершаемая силой 1Н на пути 1м: 1Дж-1Нс.

Рисунок 13.3
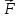 ,
действующую на материальную точку,
называют консервативной или потенциальной,
если работа
,
действующую на материальную точку,
называют консервативной или потенциальной,
если работа  ,
совершаемая этой силой при перемещении
этой точки из произвольного положения
1 в другое 2, не зависит от того, по какой
траектории это перемещение произошло:
,
совершаемая этой силой при перемещении
этой точки из произвольного положения
1 в другое 2, не зависит от того, по какой
траектории это перемещение произошло: 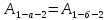 =
=
Изменение направления
движения точки вдоль траектории на
противоположное вызывает изменение
знака консервативной силы, так как
величина 

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности. Мощность равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.
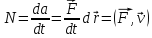
Единица мощности — ватт (Вт): 1 Вт – мощность, при которой за время 1с совершается работа 1 Дж:=1Вт=1Дж/с.
Силы в механике (основная школа)
Силы в механике
В механике обычно имеют дело с тремя основными видами сил: силой тяжести, силой упругости и силой трения.
Закон всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния r между ними:
Закон всемирного тяготения справедлив для точечных, а также сферически симметричных тел. Приближенно он выполняется для любых тел, если расстояние между ними значительно больше их размеров.
|
Рис. 1. Гравитационное взаимодействие двух тел |
Одним из проявлений закона всемирного тяготения является сила тяжести. Сила тяжести направлена к центру Земли и на поверхности Земли равна:
где ускорение свободного падения Здесь масса Земли равна а ее радиусВблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с2.
|
Рис. 2. Сила тяжести на различных расстояниях от Земли. При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Масса тела принята равной m = 70 кг |
Сила, с которой тело действует на горизонтальную опору или подвес, называется весом тела По третьему закону Ньютона с той же по модулю силой опора или подвес действует на тело; эта сила называется реакцией опоры При неподвижной опоре или подвесе эта сила равна силе тяжести Следует помнить, что эти силы приложены к разным телам (рис. 3).
|
Рис. 3. Вес тела и реакция опоры |
Если опора или подвес двигается с некоторым ускорением, то сила давления со стороны тела (то есть вес тела) изменяется.
В частности, если опора движется с ускорением направленным против силы тяжести, то вес тела обращается в нуль. Такое состояние называют невесомостью. Состояние невесомости испытывает космонавт в космическом корабле.
|
Рис. 4. Сила упругости |
|
Рис. 5. Зависимость силы упругости от удлинения |
Изменение формы или размеров тела называется деформацией. Деформации бывают упругими и пластичными. При упругих деформациях тело восстанавливает свою форму и размеры после прекращения действия силы, при пластичных – нет. При упругих деформациях справедлив закон Гука: величина деформации пропорциональна вызывающей ее силе:
| Fвнешн = –Fупр = kx. |
Силы, действующие между поверхностями соприкасающихся твердых тел, называются силами сухого трения. Они всегда направлены по касательной к соприкасающимся поверхностям.
Сила трения покоя – величина непостоянная, она растет по модулю вместе с внешней силой от нуля до некоторого максимального значения Fтр max. Сила трения покоя равна по модулю и противоположна по направлению проекции внешней силы, направленной параллельно поверхности соприкосновения его с другим телом.
Если внешняя сила больше Fтр max, то возникает движение. Силу трения в этом случае называют силой трения скольжения. Экспериментально доказано, что сила трения скольжения пропорциональна реакции опоры:
Коэффициент трения μ зависит от материалов, из которых изготовлены соприкасающиеся тела, и не зависит от размеров соприкасающихся поверхностей.Сила трения скольжения всегда направлена против относительного движения тела.
При движении в жидкости или газе возникает сила вязкого трения. При вязком трении нет трения покоя. Сила вязкого трения значительно меньше силы сухого трения и также направлена в сторону, противоположную относительной скорости тела. Зависимость от модуля скорости может быть линейной F = –βυ или квадратичной F = –αυ2.
Силы в механике. Видеоурок. Физика 11 Класс
Задачи ЕГЭ типа C проверяются экспертами, которые уделяют большое внимание правильности обозначения сил на чертеже. На данном уроке мы обсудим, какие существуют силы в механике, как правильно их обозначать в чертеже задачи. В конце урока решим несколько типовых задач из сборника для подготовки к единому государственному экзамену
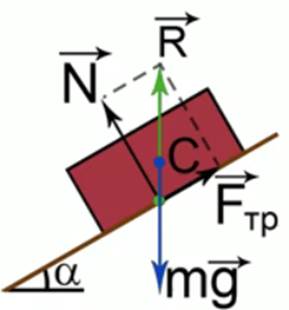
Рис. 1. Силы, действующие на тело
1. Сила притяжения тела к Земле – 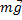 . Направлена вертикально вниз, приложена к центру масс (см. Рис. 1).
. Направлена вертикально вниз, приложена к центру масс (см. Рис. 1).
2. Сила нормальной реакции опоры – 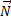 . Направлена перпендикулярно плоскости опоры или тела в точке контакта – в точке пересечения
. Направлена перпендикулярно плоскости опоры или тела в точке контакта – в точке пересечения 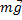 с поверхностью опоры (см. Рис. 1).
с поверхностью опоры (см. Рис. 1).
Проводить на чертеже эту силу из центра масс (т. C) допустимо только в том случае, если в условии задачи сказано, что тело можно принять за материальную точку.
3. Сила трения – 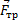 . Пропорциональна силе реакции опоры и перпендикулярна ей (см. Рис. 1).
. Пропорциональна силе реакции опоры и перпендикулярна ей (см. Рис. 1).
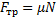 ,
,
где 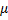 – коэффициент трения.
– коэффициент трения.
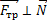
Сила трения направлена по касательной к поверхности против движения.
4. Обобщенная сила реакции опоры – 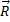 .
.
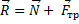
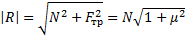
На чертеже необходимо проследить за тем, чтобы при векторном сложении 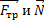 результирующая (
результирующая (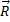 ) проходила через центр масс (т. C) (см. Рис. 1).
) проходила через центр масс (т. C) (см. Рис. 1).
5. Сила упругости – 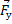
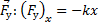 – сила упругости в проекции на ось X направлена противоположно растяжению (x) и прямо пропорциональна ему.
– сила упругости в проекции на ось X направлена противоположно растяжению (x) и прямо пропорциональна ему. 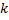 – коэффициент упругости (коэффициент жесткости, или жесткость пружины).
– коэффициент упругости (коэффициент жесткости, или жесткость пружины).
6. Сила сопротивления –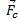 . Направлена противоположно скорости.
. Направлена противоположно скорости.
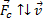
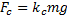 ,
,
где 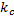 – коэффициент сопротивления.
– коэффициент сопротивления.
Сила сопротивления зависит от величины скорости и приложена к центру масс тела.
Например, парашютист выполняет затяжной прыжок (см. Рис. 2). Выпрыгивая из самолета, он некоторое время летит с ускорением. То есть сначала скорость увеличивается, а затем принимает постоянное значение. Это объясняется тем, что сила сопротивления растет с увеличением скорости и в какой-то момент приобретает значение, равное силе тяжести. И сила тяжести больше не может вызвать ускорение.
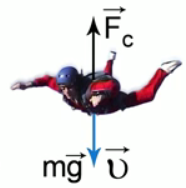
Рис. 2. Силы, действующие на парашютиста
7. Сила инерции – 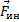
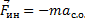 ,
,
где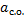 – ускорение системы отсчета.
– ускорение системы отсчета.
Например, если автобус движется вперед с ускорением относительно Земли, то в системе отсчета, связанной с автобусом, на человека будет действовать сила инерции (см. рис.3), которая отталкивает его назад. Эта сила направлена противоположно ускорению.
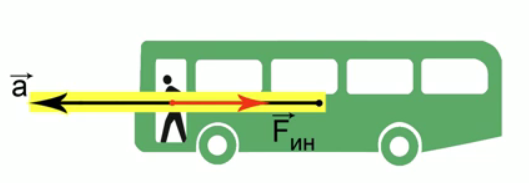
Рис. 3. Сила инерции, действующая на человека в автобусе
8. Сила тяжести – 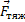
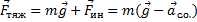
9. Вес тела – 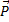
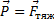
Вес тела – это сила, из-за которой под действием силы тяжести (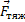 ) тело давит на опору или растягивает подвес. Вес приложен к опоре или к нити (к подвесу). Численно вес тела равен силе тяжести, рассмотренной в пункте 8.
) тело давит на опору или растягивает подвес. Вес приложен к опоре или к нити (к подвесу). Численно вес тела равен силе тяжести, рассмотренной в пункте 8.
Автомобиль трогается с места и движется с ускорением 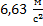 . Чему равен вес водителя, если его масса –
. Чему равен вес водителя, если его масса – 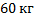 ?
?
Дано: 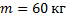 ;
; 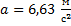
Найти: P
Решение
К центру масс водителя приложена сила тяжести (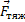 ), которая образована двумя силами: силой гравитационного притяжения (
), которая образована двумя силами: силой гравитационного притяжения (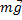 ) и силой инерции (
) и силой инерции (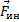 ). Сила тяжести вызывает действие на сиденье силы
). Сила тяжести вызывает действие на сиденье силы 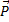 – это вес тела. Вес тела, согласно третьему закону Ньютона, вызывает силу реакции опоры (
– это вес тела. Вес тела, согласно третьему закону Ньютона, вызывает силу реакции опоры (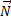 ) (см. Рис. 4).
) (см. Рис. 4).
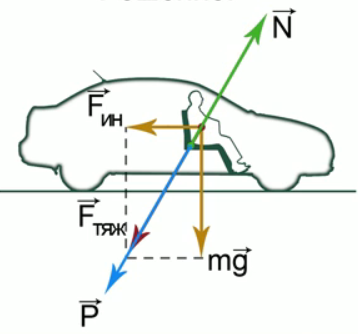
Рис. 4. Иллюстрация к задаче
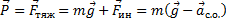
В формуле присутствует разность векторов, направленных перпендикулярно друг другу. Модуль результирующего вектора найдем по теореме Пифагора:
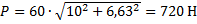
Автомобиль массой 1,2 т движется равномерно по горизонтальной дороге при коэффициенте сопротивления 0,05. Найти силу тяги двигателя. Варианты ответа: 1. 600 Н; 2. 1200 Н; 3. 3 кН; 4. 12 кН
Дано: 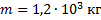 ;
; 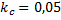
Найти: 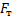 (см. Рис. 5)
(см. Рис. 5)
Решение
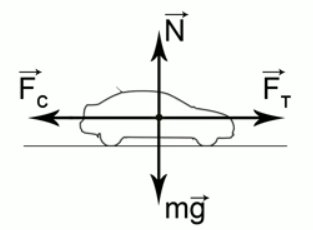
Рис. 5. Иллюстрация к задаче
При равномерном движении силы должны быть уравновешены, следовательно:
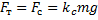
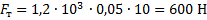
Ответ: 1. 600 Н.
Под действием груза массой 1 кг пружина растягивается на 2 см. Найти коэффициент упругости пружины. Варианты ответа: 1. 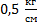 ; 2.
; 2. 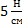 ; 3.
; 3. 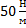 ; 4.
; 4. 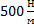 .
.
Дано: 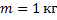 ;
; 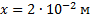
Найти: k
Решение
Сила притяжения к Земле растягивает пружину вниз, а сила упругости направлена вверх (см. Рис. 6).
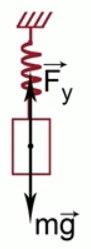
Рис. 6. Иллюстрация к задаче
Сила упругости равна по величине силе притяжения к Земле:
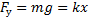
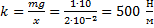
Ответ: 4. 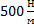 .
.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В.А., Демидова М.Ю., Никифоров Г.Г., Ханнанов Н.К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015
Домашнее задание
- Упражнение 7 (2, 3) (стр. 57) – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы)
- Тело массой m покоится на наклонной плоскости, составляющей с горизонтом угол α. Чему равна сила трения, действующая на тело?
- Тело массой
 , движущееся на восток, тормозится постоянной силой
, движущееся на восток, тормозится постоянной силой  , направленной на запад. Чему равно и куда направлено ускорение тела?
, направленной на запад. Чему равно и куда направлено ускорение тела?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Files.school-collection.edu.ru (Источник).
- Интернет-портал Eduspb.com (Источник).
- Интернет-портал Irmest.narod.ru (Источник).
- Интернет-портал Afportal.ru (Источник).
Основные типы сил в механике. Видеоурок. Физика 10 Класс
Законы Ньютона позволяют решить основную задачу механики, если известны все силы, действующие на тело. Зная эти силы, можно найти ускорение тела в любой момент времени, а зная ускорение, можно рассчитать скорость тела в любой точке траектории, зная скорость, можно определить положение тела в любой момент времени. Можно решить и обратную задачу, то есть, если нам известны координаты тела в любой момент времени, мы можем найти равнодействующую всех сил, действующих на тело. Но как же нам найти сами силы, действующие на тело? Этой теме и будет посвящен сегодняшний урок
При рассмотрении механических задач большинство сил, действующих на тела, можно отнести к трем основным разновидностям:
— сила всемирного тяготения;
— сила трения;
— сила упругости.
Рассмотрим падение некоего тела с высоты без начальной скорости (Рис. 1).
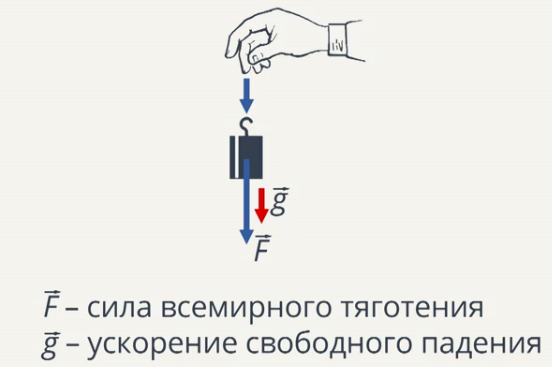
Рис. 1. Падение тела с высоты без начальной скорости (Источник)
Все окружающие нас тела притягиваются к Земле, это обусловлено действием сил всемирного тяготения. Если мы будем пренебрегать сопротивлением воздуха, то мы уже знаем, что все тела падают на Землю с одинаковым ускорением – ускорением свободного падения.
Тело, подвешенное на пружине динамометра (рис. 2):
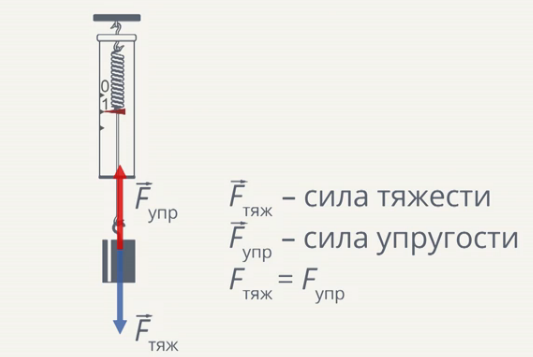
Рис. 2. Тело, подвешенное на пружине динамометра (Источник)
Как и всякий предмет, тело, подвешенное на пружине, стремится упасть вниз из-за притяжения Земли, но, когда пружина растянется до некоторой длины, тело останавливается, то есть приходит в состояние механического равновесия. Мы уже знаем, что механическое равновесие наступает, когда сумма сил, действующих на тело, равна нулю. Это означает, что сила тяжести, действующая на груз, должна уравновеситься с некоторой силой, действующей со стороны пружины. Эта сила, направленная против силы тяжести и действующая со стороны пружины, называется силой упругости.
Движение тела по шероховатой поверхности с некоторой начальной скоростью (Рис. 3):
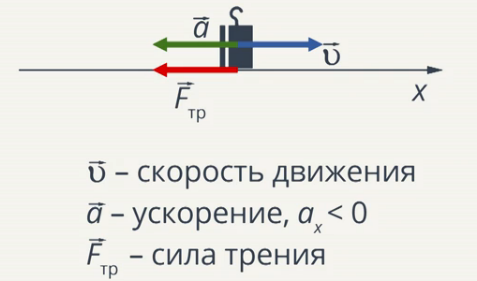
Рис. 3. Движение тела по шероховатой поверхности с некоторой начальной скоростью (Источник)
Пройдя некоторое расстояние, тело останавливается, скорость тела уменьшается от начального значения до нуля, то есть ускорение тела – величина отрицательная. Следовательно, на тело со стороны поверхности действует сила, которая стремится остановить это тело, то есть действует против его скорости. Эта сила называется силой трения.
Рассмотрим более подробно силу упругости.
Любое твердое тело оказывает противодействие попыткам изменить его размеры или форму. Изменение размеров или формы твердого тела называется деформацией. Существует пять основных видов деформации:
- Растяжение
- Сжатие
- Кручение
- Изгиб
- Сдвиг
Любые деформации, величина кот
Урок 08. Лекция 08. Силы в механике
Сила — физическая величина, которая определяет меру воздействия одного тела на другое.
Сила – векторная величина; она характеризуется:
Измеряется при помощи прибора «динамометр».
Единица измерения силы в Международной системе единиц (СИ) — Ньютон, обозначение [Н].
В природе существуют различные силы.
Гравитационные силы действуют между всеми телами – все тела притягиваются друг к другу. Но это притяжение существенно лишь тогда, когда хотя бы одно из взаимодействующих сил так же велико, как Земля или луна.
Электромагнитные силы действуют между заряженными частицами. В атомах, молекулах, живых организмах именно они являются главными.
Область ядерных сил очень ограничена. Они заметны только внутри атомных ядер (т.е. на расстоянии 10-12 см.)
Слабые взаимодействия проявляются на ещё меньших расстояниях. Они вызывают превращение элементарных частиц друг в друга.
Основные виды сил: сила тяжести, сила трения, сила упругости.
Почему мяч, выпущенный из рук, падает вниз? Почему прыгнувший вверх человек вскоре снова оказывается внизу? У этих явлений одна и та же причина – притяжение Земли. Наблюдения за природными объектами показывают, что все окружающие тела ощущают притяжение к Земле. Падает вниз вода фонтанов, водопадов и листья деревьев.
Силу притяжения тел к Земле вблизи ее поверхности называют сила тяжести.
Fтяж = m·g
Сила тяжести всегда направлена вертикально вниз к поверхности Земли. Сила тяжести направлена к центру Земли. Сила тяжести это гравитационная сила, приложенная к центру тела.
Сила тяжести – одно из проявлений силы всемирного тяготения.
Обозначим массу Земли – М, массу тела – m, радиус Земли – R, тогда сила тяготения:
Он же и есть сила тяжести.
m — масса тела
g – ускорение свободного падения.
Из закона Всемирного тяготения: , где M — масса планеты, m — масса тела, R — расстояние до центра планеты; g — ускорение силы тяжести. Значит g не зависит от массы тела.g = 9,81 м/с2 – ускорение свободного падения на поверхности Земли.
Сила тяжести это гравитационная сила, приложенная к центру тела и направленная к центру Земли.
В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2.
Значит g не зависит от массы тела.
На высоте h ускорение свободного падения равно
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли.
При соприкосновении двух движущихся тел возникает сила, направленная против движения и препятствующая движению — сила трения.
Сила трения — это сила, возникающая при движении одного тела по поверхности другого, приложенная к движущемуся телу и направлена против движения.
Сила трения — это сила электромагнитной природы.
Возникновение силы трения объясняется двумя причинами:
1) Шероховатостью поверхностей
2) Проявлением сил молекулярного взаимодействия.
Силы трения всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, силы трения скольжения, силы трения качения.
Fтр = м*N, где м – коэффициент трения , N – сила реакции опоры.
Сила упругости – сила, которая возникает при любом виде деформации тел и стремится вернуть тело в первоначальное состояние.
Fупрx = — k*x, где k – жесткость тела [Н/м], х — абсолютное удлинение тела.
Сила упругости перпендикулярна поверхности взаимодействующих тел и направлена всегда против деформации.
Механическая сила — это… Что такое Механическая сила?

Си́ла — векторная физическая величина, являющаяся мерой интенсивности взаимодействия тел. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нем деформаций.[1]
Сила, как векторная величина, характеризуется модулем и направлением. Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение движения материальной точки совпадает по направлению с приложенной силой; по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе. Деформация являются следствием возникновения в теле внутренних напряжений.[2][3][4]
Понятие силы использовали еще ученые античности в своих работах о статике и движении. Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед.[5] Представления Аристотеля о силе, связанные с фундаментальными несоответствиями, просуществовали в течение нескольких столетий. Эти несоответствия устранил в XVII в. Исаак Ньютон, используя для описания силы математические методы. Механика Ньютона оставалась общепринятой на протяжении почти трехсот лет.[4] К началу XX в. Альберт Эйнштейн в теории относительности показал, что ньютоновская механика верна лишь в при сравнительно небольших скоростях движения и массах тел в системе, уточнив тем самым основные положения кинематики и динамики и описав некоторые новые свойства пространства-времени.
С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.[2] Эксперименты по физике высоких энергий, проведенные в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия.[6]
Свойства сил
В механике силы обладают тремя основными свойствами, называемыми законами Ньютона. В ньютоновской механике они постулированы, в лагранжевой — доказываются.
Второй закон Ньютона
Второй закон Ньютона выражается следующей формулой:
Эта формула является частным случаем уравнений Эйлера—Лагранжа. Подставим в уравнение
лагранжиан
 .
.
Получим:
 .
.
По определению 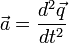 ,
, 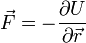 . Подставив, получим требуемое уравнение.
. Подставив, получим требуемое уравнение.
Ускорение, которое приобретает тело в результате действия на него равнодействующей силы, прямопропорционально величине этой силы, совпадает с ней по направлению и обратно пропорционально массе тела.
Ньютоновская механика
Исаак Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (знаменитые законы Ньютона).[4][7]
Первый закон Ньютона

Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.[7] Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал «покой естественным состоянием» объекта. Первый закона Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона покой физически неотличим от равномерного прямолинейного движения, связан с принципом относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.[8]
Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скорость и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга.
Третий закон Ньютона
Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что любая сила, которая обусловлена действием тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 2 со стороны тела 1.[9] Математически закон записывается так:
Этот закон означает, что силы всегда возникают парами «действие-противодействие».[7] Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:
Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.[2]
Классификация сил
Несмотря на наличие огромного количества различных типов сил, всех их можно свести к чётырём фундаментальным силам:
Источники
Примечания
- ↑ Glossary. Earth Observatory. NASA. — «Сила — любой внешний фактор, который вызывает изменение в движении свободного тела или возникновение внутренних напряжений в зафиксированном теле.» Проверено 9 апреля 2008. (англ.)
- ↑ 1 2 3 Lectures on Physics, Vol 1. — Addison-Wesley, 1963. (англ.)
- ↑ An introduction to mechanics. — McGraw-Hill. (англ.)
- ↑ 1 2 3 University Physics, Sears, Young & Zemansky, pp. 18–38 (англ.)
- ↑ Heath,T.L. The Works of Archimedes (1897). Archive.org. Проверено 14 октября 2007. (англ.)
- ↑ Weinberg, S. Dreams of a Final Theory. — Vintage Books USA, 1994. — ISBN 0-679-74408-8 (англ.)
- ↑ 1 2 3 Newton, I. The Principia Mathematical Principles of Natural Philosophy. — University of California Press, 1999. — ISBN 0-520-08817-4 (англ.)
- ↑ Мултановский, В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 80−81.
- ↑ Henderson, Tom Lesson 4: Newton’s Third Law of Motion. The Physics Classroom (1996-2007). Проверено 4 января 2008.
Wikimedia Foundation. 2010.
Силы в теоретической механике
Определение силы
В инерциальной системе отсчета, не взаимодействующие между собой, материальные точки движутся с постоянными скоростями. Пусть – радиус-вектор одной из свободных точек. Тогда вектор ее скорости есть постоянный вектор, не зависящий от времени t. Следовательно его проекции на оси прямоугольной системы координат являются постоянными, не зависящими от времени величинами: . Если мы определим вектор ускорения точки:
,
то он равен нулю: . Это означает, что его проекции на оси координат равны нулю: .
Как показывает опыт, можно создать условия, при которых материальные точки будут взаимодействовать друг с другом. Тогда их скорости не будут постоянными – движение при взаимодействии является ускоренным. У рассматриваемой нами точки, вектор скорости будет зависеть от времени, а вектор ускорения будет отличен от нуля. Тогда удобно ввести новую векторную физическую величину, пропорциональную вектору ускорения точки. Такую величину называют силой. Она определяется по формуле:
,
где m – еще одна физическая величина, называемая массой точки.
- Сила ,
- действующая на материальную точку с радиус-вектором со стороны других точек – это мера воздействия других точек на рассматриваемую точку, в результате которой она получает ускорение относительно инерциальной системы отсчета. Величина силы определяется по формуле:
(1) ,
где m – масса точки – величина, зависящая от свойств самой точки.
Формула (1) называется вторым законом Ньютона. По существу, она является определением новой физической величины – силы. Такое определение согласуется с нашим жизненным опытом, согласно которому, чем больше мы прилагаем усилий, тем быстрее разгоняется груз (например, при толкании ядра в легкой атлетике). Однако, в отличие от жизненного опыта, формула (1) дает строгое математическое определение.
Изучая движения материальных точек, мы можем экспериментально определить их ускорения, а затем по формуле (1) найти зависимость силы от положений точек системы. Так мы устанавливаем законы, описывающие взаимодействие материальных точек. Изучая и систематизируя экспериментальные данные, мы получаем правила, которые позволяют нам определять зависимость силы от времени и от координат в сложных случаях, основываясь на более простых. Так если нам известна зависимость вектора от времени и от координат: , то формула (1) представляет собой систему дифференциальных уравнений:
Решая ее, можно найти закон движения точки.
Сила – это векторная величина
В формуле (1): , m есть скаляр, то есть число, не зависящее от координат и времени. Ускорение есть вектор. Тогда сила является вектором. Это означает, что если мы выберем прямоугольную систему координат , то сила имеет три проекции на ее оси: . То есть, в математическом смысле, сила определяется тремя числами – тремя компонентами или проекциями на оси координат. Разумеется, если мы будем рассматривать движение в плоскости, то есть в двухмерном пространстве, то в нем прямоугольная система координат имеет только две оси . Тогда и сила, как и любой вектор в этой системе, имеет только две проекции (или компоненты).
Поскольку сила – это вектор, то к ней применимы все формулы, применяемые к векторам в аналитической геометрии.
Скользящие векторы
Теперь рассмотрим абсолютно твердое тело. Законы его движения имеют более сложный вид. Они описываются двумя векторными уравнениями:
(2) ;
(3) .
Здесь – ускорение центра масс тела; M – его масса; – момент импульса тела относительно произвольно выбранного центра C; – внешние силы, действующие на тело, приложенные в точках .
Вместо того, чтобы пытаться в лоб решать эти уравнения, давайте попробуем вывести некоторые закономерности, заключенные в этих уравнениях. Для этого упростим задачу. Рассмотрим тело в некоторый момент времени t. И пусть, для этого момента времени, нам известны действующие на него силы и точки их приложения .
Уравнение (2) не зависит от точек приложения Ak сил. Для его составления требуется знать только проекции сил на оси координат . А вот в уравнение (3) входят точки приложения. Они входят в виде векторов, проведенных из некоторого центра C в точку Ak. Причем входят в виде векторного произведения .
Согласно одному из свойств, векторное произведение векторов, имеющих одинаковое направление, равно нулю. Поэтому . Тогда если к вектору прибавить любой вектор, параллельный , то векторное произведение не изменится:
.
Здесь – произвольная постоянная, имеющая размерность м/Н.
Отсюда следует важный вывод. Если точку приложения силы переместить на любое расстояние вдоль линии действия силы, то уравнения движения твердого тела не изменятся. В связи с этим, вместо обычного в математическом определении вектора, можно ввести новый математический объект, называемый скользящим вектором. Скользящий вектор по существу есть множество, состоящее из двух векторов – самого вектора силы (так называемый образующий вектор) и его точки приложения относительно выбранного центра системы отсчета . В связи с этим, приводим следующие определения.
- Скользящий вектор
- – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, проведенной через образующий вектор. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на прямой, проходящей через них.
Наряду со скользящим вектором, мы можем ввести понятия закрепленных и свободных векторов.
- Закрепленный вектор
- – это множество, состоящее из образующего вектора и точки его приложения. Два фиксированных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
- Свободный вектор
- – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
Таким образом, свободный вектор не зависит от точки приложения, и является просто вектором. Для справок также приведем определение вектора.
- Вектор в трехмерном пространстве
- – это три числа, называемые компонентами, связанные с предварительно выбранной прямоугольной системой координат, которые при поворотах этой системы вокруг ее центра O, и при отражении осей, преобразуются по тому же закону, что и координаты произвольной точки A, не совпадающей с O. Компоненты вектора также называются проекциями вектора на оси координат.
Силы в теоретической механике
Если мы рассматриваем деформации в телах, то все приложенные силы нужно рассматривать как связанные векторы, поскольку внутренние напряжения и деформации зависят от точек приложения сил. Но если мы считаем тело абсолютно твердым, и нам нужно определить только траекторию его движения, то, как показано выше, силы являются скользящими векторами. То есть в теоретической механике мы можем обращаться с силами более свободно, чем при решении других задач – точки приложения сил можно перемещать вдоль линий их действия.
Таким образом, в теоретической механике, над силами мы можем выполнять следующие преобразования.
1) Переносить точку приложения силы на любое расстояние вдоль линии ее действия.
2) Раскладывать силу по правилу параллелограмма на две или более сил, каждая из которых приложена в той точке, что исходная сила – то есть можно заменить исходную силу на несколько сил, векторная сумма которых равна исходной.
3) Несколько сил, приложенных к одной точке можно объединять в одну, применяя правило параллелограмма – то есть можно заменить несколько сил, приложенных в одной точке их векторной суммой, приложенной в той же точке.
Такие преобразования называются эквивалентными преобразованиями сил. А системы, полученные в результате таких преобразований, называются эквивалентными системами сил. На странице «Аксиомы статики» приводится иллюстрация подобных преобразований. См. «Пример решения задачи, используя аксиомы статики». Таким образом, в теоретической механике, силы являются некоторыми расчетными величинами. Их можно преобразовывать для того, чтобы получить более простую систему сил и упростить уравнения движения тел.
Рассмотрим следующий пример. Пусть мы имеем тело, на которое действует сила тяжести Земли. Эта сила приложена ко всем точкам. На любую малую часть тела, массой , действует сила тяжести , где – ускорение свободного падения. То есть на тело действует система сил, равномерно распределенных по его объему. Решать уравнения движения с такими силами неудобно. Поэтому в начале, проще выполнить эквивалентные преобразования. В результате таких преобразований все силы тяжести малых элементов тела можно заменить одной силой , приложенной к центру масс тела с радиус-вектором . Тем самым мы пришли к уравнениям движения, в которых на тело действует одна сила. Естественно, что это не реальная сила, действующая в центре масс, а расчетная величина, эквивалентная распределенным по объему тела силам.
Здесь мы разбили тело на материальные точки, каждая из которых имеет массу и положение в пространстве, задаваемое радиус-вектором . Тогда – масса тела. Суммирование выполняется по всем точкам, составляющим тело.
Статика и эквивалентные преобразования сил
Снова рассмотрим уравнения движения твердого тела:
(2) ;
(3) .
Пусть в момент времени t нам известны внешние силы , действующие на тело. Далее мы можем попытаться упростить систему сил, сведя ее эквивалентными преобразованиями к новой системе . В следующий момент времени, силы могут измениться и нам потребуется выполнять новые эквивалентные преобразования. В этом, конечно, ничего хорошего нет. Но, возможно, нам удастся найти эквивалентные преобразования аналитическим способом, то есть получить аналитическое выражение для новых сил , пригодное для любого момента времени. Тогда вместо (2) и (3) мы получим систему уравнений с более простой системой сил:
(2′) ;
(3′) .
Теперь из уравнений (2) и (3) вычтем уравнения (2′) и (3′):
(4) ;
(5) .
Но это есть ни что иное, как уравнения статики, в которых к исходной системе сил добавили эквивалентную систему, изменив направления на противоположные.
Отсюда следует вывод, что для получения эквивалентной системы сил, нужно к исходной системе, добавить новую систему сил так, чтобы тело находилось в равновесии. Тогда эквивалентная система будет совпадать с новой, в которой направления сил заменены на противоположные.
Единицы измерения силы
В СИ единицей измерения силы является Ньютон. Обозначается Н. Международное обозначение N. Сила F с абсолютным значением в 1 Ньютон обозначается так:
F = 1 Н.
Из уравнения (1) получаем:
.
В СГС единицей измерения силы является дин. Обозначается дин. Международное обозначение dyn.
; .
В МКГСС единицей измерения силы является килограмм-сила. Это основная единица этой системы (наряду с метром и секундой). Обозначается кгс или кГ. Международное обозначение kgf или kgF.
.
Автор: Олег Одинцов. Опубликовано:


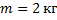 , движущееся на восток, тормозится постоянной силой
, движущееся на восток, тормозится постоянной силой 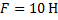 , направленной на запад. Чему равно и куда направлено ускорение тела?
, направленной на запад. Чему равно и куда направлено ускорение тела?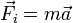
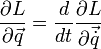
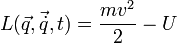 .
.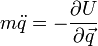 .
.