аналогия с линейным движением, примеры — OneKu

Содержание статьи:

Любая физическая величина, которая предлагается в математических уравнениях при изучении того или иного явления природы, несет некоторый смысл. Не является исключением из этого правила и момент инерции. Физический смысл этой величины подробно рассмотрен в данной статье.

Момент инерции: математическая формулировка

В первую очередь следует сказать, что рассматриваемая физическая величина используется для описания систем вращения, то есть таких движений объекта, которые характеризуются круговыми траекториями вокруг некоторой оси или точки.

Вам будет интересно:Что это — нанометр? Сравнение с метром, понятие о нанотехнологиях, интересные факты

Приведем математическую формулу момента инерции для материальной точки:

I = m*r2.

Здесь m и r — масса и радиус вращения частицы (расстояние до оси) соответственно. Любое твердое тело, каким бы сложным оно ни было, мысленно можно разбить на материальные точки. Тогда формула момента инерции в общем виде будет иметь вид:

I = ∫mr2dm.

Это выражение справедливо всегда, причем не только для трехмерных, но и для двумерных (одномерных) тел, то есть для плоскостей и стержней.

Из этих формул трудно понять смысл физический момента инерции, однако можно сделать важный вывод: он зависит от распределения массы в теле, которое вращается, а также от расстояния до оси вращения. Причем зависимость от r является более резкой, чем от m (см. знак квадрата в формулах).

Движение по окружности

Понять, каков физический смысл момента инерции, невозможно, если не рассмотреть круговое движение тел. Не вдаваясь в подробности, приведем сразу два математических выражения, описывающих вращение:

I1*ω1 = I2*ω2;

M = I *dω/dt.

Верхнее уравнение носит название закона сохранения величины L (момента импульса). Оно означает, что какие бы изменения ни происходили внутри системы (сначала был момент инерции I1, а затем он стал равным I2), произведение I на угловую скорость ω, то есть момент импульса, будет оставаться неизменным.

Нижнее выражение демонстрирует изменение скорости вращения системы (dω/dt) при воздействии на нее некоторого момента силы M, который имеет внешний характер, то есть порождается силами, не связанными с внутренними процессами в рассматриваемой системе.

И в верхнем, и в нижнем равенствах присутствует I, причем чем больше ее значение, тем меньше будет угловая скорость ω или угловое ускорение dω/dt. В этом и заключается физический смысл момента инерции тела: он отражает способность системы сохранять свою угловую скорость. Чем больше I, тем сильнее проявляется эта способность.

Аналогия с линейным импульсом

Теперь перейдем к тому же выводу, что был озвучен в конце предыдущего пункта, проведя аналогию между вращательным и поступательным движениями в физике. Как известно, последнее описывается следующей формулой:

p = m*v.

Это простое выражение определяет импульс системы. Сравним его форму с таковой для момента импульса (см. верхнее выражение в предыдущем пункте). Мы видим, что величины v и ω имеют одинаковый смысл: первая характеризует скорость изменения линейных координат объекта, вторая — угловых координат. Поскольку обе формулы описывают процесс равномерного (равноуглового) движения, то величины m и I также должны иметь одинаковый смысл.

Теперь рассмотрим 2-й закон Ньютона, который выражается формулой:

F = m*a.

Обращая внимание на форму записи нижнего равенства в предыдущем пункте, имеем подобную рассмотренной ситуацию. Момент силы M в его линейной представлении — это сила F, а линейное ускорение a полностью аналогично угловому dω/dt. И снова мы приходим к эквивалентности массы и момента инерции.

Какой смысл несет масса в классической механике? Она является мерой инерции: чем больше m, тем труднее сдвинуть предмет с места, а тем более придать ему ускорение. То же самое можно сказать и о моменте инерции применительно к движению вращения.

Физический смысл момента инерции на бытовом примере

Зададимся простым вопросом о том, как легче крутить металлический стержень, например, арматуру — когда ось вращение направлена вдоль его длины или когда поперек? Конечно же, легче раскрутить стержень в первом случае, потому что его момент инерции для такого положения оси будет очень маленьким (для тонкого стержня он равен нулю). Поэтому достаточно зажать между ладошек предмет и легким движением привести его во вращение.

Кстати, описанный факт экспериментально проверили наши предки еще в стародавние времена, когда научились добывать огонь. Они раскручивали палочку с огромными угловыми ускорениями, что приводило к созданию больших сил трения и, как следствие, к выделению значительного количества теплоты.

Маховик авто — яркий пример использования большого значения момента инерции

В завершение хотелось бы привести, пожалуй, самый важный для современной техники пример использования физического смысла момента инерции. Маховик авто представляет собой сплошной стальной диск, имеющий относительно большие радиус и массу. Эти две величины обуславливают существование значительной величины I, характеризующей его. Маховик призван «смягчать» любые силовые воздействия на коленвал автомобиля. Импульсивный характер действующих моментов сил от цилиндров двигателя на коленвал сглаживается и делается плавным благодаря тяжелому маховику.

Кстати, чем больше момент импульса, тем больше энергии находится во вращающейся системе (аналогия с массой). Этот факт хотят использовать инженеры, запасая энергию торможения авто в маховике, чтобы впоследствии направить ее на разгон транспортного средства.

Источник

17. Момент инерции тела и его физический смысл. Примеры вычисления момента инерции твердых тел. Теорема Штейнера.

а) момент инерции стержня массой m, длинойlъ

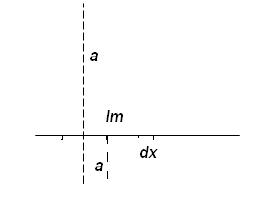Линейная плотность

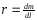
Для однородного стержня

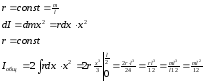
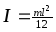для стержня

Момент инерции однородного круглого тела при вращении относительно оси походящей через центр.

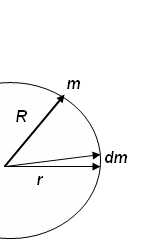
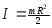— для диска

Таблица моментов инерции

Стержень относительно центра: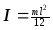Для диска: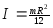

Для обода: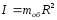

Для шара: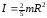

Если ось проходит через центр симметрии, то для расчёта момента инерции применяется

теорема Штейнера: I=I₀+ma² ,І₀— момент инерции относительно оси проходящей через центр;

m— масса тела; а—расстояние между осями;

Пример: Вращение стержня относительно конца

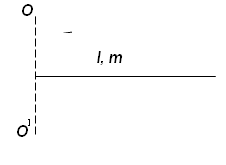
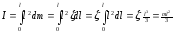
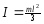— для стержня

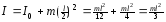
18. Момент импульса твердого тела. Вектор угловой скорости и вектор момента импульса. Гироскопический эффект. Угловая скорость прецессии. Моме́нт и́мпульса

(кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Моментом импульса тела называется величина, равная векторной сумме моментов импульса его частей. Закон сохранения момента импульса.

Система называется замкнутой, если на неё действуют внешние моменты или их действие скомпенсировано.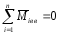

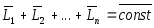—закон сохранения магнита импульса.

1. Гироскоп

—это симметричное тело, вращающегося относительно оси симметрии (волчок).

Свойства гироскопа:

а) ось гироскопа сохраняет своё положение в пространстве при любых его движениях;

Т.к. момент импульса сохраняется и по величине и по направлению, то ось гироскопа всегда занимает неизменное положение.

Используется для навигационной аппаратуры.

б) прецессия гироскопа:

— это возникновение вращения оси гироскопа в направлении перпендикулярном приложенной внешней силы.

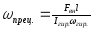
l— плечо

Гироскопический эффект вращающихся тел есть проявление коренного свойства материи — её инертности.

угловая скорость прецессии тем больше, чем больше масса подвешенного грузика Для гироскопов, применяющихся в технике, величина угловой скорости прецессии бывает в миллионы раз меньше угловой скорости вращения маховика.

К отрицательным последствиям проявления гироскопических эффектов можно отнести силы, разрушающие механические конструкции. Эти силы возникают в подшипниках при попытке изменения положения оси вращения различных валов.

19. Идеальная и вязкая жидкость. Гидростатика несжимаемой жидкости. Стационарное движение идеальной жидкости. Уравнение Бернулли.

Жидкость—агрегатное состояние вещества при котором оно сохраняет объём, но изменяет форму. Закон Бернулли.Вдоль линии тока увеличение скорости по величине приводит к изменению кинетической энергии, которая связана с изменением её потенциальной энергии жидкости, а, следовательно с изменением гидростатического давления

Замечание: Это справедливо для идеальной жидкости.

Следствие из уравнения Бернулли: чем больше скорость, тем меньше давление в жидкости.

Замечание: уравнение Бернулли не справедливо для вязких и сжимаемых жидкостей (газов). Однако следствие из него является справедливым в любом случае.

Закон Паскаля: давление, оказываемое на жидкость или газ, передаётся без изменения во все точки жидкости или газа.

Давление жидкости на глубине h

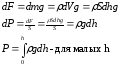
ρ=const, т.к. жидкость несжимаемая

g=const

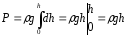
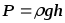
Средняя сила давления на стенку сосуда

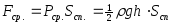
34.Что понимают под моментом инерции тела относительно некоторой оси? Какой физический смысл имеет момент инерции?

При вращении материальной точки массы т_i по окруж­ности радиуса г_i момент ее импульса в проекции на ось враще­ния равенL_i=m_i_ir_iЛинейная скорость движения _i связана с угловой скоростью  соотношением _i=r_i , поэтому L_i=m_ir_i² . Если вокруг оси 0 вращается система материаль­ных точек с одной и той же угловой скоростью , то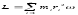, где суммирование производится по всем материальным точка системы. Величину , как одинаковую для всех матери­альных точек, можно вынести из под знака суммы, тогда получится

основной закон динамики вращательного движения в проекции на ось вращения можно записать:

,

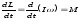где М — проекция суммарного момента внешних сил на ось вращения.

Уравнение вращения т.т. вокруг не­подвижной оси:

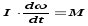или

.

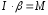Произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение  равно моменту внешних сил относительно той же оси

35. От чего зависит момент инерции тела? От чего он не зависит? Момент инерции тела- физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела,а также от выбора оси вращения, характеризует инертность тела при вращательном движении.

36.Как найти момент инерции материальной точки?

Пользуясь уравнением M=I dω/dt=Iβ и определив момент действующих сил и угловое ускорение, можно вычислить момент инерции тела. Часто в экспериментальных работах тело приводится во вращение или колебание с помощью груза, падающего с некоторой высоты. Потенциальная энергия падающего груза переходит в кинетическую энергию вращательного движения тела. Используя закон сохранения механической энергии при условии малых потерь на трение, можно вычислить момент инерции тела.

37.Как найти момент инерции тела, которое в данных условиях нельзя считать материальной точкой?

38. Какая формула упрощает расчёт момента инерции тела относительно оси, не проходящей через центр масс?

т.Гюйгенса — Штейнера, момент инерции груза относительно оси вращения:

, где R — расстояние между осью вращения и осью, проходящей через центр масс полого цилиндра параллельной оси вращения.

Момент инерции от-но произвольной оси = сумме от-но, оси параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между ними

39. В методе колебаний для определения момента инерции диска в лабораторной работе №3 «Определение момента инерции диска» применяется теория малых колебаний .Какие упрощения при этом допускаются?

Момент инерции тела – физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела, а также от выбора оси вращения, и характеризует инертность тела при вращательном движении.

Определение момента инерции диска методом колебаний

В работе используется установка, на ободе которой укреплен массивный шар

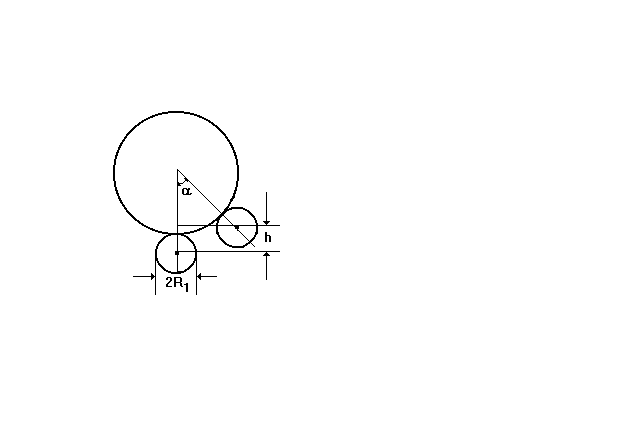
Рис.3.2. Схема экспериментальной установки для определения момента инерции диска методом колебаний.

Пренебрегая моментом сил трения, можно написать уравнение движения диска с шаром в следующем виде:

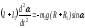, (3.5) (3.5)

где I- момент инерции диска c валом относительно оси вращения OO, I₁ — момент инерции шара относительно оси вращения OO, вычисляемый по теореме Гюйгенса – Штейнера:

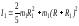, (3.6)

где R и R₁ – радиусы диска и шара соответственно, m₁ — масса шара,  – угол отклонения диска от положения равновесия.

При малых углах отклонения можно принять sin ≈  и уравнение (3.5) можно написать в виде:

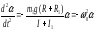. (3.7) (3.7)

Как известно, решением такого дифференциального уравнения будет периодическая функция

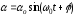, (3.8) (3.8)

где α₀— угловая амплитуда колебаний,  — начальная фаза, ω₀ — циклическая частота колебаний:

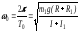. (3.9) (3.9)

Измерив период колебаний диска с шаром Т₀ и зная массу m₁ и радиус шара R₁, из формул (3.6) и (3.9) найдем момент инерции диска относительно оси вращения:

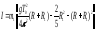. (3.10)

40.Перечислите причины, дающие погрешность в лабораторной работе №3 «Определение момента инерции диска» Скажется ли на точности измерений колебание груза при его падении, а также неуровновешенность диска?

34.Что понимают под моментом инерции тела относительно некоторой оси? Какой физический смысл имеет момент инерции?

При вращении материальной точки массы т_i по окруж­ности радиуса г_i момент ее импульса в проекции на ось враще­ния равенL_i=m_i_ir_iЛинейная скорость движения _i связана с угловой скоростью  соотношением _i=r_i , поэтому L_i=m_ir_i² . Если вокруг оси 0 вращается система материаль­ных точек с одной и той же угловой скоростью , то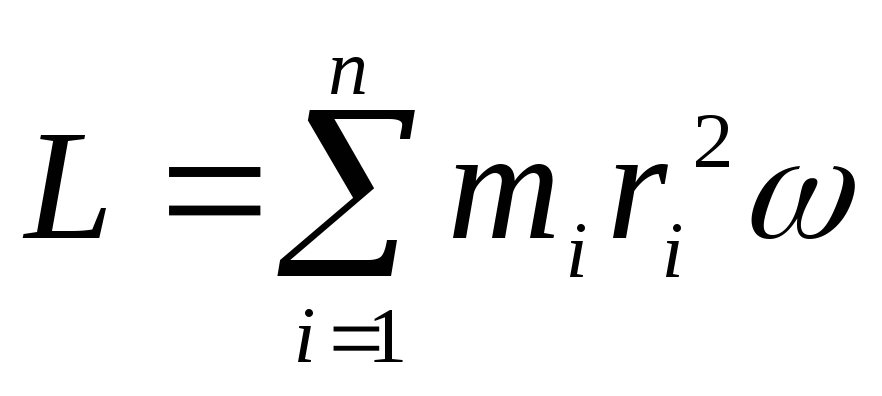, где суммирование производится по всем материальным точка системы. Величину , как одинаковую для всех матери­альных точек, можно вынести из под знака суммы, тогда получится

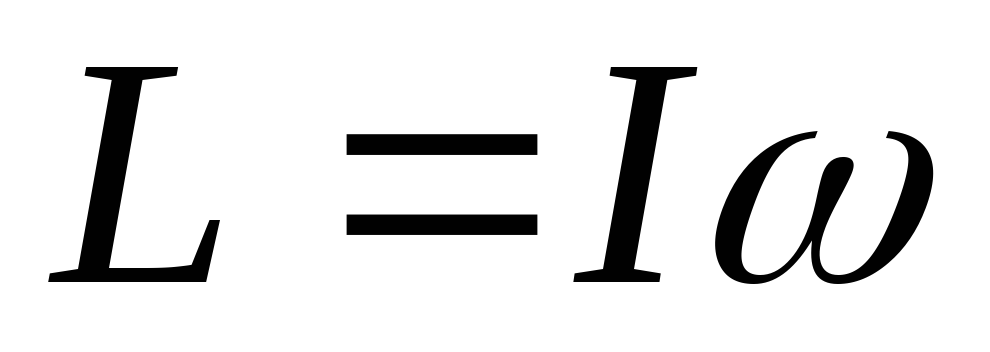
основной закон динамики вращательного движения в проекции на ось вращения можно записать:

,

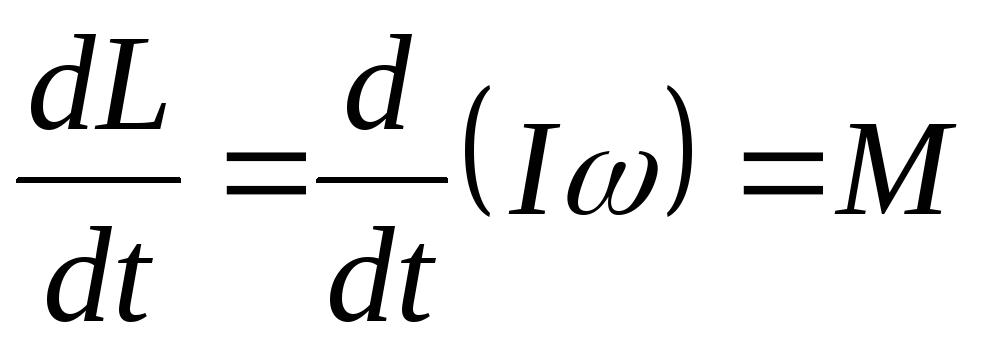где М — проекция суммарного момента внешних сил на ось вращения.

Уравнение вращения т.т. вокруг не­подвижной оси:

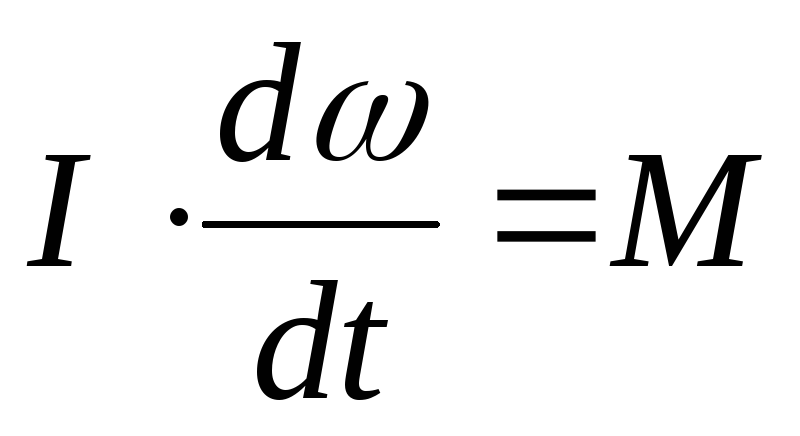или

.

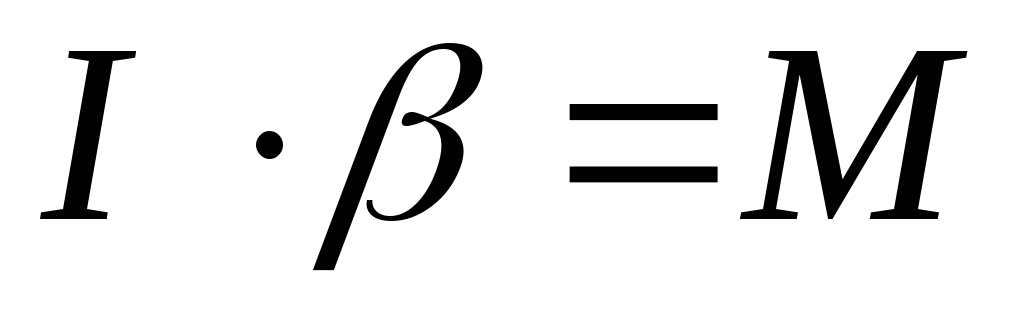Произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение  равно моменту внешних сил относительно той же оси

35. От чего зависит момент инерции тела? От чего он не зависит? Момент инерции тела- физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела,а также от выбора оси вращения, характеризует инертность тела при вращательном движении.

36.Как найти момент инерции материальной точки?

Пользуясь уравнением M=I dω/dt=Iβ и определив момент действующих сил и угловое ускорение, можно вычислить момент инерции тела. Часто в экспериментальных работах тело приводится во вращение или колебание с помощью груза, падающего с некоторой высоты. Потенциальная энергия падающего груза переходит в кинетическую энергию вращательного движения тела. Используя закон сохранения механической энергии при условии малых потерь на трение, можно вычислить момент инерции тела.

37.Как найти момент инерции тела, которое в данных условиях нельзя считать материальной точкой?

38. Какая формула упрощает расчёт момента инерции тела относительно оси, не проходящей через центр масс?

т.Гюйгенса — Штейнера, момент инерции груза относительно оси вращения:

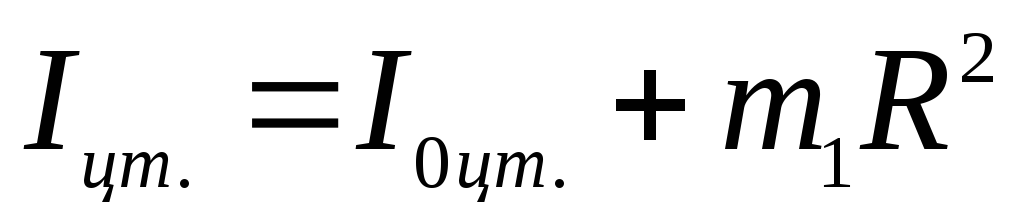, где R — расстояние между осью вращения и осью, проходящей через центр масс полого цилиндра параллельной оси вращения.

Момент инерции от-но произвольной оси = сумме от-но, оси параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между ними

39. В методе колебаний для определения момента инерции диска в лабораторной работе №3 «Определение момента инерции диска» применяется теория малых колебаний .Какие упрощения при этом допускаются?

Момент инерции тела – физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела, а также от выбора оси вращения, и характеризует инертность тела при вращательном движении.

Определение момента инерции диска методом колебаний

В работе используется установка, на ободе которой укреплен массивный шар

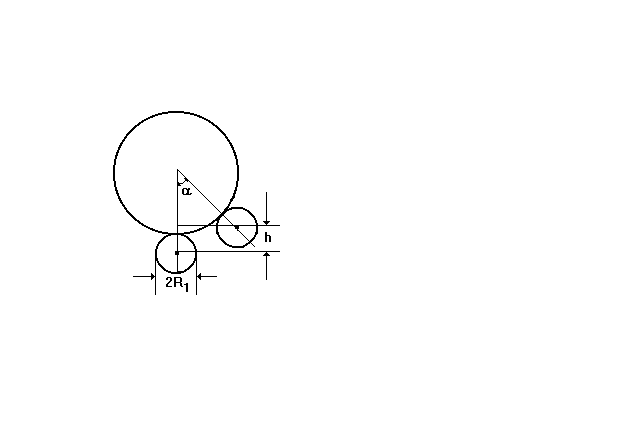
Рис.3.2. Схема экспериментальной установки для определения момента инерции диска методом колебаний.

Пренебрегая моментом сил трения, можно написать уравнение движения диска с шаром в следующем виде:

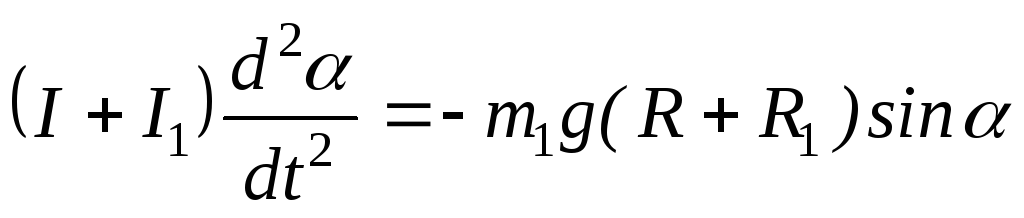, (3.5) (3.5)

где I- момент инерции диска c валом относительно оси вращения OO, I₁ — момент инерции шара относительно оси вращения OO, вычисляемый по теореме Гюйгенса – Штейнера:

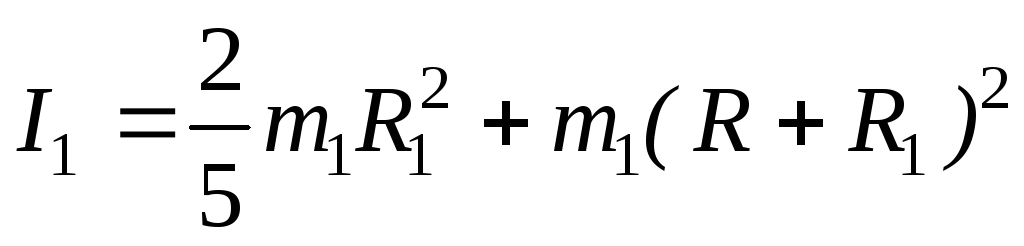, (3.6)

где R и R₁ – радиусы диска и шара соответственно, m₁ — масса шара,  – угол отклонения диска от положения равновесия.

При малых углах отклонения можно принять sin ≈  и уравнение (3.5) можно написать в виде:

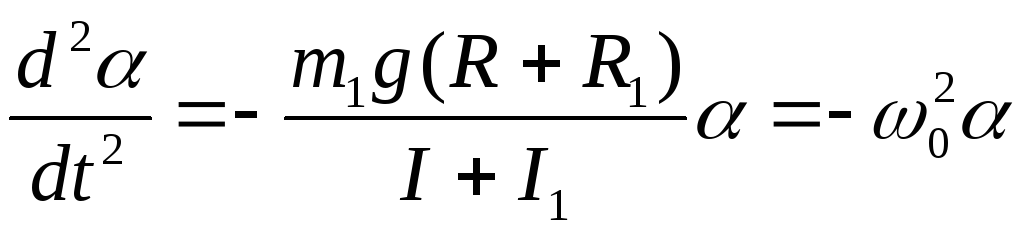. (3.7) (3.7)

Как известно, решением такого дифференциального уравнения будет периодическая функция

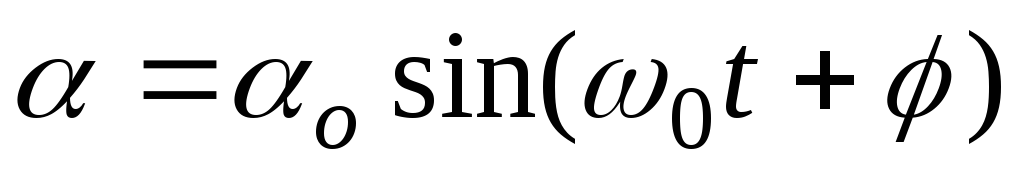, (3.8) (3.8)

где α₀— угловая амплитуда колебаний,  — начальная фаза, ω₀ — циклическая частота колебаний:

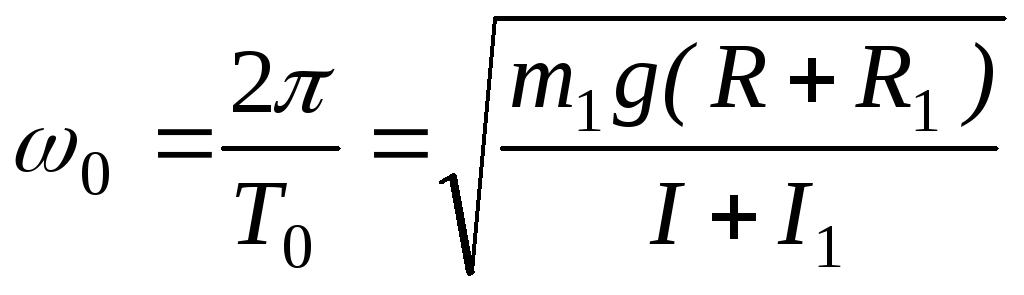. (3.9) (3.9)

Измерив период колебаний диска с шаром Т₀ и зная массу m₁ и радиус шара R₁, из формул (3.6) и (3.9) найдем момент инерции диска относительно оси вращения:

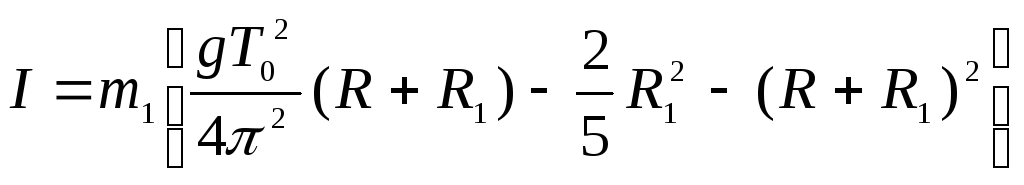. (3.10)

40.Перечислите причины, дающие погрешность в лабораторной работе №3 «Определение момента инерции диска» Скажется ли на точности измерений колебание груза при его падении, а также неуровновешенность диска?

Контрольные вопросы

Контрольные вопросы Л/р №5 Гладких Н.А.

1. Дайте определение момента инерции точечного, составного и сплошного тел. Объясните его физический смысл.

Моментом инерции материальной точки называют произведение массы точки на квадрат расстояния до оси вращения.

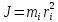
Момент инерции составного тела равен сумме моментов инерции составных частей.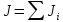

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело.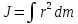 Момент инерции — величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при вращательном движении.

2. Сделайте рисунок машины Атвуда и укажите на нем все силы, действующие на грузы и блок.

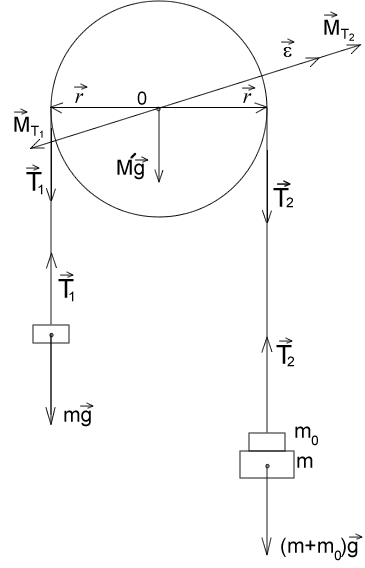
3. Дайте определение момента силы. Укажите на рисунке направления моментов сил,

действующих на блок.

Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

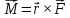
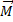
4. Используя рисунок, напишите уравнения движения грузов и блока.

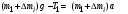_{(1) Первый груз с перегрузом}

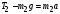_{(2) Второй груз}

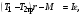_{(3) Вращение блока}

5. Используя эту систему уравнений, найдите ускорение движения грузов.

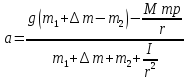
Что такое момент инерции тела. Его физический смысл.

Момент инерции — как бы «момент момента при вращении». Посмотрите на его размерность — кг умноженный на метр во 2 степени. Рассмотрим очень простой и грубый пример. Если вы открываете за ручку обычную дверь, то прикладываете обычный момент (сила умноженная на плечо) . Но если вы ее борсили с силой, то относительно петель, как оси вращения, кратковременно уже будет наблюдаться момент инерции, то есть, чтобы вам уже остановить эту дверь, первоначальной силы явно не достаточно. При вращательном движении роль массы двери теряет смысл, а получает смысл — распределение этой массы относительно оси вращения.

Момент инерции — величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело. Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен: Момент инерции всего тела относительно оси равен: или, для непрерывно распределенной массы: Момент инерции всего тела сложной конфигурации обычно определяют экспериментально. Момент инерции некоторых однородных твердых приведены в таблице 1. продолжение смотри здесь: <a rel=»nofollow» href=»http://www.effects.ru/science/230/index.htm» target=»_blank»>http://www.effects.ru/science/230/index.htm</a>

Вопросы для самостоятельной и индивидуальной работы

В чем проявляется физическое единство законов, описывающих поступательное и вращательное движения?

В чем проявляется отличие момента инерции от массы тела?

Сформулируйте теорему Гюйгенса–Штейнера. Можно ли изменять ориентацию оси АА?

В каких случаях является затруднительным аналитический расчет момента инерции тела? Как поступают в этом случае?

Под действием касательной силы F диск массой m и радиусом R приобретает угловое ускорение  относительно оси, проходящей через центр инерции диска. При каких значениях массы и радиуса диска может быть получено прежнее значение углового ускорения , если касательная вращающая сила уменьшена в k раз. Дайте обоснованный ответ в виде аналитического доказательства.

Каков физический смысл коэффициента угловой жесткости или модуля кручения подвеса?

В чем состоит метод дополнительных грузов, используемый в данной работе? Какие дополнительные грузы используются в данной работе?

В чем состоит метод проверки справедливости теоремы Гюйгенса – Штейнера, используемый в данной работе?

Зависимость Тот 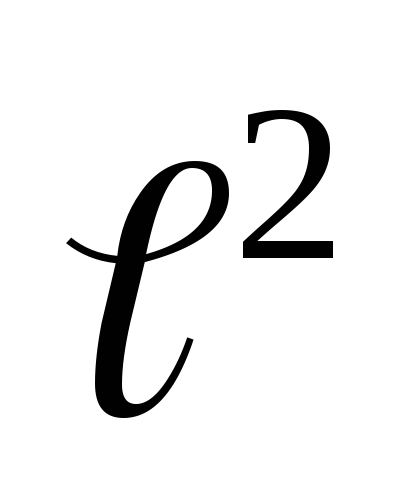в предлагаемой работе является линейной? Объясните цели, которые преследуются построением такого графика.

Объясните метод определения модуля кручения подвеса, используемый в данной работе. Как учитывается погрешность измерений данного метода?

Какие физические величины должны быть измерены для определения момента инерции цилиндра относительно оси, проходящей параллельно оси симметрии цилиндра?

Какие физические величины влияют на период колебаний маятника, используемого в данной работе?

Исследуйте зависимость периода колебаний Т от параметров маятника. Имеются ли максимумы и минимумы у Т?

Каким образом размеры стержней, по которым скользят шары, влияют на период колебаний маятника?

Докажите, что при углах поворота стержней маятника на угол, больший, чем 8–10, период колебаний зависит от амплитуды колебаний.

Каким образом влияет амплитуда колебаний на погрешности определения момента маятника инерции и его модуля жесткости подвеса.

Предложите наиболее точный метод определения радиуса шаров, используемых в данной работе.

Момент инерции маятника определяют графическим и аналитическим путем. В каком случае точность выше и почему?

При длительном пребывании в невесомости космонавты обычно худеют. Как можно измерить массы тела космонавтов в невесомости?

Как рассчитывают момент инерции шаров, имеющих внутреннюю полость в виде шара, стержня, прямоугольного параллелепипеда?

Как измерить момент инерции Земли, Луны?

Как измерить орбитальный момент импульса электрона?

Как измерить момент инерции молекулы водорода, кислорода.

Как измерить начальную (конечную) кинетическую энергию маятника, применяемого в данной работе?

Как измерить угловую скорость и угловое ускорение маятника в данной работе?