ГДЗ по информатике 7 класс, Босова, рабочая тетрадь, упр. 37. Какой сигнал соответствует таблице? – Рамблер/класс

ГДЗ по информатике 7 класс, Босова, рабочая тетрадь, упр. 37. Какой сигнал соответствует таблице? – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

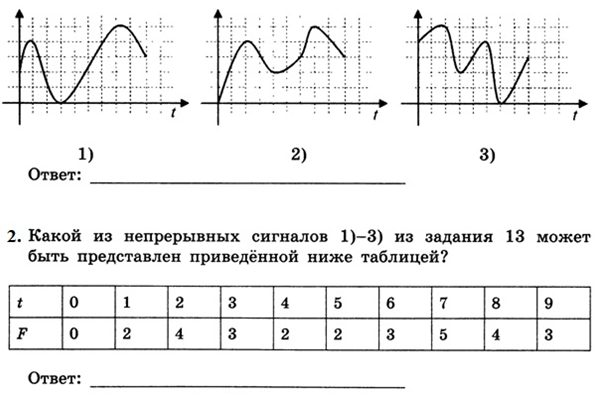
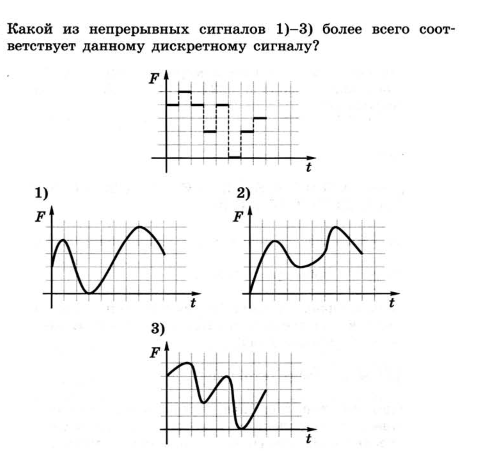
Какой из непрерывных сигналов 1)-3) из задания 36 может быть представлен приведённой ниже таблицей?

Это сигналы

ответы

Сигнал 2) может быть представлен приведённой таблицей.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

ГДЗ информатика 9 класс Босова, рабочая тетрадь, упр. 36. Переведите число 1010 из десятичной системы счисления в двоичную

Переведите число 1010 из десятичной системы счисле-

ния в двоичную систему счисления. Сколько единиц со-
держит полученное (Подробнее…)

ГДЗИнформатика9 классБосова Л.Л

ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 4 Вопрос 8 Найдите значение выражения

Привет, есть варианты, как ответить на вопрос???
Найдите значение выражения (234 — 266)2 + 4 ∙ 234 ∙ 266.

УчителяИнформатикаСеменов А. В.Ященко И.В.11 класс

Вариант 1. С-51. № 1. ГДЗ Алгебра 7 класс Звавич. помогите найти значения алгебраических дробей

 Найдите значения алгебраических дробей   при соответствующих значениях х и заполните таблицу: (Подробнее…)

ГДЗАлгебра7 классЗвавич Л.И.

Решите пожалуйста Дополнительное задание а) б) в) г)

(Подробнее…)

ГДЗЭкзамены

Помогите определить перевод. Lesson 13. № 4. ГДЗ Английский язык 4 класс Верещагина.

Read the words and guess their meaning.
 
sandals [‘sændəlz], hospital [‘hɒspɪtl], Canada [‘kænədə], rock- (Подробнее…)

ГДЗАнглийский язык4 классВерещагина И.Н.

Page

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ

2. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ С ПОМОЩЬЮ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ

3. МОДЕЛИРОВАНИЕ И АНАЛИЗ ЦИФРОВЫХ СИСТЕМ В ПАКЕТЕ SIMULINK СИСТЕМЫ MATLAB

4. ПРЕОБРАЗОВАНИЕ ФОРМ ЛИНЕЙНЫХ МОДЕЛЕЙ ЦИФРОВЫХ СИСТЕМ

Контрольные вопросы

 

Лабораторная работа № 13

Моделирование и исследование

цифровых систем управления

 

Цель работы: проанализировать линейные стационарные системы управления с дискретным временем.

 

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

 

Любая система автоматического регулирования и управления представляет собой совокупность элементов, предназначенных для преобразования сигналов, поступающих на ее вход, чтобы обеспечить выполнение цели управления [4]. Если на вход всех элементов системы поступают сигналы, которые могут быть описаны непрерывными функциями времени, система называется непрерывной. Система, содержащая, по крайней мере, один элемент, выходным сигналом которого является дискретный сигнал, называется дискретной.

Дискретный сигнал – это такой сигнал, который определяется последовательностью значений а₀, а₁, а₂, ¼, а_{n, ¼ .} Сигналы могут быть дискретными по уровню, по времени, а также одновременно по уровню и по времени.

В зависимости от способов получения дискретных сигналов может быть введена следующая классификация дискретных систем [4, 18]:

1)    импульсная система – это система, в которой используются сигналы, дискретные по времени;

2)    релейная система – это система, в которой используются сигналы, дискретные по уровню;

3)    цифровая система – это система, в которой используются сигналы, дискретные как по времени, так и по уровню.

На рис. 13.1 показана идеализированная амплитудно-импульсная модуляция непрерывного сигнала на основе идеальных импульсов, ширина которых бесконечна малая, а высота равна значениям непрерывного сигнала в дискретные моменты времени.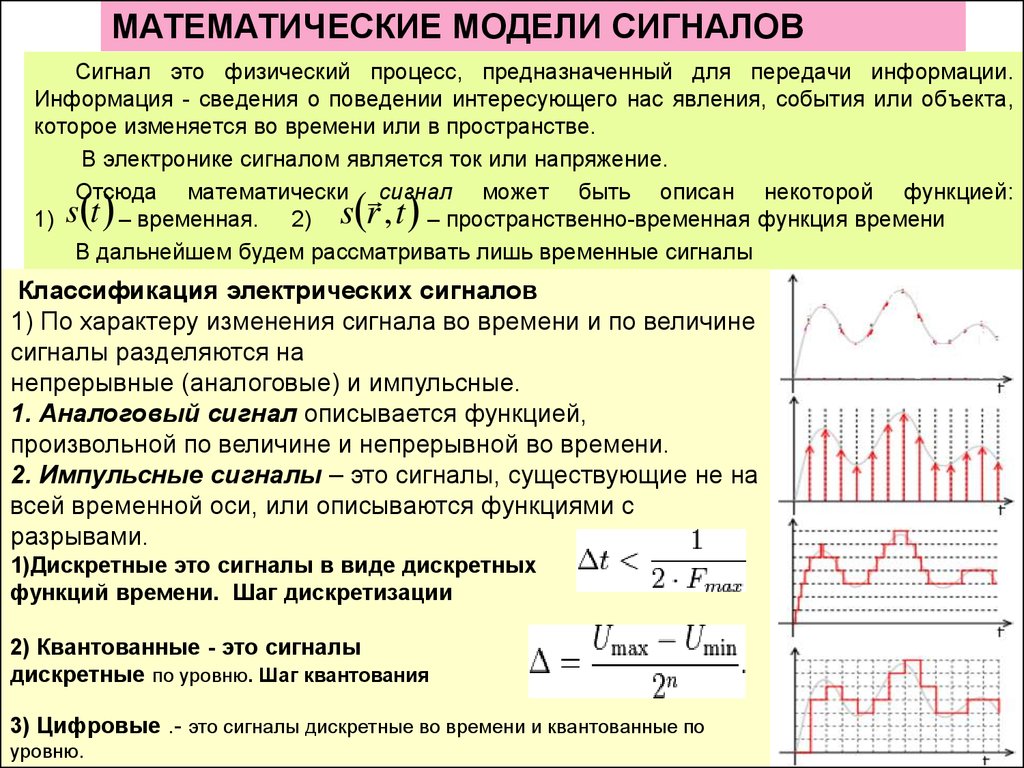 Если f(t) есть непрерывный сигнал, то выделение дискретных значений f(kT) называется квантованием сигнала f(t) по времени с постоянным шагом квантования или периодом дискретизации

Т. В то же время f(kT) называют решетчатой функцией. Другим видом импульсной модуляции является широтно-импульсная модуляция, при которой амплитуда импульсов постоянная, а их ширина пропорциональна в некоторых пределах значениям f(kT). Еще возможна фазоимпульсная модуляция сигнала, которая осуществляется за счет смещения импульсов в пределах шага квантования Т. Величина смещения пропорциональна значениям f(kT).

 

Рис. 13.1. Идеальное квантование непрерывного сигнала по времени

Квантование (дискретизация) непрерывного сигнала по уровню с шагом h показано на рис. 13.2. Оно может быть получено, если преобразовать непрерывный сигнал с помощью многоступенчатого релейного устройства.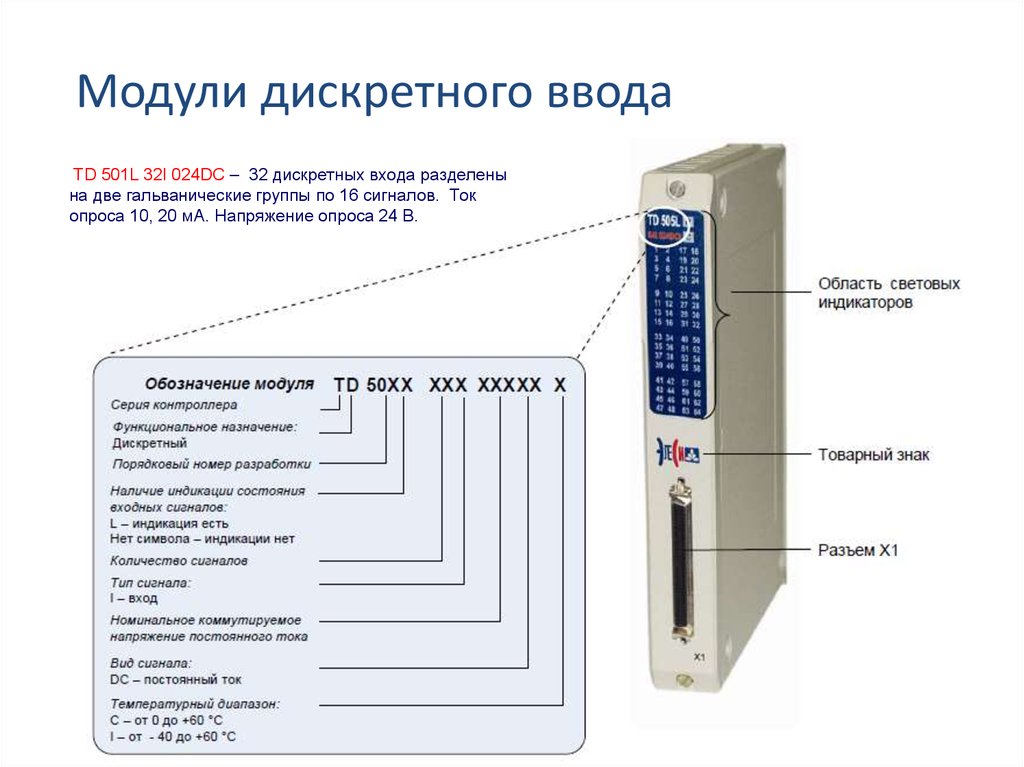 Дискретный по уровню сигнал, представленный на рис. 13.2, может быть описан в соответствии с выражением [4]:

При квантовании по уровню в произвольные моменты времени выделяются значения непрерывного сигнала при достижении им фиксированных дискретных уровней [18]. Как отмечалось, квантование по уровню характерно для релейных систем автоматического управления, которые представляют собой достаточно большой класс динамических систем, в состав которых входят нелинейные звенья с разрывной характеристикой. Основными достоинствами релейных систем автоматического управления является их простота, связанная с ней высокая надежность, а также экономичность в расходе энергии питания. В то же время к ним не могут быть применены методы анализа и синтеза

гладких систем.

Рис. 13.2. Квантование непрерывного сигнала по уровню

Характер квантования по уровню и по времени непрерывного сигнала показан на рис.

13.3. В этом случае непрерывный сигнал f(t) заменяется фиксированными дискретными (по уровню) значениями, ближайшими к значениям непрерывной функции f(t) в дискретные моменты времени 0, Т, 2Т, ¼ . Квантование по уровню и по времени осуществляется в цифровых системах управления при преобразовании непрерывных сигналов в цифровую форму или в коды. Если цифровое устройство оперирует с числовым представлением со значительным количеством разрядов (что характерно для современных компьютеров), то квантованием по уровню можно пренебречь. Тогда цифровую систему можно рассматривать как импульсную систему с амплитудно-импульсной модуляцией.

Рис. 13.3. Квантование сигнала по уровню и по времени

Цифровая система управления включает объект управления (обычно непрерывный объект или процесс), чувствительные элементы (или датчики), аналого-цифровой преобразователь (АЦП), цифровое вычислительное устройство (микропроцессор или компьютер) и цифроаналоговый преобразователь (ЦАП). Функциональная схема цифровой системы управления показана на рис. 13.4.

10.7: Дискретная обработка сигналов непрерывного времени

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

23163

• Richard Baraniuk et al.
• Университет Райса

Введение

Цифровые компьютеры могут обрабатывать дискретные сигналы времени, используя чрезвычайно гибкие и мощные алгоритмы. Однако большинство представляющих интерес сигналов представляют собой непрерывные сигналы во времени, именно так данные почти всегда появляются в природе. Теперь, когда была обсуждена теория, поддерживающая методы генерации дискретного сигнала времени из непрерывного сигнала времени путем дискретизации и последующего точного восстановления исходного сигнала из его выборок без ошибок, будет показано, как это можно применить для реализации непрерывного времени, линейного инвариантные во времени системы, использующие дискретное время, линейные инвариантные во времени системы. Это имеет ключевое значение для многих современных технологий, поскольку позволяет использовать возможности цифровых вычислений для обработки аналоговых сигналов.

Дискретная обработка сигналов непрерывного времени

Структура процесса

С целью обработки сигналов непрерывного времени с использованием системы дискретного времени мы рассмотрим одну из наиболее распространенных структур технологий цифровой обработки сигналов. В качестве обзора принятого подхода исходный сигнал непрерывного времени \(x\) преобразуется в сигнал дискретного времени \(x_s\) таким образом, что периоды спектра выборок \(X_s\) максимально близки возможным по форме к спектру \(X\). Затем применяется дискретный, линейный во времени инвариантный фильтр \(H_2\), который изменяет форму спектра отсчетов \(X_s\), но не может увеличить предел полосы пропускания \(X_s\), чтобы создать другой сигнал \(y_s\ ). Это восстанавливается с помощью подходящего фильтра реконструкции для получения выходного сигнала непрерывного времени \(y\), тем самым эффективно реализуя некоторую систему непрерывного времени \(H_1\). Этот процесс показан на рисунке \(\PageIndex{1}\), а спектры показаны для конкретного случая на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{1}\): Показана блок-схема обработки сигналов непрерывного времени с использованием систем дискретного времени.

Необходимо дальнейшее обсуждение каждого из этих шагов, и мы начнем с обсуждения аналого-цифрового преобразователя, часто обозначаемого АЦП или АЦП. Понятно, что для обработки сигнала непрерывного времени с использованием методов дискретного времени мы должны произвести выборку сигнала в качестве начального шага. По сути, это и есть цель АЦП, хотя есть и практические вопросы, которые будут обсуждаться позже. АЦП принимает аналоговый сигнал с непрерывным временем в качестве входного сигнала и формирует цифровой сигнал с дискретным временем в качестве выходного с идеальным случаем бесконечной точности, соответствующим выборке. Как утверждает теорема Найквиста-Шеннона о дискретизации, для того, чтобы сохранить всю информацию об исходном сигнале, нам обычно требуется выборка выше частоты Найквиста \(\omega_s≥2B\), где полоса исходного сигнала ограничена до \((−B, Б)\). Когда невозможно гарантировать это условие, следует использовать фильтр сглаживания.

В фильтре дискретного времени происходят преднамеренные изменения информации о сигнале. Это обычно делается в программном обеспечении для цифровых компьютеров после того, как сигнал был оцифрован аппаратным АЦП и до того, как он будет использован аппаратным ЦАП для создания выходного сигнала. Это позволяет описанной выше настройке быть достаточно гибкой в ​​фильтре, который она реализует. Если выборка выше частоты Найквиста. Любые изменения, которые дискретный фильтр вносит в эту форму, могут быть переданы в непрерывный временной сигнал, предполагающий идеальную реконструкцию. Следовательно, описанный процесс реализует непрерывный во времени линейный инвариантный во времени фильтр. Это будет объяснено более математически подробно в следующем разделе. Как обычно, есть, конечно, практические ограничения, которые будут обсуждаться позже.

Наконец, мы обсудим цифро-аналоговый преобразователь, часто обозначаемый ЦАП или ЦАП.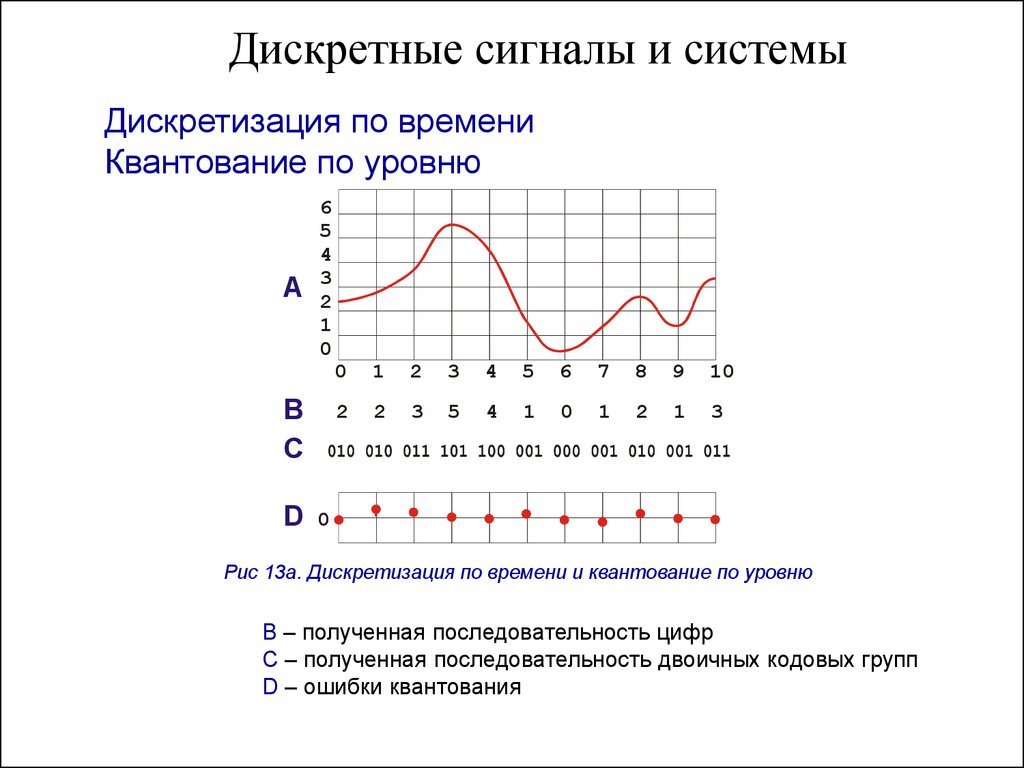 Поскольку фильтры непрерывного времени имеют входы непрерывного времени и выходы непрерывного времени, мы должны создать сигнал непрерывного времени из нашего отфильтрованного сигнала дискретного времени. Предполагая, что мы произвели выборку с ограниченной полосой пропускания с достаточно высокой скоростью, в идеальном случае это было бы сделано с использованием идеальной реконструкции с помощью интерполяционной формулы Уиттакера-Шеннона. Однако, опять же, есть практические проблемы, препятствующие этому, которые будут обсуждаться позже.

Рисунок \(\PageIndex{2}\): Спектры показаны черным цветом для каждого шага реализации фильтра непрерывного времени с использованием фильтра дискретного времени для определенного сигнала. Частотные характеристики фильтра показаны синим цветом, и обе они должны иметь максимальное значение 1, несмотря на вертикальную шкалу, предназначенную только для спектров сигналов. Предполагается, что АЦП и ЦАП идеальны.

Фильтр дискретного времени

После некоторого начального обсуждения процесса, показанного на рисунке \(\PageIndex{1}\), связь между инвариантным линейным фильтром непрерывного времени \(H_1\) и дискретным временем, линейным временем инвариантный фильтр \(H_2\) можно изучить. Мы будем предполагать использование идеальных АЦП и ЦАП с бесконечной точностью, которые выполняют дискретизацию и идеальную реконструкцию соответственно, используя частоту дискретизации \(\omega_s=2 \pi /T_s≥2B\), где входной сигнал \(x\) равен полоса ограничена до \((−B,B)\). Обратите внимание, что эти аргументы терпят неудачу, если это условие не выполняется и происходит псевдоним. В этом случае для сохранения этих аргументов необходимо предварительное применение фильтра сглаживания. 9{\infty} H_{1}\left(\frac{\omega-2 \pi k}{T_{s}}\right)(u(\omega-(2k-1) \pi) -u(\ омега-(2k+1) \pi)). \nonumber \]

Проще говоря, \(H_2\) является \(2 \pi\) периодическим и \(H_2(\omega)=H_1( \omega /T_s)\) для \(\omega \in[ -\пи, \пи)\).

При заданном непрерывном линейном инвариантном во времени фильтре \(H_1\) приведенное выше уравнение решает задачу проектирования системы при условии, что мы знаем, как реализовать \(H_2\). Фильтр \(H_2\) должен быть выбран таким, чтобы он имел частотную характеристику, где каждый период имел ту же форму, что и частотная характеристика \(H_1\) на \(\left(-\pi / T_{s}, \ pi / T_{s}\right)\). Это показано на частотных характеристиках, показанных на рисунке \(\PageIndex{2}\).

Мы могли бы также рассмотреть задачу системного анализа, в которой задан конкретный дискретный, линейный во времени инвариантный фильтр \(H_2\), и мы хотим описать фильтр \(H_1\). Таких фильтров много, но мы можем описать их частотные характеристики на \(\left(-\pi / T_{s}, \pi / T_{s}\right)\), используя приведенное выше уравнение. Выделение одного периода \(H_2(\omega)\) приводит к выводу, что \(H_{1}(\omega)=H_{2}\left(\omega T_{s}\right)\) для \(\ омега \in\left(-\pi / T_{s}, \pi / T_{s}\right)\). Поскольку предполагалось, что \(x\) ограничен полосой до \(\left(-\pi / T_{s}, \pi / T_{s}\right)\), значение частотной характеристики в другом месте не имеет значения.

Практические соображения

Как упоминалось ранее, существует несколько практических соображений, которые необходимо учитывать на каждом этапе процесса, показанного на рисунке \(\PageIndex{1}\). Некоторые из них будут кратко рассмотрены здесь, а более полная модель дискретной обработки сигналов непрерывного времени представлена ​​на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): Более полная модель того, как дискретная обработка сигналов непрерывного времени реализуется на практике. Обратите внимание на добавление фильтров сглаживания и защиты от изображения, чтобы способствовать ограничению входной и выходной полосы пропускания. Показано, что АЦП выполняет выборку с квантованием. Далее указывается, что цифровой фильтр является причинным. Показано, что ЦАП выполняет несовершенную реконструкцию, в этом случае сохраняется нулевой порядок.

Anti-Aliasing Filter

В действительности мы обычно не можем гарантировать, что входной сигнал будет иметь определенную полосу пропускания, и не всегда может быть достигнута достаточно высокая частота дискретизации. Поскольку крайне важно, чтобы высокочастотные компоненты не маскировались под более низкочастотные компоненты посредством наложения спектров, необходимо использовать сглаживающие фильтры с частотой среза, меньшей или равной \(\omega_s/2\) АЦП. Блок-схема на рисунке \(\PageIndex{3}\) отражает это дополнение.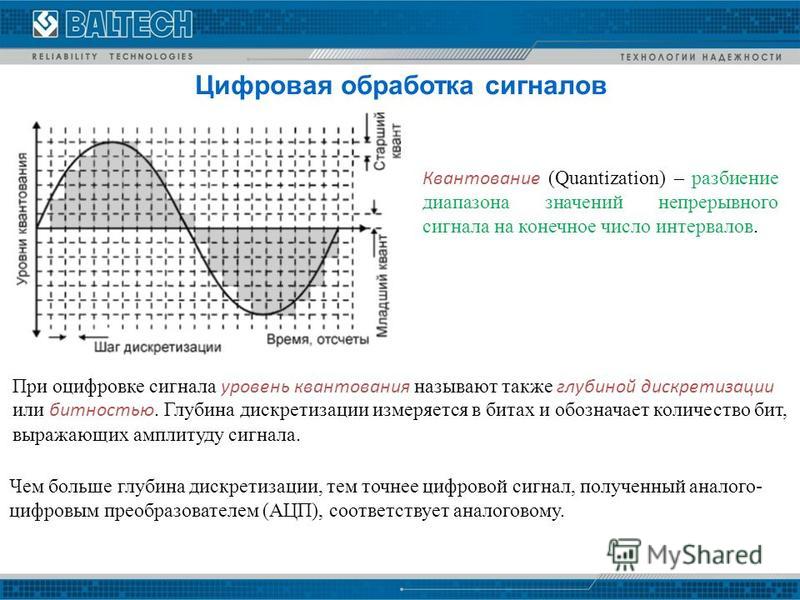

Как описано в предыдущем разделе, идеальный фильтр нижних частот, удаляющий всю энергию на частотах выше \(\omega_s/2\), был бы оптимален. Конечно, это недостижимо, поэтому необходимо принять аппроксимацию идеального фильтра нижних частот с низким коэффициентом усиления выше \(\omega_s/2\). Это означает, что некоторый алиасинг неизбежен, но его можно уменьшить до незначительного уровня.

Квантование сигнала

В нашем предыдущем обсуждении дискретной обработки сигналов с непрерывным временем мы предположили идеальный случай, в котором АЦП точно выполняет выборку. Однако, хотя АЦП преобразует непрерывный сигнал времени в сигнал дискретного времени, он также должен преобразовывать аналоговые значения в цифровые значения для использования в цифровом логическом устройстве, что называется квантованием. Подсистема ADC на блок-схеме на рисунке \(\PageIndex{3}\) отражает это дополнение.

Данные, полученные АЦП, должны храниться в виде конечного числа бит внутри цифрового логического устройства. Таким образом, существует только конечное число значений, которые может принимать цифровая выборка, а именно \(2N\), где \(N\) — количество битов, в то время как аналоговая выборка может принимать неисчислимое множество значений. Следовательно, что-то должно быть потеряно в процессе квантования. В результате квантование ограничивает как диапазон, так и точность выходного сигнала АЦП. Оба являются конечными, и улучшение одного при постоянном числе битов требует жертвовать качеством другого.

Реализуемость фильтра

В реальных условиях, если входной сигнал является функцией времени, будущие значения сигнала не могут использоваться для вычисления выходного сигнала. Таким образом, цифровой фильтр \(H_2\) и система в целом \(H_1\) должны быть причинно-следственными. Аннотация фильтра на рисунке \(\PageIndex{3}\) отражает это добавление. Если искомая система не является причинной, но имеет импульсную характеристику, равную нулю до некоторого времени \(t_0\), можно ввести задержку, чтобы сделать ее причинной.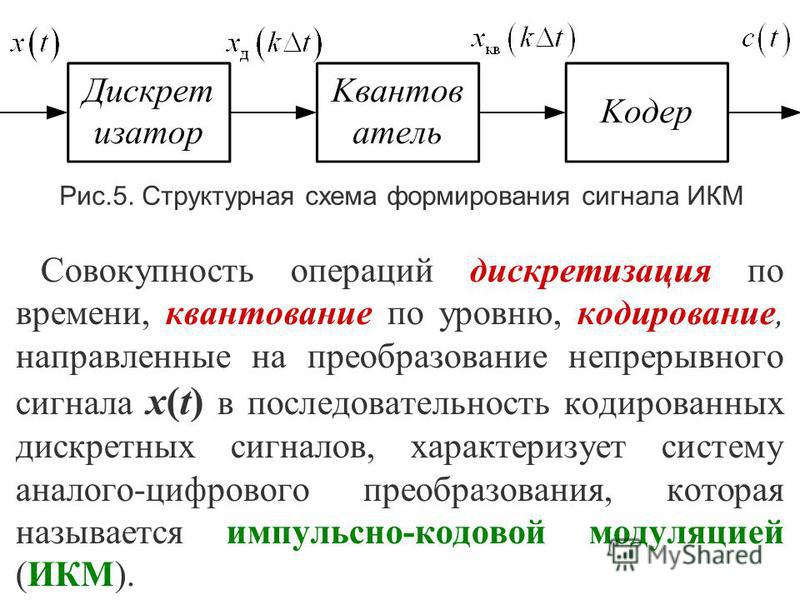 Однако, если эта задержка чрезмерна или импульсная характеристика имеет бесконечную длину, для практического решения проблемы становится необходимой оконная схема. Умножение на окно для уменьшения длины импульсной характеристики может уменьшить необходимую задержку и уменьшить требования к вычислениям.

Возьмем, к примеру, идеальный фильтр нижних частот. Она акаузальна и бесконечна по протяженности в обоих направлениях. Таким образом, мы должны довольствоваться приближением. Можно предположить, что эти аппроксимации могут быть достигнуты путем усечения синхроимпульсной характеристики фильтра нижних частот на одном из его нулей, эффективно обрабатывая его прямоугольным импульсом. Однако это приведет к плохим результатам в частотной области, так как результирующая свертка значительно расширит энергию сигнала. Другие оконные функции, которых существует множество, меньше распространяют сигнал в частотной области и, таким образом, гораздо полезнее для получения этих приближений.

Anti-Image Filter

В нашем предыдущем обсуждении дискретной обработки сигналов непрерывного времени мы предположили идеальный случай, в котором ЦАП выполняет идеальную реконструкцию. Однако при рассмотрении практических вопросов важно помнить, что функция sinc, используемая для интерполяции Уиттакера-Шеннона, бесконечна по длине и акаузальна. Следовательно, для ЦАП было бы невозможно реализовать идеальную реконструкцию.

Вместо этого ЦАП реализует причинно-следственную фиксацию нулевого порядка или другую простую схему реконструкции относительно частоты дискретизации \(\omega_s\), используемой АЦП. Однако это приведет к тому, что функция не будет ограничена пропускной способностью \((−\omega_s/2,\omega_s/2)\). Следовательно, к выходу необходимо применить дополнительный фильтр нижних частот, называемый фильтром подавления изображений. Процесс, показанный на рисунке \(\PageIndex{3}\), отражает эти добавления. Фильтр подавления изображений пытается ограничить полосу пропускания сигнала до \((−\omega_s/2,\omega_s/2)\), поэтому оптимальным будет идеальный фильтр нижних частот. Однако, как уже было сказано, это невозможно. Следовательно, должны быть приняты приближения идеального фильтра нижних частот с низким коэффициентом усиления выше \(\omega_s/2\).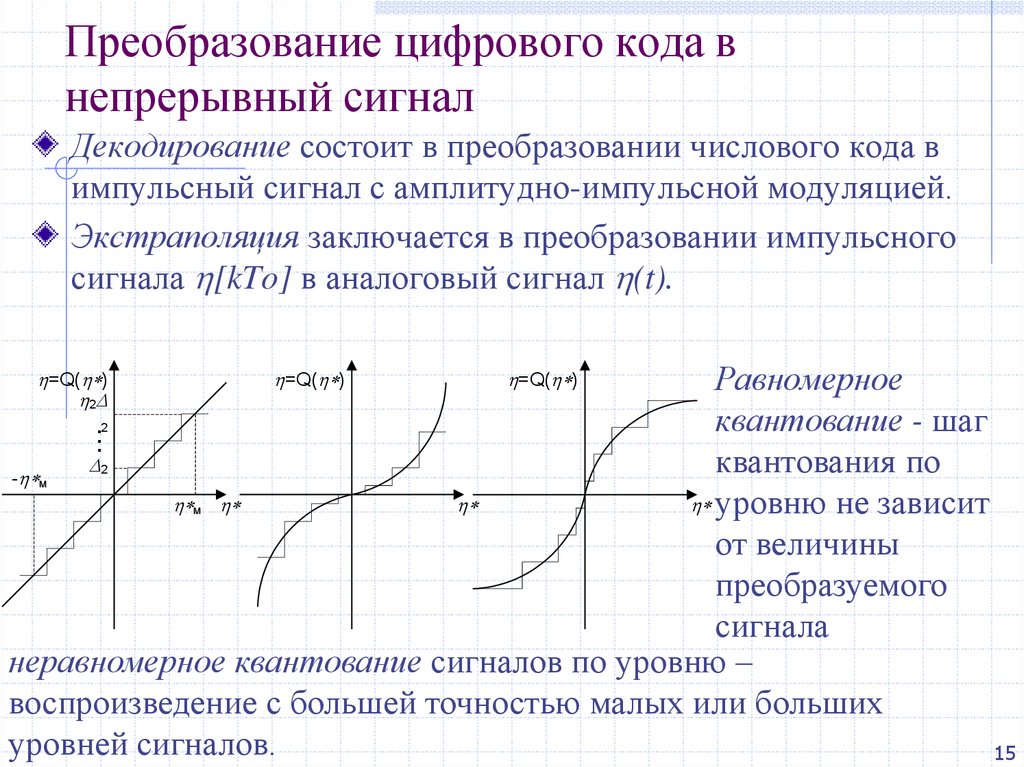 Фильтр подавления изображений обычно имеет те же характеристики, что и фильтр сглаживания.

Дискретная обработка сигналов непрерывного времени Резюме

Как было показано, выборка и реконструкция могут использоваться для реализации систем непрерывного времени с использованием систем дискретного времени, которые очень эффективны благодаря универсальности, гибкости и скорости цифровых компьютеров. . Однако существует большое количество практических соображений, которые необходимо учитывать при попытке выполнить это, включая шум квантования и сглаживание в аналого-цифровом преобразователе, реализуемость фильтра в дискретном временном фильтре, оконную реконструкцию и связанные с этим проблемы. в цифро-аналоговом преобразователе. Многие современные технологии решают эти проблемы и используют этот процесс.

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Ричард Баранюк и др.

   Лицензия

   СС BY

   Программа OER или Publisher

   OpenStax CNX

2. Теги

   На этой странице нет тегов.

scipy.signal.lti — Руководство по SciPy v1.9.3

класс scipy.signal.lti ( * система ) [источник]

Базовый класс линейной инвариантной ко времени системы с непрерывным временем.

Параметры

*system arguments

Класс lti может быть создан с 2, 3 или 4 аргументами. Ниже приводится количество аргументов и соответствующий созданный подкласс непрерывного времени:

• 2: TransferFunction : (числитель, знаменатель)

• 3: ZerosPolesGain : (нули, полюса, усиление)

• 4: StateSpace : (A, B, C, D)

Каждый аргумент может быть массивом или последовательностью.

См. также

ZerosPolesGain , StateSpace , TransferFunction , dlti

Примечания

lti экземпляров не существует напрямую. Вместо этого lti создает экземпляр одного из его подклассов: StateSpace 92 + 3s + 5 будет представлено как [1, 3, 5] ).

Изменение значения свойств, не являющихся непосредственно частью текущего представление системы (например, нулей системы StateSpace ) очень неэффективно и может привести к числовым неточностям. Лучше сначала преобразовать в конкретное системное представление. Например, позвоните sys = sys.to_zpk() перед доступом/изменением нулей, полюсов или усиления.

Примеры

 >>> из сигнала импорта scipy
 

 >>> signal.lti(1, 2, 3, 4)
StateSpaceContinuous(
массив ([[1]]),
массив ([[2]]),
массив ([[3]]),
массив ([[4]]),
дт: Нет
)
 

Построить передаточную функцию \(H(s) = \frac{5(s-1)(s-2)}{(s-3)(s-4)}\):

 >>> signal. lti([1, 2], [3, 4], 5)
ZerosPolesGainContinuous(
массив ([1, 2]),
массив ([3, 4]),
5,
дт: Нет
)
 

Построить передаточную функцию \(H(s) = \frac{3s + 4}{1s + 2}\):

 >>> signal.lti([3, 4], [1, 2])
TransferFunctionContinuous(
массив([3., 4.]),
массив([1., 2.]),
дт: Нет
)
 

Атрибуты

dt

Возвращает время выборки системы, Нет для систем lti .

полюса

полюса системы.

нули

Нули системы.

Методы

боде ([ш, н])	Расчет амплитуды Боде и данных фазы системы с непрерывным временем.
freqresp ([w, n])	Рассчитайте частотную характеристику системы с непрерывным временем.
импульс ([X0, T, N])	Возвращает импульсную характеристику системы с непрерывным временем. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника