Физика 9 кл. Явление самоиндукции

Подробности

Просмотров: 240

 

1. Какое явление изучалось на опыте?

В опыте изучается явление самоиндукции.
Рассматривается частный случай электромагнитной индукции, т.е. возникновение индукционного тока в катушке при изменении силы тока в ней.

2. Как объясняются наблюдаемые явления в опыте по самоиндукции?

При замыкании цепи:

Лампа Л1 загорится сразу, а Л2 — с опозданием.
Почему с опозданием?
При замыкании цепи все токи цепи начинают расти.
Поэтому увеличиваются индукции магнитных полей, создаваемых каждым током,
Увеличиваются и магнитные потоки, пронизывающие витки реостата и катушки.
Проходящие сквозь реостат и катушку изменяющиеся магнитные потоки создаются благодаря изменению токов в этих устройствах.
Согласно явлению электромагнитной индукции, в реостате и в катушке возникают индукционные токи.

Эти индукционные токи препятствующие увеличению токов, созданных источником тока..
В катушке индукционный ток будет значительно больше, чем в реостате, т.к. катушка имеет большее число витков и сердечник (обладает большей индуктивностью), чем реостат.
Чем больше сила индукционного тока, тем большее противодействие он оказывает изменению силы тока, созданного источником.
Ток в ветви с катушкой возрастает медленнее чем в ветви с реостатом.
В результате лампа Л2 загорается с опозданием.

При размыкании цепи:

При замыкании цепи загорится только лампа Л2.
Лампа Лн не включается, т.к. напряжение для ее зажигания требуется больше, чем дает источник тока.

Разомкнем цепь — Л2 гаснет, зато неоновая Лн дает яркую вспышку.
Уменьшение тока при размыкании цепи создает мощный индукционный ток, противодействующий уменьшению тока в катушке.
При этом напряжение на катушке становится больше напряжения источника и достаточным для зажигания Лн.

3. Что называется индуктивностью? Единицы измерения индуктивности?

Индуктивность (иначе коэффициент самоиндукции) — это физическая величина, введенная для оценивания способности катушки противодействовать изменению силы тока в ней.

Индуктивность обозначается буквой L.

Индуктивность катушки зависит от ее формы, размеров, числа витков и наличия или отсутствия сердечника.

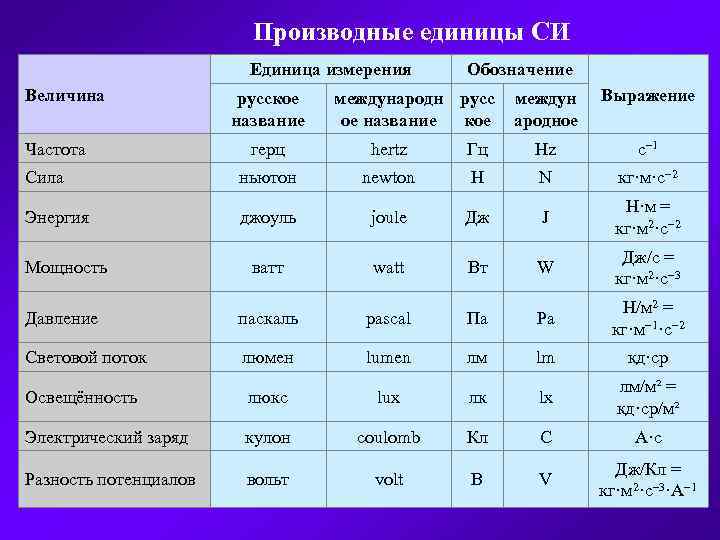
Единицей индуктивности в СИ является 1 Генри (1 Гн).

4. В чем заключается явление самоиндукции?

Явление самоиндукции заключается в возникновении индукционного тока в катушке при изменении силы тока в ней.

При этом возникающий индукционный ток называется током самоиндукции.

5. Может ли возникнуть ток самоиндукции в прямом проводнике с током? Если нет, то объясните почему; если да, то при каком условии.

Ток самоиндукции возникает не только в катушках, но и в любых других проводниках, если сила тока изменяется.

Но, в катушках с небольшим числом витков, и не имеющих сердечника, и тем более в прямых проводниках (т. е. в элементах цепи, обладающих малой индуктивностью) ток самоиндукции обычно невелик и не оказывает практического влияния на процессы в электрической цепи.

6. Что такое энергия магнитного поля тока? Как она возникает?

Магнитное поле тока в катушке обладает энергией.
Доказательство этому — появление мощного индукционного тока при размыкании цепи.

За счет уменьшения энергии магнитного поля совершается работа по созданию индукционного тока.

Накапливается энергия магнитного поля тока при замыкании цепи.
При этом за счет энергии источника тока совершается работа по преодолению тока самоиндукции, который препятствует увеличению тока в цепи и его магнитного поля.

7. Как рассчитать энергию магнитного поля тока?

Энергия магнитного поля тока определяется по формуле:

где
Е — энергия магнитного поля тока (Дж),
L — индуктивность проводника (Гн),
i — сила тока в этом проводнике (А).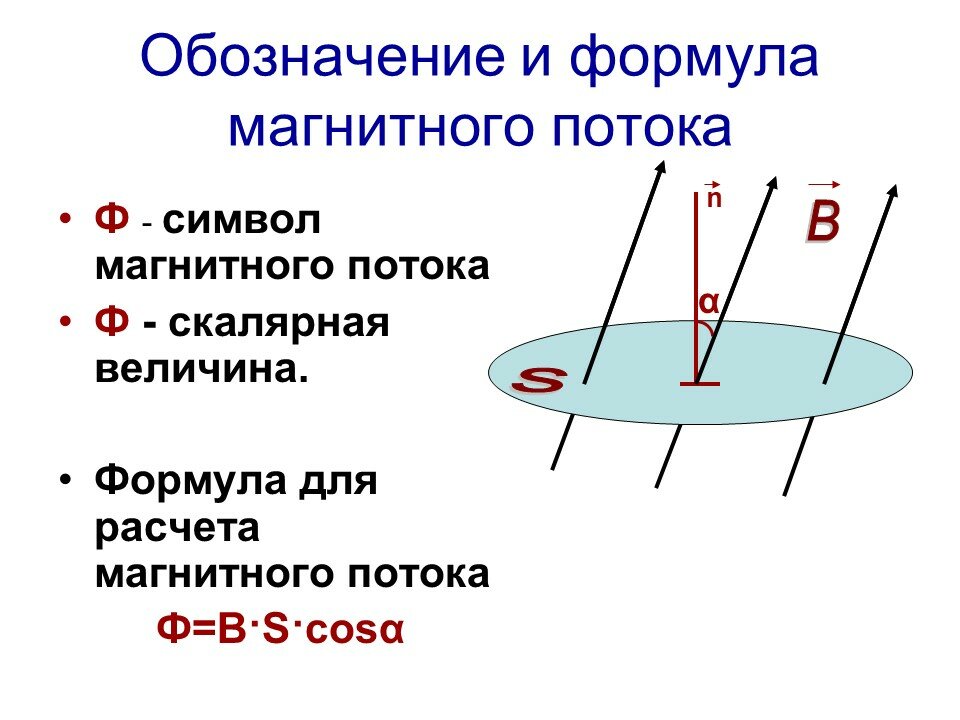

8. За счет уменьшения какой энергии совершалась работа по созданию индукционного тока при размыкании цепи?

Работа по созданию индукционного тока при размыкании цепи совершается за счет энергии магнитного поля катушки.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

Расчет катушек индуктивности в 3D с помощью COMSOL Multiphysics

При проектировании индукционных устройств важно учитывать различные электродинамические эффекты. Модуль AC/DC пакета COMSOL Multiphysics предоставляет все необходимые инструменты для эффективного и простого моделирования и проектирования катушек индуктивности, а также для расчёта их сосредоточенных характеристик в соответствии с заданными требованиями.

Базовые принципы работы катушки индуктивности

Простейшая катушка индуктивности — это электрический провод (обмотка или катушка), намотанный вокруг магнитного материала (магнитопровода). Принцип действия катушки основывается на принципе индуктивности, вокруг устройства наводится магнитное поле, которое препятствует изменению тока, текущего по проводнику.

Простейшая катушка индуктивности, состоящая из медной обмотки и железного сердечника. Красными стрелками показано направление тока, а синими — магнитное поле вокруг сердечника. Изменение тока приводит к изменению магнитного потока через обмотку, что создаёт разность потенциалов в обмотке, которая препятствует изменению тока.

Индуктивность — это параметр, который обозначается буквой L и показывает, в какой степени происходит сопротивление протеканию тока, он является ключевой характеристикой идеального индуктора. К сожалению, в нашем мире нет идеальных вещей и в реальных катушках индуктивности наблюдаются резистивные эффекты, которые больше проявляются на низких частотах и характеризуются активным сопротивлением (R), и ёмкостные эффекты, которые наблюдаются на высоких частотах и характеризуются ёмкостью (C), приводащие в т.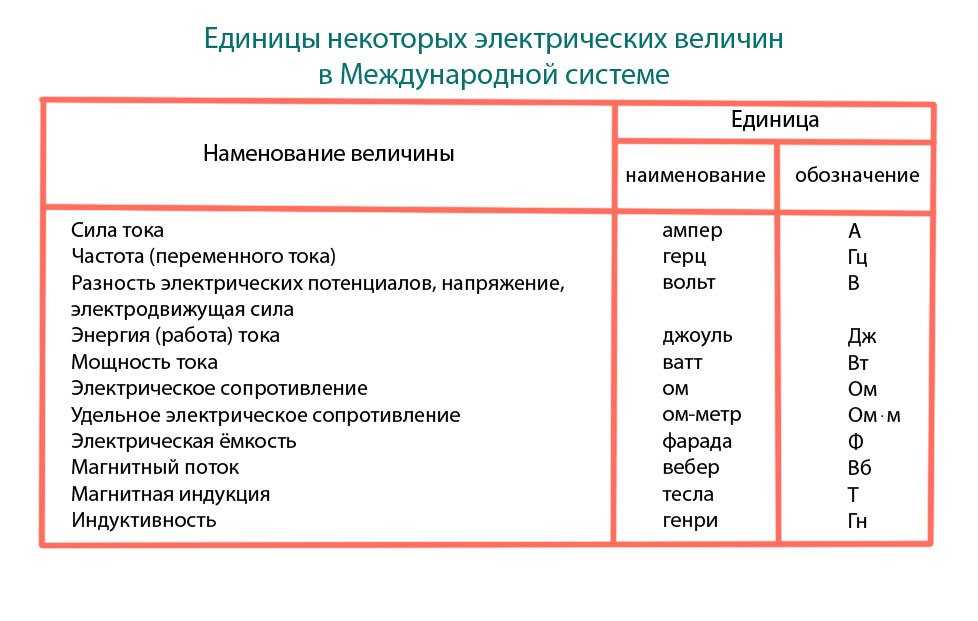 ч. авторезонансным процессам. На самом деле, принцип действия катушки индуктивности можно понять, рассмотрев простейшую RLC-цепь.

Эквивалентная схема катушки индуктивности.

С помощью набора пассивных элементов, можно собрать схему замещения, которая будет полностью соответствовать и описывать свойства индуктивности в различных приложениях. К примеру, если через катушку индуктивности протекает переменный ток, то она является низкочастотным фильтром, а последовательно соединённая с конденсатором – резонансным или полосовым фильтром. Катушки индуктивности играют очень важную роль в современном мире и повседневной жизни. Они используются в различных импульсных источниках питания и согласующих схемах, подключаемых к радиочастотным антеннам. Умный светофор, который загорается зелёным при вашем приближении, может быть индуктивным датчиком, который упрощает вашу жизнь в пути.

Оптимизация катушки индуктивности

Если в вашем устройстве присутствует катушка индуктивности, то важно знать некоторые её характеристики, чтобы полностью понимать, как работает устройство в целом. Ключевыми параметрами являются – индуктивность, активное сопротивление, электрическая ёмкость, резонансная частота и добротность (Q-factor), то есть ширина области резонанса. Эти параметры определяют частоту среза или полосу пропускания фильтра, либо просто реактивное сопротивление согласующей схемы.

Другой потенциально важной задачей при использовании катушек индуктивности является учет электромагнитных помех (ЭМП) или электромагнитной совместимости (ЭМС). Вокруг катушек индуктивности создаётся магнитное поле. При проектировании необходимо точно знать, насколько оно будет влиять на другие компоненты и близлежащие устройства. Это особенно актуально при нынешней миниатюризации всех устройств.

На данный момент существуют только грубые аналитические и эмпирические формулы, описывающие эти RLC параметры. С их помощью нельзя точно спроектировать современное устройство. Аналитические формулы в основном пригодны только для расчёта элементарных трёхмерных форм, например, куба, цилиндра, спирали и тора. Однако с помощью них невозможно рассчитать форму и поведение магнитного поля вокруг индуктивного устройства для ЭМП/ЭМС (EMI/EMC) исследований.

Дополнительно, часто требуется изготовление магнитопровода из нелинейного материала для увеличения индуктивности и ограничения окружающего магнитного поля. Это очевидно еще больше усложняет расчёты и приводит к очередной аналитической или эмпирической аппроксимации, что негативно сказывается на результате. Для получения точных рабочих характеристик трёхмерного индукционного устройства, численное моделирование является более надёжным и корректным решением.

3D-моделирование катушки индуктивности в COMSOL Multiphysics

COMSOL Multiphysics предлагает пользователю все необходимые инструменты для получения полных рабочих характеристик катушки индуктивности. Давайте рассмотрим данный функционал программы на учебном примере Modeling of a 3D Inductor (Моделирование катушки индуктивности в 3D). Он доступен в Application Gallery (Галерее моделей и приложений) для модуля AC/DC. Он как раз служит для наглядной иллюстрации процесса проектирования катушки индуктивности и расчета ее рабочих характеристик.

Геометрия катушки индуктивности для конечно-элементной модели.

В реальных устройствах протекающий через катушку ток можно задавать разными способами. Например, приложением напряжения, тока или мощности. Это может быть либо постоянная, либо периодическая величина, или какая-нибудь сложная функция, зависящая от времени. В нашем примере для задания тока используются условия Coil с опцией Single Turn (Одиночный проводник) и Lumped Port (Сосредоточенный порт) для низких и высоких частот соответственно. Таким образом, вы можете управлять катушками.

На видео продемонстрирована последовательность шагов по моделированию трёхмерной катушки индуктивности в COMSOL Multiphysics.

COMSOL Multiphysics позволяет легко добавлять в модель электрические сосредоточенные компоненты и цепи, которые можно как создать в самой программе, так и импортировать, как список SPICE. Благодаря мультифизическим связкам можно подключать данные цепи к распределенным устройствам, котороме моделируются методом конечных элементов. Всё это можно делать с помощью встроенных функций взаимосвязи. К примеру, вы можете подключить вашу катушки индуктивности к цепи управления, приложив минимум усилий. Программа сама находит те части, которые вы можете связать, и предлагает вам выбрать нужные из выпадающего списка.

При выборе нужной опции из выпадающего списка терминал катушки индуктивности (показан синим цветом) автоматически связывается с электрической цепью.

На высоких частотах (на которых может работать ваша катушка индуктивности) в проводниках с током в следствие скин-эффекта ток вытесняется к поверхности. В данном примере мы можем учесть данный эффект с помощью использования граничного условия Impedance boundary condition (Импедансное граничное условие). Решение задачи растекания тока в тонких слоях — это очень ресурсоёмкая задача. Но переходя к упрощенному описанию проводника с помощью граничного условия мы упрощаем данную задачу и значительно экономим время расчёта.

На рисунке изображён график распределения плотности тока (Am^-2) в катушке на высокой частоте. Обратите внимание, что учитывается неравномерное протекание тока.

Добротность катушки индуктивности во многом зависит от свойств материала магнитопровода, в частности от потерь. Возможности COMSOL Multiphysics позволяют отредактировать любой материал из библиотеки, чтобы добавить или заменить необходимые свойства. Любые потери на вихревые токи автоматически учитываются в расчёте. В данном примере диэлектрические потери в магнитопроводе задаются пользователем с помощью добавления мнимой части к диэлектрической постоянной, ε_r. Таким же образом вы можете добавить магнитные потери в вашу модель, задав комплексное значение магнитной проницаемости μ_r.

Постобработка и анализ результатов расчёта модели индуктора

Если вам необходимо произвести впечатление на клиентов или завоевать их доверие, буквально в несколько кликов вы можете создать красивейшие графики, благодаря встроенным возможностям постобработки результатов в COMSOL Multiphysics. Программное обеспечение автоматически вычисляет и предоставляет вам доступ к переменным, которые в полной мере характеризуют работу вашей спроектированной катушки индуктивности — магнитное поле, токи и величина потерь. В учебном примере трёхмерной катушки индуктивности продемонстрировано, как настроить детализированной изоражение ниже.

Чем тоньше магнитопровод, тем больше в нём магнитная индукция на поверхности (Тл). В катушке также показано распределение потенциала (В).

Для лучшей наглядности вы можете добавить другие типы трёхмерных графиков, например, Streamline (Силовые линии) или Arrow (Векторная диаграмма).

Магнитная индукция на поверхности магнитопровода (Тл). Силовые линии плотности тока (Aмм^-2) в катушке показывают более высокую плотность в закруглённых частях. Красными стрелками показано магнитное поле.

Наконец, для получения полных характеристик катушки индуктивности вам необходимо определиеть значения импеданса и резонансных частот. Одна из переменных в COMSOL Multiphysics автоматически рассчитывает точный импеданс для каждой частоты. Таким образом, графики данных величин можно построить очень легко. Используя встроенные операторы real (действительная часть) и imag (мнимая часть), можно строить графики активного (резистивного) и реактивного (индуктивного/ёмкостного) импеданса, на которых легко увидеть резонанс.

Действительная (слева) и мнимая (справа) части импеданса (Z) показывают резонанс и переключение между индуктивным и ёмкостным поведением.

На графике мнимой части можно также заметить, что после прохождения через резонансную частоту знак изменяется с положительного на отрицательный. Это значит, что на высоких частотах устройство больше проявляет ёмкостный характер, чем индуктивный, что вполне ожидаемо.

Учёт термических эффекто в модели катушки индуктивности

COMSOL Multiphysics специально проектировался, чтобы пользователям было легко связывать различные физические интерфейсы в одной модели. Как раз поэтому второе слово в названии — «multiphysics». Дальнейшим расширением модели может являться добавление и учет электромагнитного нагрева. Протекающие в катушке токи, вихревые токи и диэлектрические/магнитные потери в магнитопроводе, все они приводят к выделению тепла, которое распространяется по проводящим металлическим компонентам с высокой теплопроводностью и, отчасти, нагревает окружающие устройства и платы. Используя физический интерфейс Induction Heating (Индукционный нагрев), вы запросто сможете рассчитать интенсивность теплопередачи и распределение температур в индукционных устройствах.

Узнайте больше о моделировании индукционных устройств в COMSOL Multiphysics

• Ознакомьтесь с другими учебными моделями катушек индуктивности в галерее моделей и приложений:
  • Моделирование спиральной катушки индуктивности
  • Интегрированный индуктор квадратной формы в виде спирали
• Посмотрите, как используют COMSOL Multiphysics для проектирования индукционных устройств:
  • Упрощая переключение с помощью индукционной передачи энергии
  • Трансформатор тока, разработанный на основе конечно-элементного анализа и моделирования электрических цепей

23.

12: Индуктивность — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2715

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Рассчитать индуктивность катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Катушки индуктивности

Индукция — это процесс, при котором ЭДС индуцируется за счет изменения магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется индуктивностью.

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, когда первичная катушка передает энергию вторичной обмотке в трансформаторе. См. рисунок, где простые катушки наводят друг в друге ЭДС.

Рисунок \(\PageIndex{1}\): Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что «\(E_2\) индуцируется» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока \(\Delta I/\delta t\) как причине индукции. Изменение тока \(I_1\) в одном устройстве, катушка 1 на рисунке, индуцирует \(I_2\) в другом. Мы выражаем это в форме уравнения как

\[ЭДС_2 = — M\dfrac{\Delta I_1}{\Delta t},\], где \(M\) определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность \(M\), тем эффективнее связь. Например, катушки на рисунке имеют небольшой \(M\) по сравнению с катушками трансформатора в [ссылка]. Единицами для \(M\) являются (V\cdot s)/A = \Omega \cdot s\), который называется генри (H) в честь Джозефа Генри. То есть \(1 \, H = 1 \, \Omega \cdot s\).

Природа здесь симметрична. Если мы изменим ток \(I_2\) в катушке 2, мы индуцируем \(ЭДС_1\) в катушке 1, которая определяется как

\[ЭДС_1 = -M \dfrac{\Delta I_2}{\Delta t} ,\] где \(М\) то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью \(M\).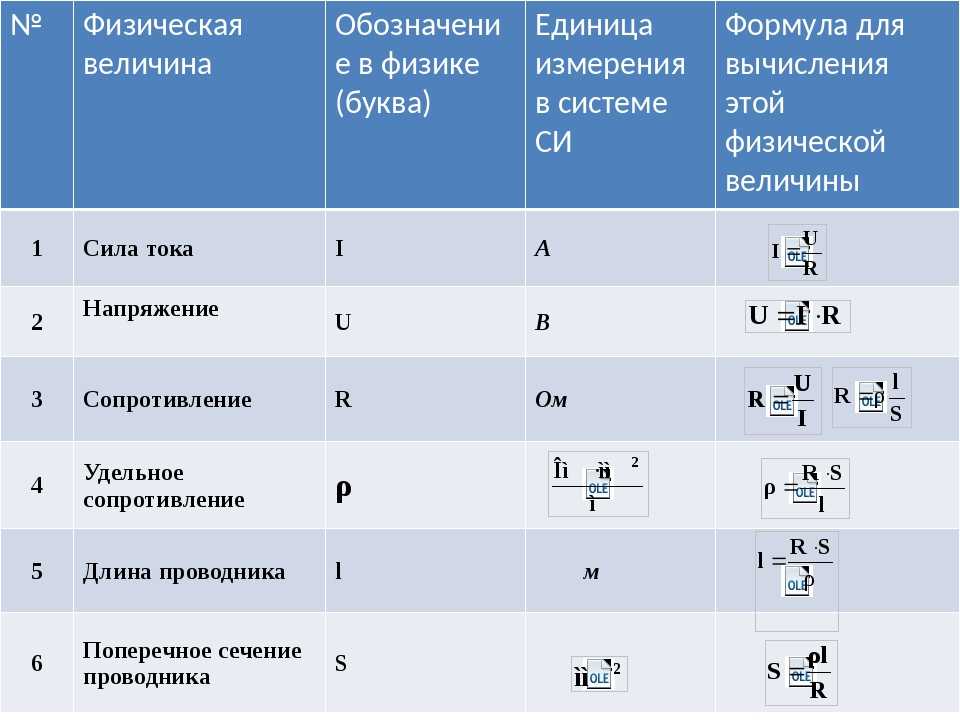

Большая взаимная индуктивность \(M\) может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность \(M\) состоит в том, чтобы встречно обмотать катушки, чтобы нейтрализовать создаваемое магнитное поле. (См. рис.)

Рисунок \(\PageIndex{2}\): Нагревательные спирали электрической сушилки для белья могут быть намотаны в противоположных направлениях, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока \(\Delta I\) через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

\[ЭДС = -L \dfrac{\Delta I}{\Delta t},\] где \(L\) — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначается символом на рисунке.

Рисунок \(\PageIndex{3}\):

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность \(L\) устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большое \(L\) и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться малого \(L\), например, за счет встречной обмотки катушек, как показано на рисунке.

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с \(L = 1,0 \, H\), через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная выражением \(ЭДС = -L(\Delta I/\Delta t)\), будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться по формуле \). Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. ) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис.)

Рисунок \(\PageIndex{4}\): Благодаря быстрому переключению катушки индуктивности батареи на 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать \(L\) для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность \(L\) обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как \(ЭДС = -N(\Delta \Phi /\Delta t)\) и, по определению самоиндукции, как \(ЭДС = — L(\Дельта I/\Дельта t)\). Приравнивая эти выходы

\[ЭДС = -N\dfrac{\Delta \Phi}{\Delta t} = -L \dfrac{\Delta I}{\Delta t}.\]

Решение для \(L\) дает \ [L = N\dfrac{\Delta \Phi}{\Delta I}.\]

Это уравнение для собственной индуктивности \(L\) устройства всегда справедливо. Это означает, что собственная индуктивность \(L\) зависит от того, насколько эффективно ток создает поток; чем эффективнее, тем больше \(\Delta \phi /\Delta I\).

Воспользуемся последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь \(A\) соленоида фиксирована, изменение потока равно \(\Delta \Phi = \Delta (BA) = A\Delta B\). Чтобы найти \(\Delta B\), заметим, что магнитное поле соленоида определяется выражением \(B = \mu_0 n I = \mu_0 \frac{\Delta I}{l}\). 2 A}{l}\), поскольку все величины в уравнении, кроме \(L\), известны. 92)}{0,100 \, м}\]

\[= 0,632 \, мГн.\]

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных применений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была найдена на «подрывнике в нижнем белье».) См. рисунок.

Рисунок \(\PageIndex{5}\): Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Энергия, запасенная в катушке индуктивности

Из закона Ленца мы знаем, что индуктивность сопротивляется изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что энергия 92 = 0,284 \, Дж.\]

Обсуждение

Этого количества энергии, безусловно, достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

Резюме

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока \(\Delta I_1/\Delta t\) в одном индуцирует \(ЭДС_2\) во втором: \[ЭДС_2 = — M\dfrac{\Delta I_1}{\Delta t},\] где \(M\) определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.
• Симметрично изменение тока \(\Delta I_2/\Delta t\) через второе устройство индуцирует \(ЭДС_2\) в первом: \[ЭДС_1 = -M\dfrac{\Delta I_2}{\Delta t },\] где \(M\) — та же взаимная индуктивность, что и в обратном процессе.
• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Устройство называется катушкой индуктивности, а ЭДС, индуцируемая в нем изменением тока через него, равна \[ЭДС = -L\dfrac{\Delta I}{\Delta t},\], где \(L\) собственная индуктивность катушки индуктивности, а \(\Delta I/\Delta t\) — скорость изменения тока через нее. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца. 92.\]

Глоссарий

индуктивность

свойство устройства, описывающее, насколько эффективно оно создает ЭДС в другом устройстве

взаимная индуктивность

насколько эффективно пара устройств индуцирует ЭДС друг в друге

Генри

единица индуктивности; \(1 \, H = 1 \Омега \cdot s\)

самоиндукция 92\)

Авторы

Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрихс (Государственный университет Нью-Йорка, Колледж в Освего) с соавторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет) ). Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4. 0).

---

Эта страница под названием 23.12: Inductance распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. энергия, запасенная в катушке индуктивности
   2. Генри
   3. индуктивность
   4. индуктор
   5. взаимная индуктивность
   6. самоиндукция
   7. источник@https://openstax. org/details/books/college-physics

Понимать понятие индуктивности

Когда электрический ток проходит через элемент, он представляет собой индуктор. Он описывается как пассивный электрический элемент с двумя клеммами, который накапливает энергию в виде магнитного поля. Он также известен как катушка, дроссель или реактор. Индуктивность относится к магнитному полю, аналогичному скорости изменения магнитного поля. Индуктивность обозначается буквой L, а ее единицей в системе СИ является Генри. Он состоит из взаимной индуктивности и самоиндукции.

Закон Фарадея об электромагнитной индукции утверждает, что в цепи возникает электродвижущая сила за счет изменения магнитного потока. Индуктивность относится к электродвижущей силе, индуцируемой для противодействия изменению тока в определенное время.

Факторы, влияющие на индуктивность

На индуктивность влияют несколько факторов:

1. Форма сердечника
2. Материал сердечника
3. Сумма витков провода в индукторе

Закон электромагнитной индукции Фарадея

Когда электрический ток, протекающий через индуктор или катушку, изменяется, изменяющееся во времени магнитное поле создает в нем ЭДС (электродвижущую силу) или напряжение в соответствии с законом электромагнитной индукции Фарадея. Скорость изменения электрического тока, протекающего через индуктор, точно пропорциональна наведенному напряжению или ЭДС на индукторе.

Самоиндукция  

Магнитное поле индуцируется, когда ток течет через индуктор. Он подключается к окружающим цепям через концентрические петли, а также соединяется с цепью, от которой он питается.

Результатом самоиндукции является то, что при изменении тока в разных витках катушки индуцируется напряжение.

Когда одна катушка подвергается влиянию индуктивности, это называется самоиндукцией. Эффект известен как самоиндукция, потому что он возникает в том же проводе или катушке, которая генерирует магнитное поле.

Самоиндукция вызывает электродвижущую силу в том же проводе или катушке, что приводит к тому, что известно как противо-ЭДС.

Взаимная индуктивность 

Взаимная индуктивность двух катушек определяется как ЭДС индукции в одной катушке, противодействующая изменению тока и напряжения в другой катушке. Две катушки магнитно связаны из-за сдвига магнитного потока. Магнитное поле одной катушки взаимодействует с полем другой катушки и обозначается буквой М.

Из-за сдвига магнитного потока ток, протекающий в одной катушке, вызывает повышение напряжения в другой катушке. Взаимная индуктивность и изменение тока точно пропорциональны величине магнитного потока, связанного с двумя катушками.

Если ток в одной катушке колеблется во времени, ЭДС будет индуцировать в другой катушке в соответствии со свойством индуктивности.

Разница между взаимной индуктивностью и собственной индуктивностью

 

Индуктивность	Взаимная индуктивность
90	Взаимная индуктивность относится к свойствам пары катушек.
Противодействует увеличению или уменьшению тока в катушке при повышении основного тока в катушке.	Препятствует спаду тока в катушке при снижении основного тока в катушке. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника