опишите свойства сопротивлений r_u и r_i. Что называется статическим сопротивлением и что динамическим? Чем характеризуется степень нелинейности сопротивлений?
Существенное
отличие нелинейных сопротивлений от
линейных в том, что значение сопротивления
такой цепи зависит от величины протекающего
по ней тока или приложенного напряжения.
Нелинейные сопротивления различаются
своей вольтамперной характеристикой.
Нелинейные сопротивления вида Ru,обладают
тем свойством, что при изменении
протекающего через них тока в заданных
пределах напряжение на них изменяется
весьма незначительно. Нелинейные же
сопротивления вида Ri, наоборот,
обуславливают весьма незначительные
изменения протекающего через него тока
при изменении напряжения на нем в
заданных пределах. В отличие от линейного
активного сопротивления, нелинейное
активное сопротивление имеет различные
значения для постоянного тока и изменений
его.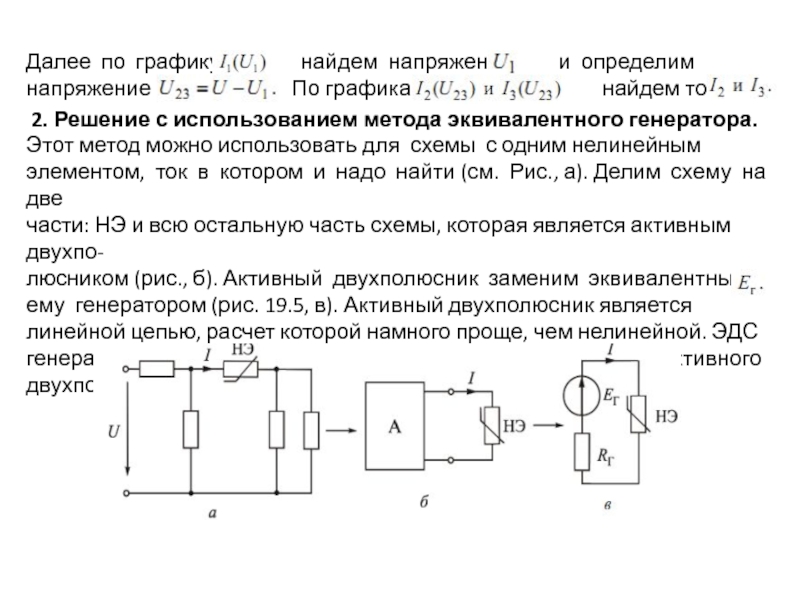 Сопротивление постоянному току
называется статическим Rст=U/I . Сопротивление
изменению постоянного тока называют
динамическим сопротивлением Rдин=delta
U/delta I.
Сопротивление постоянному току
называется статическим Rст=U/I . Сопротивление
изменению постоянного тока называют
динамическим сопротивлением Rдин=delta
U/delta I.
Статическое сопротивление определяется тангенсом угла между осью тока и прямой, проходящей через начало координат и рабочую точку вольтамперной характеристики. Динамическое сопротивление определяется тангенсом угла между осью тока и касательной, проведенной через ту же точку. У сопротивлений вида Ri:Rст<Rдин, а у сопротивлений вида Ru наоборот Rдин<Rст. Степень нелинейности характеризуется добротностью ( или качеством) нелинейного сопротивления Q. Этот параметр подсчитывается так: для лампы :Q=Rдин/Rст, для диода Rст/Rдин и показывает во сколько раз одно сопротивление в одной и той же рабочей точке на вольтамперной характеристике больше другого.
8. Ферромагнетики. Что вы понимаете под основной кривой намагничивания? Под остаточной магнитной индукции?
Ферромагнетики
– это вещества, обладающие самопроизвольной
намагниченностью, которая сильно
изменяется под влиянием внешних
воздействий – магнитного поля, деформации,
температуры.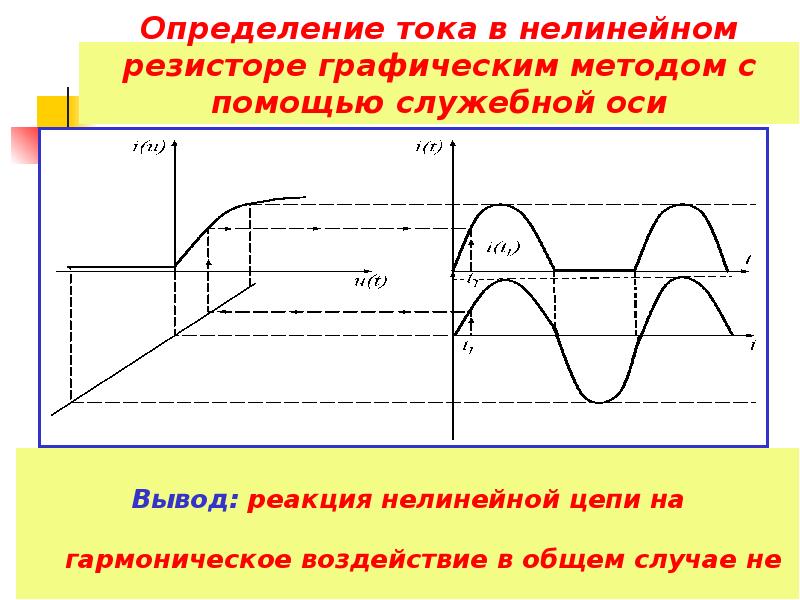 Ферромагнетики, в отличие
от слабо магнитных диа- и парамагнетиков,
являются сильно магнитными веществами:
внутреннее магнитное поле в них может
в сотни раз превосходить внешнее поле.
Ферромагнетики, в отличие
от слабо магнитных диа- и парамагнетиков,
являются сильно магнитными веществами:
внутреннее магнитное поле в них может
в сотни раз превосходить внешнее поле.
Кривая, представляющая собой геометрическое место вершин симметричных петель гистерезиса, называется основной кривой намагничивания
9. Ферромагнетики. В чем заключается явление магнитного гистерезиса? Что характеризует площадь петли гистерезиса?
Ферромагнетики — это вещества, обладающие спонтанной намагниченностью, то есть они сохраняют намагниченность при отсутствии внешнего магнитного поля. К ферромагнетикам относятся, например, кристаллы железа, никеля, кобальта.
Магнитный
гистерезис — явление зависимости
вектора намагничивания и вектора
напряженности магнитного поля в веществе
не только от приложенного внешнего
поля, но и от предыстории данного образца.
Магнитный гистерезис обычно проявляется
в ферромагнетиках — Fe, Co, Ni и сплавах на
их основе. Именно магнитным гистерезисом
объясняется существование постоянных
магнитов.
Петля гистерезиса это кривая изменение магнитного момента образца под действием периодического изменения напряжённости поля. Слово гистерезис обозначает запаздывание или отставание. При воздействии магнитного поля на ферромагнетики их магнитный момент меняется не сразу, а с некоторой задержкой.
магнитный момент М
напряжённость Н
Какое сопротивление называется линейным — MOREREMONTA
Все резисторы делятся на линейные и нелинейные. Линейными называются резисторы, сопротивления которых не зависят (т. е. не изменяются) от значения протекающего тока или приложенного напряжения. В аппаратуре связи и других электронных устройствах (радиоприемниках, транзисторах, магнитофонах и т. п.) широко используются малогабаритные линейные резисторы, например типа МЛТ (металлизированные, лакированные, термостойкие). Сопротивление этих резисторов остается неизменным при изменении приложенных к ним напряжений или протекающих через них токов и поэтому данные резисторы являются линейными.
Нелинейными называются резисторы, сопротивление которых изменяется в зависимости от значения, приложенного напряжения или протекающего тока. Так, сопротивление осветительной лампы накаливания при отсутствии тока в 10—15 раз меньше, чем при нормальном горении. К нелинейным элементам относятся многие полупроводниковые приборы.
Экспериментально было установлено, что в линейных резистивных цепях мгновенные напряжения и токи пропорциональны друг другу . Это означает, что при изменении напряжения в некоторое число раз ток в цепи изменяется в такое же число раз и, следовательно, форма тока, протекающего в цепи, повторяет форму напряжения, приложенного к этой цепи. Например, если к резистивной цепи приложено напряжение треугольной формы, то ток будет также треугольной формы, постоянное во времени напряжение вызывает постоянный во времени ток и т. д.
Таким образом, в линейных резистивных цепях форма тока повторяет форму напряжения, вызвавшего этот ток .
Могут возникнуть вопросы: «А разве не очевидно, что ток и напряжение имеют одну и ту же форму? Разве такое само собой не разумеется? Почему это обстоятельство следует оговаривать особо?».
В цепях с иными элементами, например с конденсаторами, форма тока, в общем случае, всегда отличается от формы приложенного напряжения, поэтому совпадение форм напряжения и тока — скорее исключение, нежели правило.
Следует запомнить, что линейная резистивная цепь — это частный случай, при котором формы тока и напряжения идентичны и наличие такой идентичности оказывается сравнительно редко и вовсе не является само собой разумеющейся.
Кроме того, экспериментально было установлено, что в линейной резистивной цепи ток обратно пропорционален сопротивлению, т. е. при увеличении сопротивления в некоторое число раз (при неизменном напряжении) ток уменьшается в такое же число раз. Связь между мгновенными токами i, мгновенными напряжениями и и сопротивлением цепи R выражается формулой
Данное соотношение называется законом Ома для участка цепи.
где Im и Um — максимальные значения тока и напряжения соответственно; Ip и Up — размах тока и напряжения.
В частном случае напряжения и токи могут не меняться во времени (режим постоянного тока), тогда мгновенные значения напряжения становятся величинами постоянными и их обозначают не и (т. е. малой буквой, как всякую переменную величину), a U (большая буква, величина постоянная), в этом частном случае закон Ома записывается так:
Таким образом, в общем случае при напряжениях, а следовательно и токах, произвольной формы следует использовать основной вид формулы, выражающей закон Ома:
При напряжениях и токах, неизменных во времени
Важное правило: закон Ома для мгновенных значений справедлив только в резистивных цепях.
Резистивные элементы необратимо превращают электрическую энергию в тепловую, но не накапливают какую-либо энергию, поэтому их называют неэнергоемкими. Из сказанного следует, что закон Ома для мгновенных значений справедлив только в цепях с неэнергоемкими элементами.
Из сказанного следует, что закон Ома для мгновенных значений справедлив только в цепях с неэнергоемкими элементами.
Поделитесь с друзьями:
Школа для электрика в Facebook:
Если связь между током и напряжение на сопротивлении линейна, т.е. может быть описана функцией вида y=kx+b, где k и b — постоянные величины, то такой элемент называется линейным.
Если нарисовать вольтамперную характеристику линейного сопротивления, то это будет прямая линия.
Идеальные резисторы не бывают линейными. У них всегда нелинейная вольт-амперная характеристика. Даже если вы покупаете сопротивление с линейной ВАХ, ее ВАХ на самом деле нелинейна в пределах погрешности, указанной на резисторе.
Внешняя цепь, нагрузка или приёмник электрической энергии — часть электрической цепи, которая подключена к зажимам источника. В нагрузке энергия электрического поля преобразуется в другие виды энергии (тепловую, звуковую, механическую и др.). Приёмники энергии являются пассивными элементами.
Пассивные элементы – это сопротивление, ёмкость, индуктивность.
В теории электрических цепей рассматриваются пассивные элементы: сопротивление – это идеальный элемент цепи, характеризующий потери энергии на нагрев, механическую работу или излучение электромагнитной энергии.
Единицы измерения сопротивления – Ом
проводимость – величина, обратная сопротивлению.
Единицы измерения проводимости – Сименс
Мощность, выделяемая на сопротивлении, всегда положительна. Мгновенная мощность равна:
Единицы измерения мощности – Ватт
Сопротивления делятся на: линейные и нелинейные.
Линейное сопротивление – сопротивление, которое не зависит от величины, направления тока и величины напряжения. Оно имеет прямую пропорциональную зависимость между напряжением и током, выражающееся законом Ома.
Рисунок 2. 2 Условное обозначение сопротивления
2 Условное обозначение сопротивления
Индуктивность – идеализированный элемент электрической цепи, способный накапливать энергию магнитного поля, причем накопление энергии электрического поля и преобразование её в другие виды энергии в нём не происходит. Связь между током и напряжением на зажимах индуктивности определяется из закона электромагнитной индукции: при изменении магнитного потока, пронизывающего витки катушки индуктивности, на её зажимах образуется ЭДС прямо пропорциональная скорости изменения потокосцепления и направленная таким образом, чтобы вызываемый ток препятствовал изменению магнитного потока.
Для катушки, состоящей из витков, справедливо равенство:
;
где – потокосцепление, т. е. суммарный магнитный поток, который сцеплен с витками. – магнитный поток одного витка.
Единица измерения магнитного потока и потокосцепления – Вебер (Вб).
Коэффициент пропорциональности между и называется индуктивностью, и, обозначается . Единицы измерения индуктивности – Генри . Из формулы получим выражение для напряжения на индуктивном элементе:
Единицы измерения индуктивности – Генри . Из формулы получим выражение для напряжения на индуктивном элементе:
Энергия, которая накапливается в индуктивном элементе, вычисляется по формуле:
Для постоянного тока , поэтому напряжение , т. е. индуктивность эквивалентна короткому замыканию. Физический аналог индуктивности – катушка индуктивности, эквивалентная схема которой изображена на рисунке 2.3.
Катушка индуктивности – устройство, основным свойством которого является индуктивность (кроме индуктивности , обладает сопротивлением потерь ).
Рисунок 2.3 Условное графическое обозначение катушки индуктивности
Ёмкость – идеализированный элемент электрической цепи, способный запасать энергию электрического поля. При этом накоплении энергии электрического поля преобразование электрической энергии в тепловую в нем не происходит. Свойства емкостного элемента обусловлены возможностью накопления в нем электрического заряда , пропорционального напряжению на элементе:
Коэффициент пропорциональности называется емкостью, измеряется в Фарадах .
Из формулы найдем связь между током и напряжением для линейной емкости :
Энергия, которая накапливается в линейной емкости, вычисляется по формуле:
В отличие от сопротивления идеальные реактивные элементы не рассеивают, а накапливают электрическую энергию и могут возвращать ее в цепь или источник. Мощность реактивных элементов , называется мгновенной реактивной мощностью и измеряется в вольт – амперах реактивных (Вар).
Для постоянного напряжения ток , т. е. емкость эквивалентна разрыву цепи (холостому ходу). Физический аналог емкости – конденсатор. Конденсатор — устройство, основным свойством которого является электрическая емкость; кроме емкости он обладает сопротивлением утечки
Рисунок 2.4 Условное графическое изображение конденсатора
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете.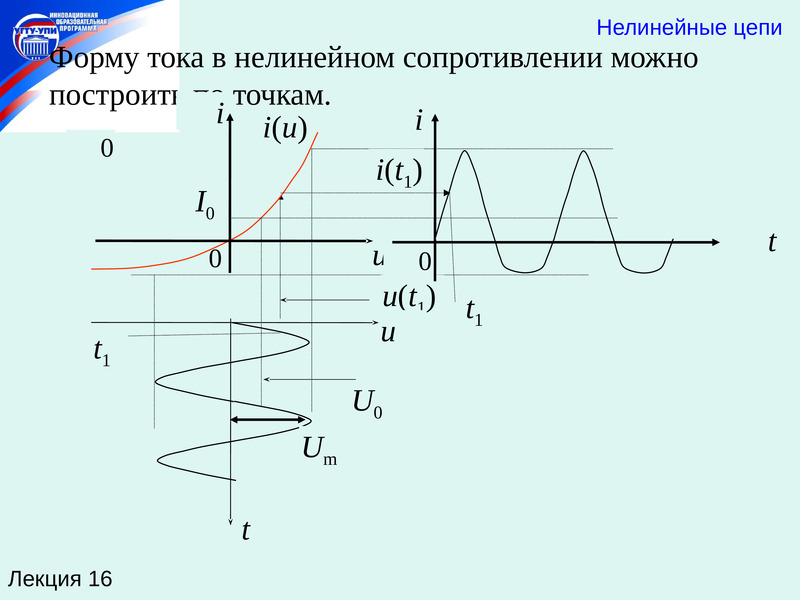 8460 — | 7349 — или читать все.
8460 — | 7349 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
4.1. Нелинейные электрические цепи основные понятия и определения
Цепь называют нелинейной, если хотя бы один из её элементов обладает нелинейной характеристикой.
Активные нелинейные сопротивления характеризуются вольтамперной характеристикой
(рис. 4.1).
Характеристики элементов могут быть симметричными и несимметричными. Они располагаются в первом и в третьем квадрантах. У нелинейных элементов их сопротивление зависит от напряжения r(u) или от тока, r(i).
Примером активного нелинейного сопротивления является полупроводниковый диод.
Его вольтамперная характеристика (ВАХ) несимметрична (рис. 4.2) и содержит рабочие (сплошная линия) и нерабочие зоны (штриховая линия). На электрических схемах диод изображается, как показано на рис. 4.3. Он относится к неуправляемым элементам.
Примером управляемого активного нелинейного сопротивления является транзистор (рис. 4.4). Током базы (Б) изменяют сопротивление между эмиттером (Э) и коллектором (К).
Другим примером управляемого активного нелинейного сопротивления является тиристор (рис. 4.5).
В нем с помощью управляющего электрода (УЭ) можно только уменьшить сопротивление между анодом и катодом Rak, а увеличить его нельзя. Это не полностью управляемое активное сопротивление.
Существуют и запираемые тиристоры (рис. 4.6). Запираемый тиристор (может увеличивать и уменьшать Rak).
Нелинейные индуктивные элементы характеризуются вебер-амперной характеристикой (рис. 4.7).
Потокосцепление связано с током следующей зависимостью: y = Li. Эта формула и определяет вебер-амперную характеристику (ВбАХ). Если индуктивность L = сonst, то характеристика – прямая (рис. 4.7, а, сплошная линия), но если в ее основе есть ферромагнетик, то это неуправляемая нелинейная индуктивность (рис. 4.7, б).
Эта формула и определяет вебер-амперную характеристику (ВбАХ). Если индуктивность L = сonst, то характеристика – прямая (рис. 4.7, а, сплошная линия), но если в ее основе есть ферромагнетик, то это неуправляемая нелинейная индуктивность (рис. 4.7, б).
Нелинейная индуктивность, зависящая от тока, может быть изображена на схемах в виде (рис. 4.8). Нелинейная индуктивность может быть управляемой (рис. 4.9). Постоянным током управления Iу можно изменять рабочий ток iр. Характеристика такой индуктивности при изменении Iу смещается (рис. 4.10).
С помощью нелинейных элементов в электрических цепях осуществляется ряд преобразований электромагнитной энергии. Основные из них: выпрямление переменного напряжения или тока; инвертирование постоянного напряжения или тока; усиление напряжений и токов; регулирование постоянных и переменных напряжений и токов; стабилизация напряжений и токов; преобразование частоты; модуляции и так далее.
Линейные и нелинейные резистивные сопротивления
Все резисторы делятся на линейные и нелинейные. Линейными
Линейными
называются резисторы, сопротивления которых не зависят (т. е. не
изменяются) от значения протекающего тока или приложенного напряжения. В
аппаратуре связи и других электронных устройствах (радиоприемниках,
транзисторах, магнитофонах и т. п.) широко используются малогабаритные
линейные резисторы, например типа МЛТ (металлизированные, лакированные,
термостойкие). Сопротивление этих резисторов остается неизменным …
Все резисторы делятся на линейные и нелинейные. Линейными называются резисторы, сопротивления которых не зависят (т. е. не изменяются) от значения протекающего тока или приложенного напряжения. В аппаратуре связи и других электронных устройствах (радиоприемниках, транзисторах, магнитофонах и т. п.) широко используются малогабаритные линейные резисторы, например типа МЛТ (металлизированные, лакированные, термостойкие). Сопротивление этих резисторов остается неизменным при изменении приложенных к ним напряжений или протекающих через них токов и поэтому данные резисторы являются линейными.
Нелинейными называются резисторы, сопротивление которых изменяется в зависимости от значения, приложенного напряжения или протекающего тока. Так, сопротивление осветительной лампы накаливания при отсутствии тока в 10—15 раз меньше, чем при нормальном горении. К нелинейным элементам относятся многие полупроводниковые приборы.
Экспериментально было установлено, что в линейных резистивных цепях мгновенные напряжения и токи пропорциональны друг другу. Это означает, что при изменении напряжения в некоторое число раз ток в цепи изменяется в такое же число раз и, следовательно, форма тока, протекающего в цепи, повторяет форму напряжения, приложенного к этой цепи. Например, если к резистивной цепи приложено напряжение треугольной формы, то ток будет также треугольной формы, постоянное во времени напряжение вызывает постоянный во времени ток и т. д.
Таким образом, в линейных резистивных цепях форма тока повторяет форму напряжения, вызвавшего этот ток.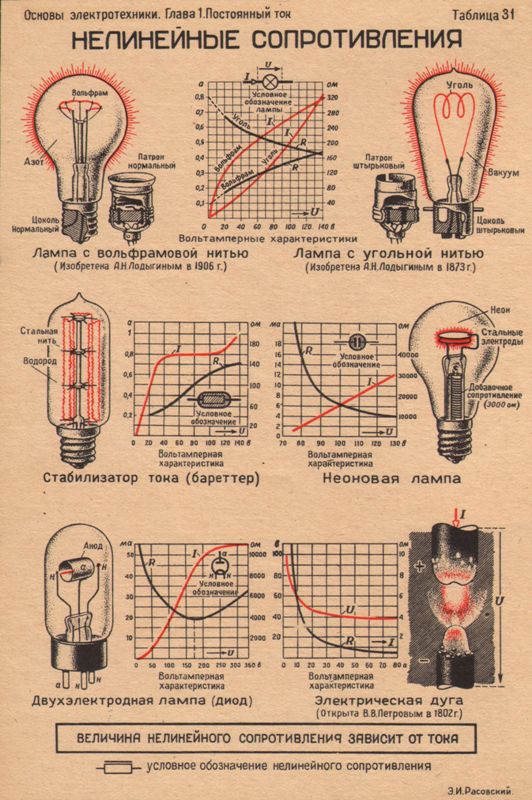
Могут возникнуть вопросы: «А разве не очевидно, что ток и напряжение имеют одну и ту же форму? Разве такое само собой не разумеется? Почему это обстоятельство следует оговаривать особо?». Ответим сразу на эти вопросы. Дело в том, что форма тока повторяет форму напряжения только в одном частном случае, именно в линейных резистивных цепях.
В цепях с иными элементами, например с конденсаторами, форма тока, в общем случае, всегда отличается от формы приложенного напряжения, поэтому совпадение форм напряжения и тока — скорее исключение, нежели правило.
Следует запомнить, что линейная резистивная цепь — это частный случай, при котором формы тока и напряжения идентичны и наличие такой идентичности оказывается сравнительно редко и вовсе не является само собой разумеющейся.
Кроме того, экспериментально было установлено, что в линейной резистивной цепи ток обратно пропорционален сопротивлению, т. е. при увеличении сопротивления в некоторое число раз (при неизменном напряжении) ток уменьшается в такое же число раз. Связь между мгновенными токами i, мгновенными напряжениями и и сопротивлением цепи R выражается формулой
Связь между мгновенными токами i, мгновенными напряжениями и и сопротивлением цепи R выражается формулой
Данное соотношение называется законом Ома для участка цепи. Поскольку наибольшие мгновенные значения называются максимальными, закон Ома может иметь вид
где Im и Um — максимальные значения тока и напряжения соответственно; Ip и Up — размах тока и напряжения.
В частном случае напряжения и токи могут не меняться во времени (режим постоянного тока), тогда мгновенные значения напряжения становятся величинами постоянными и их обозначают не и (т. е. малой буквой, как всякую переменную величину), a U (большая буква, величина постоянная), в этом частном случае закон Ома записывается так:
Таким образом, в общем случае при напряжениях, а следовательно и токах, произвольной формы следует использовать основной вид формулы, выражающей закон Ома:
или
При напряжениях и токах, неизменных во времени
или
Важное правило: закон Ома для мгновенных значений справедлив только в резистивных цепях.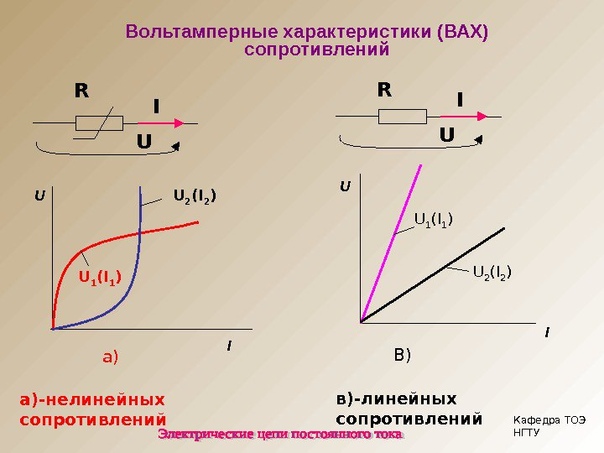
Резистивные элементы необратимо превращают электрическую энергию в тепловую, но не накапливают какую-либо энергию, поэтому их называют неэнергоемкими. Из сказанного следует, что закон Ома для мгновенных значений справедлив только в цепях с неэнергоемкими элементами.
10.12.2016 Без рубрики
Теория электрических цепей
Теория электрических цепей| Теория электрических цепей |
| ГЛАВА 10. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ В РЕЖИМЕ ПОСТОЯННОГО ТОКА |
Вопросы и задания для самопроверки
1. Какими уравнениями описываются нелинейные резистивные цепи, какими – нелинейные цепи, содержащие реактивные элементы?
2. Какие
значения может принимать дифференциальное сопротивление нелинейного элемента?
Какие
значения может принимать дифференциальное сопротивление нелинейного элемента?
3. Какой элемент цепи обладает одинаковыми статическим и дифференциальным сопротивлением?
4. Что называется рабочей точкой вольт-амперной характеристики нелинейного элемента?
5. Приведите пример многозначной вольт-амперной характеристики нелинейного элемента?
6. Объясните на примерах трехзначных характеристик N-типа и S-типа возможность получения неоднозначного решения задачи нахождения рабочей точки вольт-амперной характеристики резистивных нелинейных элементов?
7. В каком режиме (постоянного или переменного тока) могут быть сняты статические вольт-амперные характеристики резистивных нелинейных элементов?
8. Нарисуйте схему измерительной установки для снятия статической вольт-амперной характеристики резистивного двухполюсника.
9. Применим ли метод эквивалентного генератора к нелинейной цепи? К ее линейной части? Как определяются характеристики этого генератора?
10. Какие
из указанных ниже законов справедливы для нелинейной цепи (нелинейного элемента):
закон Ома, закон Кирхгофа, закон Джоуля-Ленца?
Какие
из указанных ниже законов справедливы для нелинейной цепи (нелинейного элемента):
закон Ома, закон Кирхгофа, закон Джоуля-Ленца?
11. В чем отличие метода эквивалентных преобразований для линейной и нелинейной цепей?
12. Найдите ток i2 и напряжение u2 на нелинейном элементе (рис. 10.37), если U0 = 6 В, I0 = 3 А, R1 = 8 Ом, R2 = 6 Ом, R3 = 3 Ом, i = 0,1u2 А.
Ответ: i2 = 1,6 А, u2 = 4 В.
13.
Найдите токи и напряжения в ветвях
цепи (рис. 10.38), если U0 = 6 В, IА = 6 мА, R = 1 кОм, i = 0,001u2 А. Найдите алгебраические суммы частичных токов и напряжений, вызванных действием
каждого источника в отдельности и убедитесь, что метод наложения дает неверные
результаты.
Ответ: I = 9 мА, U = 3 В.
Ток и напряжение, вызванные генератором тока II = 4 мА, UI = 2 В; ток и напряжение, вызванные генератором напряжения, имеют те же значения III = 4 мА, UII = 2 В. В результате получаем
I = II + III = 8 мА,
U = UI + UII = 4 В.
Cледовательно, принцип наложения для нелинейной цепи не справедлив.
14.
Найдите токи и напряжения в цепи (рис. 10.39), если I0 = 0,2 А, R1 = 100 Ом, i = 0,01u2 А и определите соответствующие значения статических
и дифференциальных сопротивлений нелинейного элемента и параллельного соединения
сопротивления R1 и нелинейного элемента.
Ответ: I = 0,16 А, I1 = 0,04 А, Rст = 25 Ом,
Rст экв = 20 Ом, Rд = 12,5 Ом, Rд экв = 11,1 Ом.
15. Найдите ток и напряжение в цепи (рис. 10.40), если u = i2 В, U0 = 11 В, R1 = 10 Ом. Определите новое значение R1, при котором дифференциальное сопротивление в новой рабочей точке вольт-амперной характеристики нелинейного элемента будет равно 1 Ом.
Ответ: I = 1 А, U1 =
10 В, R1 = 21,5 Ом.
16.
На рис.10.41 изображена вольт-амперная
характеристика стабилитрона – нелинейного полупроводникового прибора, используемого
для стабилизации постоянного напряжения на входе питаемой цепи. Найдите, в каких
пределах может изменяться сопротивление нагрузки Rн при неизменном напряжении Uн = 6 В, если U0 = 12 В, R = 100 Ом, U = 6 В, Imax = = 50 мА, Imin = 10 мА.
Найдите, в каких
пределах может изменяться сопротивление нагрузки Rн при неизменном напряжении Uн = 6 В, если U0 = 12 В, R = 100 Ом, U = 6 В, Imax = = 50 мА, Imin = 10 мА.
Ответ: 120 Ом Rн 600 Ом.
17. Найдите величину сопротивления R3 (рис. 10.42), при которой I = 3 мА, если U0 = 16 В, R1 = R2 = 2 кОм, I = (2U – 1)×10—3 А. Определите в рабочей точке дифференциальное и статическое сопротивление нелинейного элемента.
Ответ: R3 = 1 кОм, Rст = 666,7 Ом, Rд = 364 Ом.
18.
Найдите
вольт-амперную характеристику параллельного соединения НЭ (рис. 10.43), если i1 = 0,02u2 А, i2 = 0,08u2 А. Определите величину R,
при которой i = 0,4А, если u0 =
6В.
10.43), если i1 = 0,02u2 А, i2 = 0,08u2 А. Определите величину R,
при которой i = 0,4А, если u0 =
6В.
Ответ: R = 10 Ом.
19. Найдите токи и напряжения в цепи (рис. 10.44), если U0 = 30 В, I0 = 3 А, u1 = В, i2 = 0,01u22 В.
Ответ: i1 = 1 А, u1 = 10 В, i2 = 4 А, u2 = 20 В.
20.
Найдите
токи и напряжения в цепи (рис. 10.45), если U01 =
= U02 = 6 В, u1 =
В, u2 =
В, R = 0,8 Ом.
Ответ: I1 = 1 А, I2 = 4 А, I3 = 5 А, U1 = U2 = 2В, UR = 4 В.
21.
Применив интерполяционный метод,
аппроксимируйте ВАХ нелинейного резистивного элемента (рис. 10.45) полиномом
вида .
Ответ: a0 = i0; ;
;
.
22. Заданную в виде таблицы (Uk, Ik) ВАХ нелинейного резистивного элемента аппроксимируйте линейной функцией .
Uk | 0 | 0.1 | 0. | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
Ik | 0 | 0.26 | 0.54 | 0.72 | 0.93 | 1.1 | 1.18 | 1.28 | 1.36 |
Коэффициент а1 определить методом наименьших квадратов.
Ответ: i = 1,94u.
23. Падающий участок ВАХ нелинейного резистивного элемента i = F(u) задан таблицей:
Uk | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 |
Ik | 9.0 | 6.75 | 4.6 | 3.0 | 2.0 |
Аппроксимируйте характеристику на отрезке [0.2; 0.4] линейной функцией методом наименьших квадратов.
Ответ: i = -35,3
+ 15,7u.
Как по вах определить сопротивление цепи
В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями.
В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения.
Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат.
Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.1), а полупроводниковые диоды — несимметричные характеристики (рис. 5.2).
Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3)
Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3)
.
Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока.
Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики (рис. 5.4).
.
При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения.
5.2. Графический метод расчета нелинейных цепей
постоянного тока
Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения.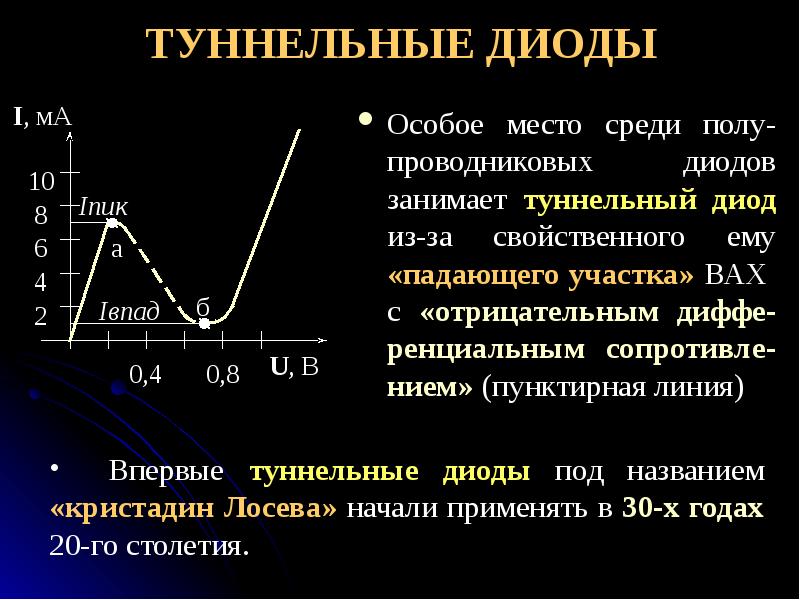 Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6.
Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6.
К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:
(5.1)
По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).
При параллельном соединении двух нелинейных элементов (рис.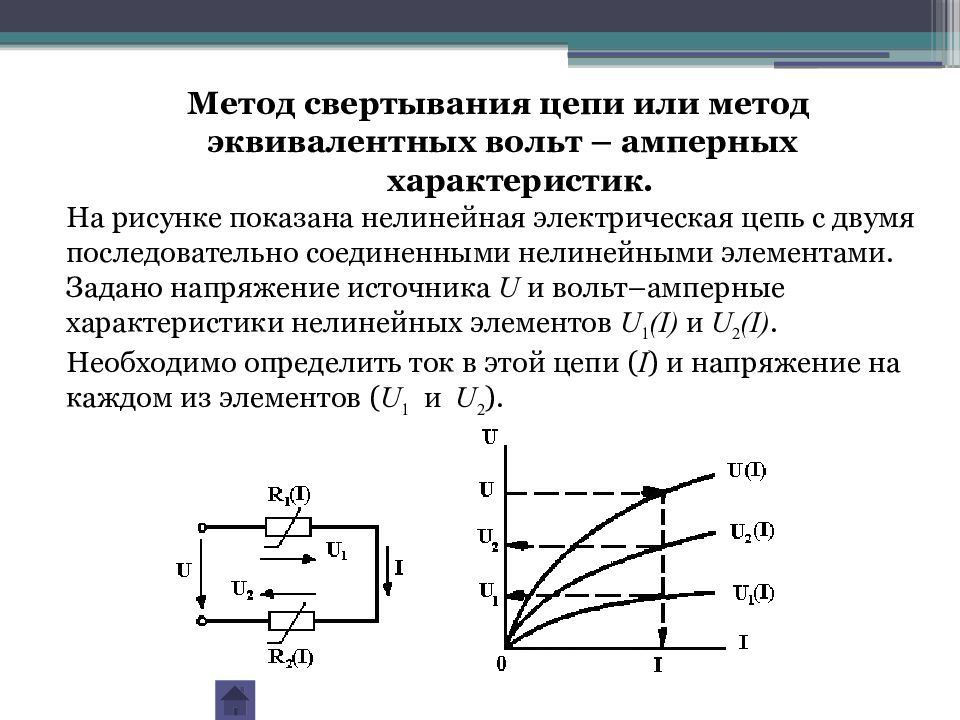 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3.
5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3.
(аг = ав + аб)
Далее задаваясь произвольным значением напряжения больше и меньше U’, можно построить ВАХ всей цепи (кривая 3). Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I1 и I2 в отдельных ветвях с учетом масштаба тока mI.
В случае смешанного (рис. 5.9) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.
5.9) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.
6. Электрические цепи однофазного
переменного тока
Не нашли то, что искали? Воспользуйтесь поиском:
В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями.
В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения.
Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат.
Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.1), а полупроводниковые диоды — несимметричные характеристики (рис. 5.2).
Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3)
.
Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока.
Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики (рис. 5.4).
.
При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения.
5.2. Графический метод расчета нелинейных цепей
постоянного тока
Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения. Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6.
К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:
(5.1)
По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).
Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3).
При параллельном соединении двух нелинейных элементов (рис. 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3.
(аг = ав + аб)
Далее задаваясь произвольным значением напряжения больше и меньше U’, можно построить ВАХ всей цепи (кривая 3).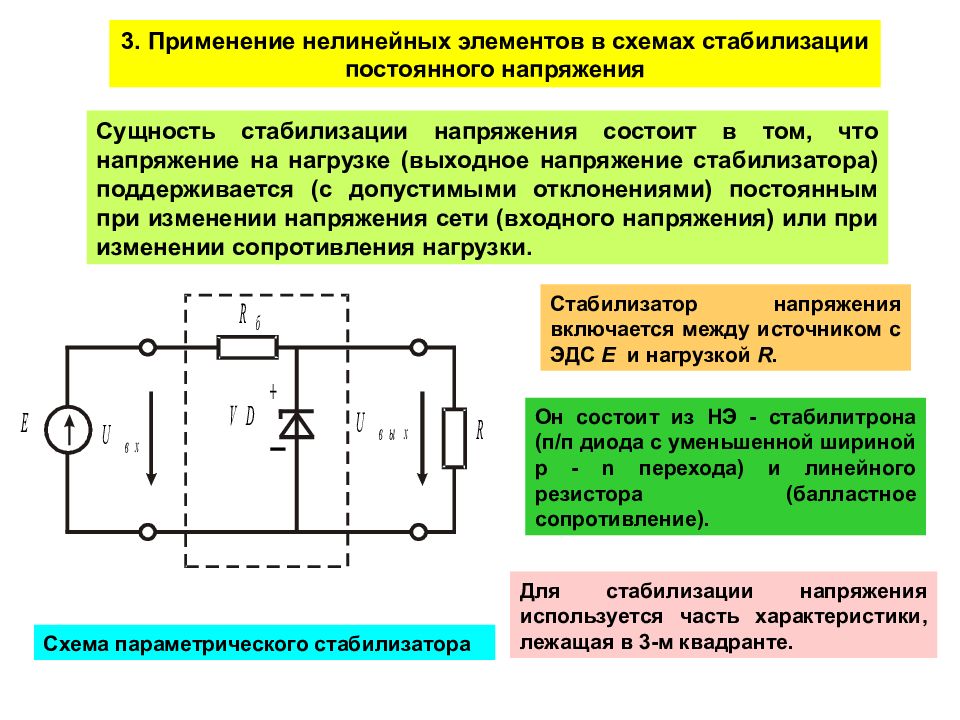 Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I1 и I2 в отдельных ветвях с учетом масштаба тока mI.
Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I1 и I2 в отдельных ветвях с учетом масштаба тока mI.
В случае смешанного (рис. 5.9) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.
6. Электрические цепи однофазного
переменного тока
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8832 — | 7545 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.
Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется.
Кроме того речь может идти не только об элементах, обладающих чисто активными сопротивлениями R, но и о линейных индуктивностях L и емкостях C, где постоянными будут зависимость магнитного потока от тока — Ф(I) и зависимость заряда конденсатора от напряжения между его обкладками — q(U).
Яркий пример линейного элемента — проволочный резистор. Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.
Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью.
Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется.
В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.
Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.
Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи нелинеен.
Для нелинейных элементов свойственно определенное статическое сопротивление в каждой точке их ВАХ, то есть каждому отношению напряжения к току, в каждой точке на графике, — ставится в соответствие определенное значение сопротивления. Оно может быть посчитано как тангенс угла альфа наклона графика к горизонтальной оси I, как если бы эта точка лежала на линейном графике.
Еще у нелинейных элементов есть так называемое дифференциальное сопротивление, которое выражается как отношение бесконечно малого приращения напряжения — к соответствующему изменению тока.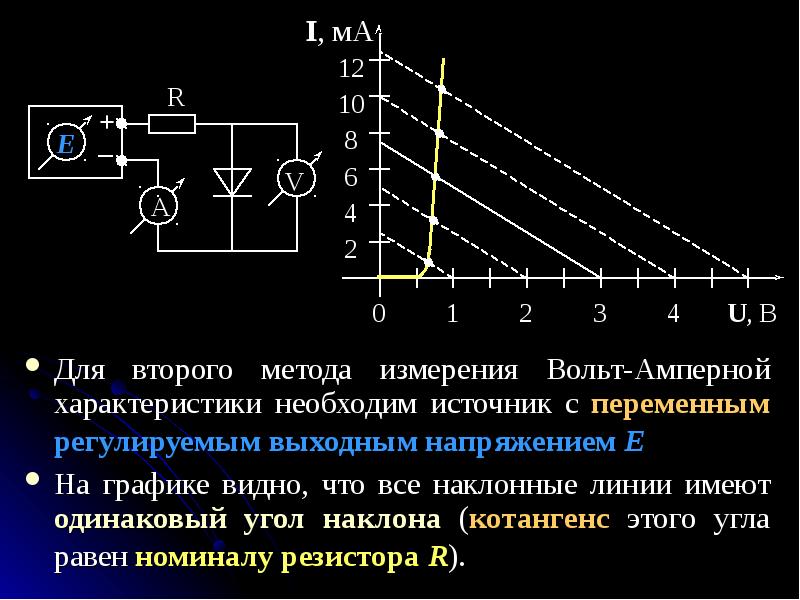 Данное сопротивление можно посчитать как тангенс угла между касательной к ВАХ в данной точке и горизонтальной осью.
Данное сопротивление можно посчитать как тангенс угла между касательной к ВАХ в данной точке и горизонтальной осью.
Такой подход делает возможным простейший анализ и расчет простых нелинейных цепей.
На рисунке выше показана ВАХ типичного диода. Она располагается в первом и в третьем квадрантах координатной плоскости, это говорит нам о том, что при положительном или отрицательном приложенном к p-n-переходу диода напряжении (в том или ином направлении) будет иметь место прямое либо обратное смещение p-n-перехода диода. С ростом напряжения на диоде в любом из направлений ток сначала слабо увеличивается, а после резко возрастает. По этой причине диод относится к неуправляемым нелинейным двухполюсникам.
На этом рисунке показано семейство типичных ВАХ фотодиода в разных условиях освещенности. Основной режимом работы фотодиода — режим обратного смещения, когда при постоянном световом потоке Ф ток практически неизменен в довольно широком диапазоне рабочих напряжений.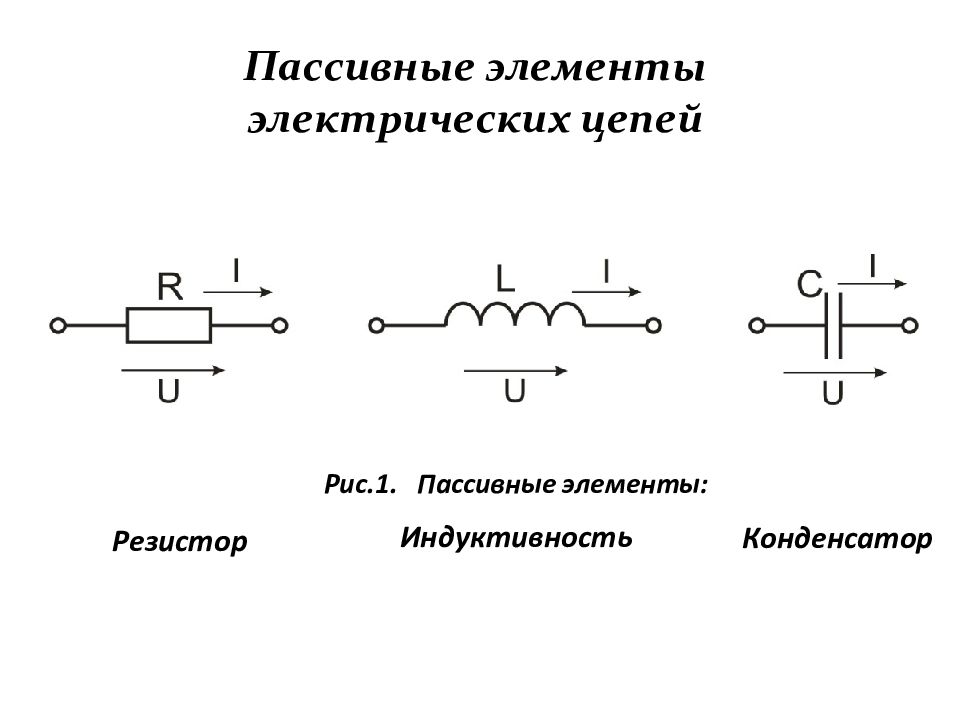 В данных условиях модуляция освещающего фотодиод светового потока, приведет к одновременной модуляции тока через фотодиод. Таким образом, фотодиод — это управляемый нелинейный двухполюсник.
В данных условиях модуляция освещающего фотодиод светового потока, приведет к одновременной модуляции тока через фотодиод. Таким образом, фотодиод — это управляемый нелинейный двухполюсник.
Это ВАХ тиристора, здесь видна ее явная зависимость от величины тока управляющего электрода. В первом квадранте — рабочий участок тиристора. В третьем квадранте начало ВАХ — малый ток и большое приложенное напряжение (в запертом состоянии сопротивление тиристора очень велико). В первом квадранте ток велик, падение напряжения мало — тиристор в данный момент открыт.
Момент перехода из закрытого — в открытое состояние наступает тогда, когда на управляющий электрод подан определенный ток. Переключение из открытого состояния — в закрытое происходит при снижении тока через тиристор. Таким образом, тиристор — это управляемый нелинейный трехполюсник (как и транзистор, у которого ток коллектора зависит от тока базы).
Нелинейное активное сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Нелинейное активное сопротивление
Cтраница 1
Нелинейные активные сопротивления, изменяющие ивою величину под влиянием нагрева, называют термосопротивлениями ( терморезисторами) иди термистовами, а под влиянием напряженности поля — варисторами, Нелинейные сопротивления емкостного характера называют варикондами. К нелинейным сопротивлениям индуктивного характера относятся катушки индуктивности с ферромагнитными сердечниками в режиме насыщения.
[2]
К нелинейным сопротивлениям индуктивного характера относятся катушки индуктивности с ферромагнитными сердечниками в режиме насыщения.
[2]
Неуправляемыми нелинейными активными сопротивлениями являются электрическая дуга, меднозакисные и селеновые выпрямители, тиритовые и вилитовые сопротивления, термисторы, бареттеры, лампы накаливания и др. Основные свойства и вольт-амперные характеристики их обсуждались в гл. [3]
Неуправляемыми нелинейными активными сопротивлениями являются электрическая дуга, германиевые и кремниевые, медно-закисные и селеновые выпрямители, тиритовые и вилитовые сопротивления, термисторы, бареттеры, лампы накаливания и др. Основные свойства и вольтамперные характеристики их обсуждались в гл. [4]
Неуправляемыми нелинейными активными сопротивлениями являются электрическая дуга, германиевые и кремниевые, меднозакис-ные и селеновые выпрямители, тиритозые и вилитовые сопротивления, термисторы, бареттеры, лампы накаливания и др. Основные свойства и вольтамперные характеристики их обсуждались в гл.
[5]
Основные свойства и вольтамперные характеристики их обсуждались в гл.
[5]
Неуправляемыми нелинейными активными сопротивлениями являются электрическая дуга, германиевые и кремниевые выпрямители, тирито-вые сопротивления, термисторы, бареттеры, лампы накаливания и др. Их основные свойства и вольт-амперные характеристики обсуждались в гл. [6]
Для нелинейных активных сопротивлений ( например, тиритовых и вилитовых сопротивлений) роль х выполняет напряжение, роль У-ток. [7]
Для нелинейных активных сопротивлений ( например, тири-товых и вилитовых сопротивлений) роль х играет напряжение, роль у — ток. [8]
Как классифицируются нелинейные активные сопротивления по степени влияния температуры нагрева ( проходящим током) на форму характеристики. [9]
[9]
Кроме классификации нелинейных активных сопротивлений по принципу управляемости, они могут быть классифицированы по степени влияния температуры нагрева сопротивления, обусловленной протекающим по сопротивлению током, на форму вольт-амперной характеристики его. [10]
Кроме классификации нелинейных активных сопротивлений по принципу управляемости, они могут быть классифицированы по степени влияния температуры нагрева сопротивления, обусловленной протекающим по сопротивлению током, на форму вольтам-перной характеристики. [11]
С помощью нелинейных активных сопротивлений с несимметричной вольт-амперной характеристикой можно осуществлять выпрямление напряжения и тока, так как в кривых напряжений и токов цепи появляются постоянные составляющие, которые можно выделить. [12]
К числу нелинейных активных сопротивлений относятся: лампы накаливания, электронные лампы, полупроводниковые триоды, медно-закисные, купроксные, селеновые, германиевые и кремниевые вентили, барретеры, термисторы и др. Под нелинейными индуктивными сопротивлениями понимают катушки, намотанные на сердечники из ферромагнитных материалов. У нелинейных конденсаторов пространство между обкладками заполнено сегнетодиэлектриками.
[13]
Под нелинейными индуктивными сопротивлениями понимают катушки, намотанные на сердечники из ферромагнитных материалов. У нелинейных конденсаторов пространство между обкладками заполнено сегнетодиэлектриками.
[13]
Последовательно с нелинейным активным сопротивлением включено линейное сопротивление К 10 ом. [14]
Последовательно с нелинейным активным сопротивлением включено линейное сопротивление R 10 ом. [15]
Страницы: 1 2 3 4
Нелинейный резистор— обзор
5.6 Нелинейные резистивные схемы
В предыдущих разделах мы проанализировали электрические цепи, содержащие только линейных элементов цепи , таких как резисторы, катушки индуктивности и конденсаторы. Термин «линейный» означает, что значения сопротивлений, индуктивностей и емкостей не зависят от напряжений на соответствующих элементах схемы или токов через эти элементы. По этим причинам клеммы для таких элементов являются линейными, и схемы с этими элементами описываются линейными уравнениями, такими как уравнения (2.29) — (2.34) 2.292.302.312.322.332.34. В наших предыдущих обсуждениях также предполагалось, что значения сопротивлений, индуктивностей и емкостей не меняются со временем. Такие элементы схемы называются инвариантными во времени, а схемы с линейными и неизменяющимися во времени элементами описываются линейными уравнениями с постоянными коэффициентами . Уравнения (2.29) — (2.34) 2.292.302.312.322.332.34 можно снова использовать в качестве примера. Линейные и инвариантные во времени (LTI) схемы являются важными представителями систем LTI, и всестороннее математическое изучение этих систем относится к курсу линейных систем и сигналов.Однако здесь полезно подчеркнуть два наиболее фундаментальных свойства таких схем и систем. Первым свойством является инвариантность относительно сдвига во времени , а вторым свойством является принцип суперпозиции .
По этим причинам клеммы для таких элементов являются линейными, и схемы с этими элементами описываются линейными уравнениями, такими как уравнения (2.29) — (2.34) 2.292.302.312.322.332.34. В наших предыдущих обсуждениях также предполагалось, что значения сопротивлений, индуктивностей и емкостей не меняются со временем. Такие элементы схемы называются инвариантными во времени, а схемы с линейными и неизменяющимися во времени элементами описываются линейными уравнениями с постоянными коэффициентами . Уравнения (2.29) — (2.34) 2.292.302.312.322.332.34 можно снова использовать в качестве примера. Линейные и инвариантные во времени (LTI) схемы являются важными представителями систем LTI, и всестороннее математическое изучение этих систем относится к курсу линейных систем и сигналов.Однако здесь полезно подчеркнуть два наиболее фундаментальных свойства таких схем и систем. Первым свойством является инвариантность относительно сдвига во времени , а вторым свойством является принцип суперпозиции . Чтобы выразить эти свойства математически, рассмотрим электрическую цепь LTI с двумя выводами, показанную на рис. 5.22. Предположим, что напряжение на клеммах v (t) приводит к отклику i (t) тока на клеммах. Тогда инвариантность относительно сдвига по времени означает, что напряжение на клеммах v ( t — τ) приведет к отклику тока на клеммах i ( t — τ), где τ — произвольный сдвиг во времени.Это свойство прозрачно с физической точки зрения и просто утверждает, что для линейных инвариантных во времени схем нет ничего, что указывало бы на происхождение времени. Это начало координат может быть выбрано произвольно, не влияя на математическое описание электрических цепей LTI , а изменение начала координат времени эквивалентно сдвигу во времени.
Чтобы выразить эти свойства математически, рассмотрим электрическую цепь LTI с двумя выводами, показанную на рис. 5.22. Предположим, что напряжение на клеммах v (t) приводит к отклику i (t) тока на клеммах. Тогда инвариантность относительно сдвига по времени означает, что напряжение на клеммах v ( t — τ) приведет к отклику тока на клеммах i ( t — τ), где τ — произвольный сдвиг во времени.Это свойство прозрачно с физической точки зрения и просто утверждает, что для линейных инвариантных во времени схем нет ничего, что указывало бы на происхождение времени. Это начало координат может быть выбрано произвольно, не влияя на математическое описание электрических цепей LTI , а изменение начала координат времени эквивалентно сдвигу во времени.
Рисунок 5.22. Входное напряжение и ток на клеммах для электрической цепи LTI.
Чтобы продемонстрировать принцип суперпозиции, предположим, что два напряжения на клеммах v 1 ( t) и v 2 ( t ) приводят к двум характеристикам тока на клеммах i 1 ( t) и и 2 (t) соответственно. Тогда, согласно принципу суперпозиции, напряжение на клеммах
Тогда, согласно принципу суперпозиции, напряжение на клеммах
(5,40) v (t) = c1v1 (t) + c2v2 (t)
приведет к отклику тока на клеммах
(5,41) i (t) = c1i1 (t) + c2i2 (t),
, где c 1 и c 2 — произвольные числа.
Ранее подчеркивалось, что принцип суперпозиции является математическим следствием линейности уравнений схемы.
Инвариантность сдвига во времени и принцип суперпозиции можно объединить в следующее утверждение: если i 1 (t) и i 2 (t) — это отклики тока на клеммах на напряжения на клеммах v 1 (t) и v 2 (t) соответственно, затем
(5.42) i (t) = c1i1 (t − τ1) + c2i2 (t − τ2)
будет текущей реакцией на напряжение на клеммах
(5,43) v (t) = c1v1 (t − τ1) + c2v2 ( t − τ2),
, где τ 1 и τ 2 — произвольные временные сдвиги. Последнее утверждение можно рассматривать как еще одно определение схем LTI, определение, которое широко используется в теории линейных систем.
Во многих приложениях значения сопротивлений, индуктивностей и емкостей могут зависеть от напряжений или токов через элементы схемы.Такие элементы схемы являются нелинейными, а электрические цепи с нелинейными элементами описываются нелинейными дифференциальными и алгебраическими уравнениями, для которых принцип суперпозиции не выполняется. По этой причине теория нелинейных электрических цепей намного сложнее. В этом разделе мы рассмотрим только некоторые простые факты и результаты, относящиеся к нелинейным резистивным цепям . Такие схемы описываются нелинейными алгебраическими уравнениями.
Сначала напомним определение линейных резисторов.Эти резисторы характеризуются следующим соотношением выводов:
, где v и i — мгновенное напряжение на резисторе и ток через резистор, а R — сопротивление, которое не зависит от значений v. и и .
Выражение (5.44) можно графически проиллюстрировать прямой линией, показанной на рис. 5.23. Наклон этой прямой равен значению сопротивления:
5.23. Наклон этой прямой равен значению сопротивления:
Рисунок 5.23. v по сравнению с i представление линейного резистора.
Обозначение схемы для нелинейного резистора, который будет использоваться в этом разделе, показано на рисунке 5.24. Нелинейный резистор нельзя полностью охарактеризовать одним значением сопротивления. Обычно нелинейный резистор характеризуется кривой «v (i) », подобной кривой, показанной на рисунке 5.25. Из этого рисунка видно, что если мы определим сопротивление как отношение
Рисунок 5.24. Условные обозначения нелинейного резистора.
Рисунок 5.25. v (i) кривая для нелинейного резистора.
значение этого сопротивления будет изменяться в зависимости от тока через резистор. Этот факт подчеркивается обозначением R (i) . Действительно, значения сопротивления для двух разных
значений i 1 и i 2 тока через резистор будут равны двум разным наклонам:
Это объясняет, почему v (i) Кривые используются для характеристики нелинейных резисторов.
Существует множество физических механизмов, которые приводят к нелинейной зависимости сопротивления от электрического тока через резистор. Например, один простой механизм основан на том факте, что сопротивление обычно увеличивается с температурой. По мере увеличения тока через резистор количество рассеиваемой мощности (в виде тепла) увеличивается, а его температура повышается. Это приводит к увеличению сопротивления.
Анализ электрических цепей с нелинейными резисторами требует решения нелинейных алгебраических уравнений.По этой причине этот анализ сталкивается с некоторыми трудностями, которые можно в некоторой степени обойти, используя графические методы. Проиллюстрируем это на примере простой нелинейной схемы, показанной на рис. 5.26.
Рисунок 5.26. Электрическая схема с нелинейным резистором.
Применяя KVL к этой схеме, мы получаем уравнение:
Это нелинейное алгебраическое уравнение. Нелинейность этого уравнения проистекает из последнего члена v 1 ( i ), который представляет собой описание нелинейного резистора «напряжение в зависимости от тока». Решим это нелинейное уравнение графически. Для этого преобразуем его следующим образом:
Решим это нелинейное уравнение графически. Для этого преобразуем его следующим образом:
Затем мы построим левую и правую части этого уравнения, как показано на рисунке 5.27. Прямая, соответствующая левой части (5.50), обычно называется «линией нагрузки». Решением уравнения (5.50) является значение — тока, при котором обе части в (5.50) равны. Из рисунка 5.27 видно, что обе стороны в (5.50) будут равны друг другу для значения тока, которое соответствует пересечению графиков этих сторон.Таким образом, мы можем графически найти ток – в цепи и напряжение – на нелинейном резисторе (см. Рис. 5.27).
Рисунок 5.27. Графический метод анализа нелинейной электрической цепи.
Обсуждаемая проблема очень проста. Однако произвольные резистивные электрические цепи с одиночными нелинейными резисторами могут быть сведены к схеме, показанной на рисунке 5.26. Это утверждение является теоремой Тевенина для резистивных цепей с одиночными нелинейными резисторами.
Чтобы доказать эту теорему, рассмотрим схему, показанную на рис. 5.28. Предположим, что и — это ток через нелинейный резистор. Напряжение v на клеммах «A-B» останется прежним , если мы заменим этот резистор источником тока i s = i (см. Рисунок 5.29). Это верно, потому что эта замена сохраняет ток через клеммы A-B активной линейной резистивной цепи. Другими словами, эта линейная резистивная схема не может отличить нелинейный резистор от источника тока, если каждый из них дает одинаковый ток на клеммах.Следовательно, в обоих случаях напряжение на клеммах A-B будет одинаковым. С чисто математической точки зрения это верно, потому что линейные резистивные цепи на рисунках 5.28 и 5.29 описываются идентичными линейными алгебраическими уравнениями. Следовательно, решая эти уравнения, мы находим одинаковое напряжение на клеммах A-B.
Рисунок 5.28. Резистивная схема с одним нелинейным резистором.
Рисунок 5.29. Замена нелинейного резистора источником тока.
Далее мы применим принцип суперпозиции к схеме на рис. 5.29. Для этого мы разделим все источники в этой схеме на две группы: 1) все источники в активной линейной резистивной цепи, 2) один источник тока i s = i . Теперь рассмотрим два отдельных режима, показанных на рисунке 5.30. Согласно принципу суперпозиции, напряжение v на выводах AB равно сумме напряжений v (1) и v (2) на одних и тех же выводах для первого и второго режимов соответственно:
Рисунок 5.30. Два режима.
Ясно, что v (1) равно напряжению холостого хода
, тогда как v (2) может быть выражено через эквивалентное входное сопротивление R в пассивная линейная резистивная цепь и ток i следующим образом:
Обратите внимание, что знак минус в (5.53) появился, потому что опорные направления тока i через R в и напряжения v (2) через одно и то же сопротивление не согласованы (противоположны).
Подставляя (5.52) и (5.53) в (5.51), мы получаем:
Если мы рассмотрим эквивалентную схему Тевенина, показанную на рисунке 5.26, мы обнаружим, что:
Формула (5.54) является выражением зависимости напряжения от ток на выводах AB исходной схемы, показанной на рисунке 5.28, тогда как формула (5.55) является выражением зависимости напряжения от тока на выводах AB схемы, показанной на рисунке 5.26. Эти два выражения будут идентичны, если:
При условиях (5.56) и (5.57), соотношение напряжения и тока на клеммах A-B в схемах, показанных на рисунках 5.28 и 5.26, будет одинаковым. Это гарантирует одинаковые токи через нелинейный резистор для обеих цепей. Таким образом, доказательство теоремы Тевенина для резистивных цепей с одиночными нелинейными резисторами завершено.
Данное доказательство теоремы Тевенина более тонкое, чем приведенное в разделе 5.4. Основное отличие состоит в том, что это доказательство использует принцип суперпозиции только для активной (линейной) части схемы, а не для всей схемы.
Мы также установили уже знакомые выражения (5.56) и (5.57) для напряжения Тевенина v s и сопротивления R s .
Используя теорему Тевенина, мы можем сформулировать следующий двухэтапный алгоритм для анализа общей схемы, показанной на рис. 5.28.
Шаг I:
Найдите напряжение холостого хода на клеммах A-B для активной линейной резистивной цепи и эквивалентное входное сопротивление на тех же клеммах для соответствующей пассивной линейной резистивной цепи.
Шаг II:
Замените активную линейную резистивную схему эквивалентной схемой Тевенина (см. Рисунок 5.26) и используйте графический метод, показанный на рисунке 5.27, для анализа преобразованной схемы.
Проиллюстрируем описанный выше алгоритм двумя следующими примерами.
ПРИМЕР 5.5 Схема регулятора напряжения
Рассмотрим схему, показанную на рисунке 5.31, где нагрузочный резистор R L подключен параллельно с нелинейным резистором, характеризуемым v 1 ( i ) кривая, показанная на рисунке 5. 32. Эта кривая демонстрирует «насыщение напряжения». Другими словами, он имеет почти горизонтальный (плоский) участок, который начинается с малых значений тока. Мы хотели бы найти все токи и напряжения в этой цепи.
32. Эта кривая демонстрирует «насыщение напряжения». Другими словами, он имеет почти горизонтальный (плоский) участок, который начинается с малых значений тока. Мы хотели бы найти все токи и напряжения в этой цепи.
Рисунок 5.31. Схема регулятора напряжения.
Рисунок 5.32. Соотношение напряжение-ток для нелинейного резистора, используемого в цепи постоянного тока регулятора напряжения.
Сначала мы перерисовываем эту схему, чтобы представить ее в форме, аналогичной общей схеме на рис. 5.28. Перерисованная схема показана на рисунке 5.33. Затем мы найдем напряжение Тевенина v s , которое согласно (5.56) равно напряжению холостого хода, то есть напряжению на нагрузочном резисторе R L , когда нелинейный резистор удаленный. Используя правило делителя напряжения, легко найти, что:
Рисунок 5.33. Перерисована схема регулятора напряжения.
Теперь мы найдем сопротивление Тевенина R s , которое равно сопротивлению на выводах A-B, когда нелинейный резистор удален и источник постоянного напряжения В, s замкнут накоротко. Легко видеть, что это сопротивление равно эквивалентному сопротивлению R и R L , соединенных параллельно:
Легко видеть, что это сопротивление равно эквивалентному сопротивлению R и R L , соединенных параллельно:
Таким образом, мы нашли параметры эквивалентной схемы, показанной на рисунке 5.26, и теперь можем используйте графическую технику, показанную на Рисунке 5.27. В нашем случае этот метод проиллюстрирован на рис. 5.34. Ток i через нелинейный резистор соответствует точке пересечения прямой линии нагрузки и кривой v 1 ( i ).Напряжение v L , которое соответствует этой точке, является напряжением на сопротивлении нагрузки. Таким образом, разделив это напряжение на R L , мы находим ток i L через сопротивление нагрузки. Суммируя этот ток с и , мы находим ток через резистор R , и на этом завершаем анализ вышеуказанной схемы.
Рисунок 5.34. Графический анализ схемы регулятора напряжения.
Продемонстрируем особенность этой схемы. Предположим, что напряжение источника В, с , не остается постоянным и несколько изменяется со временем. Затем линия нагрузки изменит свое положение, но останется параллельной исходной линии нагрузки (см. Рисунок 5.34). Новое напряжение нагрузки v L будет соответствовать новой точке пересечения. Однако, поскольку кривая v 1 ( i ) демонстрирует насыщение напряжения, это новое напряжение нагрузки будет практически таким же, как и раньше.Это объясняет, почему эта схема называется схемой регулятора напряжения. Для построения подобных схем необходимы нелинейные резисторы со свойством насыщения по напряжению. Оказывается, этим свойством обладают стабилитроны, которые могут быть использованы для построения схем регуляторов напряжения. Стабилитроны обычно достаточно подробно изучаются в курсах по электронным схемам.
Предположим, что напряжение источника В, с , не остается постоянным и несколько изменяется со временем. Затем линия нагрузки изменит свое положение, но останется параллельной исходной линии нагрузки (см. Рисунок 5.34). Новое напряжение нагрузки v L будет соответствовать новой точке пересечения. Однако, поскольку кривая v 1 ( i ) демонстрирует насыщение напряжения, это новое напряжение нагрузки будет практически таким же, как и раньше.Это объясняет, почему эта схема называется схемой регулятора напряжения. Для построения подобных схем необходимы нелинейные резисторы со свойством насыщения по напряжению. Оказывается, этим свойством обладают стабилитроны, которые могут быть использованы для построения схем регуляторов напряжения. Стабилитроны обычно достаточно подробно изучаются в курсах по электронным схемам.
Схема регулятора типа, показанного на рис. 5.33, часто считается неэффективной. Причина в следующем. Если V s имеет тенденцию к увеличению, это приводит к значительному увеличению тока i через нелинейный резистор (стабилитрон). Поскольку напряжение нагрузки и, следовательно, ток нагрузки остаются прежними, это приводит к увеличению тока через резистор R . Это вызывает увеличение падения напряжения на этом резисторе, которое компенсирует увеличение В, , , . Таким образом, мы можем видеть, что регулирование напряжения достигается за счет увеличения токов через нелинейный резистор R и, следовательно, за счет увеличения рассеиваемой мощности в этих резисторах.По этой причине эти схемы регуляторов напряжения в основном используются в приложениях с низким энергопотреблением. Для приложений большой мощности были разработаны более эффективные схемы регулятора напряжения.
Если V s имеет тенденцию к увеличению, это приводит к значительному увеличению тока i через нелинейный резистор (стабилитрон). Поскольку напряжение нагрузки и, следовательно, ток нагрузки остаются прежними, это приводит к увеличению тока через резистор R . Это вызывает увеличение падения напряжения на этом резисторе, которое компенсирует увеличение В, , , . Таким образом, мы можем видеть, что регулирование напряжения достигается за счет увеличения токов через нелинейный резистор R и, следовательно, за счет увеличения рассеиваемой мощности в этих резисторах.По этой причине эти схемы регуляторов напряжения в основном используются в приложениях с низким энергопотреблением. Для приложений большой мощности были разработаны более эффективные схемы регулятора напряжения.
ПРИМЕР 5.6 Мостовая схема
Эта схема показана на рисунке 5.35. Было бы очень сложно проанализировать эту схему без использования теоремы Тевенина. Использование этой теоремы значительно упрощает анализ.
Использование этой теоремы значительно упрощает анализ.
Рисунок 5.35. «Мостовая» схема с нелинейным резистором.
Сначала мы найдем напряжение Thevenin v s , которое равно напряжению холостого хода, то есть напряжению на выводах A-B, когда нелинейный резистор удален (см. Рисунок 5.36). Нетрудно заметить, что
Рисунок 5.36. Электрическая схема для расчета v oc .
Используя (5.60), (5.61) и KVL для контура, состоящего из R 1 , открытых клемм и R 2 , получаем:
(5.62) vs = вок = R2i2 − R1i1 = v0 (R2R2 + R4 − R1R1 + R3).
Теперь мы найдем сопротивление Тевенина R s , которое равно входному сопротивлению на клеммах A-B, когда источник напряжения v 0 замкнут накоротко (см. Рисунок 5.37). Легко видеть, что это сопротивление определяется по формуле:
Рисунок 5.37. Схема электрическая для расчета R в .
(5,63) Rs = Rin = R1R3R1 + R3 + R2R4R2 + R4.
Наконец, с помощью графической техники, показанной на Рисунке 5.27, мы можем найти ток и напряжение на нелинейном резисторе. Тогда легко найти все остальные напряжения и токи в цепи.
Линейный и нелинейный резистор | Определение | Характеристическая кривая
Для большинства проводников график зависимости тока от напряжения представляет собой прямую линию, указывающую на постоянное сопротивление (см. , рис. 1, ). Чем меньше сопротивление, тем круче наклон графика.
Определение: Резистор, поддерживающий постоянное отношение V / I, является линейным резистором.
По мере увеличения тока через резистор в резисторе выделяется больше тепла, что приводит к повышению его температуры. Это повышение температуры вызывает небольшое увеличение сопротивления большинства проводящих материалов.
Для обычных проводниковых материалов, таких как медь и алюминий, изменение сопротивления в диапазоне рабочих температур для большинства цепей настолько мало, что эти материалы обычно считаются линейными резисторами.
Рисунок 1 Зависимость тока от напряжения Характеристическая кривая для линейных резисторов
Как следует из названия, резисторы с проволочной обмоткой имеют металлическую проволоку, намотанную на полую фарфоровую трубку и герметизированную фарфоровым покрытием.Эти резисторы обычно изготавливаются из константана или других сплавов с почти нулевым температурным коэффициентом.
Чем больше размер резистора, тем легче он может рассеивать тепло в окружающий воздух и, следовательно, тем выше номинальная мощность.
Недорогие резисторы массового производства часто имеют сопротивление, которое на 10% или более отличается от их номинальных значений.
Хотя такие резисторы подходят для многих типов цепей, для таких приложений, как измерительные приборы, требуются резисторы с точностью до 1% или менее от номинального сопротивления.Такие прецизионные резисторы часто изготавливаются путем нанесения тонкой пленки металла или углерода на небольшой керамический цилиндр, к которому прикреплены выводы.
Пленку можно протравить для доведения сопротивления до заданного значения перед нанесением слоя изоляционного материала.
Резисторы, используемые в электронных устройствах, обычно имеют сопротивление более килом (тысячи Ом) и пропускают ток всего в несколько миллиампер.
Резистор на основе углерода обычно используется, когда ток через резистор выделяет менее 2 Вт тепла.Элемент сопротивления состоит из мелко измельченного углерода, смешанного с изолирующим связующим, например фенольным, и спрессованного в цилиндрическую форму с проволочным выводом, встроенным в каждый конец. Затем резистивный элемент герметизируется пластиковой оболочкой.
Длина и ширина цилиндра, доля углерода в смеси и способ сжатия смеси для определения сопротивления.
Резисторы из углеродного состава намного дешевле, чем проволочные и пленочные резисторы, но сопротивление резистора из углеродного состава увеличивается, если температура заметно изменяется от 20 ° C, как показано на , рис. 2 .
2 .
При умеренных колебаниях температуры сопротивление изменяется всего на несколько процентов, поэтому мы обычно можем рассматривать резисторы из углеродистой композиции как линейные резисторы.
Рисунок 2 Кривая зависимости сопротивления от температуры углеродных резисторов
Составные резисторы также изготавливаются из керамики, состоящей из оксида олова и сурьмы, связанных стеклом. Резисторы из керамической композиции особенно полезны в схемах, в которых резисторы должны выдерживать скачки напряжения или энергии.
Интегральные схемы (ИС) варьируются от простых резисторных цепей до микропроцессоров, содержащих миллионы микроскопических резисторов и транзисторов. ИС начинаются как пластина из высокоочищенного кремния.
Чистый кремний — плохой проводник, поскольку в нем мало свободных носителей заряда. Резисторы изготавливаются путем рассеивания крошечных областей кремния с точно контролируемым количеством элементов, которые поставляют свободные электроны, что делает области более проводящими.
Резисторы нелинейныеЛампа накаливанияОпределение: Свойство, проявляемое устройствами, сопротивление которых не изменяется равномерно при изменении напряжения или тока.
При включении лампы накаливания температура и сопротивление ее вольфрамовой нити резко возрастают.
Раскаленная добела нить накала обычной 60-ваттной 120-вольтовой лампы имеет сопротивление 240 Ом, но ее сопротивление при комнатной температуре составляет около 18 Ом.
Лампа накаливания — это нелинейный резистор . Пусковой ток в момент включения лампы намного превышает нормальный рабочий ток:
$ \ begin {align} & Normal \ text {} I = \ frac {V} {R} = \ frac {120V} {240 \ Omega} = 0.5A \\ & бросок \ text {} I = \ frac {V} {R} = \ frac {120V} {18 \ Omega} = 6.6A \\\ end {align} $
К счастью, масса нити лампы настолько мала, что она нагревается добела менее чем за миллисекунду. Следовательно, скачок тока кратковременный, как показано на Рис. 3 .
Тем не менее, переключатели, используемые с лампами накаливания, должны быть спроектированы так, чтобы выдерживать пусковой ток. Чтобы избежать больших пусковых токов, нагревательные элементы, например, в печах, обычно изготавливаются из сплава с очень малым температурным коэффициентом.
Рисунок 3 Пусковой ток лампы накаливания мощностью 60 Вт
Кривая на рис. 4 показывает, как сопротивление лампы накаливания изменяется с напряжением.
Рисунок 4: Кривая вольт-амперной характеристики лампы накаливания
ТермисторРезистор с большим отрицательным температурным коэффициентом, называемый термистором , может использоваться для ограничения пусковых токов.
Обычно , такие термисторы имеют сопротивление более 100 Ом при комнатной температуре, но при токе через них 1 А их сопротивление падает до менее 1 Ом через 10–15 с.
Эти термисторы содержат полупроводящие оксиды металлов с керамической связкой. Тепло, выделяемое током через резистор, разрывает ковалентные связи в оксидах металлов, создавая достаточно свободных электронов, чтобы снизить сопротивление до доли от его значения при комнатной температуре.
Маленькие термисторы используются для измерения температуры, поскольку снижение температуры ниже 20 ° C увеличивает их сопротивление более чем в два раза.
Рисунок 5: Кривая зависимости сопротивления термистора от температуры
ВаристорВаристоры зависят от нелинейной характеристики сопротивления кристаллов оксида цинка или карбида кремния, которые формуются в пластины с глиняной связкой.
Варисторы на основе оксида цинка(также называемые варисторами на основе оксида цинка или MOV) используются для защиты чувствительной электроники от скачков напряжения.
Варисторы из карбида кремния (широко известные под торговым названием тирит) могут защищать высоковольтные системы. Они используются в качестве грозовых разрядников на линиях электропередачи.
Температура мало влияет на сопротивление варистора. Вместо этого происходит быстрое увеличение количества носителей заряда, когда разность потенциалов на варисторе становится больше, чем пороговое значение варистора. Как видно из , рис. 6, , результирующее уменьшение сопротивления таково, что ток через варистор сильно увеличивается без заметного увеличения падения напряжения на нем.
Таким образом, варистор, подключенный к источнику питания устройства, может защитить его от скачков напряжения.
Рисунок 6 Типичная характеристика варистора
ФоторезисторФоторезистор , фотопроводник или светозависимый резистор (LDR) содержит тонкую зигзагообразную полоску из сульфида кадмия или селенида кадмия.
Свет, падающий на полоску, разрушает валентные связи в соединении кадмия, создавая дополнительные носители заряда.
Сопротивление может составлять от сотен кОм в темноте до менее 100 Ом при ярком дневном свете. Фоторезисторы широко используются в люксметрах, схемах автоэкспозиции в камерах и контроллерах уличного освещения.
Рисунок 7: Характеристическая кривая фоторезистора
Во всех термисторах, варисторах и фоторезисторахиспользуются полупроводники, которые в определенных условиях становятся более проводящими. Схематические обозначения этих нелинейных резисторов показаны в Таблице 1 .
Таблица 1 Условные обозначения нелинейных резисторов
Сопротивление и резисторы | Безграничная физика
Закон Ома
ЗаконОма гласит, что ток пропорционален напряжению; схемы являются омическими, если они подчиняются соотношению V = IR.
Цели обучения
Контрастная форма вольт-амперных графиков для омических и неомических цепей
Ключевые выводы
Ключевые моменты
- Напряжение управляет током, а сопротивление препятствует ему. Закон
- Ома относится к пропорциональному соотношению между напряжением и током. Это также относится к конкретному уравнению V = IR, которое справедливо при рассмотрении схем, содержащих простые резисторы (сопротивление которых не зависит от напряжения и тока).
- Цепи или компоненты, которые подчиняются соотношению V = IR, известны как омические и имеют линейные зависимости тока от напряжения, проходящие через начало координат.
- Есть неомические компоненты и схемы; их графики I-V не являются линейными и / или не проходят через начало координат.
Ключевые термины
- простая схема : Схема с одним источником напряжения и одним резистором.
- омический : То, что подчиняется закону Ома.
Закон Ома
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов V, которая создает электрическое поле.Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток. Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению V. Немецкий физик Георг Симон Ом (1787-1854) был первым, кто экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению: [латекс] \ text {I} \ propto \ text {V} [/ latex ].
Это важное соотношение известно как закон Ома. Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием.Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда. Напомним, что в то время как напряжение управляет током, сопротивление ему препятствует. Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Следовательно, ток обратно пропорционален сопротивлению: [latex] \ text {I} \ propto \ frac {1} {\ text {R}} [/ latex].
Простая схема : Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленными красными параллельными линиями.Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Единицей измерения сопротивления является Ом, где 1 Ом = 1 В / А. Мы можем объединить два приведенных выше соотношения, чтобы получить I = V / R. Это соотношение также называется законом Ома. В этой форме закон Ома действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах.Омические материалы имеют сопротивление R, которое не зависит от напряжения V и тока I. Объект с простым сопротивлением называется резистором, даже если его сопротивление невелико.
Падение напряжения : Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Дополнительное понимание можно получить, решив I = V / R для V, что дает V = IR. Это выражение для V можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I.Для обозначения этого напряжения часто используется фраза «падение ИК-излучения». Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию).В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку E = qΔV, и через каждую из них протекает одинаковое q. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.
В истинно омическом устройстве одно и то же значение сопротивления будет вычислено из R = V / I независимо от значения приложенного напряжения V. То есть отношение V / I является постоянным, и когда ток отображается как В зависимости от напряжения кривая является линейной (прямая линия).Если напряжение принудительно устанавливается равным некоторому значению V, тогда это напряжение V, деленное на измеренный ток I, будет равно R. Или, если ток принудительно установлен до некоторого значения I, тогда измеренное напряжение V, деленное на этот ток I, также будет R. график I против V как прямая линия. Однако есть компоненты электрических цепей, которые не подчиняются закону Ома; то есть их соотношение между током и напряжением (их ВАХ) нелинейное (или неомическое). Примером может служить диод с p-n переходом.
Кривые вольт-амперной характеристики : ВАХ четырех устройств: двух резисторов, диода и батареи.Два резистора подчиняются закону Ома: график представляет собой прямую линию, проходящую через начало координат. Два других устройства не подчиняются закону Ома.
Закон Ома : Краткий обзор закона Ома.
Температура и сверхпроводимость
Сверхпроводимость — это явление нулевого электрического сопротивления и выброс магнитных полей в некоторых материалах при температуре ниже критической.
Цели обучения
Описать поведение сверхпроводника при температуре ниже критической и в слабом внешнем магнитном поле.
Ключевые выводы
Ключевые моменты
- Сверхпроводимость — это термодинамическая фаза, обладающая определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей.
- В сверхпроводящих материалах характеристики сверхпроводимости проявляются при понижении температуры ниже критической. Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств.
- Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже температуры перехода, магнитное поле выбрасывается.
- Сверхпроводники могут поддерживать ток без приложенного напряжения.
Ключевые термины
- высокотемпературные сверхпроводники : материалы, которые ведут себя как сверхпроводники при необычно высоких температурах (выше примерно 30 K).
- критическая температура : В сверхпроводящих материалах характеристики сверхпроводимости проявляются при этой температуре (и сохраняются ниже).
- сверхпроводимость : Свойство материала, при котором он не оказывает сопротивления прохождению электрического тока.
Сверхпроводимость — это явление точно нулевого электрического сопротивления и выброса магнитных полей, возникающее в некоторых материалах при охлаждении ниже критической температуры.Он был обнаружен Хайке Камерлинг-Оннес (на фото) 8 апреля 1911 года в Лейдене.
Хайке Камерлинг-Оннес : Хайке Камерлинг-Оннес (1853-1926).
Большинство физических свойств сверхпроводников варьируются от материала к материалу, например теплоемкость и критическая температура, критическое поле и критическая плотность тока, при которых сверхпроводимость разрушается. С другой стороны, существует класс свойств, не зависящих от основного материала.Например, все сверхпроводники имеют точно нулевое удельное сопротивление по отношению к низким приложенным токам, когда нет магнитного поля или если приложенное поле не превышает критического значения. Существование этих «универсальных» свойств подразумевает, что сверхпроводимость является термодинамической фазой и, таким образом, обладает определенными отличительными свойствами, которые в значительной степени не зависят от микроскопических деталей.
В сверхпроводящих материалах характеристики сверхпроводимости проявляются, когда температура T понижается ниже критической температуры T c .Возникновение сверхпроводимости сопровождается резкими изменениями различных физических свойств — отличительным признаком фазового перехода. Например, электронная теплоемкость пропорциональна температуре в нормальном (несверхпроводящем) режиме. При сверхпроводящем переходе он испытывает прерывистый скачок и после этого перестает быть линейным, как показано на.
Когда сверхпроводник помещается в слабое внешнее магнитное поле H и охлаждается ниже температуры перехода, магнитное поле выбрасывается.Эффект Мейснера не вызывает полного выброса поля. Скорее, поле проникает в сверхпроводник на очень малое расстояние (характеризуемое параметром λ), называемое лондонской глубиной проникновения. Он экспоненциально спадает до нуля в объеме материала. Эффект Мейснера — определяющая характеристика сверхпроводимости. Для большинства сверхпроводников лондонская глубина проникновения составляет порядка 100 нм.
Сверхпроводящий фазовый переход : Поведение теплоемкости (cv, синий) и удельного сопротивления (ρ, зеленый) при сверхпроводящем фазовом переходе.
Сверхпроводники также способны поддерживать ток без какого-либо приложенного напряжения — свойство, используемое в сверхпроводящих электромагнитах, таких как те, что используются в аппаратах МРТ. Эксперименты показали, что токи в сверхпроводящих катушках могут сохраняться годами без какого-либо измеримого ухудшения. Экспериментальные данные указывают на то, что в настоящее время продолжительность жизни составляет не менее 100 000 лет. Теоретические оценки времени жизни постоянного тока могут превышать расчетное время жизни Вселенной, в зависимости от геометрии провода и температуры.
Значение этой критической температуры варьируется от материала к материалу. Обычно обычные сверхпроводники имеют критические температуры в диапазоне от примерно 20 К до менее 1 К. Твердая ртуть, например, имеет критическую температуру 4,2 К. По состоянию на 2009 год самая высокая критическая температура, обнаруженная для обычного сверхпроводника, составляет 39 К. для магния. диборид (MgB 2 ), хотя экзотические свойства этого материала вызывают некоторые сомнения в правильности его классификации как «обычного» сверхпроводника.Высокотемпературные сверхпроводники могут иметь гораздо более высокие критические температуры. Например, YBa 2 Cu 3 O 7 , один из первых открытых купратных сверхпроводников, имеет критическую температуру 92 К; Были обнаружены купраты на основе ртути с критическими температурами, превышающими 130 К. Следует отметить, что химический состав и кристаллическая структура сверхпроводящих материалов могут быть довольно сложными, как показано в.
Элементарная ячейка сверхпроводника YBaCuO : Элементарная ячейка сверхпроводника YBaCuO.Атомы обозначены разными цветами.
Сопротивление и удельное сопротивление
Сопротивление и удельное сопротивление описывают степень, в которой объект или материал препятствуют прохождению электрического тока.
Цели обучения
Определить свойства материала, которые описываются сопротивлением и удельным сопротивлением
Ключевые выводы
Ключевые моменты
- Сопротивление объекта (т. Е. Резистора) зависит от его формы и материала, из которого он состоит.
- Удельное сопротивление ρ является внутренним свойством материала и прямо пропорционально общему сопротивлению R, внешней величине, которая зависит от длины и площади поперечного сечения резистора.
- Удельное сопротивление разных материалов сильно различается. Точно так же резисторы могут иметь разные порядки величины.
- Резисторы расположены последовательно или параллельно. Эквивалентное сопротивление цепи последовательно включенных резисторов является суммой всех сопротивлений.Сопротивление, обратное эквивалентному сопротивлению цепи параллельно включенных резисторов, является суммой обратных сопротивлений каждого резистора.
Ключевые термины
- Эквивалентное сопротивление серии : Сопротивление сети резисторов, расположенных таким образом, что напряжение в сети является суммой напряжений на каждом резисторе. В этом случае эквивалентное сопротивление — это сумма сопротивлений всех резисторов в сети.
- параллельное эквивалентное сопротивление : сопротивление сети, при котором на каждый резистор действует одинаковая разность потенциалов (напряжение), так что токи, проходящие через них, складываются.В этом случае сопротивление, обратное эквивалентному сопротивлению, равно сумме обратных сопротивлений всех резисторов в сети.
- удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.
Сопротивление и удельное сопротивление
Сопротивление — это электрическое свойство, препятствующее прохождению тока. Ток, протекающий через провод (или резистор), подобен воде, протекающей по трубе, а падение напряжения на проводе подобно перепаду давления, которое проталкивает воду по трубе.Сопротивление пропорционально тому, сколько давления требуется для достижения заданного потока, в то время как проводимость пропорциональна тому, сколько потока возникает при заданном давлении. Проводимость и сопротивление взаимны. Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L, подобно сопротивлению трубы потоку жидкости.Чем длиннее цилиндр, тем больше зарядов соударяется с его атомами. Чем больше диаметр цилиндра, тем больше тока он может пропускать (опять же, аналогично потоку жидкости по трубе). Фактически, R обратно пропорционально площади поперечного сечения цилиндра A.
Цилиндрический резистор : однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление протеканию тока аналогично сопротивлению, оказываемому трубой потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление.Чем больше площадь его поперечного сечения A, тем меньше его сопротивление.
Как уже упоминалось, для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы обладают разным сопротивлением потоку заряда. Мы определяем удельное сопротивление вещества ρ так, чтобы сопротивление объекта R было прямо пропорционально ρ. Удельное сопротивление ρ является внутренним свойством материала, независимо от его формы или размера. Напротив, сопротивление R — это внешнее свойство, которое действительно зависит от размера и формы резистора.(Аналогичная внутренняя / внешняя связь существует между теплоемкостью C и удельной теплоемкостью c). Напомним, что объект, сопротивление которого пропорционально напряжению и току, называется резистором.
Типичный резистор : Типовой резистор с осевыми выводами.
Что определяет удельное сопротивление? Удельное сопротивление разных материалов сильно различается. Например, проводимость тефлона примерно в 1030 раз ниже, чем проводимость меди. Почему такая разница? Грубо говоря, металл имеет большое количество «делокализованных» электронов, которые не застревают в каком-либо одном месте, но могут свободно перемещаться на большие расстояния, тогда как в изоляторе (например, тефлоне) каждый электрон прочно связан с одним атомом и требуется большая сила, чтобы оторвать его.Точно так же резисторы могут иметь разные порядки величины. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление сухого человека может составлять 10 5 Ом, в то время как сопротивление человеческого сердца составляет примерно 10 3 Ом. Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Разность потенциалов (напряжение), наблюдаемая в сети, является суммой этих напряжений, поэтому общее сопротивление (последовательное эквивалентное сопротивление) можно найти как сумму этих сопротивлений:
[латекс] \ text {R} _ {\ text {eq}} = \ text {R} _ {1} + \ text {R} _ {2} + \ cdots + \ text {R} _ {\ text {N}} [/ латекс].
В качестве особого случая сопротивление N резисторов, соединенных последовательно, каждый из которых имеет одинаковое сопротивление R, определяется как NR. Каждый резистор в параллельной конфигурации подвержен одной и той же разности потенциалов (напряжению), однако протекающие через них токи складываются. . Таким образом, можно вычислить эквивалентное сопротивление (Req) сети:
[латекс] \ frac {1} {\ text {R} _ {\ text {eq}}} = \ frac {1} {\ text {R} _ {1}} + \ frac {1} {\ text {R} _ {2}} + \ cdots + \ frac {1} {\ text {R} _ {\ text {N}}} [/ latex].
Параллельное эквивалентное сопротивление может быть представлено в уравнениях двумя вертикальными линиями «||» (как в геометрии) как упрощенное обозначение.Иногда вместо «||» используются две косые черты «//», если на клавиатуре или шрифте отсутствует символ вертикальной линии. Для случая, когда два резистора включены параллельно, это можно рассчитать по формуле:
[латекс] \ text {R} _ {\ text {eq}} = \ text {R} _ {1} \ parallel \ text {R} _ {2} = \ frac {\ text {R} _ {1 } \ text {R} _ {2}} {\ text {R} _ {1} + \ text {R} _ {2}} [/ latex].
В качестве особого случая сопротивление N резисторов, подключенных параллельно, каждый из которых имеет одинаковое сопротивление R, определяется как R / N. Сеть резисторов, которая представляет собой комбинацию параллельного и последовательного соединения, может быть разбита на более мелкие части, которые являются одним или другим, например, как показано на.
Схема резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный компонент и параллельный компонент.
Однако некоторые сложные сети резисторов не могут быть решены таким образом. Это требует более сложного анализа схем. Одним из практических применений этих соотношений является то, что нестандартное значение сопротивления обычно может быть синтезировано путем соединения ряда стандартных значений последовательно или параллельно. Это также можно использовать для получения сопротивления с более высокой номинальной мощностью, чем у отдельных используемых резисторов.В частном случае N идентичных резисторов, все подключенных последовательно или все подключенных параллельно, номинальная мощность отдельных резисторов умножается на N.
Сопротивление, резисторы и удельное сопротивление : краткий обзор сопротивления, резисторов и удельного сопротивления.
Зависимость сопротивления от температуры
Удельное сопротивление и сопротивление зависят от температуры, причем зависимость линейна для малых изменений температуры и нелинейна для больших.
Цели обучения
Сравнить температурные зависимости удельного сопротивления и сопротивления при больших и малых изменениях температуры
Ключевые выводы
Ключевые моменты
- При изменении температуры на 100ºC или менее удельное сопротивление (ρ) изменяется с изменением температуры ΔT как: [latex] \ text {p} = \ text {p} _ {0} (1 + \ alpha \ Delta \ text {T }) [/ latex] где ρ 0 — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления.
- При больших изменениях температуры наблюдается нелинейное изменение удельного сопротивления с температурой.
- Сопротивление объекта демонстрирует такую же температурную зависимость, как и удельное сопротивление, поскольку сопротивление прямо пропорционально удельному сопротивлению.
Ключевые термины
- удельное сопротивление : Обычно сопротивление материала электрическому току; в частности, степень сопротивления материала потоку электричества.
- температурный коэффициент удельного сопротивления : эмпирическая величина, обозначаемая α, которая описывает изменение сопротивления или удельного сопротивления материала в зависимости от температуры.
- полупроводник : Вещество с электрическими свойствами, промежуточными между хорошим проводником и хорошим изолятором.
Удельное сопротивление всех материалов зависит от температуры. Некоторые материалы могут стать сверхпроводниками (нулевое сопротивление) при очень низких температурах (см.). И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы колеблются быстрее и на больших расстояниях при более высоких температурах, электроны, движущиеся через металл, например, создают больше столкновений, эффективно увеличивая удельное сопротивление.При относительно небольших изменениях температуры (около 100 ° C или менее) удельное сопротивление ρ изменяется с изменением температуры ΔT, как выражается в следующем уравнении:
Сопротивление образца ртути : Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает внезапный скачок, а затем увеличивается почти линейно. с температурой.
[латекс] \ text {p} = \ text {p} _ {0} (1 + \ alpha \ Delta \ text {T}) [/ latex]
, где ρ 0 — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления.Для более значительных изменений температуры α может изменяться, или для нахождения ρ может потребоваться нелинейное уравнение. По этой причине обычно указывается суффикс для температуры, при которой измерялось вещество (например, α 15 ), и соотношение сохраняется только в диапазоне температур вокруг эталона. Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Температурный коэффициент обычно составляет от + 3 · 10 −3 K −1 до + 6 · 10 −3 K −1 для металлов, близких к комнатной температуре.Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Например, манганин (состоящий из меди, марганца и никеля) имеет α, близкое к нулю, поэтому его удельное сопротивление незначительно меняется с температурой. Это полезно, например, для создания не зависящего от температуры эталона сопротивления.
Обратите также внимание на то, что α отрицательна для полупроводников, что означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока.Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.
Сопротивление объекта также зависит от температуры, поскольку R 0 прямо пропорционально ρ. Для цилиндра мы знаем, что R = ρL / A, поэтому, если L и A не сильно изменяются с температурой, R будет иметь ту же температурную зависимость, что и ρ. (Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, и поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ.) Таким образом,
[латекс] \ text {R} = \ text {R} _ {0} (1 + \ alpha \ Delta \ text {T}) [/ latex]
— это температурная зависимость сопротивления объекта, где R 0 — исходное сопротивление, а R — сопротивление после изменения температуры T. Многие термометры основаны на влиянии температуры на сопротивление (см.). Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры.Устройство небольшое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Термометры : Эти знакомые термометры основаны на автоматическом измерении сопротивления термистора в зависимости от температуры.
Нелинейные резисторы — Блог пассивных компонентов
Источник: EPCI ABC статьи онлайн-справочника CLR
. R 5.1 ТЕРМИСТОРЫ NTCВ этом разделе мы опишем некоторые стили нелинейных резисторов, что означает, что они не подчиняются закону Ома.Упрощенно, материал резистора состоит из легированных гранул, содержащих различные оксиды, которые с помощью связующих были спрессованы до желаемой формы и затем спечены. Клеммы либо вставляются в корпус резистора, либо припаиваются к металлизированным поверхностям. Есть несколько типов инкапсуляции.
R 5.1.1 Конструкции ТермисторыNTC существуют в виде стержней, дисков, шариков, покрытых лаком, эпоксидной смолой, глазурью или расплавленным стеклом, а также в виде SMD.
Рисунок R5-1.Примеры конструкции термистора.
ТермисторыSMD с низким сопротивлением имеют ряд внутренних электродов, как показано на рисунке R5-2. Пониженное сопротивление достигается за счет конструкции, которая параллельно соединяет «резистивные элементы» внутри корпуса термистора.
Рисунок R5-2. Конструкция термистора микросхемы с низким сопротивлением.
Р 5.1.2. Температурная зависимость и допускиNTC означает отрицательный TCR (отрицательный температурный коэффициент).Температурная зависимость сильная, экспоненциальная и соответствует формуле
Постоянная материала A определяет сопротивление, а B — его температурную зависимость, то есть наклон кривой зависимости сопротивления от температуры. T означает температуру в Кельвинах (° C + 273). Если мы применим формулу [R5-1] к эталонной температуре T0 и общей температуре T и объединим два выражения, мы получим формулу
Константа B обычно определяется измерениями при 25 и 50 ° C.Обычно он имеет значения от 2500 до 5000. Значение немного меняется в зависимости от температуры. Следовательно, в формулах стоит символ ≈. Материал термистора сильно сжимается во время процесса спекания, что вызывает большие трудности с соблюдением допусков как для R 25 , так и для значения B в заданных пределах. Значение B указано с допусками, которые обычно составляют 5%. Контрольное значение R 0 относится к 20 или 25 ° C и имеет допуски 5, 10 или 20%. Однако, распиливая уже спеченную стружку до близких размеров, можно значительно повысить точность.R 25 допуски 0,2–1% больше не являются исключительными, равно как и допуск 1% для значения B. Результат этих наложенных допусков выглядит как на рисунках R5-3… R5-5.
Рисунок R5-3. Допуски термистора при эталонной температуре T25.
Рисунок R5-4. Эффект толерантности B.
Рисунок R5-5. Комбинированный эффект допусков R25 и B.
Для более точных применений указаны две или более точек на кривой сопротивления / температуры (сокращенно R / T-кривая), так называемое приложение отслеживания кривой.Тогда допуски B менее важны. Допуски такого двух- или трехточечного датчика могут быть указаны либо как отклонение сопротивления ∆R в процентах от R, либо как отклонение температуры ∆T в ° C при рассматриваемых температурах (рисунок R5-6). В последнем случае мы должны рассчитать ∆R с помощью температурного коэффициента α в формуле R5-3.
Рисунок R5-6. Пример задания альтернативного допуска с помощью так называемой кривой «бабочка».
Крутизна и температурный коэффициент
Наклон кривой R / T для термистора NTC определяется значением B.Иногда также указывается температурный коэффициент a. Если мы выведем выражение в уравнении R5-1, мы получим:
По сравнению с формулой R1-4, где TCR = 1 / R x ∆R / ∆T, мы находим то же основное выражение, что и для α. Как следует из уравнения R5-3, α сильно зависит от температуры. Около 25 ° C α обычно имеет значения от –3 до –5,5% / ° C. Еще один способ указать наклон кривой R / T — использовать отношения сопротивлений. Например, сравниваются отношения 0 R 50 R 25 R 125 .Коэффициенты указаны с допусками.
R 5.1.3 Эффекты самонагреваСамонагрев термистора NTC влияет на сопротивление. Если мы подадим напряжение на термистор, ток вначале линейно возрастет по закону Ома. Но как только внутренняя энергия генерирует ощутимое тепло, сопротивление начинает уменьшаться. Дальнейшее постепенное повышение напряжения вызывает уменьшение сопротивления, которое происходит быстрее, чем увеличивается ток. Кривая V / I начинает снижаться (Рисунки R5-7 и R5-8).
Рисунок R5-7. Эффект самонагрева на кривой V / I термистора NTC
Рисунок R5-8. Пример термистора NTC на диаграмме V / I в логарифмическом масштабе вместе с градацией мощности и сопротивления.
Пример на рисунке R5-8 помогает нам понять, как параметры V, I, P и R связаны друг с другом.
Р 5.1.4- Постоянная времени теплового охлаждения, т
- Теплоемкость, ч
- Коэффициент рассеяния, D
Еще два параметра связаны с рисунком R5-8, а именно, время и температура.Размер, форма и окружающая среда влияют на скорость изменения температуры. Мерой скорости изменения является тепловая постоянная времени t. Он указан для свободно установленного корпуса термистора в неподвижном воздухе в условиях нулевой мощности и определяется как время, необходимое для изменения температуры на 63,2% — точно (1-1 / e) — разницы ∆T между начальная и конечная температура тела T0 соответственно T∞ (Рисунок R5-9).
Фигура R5 -9.Постоянная времени t термистора NTC
С обозначениями на Рисунке R7-9 можно записать температуру термистора:
t также можно вывести из двух констант материала: теплоемкости H (Дж / ° C) и коэффициента рассеяния D (мВт / ° C).
Теплоемкость описывает, сколько джоулей (Вт) необходимо передать корпусу термистора, чтобы повысить его среднюю температуру на 1 ° C. Коэффициент рассеяния D выражается в мВт / ° C (или мВт / K) и определяется как мощность, повышающая среднюю температуру корпуса термистора на 1 ° C (или 1 K) при свободном монтаже в неподвижном воздухе.Разумеется, способность рассеивания мощности может быть увеличена с помощью вентиляторов, радиаторов или другой охлаждающей среды, например подходящей жидкости. В этом случае можно получить практическую постоянную времени. Если термистор помещен в подходящую жидкость, постоянная времени резко уменьшается. Помимо прочего, это используется при производственном контроле. Термистор погружается в ванну с точным контролем температуры и, таким образом, за очень короткое время доводится до стабильной температуры измерения.
R 5.1.5 Применение / выбор типаМожно выделить три основные группы приложений:
1. Использована температурная зависимость сопротивления R = f (T). Тогда может быть определена температура
- либо по окрестностям
- или внутренним питанием термистора.
2. Используется временная зависимость R = f (t), т.е. мы используем внутреннюю тепловую инерцию материала.
3.Используются типичные NTC характеристики материала.
При выборе термистора необходимо учитывать следующие требования.
- Требования к окружающей среде и герметичности. Стекло, глазурь, лак / эпоксидная смола, без инкапсуляции.
- Диапазон температур.
- Форма и дизайн. Чип / SMD, стержневой, дисковый или бортовой термистор.
- Пайка, точечная сварка или склеивание.
- Эталонная температура R 25 и температурный коэффициент α (-B / T2).
- Требования к допуску по R 25 и значение B. Это приложение R / T для сопоставления точек или отслеживания кривой?
- Рассеиваемая мощность а) без ощутимого нагрева. б) с максимальным изменением значения сопротивления.
- Тепловая постоянная времени τ.
Линеаризация R / T характеристики
Если нам нужна температурная зависимость с определенным наклоном характеристики R / T в более широком диапазоне температур, обычно трудно найти подходящую форму кривой.Однако с помощью постоянных резисторов в сочетании с термистором можно настроить кривую R / T в желаемом направлении. На рисунке R5-10 показаны некоторые примеры простых схем для этого.
Рисунок R5-10. Цепи коррекции R / T характеристики термисторов NTC.
При альтернативе c) можно получить интересное решение, задав размеры R p в соответствии с уравнением R5-6 ниже. Результирующее параллельное сопротивление дает кривую, которая пересекает прямую в трех точках, как показано на Рисунке R5-11.
Рисунок R5-11. Линеаризация кривой R / T термистора NTC.
R 5.1.6 Виды отказа Термисторычасто имеют очень маленькие размеры и высокие значения сопротивления. Они чувствительны к каждому «беспорядку» в материале. Открытая часть тела — это конечная область, особенно для маленьких размеров. Если корпус не герметизирован таким образом, чтобы любые изгибы свинца механически разгружались перед входом в корпус термистора, можно легко создать небольшие трещины вокруг входа для свинца.С этими трещинами сопротивление изменяется; также остается возможность для влаги и жидкостей проникать в организм.
Бусины, покрытые глазурью, и диски без покрытия с выводами, припаянными непосредственно поверх металлизированных контактных площадок, являются примерами уязвимых конструкций. Дисковые термисторы без покрытия не рекомендуется использовать в проводящих жидкостях и агрессивных газах. Спеченный материал иногда оседает в кристаллической структуре. Такие события проявляются в виде внезапных изменений сопротивления величиной от 3 до 10% и могут высвобождаться из-за тепла, изменений температуры и механических ударов.Частота отказов для необработанных партий поставки колеблется от 30 до 60%. Отверждение — это процесс пригорания, который обычно проводится в виде термической обработки.
Термисторы с шариками, заключенные в корпус из расплавленного стекла, часто имеют небольшие размеры и соответствующие тонкие выводы, состоящие из сплавов, которые часто трудно паять. В таких случаях единственным выходом может быть точечная сварка. Осторожность. Никогда не пытайтесь подключать термисторы NTC параллельно, чтобы увеличить рассеиваемую мощность.Термистор, который на данный момент имеет наименьшее сопротивление, получит более высокую токовую нагрузку, более сильный самонагрев, большее уменьшение сопротивления, еще более высокую нагрузку по току и т. Д., Пока эффект лавины не разрушит компонент.
R 5.1.7 НадежностьНадежность термисторов NTC сегодня считается хорошей. Это зависит не в последнюю очередь от серьезных производителей, имеющих программы на основе статистического управления процессами (SPC) для производства и проверенных типовых квалификаций.Если мы определим, что компоненты обработаны при выгорании, и если мы приобретем их с герметичными уплотнениями, то есть в стеклянном или стеклянном / металлическом корпусе, надежность таких термисторов следует отнести к той же группе, что и фиксированные металлизированные пленочные резисторы.
ТермисторыSMD устраняют некоторые проблемы, связанные с выводами чувствительных выводов. Вначале были некоторые проблемы с пайкой, но сегодня их можно считать преодоленными. Теперь у нас есть компонент, который конструктивно напоминает керамический конденсатор микросхемы, однако с меньшим количеством источников ошибок.Послойный вариант с низким сопротивлением имеет электроды, встроенные в материал, и с точки зрения надежности может быть сопоставим с гомогенным типом.
Ядерная радиация
Испытания с радиоактивным излучением в виде нейтронного, β- и γ-излучения показывают, что термисторы способны выдерживать высокие нагрузки без какого-либо влияния на характеристики.
Таблица R5-1. ТЕРМИСТОРЫ NTC
ABC CLR: Глава R Резисторы
Резисторы нелинейные
Контент, лицензируемый EPCI:
[1] EPCI Эксперты Европейского института пассивных компонентов оригинальные статьи
[2] Справочник по пассивным компонентам CLR от P-O.Fagerholt *
[one_third]
см. Предыдущую страницу:
Подстроечные потенциометры
[/ одна_третья] [одна_третья]
см. Следующую страницу:
[/ one_third_last]
* используется под авторским правом EPCI от CTI Corporation, США
Содержание этой страницы находится под международной лицензией Creative Commons Attribution-Share Alike 4.0.
Нелинейные резисторы | Кривые характеристик нелинейных устройств
В большинстве схем мы можем предположить, что сопротивление является постоянным по отношению к току и напряжению. Это линейное соотношение может быть графически показано на рисунке 1.
Рис.1: График линейной зависимости между током и напряжением
Например, если 3 В подается на определенный резистор и течет 1 А, то 6 В подается на тот же через резистор будет течь удвоенный ток, или 2А.
Нелинейное сопротивлениеСвойство, проявляемое устройствами, сопротивление которых не изменяется равномерно при изменении напряжения или тока.
Многие различные устройства имеют характеристические кривые (графики ВАХ), которые не являются прямыми линиями, и, следовательно, они не являются линейными устройствами. Такие устройства называются нелинейными, поскольку их сопротивления являются нелинейными сопротивлениями.
Типичные нелинейные устройства — это нить накаливания, диод, термистор и варистор (специальный резистор, сделанный из кристаллов карборунда, скрепленных связкой).Кривая на рисунке 2 показывает, как ток через варистор очень быстро увеличивается, когда напряжение на устройстве превышает определенную величину (в данном случае около 100 В). Также происходит соответствующее быстрое снижение сопротивления. Варисторы используются для защиты от перенапряжения в определенных цепях.
Рис. 2: Кривая ВАХ варистора
Термистор — еще один специальный резистор. Он изготовлен из оксидов металлов в подходящем связующем и имеет большой отрицательный коэффициент сопротивления (то есть сопротивление уменьшается с повышением температуры).Рисунок 3 иллюстрирует эту зависимость сопротивления от температуры.
Рис. 3. Зависимость сопротивления термистора от температуры
Кривая на рис. 4 показывает, как сопротивление лампы накаливания изменяется с напряжением.
Рис.4: ВАХ лампы накаливания
На рисунке 5 показана ВАХ типичного кремниевого диода.
Рис. 5: Кривая I-V кремниевого диода
При любом нелинейном сопротивлении важно помнить, что сопротивление, рассчитанное для одного значения V и I, нельзя использовать при изменении V и I.Но, сделав ряд изменений напряжения и тока, мы можем построить кривую сопротивления, подобную кривым на рисунках выше.
Закон Ома — сопротивление
Интуитивно понятно, что напряжение и ток каким-то образом связаны. Например, если увеличить разность потенциалов между двумя концами провода, мы ожидаем, что будет течь больший ток, точно так же, как скорость потока газа по трубопроводу увеличивается, когда применяется большая разница давлений.
Для большинства материалов, включая металлические проводники, эта взаимосвязь между напряжением и током является линейной: по мере увеличения разности потенциалов между двумя концами проводника пропорционально увеличивается ток через проводник.
Фактически, постоянная по току и напряжению. Некоторые материалы и электронные устройства демонстрируют нелинейную зависимость между током и напряжением, то есть их сопротивление изменяется в зависимости от приложенного напряжения.
Соотношение V = IR будет по-прежнему сохраняться в любой момент времени, но значение R будет другим для разных значений V и I .
Эти нелинейные устройства имеют специализированное применение и не будут обсуждаться в этой статье. Сопротивление также имеет тенденцию меняться в зависимости от температуры, хотя проводник может подчиняться закону Ома при любой температуре.
Например, сопротивление медного провода увеличивается по мере нагрева. В большинстве режимов работы эти отклонения незначительны. Как правило, в любой ситуации, когда изменения сопротивления значительны, это прямо упоминается. Таким образом, всякий раз, когда кто-то сталкивается с термином «сопротивление» без дальнейшей разработки, можно с уверенностью предположить, что в данном контексте это сопротивление является фиксированным, неизменным свойством рассматриваемого объекта.
Сопротивление зависит от состава материала объекта, а также от его формы. Для провода сопротивление увеличивается с увеличением длины и уменьшается с увеличением площади поперечного сечения.
Опять же, аналогия с газовой или водопроводной трубой удобна: мы знаем, что труба допускает более высокую скорость потока при той же разнице давлений, если она имеет больший диаметр, в то время как скорость потока будет уменьшаться с увеличением длины трубы. . Это происходит из-за трения в трубе, и фактически аналогичное «трение» возникает, когда электрический ток проходит через материал.
Это трение можно объяснить, сославшись на микроскопическое движение электронов или ионов и отметив, что они взаимодействуют или сталкиваются с другими частицами в материале по мере их движения. Возникающие в результате силы имеют тенденцию препятствовать движению носителей заряда и, по сути, ограничивают скорость их прохождения. Эти силы различаются для разных материалов из-за разного пространственного расположения электронов и ядер, и они определяют способность материала проводить.
Это внутреннее свойство материала, не зависящее от размера или формы, называется удельным сопротивлением и обозначается как ρ (греческое rho в нижнем регистре).
Фактическое сопротивление объекта определяется как удельное сопротивление, умноженное на длину объекта ( l ) и деленное на его площадь поперечного сечения ( A ):
Единицы измерения сопротивления — Ом, сокращенно Ом (греческая заглавная омега). Изменив закон Ома, мы увидим, что сопротивление равно напряжению, деленному на ток. Таким образом, единицы сопротивления эквивалентны единицам напряжения, разделенным на единицы тока. По определению, один Ом равен одному вольт на ампер ( Ом = В / А ).
Единицы измерения удельного сопротивления — ом-метры ( Ом-м ), которые можно восстановить по предыдущей формуле: когда ом-метры умножаются на метры (для l ) и делятся на квадратные метры (для A). ), результат будет просто ом. Удельное сопротивление, которое является неотъемлемым свойством материала, не следует путать с сопротивлением на единицу длины (обычно провода), выраженным в единицах Ом на метр ( Ом / м ).
Последняя мера уже учитывает диаметр проволоки; фактически он представляет собой величину ρ / A .Удельное сопротивление различных материалов в Ом-м можно найти в технических таблицах.
ИСТОЧНИК: Electric Power Systems — A. Von Meir
chet_boylestad_introduct_10 | Сопротивление | Глоссарий
Абсолютный ноль Температура, при которой прекращается любое движение молекул; 2273,15 ° С.
Круглый мил (СМ) Площадь поперечного сечения проволоки диаметром один мил.
Цветовое кодирование Метод, использующий цветные полосы для обозначения уровней сопротивления и допусков резисторов.
Электропроводность ( G ) Показатель относительной легкости, с которой ток может быть установлен в материале. Измеряется в сименсах (S).
Эффект Купера «Спаривание» электронов при их движении через среду.
Пластичность Свойство материала, позволяющее вытягивать его в длинные тонкие проволоки.
Предполагаемая абсолютная температура Температура, через которую прямолинейная аппроксимация фактической кривой зависимости сопротивления от температуры будет пересекать ось температуры.
Пластичность Свойство материала, которое позволяет ему обрабатывать множество различных форм.
Отрицательный температурный коэффициент сопротивления Величина, показывающая, что сопротивление материала будет уменьшаться с увеличением температуры.
Ом (В) Единица измерения, применяемая к сопротивлению.
Омметр Прибор для измерения уровней сопротивления.
Фотопроводящий элемент Двухконтактный полупроводниковый прибор, оконечное сопротивление которого определяется интенсивностью падающего света на его открытую поверхность.
Положительный температурный коэффициент сопротивления Значение, показывающее, что сопротивление материала увеличивается с увеличением температуры.
Потенциометр Устройство с тремя выводами, с помощью которого уровни потенциала могут изменяться линейным или нелинейным образом.
PPM / ° C Температурная чувствительность резистора в частях на миллион на градус Цельсия.
Сопротивление Мера сопротивления потоку заряда через материал.
Удельное сопротивление (r) Константа пропорциональности между сопротивлением материала и его физическими размерами.
Реостат Элемент, оконечное сопротивление которого может изменяться линейным или нелинейным образом.
Сопротивление листа Определено r / d для тонкопленочных и интегральных схем.
Сверхпроводник Проводники электрического заряда, которые имеют практически нулевое сопротивление.
Термистор Двухконтактный полупроводниковый прибор, сопротивление которого чувствительно к температуре.


 2
2