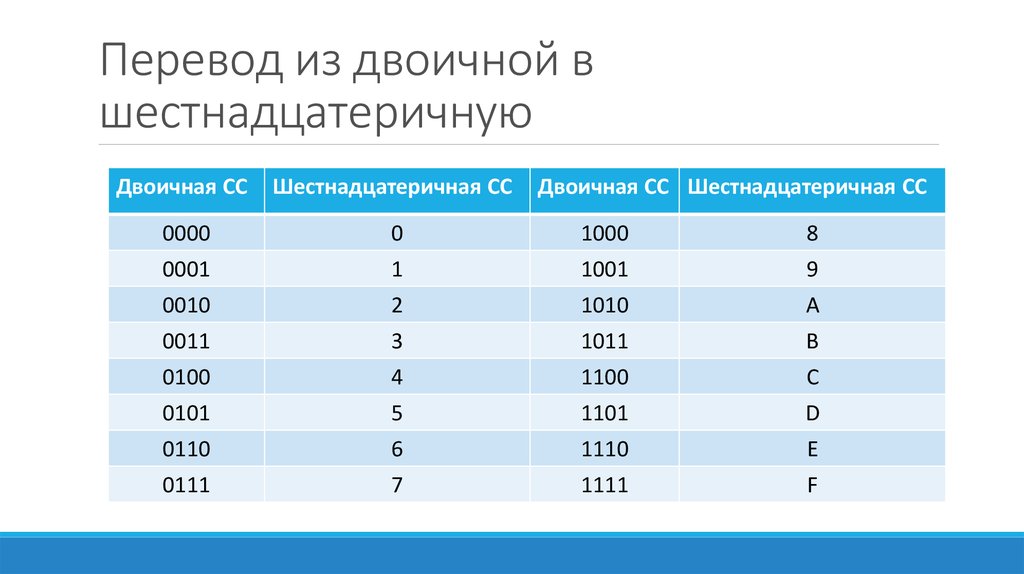
Урок-контрольная работа по дисциплине информатика и ИКТ «Системы счисления»
Филатова Юлия Александровна
преподаватель математики, информатики и ИКТ
ГБПОУ ВО «Лискинский аграрно-технологический техникум»
Урок — контрольная работа
по дисциплине информатика и ИКТ
«Системы счисления»
Цель урока:
- проверить знания, умения и навыки учащихся по теме «Системы счисления».
Задачи:
- образовательные: выявить качество и уровень овладения знаниями и умениями, полученными на уроках;
- воспитательные: способствовать формированию ответственного отношения к учению, готовности и мобилизации усилий на безошибочное выполнение заданий;
- развивающие: развить логическое мышление, память, способность к анализу и синтезу.

Тип урока: урок контроля и проверки знаний и умений.
Формы урока: контрольная работа.
Форма организации совзаимодействия на уроке: индивидуальная
Ход урока
Организационный момент
Выполнение контрольной работы
Инструкция к заданиям
На выполнение контрольной работы отводится 45 минут. Работа состоит из 15 заданий. В заданиях требуется выбрать один вариант ответа. За выполнение каждого задания вы получаете 1 балл. Баллы, полученные за выполненные задания, суммируются. Максимальное количество 15 баллов.
Оценивание работы:
0-7 баллов – «2» |
8-10 баллов – «3» |
11-13 баллов – «4» |
14-15 баллов – «5» |
Контрольно-измерительный материал
Задание 1
Вопрос: Какое десятичное число в двоичной системе счисления записывается как 1101?
1) 17
2) 13
3) 26
4) 8
Задание 2
Вопрос: Как записывается в двоичной системе счисления число 15?
1) 1111
2) 1010
3) 1110
4) 1000
Задание 3
Вопрос: Умножьте два числа в двоичной системе счисления 110112*1012
1) 10000111
2) 11111111
3) 11011101
4) 10011111
Задание 4
Вопрос: Укажите самое большое число
1) 756 в 8-ричной системе счисления
2) 756 в 16-ричной системе счисления
3) 756 в 10-ричной системе счисления
4) 756 в 12-ричной системе счисления
Задание 5
Вопрос: Число, записанное в римской системе счисления CDX, равно:
1) 610
2) 410
3) 510
4) 730
Задание 6
Вопрос: Число байт, необходимых для записи числа 244 равно.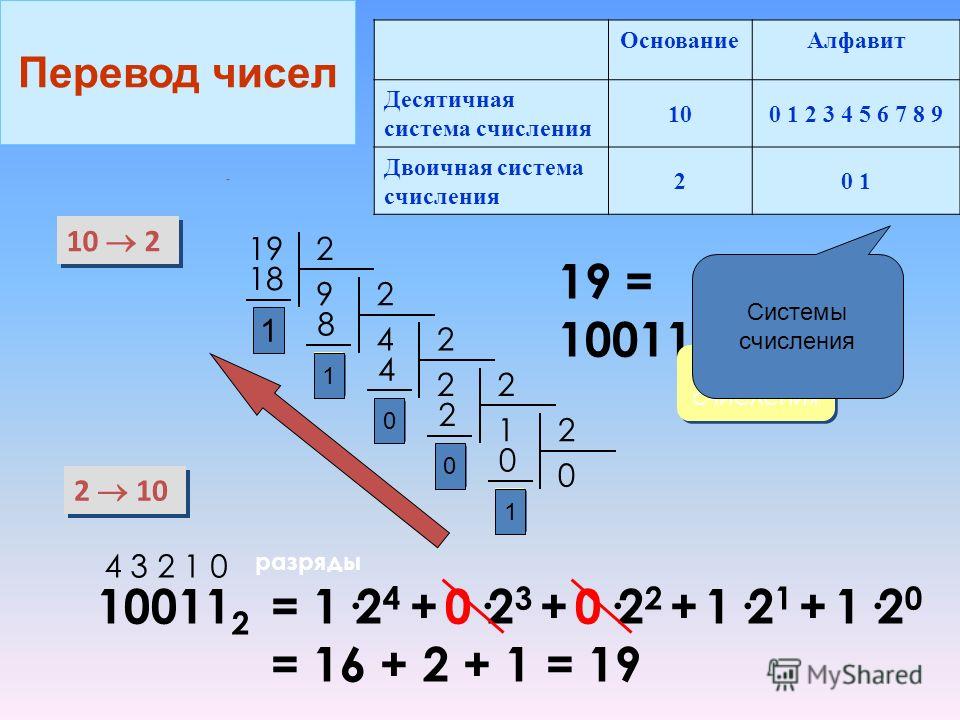 ..
..
1) 10
2) 11
3) 82
4) 256
Задание 7
Вопрос: Перевести число 101,12 в десятичную систему счисления:
1) 5,5
2) 6,5
3) 5,2
4) 6,2
Задание 8
Вопрос: Для перевода целых десятичных чисел из одной системы счисления в любую другую используется метод, основанный на
1) делении переводимого числа на основание новой системы счисления
2) сложении переводимого числа с основанием новой системы счисления
3) умножении переводимого числа с основанием новой системы счисления
4) замене каждой цифры переводимой дроби ее эквивалентом в новой системе счисления
Задание 9
Вопрос: Увеличение основания системы счисления делает запись числа более…
1) детальной
2) читаемой
3) компактной
4) длинной
Задание 10
Вопрос: Выбрать правильную запись числа 21310 в развернутой форме
1) 2∙102+1∙101+3∙100
2) 2∙103+1∙102+3∙101
3) 3∙102+1∙101+2∙100
Задание 11
Вопрос: Как представлено число 4210 в восьмеричной системе счисления?
278
528
478
368
Задание 12
Вопрос: Какое из чисел следует за числом 1278 в восьмеричной системе счисления?
1318
1378
1308
1288
Задание 13
Вопрос: Сколько единиц в двоичной записи числа 20510?
5
2
3
4
Задание 14
Вопрос: Чему равна сумма чисел X и Y при x=110112, y=10102?
1110012
1001012
100012
1110112
Задание 15
Вопрос: Определите систему счисления p, в которой число 2210 записывается как 42p
Двоичная
Троичная
Пятиричная
Девятиричная
Правильные ответы
задание | ответ |
1 | 2 |
2 | 1 |
3 | 1 |
4 | 2 |
5 | 2 |
6 | 2 |
7 | 1 |
8 | 1 |
9 | 3 |
10 | 1 |
11 | 2 |
12 | 3 |
13 | 1 |
14 | 2 |
15 | 3 |
3. Подведение итогов урока
Подведение итогов урока
4. Домашнее задание
Подготовить реферат по одной из тем:
История систем счисления.
Позиционные и непозиционные системы счисления.
Римская система счисления.
9 класс: Системы счисления. Вариант 2
Системы счисления
Вариант 2
1. Как представляется число 4210 в восьмеричной системе счисления?
1) 278 2) 528 3) 478 4) 368
2. Какое из чисел следует за числом 1278 в восьмеричной системе счисления?
1) 1318 2) 1378 3) 1308 4) 1288
3. Сколько единиц в двоичной записи числа 20510?
1) 5 2) 2 3) 3 4) 4
4. Чему равна сумма чисел x и y при x=110112, y=10102?
1) 1110112 2) 1001012 3) 100012 4) 1110112
5.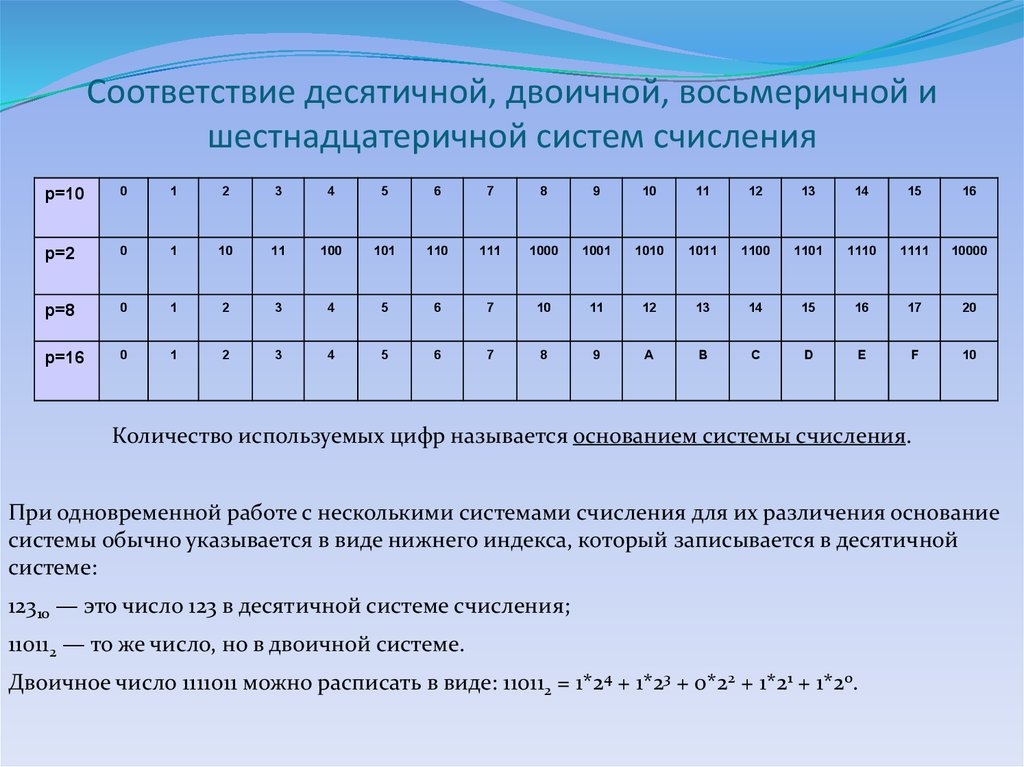
6. Как представлено число 1008 в десятичной системе счисления?
1) 6410 2) 5210 3) 7710 4) 6010
7. Какое из чисел следует за числом 9F16 в шестнадцатеричной системе счисления?
1) 10016 2) AF16 3) A016 4) 9116
8. Сколько значащих нулей в двоичной записи числа 10010?
1) 1 2) 2 3) 5 4) 4
9. Чему равна сумма чисел x и y при x=111002, y=148?
1) 2416 2) 4110 3) 448 4) 4010
10. Определите
систему счисления р, в которой число 2710 записывается как 36р.
11. Как записывается в двоичной системе счисления число 6310?
1) 11112 2) 10000112 3) 111101
12. Какое из десятичных чисел больше двоичного числа 11112?
1) 1410 2) 1310 3) 1510 4) 1710
13. Сколько единиц в восьмеричной записи числа 128116?
1) 5 2) 2 3) 3 4) 4
14. Дано а=ВВ16, b=258, с=а+b. Найдите значение с.
1) DD16 2) 20810 3) 32010 4) 11010002
15. Запишите
через запятую в порядке возрастания основания всех систем счисления, в которых
запись числа 31
16. Как записывается в шестнадцатеричной системе десятичное число 5710?
1) 3А16 2) 4016 3) 3916 4) 2F16
17.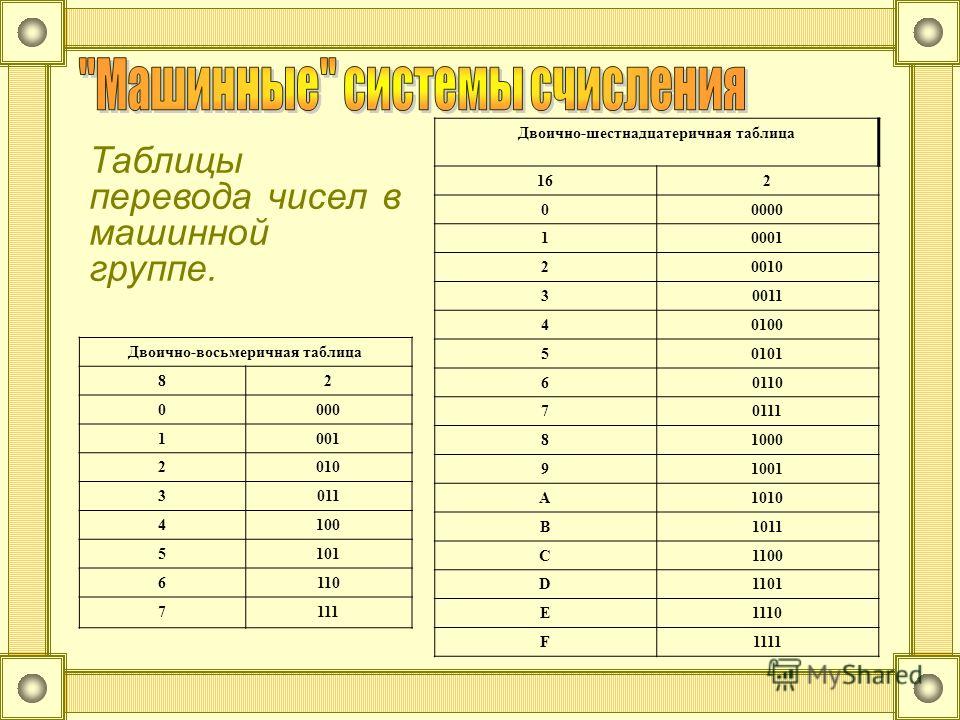 Дано
х=518. Какое из чисел y удовлетворяет условию y>x?
Дано
х=518. Какое из чисел y удовлетворяет условию y>x?
1) 4110 2) 3116 3) 2216 4) 1000002
18. Сколько значащих нулей в двоичной записи числа СЕ16?
1) 8 2) 2 3) 3 4) 5
19. Чему равна сумма 112 + 1018 + 110116?
1) 442110 2) 1010116 3) 121310 4) 101012
20. Запишите через запятую в порядке возрастания основания всех систем счисления, в которых запись числа 2110 оканчивается на 5.
АДС1278-НТ | Купить TI Parts
ТЕХНИЧЕСКИЕ ДАННЫЕ
| Кол-во | Цена |
|---|---|
| — | |
| — | |
| + |
*Только для справки
- ECCN США: 3A001A2A
| Пакет | Пины СФП (ГКП) | 84 |
| Диапазон рабочих температур (°C) от -55 до 210 |
| Количество в упаковке | Перевозчик 1 | ПОДНОС ДЖЕДЕК (5+1) |
- Одновременное измерение восьми каналов
- Скорость передачи данных до 128 тыс.

- Характеристики переменного тока:
Полоса пропускания 62 кГц
111 дБ SNR (режим высокого разрешения)
–108 дБ THD - DC Точность:
Дрейф смещения 0,8 мкВ/°C
Дрейф коэффициента усиления 1,3 ppm/°C - Выбираемые режимы работы:
Высокоскоростной: 128 тыс. выборок в секунду, отношение сигнал/шум 106 дБ
Высокое разрешение: 52 тыс. выборок в секунду, отношение сигнал-шум 111 дБ
Маломощный: 52 кГц, 31 мВт/канал
Низкая скорость: 10 тыс. выборок в секунду, 7 мВт/канал - Линейно-фазовый цифровой фильтр
- SPI или последовательный интерфейс Frame-Sync
- Ошибка низкой апертуры выборки
- Опция выхода модулятора (обход цифрового фильтра)
- Аналоговый источник питания: 5 В
- Цифровое ядро: 1,8 В
- Питание ввода/вывода: от 1,8 В до 3,3 В
- В настоящее время доступно в корпусе HTQFP-64 PowerPAD™,
84-контактный корпус HFQ и опция KGD Chiptray - поддерживает приложения с экстремальными температурами
- Контролируемый базовый уровень
- Одна сборочная/испытательная площадка
- Одна производственная площадка
- Доступен в диапазоне экстремальных (–55°C/210°C) температур
- Увеличенный жизненный цикл продукта
- Расширенное уведомление об изменении продукта
- Отслеживаемость продукции
- Высокотемпературные продукты Texas Instruments широко используются
Оптимизированные кремниевые (кристаллы) решения с Dsign и процессом Усовершенствования
для повышения производительности при длительном диапазоне температур
- ПРИЛОЖЕНИЙ
- Бурение вниз по скважине
- Высокотемпературная среда
- Вибрационный/модальный анализ
- Многоканальный сбор данных
- Акустические/динамические тензодатчики
- Датчики давления
(1) Доступны настраиваемые диапазоны температур
Все другие товарные знаки являются собственностью их соответствующих владельцев
Основан на одноканальном
АДС1271,
ADS1278 (восьмеричный) представляет собой 24-битный дельта-сигма (ΔΣ) аналого-цифровой преобразователь (АЦП) со скоростью передачи данных
до 128 тыс.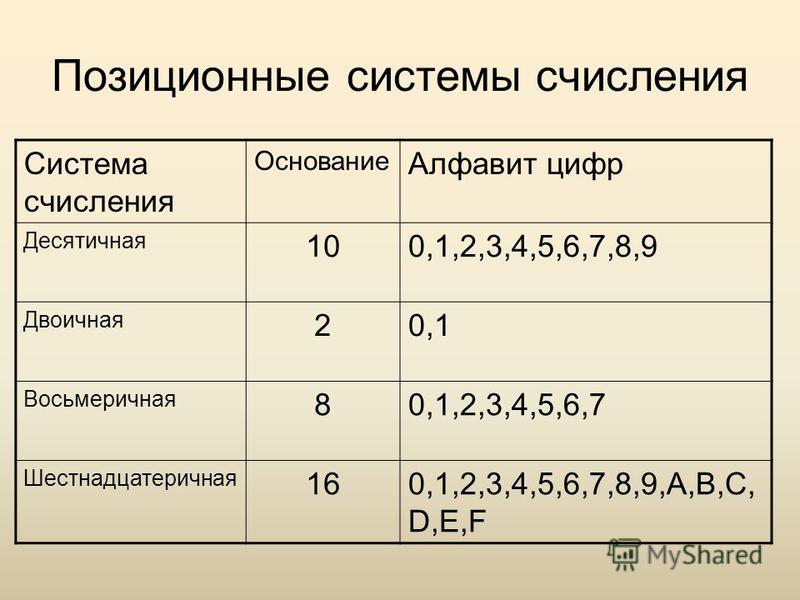 выборок в секунду (SPS), что позволяет осуществлять одновременную выборку восьми каналов.
выборок в секунду (SPS), что позволяет осуществлять одновременную выборку восьми каналов.
Традиционно промышленные дельта-сигма АЦП с хорошим дрейфом используют цифровые фильтры с большим спадом в полосе пропускания. В результате они имеют ограниченную полосу пропускания сигнала и в основном подходит для измерения постоянного тока. АЦП высокого разрешения в аудиоприложениях предлагают большую полезную полосы пропускания, но характеристики смещения и дрейфа значительно слабее, чем соответствующие промышленные аналоги. ADS1278 сочетает в себе эти типы преобразователей, обеспечивая высокую точность промышленные измерения с превосходными характеристиками постоянного и переменного тока.
Модулятор высокого порядка, стабилизированный прерывателем, обеспечивает очень низкий дрейф с низким внутриполосным
шум. Встроенный децимирующий фильтр подавляет модулятор и внеполосный шум сигнала. Эти АЦП
обеспечивают полезную полосу пропускания сигнала до 90% скорости Найквиста с менее чем 0,005 дБ
рябь.
Четыре режима работы позволяют оптимизировать скорость, разрешение и мощность. Все операции контролируются непосредственно штифтами; нет регистров для программирования. Устройство полностью указан в расширенном промышленном диапазоне (от –55°C до 210°C) и доступен в корпусе HTQFP-64. Пакет PowerPAD (от 55°C до 175°C), 84-контактный пакет HFQ и опциональный лоток для чипов KGD.
| Кол-во | Цена |
|---|---|
| — | |
| — | |
| + |
Варианты держателя
Вы можете выбрать различные варианты держателей в зависимости от количества деталей, включая полную катушку, индивидуальную катушку, обрезанную ленту, трубку или лоток.
Индивидуальная катушка представляет собой непрерывный отрезок ленты из одной катушки для обеспечения прослеживаемости по коду партии и даты, созданный для точного запрошенного количества. В соответствии с отраслевыми стандартами латунная прокладка соединяет 18-дюймовую ведущую и концевую части по обеим сторонам отрезанной ленты для прямой подачи в автоматизированные сборочные машины. TI включает плату за намотку для индивидуальных заказов на катушки.
Обрезная лента представляет собой отрезок ленты, отрезанный от катушки. TI может выполнять заказы, используя несколько полос разрезанных лент или коробок, чтобы удовлетворить запрошенное количество.
TI часто поставляет устройства в трубке или в лотке в коробке, в тубе или лотке, в зависимости от наличия на складе. Мы упаковываем все ленты, трубки или коробки для образцов в соответствии с требованиями защиты от внутреннего электростатического разряда и уровня чувствительности к влаге.
Узнать больше
Может быть доступен выбор кода партии и даты
Добавьте количество в корзину и начните процесс оформления заказа, чтобы просмотреть варианты, доступные для выбора кодов партий или дат из существующих запасов.
Узнать больше
1278 (номер)
1,278 ( одна тысяча двести семьдесят восемь ) — четное четырехзначное составное число, расположенное между числами 1277 и 1279. В экспоненциальной записи оно записывается как 1,278 × 10 9 .0106 3 . Сумма его цифр равна 18. Всего у него 4 простых делителя и 12 положительных делителей. Существует 420 положительных целых чисел (до 1278), взаимно простых с 1278.
- Прайм? №
- Числовая четность Четный
- Длина номера 4
- Сумма цифр 18
- Цифровой корень 9
| Краткое имя | 1 тыс.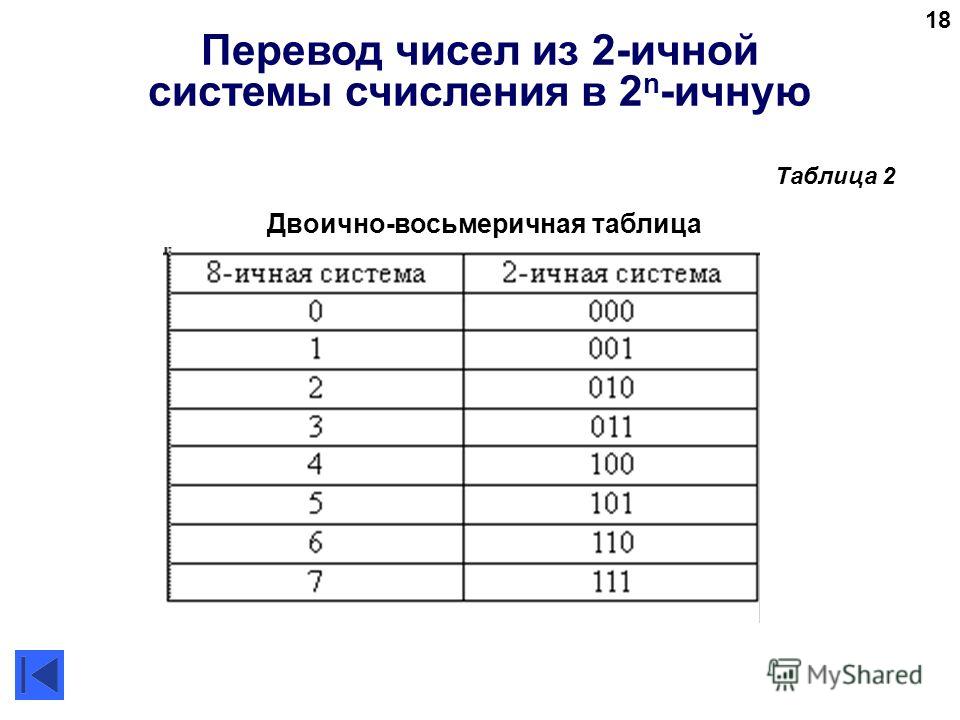 278 278 |
|---|---|
| Полное наименование | одна тысяча двести семьдесят восемь |
| Научное обозначение | 1,278 × 10 3 |
|---|---|
| Техническое обозначение | 1,278 × 10 3 |
Простые множители 2 × 3 2 × 71
Составное число
| ω(n) | Отличительные факторы | 3 | Общее количество различных простых множителей |
|---|---|---|---|
| Ом(n) | Всего факторов | 4 | Общее количество простых множителей |
| рад(н) | Радикальный | 426 | Произведение различных простых чисел |
| λ(n) | Лиувилль Лямбда | 1 | Возвращает четность Ω(n), такую, что λ(n) = (-1) Ом(n) |
| мк(н) | Мебиус Мю | 0 | Возвращает:
|
| Л(н) | Функция Мангольдта | 0 | Возвращает log(p), если n является степенью p k любого простого числа p (для любого k >= 1), в противном случае возвращает 0 |
Разложение числа 1278 на простые множители равно 2 × 3 2 × 71.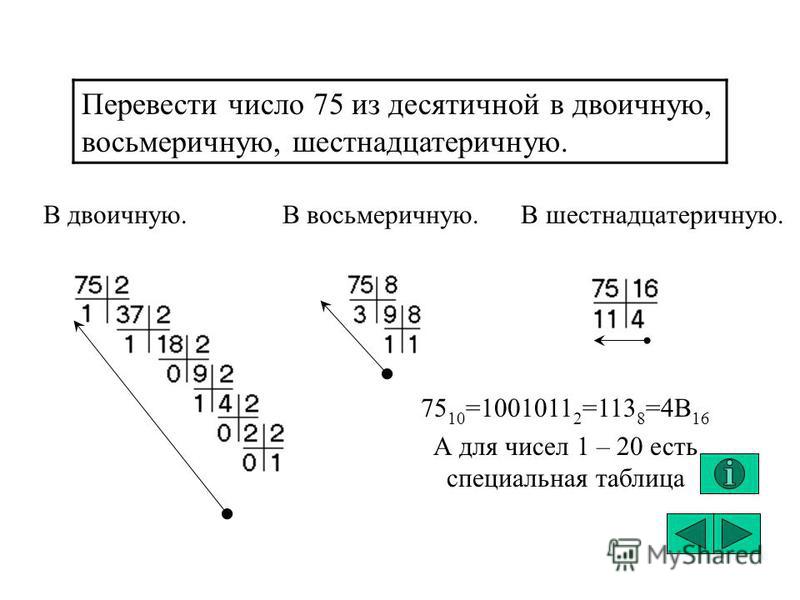 Поскольку всего 4 простых делителя, 1278 является составным числом.
Поскольку всего 4 простых делителя, 1278 является составным числом.
1, 2, 3, 6, 9, 18, 71, 142, 213, 426, 639, 1278
12 делителей
| Четный делитель | 6 |
|---|---|
| Нечетные делители | 6 |
| 4k+1 делитель | 3 |
| 4k+3 делителя | 3 |
| τ(n) | Всего делителей | 12 | Общее число положительных делителей n |
|---|---|---|---|
| σ(n) | Сумма делителей | 2808 | Сумма всех положительных делителей n |
| с(н) | Аликвотная сумма | 1530 | Сумма собственных положительных делителей n |
| А(н) | Среднее арифметическое | 234 | Возвращает сумму делителей (σ(n)), деленную на общее количество делителей (τ(n)) |
| Г(н) | Среднее геометрическое | 35,749125863439 | Возвращает корень n из произведения n делителей |
| Н(н) | Среднее гармоническое | 5. 4615384615385 4615384615385 | Возвращает общее количество делителей (τ(n)), деленное на сумму обратной величины каждого делителя |
Число 1278 можно разделить на 12 положительных делителей (из них 6 четных и 6 нечетных). Сумма этих делителей (считая 1278) равна 2808, среднее значение равно 234.
1 ф (п) п
| φ(n) | Эйлер Тотиент | 420 | Общее количество положительных целых чисел, не превышающих n, взаимно простых с n |
|---|---|---|---|
| λ(n) | Кармайкл Лямбда | 210 | Наименьшее положительное число такое, что λ(n) ≡ 1 (mod n) для всех чисел, взаимно простых с n |
| п(н) | Прайм Пи | ≈ 210 | Общее количество простых чисел меньше или равно n |
| р 2 (н) | Сумма 2 квадратов | 0 | Количество способов n представить в виде суммы двух квадратов |
Существует 420 натуральных чисел (меньше 1278), взаимно простых с 1278. И есть примерно 210 простых чисел, меньших или равных 1278.
И есть примерно 210 простых чисел, меньших или равных 1278.
| м | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| н мод м | 0 | 0 | 2 | 3 | 0 | 4 | 6 | 0 |
Число 1278 делится на 2, 3, 6 и 9.
С помощью арифметических функций
- Арифметика
- Обильный
Выражается через конкретные суммы
- Вежливый
- Не гипотенуза
| Основание | Система | Значение |
|---|---|---|
| 2 | Двоичный | 10011111110 |
| 3 | Тернарный | 1202100 |
| 4 | Четвертичный | 103332 |
| 5 | Квинарий | 20103 |
| 6 | Сенар | 5530 |
| 8 | Окталь | 2376 |
| 10 | Десятичный | 1278 |
| 12 | Двенадцатеричный | 8а6 |
| 16 | Шестнадцатеричный | 4фе |
| 20 | Десятичное число | 33i |
| 36 | База36 | и |
Умножение
п × у| n×2 | 2556 |
|---|---|
| n×3 | 3834 |
| n×4 | 5112 |
| n×5 | 6390 |
Отдел
n÷y| н÷2 | 639.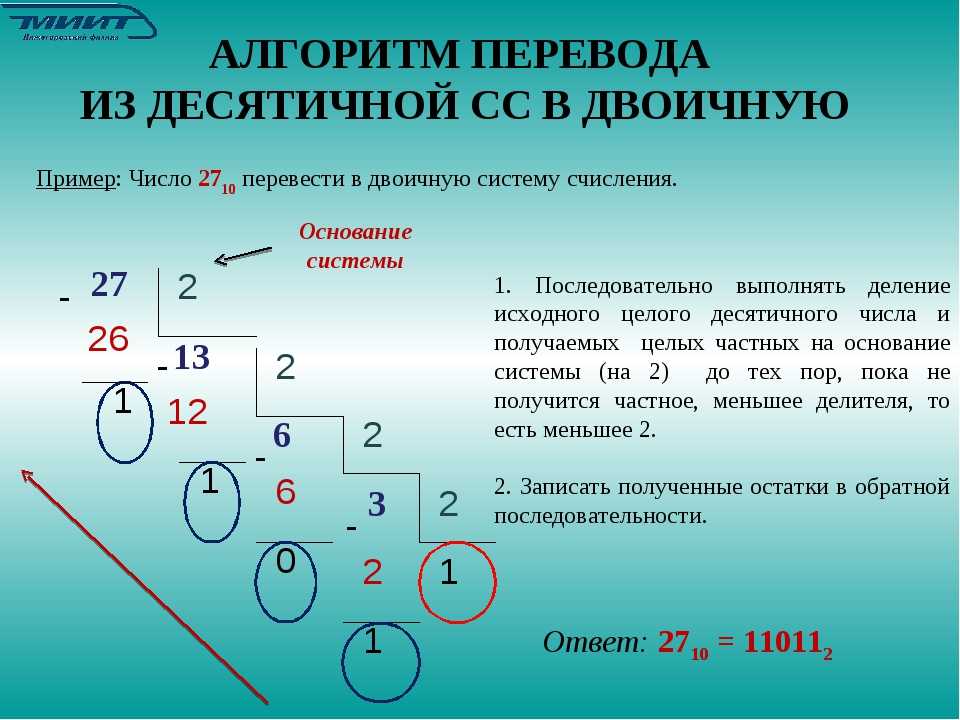 000 000 |
|---|---|
| н÷3 | 426.000 |
| н÷4 | 319.500 |
| н÷5 | 255.600 |
Возведение в степень
п г| п 2 | 1633284 |
|---|---|
| п 3 | 2087336952 |
| п 4 | 2667616624656 |
| п 5 | 3409214046310368 |
N-й корень
г √n| 2 √n | 35,749125863439 |
|---|---|
| 3 √n | 10. 852012481787 852012481787 |
| 4 √n | 5,97721324 |
| 5 √n | 4.1812503432518 |
Круг
Радиус = n| Диаметр | 2556 |
|---|---|
| Окружность | 8029.9108225755 |
| Зона | 5131113.0156258 |
Сфера
Радиус = n| Том | 8743416578.6263 |
|---|---|
| Площадь поверхности | 20524452. 062503 062503 |
| Окружность | 8029.9108225755 |
Квадрат
Длина = n| Периметр | 5112 |
|---|---|
| Зона | 1633284 |
| Диагональ | 1807.3649327128 |
Куб
Длина = n| Площадь поверхности | 9799704 |
|---|---|
| Том | 2087336952 |
| Диагональ пространства | 2213. |