Тест: Кодирование числовой информации с помощью систем счисления
Тест: Кодирование числовой информации с помощью систем счисления — Информатика 11 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Информатика »
- 11 класс »
- Кодирование числовой информации с помощью систем счисления
Кодирование числовой информации с помощью систем счисления
Информатика 11 класс | Автор: Власов Сергей Евгеньевич | ID: 9053 | Дата: 31.12.2016
Помещать страницу в закладки могут только зарегистрированные пользователи
В зависимости от способа изображения чисел системы счисления делятся на:
арабские и римские;позиционные и непозиционные;
представление в виде ряда и в виде разрядной сетки.
Вопрос № 2
Для представления чисел в шестнадцатеричной системе счисления используются:
цифры 0 — 9 и буквы А — F;буквы А — Q;
числа 0 — 15.
Вопрос № 3
Чему равно число DXXVII в десятичной системе счисления?
527;499;
474.
Вопрос № 4
Какие цифры используются в шестеричной системе счисления?
0, 6, 5, 2;8, 6, 1, 0;
0, 3, 2, 1.
Вопрос № 5
Система счисления — это:
представление чисел в экспоненциальной форме;представление чисел с постоянным положением запятой;
способ представления чисел с помощью символов, имеющих определенное количественное значение.
Вопрос № 6
Для перевода целых десятичных чисел из одной системы счисления в любую другую используется метод, основанный на
делении переводимого числа на основание новой системы счислениясложении переводимого числа с основанием новой системы счисления
замене каждой цифры переводимой дроби ее эквивалентом в новой системе счисления
Вопрос № 7
Совокупность правил для обозначения и наименования чисел, называется
Алфавитом;Системой счисления;
Алгоритмом.
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.ru 2013-2023
E-mail администратора: [email protected]
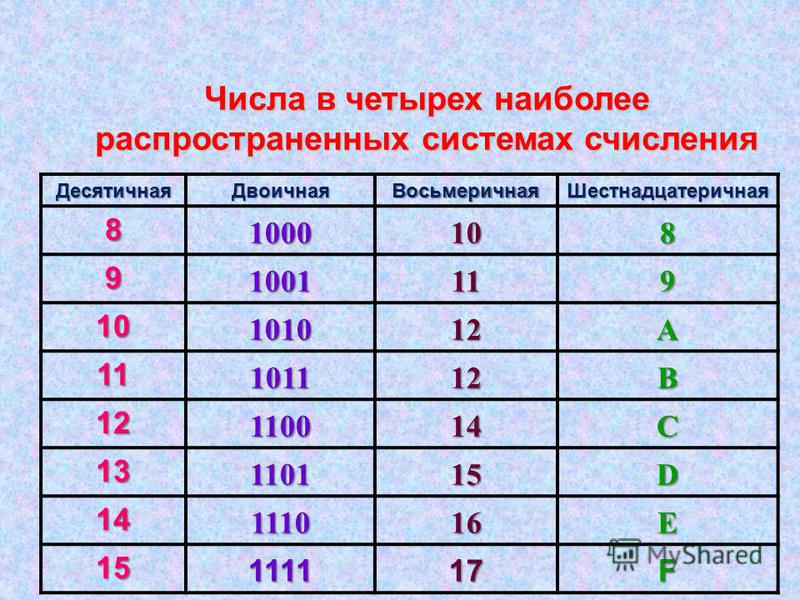
Во многих системах счисления выбирается некоторое число p – основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, принимающими значение от 0 до p-1, т. е. в виде ak * pk + ak-1 * pk-1 + … + a1 * p + a0. Такая форма записи называется развёрнутой формой числа. Далее такое число сокращённо записывается в виде (akak-1 … a1a0)p. В этой записи значение каждой цифры
зависит от того места, которое эта цифра занимает. Например, в числе 222 двойка учaствует три раза. Но самая правая из них означает две единицы, вторая справа – два десятка, т. е. двадцать, а третья – две сотни: 22210 = 2 * 102 + 2 * 101 + 2 * 100.Системы счисления, построенные таким образом, называются позиционными. Для дробных чисел развёрнутая форма числа будет выглядеть следующим образом: ak Например: 555,5510 = 5 * 102 + 5 * 101 + 5 * 100+ 5 * 10-1 + 5 * 10-2 . Итак: позиционная система счисления — это система счисления, в которой
числовое значение каждой цифры зависит от номера её позиции (разряда) в
последовательности цифр, представляющей число. Самой распространенной позиционной системой счисления является современная десятичная система счисления, в которой используется 10 арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например, в записи числа 555 в десятичной системе счисления используется одна цифра 5, но в зависимости от занимаемого ею места, она имеет разное значение — 5 сотен, 5 десятков, 5 единиц. Рассмотрим некоторые позиционные системы счисления:
Задания для самоконтроля: Что обозначает вторая цифра в десятичной записи числа 256? Количество сотен Назовите самую большую цифру шестеричной системы счисления 5 Какой системе счисления позволил появиться счет на пальцах? Пятеричной системе счисления В какой системе счисления для записи цифр используются латинские буквы? Шестнадцатеричная система счисления Назовите самую большую цифру двенадцатеричной системы счисления 12 |
Числовое значение цифры
определяется по строгому правилу.Двоичная система счисления, Десятичная система счисления, Восьмеричная система счисления, Шестнадцатеричные системы счисления : Pharmaguideline
В двоичной системе число определяется с использованием двоичной системы счисления.
Двоичная система использует только две цифры, 0 и 1, для представления числа.Двоичная система счисления
В двоичной системе число определяется с помощью двоичной системы счисления. Двоичная система использует только две цифры, 0 и 1, для представления числа. Многие компьютерные языки используют двоичные системы счисления, включая Java и C++. Компьютер может понимать только двоичный язык (0 или 1), то есть 0 и 1, поэтому все входные данные перед дальнейшей обработкой преобразуются в последовательность 0 и 1. Чтобы понять смысл информации в этом уроке, я преобразовал десятичное число в двоичное число, а затем вернул двоичное число в десятичное число. Двоичный символ «Би» означает «два». Таким образом, линия возвращается к 0 и 1 как к единственным способам представления числа. Двоичные числа могут быть легко выражены в виде десятичных чисел. Различия между двоичной и десятичной системами счисления. Двоичные числа представлены по основанию двойки, а десятичные числа представлены по основанию 10.
Ниже показано, как числа от 1 до 10 выражаются в двоичной системе счисления:
Десятичная система счисления
Числа представлены своими основаниями в системе счисления. Существует четыре основы для чисел: двоичная, восьмеричная, десятичная и шестнадцатеричная. Если основание равно 2, оно двоичное, если 8 — восьмеричное, если 10 — десятичное, а если 16 — шестнадцатеричное. Взять десятичные числа и преобразовать их в другую систему счисления несложно. Однако преобразование десятичных чисел из других систем счисления требует практики. В этой статье мы более подробно рассмотрим десятичные числа и то, как их можно преобразовать в другие системы. Основа 10 представляет десятичные числа в десятичной системе счисления. Также известная как десятичная запись, это способ представления десятичных чисел с основанием 10. Многие компьютерные программы используют этот числовой формат. База-10 — это система счисления, состоящая из 10 цифр, например, 0,1,2,3,4,5,6,7,8,9.
Десятичные числа имеют четкую позицию для каждой цифры, и каждая цифра в 10 раз значительнее, чем любая предыдущая цифра. Два в десять раз больше, чем пять, если 25 — десятичное число. Число в десятичной системе представляет собой число от 0 до 9 с использованием цифр от 0 до 9.
В системе счисления с основанием 10 число записывается с нулем или первыми девятью положительными целыми числами, представляющими каждое значение. В конце каждого значения ставится степень 10. Десятикратный размер цифры в разряде десятков означает, что он в десять раз больше десятого в разряде единиц. Подсчет в порядке убывания мощности каждой цифры, которая следует за десятичным нулем (.) в десятичном числе.
Восьмеричная система счисления
В восьмеричной системе счисления числа от 0 до 7 представляют собой восьмизначные числа. Всякий раз, когда восьмеричные числа сгруппированы по три, в качестве представления используются двоичные числа. Системы счисления с основанием «восемь» называются восьмеричными числами.
Эта система работает с числами от нуля до семи. По основанию 2 двоичное число является десятичным, по основанию 10 и по основанию 16 — шестнадцатеричным числом. Основание 2 такое же, как основание 8, когда дело доходит до описания восьмеричного числа.Группируя последовательные двоичные числа в группы по три (для целых чисел, начиная справа), восьмеричные числа легко преобразуются из двоичных представлений (аналогично четверичным числам). Двоичное представление десятичного числа 74, например, 1001010. Прибавив два нуля слева: (00)1 001 010, что соответствует восьмеричным числам 1 1 2, можно получить восьмеричное число 112.
Число с основанием 8, например 248, 1098 или 558, является восьмеричным. число. В восьмеричной системе счисления используются только семь цифр. Больше 7, например 8 или 9, восьмеричные цифры не используются. Единица, деленная на 10, называется восьмеричным числом. Число 19 не представляет собой восьмеричное число.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления существует значение основания 16 для метода представления чисел.
Единственными возможными значениями являются 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Например, A представляет собой однобитовое представление десятичных значений 10. , 11, 12, 13, 14 и 15, тогда как B представляет собой двухбитное представление десятичных значений 14 и 15. Значение любой цифры может быть представлено только 4 битами. Префиксы 0x и суффиксы h используются в качестве шестнадцатеричной записи. Вес каждой цифры в степени 16, Шестнадцатеричные числа имеют в 16 раз большее значение, чем предшествующие позиции, поэтому, чтобы вычислить значение шестнадцатеричного числа, умножьте каждую цифру на значение позиции, в которой она стоит, а затем сложите произведения. Помимо взвешенной системы счисления, у нас также есть позиционная система счисления. Для шестнадцатеричных чисел используется только четыре бита, причем каждая группа битов имеет разные значения от 0000 (для 0) до 1111 (для F = 15 = 8+4+2+1). Ниже приведена таблица в двоичной форме эквивалентов шестнадцатеричных чисел.
Как и восьмеричные числа, шестнадцатеричные числа также являются системой чисел. Используя шестнадцатеричные числа, можно преобразовать большие двоичные числа в более мелкие и компактные группы.
Получить тематические печатные документы в формате PDFПросмотреть здесь
Шестнадцатеричный: определения и примеры — Club Z! Репетиторство
Введение
В области информатики и программирования особая система нумерации играет важную роль в представлении значений и передаче данных. Шестнадцатеричная система счисления, часто называемая шестнадцатеричной, представляет собой систему счисления с основанием 16, получившую известность благодаря своим уникальным характеристикам. В этой статье мы углубимся в глубины шестнадцатеричной системы счисления, изучая ее определение, приложения и предоставляя примеры для лучшего понимания. Кроме того, раздел часто задаваемых вопросов и викторина позволят читателям закрепить свои знания и проверить свое понимание. Итак, давайте отправимся в это путешествие и разгадаем тайны шестнадцатеричной системы счисления.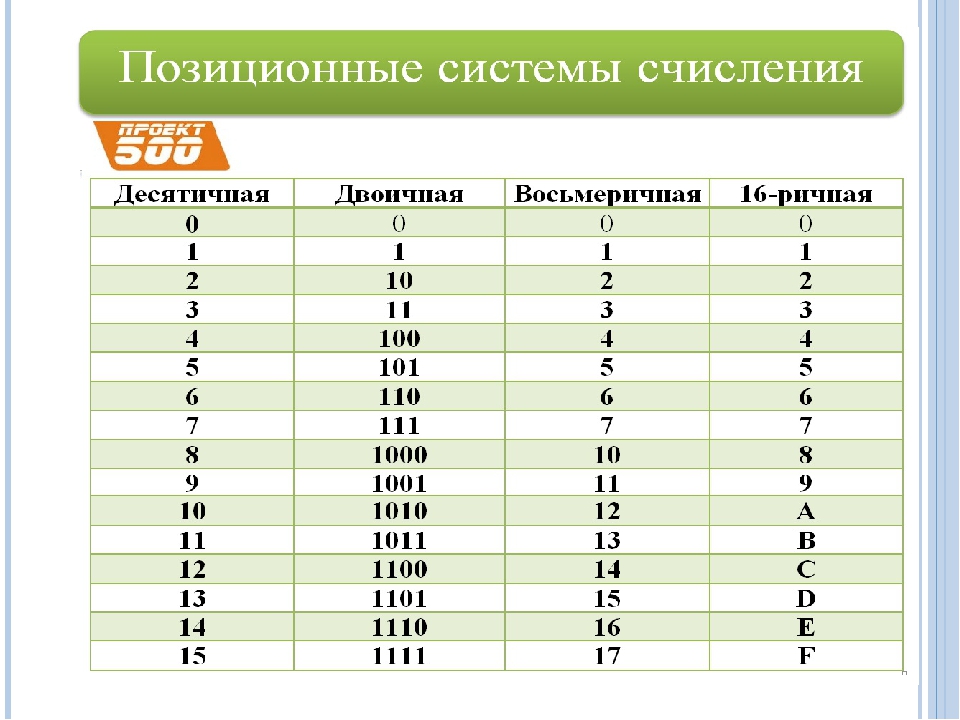
Шестнадцатеричная и десятичная: Шестнадцатеричная система часто используется в сочетании с двоичной и десятичной системами. В то время как десятичная система использует основание 10, а двоичная система использует основание 2, шестнадцатеричная система использует основание 16. Это различие позволяет шестнадцатеричной системе выражать большие двоичные значения более кратко.
Представление шестнадцатеричных чисел: Шестнадцатеричные числа представляются путем добавления префикса «0x» или «0X» к значению. Например, 15 в шестнадцатеричном формате записывается как 0xF, а 255 представляется как 0xFF. Префикс используется для отличия шестнадцатеричных значений от десятичных или двоичных значений.
Преобразование шестнадцатеричной системы в двоичную: Шестнадцатеричная и двоичная системы тесно связаны. Каждая шестнадцатеричная цифра соответствует 4-битной двоичной последовательности. Сгруппировав 4 двоичных числа, мы можем сопоставить их с их шестнадцатеричными аналогами.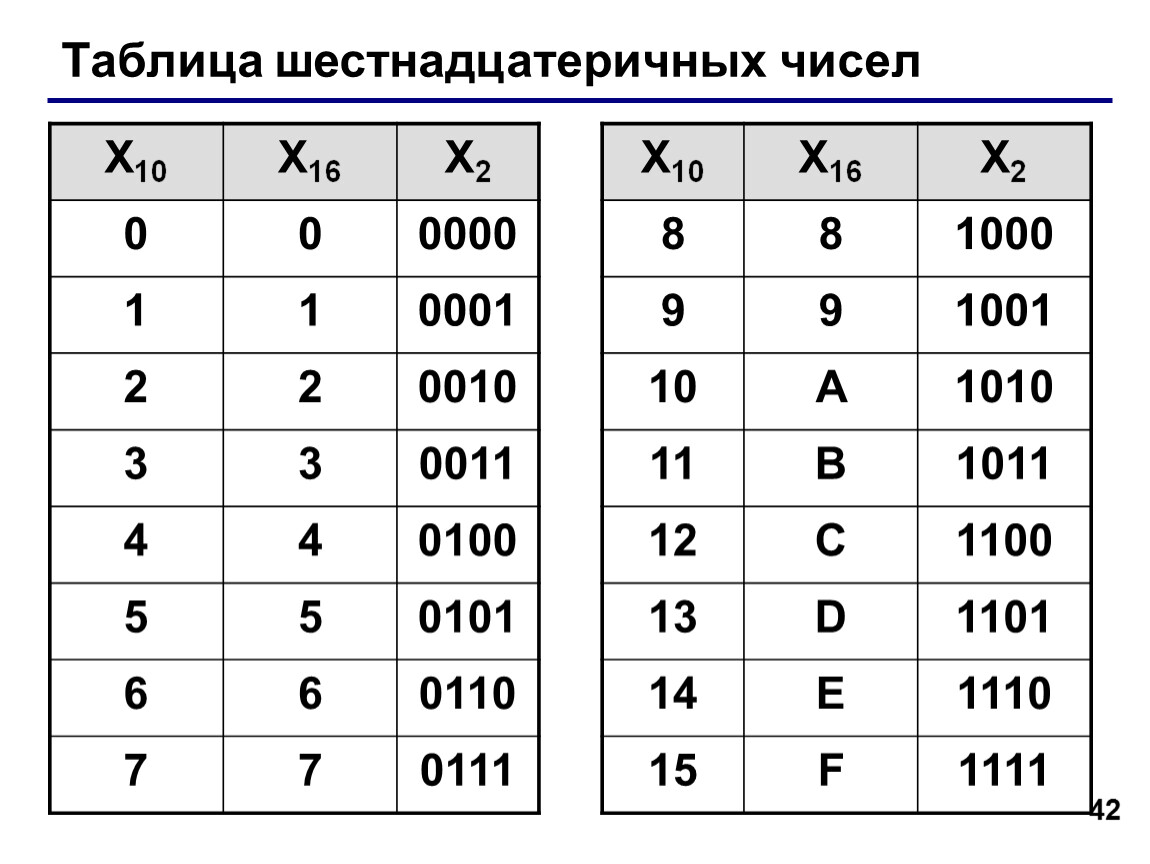
Например, двоичное число 1010 может быть представлено как шестнадцатеричная цифра A.
Применение шестнадцатеричной системы счисления
Шестнадцатеричная система счисления широко используется в различных областях, включая:
a. Адресация памяти: Шестнадцатеричный формат широко используется в адресации компьютерной памяти для представления ячеек памяти.
б. Представление цвета: в компьютерной графике и веб-дизайне для представления цветов используется шестнадцатеричный формат. Каждому цветовому каналу (красному, зеленому и синему) назначается шестнадцатеричное значение в диапазоне от 00 до FF.
в. Языки ассемблера: шестнадцатеричный код обычно используется в языках ассемблера для представления машинных инструкций и адресов памяти.
д. Сетевая адресация: в администрировании сети IP-адреса часто представляются в шестнадцатеричном формате для упрощения связи и настройки.
Примеры:
а. Пример 1: Двоичный: 1101 Шестнадцатеричный: 0xD
b.
Пример 2: Двоичный: 10011011 Шестнадцатеричный: 0x9B
c. Пример 3: Десятичный: 255 Шестнадцатеричный: 0xFF
d. Пример 4: Десятичный: 4096 Шестнадцатеричный: 0x1000
e. Пример 5: Шестнадцатеричный: 0xAB Двоичный: 10101011
f. Пример 6: Шестнадцатеричный: 0x1F Десятичный: 31
g. Пример 7: Шестнадцатеричный: 0xC0 Двоичный: 11000000
h. Пример 8: Шестнадцатеричный: 0x10 Десятичный: 16
я. Пример 9: Шестнадцатеричный: 0xE5 Двоичный: 11100101
j. Пример 10: Десятичный: 32768 Шестнадцатеричный: 0x8000
Часто задаваемые вопросы:
Q1: Почему шестнадцатеричный формат важен для компьютерного программирования и систем?
A1: Шестнадцатеричное число играет решающую роль в компьютерном программировании и системах по нескольким причинам:
i. Компактное представление: шестнадцатеричное представление позволяет сжато представлять большие двоичные числа. Поскольку каждая шестнадцатеричная цифра соответствует 4 двоичным цифрам, это обеспечивает компактный и удобочитаемый способ выражения двоичных значений.
ii. Адресация памяти: в компьютерной памяти для представления адресов памяти обычно используется шестнадцатеричный формат. Это упрощает идентификацию и доступ к определенным ячейкам памяти.
III. Выравнивание байтов. Многие компьютерные архитектуры и системы организуют данные в байтах, состоящих из 8 бит. Шестнадцатеричный формат идеально соответствует этой структуре байтов, поскольку 2 шестнадцатеричных цифры точно представляют байт. Такое выравнивание делает его удобным для операций на уровне байтов и манипулирования памятью.
iv. Отладка и низкоуровневое программирование. Шестнадцатеричное число часто используется в процессах отладки и задачах низкоуровневого программирования. При изучении дампов памяти или инструкций машинного кода шестнадцатеричное представление обеспечивает более удобочитаемое и удобное представление по сравнению с двоичным.
Q2: Как шестнадцатеричный формат используется для представления цвета?
A2: шестнадцатеричный формат широко используется для представления цветов в компьютерной графике и веб-дизайне.
Широко используется цветовая модель RGB, в которой каждому цветовому каналу (красному, зеленому и синему) присваивается шестнадцатеричное значение в диапазоне от 00 до FF. Комбинируя эти три цветовых канала, можно представить широкий спектр цветов. Шестнадцатеричное представление позволяет точно контролировать значения цвета и упрощает спецификацию цвета в различных приложениях.
Q3: Могу ли я преобразовывать шестнадцатеричные числа в десятичные и наоборот?
A3: Да, преобразование шестнадцатеричных чисел в десятичные и наоборот выполняется просто. Чтобы преобразовать шестнадцатеричное число в десятичное, умножьте каждую цифру на соответствующую степень числа 16 и просуммируйте результаты. И наоборот, чтобы преобразовать десятичное число в шестнадцатеричное, нужно несколько раз разделить десятичное число на 16 и записать остаток. Остатки при чтении в обратном порядке представляют собой шестнадцатеричный эквивалент.
Q4: Как преобразовать шестнадцатеричное число в двоичное и наоборот?
A4: Преобразование шестнадцатеричных чисел в двоичные и наоборот включает простой процесс отображения.
Каждая шестнадцатеричная цифра соответствует 4-битной двоичной последовательности. Чтобы преобразовать шестнадцатеричное число в двоичное, замените каждую шестнадцатеричную цифру эквивалентной ей 4-битной двоичной последовательностью. И наоборот, чтобы преобразовать двоичное число в шестнадцатеричное, сгруппируйте двоичные числа в наборы по 4 и замените каждый набор соответствующим шестнадцатеричным числом.
Q5: Могу ли я выполнять арифметические операции напрямую, используя шестнадцатеричные числа?
A5: Да, арифметические операции, такие как сложение, вычитание, умножение и деление, могут выполняться с использованием шестнадцатеричных чисел. Процесс аналогичен десятичной арифметике, где учитываются соответствующие разрядные значения. Однако важно преобразовать шестнадцатеричные числа в десятичные, выполнить операцию, а затем преобразовать результат обратно в шестнадцатеричный для точных вычислений.
Q6: Используется ли шестнадцатеричный формат в сетевой адресации?
A6: Да, шестнадцатеричный формат используется в сетевой адресации, особенно в IPv6 (Интернет-протокол версии 6).
Адреса IPv6 представляют собой 128-битные значения и представлены в шестнадцатеричном формате для удобства чтения. Шестнадцатеричное представление упрощает настройку и передачу сетевых адресов, особенно в сложных сетевых средах.
Q7: Могу ли я смешивать шестнадцатеричную систему с другими системами счисления при программировании?
A7: Да, языки программирования часто предоставляют встроенные функции или синтаксис для преобразования между различными системами счисления, включая шестнадцатеричную, десятичную и двоичную. Такая гибкость позволяет программистам беспрепятственно работать с различными системами нумерации и при необходимости использовать преимущества каждой из них.
Q8: Существуют ли какие-либо языки программирования, которые в основном используют шестнадцатеричный формат?
A8: Хотя в большинстве языков программирования в качестве системы нумерации по умолчанию используется десятичная система счисления, существуют специальные языки и инструменты, ориентированные на шестнадцатеричное и низкоуровневое программирование.
Например, языки ассемблера и низкоуровневые среды программирования часто сильно зависят от шестнадцатеричных представлений адресов памяти, машинных инструкций и побитовых операций.
Q9: Используются ли шестнадцатеричные числа в криптографии?
A9: Да, шестнадцатеричный код широко используется в криптографии. Криптографические алгоритмы часто манипулируют двоичными данными, а шестнадцатеричное представление обеспечивает удобное и краткое представление для работы с двоичными значениями. Хэш-функции, алгоритмы шифрования и криптографические ключи обычно представлены в шестнадцатеричном формате. Кроме того, криптографические протоколы и библиотеки часто используют шестнадцатеричные строки для представления криптографических значений и параметров.
Q10: Можно ли преобразовать шестнадцатеричные символы в символы ASCII?
A10: Да, шестнадцатеричные значения могут быть преобразованы в символы ASCII. Каждая пара шестнадцатеричных цифр представляет собой байт, который может быть сопоставлен с соответствующим символом ASCII.
Например, шестнадцатеричное значение 41 соответствует символу ASCII «A», 42 соответствует «B» и так далее. Это преобразование особенно полезно при работе с кодировкой символов, форматами файлов и манипулированием текстовыми данными в программировании.
Тест:
Что является основой шестнадцатеричной системы счисления? а) 2 б) 8 в) 10 г) 16
Какую систему счисления часто сопровождает шестнадцатеричная? a) Двоичный b) Восьмеричный c) Десятичный d) Шестнадцатеричный является автономным
Сколько различных символов используется в шестнадцатеричном формате? а) 6 б) 8 в) 10 г) 16
Как число 15 представлено в шестнадцатеричном формате? а) 0xF б) 0xА в) 0хЕ г) 0хFF
Сколько шестнадцатеричных цифр используется в цветовой модели RGB для каждого цветового канала? а) 2 б) 4 в) 6 г) 8
Какой домен широко использует шестнадцатеричный формат для представления адресов памяти? a) Компьютерная графика b) Работа в сети c) Криптография d) Языки ассемблера
Сколько бит представлено одной шестнадцатеричной цифрой? а) 2 б) 4 в) 8 г) 16
Как шестнадцатеричное число преобразовать в двоичное? a) Умножить на 2 b) Разделить на 2 c) Заменить каждую цифру ее 4-битным двоичным эквивалентом d) Вычесть 2
Какое шестнадцатеричное значение эквивалентно двоичному числу 1011? а) 0x3 б) 0xB в) 0xA г) 0xF
Какое поле часто использует шестнадцатеричный формат для представления криптографических ключей и параметров? a) Искусственный интеллект b) Сетевое администрирование c) Управление базой данных d) Криптография
Вывод: Шестнадцатеричная система счисления с основанием 16 и уникальное представление играет жизненно важную роль в различных аспектах информатики и программирования.
