Динамика твёрдого тела. Лекция 4

1. Динамика твёрдого тела

Составила: ОБОЛОНСКАЯ О.С.
к.ф.-м.н.

2. Содержание:

1. Введение.
2. Моментом силы.
3. Основной закон динамики вращательного
движения.
4. Момент инерции твердого тела.
5. Момент инерции тонкостенного полого
цилиндра (кольца).
6. Момент инерции однородного диска (
сплошного цилиндра).
7. Момент инерции шара относительно оси
симметрии.
8. Момент инерции тонкого однородного стержня.
9. Теорема Штейнера.
10. Кинетическая энергия вращения.
11. Момент импульса и закон его сохранения.
До сих пор мы рассматривали движение
материальной
точки.
Далее
мы
будем
рассматривать движение абсолютно твёрдого
тела.
В механике под абсолютно твёрдым
телом понимают такую идеальную систему
материальных точек, расстояние между которыми
при любых движениях остаются неизменными.
Вращательное движение вокруг оси – это
такое движение твёрдого тела, при котором
траектория
любой
его
точки
является
окружностью. Центры всех окружностей лежат на
одной прямой, названной осью вращения.

5. 1.Момент силы

Для того чтобы вызвать вращение тела,
недостаточно просто приложить силу, необходимо
создать так называемый вращательный момент или
момент силы.
Различают понятие момента силы относительно
центра точки О и силы относительно оси.
Моментом силы относительно центра точки О
будем считать векторную физическую величину
,
определяемую векторным произведением радиусвектора
, проведённого из центра О в точку
приложения силы на вектор силы
.
Направление
определяется правилом правого
винта. Модуль момента силы по определению
векторного произведения.
где
— плечо силы.
Кратчайшее расстояние (перпендикуляр) от точки
вращения до линии действия силы называется плечом
силы.
Моментом
силы относительно оси называется
проекция
момента силы относительно точки на
эту ось.
— величина алгебраическая, берётся со
знаком «плюс» если поворот под действием
с
положительным направлением оси z виден против
часовой стрелки.

9. Основной закон динамики вращательного движения.

Рассмотрим вращательное движение твёрдого тела
относительно неподвижной вертикальной оси z.
Пусть
— внешняя сила, действующая на i-ю
материальную точку mi. Направление в общем случае
произвольно. Эту силу можно разложить на 3
компонента. Один из них параллелен оси вращения ,
другой
перпендикулярен
ей
,
а
также
перпендикулярен траектории тела в данной точке.
Третий компонент
совпадает по направлению с
касательной к траектории рассматриваемого элемента
. Два первых компонента будут только воздействовать
на ось вращения, деформируя её, а 3-й компонент,
направленный по касательной, будет создавать
тангенциальное ускорение (
) и для неё можно
записать уравнение 2-го закона Ньютона
.
Умножив обе части этого уравнения на
:
Аналогичные уравнения можно написать для всех
остальных материальных точек, затем просуммируем
их, вынося
(т. к. оно постоянно для всех
материальных точек вращающегося твёрдого тела) за
знак суммы, получим:
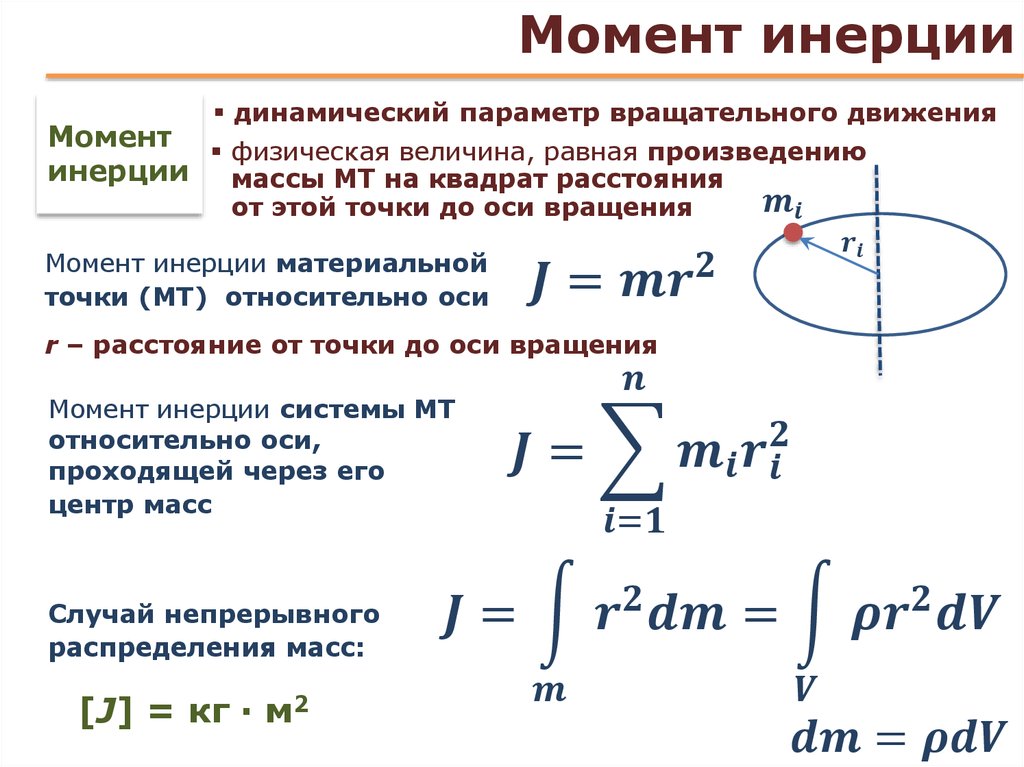
Величина
равная произведению массы
материальной точки на квадрат её расстояния до оси
вращения, называется моментом инерции точки
относительно этой оси.
Величина
, равная сумме моментов
инерции материальной точки твёрдого тела,
называется моментом инерции тела относительно
оси z.
по определению момента силы F
относительно оси z.
— представляет собой полный момент
внешних сил относительно оси вращения z. Он равен
алгебраической сумме моментов сил, действующих на
материальные точки твердого тела. Тогда используя
введенные понятия момента инерции тела и момента
силы, уравнение можно переписать в виде:
или в векторном виде:
Это
соотношение является основным законом
динамики вращения движения или 2-ым законом
Ньютона для вращения движения. Он аналогичен
2-ому закону Ньютона поступательного движения.
— момент силы характеризует вращательный
эффект силы.
— роль линейного ускорения играет при
вращении твёрдого тела угловое ускорение.
— момент инерции является мерой инертного
вращения тела, аналогично m при поступательном
движении. Кроме того, заметим, что любое тело
обладает
определённым
моментом
инерции
относительно любой оси независимо от того,
вращается оно или покоится, подобно тому, что тело
обладает массой независимо от того движется оно или
покоится.

14. Момент инерции твердого тела

Момент инерции твердого тела:
— есть величина аддитивная. Это значит,
что момент инерции тела равен сумме моментов
инерции его частей. Судя по определению, момент
инерции относительно данной оси зависит не только
от массы тела, но и от распределения масс
относительно оси.
Для расчётов момент инерции однородных твёрдых
тел преобразуем формулу
, используя
понятие плотности вещества
,
где
— элементарный объём, получим:
это соотношение является приближенным, причём тем
больше точным, чем меньше элементарные объёмы .
Следовательно, если перейти к пределу
→0,
получим для момента инерции
Таким образом вычисляется момент инерции
однородного твёрдого тела (однородным называется
твёрдое тело свойства которого во всех точках
одинаковые, то есть
для каждой точки
твёрдого тела ).
Выведем формулы момента инерции некоторых
тел правильной геометрической формы.

16. Момент инерции тонкостенного полого цилиндра (кольца)

Относительно оси z, перпендикулярной плоскости
цилиндра, проходящей через центр. Пусть масса
цилиндра m равномерно распределена по ободу,
радиус его R. Разобьем цилиндр на элементарные
полоски mi. Ввиду малой толщины стенок цилиндра
можно считать, что все части такой полоски лежат на
одинаковом расстоянии от оси z, равном R. Тогда
момент инерции такой полоски Ii=miR2
Тогда полный момент инерции цилиндра равен ∑
моментов инерции полосок:
— масса
цилиндра.

18. Момент инерции однородного диска ( сплошного цилиндра)

Относительно оси z, проходящей через центр и
перпендикулярно диску (цилиндру). Найдём момент
инерции однородного диска массой m и толщиной b,
относительно оси ОО′. Разобьем диск на тонкие
кольцевые слои толщиной dr, все точки одного слоя
находятся на одинаковом расстоянии r от оси.
Объём такого слоя равен:
Тогда момент инерции всего диска:
Так как масса диска
, то
Момент инерции толстостенного диска, радиусами R1
и R2, определяется интегрированием от R1 до R2 только
надо учесть, что масса диска равна
Тогда
Тогда
диска (цилиндра).
— момент инерции толстостенного

20. Момент инерции шара относительно оси симметрии.

— момент инерции шара.

21. Момент инерции тонкого однородного стержня

Момент инерции тонкого стержня относительно оси,
перпендикулярной стержню и проходящей через его
середину:
Пусть масса стержня m и длины его l , площадь
поперечного сечения S.
Разобьём стержень на элементарные объёмы
находящегося на расстоянии r от оси ОО´ , тогда
,
— момент инерции тонкого стержня.

23. Теорема Штейнера

Если
определён
момент
инерции
тела
относительно оси, проходящей через центр тяжести
тела, то очень просто определить момент инерции
этого тела относительно любой параллельной ей оси.
Определение момента инерции таким образом
производится по теореме Штейнера:
Момент инерции тела I относительно
произвольной оси равен сумме момента инерции I0
относительно оси, параллельной данной и
проходящей через центр инерции тела и
произведения массы тела на квадрат расстояния
между осями.
Рассмотрим пример.
Момент инерции тонкого стержня относительно
оси, перпендикулярна стержню и проходящей через
его конец.

25. Кинетическая энергия вращения

Рассмотрим абсолютно твердое
тело вращающееся около неподвижной
оси z, проходящей через него. Мысленно
разобьем это тело на маленькие объемы
с элементарными массами m1, m2,…, mn,
находящиеся на расстоянии r1, r2,…, rn от
оси.
При вращении твердого тела относительно
неподвижной оси отдельные его элементарные
объемы массами mi опишут окружности различных
радиусов ri, и имеют различные линейные скорости .
Но так как мы рассматриваем абсолютно твердое тело,
то угловая скорость вращения этих объемов
одинакова:
Кинетическую энергию вращающегося тела
найдем как сумму кинетических энергий его
элементарных объемов:
или
где
— момент инерции тела относительно оси z.
— элементарные массы, находящиеся на расстоянии
от оси,
υi — линейные скорости материальной точки,
ω – угловая скорость вращения.
Таким
образом,
кинетическая
энергия
вращающегося тела
Из
сравнения формулы (*) с выражением для
кинетической энергии
тела, движущегося
поступательно, следует, что момент инерции –
мера
инертности тела при вращательном
движении. Формула (*) справедлива для тела,
вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например
цилиндра, скатывающегося с наклонной плоскости без
скольжения, энергия движения складывается из
энергии поступательного движения и энергии
вращения:
где m — масса катящегося тела;
υс — скорость центра масс тела;
— момент инерции тела относительно оси,
проходящей через его центр масс;
ω — угловая скорость тела.

29. Момент импульса и закон его сохранения.

Аналогом импульса во вращательном движении
«играет» момент импульса тела относительно оси.
Моментом импульса (количества движения)
материальной точки А относительно неподвижной
точки
О
называется
физическая
величина,
определяемая векторным произведением:
,
где
— радиус-вектор, проведённый из точки О в
точку А;
— импульс материальной точки.
— псевдовектор, его направление совпадает с
направлением поступательного движения правого
винта при его вращении от к .
Модуль вектора момента импульса
где α – угол между векторами
l – плечо вектора
и ,
относительно точки О.
Моментом импульса относительно неподвижной
оси z называется скалярная величина
, равная
проекции на эту ось вектора момента импульса,
определённого относительно произвольной точки О
данной оси. Момент импульса
не зависит от
положения точки О на оси z.
При вращении абсолютно твёрдого тела вокруг
неподвижной оси z каждая отдельная точка тела
движется по окружности постоянного радиуса с
некоторой скоростью
. Скорость
и импульс
перпендикулярны этому радиусу, то есть радиус
является плечом вектора
. Поэтому можем
записать, что момент импульса отдельной частицы
равен
и направлен по оси в сторону, определяемую правилом
правого винта.
Момент импульса твёрдого тела относительно
оси есть сумма моментов импульса отдельных частиц:
Используя формулу
, получим
, то есть
Таким образом, момент импульса твёрдого тела
относительно оси равен произведению момента
инерции тела относительно той же оси на угловую
скорость.
Продифференцируем уравнение (**) по времени:
,
— уравнение динамики вращательного
движения твёрдого тела относительно неподвижной
оси.
Производная момента импульса твёрдого тела
относительно оси равна моменту силы относительно
той же оси.
Имеет место векторное равенство:
В замкнутой системе внешних сил
откуда
импульса.
и
— закон сохранения момента
,
Момент импульса замкнутой системы сохраняется,
то есть не изменяется с течением времени.
Аналогично, гимнаст во время прыжка через
голову поджимает к туловищу руки и ноги, чтобы
уменьшить свой момент инерции и увеличить тем
самым угловую скорость вращения.

36. Спасибо за внимание!!!

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

%PDF-1.6 % 1 0 obj > /Metadata 4 0 R /OCProperties > > > ] /ON [ 5 0 R ] /Order [ ] /RBGroups [ ] >> /OCGs [ 5 0 R ] >> /Pages 7 0 R /StructTreeRoot 44 0 R /Type /Catalog >> endobj 2 0 obj /CreationDate (D:20130426110108+03’00’) /Creator (Microsoft Word 2013) /ModDate (D:20130426110422+03’00’) /Producer (Microsoft Word 2013) /Title >> endobj 3 0 obj > /Font > >> /Fields [ ] >> endobj 4 0 obj > stream application/pdf

Бобученко Дмитрий Степанович

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

2013-04-26T11:01:08+03:00Microsoft® Word 20132013-04-26T11:04:22+03:002013-04-26T11:04:22+03:00Microsoft® Word 2013uuid:52ce5e78-968e-426c-99ad-9fc809de3b58uuid:081cd9c5-d6e4-4518-b9a7-cb26101cdbe6 endstream endobj 5 0 obj > /PageElement > /Print > /View > >> >> endobj 6 0 obj > stream x͛n7} >AEr|SFQ4|(PE2dH޾CŻ%;^b1Kqsg~RAiEʁ QF

вращательная динамика — Достаточно ли массы и момента инерции для описания движения твердого тела?

$\begingroup$

Контекст: как построить VR-контроллер, чтобы размахивание им было неотличимо от размахивания мечом.

Достаточно ли того, что контроллер соответствует массе меча и моменту инерции относительно центра масс, чтобы гарантировать, что взмах одного ощущается как взмах другого?

Нужны ли мне моменты более высокого порядка распределения масс и насколько вероятно, что они приведут к заметным различиям?

Обратите внимание, что мы можем предположить, что контроллер всегда будет удерживаться одинаково (например, нам не нужно сопоставлять момент инерции виртуального меча, удерживаемого лезвием).

• динамика вращения
• масса
• момент инерции
• динамика твердого тела

$\endgroup$

1

$\begingroup$

Чтобы точно учесть, как объект ощущается при вращении более чем по одной оси (например, поворот запястья будет ощущаться иначе, чем поворот рукой), вам также понадобится полный тензор инерции. Это может быть полностью определено тремя числами, моментами инерции относительно главных осей, вместо одного числа для момента инерции, которое вы рассматривали в своем вопросе.

Вам также потребуется указать вектор смещения центра масс виртуального меча относительно места захвата контроллера и ориентацию главных осей, чтобы можно было определить величину вращения вокруг каждой оси через центр масс для любой заданной траектории движения

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Жесткий материал

Жесткий материал

Жесткий материал

Твердая область или твердое тело — это идеализация тела, в которой пренебрегают деформацией. Другими словами, расстояние между любыми двумя заданными точками твердого тела остается постоянным во времени независимо от действующих на него внешних сил. Объект можно считать абсолютно жестким, если его податливостью можно пренебречь по сравнению с другими податливостью системы и когда нет необходимости вычислять напряжение в объекте. Чтобы смоделировать жесткий домен, вы используете модель материала Rigid Material.

Rigid Material доступен как модель материала в интерфейсах Solid Mechanics, Shell, Beam и Multibody Dynamics. Этот теоретический раздел применим ко всем интерфейсам. Между версиями Rigid Material есть небольшие различия, которые будут описаны по мере их появления. В дальнейшем, говоря о жестких доменах, геометрическим объектом может быть домен, граница или ребро, в зависимости от физического интерфейса и пространственного измерения. Жесткая область может состоять из набора нескольких геометрических областей. Эти домены будут действовать как единый жесткий объект, независимо от того, связаны они геометрически или нет. Смежные геометрические объекты, выбранные в разных узлах жесткого материала, независимы и даже могут проникать друг в друга.

Жесткий материал — это модель материала, которая является взаимоисключающей для всех других моделей материалов. Единственным необходимым свойством материала является массовая плотность.

Жесткая доменная кинематика

Когда тело твердое, достаточно описать движение не менее трех неколлинеарных частиц. Тогда можно реконструировать движение всех других частиц в теле. Обычно используется математически более удобный, но эквивалентный подход.

Движение всего тела представлено:

•	Линейное движение тела. Движение одной из частиц тела, выбранной в качестве точки отсчета (часто совпадающей с центром масс).

•	Угловое движение (также известное как ориентация или положение) тела.

Степени свободы, необходимые для представления линейного и углового движения, известны как степени свободы перемещения твердого тела и вращения твердого тела.

В двумерных осесимметричных интерфейсах жесткая область имеет только одну степень свободы: перемещение по оси Z. Следующие разделы теории описывают только более общие случаи. Осесимметричная формулировка является тривиальной специализацией, в которой отбрасываются все вращательные части выражений.

В 2D это представлено двумя перемещениями в плоскости и скалярным вращением вокруг оси Z.

В 3D ситуация сложнее. Необходимо шесть степеней свободы. Обычно выбирают три перевода и три параметра поворота. Для конечных поворотов любой выбор из трех параметров поворота даст сингулярность при некотором определенном наборе углов. По этой причине для вращения в COMSOL Multiphysics используется четырехпараметрическое кватернионное представление. Таким образом, каждая жесткая область в 3D на самом деле имеет семь степеней свободы: три для перемещения и четыре для вращения. Параметры кватерниона называются a, b, c и d. Эти четыре параметра не являются независимыми, поэтому дополнительное уравнение, утверждающее, что

добавлен.

Связь между параметрами кватерниона и матрицей вращения R:

Для геометрически линейного случая ограничение кватерниона и определение матрицы вращения сводятся к:

В 2D вращательная степень свободы — это угол поворота вокруг оси Z, и его соотношение с матрицей вращения R:

Для геометрически линейного случая двумерная матрица вращения уменьшается до:

При перемещении и вращении твердой области полное выражение для смещения любой точки твердого тела имеет вид:

, где X — материальные координаты любой точки жесткой области, XM — центр масс жесткой области, u — вектор смещения в центре масс, а I — единичная матрица.

Перемещения твердого тела в центре масс (u) являются степенями свободы. Таким образом, поступательную скорость и ускорение твердого тела можно оценить, непосредственно взяв производные по времени от u. Во временной области это может быть выражено как:

В частотной области их можно выразить через частоту (ω):

То же верно и для вращения в 2D, поскольку вращение твердого тела является степенью свободы. Угловую скорость и ускорение твердого тела можно оценить, непосредственно взяв производные по времени от .

В 3D ситуация иная, и полное вращение жесткого домена можно представить как функцию кватерниона:

Параметр a можно рассматривать как измерение вращения, тогда как b, c и d можно интерпретировать как ориентацию вектора вращения. Для малых оборотов это соотношение упрощается до:

Угловая скорость твердого домена вычисляется как:

Здесь — сопряженное число q, обозначающее умножение кватернионов.

Угловое ускорение твердого домена можно оценить, взяв производную по времени от угловой скорости.

Жесткая доменная динамика

Основное уравнение для жесткого домена может быть записано как баланс между инерционными (внутренними) силами и приложенными внешними силами. Жесткий домен имеет только одну внутреннюю силу, силу инерции. Это означает, что для определения модели материала жесткого домена требуется только массовая плотность домена.

Силы инерции и моменты инерции относительно центра масс равны:

где и – линейное и угловое ускорения жесткого домена.

Масса инерционных свойств (m) и тензор момента инерции (I) твердого домена вычисляются как:

, где E3 и XM — единичная матрица и центр масс жесткого домена соответственно. Особый случай для интерфейса оболочки описан в разделе Жесткий домен для оболочек.

В 2D выражения для сил инерции, моментов инерции и момента инерции сводятся к:

, где интегрирование по объему было заменено интегрированием по площади, умноженным на толщину вне плоскости h.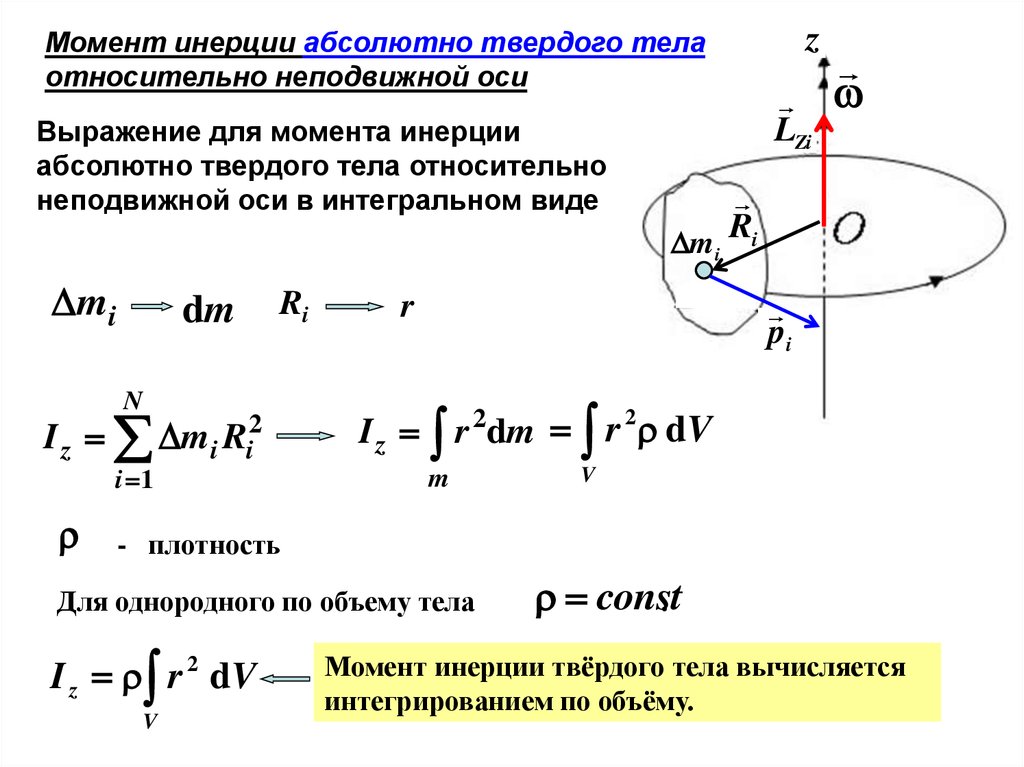

Уравнения движения твердой области:

и

Здесь индексы I и ext обозначают инерционную и внешнюю силы соответственно, а R — матрица текущего вращения. Силы инерции являются вкладами узлов Mass и Moment of Inertia.

В 2D уравнения моментов упрощаются до скалярного уравнения

Начальное значение

Жесткий материал — это отдельная модель материала, которая переопределяет узел линейного эластичного материала по умолчанию и узел исходных значений по умолчанию в физическом интерфейсе. Начальные значения задаются в отдельном подузле Initial Values ​​для каждого жесткого материала.

В версии Rigid Material интерфейса Multibody Dynamics также можно получить начальные значения для всех доменов из раздела Initial Values ​​на уровне интерфейса. Это опция по умолчанию. Подузел «Исходные значения» присутствует только в разделе «Жесткий материал», если выбран параметр «Определено локально». Если в системе присутствует много жестких доменов и они имеют одинаковые начальные значения, то часто лучше один раз определить начальные значения на уровне интерфейса и ссылаться на них во всех функциях.

Начальные значения для перемещения твердого тела, вращения твердого тела и первых производных по времени могут быть заданы относительно любой точки — центра вращения — в выбранной системе координат. Центр вращения можно определить с помощью

•	Центр масс жесткого домена

•	Глобальные координаты центра вращения

•	Центр тяжести набора выбранных объектов (границ, ребер или точек)

При заданных начальных значениях смещения (u), вращения (), поступательной скорости () и угловой скорости (ω) относительно центра вращения (Xc), перемещение твердого тела и кватернионные степени свободы инициализируются как:

В 2D выражения для начальных значений уменьшаются до:

Переменная ur представляет собой смещение центра масс из-за вращения вокруг центра вращения и, таким образом, равно нулю, когда две точки совпадают. В том случае, если вы вводите данные, используя отдельный центр вращения, вы должны обратить особое внимание на то, как складываются начальное перемещение и скорость, если присутствуют начальные вращения и скорости вращения.

Рисунок 3-27: Начальное перемещение твердого тела

Масса и момент инерции

Иногда для жесткой области требуется дополнительный эффект связанного абстрактного жесткого объекта, который физически не моделируется и для которого известны инерционные свойства. Вы можете смоделировать это, используя Массу и Момент инерции, где можно напрямую ввести инерционные свойства этой абстрактной области (центр масс, масса и тензор момента инерции).

Формулировка абстрактного жесткого объекта аналогична физической жесткой области со следующими исключениями:

•	Инерционные свойства абстрактного твердого объекта вводятся пользователем, а не вычисляются из физической области.

•	Дополнительные степени свободы не создаются. Силы инерции, создаваемые этой функцией, будут рассчитываться на основе расстояния от центра тяжести жесткой области, к которой она принадлежит, и значений степеней свободы в ней.

Вклад инерционной силы составляет

где Xmc — вектор от центра масс жесткого домена (XM) к центру масс этого вклада (Xm),

Вклад инерционного момента составляет

В 2D присутствует только скалярный вклад момента:

Ограничения

Ограничения для жесткого домена по своей природе отличаются от ограничений, применяемых к гибким доменам. В гибком домене ограничение может применяться на различных уровнях объектов: доменах, границах, ребрах или точках. Поскольку степени свободы жесткой области являются глобальными и присутствуют только в центре масс, для ограничения этих глобальных степеней свободы используются граничные условия, поэтому необходим глобальный выбор.

Ограничения, используемые для гибкого домена, например «Фиксированное ограничение», «Предписанное смещение», «Жесткий соединитель» или «Присоединение», неприменимы к жесткому домену. В жесткой области вместо этого используется подузел Prescribed Displacement/Rotation или Fixed Constraint для ограничения его степеней свободы.

Узел Prescribed Displacement/Rotation можно использовать для:

•	Задать компоненты смещения в произвольных направлениях в заданной точке.

•	Ограничение вращения в произвольном направлении.

•	Задать ненулевой поворот вокруг произвольной оси.

Перемещение и поворот можно задать в выбранной системе координат относительно произвольного центра вращения. Центр вращения можно определить с помощью

•	Центр масс жесткого домена.

•	Глобальные координаты центра вращения.

•	Центроид набора выбранных объектов (границы, ребра или точки).

Смещение в центре вращения вычисляется как:

(3-111)

Компоненты этого вектора смещения задаются индивидуально в выбранной системе координат. Согласно уравнению 3-111, ограничение на поступательное движение наложит связь между поступательными и вращательными степенями свободы, если центр вращения отличается от центра масс.

Чтобы задать вращение в 3D, мнимая часть кватерниона задается как:

где и — ось вращения и угол поворота соответственно.

В 2D угол поворота вне плоскости напрямую ограничивается заданным значением поворота.

Нагрузки

Нагрузки, доступные для гибкого домена, также можно использовать для жесткого домена. Помимо этих граничных условий, жесткая область также имеет глобальные подузлы для приложения сил и моментов. Если вы используете Applied Force, силу и ее местоположение можно задать в выбранной системе координат. Сила неявно также вносит вклад в момент, если только она не приложена к центру масс жесткой области. Если используется узел Applied Moment, момент может быть задан в выбранной системе координат.

Подключение к другим телам

Когда жесткий домен и гибкий домен имеют общую границу (Оболочка: ребро, Балка: точка), соединение устанавливается автоматически. Все перемещения в гибкой области контролируются степенями свободы жесткой области, так что

, где X — координата на границе. При наличии вращательных степеней свободы, что имеет место в интерфейсах Shell и Beam, повороты задаются равными поворотам жесткой области.