Чем отличаются внутренние и внешние силы. Механическая система. Силы внешние и внутренние
Силы внутренние и внешние. Внешние и внутренние силы Внешняя сила это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. Внешние силы делятся на объемные и поверхностные.
9.Законы сохранения. Силы внутренние и внешние. Замкнутая система. Сохраняющиеся величины. Связь законов сохранения со свойствами пространства и времени.
Законы сохранения фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени.
Некоторые из законов сохранения выполняются всегда и при всех условиях (например, законы сохранения энергии, импульса, момента импульса, электрического заряда), или, во всяком случае, никогда не наблюдались процессы, противоречащие этим законам. Другие законы являются лишь приближёнными и выполняющимися при определённых условиях.
Внешние и внутренние силы
Внешняя сила это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор.
Внешние силы делятся на
объемные
и
поверхностные
.
Объемные силы
приложены к каждой частице тела по всему его объему. Примером объемных сил являются силы веса и силы инерции.
Поверхностные силы
делятся на
сосредоточенные
и
распределенные
.
Сосредоточенными
считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела. Однако при расчете напряжений вблизи зоны приложения силы нагрузку следует считать распределенной. К сосредоточенным нагрузкам относят не только сосредоточенные силы, но и пары сил, примером которых можно считать нагрузку, создаваемую гаечным ключом при закручивании гайки. Сосредоточенные усилия измеряются в
кН
.
В результате действия внешних сил в теле возникают
внутренние силы
.
Внутренняя сила
мера взаимодействия между частицами одного тела.
Замкнутая система термодинамическая система, которая не обменивается с окружающей средой ни веществом , ни энергией . В термодинамике постулируется (как результат обобщения опыта), что изолированная система постепенно приходит в состояние термодинамического равновесия, из которого самопроизвольно выйти не может (нулевое начало термодинамики ).
Адиабатически изолированная система термодинамическая система , которая не обменивается с окружающей средой энергией в форме теплоты. Изменение внутренней энергии такой системы, равно производимой над ней работе. Всякий процесс в адиабатически изолированной системе называется адиабатическим процессом .
А также другие работы, которые могут Вас заинтересовать | |||
| 41636. | Попередні обчислення в тріангуляції | 1.68 MB | |
| Попередні о | |||
22Внешние и внутренние силы. Главный вектор, момент. Работа
Внутренние силы — это такие силы, которые действуют сразу на все атомы передвигаемого предмета независимо от того, где они находятся: на поверхности или в середине предмета. К этим силам относятся силы инерции и силы поля: гравитационного, электрического, магнитного. И происходит это потому, что поле и носитель инерции физвакуум свободно проникают внутрь любого тела.
В механике внешними силами по отношению к данной системе материальных точек
Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы. Подразделение сил на внешние и внутренние является совершенно условным: при изменении заданного состава системы некоторые силы, ранее бывшие внешними, могут стать внутренними, и обратно. Так, например, при рассмотрении
PRIMER движения системы, состоящей из земли и ее спутника луны, силы взаимодействия между этими телами будут внутренними силами для этой системы, а силы притяжения солнца, остальных планет, их спутников и всех звезд будут внешними силами по отношению к указанной системе. Но если изменить состав системы и рассматривать движение солнца и всех планет как движениеодной общей системы, то внешн. силами будут только силы притяжений, оказываемых


Если нагруженное тело находится в равновесии, то внутренние силы равны по значению внешним силам и противоположны им по направлению. Очевидно, что они препятствуют развитию деформации.
Работа внешних сил равна взятой с обратным знаком работе внутренних сил:
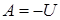 .
.
Пусть
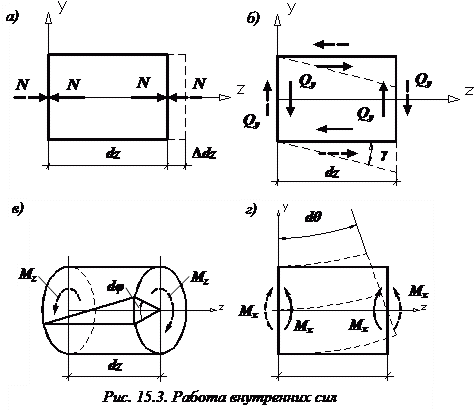
элемент стержня длиной 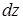 испытывает
растяжение (рис. 15.3, а).
испытывает
растяжение (рис. 15.3, а).
Действие
отброшенных частей стержня на
рассматриваемый элемент заменим
продольными силами N. Эти усилия показаны
на рисунке штриховыми линиями. По
отношению к элементу они являются как
бы внешними. Вызываемое ими удлинение
элемента равно: 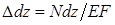
 Действие
рассматриваемого элемента на отброшенные
части показано на рисунке сплошными
линиями. Элементарная работа внутренних
продольных сил, постепенно увеличивающихся,
и противодействующих развитию удлинения,
согласно теореме Клапейрона, выразится
формулой:
Действие
рассматриваемого элемента на отброшенные
части показано на рисунке сплошными
линиями. Элементарная работа внутренних
продольных сил, постепенно увеличивающихся,
и противодействующих развитию удлинения,
согласно теореме Клапейрона, выразится
формулой: 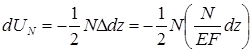 .
.
ЭЛЕМЕНТАРНАЯ
РАБОТА ВНУТРЕННИХ ПОПЕРЕЧНЫХ СИЛ (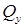
При чистом
сдвиге касательные напряжения равномерно
распределены по всему сечению и
определяются по формуле: 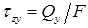 .
.
Абсолютный
сдвиг правого сечения элемента по
отношению к левому сечению, с учетом
закона Гука, равен: 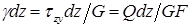 ,
,
тогда 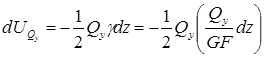 .
.
При поперечном
изгибе касательные напряжения распределены
по сечению неравномерно. В этом случае
выражение для элементарной работы
внутренних перерезывающих сил может
быть представлено в виде: 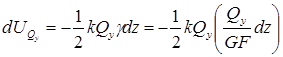
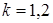 .
.ЭЛЕМЕНТАРНАЯ РАБОТА ВНУТРЕННИХ УСИЛИЙ ПРИ КРУЧЕНИИ
Поворот
правого сечения элемента по отношению
к левому сечению, происходящий под
действием внешних по отношению к нему
крутящих моментов (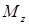 ),
показанных (см. рис. 15.3, в) штриховыми
линиями, равен:
),
показанных (см. рис. 15.3, в) штриховыми
линиями, равен: 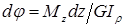
Тогда работа
внутренних крутящих моментов (они на
рисунке не показаны) на этом угле поворота
определяется по формуле: 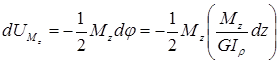 .
.
Пусть теперь
элемент стержня испытывает изгиб. И
пусть его правое поперечное сечение
повернется на угол поворота 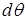 по
отношению к левому сечению (см. рис.
15.3, г).
по
отношению к левому сечению (см. рис.
15.3, г).
Тогда внутренние изгибающие моменты, показанные (см. рис. 15.3, г) сплошными линиями, совершат на этом угле поворота работу:

При одновременном растяжении, кручении и прямом поперечном изгибе стержня (с учетом того, что работа каждого из внутренних усилий на перемещениях, вызываемых остальными усилиями, равна нулю) получим следующее выражение для элементарной работы внутренних сил упругости:
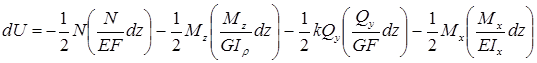 .
.
Интегрируя выражение по всей длине стержня, окончательно получим формулу работы внутренних сил:
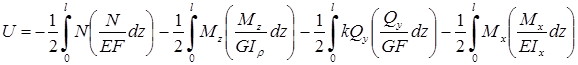 .
.
Внешние силы — Лекции и примеры решения задач технической механики
Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).
Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.
В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.
Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.
Распределённые нагрузки обозначаются буквой q и они бывают:
- поверхностными (например, давление ветра, воды на стенку). Размерность [FL-2].
- объёмными. Их размерность [FL-3].
- распределенными по длине (например, силу тяжести стержня, учитывая небольшие размеры его поперечного сечения, рассматривают как распределённую нагрузку по длине). Размерность [FL-1].
Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.
Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.
Законы изменения нагрузок во времени могут иметь весьма сложный характер.
В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.
Классификация внешних нагрузок
Внешние силы делятся на активные и реактивные (реакции связей). Активные связи принято называть нагрузками.
По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.
Примеры решения задач >
Внутренние силовые факторы >
За счет чего возникает сила, действующая на тело? — КиберПедия
За счет чего возникает сила, действующая на тело?
Если тело движется равномерно и прямолинейно, то:
· Либо на него не действуют никакие силы
· Либо действуют 2 силы: сила тяги и сила трения. Они уравновешивают друг друга по 3 закону.
Какие силы называют внутренними, а какие внешними?
Внутренние силы – это такие силы, которые действуют сразу на все атомы передвигаемого предмета независимо от того, где они находятся: на поверхности или в середине предмета. К этим силам относятся сила инерции и сила покоя.
Внешние силы – это такие силы, которые действуют только на поверхности предмета, не проникая внутрь. К этим силам относятся все силы, развиваемые материальным объектом.
Какие системы тел называют замкнутыми?
Механическая система называется замкнутой (или изолированной), если на неё не действуют внешние силы, т.е. она не взаимодействует с внешними телами.
Как приращение импульса материальной точки связано с импульсом силы? О какой силе при этом идет речь?
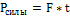 ;
; 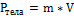 ;
;
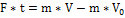 — 2 закон Ньютона
— 2 закон Ньютона
( 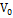 — начальная скорость, V — конечная скорость)
— начальная скорость, V — конечная скорость)
Изменение времени приводит к изменению импульса силы, и следовательно к изменению импульса тела:
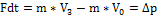
( 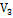 — конечная скорость спустя время dt)
— конечная скорость спустя время dt)
Сформулируйте закон сохранения импульса для системы тел.
Закон сохранения импульса: импульс замкнутой системы тел остаётся постоянным при любых взаимодействиях этих тел между собой.
Что такое работа силы? Что такое мощность? В каких единицах они измеряются?
Работы силы (Дж) – это мера действия силыпри превращении механического движения в другую форму движения, зависящая от модуля и направления силы, а также от перемещения точки приложения силы.
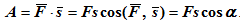
Мощность (Вт) – это физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
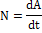
Что такое кинетическая энергия материальной точки? С работой какой силы она связана и как?
· Кинетическая энергия материальной точки – это мера механического движения точки, зависящей от скорости ее движения в ИСО.
· Кинетическая энергия материальной точки – физ. величина, изменение которой = работе всех сил, действующих на материальную точку.
Приращение 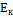 материальной точки при ее перемещении из положения 1 в положение 2 = работе силы, действующей на точку на этом перемещении.
материальной точки при ее перемещении из положения 1 в положение 2 = работе силы, действующей на точку на этом перемещении.
24. Какие силы называют консервативными? Приведите примеры таких сил.
Консервативные силы — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки.
Примеры: сила тяжести, сила упругости, сила гравитации, кулоновская сила.
За счет чего возникает сила, действующая на тело?
Если тело движется равномерно и прямолинейно, то:
· Либо на него не действуют никакие силы
· Либо действуют 2 силы: сила тяги и сила трения. Они уравновешивают друг друга по 3 закону.
1.3 Классификация внешних сил
Силы являются мерой механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих её тел, то действие последних на неё заменяется силами, которые называются внешними. К внешним силам относятся и реакции опорных устройств.
Классификацию сил можно провести по нескольким признакам.
1. Внешние силы могут быть поверхностными или объёмными.
Поверхностные силы —это силы, действующие по поверхности тела или по её значительной части (давление воды на боковую поверхность плотины, давление газа на лопатку компрессора и т.д.).
Объёмные силыраспределены по всему объёму тела, т.е., приложены к каждой его частице (силы тяжести, силы инерции, силы электромагнитных полей).
2. Силысосредоточенные и распределённые.
Сосредоточенные силы —это силы, приложенные к малой части поверхности конструкции (сила давления колеса железнодорожного вагона на рельс). В расчетной схеме такая сила принимается приложенной в точке.
Распределенные силы– это силы, приложенные к достаточно большой части поверхности конструкции (подъемная сила крыла самолета).
3. Силы постоянные и временные.
Постоянная сила действует, не изменяясь, в течение длительного промежутка времени (например, вес железнодорожного моста, передающийся на его опоры).
Временная сила –это сила, действующая в течение сравнительно небольшого промежутка времени (вес железнодорожного состава, проходящего через мост).
4. Силы статические и динамические.
Статические силы–это силы, постепенно возрастающие от нуля до конечного значения, а затем почти не изменяющие своей величины (действие силы тяжести строящегося здания на фундамент).
Динамические силы— это ударные, инерционные, либо циклически изменяющиеся нагрузки.
Ударные нагрузкивозникают в том случае, когда скорости соприкасающихся тел изменяется существенно за короткий промежуток времени (например, усилия, возникающие при ковке и штамповке деталей).
Циклически изменяющиеся — это силы, которые периодически изменяются от одного крайнего значения до другого и обратно. Это наиболее часто встречающиеся нагрузки, действующие на детали машин.
4.Силы активные (обычно бывают заданными) исилы реактивные (силы, действующие со стороны опорных устройств, которые, как правило, подлежат определению).
1.4 Метод сечений
Внешние силы, деформируя тело, вызывают в нем внутренние силы –силы взаимодей-
ствия одной части тела с другой. Прочность тела, в конечном счете, зависит именно от этих сил.
Внутренние усилия
определяются методом сечений. Рассмотрим
его на примере тела произвольной формы,
нагруженного системой внешних сил,
удовлетворяющей условиям равнов-есия.
Мысленно рассечем его некоторой
плоскостью на две части (рис.1.5, α). Так
как связи между частями тела устранены,
то действие их друг на друга необходимо
заменить системой внутренних сил.
Воспользовавшись правилами статики,
приведем эту систему сил к центру
тяжести сечения. В результате получим
главный вектор 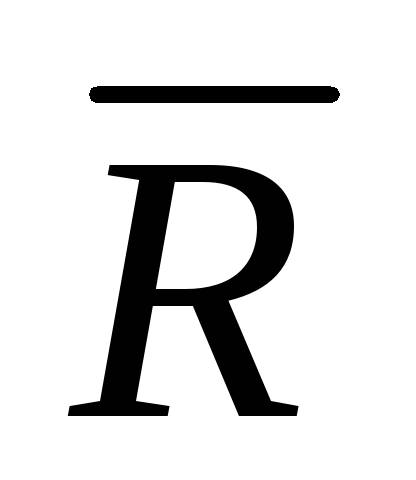 и главный момент
и главный момент (рис1.5,b),
проекциями которых на координатные
оси Х,Y,Zявляются силыQx ,Qy ,N(проекции главного
вектора) и моментыMx,My,Mz(проекции главного момента). Эти
составляющие называются внутренними
силовыми факторами в сечении бруса или
внутренними усилиями:N-
нормальная или продольная сила;Qx, Qy— поперечные силы;Mx,My— изгибающие моменты;Mz— крутящий момент.
(рис1.5,b),
проекциями которых на координатные
оси Х,Y,Zявляются силыQx ,Qy ,N(проекции главного
вектора) и моментыMx,My,Mz(проекции главного момента). Эти
составляющие называются внутренними
силовыми факторами в сечении бруса или
внутренними усилиями:N-
нормальная или продольная сила;Qx, Qy— поперечные силы;Mx,My— изгибающие моменты;Mz— крутящий момент.
При известных внешних силах все рассмотренные силовые факторы определяются из шести уравнений равновесия, которые могут быть составлены для отсеченной части бруса.
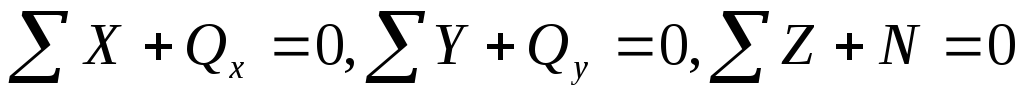 ,
,
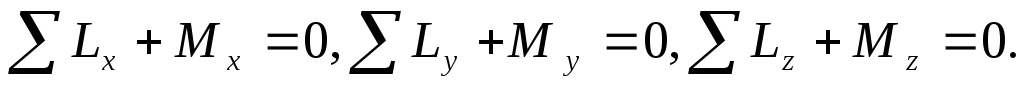
Здесь
∑Х, ∑У, ∑Z– сумма проекций
внешних сил на координатные оси Х, У,Z,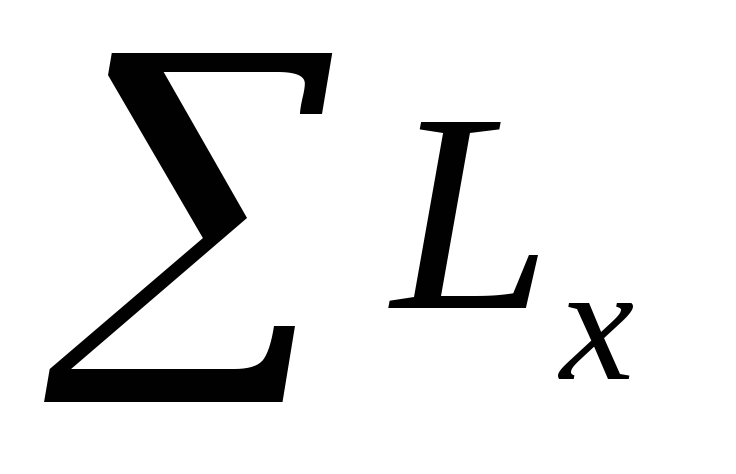
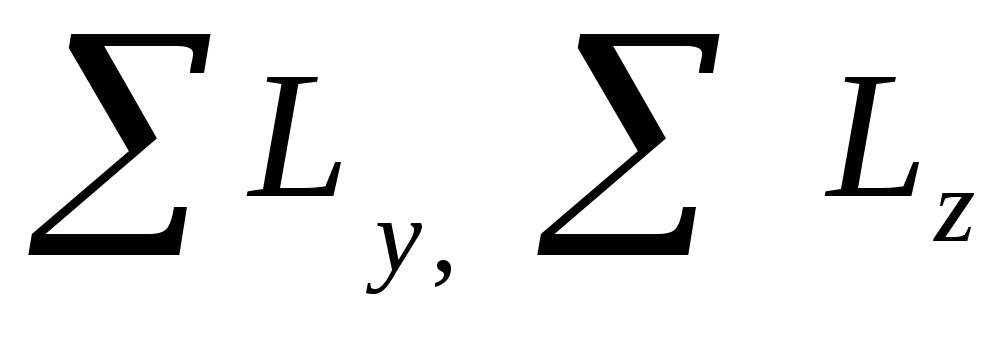 — сумма проекций моментов внешних сил
относительно координатных осей Х, У,Z
— сумма проекций моментов внешних сил
относительно координатных осей Х, У,Z
Из приведенных уравнений равновесия следует, что внутренние усилия правой и левой части бруса равны по величине, но противоположны по знаку.
Наиболее подробно определение внутренних усилий будет рассмотрено при изучении простых деформаций бруса – центрального растяжения, сжатия, изгиба и кручения.
Если на каком-то участке бруса в поперечных сечениях возникает только нормальная сила N, а остальные силовые факторы обращаются в нуль, то на этом участке брус испытывает деформацию растяжения или сжатия. Если в поперечном сечении будет отличным от нуля только крутящий момент Мк, то брус в этом сечении будет испытывать деформацию кручения. Если в поперечных сечениях возникает только изгибающий момент Mх (или Mу), то брус будет испытывать деформацию чистого изгиба в плоскостиYZ(илиXZ). Обычно в поперечном сечении наряду с изгибающим моментом возникает поперечная силаQy(Qx). В этом случае брус испытывать поперечный изгиб.

Понятие о напряжении
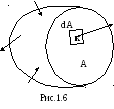
ΔR
Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимаетсянапряжение – это величина внутреннего усилия, приходящаяся на единицу площади сечения.Рассмотрим
сечение А некоторого тела. В окрестности
точки К выделим элементарную площадку
dА, в пределах которой действует внутреннее
усилие ΔR (рис.1.6). За среднее напряжение
на площадке dА принимается отношение
рср= 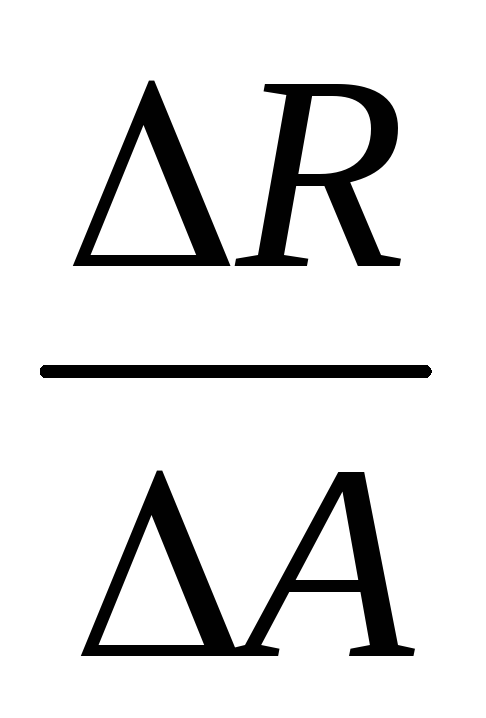 .Уменьшая эту площадку, стянем её в
точку К. В пределе получим:р=ℓim
.Уменьшая эту площадку, стянем её в
точку К. В пределе получим:р=ℓim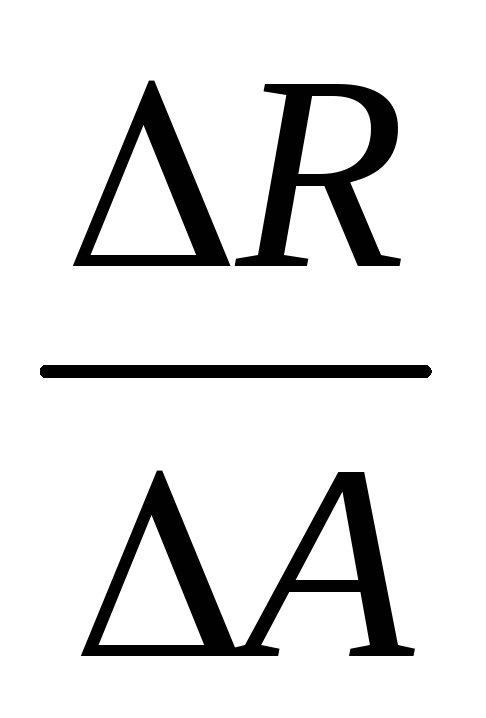 при ΔA→0.Векторная величина
рпредставляет собойполное напряжение в
точке К сечения А. Размерность напряжения
[H/м2]. Единицей измерения является
Па =1Н/м2. Эта единица измерения
мала, поэтому на практике используется
1 МПа = 106Па.
при ΔA→0.Векторная величина
рпредставляет собойполное напряжение в
точке К сечения А. Размерность напряжения
[H/м2]. Единицей измерения является
Па =1Н/м2. Эта единица измерения
мала, поэтому на практике используется
1 МПа = 106Па.
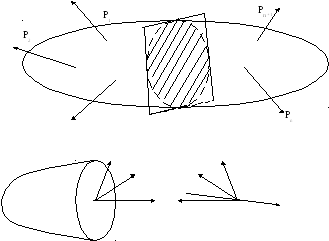
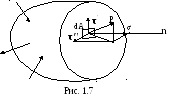 Полное
напряжение рможет быть разложено на три составляющие:
по нормали к плоскости сечения и по двум
осям в плоскости сечения (рис1.7)
Полное
напряжение рможет быть разложено на три составляющие:
по нормали к плоскости сечения и по двум
осям в плоскости сечения (рис1.7)
Перемещения и деформации
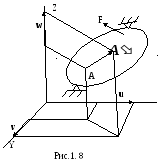
Все тела под действием внешних сил в какой — то мере меняют свои форму и размеры (деформируются). В этом случае точки тела меняют свое положение в пространстве. Вектор , начало которого находится в точке недеформированного тела, а конец в той же точке
деформированного тела, называется вектором полного перемещенияточки (рис. 1.8).
Проекции этого вектора на координатные оси X,Y,Zобозначаются соответственно черезu,v,w. Если на систему тел наложены связи, исключающие её перемещения в пространстве как жесткого целого, то такая система назы- вается кинематически неизменяемой. Именно такие системы рассматриваются в сопротив-лении материалов. В этом случае из перемеще-ний всех точек исключаются составляющие перемещений тела как абсолютно жесткого и остаются лишь перемещения, свойственные только деформируемому телу. Тогда переме-щенияu,v,wявляются малыми по отношению к общим геометрическим размерам тела. На основе малости таких перемещений и принята сформулированная ранее гипотеза неизмен-ности начальных размеров, которая позволяет
при составлении уравнений статики рассматривать тело как недеформированное, имеющее
геометрические размеры такие же, как и до нагружения внешними силами.
Интенсивность изменения формы и размеров тела характеризуется линейными и угловыми деформациями.
Рассмотрим
точки А и В недеформированного тела,
расстояние между которыми равно 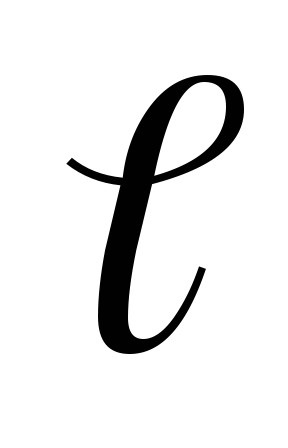 (рис.1.9).
После деформации тела это расстояние
изменится на величину
(рис.1.9).
После деформации тела это расстояние
изменится на величину .
Отношение
.
Отношение к начальной длине
к начальной длине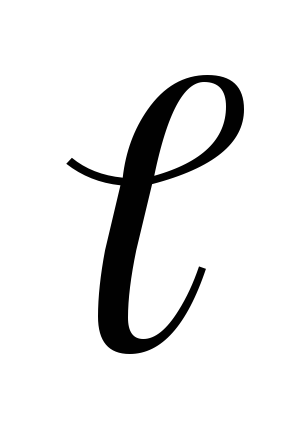 называется
средним удлинением на отрезке
называется
средним удлинением на отрезке 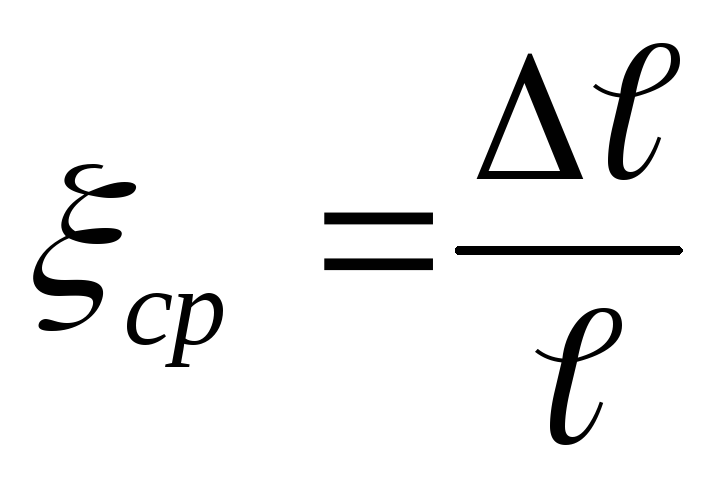 .
Уменьшая отрезок
.
Уменьшая отрезок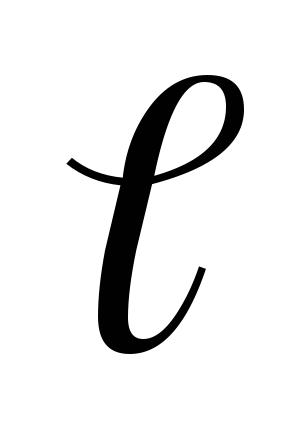 ,
будем приближать точку В к точке А, тогда
в пределе получим
,
будем приближать точку В к точке А, тогда
в пределе получим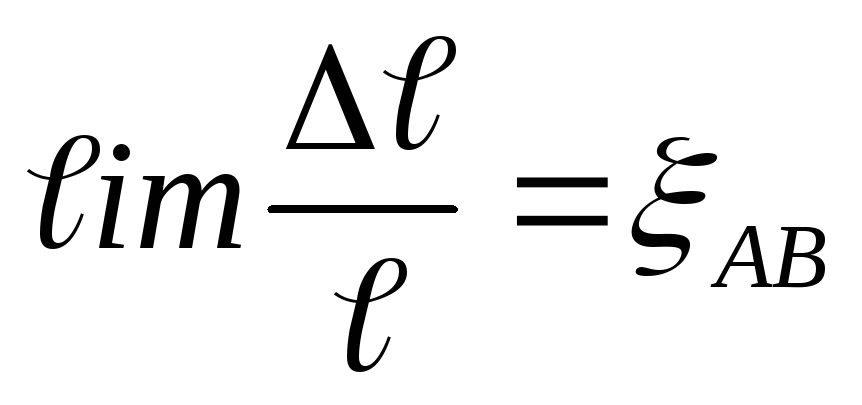 при ℓ →0.
при ℓ →0.
Величина ξАВ называется линейной деформацией в точке А по направлению АВ. В этой же точке, но в другом направлении деформация будет другой. Если рассматриваются деформации в направлении координатных осейx,y,z, то в их обозначение вводятся соответствующие индексы: ξx,ξy,ξz.
Следует отметить, что слово «деформация» имеет два значения. В обиходном языке оно обозначает всякое изменение формы без количественной оценки. В сопротивлении материалов имеет данное выше строгое определение и выступает как количественная мера изменения геометрических размеров в окрестности точки.
Кроме линейной
деформации в теле возникают также и
угловые деформации. Прямой угол,
образованный в недеформированном теле
отрезками СDиDE,
после нагружения его внешними силами
изменит свою величину и примет значение,
равное углу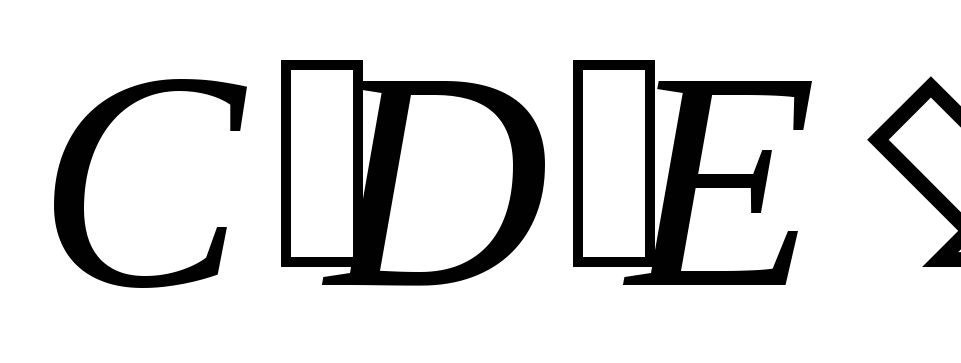 (рис.
1.9).
(рис.
1.9).

Контрольные вопросы
1.Чем занимается наука о сопротивлении материалов?
2.Что такое прочность, жёсткость и устойчивость элементов конструкций?
3. Что понимается под расчётной схемой?
4. Какие силы называются внешними? Какие внутренними?
5. Для чего используется в сопротивлении материалов метод сечений? В чём он
заключается?
6. Количество внутренних усилий в поперечном сечении бруса, как они определяются?
7. Что такое напряжение? Какова его размерность?
8. Какие простые деформации может испытывать брус при его нагружении внешними силами?
Внешние и внутренние силы в сопромате.
В сопромате силы, приложенные к телу в результате взаимодействия тел, называются внешними. Внешние силы бывают объемными (например, собственный вес) и поверхностными. Поверхностные силы делятся на сосредоточенные (теоретически действующие в точке), и на распределенные (приложенные по длине или на площади). Величина распределенной нагрузки, приходящейся на единицу длины или площади, называется интенсивностью нагрузки. Сопротивление материалов изучает не только статические , но и динамические нагрузки. По времени действия нагрузки делятся на постоянные и временные. По характеру действия нагрузки подразделяются на статические и динамические. Статические нагрузки прилагаются постепенно, они не меняются, или меняются незначительно. Динамические нагрузки меняют величину в течение короткого промежутка времени. Под действием внешних сил в материале возникают внутренние силы, сопровождающие деформацию.
Метод сечений, напряжения.
Для определения внутренних сил, возникающих в брусе от действия внешних сил, в сопромате применяется метод сечений.
Изучаемый брус мысленно рассекаем плоскостью на две части. Предполагаем, что каждая из частей находится в равновесии под действием внешних сил, приложенных к этой части, и внутренних сил, возникающих в сечении и представляющих собой силы взаимодействия между оставшейся и отброшенной частями. Равнодействующая внутренних сил в сечении называется внутренним усилием. Рассмотрим пространственный брус, находящийся в равновесии под действием внешних сил (рис. 1).
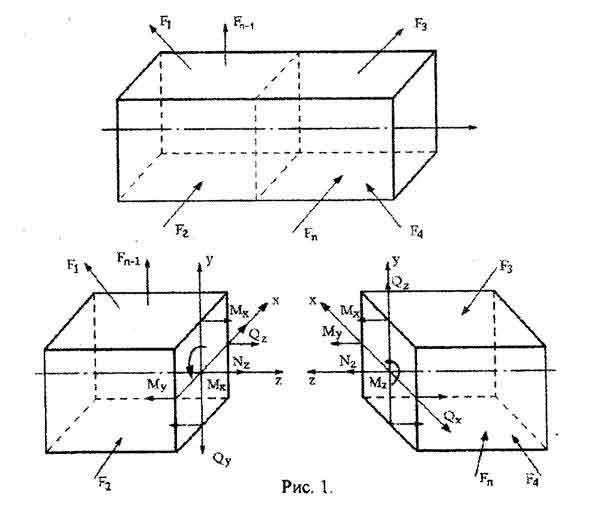
Если брус рассечь плоскостью (использование метода сечений), перпендикулярной оси, т.е. поперечным сечением (рис. 1) и разложить главный вектор и главный момент внутренних сил по осям x,y,z, то на каждой стороне сечения получим шесть внутренних силовых факторов: три силы (N, Qx, Qy) и три момента (Mx, My, Mz).
Эти шесть усилий, совместно с внешними силами, действующими на отсеченную часть бруса, должны обеспечить равновесия этой части. Таким образом, для каждой части бруса должны быть выполнены шесть условий равновесия: сумма моментов сил относительно осей координат, сумма проекций сил на оси координат равна нулю. В этом и есть суть метода сечений сопромата.
Усилия, возникающие в сечении бруса, имеют в сопромате следующие наименования:
N — продольная сила; Qу, Qх — поперечные силы;
Мz — крутящий момент; Мх, Му — изгибающие моменты.
Внутренняя сила (Nz, Qу , Qх) численно равна алгебраической сумме проекций на соответствующую ось бруса всех внешних сил, расположенных по одну сторону от сечения.
Момент (Мz Мx Мy) в любом сечении численно равен алгебраической сумме моментов относительно соответствующей оси бруса от всех внешних сил, расположенных по одну сторону от сечения.
Графики, показывающие как изменяются внутренние усилия при переходе от сечения к сечению, в сопромате называются эпюрами.
Интенсивность
внутренних сил, приходящихся на единицу
площади, в сопротивление материалов
называется напряжением.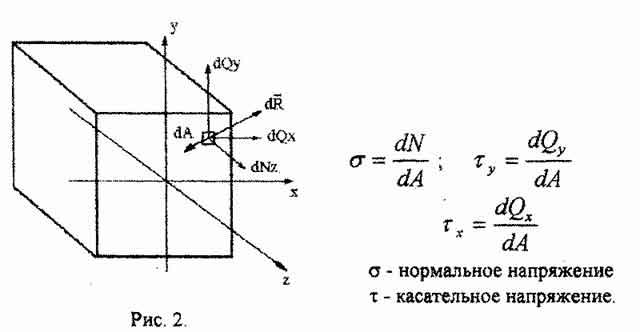
Допустим, что около некоторой точки поперечного сечения бруса, выделена элементарная площадка dА (рис.2). Равнодействующая внутренней силы, действующая на данной площадке, равна dR.. Проекциями dR на оси будут dN, dQy и dQx.
Разделив величины dN, dQy и dQx на площадь dA, получим величины продольных и попе-
речных сил, приходящихся на единицу площади:
Их измеряют в единицах напряжения — паскалях (Па) и кратных ему — (кПа и мПа)
Полное напряжение в данной точке рассматриваемого сечения:
Сила —
величина векторная, следовательно, и
напряжение – вектор того же направления.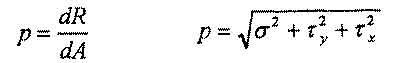
Между напряжениями и деформациями существует зависимость. В случае упругой деформации эта зависимость выражается законом Гука.
Закон Гука при линейной деформации (растяжение или сжатие) выражает прямолинейную зависимость между нормальными напряжениями и относительными деформациями.
При угловой деформации (сдвиг) существует прямолинейная зависимость между касательными напряжениями и углами сдвига: т = уе.
В этих выражениях Е и G — коэффициенты пропорциональности,
характеризующие упругие свойства материалов:
Е — модуль нормальной упругости или модуль Юнга;
G — модуль упругости при сдвиге или модуль сдвига;
е — относительная продольная деформация;
у — относительная угловая деформация.

