ПОЛЯ ФИЗИЧЕСКИЕ • Большая российская энциклопедия

Авторы: В. П. Павлов

ПОЛЯ́ ФИЗИ́ЧЕСКИЕ, фи­зич. сис­те­мы, об­ла­даю­щие бес­ко­неч­но боль­шим чис­лом сте­пе­ней сво­бо­ды. От­но­ся­щие­ся к та­кой сис­те­ме фи­зич. ве­ли­чи­ны не ло­ка­ли­зо­ва­ны на к.-л. отд. ма­те­ри­аль­ных час­ти­цах с ко­неч­ным чис­лом сте­пе­ней сво­бо­ды, а не­пре­рыв­но рас­пре­де­ле­ны по не­ко­то­рой об­лас­ти про­стран­ст­ва. При­ме­ра­ми та­ких сис­тем мо­гут слу­жить гра­ви­тац. и элек­тро­маг­нит­ные по­ля и вол­но­вые по­ля час­тиц в кван­то­вой фи­зи­ке (элек­трон­но-по­зи­трон­ное, ме­зон­ное и т. п.).

При рас­смот­ре­нии не­ре­ля­ти­ви­ст­ских про­цес­сов по­ня­тие по­ля обыч­но не вво­дят. Напр., при рас­смот­ре­нии гра­ви­тац. или ку­ло­нов­ско­го взаи­мо­дей­ст­вия двух час­тиц мож­но счи­тать, что си­ла взаи­мо­дей­ст­вия воз­ни­ка­ет лишь при на­ли­чии обе­их час­тиц, по­ла­гая, что про­стран­ст­во во­круг час­тиц не иг­ра­ет осо­бой ро­ли в пе­ре­да­че взаи­мо­дей­ст­вия (см. Взаи­мо­дей­ст­вие в фи­зи­ке). Та­кое пред­став­ле­ние со­от­вет­ст­ву­ет кон­цеп­ции даль­но­дей­ст­вия, или дей­ст­вия на рас­стоя­нии. По­ня­тие о даль­но­дей­ст­вии, од­на­ко, яв­ля­ет­ся при­бли­же­ни­ем толь­ко в не­ре­ля­ти­ви­ст­ском слу­чае, фи­зи­че­ски эк­ви­ва­лент­ным пред­став­ле­нию о том, что дей­ст­вие за­ря­да про­яв­ля­ет­ся лишь при по­ме­ще­нии вто­рой, проб­ной час­ти­цы в об­ласть про­стран­ст­ва, свой­ст­ва ко­то­ро­го уже из­ме­не­ны из-за на­ли­чия пер­вой час­ти­цы.

По­ня­тие по­ля вве­де­но М. Фа­ра­де­ем и Дж. К. Мак­свел­лом в 1830–60-х гг. для опи­са­ния ме­ха­низ­ма дей­ст­вия элек­трич. и маг­нит­ных сил. Кон­цеп­ция си­ло­во­го по­ля как по­сред­ни­ка при пе­ре­да­че взаи­мо­дей­ст­вия воз­ник­ла в ка­че­ст­ве аль­тер­на­ти­вы идее даль­но­дей­ст­вия. Она под­ра­зу­ме­ва­ет, что са­мо на­ли­чие за­ря­жен­ной час­ти­цы ме­ня­ет свой­ст­ва про­стран­ст­ва: час­ти­ца соз­да­ёт во­круг се­бя си­ло­вое элек­трич. по­ле. Ка­ж­дая точ­ка из­ме­нён­но­го про­стран­ст­ва об­ла­да­ет по­тен­ци­аль­ной спо­соб­но­стью про­явить дей­ст­вие си­лы. Для это­го дос­та­точ­но по­мес­тить в эту точ­ку вто­рой, проб­ный за­ряд. Проб­ный за­ряд взаи­мо­дей­ст­ву­ет не не­по­сред­ст­вен­но с за­ря­дом – соз­да­те­лем по­ля, а с по­лем в точ­ке, где этот проб­ный за­ряд на­хо­дит­ся. По­ле вы­пол­ня­ет роль по­сред­ни­ка: оно от точ­ки к точ­ке пе­ре­да­ёт дей­ст­вие од­но­го за­ря­да на дру­гой. Та­кой ме­ха­низм на­зы­ва­ет­ся близ­ко­дей­ст­ви­ем. Взаи­мо­дей­ст­вие при этом пе­ре­да­ёт­ся по­сте­пен­но, от точ­ки к точ­ке в та­ком из­ме­нён­ном про­стран­ст­ве. Это и оз­на­ча­ет, что пер­вая час­ти­ца соз­да­ёт во­круг се­бя си­ло­вое гра­ви­тац. или элек­трич. по­ле.

Кон­цеп­ция близ­ко­дей­ст­вия на­хо­дит под­твер­жде­ние при рас­смот­ре­нии ре­ля­ти­ви­ст­ских про­цес­сов. При дви­же­нии ис­точ­ни­ков со ско­ро­стью, срав­ни­мой со ско­ро­стью пе­ре­да­чи взаи­мо­дей­ст­вия, го­во­рить о даль­но­дей­ст­вии уже нель­зя. Из­ме­не­ние со­стоя­ния од­ной час­ти­цы со­про­во­ж­да­ет­ся, во­об­ще го­во­ря, из­ме­не­ни­ем её энер­гии и им­пуль­са, а из­ме­не­ние си­лы, дей­ст­вую­щей на др.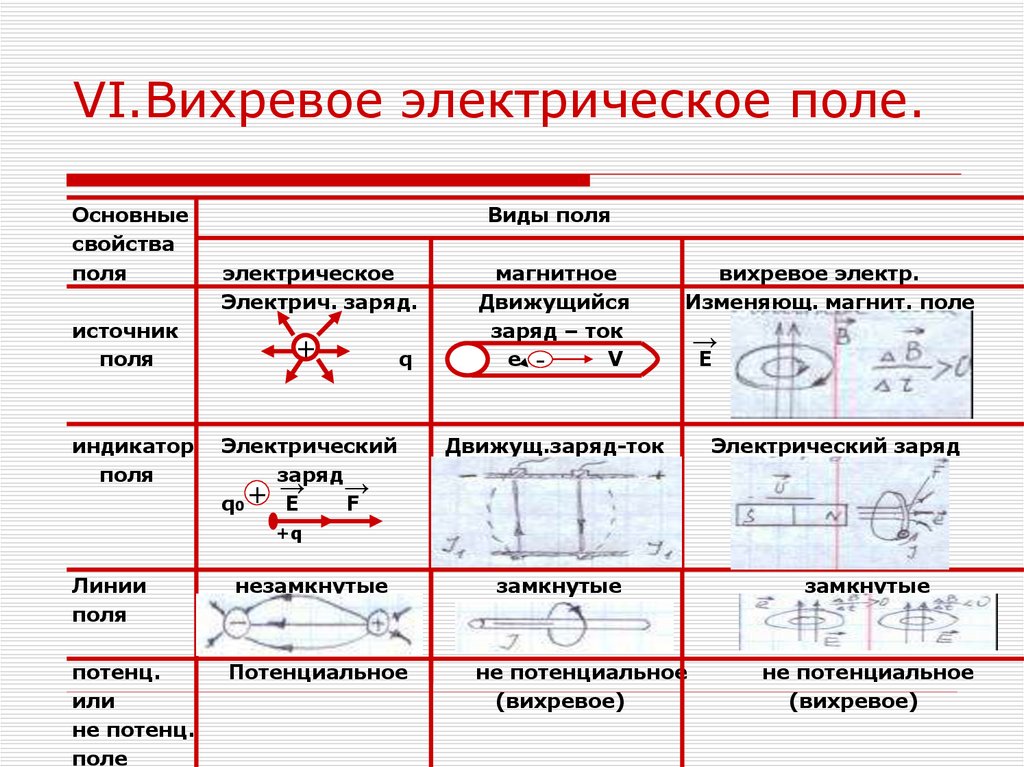 час­ти­цу, на­сту­па­ет лишь че­рез ко­неч­ный про­ме­жу­ток вре­ме­ни. До­ли энер­гии и им­пуль­са, от­дан­ные од­ной час­ти­цей и ещё не при­ня­тые вто­рой, при­над­ле­жат в те­че­ние это­го вре­ме­ни пе­ре­но­ся­ще­му их по­лю. По­ле, пе­ре­но­ся­щее взаи­мо­дей­ст­вие, яв­ля­ет­ся, т. о., са­мо по се­бе фи­зич. ре­аль­но­стью.

По­ня­тие «П. ф.» при­ме­ни­мо при опи­са­нии свойств лю­бой сплош­ной сре­ды. Ес­ли со­пос­та­вить с ка­ж­дой точ­кой сре­ды оп­ре­де­ляю­щие её со­стоя­ние фи­зич. ве­ли­чи­ны (темп-ру, дав­ле­ние, на­тя­же­ние и др.), то по­лу­чит­ся по­ле этих ве­ли­чин. В этом слу­чае роль уп­ру­гой сре­ды для пе­ре­да­чи взаи­мо­дей­ст­вия оче­вид­на. Пер­во­на­чаль­ная труд­ность пред­ста­вить не­ме­ха­нич. сре­ду, спо­соб­ную пе­ре­но­сить энер­гию и им­пульс, по­ро­ди­ла разл. ме­ха­нич. мо­де­ли эфи­ра как сре­ды, пе­ре­но­ся­щей элек­тро­маг­нит­ные взаи­мо­дей­ст­вия (см. Эфир ми­ро­вой). Од­на­ко все ме­ха­нич. мо­де­ли эфи­ра про­ти­во­ре­чат прин­ци­пу от­но­си­тель­но­сти Эйн­штей­на (см. От­но­си­тель­но­сти тео­рия), и от них при­шлось от­ка­зать­ся.

Про­стей­ший тип дви­же­ния по­ля – вол­но­вое, для ко­то­ро­го по­ле­вая функ­ция пе­рио­ди­че­ски ме­ня­ет­ся во вре­ме­ни и от точ­ки к точ­ке. Лю­бое со­стоя­ние по­ля удоб­но пред­ста­вить в ви­де су­пер­по­зи­ции волн. Для вол­но­во­го дви­же­ния ха­рак­тер­ны яв­ле­ния ди­фрак­ции и ин­тер­фе­рен­ции, не­воз­мож­ные в клас­сич. ме­ха­ни­ке. С др. сто­ро­ны, ди­на­мич. ха­рак­те­ри­сти­ки волн (энер­гия, им­пульс и т. д.) «раз­ма­за­ны» в про­стран­ст­ве, а не ло­ка­ли­зо­ва­ны, как у клас­сич. час­тиц.

Та­кое про­ти­во­пос­тав­ле­ние вол­но­вых и кор­пус­ку­ляр­ных свойств, при­су­щее клас­сич. ме­ха­ни­ке, от­ра­жа­ет­ся в ней как ка­че­ст­вен­ное раз­ли­чие ме­ж­ду П. ф. и час­ти­ца­ми. Од­на­ко опыт по­ка­зы­ва­ет, что на ма­лых рас­стоя­ни­ях, в атом­ных мас­шта­бах, это раз­ли­чие ис­че­за­ет: у по­ля вы­яв­ля­ют­ся кор­пус­ку­ляр­ные свой­ства (см., напр., Ком­пто­на эф­фект), у час­тиц – вол­но­вые (см. Ди­фрак­ция час­тиц).

Кван­то­вая ме­ха­ни­ка ста­вит в со­от­вет­ст­вие ка­ж­дой час­ти­це по­ле её вол­но­вой функ­ции, даю­щее рас­пре­де­ле­ние разл. от­но­ся­щих­ся к час­ти­це фи­зич. ве­ли­чин. Дви­же­ние час­ти­цы пред­став­ля­ет­ся при этом как рас­про­стра­няю­щие­ся ко­ле­ба­ния её вол­но­вой функ­ции. Од­на­ко вол­но­вую функ­цию нель­зя трак­то­вать как ре­аль­ное П. ф., и в сво­ей обыч­ной фор­ме кван­то­вая ме­ха­ни­ка не пол­но­стью сня­ла про­ти­во­пос­тав­ле­ние по­лей и час­тиц. Она ока­за­лась спо­соб­ной лишь от­ра­зить вол­но­вые свой­ст­ва час­тиц как на­мёк на пол­ное един­ст­во по­ля и час­ти­цы – кор­пус­ку­ляр­но-вол­но­вой дуа­лизм.

Еди­ную кор­пус­ку­ляр­но-вол­но­вую точ­ку зре­ния осу­ще­ст­в­ля­ет кван­то­вая тео­рия по­ля в тер­ми­нах но­во­го фи­зич. объ­ек­та – кван­то­ван­но­го по­ля, опи­сы­ваю­ще­го на рав­ной ос­но­ве и по­ля, и час­ти­цы. Имен­но на кван­то­ван­ное по­ле пе­ре­но­сят­ся тре­бо­ва­ния сим­мет­рии и ин­ва­ри­ант­но­сти, ко­то­рые яв­ля­ют­ся обоб­ще­ни­ем экс­пе­рим. дан­ных, опи­сы­ваю­щих раз­но­об­ра­зие эле­мен­тар­ных час­тиц и их взаи­мо­дей­ст­вий.

Магнитные поля и Капица в рамках погрешности

Капица — ученик сразу двух ученых, почитаемых за «отцов физики». Первым был Абрам Иоффе, воспитавший первое поколение советских физиков: кроме Капицы у него, например, учились Курчатов, Семенов, Александров. Вторым — Эрнест Резерфорд, среди воспитанников которого 12 (!) нобелевских лауреатов по физике и химии, включая и самого Капицу. К Резерфорду Капица отправился в 1921-м, по рекомендации Иоффе.

На этом фото 1916 года — участники семинара Иоффе в Политехническом институте; двое из них станут нобелевскими лауреатами: сначала Николай Семенов (справа, в первом ряду), потом Капица (тоже справа, во втором ряду)

Впрочем, для того чтобы таки стать сотрудником легендарной Кавендишской лаборатории, Капице пришлось Резерфорда убеждать — лорд ссылался на то, что ставок у него для нового сотрудника нет. Как вспоминал потом Капица, диалог их выглядел следующим образом:

 

— Какую точность Вы считаете приемлемой в своей работе?

 

— Два-три процента.

 

— В таком случае один лишний исследователь не будет заметен, он будет поглощен допустимой неточностью опыта.

 

С этим Резерфорд не смог не согласиться, и молодой физик стал заниматься исследованиями под его началом.

 

На тот момент передним краем физики было изучение свойств атомов и развитие квантовой механики — магнитные поля в этом играли ключевую роль.

 

Магнитное поле отклоняет в сторону заряженные частицы и меняет структуру энергетических уровней в атомах. Наблюдение за этими явлениями позволило физикам разработать фундаментальную теорию микромира, но для этого пришлось решить ряд чисто инженерных задач.

 

Современные бытовые магниты — скажем, в динамиках или жестких дисках — создают поле около одного тесла. В аппарате для МРТ бывают поля до десяти тесла. Такие магниты уже далеко не просты в обращении: на гаечный ключ вблизи томографа будет действовать сила, достаточная для отрыва от земли груза в центнер!

 

Капица в Кавендишской лаборатории смог получить, пусть и на короткое время, поле в пятьдесят тесла. Конечно, сейчас есть магниты, создающие поле в 100 тесла, и даже установки, которые позволяют получить более двух с половиной тысяч тесла (с разрушением магнита и всего вокруг), но для 1920-х это был выдающийся результат.

 

Успех этот был столь впечатляющим, что уже в 1930 году Капица, еще недавно чуть было не «завернутый» Резерфордом, получил уже свою собственную лабораторию.

 

Портрет Капицы и Николая Семенова кисти Бориса Кустодиева, 1921 год. Будущие нобелевские лауреаты заявили художнику, что они только «пока» не знамениты — и оказались правы

 

Самое холодное вещество в мире

Довольно быстро Капица стал признанным физиком-экспериментатором, способным проводить тонкие и сложные опыты. В 1930-е годы он занялся темой, требовавшей экстраординарных навыков, — изучением жидкого гелия и процессов при сверхнизких температурах.

 

Работать с гелием сложно по целому ряду причин, начиная от его дороговизны и заканчивая тем, что в жидком виде он имеет температуру всего на четыре градуса выше абсолютного нуля. Капице и британским физикам Джону Аллену и Остину Майзнеру удалось не просто измерить характеристики жидкого гелия, но открыть новое состояние вещества, сверхтекучую жидкость.

 

Сверхтекучий гелий утрачивает вязкость и без сопротивления протекает через отверстия шириной всего в три атома, а еще может вытечь из емкости, «вскарабкавшись» по смачиваемой стенке. Теоретический анализ этого феномена позволил продвинуться в разработке квантовой теории. В 1978 году Капицу наградили за открытие Нобелевской премией. А теория сверхтекучести собрала целых две Нобелевки с интервалом в 40 лет, причем обе ушли в том числе ученым из России: Льву Ландау, Виталию Гинзбургу и Алексею Абрикосову (последний с 1991 года жил и работал в США).

 

Говоря о выборе физики низких температур в качестве своей области, Капица в 1974 году написал следующее (орфография сохранена):

 

«Когда мы изучаем вещество при комнатной температуре, квантовая природа процессов не может обычно выявляться. Тепловое движение атомов как бы стушевывает те особенности в процессах, которые накладываются их квантовой природой, и они неощутимы. Это так же, как если бы на качающемся в море корабле мы вздумали изучать на биллиардном столе законы соударений шаров. Очевидно, эта затея осуществима только тогда, когда море спокойно. Так и при изучении квантовой природы явлений течения процессов, происходящих в конденсированном состоянии. Только тогда они себя полностью проявляют, когда тепловое движение атомов достаточно мало. Отсюда очевиден тот большой интерес в физике к изучению явлений в веществе при очень низких температурах».

 

Турбодетандер и подача кислорода

Петр Капица занимался не только и даже не столько чистой физикой, сколько передовыми технологиями. Его возвращение в СССР, кстати, не было добровольным: ученому просто не дали вернуться в Великобританию из короткой поездки в 1934 году, аннулировав его визу (а в то время они были и на выезд из страны). Капицу «приземлили» с расчетом на его участие в прикладных исследованиях.

 

Физик действительно добился важных результатов, после того как поставил встречное требование советскому правительству и заставил перевезти свою британскую лабораторию со всем оборудованием (а там были инновационные приборы). Работая с низкими температурами, Капица радикально усовершенствовал турбодетандер, устройство для охлаждения газа.

 

В этом устройстве газ раскручивает турбину и из-за этого остывает, пока не превратится в жидкость. Сжижение — самый удобный и дешевый метод получения кислорода, который конденсируется до азота и других газов. Чистым кислородом продувают печи на сталелитейных заводах, его используют в производстве взрывчатки, как окислитель для ракетных двигателей, в медицине, для сварки и много где еще.

 

В 1930-е годы лучшие турбодетандеры делала немецкая фирма Linde, но их КПД не достигал и 60%. Найденные Капицей решения позволили превысить отметку 90% и обойтись без импортного оборудования. Последнее оказалось критически важным в военные годы.

 

Высокие температуры

Эксперименты с низкими и очень низкими температурами прославили Капицу, но когда ему присудили Нобелевскую премию, он занимался предметом совсем другого толка, высокотемпературной плазмой. Вопреки правилам темой его нобелевской лекции стали управляемый термоядерный синтез и плазма. «Эти работы я сделал 40 лет назад, и я их забыл», — ответил физик на предложение рассказать про сверхтекучесть.

 

Еще Капица предложил гипотезу происхождения шаровой молнии. Согласно ей, шаровая молния подпитывается энергией за счет внешнего микроволнового излучения, которое каким-то образом возникает во время гроз. Физик отмечал, что источник этого излучения неясен, но, если допустить его наличие, поведение шаровой молнии вполне объяснимо даже в части проникновения плазменного сгустка сквозь оконное стекло или иные тонкие препятствия.

 

Эту гипотезу, в отличие от многого другого из научного наследия ученого, не удалось ни подтвердить, ни опровергнуть. Теории, объясняющей природу шаровой молнии, нет и по сей день. Редкость явления не позволяет изучить его в природных условиях, а все попытки создать нечто подобное в лаборатории успехом не увенчались. Правда, можно смело отвергнуть предположение, что светящийся объект лишь галлюцинация. На сегодня есть и видеозаписи, и даже данные о спектрах шаровой молнии.

 

Борьба за коллег и принципиальность

Капица писал, что после вынужденного возвращения в СССР его поначалу недолюбливали. Во-первых, ученый открыто требовал приличных условий для работы: отдельного здания под институт и выкупа британского оборудования. Во-вторых, он этого добивался и получал больше, чем многие другие физики.

 

Однако спустя некоторое время он получил признание не только как хороший исследователь и грамотный организатор — Капицу стали уважать за стойкость. Когда Льва Ландау арестовали за составление листовок, где Сталин сравнивался с Гитлером (!), Капица добился освобождения ученого под свою ответственность. В разгар репрессий это был крайне рискованный шаг, но ни Капицу, ни большинство его сотрудников НКВД не трогало.

 

Капица вел переписку с иностранными коллегами и обращался к руководителям страны вплоть до самого Иосифа Сталина, указывая, как стоит развивать науку и технологии. В 1946 году он ушел из атомного проекта и попал в опалу до самой смерти Сталина и ареста Берии, но опять-таки не был арестован или убит.

 

В Институте физических проблем Капица, будучи директором и основателем, пошел против советских принципов хозяйствования. Чтобы разделаться с грязью, он уволил двух дворников и втрое поднял оклад оставшемуся. А когда создаваемая Капицей система подготовки будущих инженеров не прижилась в МГУ, тамошний физико-технический факультет сделали отдельным Московским физико-техническим институтом, МФТИ.

 

Капица был талантлив, обладал организаторскими способностями, у него были дипломатические навыки и гражданская позиция. Сочетание этих качеств выделяло его даже среди нобелевских лауреатов.

Источник: chrdk.ru

образование — Что такое квантовое поле?

спросил 8 лет, 3 месяца назад

Изменено 7 лет назад

Просмотрено 3к раз

$\begingroup$

Я только пробую QFT и хочу начать. Я застрял в самом начале: что такое квантовое поле и как на него смотреть? Этот вопрос может быть продолжением вопроса Что такое поле? вопрос.

Для меня поле можно рассматривать как функцию. Таким образом, выражение «векторное поле» — это сокращение от выражения «функция, которая отображает любую область в векторы некоторых измерений».

Какой тип значения отображает эта функция, когда речь идет о квантовых полях?

В этом еще вопрос. Они говорят, что это ценится оператором.

Насколько я помню, операторы можно рассматривать как «кет-брас», то есть матричное произведение бесконечно длинного столбца и вектора-строки. Итак, бесконечно большая матрица. Или, другими словами, функция, которая принимает 2 параметра и возвращает скаляр. Это правильно?

Итак, если я прав, квантовое поле — это «поле скалярного поля». Итак, функция, которая отображает координаты пространства-времени, в функции, которые отображают 2 скаляра в скаляр.

В этом еще вопрос. Говорят, что это скаляр, оцененный в формализме интеграла по путям. Мне еще предстоит понять этот формализм до сих пор. Но пока я не понимаю, как скаляр и поле с функциональным значением могут быть эквивалентны…

С другой стороны, просто из любопытства, сколько полей нам нужно иметь в QFT? В классической электромагнетике у нас было два векторных поля, электрическое и магнитное, и уравнения Максвелла, описывающие эволюцию во времени. После некоторого поиска в Google я вижу, что есть бозонные поля, фермионные поля, поле Хиггса, любое другое поле. .. Все ли эти квантовые поля (значатся оператором)? Есть ли у нас уравнения поля, описывающие все взаимосвязи между этими полями (так же, как уравнения Максвелла в ЭМ)?

• квантовая теория поля
• образование

$\endgroup$

8

$\begingroup$

Квантовое поле, вообще говоря, не является полем скалярных функций (можно построить игрушечные модели). Его можно понимать как поле операторов или как фоковское пространство, присоединенное к каждой пространственно-временной точке. Хорошая новость заключается в том, что для многих целей нам не нужно иметь дело со всей сложностью такого объекта. Многие физически релевантные взаимодействия можно понимать как сходящиеся ряды возмущений взаимодействий отдельных частиц (но не следует создавать впечатление, что этот подход теории возмущений поля полон, за исключением нескольких небольших проблем «сходимости»).

Другая хорошая новость заключается в том, что многие свойства квантовых полей можно изучать с помощью формализмов, которые выглядят так, как если бы поля были скалярнозначными, или, по крайней мере, можно абстрагироваться от полного рассмотрения из-за свойств симметрии.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Из чего состоят квантовые поля?

спросил 1 год, 8 месяцев назад

Изменено 1 год, 8 месяцев назад

Просмотрено 2к раз

$\begingroup$

Если квантовые поля являются математическими объектами, созданными для объяснения природы, то то, что они объясняют, определенно является чем-то физическим и из чего-то состоит. Так почему же не может быть ответа на вопрос, из чего состоят эти математические квантовые поля?

Я имею в виду, что если физики их придумывают, то у них определенно есть определенные критерии того, из чего состоят эти математические поля, не так ли?

• квантовая теория поля

$\endgroup$

3

$\begingroup$

«Книга природы написана в математике», — сказал Галилей. Трудно петь песню о книге, которую нельзя прочитать; вот песня.

Квантовые поля состоят из бесконечного множества квантовых осцилляторов. Эти осцилляторы — повсюду маленькие гаджеты, которые извергают и потребляют квантов , строительных блоков нашего мира (ноты/тоны песни?).

Их понимание существует почти столетие (Джордан), но до сих пор трудно понять интуитивно: вот почему требуются годы обучения физике, чтобы обращаться с ними вслепую. Эти кванты — фотоны, материальные частицы, гравитоны и тому подобное.

Они более физические и могут давать более точные ответы, чем инженерные и любые другие физические теории. На самом деле, большая часть интуитивных представлений инженера/дилетанта о физическом мире представляет собой сложное эмпирическое, но ошибочное обобщение квантовых полей, и настоящая проблема заключается в том, как это возникает из более реальных квантовых полей. То, что вы/мы видим в свое время, является всего лишь искаженным изображением/блефом их коллективов, но вы/мы избалованы с самого рождения, чтобы предположить, что это более реально. Как сказал Стив Вайнберг, покойный (просто) супергерой понимания таких квантовых полей: «Вселенная — огромный прямой продукт представлений групп симметрии». Эти представления и есть квантовые поля».0005

В принципе, они лежат в основе всего, но выяснить, как из них возникает наш макроскопический мир коттивампус, «появление», иногда бывает непросто, а редко нет. Но вряд ли есть им заслуживающие доверия, полные, эффективные, логичные альтернативы.

Эта песня лучше.

$\endgroup$

10

$\begingroup$

Я собираюсь занять совсем другую позицию, чем удивительный ответ Космаса Захоса. Это не означает, что я думаю, что ответ неверен, но скорее я считаю, что есть несколько совершенно разных ответов на этот вопрос, потому что на самом деле это не

физика вопрос, а философия вопрос. Следовательно, я предлагаю дополнительную точку зрения.

Моя точка зрения: мы не только не знаем, из чего состоят квантовые поля, но мы даже не знаем, существуют ли они (что бы ни значило «существующее»), и нам все равно. Задача физики не в том, чтобы описать, как Вселенная на самом деле является , а в том, чтобы сказать , на что она похожа на .

Выберите, например, ньютоновскую гравитацию. Он говорит вам, что существует классическое поле, пронизывающее пространство-время, которое мы называем гравитационным полем, которое создает силу между любыми двумя телами, которая действует как произведение их масс, деленное на квадрат их расстояния. Так ли уж устроена Вселенная? Не обязательно, но для широкого круга явлений это в значительной степени работает, как если бы это была вся картина. Вы можете долгое время ничего не знать об общей теории относительности (ОТО). В качестве альтернативы вы также можете сформулировать ньютоновскую гравитацию геометрически, как мы получаем ее из ОТО в пределе слабого поля, а затем сделать вывод, что силы нет, а вместо этого пространство-время искривлено, а гравитация — это именно то, что нужно.

Что является истинной природой Вселенной? Можно спорить об искривленном пространстве-времени из-за ОТО, а затем другой может начать спорить о том, какова природа той или иной теории, лежащей ниже ОТО, или об альтернативных формулировках гравитации. Какой из них правильный? Нет никакого способа узнать, и, хотя это увлекательная задача, это не проблема физики.

Квантовые поля — почти то же самое. Мы не наблюдаем поля напрямую. То, что мы можем измерить, — это такие величины, как сечения или скорость затухания, которые являются числами, которые говорят нам о свойствах того, как «частицы» рассеиваются друг от друга или как быстро они распадаются (кавычки взяты потому, что мы интерпретируем возбуждения поля как частицы, но фундаментальные количества на самом деле являются полями). Поскольку мы не измеряем фактические поля, у нас нет способа узнать, существуют ли они. Суть в том, что Вселенная работает таким образом, который невероятно хорошо согласуется с тем, что было бы, если бы поля действительно существовали. Мы не знаем, существуют ли они, но это действительно похоже на то, если бы они были на самом деле.

Как я уже сказал, это скорее философский вопрос, в котором я не эксперт. Позиция, которую я занимаю, ближе к так называемому антиреализму (где я скептически отношусь к тому, можем ли мы сказать, действительно ли существует что-то, что мы не измеряем), в то время как ответ Космаса Захоса ближе к реалистической точке зрения. точка зрения (которая ближе к представлению о том, что если теория использует такое понятие, оно должно каким-то образом существовать).

Эти идеи гораздо шире, чем я изложил в этом комментарии, но, как я уже сказал, я не эксперт. Стоит отметить, что мы часто меняем свое мнение, когда говорим о разных теориях: тот же физик может сказать, что ОТО подразумевает, что пространство-время на самом деле искривлено (более реалистично), в то время как отрицание волновой функции является чем-то большим, чем просто математическим удобством. (антиреалист).

Таким образом, мы не знаем, из чего они сделаны, и попытка ответить на вопрос требует философского выбора.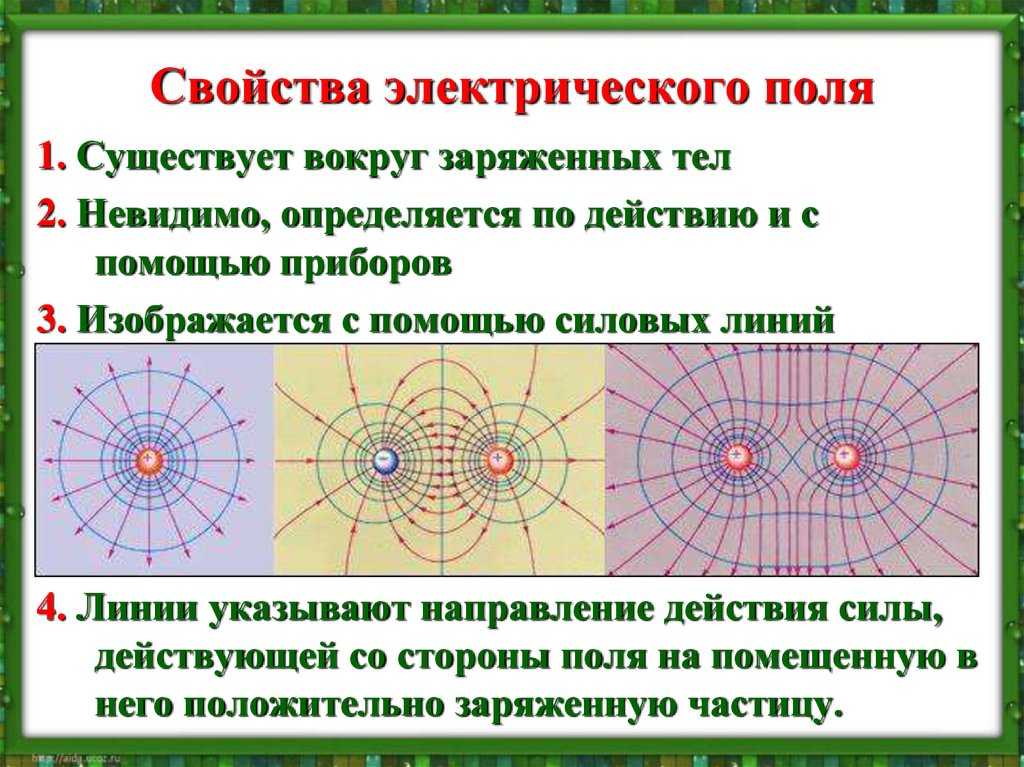 Что мы знаем, так это то, что Вселенная ведет себя так, как если бы эти вещи существовали с гигантской точностью. Может быть, однажды мы найдем более глубокую теорию, которая заменит КТП и объяснит, из чего состоят поля, может быть, мы застрянем на ней навсегда.

$\endgroup$

4

$\begingroup$

Квантовые поля — это математические конструкции, представляющие квантовые степени свободы. В релятивистской квантовой теории поля квантовое поле может использоваться для представления неопределенного числа идентичных релятивистских частиц. Кроме того, квантовые поля позволяют нам кодировать взаимодействия, которые являются локальными.

В Стандартной модели некоторые частицы (например, электрон) являются «фундаментальными», поэтому поле, связанное с этими частицами, также является «фундаментальным», то есть они не состоят из чего-то более глубокого, о чем мы знаем.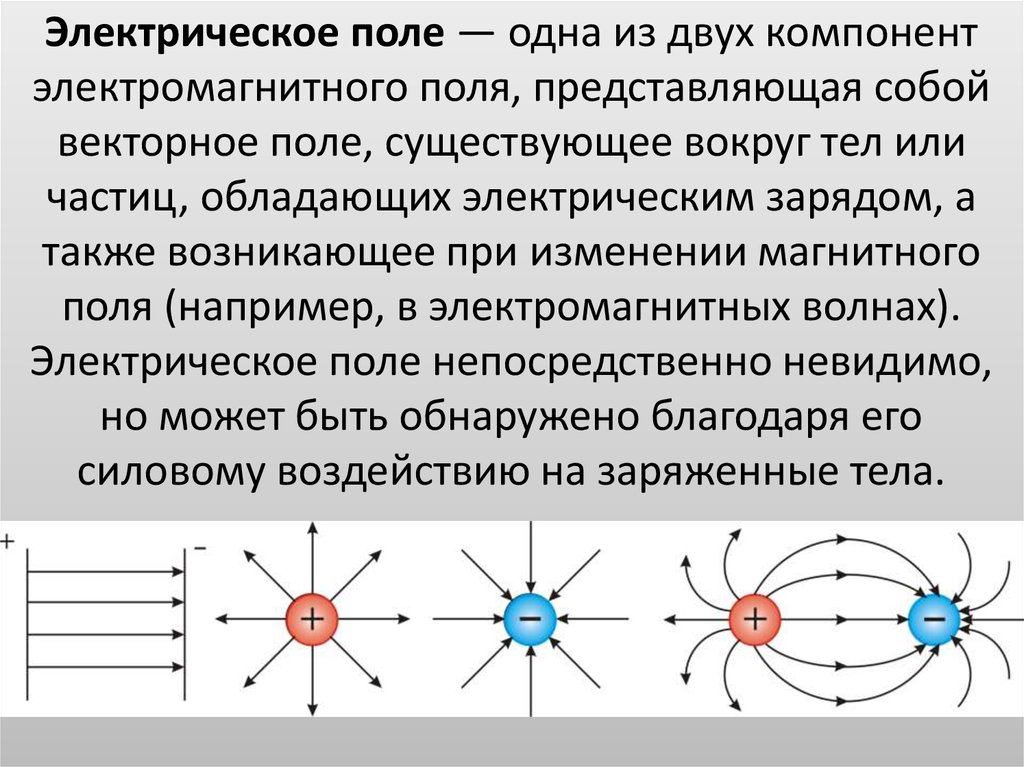

Это не означает, что за Стандартной моделью не существует более глубокого уровня реальности, из которого возникает наш нынешний набор фундаментальных полей. Это может быть другая квантовая теория поля, или теория струн, или что-то еще. На данный момент мы не знаем, существует ли этот более глубокий уровень реальности (хотя большинство физиков считают, что за пределами Стандартной модели есть физика, по крайней мере, темная материя, возможно, темная энергия, а также квантовая гравитация).

Таким образом, предварительный ответ состоит в том, что одни квантовые поля состоят из других квантовых полей, а другие являются «фундаментальными», то есть (насколько нам известно сейчас) за ними нет более глубоких объяснений.

Однако существуют и другие математические конструкции, которые могут представлять ту же физику. Точнее: существуют рамки для вычисления амплитуд рассеяния — результаты экспериментов по релятивистскому квантовому рассеянию — где поля вообще не проявляются. Кроме того, в квантовой теории поля существует огромное вырождение, когда поля могут быть переопределены , но не изменить физику. Одним из способов сказать это является то, что поля являются фиктивными переменными в интеграле по путям, и поэтому сами поля могут быть преобразованы бесконечным числом различных способов без изменения результатов физической наблюдаемой. Так что я бы не стал придавать слишком много «реальности» понятию квантового поля, даже несмотря на то, что формализм невероятно полезен и мощен.

На мой взгляд, гораздо более интересным вопросом, чем вопрос о том, реальны ли поля или из чего они сделаны, является вопрос о том, полезны ли поля. Ответ, несомненно, да.

$\endgroup$

$\begingroup$

Я собираюсь дать немного более буквальный ответ и немного меньше истории, так как это мой вкус. То, что мы называем квантовым полем, является оператором как функцией положения и/или времени, т.