Вращающий момент — Википедия

Материал из Википедии — свободной энциклопедии

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

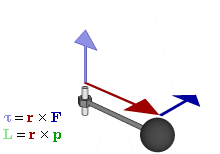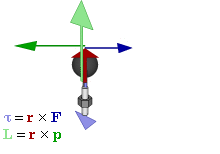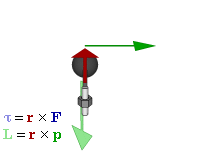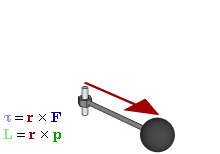
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению вектора силы и радиус-вектора, проведённого от оси вращения к точке приложения этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Общие сведения[ | ]

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:

M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}

где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} —

5.2. Вращающий момент (или момент силы)

Пусть на тело, в плоскости перпендикулярной оси вращения действует сила (рис.5.2). Разложим эту силу на две составляющие: и

Сила

пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей тело будет совершать вращательное движение вокруг оси . Расстояние от оси вращения до линии вдоль которой действует сила называется плечом силы . Моментом силы относительно точки О называется произведение модуля силы на плечо

С учетом, что

момент силы

.

С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора

, проведенного в точку приложения силы на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен

(5.1)

Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы и , и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от

к происходит против часовой стрелки).

Вращающий момент — это… Что такое Вращающий момент?



Вращающий момент

        мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. В. м. равен алгебраической сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см. Момент силы, Вращательное движение). В. м. связан с угловым ускорением тела ε равенством М_вр

= Iε, где I — Момент инерции тела относительно оси вращения.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Вращающееся магнитное поле
• Вращающийся вольтметр

Смотреть что такое «Вращающий момент» в других словарях:

• Вращающий момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент)  физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы …   Википедия

• ВРАЩАЮЩИЙ МОМЕНТ

  — мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. Вращающий момент Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела ? равенством Мвр = I?, где I момент… …   Большой Энциклопедический словарь

• ВРАЩАЮЩИЙ МОМЕНТ — ВРАЩАЮЩИЙ МОМЕНТ, вращающее действие силы. Так, турбина при повороте генератора создает вращающий момент по оси вращения. Мощность ротационного двигателя, к примеру, ЧЕТЫРЕХТАКТНОГО ДВИГАТЕЛЯ или электрического мотора, определяется вращающим… …   Научно-технический энциклопедический словарь

• ВРАЩАЮЩИЙ МОМЕНТ — мера внеш. воздействия, изменяющего угл. скорость вращающегося тела. В. м. равен алгебр. сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см. МОМЕНТ СИЛЫ, ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ). В. м. связан с угл. ускорением… …   Физическая энциклопедия

• вращающий момент — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN rotational momentturning momentdriving torque …   Справочник технического переводчика

• ВРАЩАЮЩИЙ МОМЕНТ — мера внешнего воздействия, изменяющего частоту вращения тела вокруг оси. В. м. равен произведению составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на расстояние от оси вращения до линии действия силы …   Большая политехническая энциклопедия

• вращающий момент — мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. Вращающий момент Мвр равен сумме моментов всех действующих на тело сил относительно оси вращения и связан с угловым ускорением тела ε равенством Мвр = Iε, где I  момент… …   Энциклопедический словарь

• вращающий момент — sukimo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Išorinio poveikio, dėl kurio kinta besisukančio kūno kampinis greitis, matas. Jis lygus visų besisukantį kūną veikiančių jėgų momentų sukimosi ašies atžvilgiu algebrinei… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• вращающий момент — sukimo momentas statusas T sritis fizika atitikmenys: angl. torque moment; turning moment vok. Drallmoment, n; Drehmoment, n rus. вращательный момент, m; вращающий момент, m; момент вращения, m pranc. couple moteur, m; moment de rotation, m;… …   Fizikos terminų žodynas

• вращающий момент — sukimo momentas statusas T sritis automatika atitikmenys: angl. torque; torque moment; turning moment vok. Drehmoment, n rus. вращающий момент, m; крутящий момент, m pranc. couple, m; couple moteur, m …   Automatikos terminų žodynas

Момент силы Википедия

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Общие сведения

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:

M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}

где

1.3.1 Момент силы относительно оси вращения

Видеоурок 1: Вращающий момент

Видеоурок 2: Момент силы

Лекция: Момент силы

Момент силы (МС) — это векторная ФВ, которая определяется силой, приложенной к телу, на радиус-вектор, соединяющий ось вращения с точкой, к которой приложена сила.

Данная величина объясняет причины, по которым тело может вращаться вокруг оси.

Единицей измерения момента силы является [М] = 1 Н*м.

Величина момента силы зависит от модуля прикладываемой силы, а также от величины плеча, к которому данная сила была приложена относительно оси вращения.

Момент силы на примере поворачивания гаечного ключа:

Существует иное название у данной величины — вращающая сила. Иногда под моментом сил понимают действие пары сил, приводящее к вращению или наоборот равновесию.

Под парой сил можно понимать две параллельные силы, направленные в противоположные направления относительно оси, которые равны по величине. Самое короткое расстояние между парой сил называется плечом данной пары.

Для определения момента пары сил необходимо найти произведение одной из сил на плече пары.

Данный раздел физики имеет огромное применение даже в быту. Например, именно поэтому ручка на двери располагается не возле креплений, а со стороны свободной части. Этот принцип рассматривался многими детьми при катании на качелях.

Направление момента силы

Для определения направления данной физической величины не подойдут, известные нам правила проекции на ось. В данном случае следует запомнить:

При вращении тела по часовой стрелке момент принимает положительное направление, в случае вращения против часовой стрелки — отрицательное.

Характеристика момента силы

Для характеристики момента силы следует знать следующие сведения о нем:

• Величина момента по модулю.
• В какой плоскости происходит поворот.
• В каком направлении вращается тело.

Момент силы относительно оси

Данный момент можно определить для любой, приложенной силы, которая не совпадает с осью, не пересекает её или не является параллельной ей.

Вращательное движение — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 октября 2016; проверки требуют 10 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 октября 2016; проверки требуют 10 правок.

Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.

Основной закон динамики вращательного движения[править | править код]

Производная по времени от момента количества движения механической системы относительно неподвижной относительно инерциальной системы отсчёта точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе.

Кинематические характеристики[править | править код]

Вращение характеризуется углом φ{\displaystyle \varphi }, измеряющимся в градусах или радианах, угловой скоростью ω=dφdt{\displaystyle \omega ={\frac {d\varphi }{dt}}} (измеряется в рад/с) и угловым ускорением ϵ=d2φdt2{\displaystyle \epsilon ={\frac {d^{2}\varphi }{dt^{2}}}} (единица измерения — рад/с²).

При равномерном вращении (T{\displaystyle T} — период вращения),

• Частота вращения — число оборотов в единицу времени.

ν=1T=ω2π,{\displaystyle \nu ={1 \over T}={\omega \over 2\pi },}

• Период вращения — время одного полного оборота. Период вращения T{\displaystyle T} и его частота ν{\displaystyle \nu } связаны соотношением T=1/ν{\displaystyle T=1/\nu }.

v=2πνR=2πRT,{\displaystyle v={2\pi \nu R}={2\pi R \over T},}

ω=2πν=2πT.{\displaystyle \omega ={2\pi \nu }={2\pi \over T}.}

Динамические характеристики[править | править код]

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:

E=ω2J2=2π2ν2J.{\displaystyle E={\frac {\omega ^{2}J}{2}}={2\pi ^{2}\nu ^{2}J}.}

В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы

J=∫r2dm.{\displaystyle J=\int r^{2}dm.}

• Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:

Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}

где mi{\displaystyle m_{i}} — масса, ri{\displaystyle r_{i}} — расстояние от i{\displaystyle i}-й точки до оси^[1].

Слободянюк А.И. Физика 10/4.6 — PhysBook

Содержание книги

Предыдующая страница

§4. Основные законы динамики

4.6 Вращательное движение твердого тела. Момент силы.

Конечно, положение одной, даже «особой», точки далеко не полностью описывает движение всей рассматриваемой системы тел, но все-таки, лучше знать положение хотя бы одной точки, чем не знать ничего. Тем не менее, рассмотрим применение законов Ньютона к описанию вращения твердого тела вокруг фиксированной оси ^[1].

Начнем с простейшего случая: пусть материальная точка массы m прикреплена с помощью невесомого жесткого стержня длиной r к неподвижной оси OO’ (рис. 46). Материальная точка может двигаться вокруг оси, оставаясь от нее на постоянном расстоянии, следовательно, ее траектория будет являться окружностью с центром на оси вращения.

Безусловно, движение точки подчиняется уравнению второго закона Ньютона \(~m \vec a = \vec F_0\). Однако, непосредственное применение этого уравнения не оправдано: во-первых, точка обладает одной степенью свободы, поэтому в качестве единственной координаты удобно использовать угол поворота, а не две декартовые координаты; во-вторых, на рассматриваемую систему действуют силы реакции в оси вращения, а непосредственно на материальную точку – сила натяжения стержня. Нахождение этих сил представляет собой отдельную проблему, решение которой излишне для описания вращения. Поэтому имеет смысл получить на основании законов Ньютона специальное уравнение, непосредственно описывающее вращательное движение.

Пусть в некоторый момент времени на материальную точку действует некоторая сила \(~\vec F\), лежащая в плоскости перпендикулярной оси вращения (рис. 47). При кинематическом описании криволинейного движения вектор полного ускорения \(~\vec a\) удобно разложить на две составляющих: нормальную \(~\vec a_n\), направленную к оси вращения, и тангенциальную \(~\vec a_{\tau}\) , направленную параллельно вектору скорости. Значение нормального ускорения для определения закона движения нам не нужно. Конечно, это ускорение также обусловлено действующими силами, одна из которых неизвестная сила натяжения стержня.

Запишем уравнение второго закона в проекции на тангенциальное направление:

\(~m a_{\tau} = F_{\tau}\) , (1)

заметим, что сила реакции стержня не входит в это уравнение, так как она направлена вдоль стержня и перпендикулярна выбранной проекции. Изменение угла поворота φ непосредственно определяется угловой скоростью \(~\omega = \frac{\Delta \varphi}{\Delta t}\) , изменение которой в свою очередь описывается угловым ускорением \(~\varepsilon = \frac{\Delta \omega}{\Delta t}\) . Угловое ускорение связано с тангенциальной составляющей ускорения соотношением a_τ = rε. Если подставить это выражение в уравнение (9), то получим уравнение, пригодное для определения углового ускорения. Удобно ввести новую физическую величину, определяющую взаимодействие тел при их повороте. Для этого умножим обе части уравнения (1) на r

\(~m r^2 \varepsilon = F_{\tau} r\) . (2)

и рассмотрим выражение в его правой части F_τr, имеющего смысл произведения тангенциальной составляющей силы, на расстояние от оси вращения до точки приложения силы. Это же произведение можно представить несколько иной форме (см. рис. 48)

M = F_τr = Fr cos α = Fd, здесь d — расстояние от оси вращения до линии действия силы, которое также называют плечом силы. Эта физическая величина, произведение модуля силы на расстояние от линии действия силы до оси вращения (плечо силы) M = Fd называется моментом силы. Действие силы может приводить к вращению, как по часовой стрелке, так и против часовой стрелки. В соответствии с выбранным положительным направлением вращения следует определять и знак момента силы. Заметьте, что момент силы определяется той составляющей силы, которая перпендикулярна радиус-вектору точки приложения. Составляющая вектора силы, направленная вдоль отрезка, соединяющего точку приложения и ось вращения, не приводит к раскручиванию тела. Эта составляющая при закрепленной оси компенсируется силой реакции в оси, поэтому она не влияет на вращение тела.

Запишем еще одно полезное выражения для момента силы. Пусть сила \(~\vec F\) приложена к точке А, декартовые координаты которой равны x,y (рис. 49). Разложим силу \(~\vec F\) на две составляющие \(~\vec F_x, \vec F_y\) , параллельные соответствующим осям координат. Момент силы \(~\vec F\) относительно оси, проходящей через начало координат, очевидно равен сумме моментов составляющих \(~\vec F_x, \vec F_y\) , то есть M = xF_y — yF_x.

Аналогично, тому, как нами было введено понятие вектора угловой скорости, можно определить также и понятие вектора момента силы. Модуль этого вектора соответствует данному выше определению, направлен же он перпендикулярно плоскости, содержащей вектор силы и отрезок, соединяющий точку приложения силы с осью вращения. Вектор момента силы также может быть определен как векторное произведение радиус-вектора точки приложения силы на вектор силы

\(~\vec M = \vec r \times \vec F\) .

Заметим, что при смещении точки приложения силы вдоль линии ее действия момент силы не изменяется.

Обозначим произведение массы материальной точки на квадрат расстояния до оси вращения mr² = I (эта величина называется моментом инерции материальной точки относительно оси). С использованием этих обозначений уравнение (2) приобретает вид, формально совпадающий с уравнением второго закона Ньютона для поступательного движения

\(~I \varepsilon = M\) . (3)

Это уравнение называется основным уравнением динамики вращательного движения. Итак, момент силы во вращательном движении играет такую же роль, как и сила в поступательном движении, именно он определяет изменение угловой скорости. Оказывается, (и это подтверждает наш повседневный опыт) влияние силы на скорость вращения определяет не только величина силы, но и точка его приложения. Момент инерции определяет инерционные свойства тела по отношению к вращению (говоря простым языком – показывает, легко ли раскрутить тело) — чем дальше от оси вращения находится материальная точка, тем труднее привести ее во вращение.

Уравнение (3) допускает обобщение на случай вращения произвольного тела. При вращении тела вокруг фиксированной оси угловые ускорения всех точек тела одинаковы. Поэтому, аналогично тому, как мы проделали при выводе уравнения Ньютона для поступательного движения тела, можно записать уравнения (3) для всех точек вращающегося тела и затем их просуммировать. В результате мы получим уравнение, внешне совпадающее с (3), в котором I — момент инерции всего тела, равный сумме моментов составляющих его материальных точек, M — сумма моментов внешних сил, действующих на тело.

Покажем, каким образом вычисляется момент инерции тела. Важно подчеркнуть, момент инерции тела зависит не только от массы, формы и размеров тела, но и от положения и ориентации оси вращения. Формально процедура расчета сводится к разбиению тела на малые части, которые можно считать материальными точками (рис. 51), и суммированию моментов инерций этих материальных точек, которые равны произведению массы на квадрат расстояния до оси вращения

\(~I = m_1 r^2_1 + m_2 r^2_2 + m_3 r^2_3 + \ldots\) .

Для тел простой формы такие суммы давно подсчитаны, поэтому часто достаточно вспомнить (или найти в справочнике) соответствующую формулу для нужного момента инерции. В качестве примера: момент инерции кругового однородного цилиндра массы m и радиуса R для оси вращения совпадающей с осью цилиндра равен \(~I = \frac{1}{2} m R^2\) .

Примечания

1. ↑ В данном случае мы ограничиваемся рассмотрением вращения вокруг фиксированной оси, потому, что описание произвольного вращательного движения тела представляет собой сложную математическую проблему, далеко выходящую за рамки курса математики средней школы. Знания же других физических законов, кроме рассматриваемых нами, это описание не требует.

Следующая страница