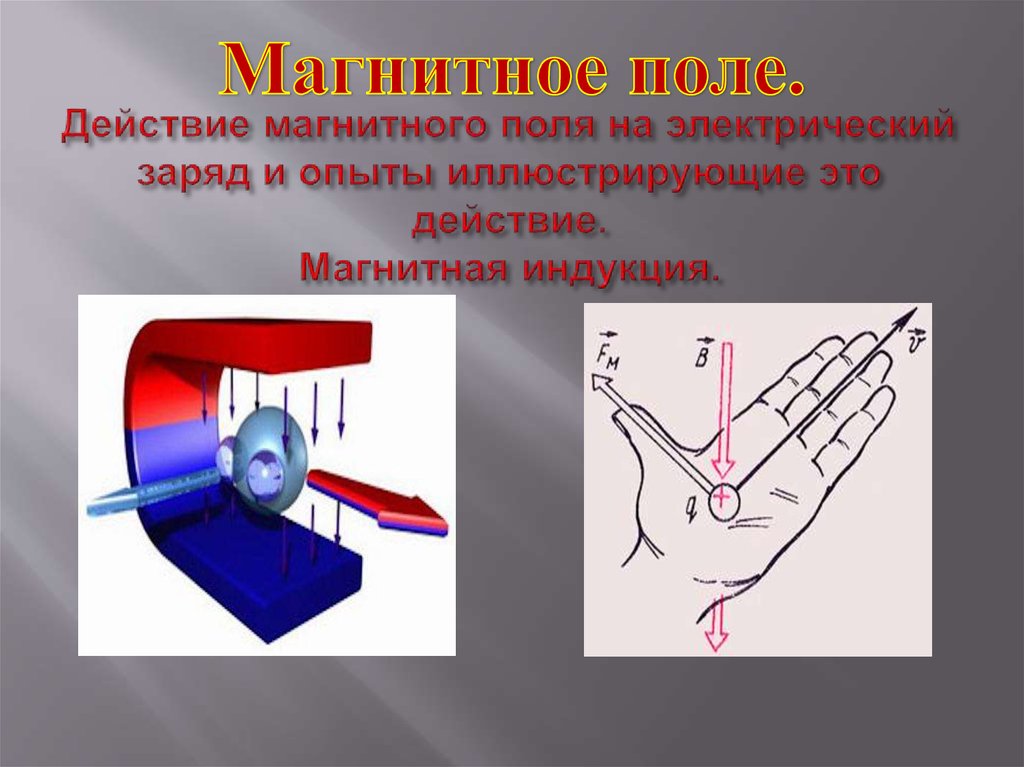
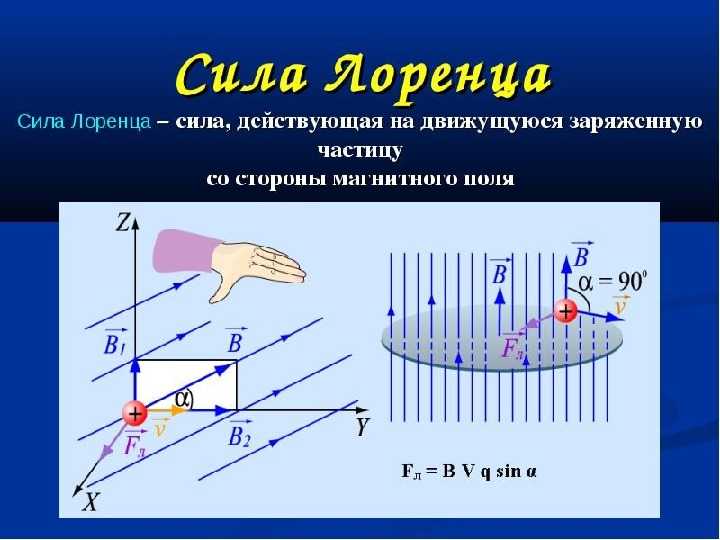
Действие магнитного поля на движущийся заряд кратко – определение силы Лоренца (11 класс)
4.7
Средняя оценка: 4.7
Всего получено оценок: 300.
4.7
Средняя оценка: 4.7
Всего получено оценок: 300.
Электричество и магнетизм долгое время считались мало связанными явлениями. Однако в середине XIX в. было обнаружено, что, хотя статичные электрические заряды никак не реагируют на магнитное поле, движущиеся заряды с ним взаимодействуют. Расскажем кратко о действии магнитного поля на движущийся электрический заряд.
Сила Ампера
Связь между электричеством и магнетизмом обнаружили после того, как в начале XIX в. были сконструированы гальванические элементы и физики научились создавать в проводниках электрический ток, текущий долгое время. В середине XIX в. Х. Эрстед показал, что ток, протекающий по проводнику, порождает магнитное поле, которое отклоняет стрелку компаса. Обратное явление — отклонение проводника с током в магнитном поле — открыл А.
Ампер. Кроме того, Ампер вывел математические формулы, устанавливающие связь между силой тока, вектором индукции магнитного поля и вектором силы, действующей на проводник.
Несмотря на правильное математическое описание, закон Ампера не раскрывает механизма возникновения силы, действующей на проводник в магнитном поле. Механизм возникновения силы Ампера был установлен только к концу XIX в., когда было доказано, что электрический ток представляет собой движение носителей заряда в проводнике, а на любой движущийся заряд со стороны магнитного поля действует сила, названная впоследствии силой Лоренца. Кратко говоря, сложение всех сил Лоренца, действующих на все заряды в проводнике, дает в итоге силу Ампера.
Сила Лоренца
Для определения действия магнитного поля на движущийся заряд можно использовать закон Ампера. Очевидно, что сила Лоренца, действующая на отдельный заряд, равна отношению силы Ампера, действующей на проводник, к количеству зарядов в этом проводнике.
$$F= I |\overrightarrow B| Δl sin \alpha$$
А ток в проводнике связан с зарядом $q$ и концентрацией носителей $n$ соотношением:
$$I = qnvS$$
В этой формуле $v$ — это линейная скорость движения носителей, а $S$ — площадь поперечного сечения проводника. Подставив значение тока в предыдущую формулу, получим выражение для силы Ампера:
$$F_A= |q| nvS |\overrightarrow B| Δl sin \alpha$$
Число носителей заряда в проводнике равно:
$$N = nSΔl$$
Чтобы найти силу, действующую на каждый носитель (силу Лоренца), необходимо силу Ампера поделить на число носителей. В результате имеем:
$$F_Л={F_A\over N}= |q| v B sin \alpha$$
Поскольку носители заряда движутся в направлении электрического тока, то угол $\alpha$ равен углу между вектором скорости движения заряда и вектором магнитной индукции.
Направление силы Лоренца определяется так же, как и направление силы Ампера, по правилу левой руки.
Направление силы Лоренца всегда перпендикулярно скорости, а значит, траекторией движения заряда в магнитном поле является окружность (или спираль) некоторого радиуса. Отметим также, что сила Лоренца не совершает работы и не меняет кинетическую энергию частицы. Она лишь меняет направление ее движения.
Что мы узнали?
На заряд, движущийся в магнитном поле, действует сила Лоренца. Ее направление перпендикулярно векторам скорости и магнитной индукции. Определяется оно так же, как сила Ампера: мнемоническим правилом левой руки.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 300.
Физика, 9 кл. (Буховерцев Б.Б.)
Физика, 9 кл. (Буховерцев Б.Б.)
ОглавлениеТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКАГлава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ 2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 13.  ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17. КОЛИЧЕСТВО ТЕПЛОТЫ 18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII.  ТВЕРДЫЕ ТЕЛА29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА? Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47.  48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ 52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62.  ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ 68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI.  МАГНИТНОЕ ПОЛЕ83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА 90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ |
примеров и приложений — College Physics: OpenStax
Глава 22 Магнетизм
Резюме
- Описать влияние магнитного поля на движущийся заряд.
- Рассчитайте радиус кривизны пути заряда, движущегося в магнитном поле.
Магнитная сила может заставить заряженную частицу двигаться по круговой или спиральной траектории. Космические лучи — это энергичные заряженные частицы в космическом пространстве, некоторые из которых приближаются к Земле. Магнитное поле Земли может заставить их двигаться по спирали. Протоны в гигантских ускорителях удерживаются на круговой траектории благодаря магнитной силе. На фотографии пузырьковой камеры на рис. 1 показаны заряженные частицы, движущиеся по таким изогнутым траекториям. Искривленные траектории заряженных частиц в магнитных полях лежат в основе ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре.
Рисунок 1. Следы пузырьков образуются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород в этом художественном исполнении пузырьковой камеры. Существует сильное магнитное поле, перпендикулярное странице, что приводит к искривлению траекторий частиц.
2/r}[/латекс]. Отметив, что [латекс]\boldsymbol{\textbf{sin} \;\theta = 1}[/latex], мы видим, что [латекс]\boldsymbol{F = qvB}[/латекс]. Рис. 2. Отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиком — как хвосты стрелок). Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат равномерного кругового движения.Поскольку магнитная сила [латекс]\boldsymbol{F}[/латекс] обусловливает центростремительную силу [латекс]\boldsymbol{F_c}[/латекс], мы имеем 92}{г}}.[/латекс]
Решение для [латекс]\boldsymbol{r}[/латекс] дает
[латекс]\boldsymbol{r =}[/латекс] [латекс]\boldsymbol{\frac{mv}{qB}}.[/латекс]
Здесь [latex]\boldsymbol{r}[/latex] — радиус кривизны пути заряженной частицы с массой [latex]\boldsymbol{m}[/latex] и зарядом [latex]\boldsymbol{q }[/latex], движущийся со скоростью [latex]\boldsymbol{v}[/latex] перпендикулярно магнитному полю напряженностью [latex]\boldsymbol{B}[/latex].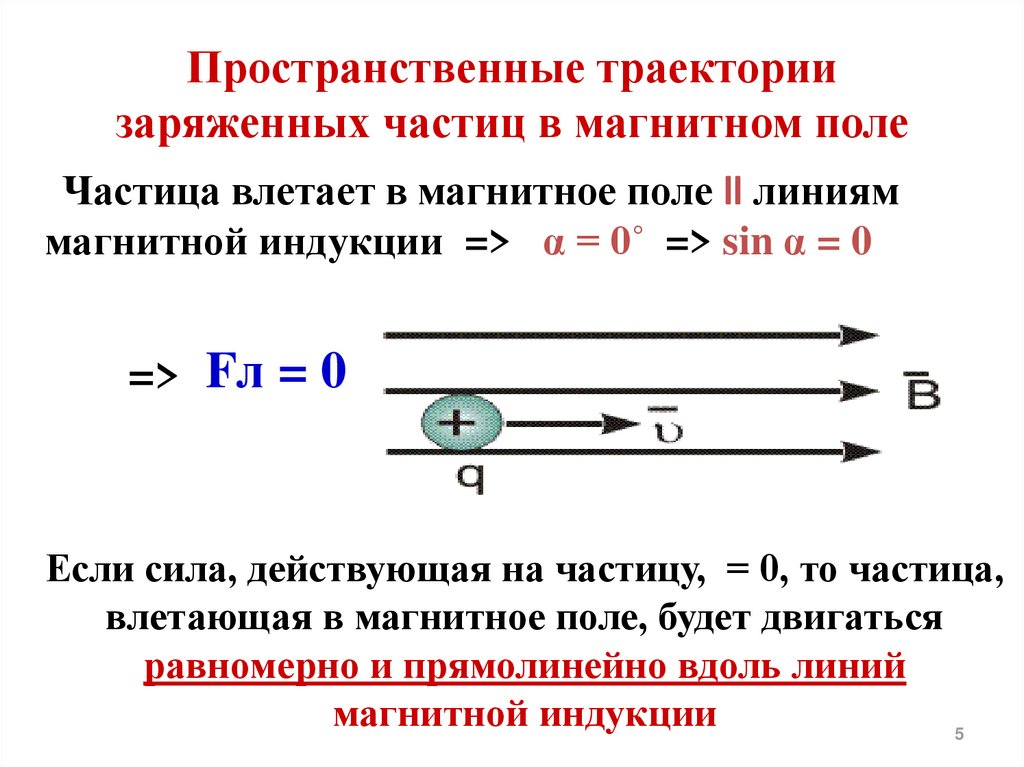
7 \;\textbf{м/с}}[/latex] (соответствует ускоряющему напряжению около 10,0 кВ, используемому в некоторых телевизорах) перпендикулярно магнитному полю напряженностью [латекс]\boldsymbol{B = 0,500 \;\textbf{T}}[/latex] (доступно с постоянными магнитами).
Стратегия
Радиус кривизны [латекс]\boldsymbol{r}[/latex] можно найти непосредственно из уравнения [латекс]\boldsymbol{r = \frac{mv}{qB}}[/latex] , так как все остальные величины в нем заданы или известны. 9{-4} \;\textbf{м}} \end{массив}[/латекс]
или
[латекс]\boldsymbol{r = 0,683 \;\textbf{мм}}.[/латекс]
Обсуждение
Малый радиус указывает на большой эффект.
Электроны в кинескопе телевизора вынуждены двигаться по очень узким кругам, сильно меняя свои траектории и искажая изображение.
На рис. 4 показано, как электроны, движущиеся не перпендикулярно силовым линиям магнитного поля, следуют за силовыми линиями. Составляющая скорости, параллельная линиям, не изменяется, поэтому заряды закручиваются вдоль силовых линий. Если напряженность поля увеличивается в направлении движения, поле будет прикладывать силу для замедления зарядов, образуя своего рода магнитное зеркало, как показано ниже.
Рис. 4. Когда заряженная частица движется вдоль линии магнитного поля в область, где поле становится сильнее, на частицу действует сила, уменьшающая составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии, а здесь меняет его направление, образуя «магнитное зеркало». Свойства заряженных частиц в магнитных полях связаны с такими разными вещами, как Aurora Australis или Aurora Borealis и ускорителями частиц.
Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут попасть в ловушку на спиральных орбитах вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Это свечение возбужденных атомов и молекул можно увидеть в главе 22 «Введение в магнетизм». Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.
)Некоторые прилетающие заряженные частицы захватываются магнитным полем Земли, образуя два пояса над атмосферой, известные как радиационные пояса Ван Аллена в честь первооткрывателя. Джеймс А. Ван Аллен, американский астрофизик. (См. рис. 6.) Частицы, попавшие в эти пояса, образуют радиационные поля (аналогичные ядерному излучению) настолько интенсивные, что пилотируемые космические полеты избегают их, а спутники с чувствительной электроникой не попадают в них. За несколько минут, которые потребовались лунным миссиям для пересечения радиационных поясов Ван Аллена, астронавты получили дозы радиации, более чем в два раза превышающие допустимую годовую дозу радиационных работников. Подобные пояса есть и у других планет, особенно у тех, у которых сильные магнитные поля, таких как Юпитер.
Рис. 6. Радиационные пояса Ван Аллена представляют собой две области, в которых энергичные заряженные частицы захватываются магнитным полем Земли. Один пояс лежит на высоте около 300 км над поверхностью Земли, другой — около 16 000 км.
Заряженные частицы в этих поясах мигрируют вдоль силовых линий магнитного поля и частично отражаются от полюсов более сильными там полями. Заряженные частицы, попадающие в атмосферу, восполняются Солнцем и источниками в глубоком космосе.Вернувшись на Землю, у нас есть устройства, которые используют магнитные поля для удержания заряженных частиц. Среди них гигантские ускорители частиц, которые использовались для изучения субструктуры материи. (См. рис. 7.) Магнитные поля не только контролируют направление заряженных частиц, они также используются для фокусировки частиц в пучки и преодоления отталкивания одноименных зарядов в этих пучках.
Рис. 7. В лаборатории Фермилаб в Иллинойсе есть большой ускоритель частиц (самый мощный в мире до 2008 г.), который использует магнитные поля (магниты здесь выделены оранжевым цветом) для сдерживания и направления луча. Этот и другие ускорители используются уже несколько десятилетий и позволили нам открыть некоторые законы, лежащие в основе всей материи.
(кредит: ammcrim, Flickr)Термоядерный синтез (подобный происходящему на Солнце) — это надежда на будущий источник чистой энергии. Одним из самых перспективных устройств является 9Токамак 0023 , который использует магнитные поля для удержания (или захвата) и направления реактивных заряженных частиц. (См. рис. 8.) Менее экзотические, но более практичные усилители в микроволновых печах используют магнитное поле для сдерживания колеблющихся электронов. Эти колеблющиеся электроны генерируют микроволны, направляемые в духовку.
Рисунок 8. Токамаки, подобные показанному на рисунке, изучаются с целью экономичного производства энергии путем ядерного синтеза. Магнитные поля в устройстве в форме пончика удерживают и направляют реактивные заряженные частицы. (кредит: Дэвид Меллис, Flickr) Масс-спектрометры имеют различные конструкции, и многие из них используют магнитные поля для измерения массы. Кривизна пути заряженной частицы в поле связана с ее массой и измеряется для получения информации о массе.
(См. главу 22.11 «Другие применения магнетизма».) Исторически такие методы применялись при первых прямых наблюдениях заряда и массы электрона. Сегодня масс-спектрометры (иногда в сочетании с газовыми хроматографами) используются для определения состава и последовательности крупных биологических молекул.
- Магнитная сила может создавать центростремительную силу и заставлять заряженную частицу двигаться по круговой траектории радиусом
[латекс]\boldsymbol{r =}[/латекс] [латекс]\boldsymbol{\frac{mv}{qB}},[/латекс]
где [latex]\boldsymbol{v}[/latex] — составляющая скорости, перпендикулярная [latex]\boldsymbol{B}[/latex] для заряженной частицы с массой [latex]\boldsymbol{m}[/ латекс] и заряжать [латекс]\boldsymbol{q}[/латекс].
Задача и упражнения 97 \;\textbf{м/с}}[/latex] перпендикулярно магнитному полю. Поле заставляет протон двигаться по круговой траектории радиусом 0,800 м. Какова напряженность поля?
3: (a) Зрители Star Trek слышат о приводе антиматерии на звездолете Enterprise .
6\;\textbf{м/с}}[/латекс]? б) Чему равно напряжение между пластинами, если расстояние между ними 1 см? 9{-5} \;\textbf{T}}[/latex]. а) Электрическое поле какой напряженности необходимо приложить перпендикулярно полю Земли, чтобы заставить электрон двигаться прямолинейно? (b) Если это сделать между пластинами, расстояние между которыми составляет 1,00 см, какое напряжение будет приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом, чтобы защитить от внешних магнитных полей и избежать необходимости такой коррекции.)
8: (а) С какой скоростью будет двигаться протон по круговой траектории того же радиус, как у электрона в главе 22.5 Упражнение 1? б) Каким был бы радиус пути, если бы скорость протона была такой же, как у электрона? в) Чему был бы равен радиус, если бы протон имел ту же кинетическую энергию, что и электрон? г) один и тот же импульс? 95 \;\textbf{м/с}}[/latex] в поле 0,250 Тл. Каково расстояние между их путями, когда они попадают в цель после прохождения полукруга? (b) Обсудите, кажется ли это расстояние между их путями достаточно большим, чтобы его можно было использовать при отделении урана-235 от урана-238.
Сила, действующая на движущийся заряд в магнитном поле – Колледж физики, главы 1-17
22 Магнетизм
Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле
- Описать влияние магнитных полей на движущиеся заряды.
- Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
- Рассчитайте магнитную силу, действующую на движущийся заряд.
Каков механизм, посредством которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила.
И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы FF размером 12{F} {} на заряд qq размером 12{q} {}, движущийся со скоростью vv размером 12{v} {} в магнитном поле напряженностью BB размером 12{B} { } задается
F=qvBsinθ,F=qvBsinθ, размер 12{F= ital “qvB””sin”θ} {}
, где θθ размер 12{θ} {} — угол между направлениями vv и B.B. размер 12{B} {} Эту силу часто называют силой Лоренца. Собственно, так мы определяем напряженность магнитного поля ВВ размером 12{B}{} — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля BB размера 12{B} {} называется тесла (Т) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F=qvBsinθF=qvBsinθ size 12{F= ital «qvB»»sin»θ} {} для размера BB 12{B} {}.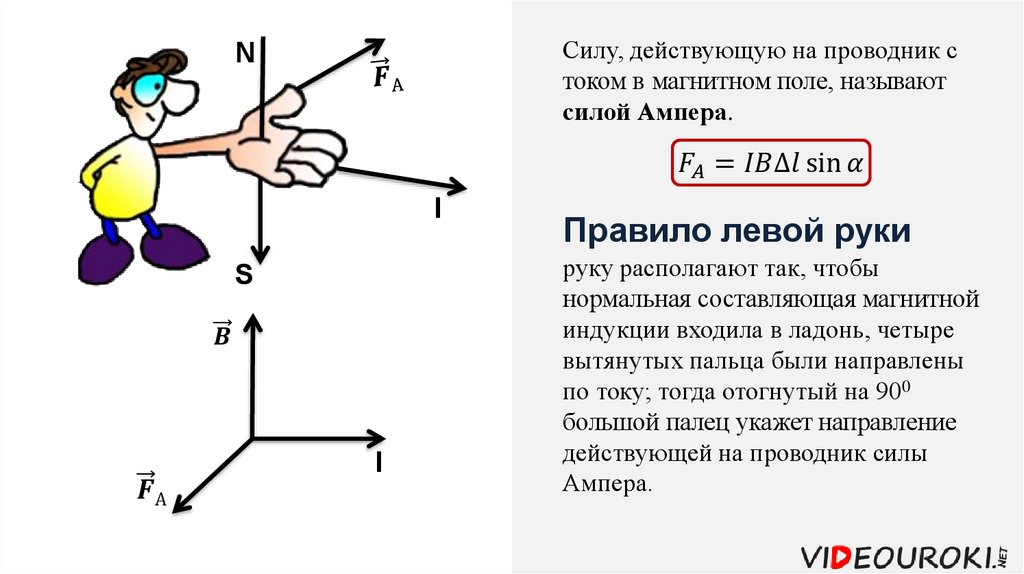
B=FqvsinθB=Fqvsinθ размер 12{B= {{F} над { ital «qv»»sin»θ} } } {}
Поскольку
sinθsinθ size 12{θ} {}
безразмерно, тесла составляет
1 T=1 NC⋅м/с=1 NA⋅м1 T=1 NC⋅м/с=1 NA⋅м размер 12{«1 T»= {{«1 N»} над {C cdot «m/ s”} } = {{1″ N”} более {A cdot m} } } {}
(обратите внимание, что C/s = A).
Другая меньшая единица, называемая гауссом (Г), где иногда используется. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5×10−5T5×10−5T, размер 12{5, умноженный на «10» rSup { размер 8{ – 5} } `T} {}, или 0,5 G.
Направление магнитной силы FF размера 12{F} {} перпендикулярно плоскости, образованной vv размера 12{v} {} и BB, как определено правилом правой руки 1 (или RHR-1), который проиллюстрирован в [ссылка]. RHR-1 утверждает, что для определения направления магнитной силы на положительно движущемся заряде вы указываете большим пальцем правой руки в направлении vv, остальными пальцами в направлении BB, а перпендикуляр к ладони указывает на направление ФФ.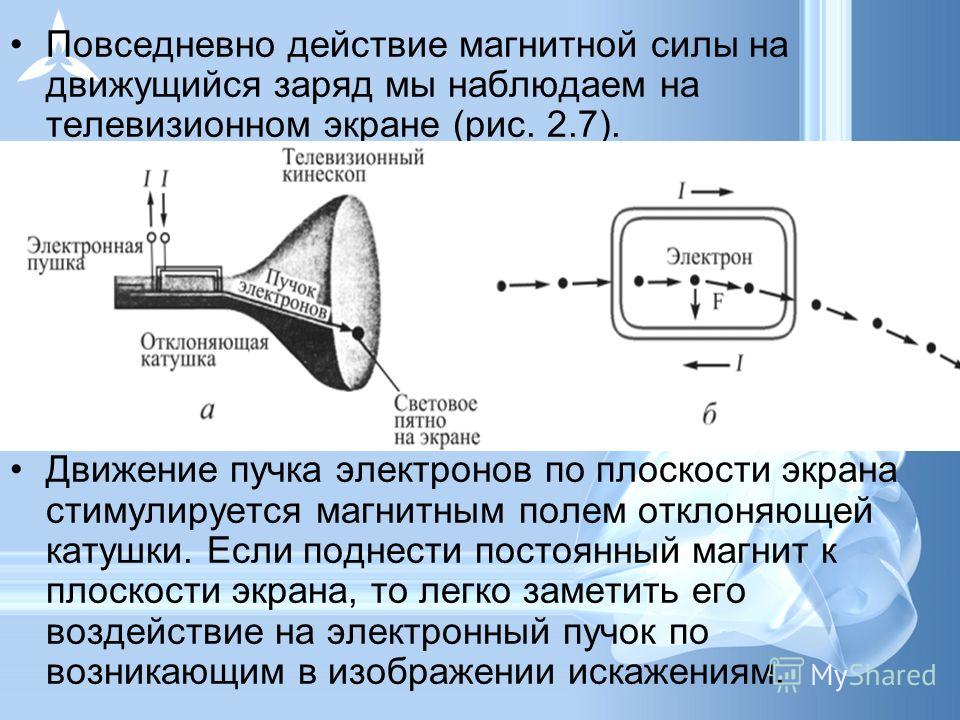
Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Выполнение соединений: заряды и магниты
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты.
Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на [ссылка].)
Положительно заряженный объект, движущийся строго на запад в районе, где магнитное поле Земли направлено строго на север, подвергается действию силы, направленной строго вниз, как показано на рисунке.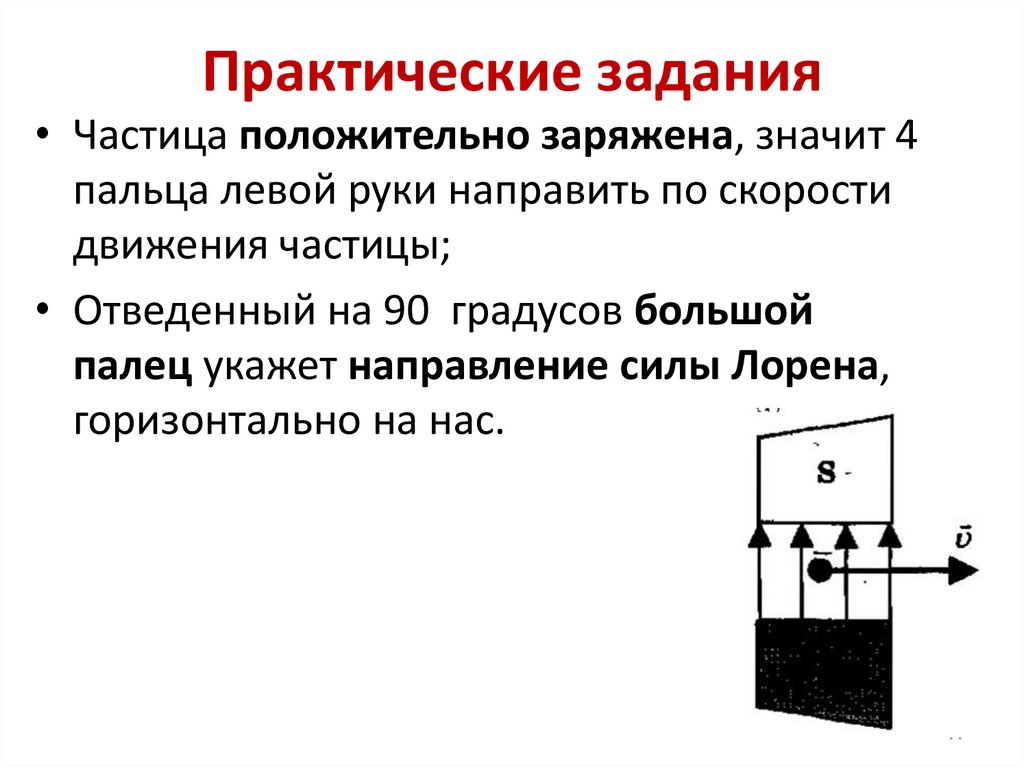
Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх. Стратегия
Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F=qvBsinθF=qvBsinθ size 12{F= ital “qvB””sin”θ} {}, чтобы найти силу.
Решение
Магнитная сила равна
F=qvbsinθ.F=qvbsinθ. size 12{F= ital «qvb»»sin»θ} {}
Мы видим, что sinθ=1sinθ=1 size 12{«sin»θ=1} {}, так как угол между скоростью и направлением поле 90º90º размер 12{«90» rSup { размер 8{ circ } } } {}. Ввод остальных заданных величин дает
F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1×10–11N.F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1×10–11N.alignl { стек {
размер 12{F= слева («20» умножить на «10» rSup { размер 8{- 9} } `C вправо ) влево («10″`”м/с” вправо ) влево (5 раз “10” rSup {размер 8{ – 5} } `T вправо )} {} #
” “=1 раз “ 10” rSup {размер 8{ – “11”} } ` влево (C cточка “м/с” вправо) влево ( { {N} над {C cточка “м/с”} } вправо )=1 раз “10” rSup {размер 8{ — «11»} } `N «.
» {}
} } {}
Обсуждение
Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное влияние, особенно на субмикроскопические частицы. Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».
- Магнитные поля воздействуют на движущийся заряд силой q , величина которой равна
F=qvBsinθ,F=qvBsinθ, размер 12{F= ital “qvB””sin”θ} {}
, где θθ размер 12{θ} {} — угол между направлениями vv размера 12{v} {} и BB размера 12{B} {}.
- Единицей СИ для напряженности магнитного поля BB размера 12{B} {} является тесла (Т), которая связана с другими единицами соотношения
1 T=1 NC⋅м/с=1 NA⋅м.1 T=1 NC⋅м/с=1 NA⋅м.
- направление силы на движущийся заряд задается правилом правой руки 1 (RHR-1): Укажите большой палец правой руки в направлении vv размера 12 {v} {}, пальцы в направлении BB размера 12 {B} {}, а перпендикуляр к ладони указывает в направлении размера FF 12{F} {}.
- Сила перпендикулярна плоскости, образованной vv и BB размером 12{B} {}. Поскольку сила равна нулю, если размер vv 12{v} {} параллелен размеру BB 12{B} {}, заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.
Если заряженная частица движется прямолинейно через некоторую область пространства, можете ли вы сказать, что магнитное поле в этой области обязательно равно нулю?
Каково направление магнитной силы на положительный заряд, который движется, как показано в каждом из шести случаев, показанных в [ссылка]?
(a) Влево (Запад)
(b) На страницу
(c) Вверх (Север)
(d) Без силы
(e) Вправо (Восток)
(f) Вниз ( Юг)
Повторить [ссылка] для отрицательного заряда.
Каково направление скорости отрицательного заряда, на который действует магнитная сила, показанная в каждом из трех случаев в [ссылка], если предположить, что он движется перпендикулярно B?B? размер 12{B?} {}
(a) Восток (справа)
(b) На страницу
(c) Юг (вниз)
Повторите [ссылка] для положительного заряда.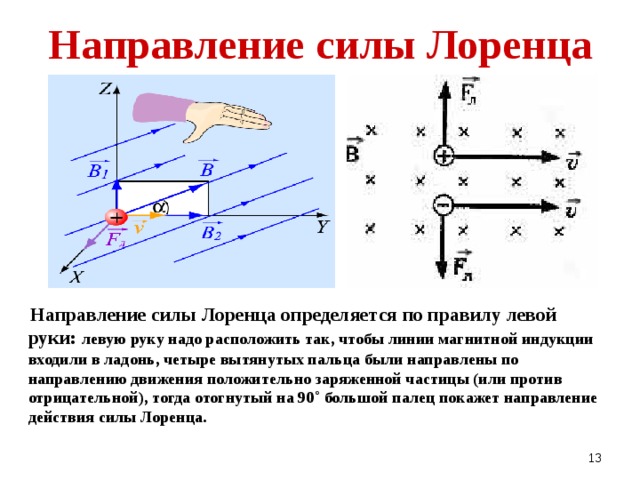
Каково направление магнитного поля, которое создает магнитную силу на положительном заряде, как показано в каждом из трех случаев на рисунке ниже, при условии, что размер BB 12{B} {} перпендикулярен размеру vv 12{v} { }?
(a) На страницу
(b) Запад (слева)
(c) Вне страницы
Повторите [ссылка] для отрицательного заряда.
Какое максимальное усилие действует на алюминиевый стержень размером 0,100 мкКл 0,100 мкКл размером 12{0″.) «100””-мкКл”} {} заряд, который вы проходите между полюсами постоянного магнита 1,50-T со скоростью 5,00 м/с? В каком направлении сила?
7,50×10-7 N7,50×10-7 размер N 12{7 «.» «50» умножить на «10» rSup {размер 8{ – 7} } ”N”} {} перпендикулярно обеим силовым линиям магнитного поля и скорости
(a) Самолеты иногда приобретают небольшие статические заряды. Предположим, что сверхзвуковая струя имеет размер 0,500 мкКл 0,500 мкКл 12{0″. «500””-мкКл”} {} заряжается и летит строго на запад со скоростью 660 м/с над южным магнитным полюсом Земли, где находится 8,00×10−5-T8,00×10−5-T размером 12{ 8 «.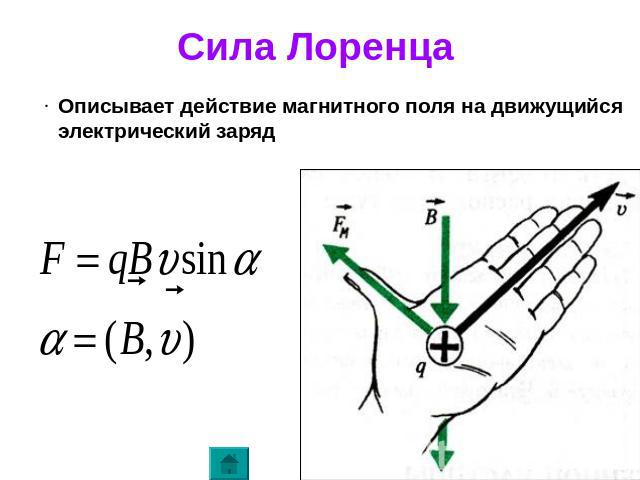
» «00» умножить на «10» rSup {размер 8{ – 5} } «-T»} {} магнитное поле указывает прямо вверх. Каковы направление и величина магнитной силы на плоскости? (b) Обсудите, подразумевает ли значение, полученное в части (а), это значительный или незначительный эффект.
(a) Протон космических лучей, движущийся к Земле со скоростью 5,00×107 м/с5,00×107 м/с размером 12{5″. «00» умножить на «10». «70» умножить на «10» rSup {размер 8{ – «16»} } `N} {}. Какова сила магнитного поля, если между ним и скоростью протона существует угол 45º45º размером 12{«45» rSup { size 8{ circ } } } {}? (b) Соответствует ли значение, полученное в части (а), известной напряженности магнитного поля Земли на ее поверхности? Обсуждать.
(a) 3,01×10-5 T3,01×10-5 размер T 12{3 «.» «01» умножить на «10» rSup {размер 8{ – 5} } ”T”} {}
(b) Это немного меньше, чем напряженность магнитного поля 5×10−5T5×10−5T размера 12{5 умножить на «10» rSup { size 8{ – 5} } `T} {} на поверхности Земли, так что это соответствует.
