Эл-ка / 05 Лекции АВТ / UE_mod_2 / l 217
L. 217. «Электротехника» Аксютин В.А.
Эквивалентные преобразования электрических цепей.
Преобразование части электрической цепи является эквивалентным, если оно не изменяет значения токов и напряжений в не преобразованной части цепи.
Преобразование электрических цепей упрощает расчёт цепи. К основным видам можно отнести следующие преобразования:
Вынесение ЭДС за узел;
Замена последовательного, параллельного и смешанного соединения сопротивлений одним эквивалентным;
Замена реального источника тока эквивалентными источниками ЭДС;
Замена участка сложной цепи с параллельным соединением ветвей расположенных между двумя узлами;
Замена треугольника сопротивлений эквивалентной звездой и наоборот;
Замена сопротивления с известным током, зависимым источником ЭДС (теорема о компенсации).
Рассмотрим более подробно нижеприведенные преобразования.
Вынесение ЭДС за узел.
Это преобразование поясняется рис. 1. В каждую ветвь, подходящую к узлу рис. 1,а можно включить ЭДС E, направленные, например, от узла рис. 1,б. В ветви с исходным источником появляется две равных по модулю и разнонаправленных ЭДС, которые можно сократить. В результате преобразований эквивалентная цепь представлена на рис. 1,в.



E




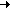



E



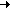


E
E
E
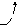
E
E
E









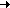





E
а б в
Рис. 1
Замена последовательного, параллельного и смешанного соединения сопротивлений одним эквивалентным.
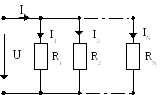

а б


в г
Рис. 2
Для всех случаев входной ток определим по закону Ома: I = U/RЭ,
где RЭ – входное сопротивление цепи
2.1. Последовательное соединение N резисторов рис. 2,а:
RЭ = R1 + R2 +…+ RN = Ri (1)
2.2. Параллельное соединение N резисторов рис. 2, б:
RЭ
где эквивалентная проводимость:
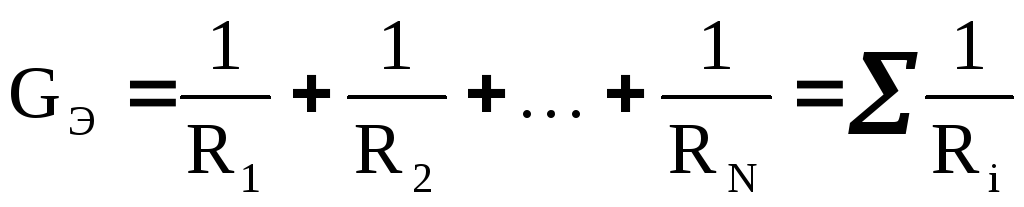 (3)
(3)
Входной ток определяется по закону Кирхгофа:
I =I1 + I2 + … +IN = Ii (4)
Токи в ветвях: Ii = U/Ri
2.3. Параллельное соединение двух резисторов рис. 2, в:
RЭ = 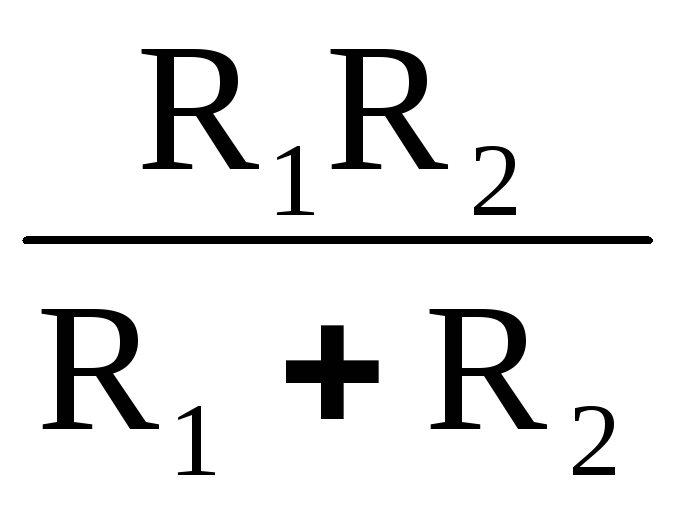 (5)
(5)
U = I RЭ = I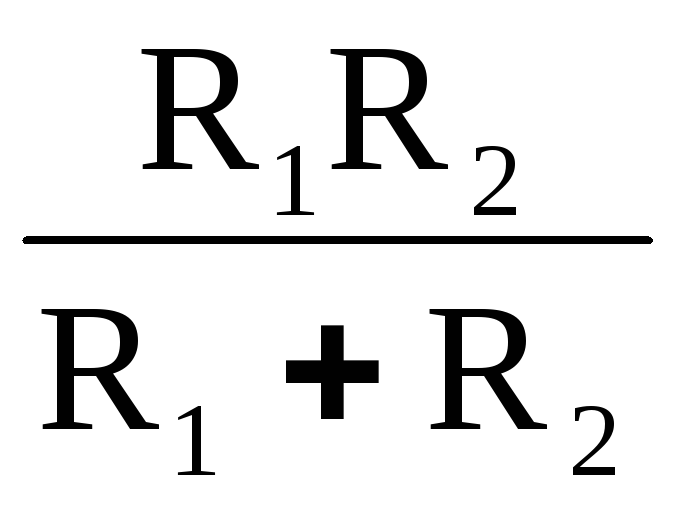
Токи в ветвях;
Ii = 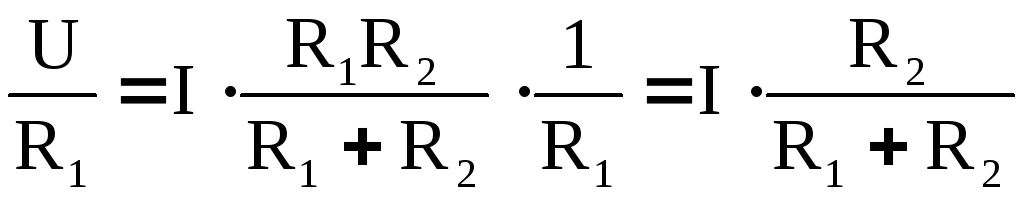 (6)
(6)
I2 = 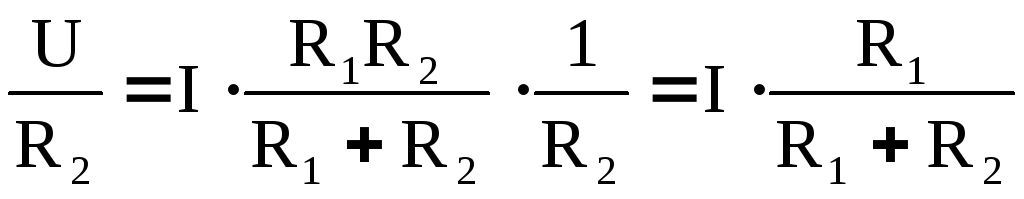 (7)
(7)
Соотношения (6) и (7) называют правилом рычага (разноса): ток в параллельной ветви равен произведению общего тока на сопротивление в противоположной ветви и делённое на сумму сопротивлений ветвей.
2.3. Параллельно-последовательное соединение трёх резисторов рис. 2, г:
RЭ = R+ (8)
(8)
Токи в параллельных ветвях определим по (6) и (7):
Ii = 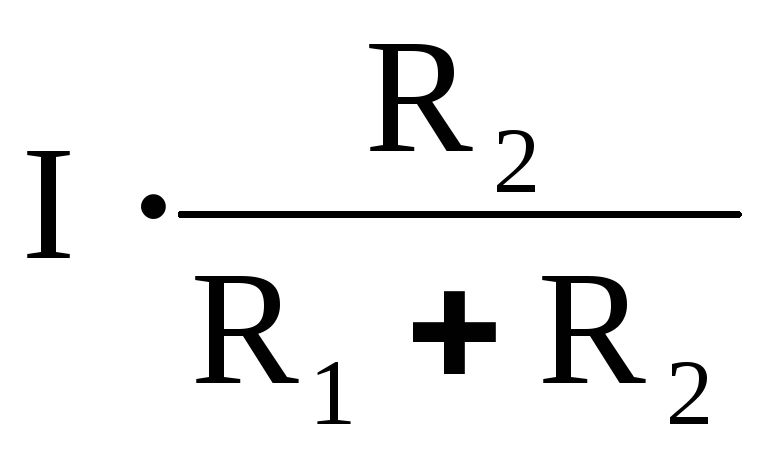 (9)
(9)
I2 =  (10)
(10)
Замена источника тока эквивалентными источниками ЭДС.
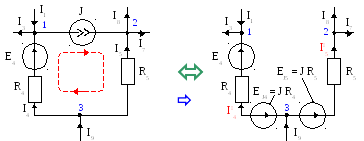
а б
Рис. 3
Рассмотрим фрагмент цепи, в который входит контур, содержащий источник тока и ряд ветвей (рис. 3,а). Источник тока можно преобразовать в источники ЭДС (рис. 3,б), если в каждую ветвь контура включить дополнительный источник ЭДС, равный произведению тока источника тока на сопротивление ветви. Направление обхода контура выбирается по направлению источника тока, а направление ЭДС задаётся на встречу обхода контура. Доказательство данного преобразования производится из аналогии уравнений метода контурных токов составленных для двух схем рис. 3,а и б.
Интерес представляет преобразование реального источника тока в источник ЭДС и наоборот. Порядок преобразования показан на рис. 4.
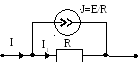
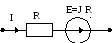
Рис. 4
Замена участка сложной цепи с параллельным соединением ветвей расположенных между двумя узлами.
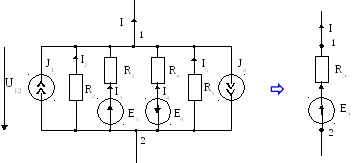
а б
Рис. 5
На рис. 5,а изображён участок цепи, имеющий параллельное соединение нескольких ветвей. Применяя метод узловых потенциалов можно получить ветвь с эквивалентным сопротивлением и ЭДС рис. 5,б:
EЭ = 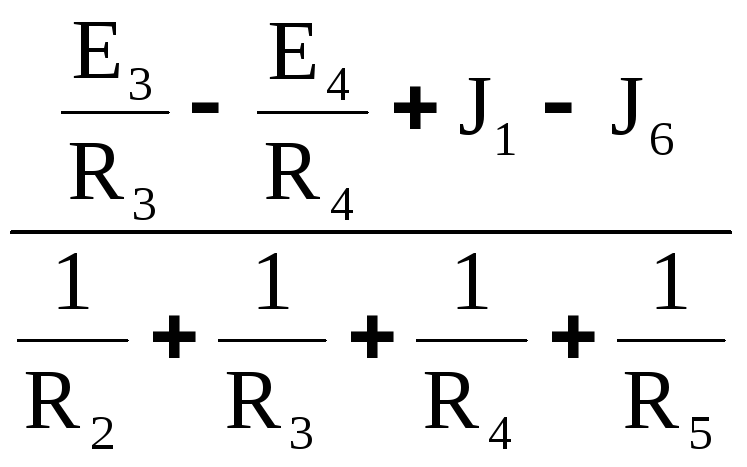 ; (11)
; (11)
RЭ = 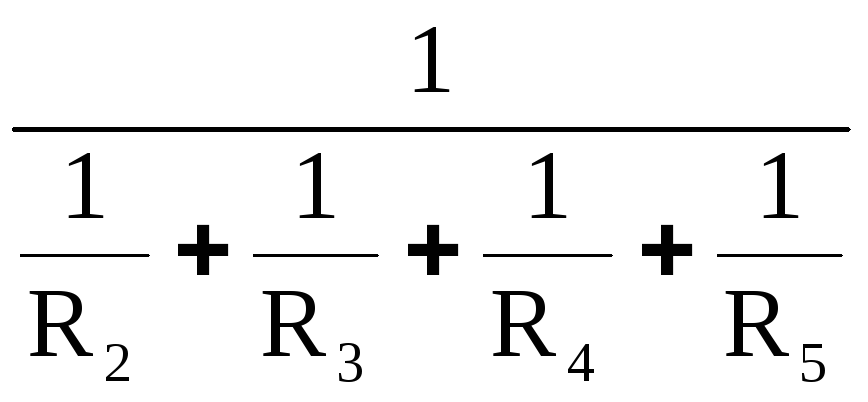 . (12)
. (12)
В общем случае:
EЭ = 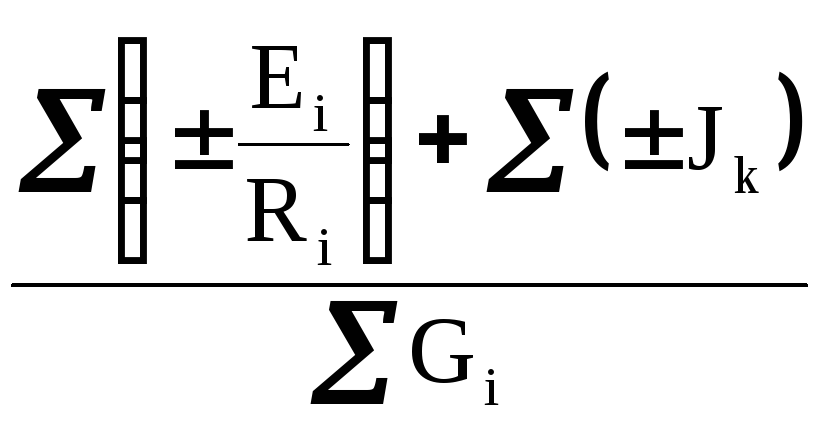 ; (13)
; (13)
RЭ =  . (14)
. (14)
З
 амена
треугольника сопротивлений эквивалентной
звездой и наоборот.
амена
треугольника сопротивлений эквивалентной
звездой и наоборот.
а б в
Рис. 6

а б в
Рис. 7
Трёхполюсник считается пассивным, если не содержит источников электрической энергии. Среди пассивных трёхполюсников наиболее часто встречаются «звезда» рис. 6 и «треугольник» сопротивлений рис. 7. Это основные схемы соединения элементов трёхфазных цепей.
Соединение в «звезду» – это соединение трёх сопротивлений, при котором они имеют общую точку и образуют три расходящихся луча. Обозначается Y (рис. 6).
Соединением
в «треугольник» называют соединение,
при котором элементы образуют
геометрический треугольник. Обозначается  (рис. 7).
(рис. 7).
Существует
вывод формул эквивалентной замены
n-лучевой
звезды m
-сторонним многоугольником, причём m
= 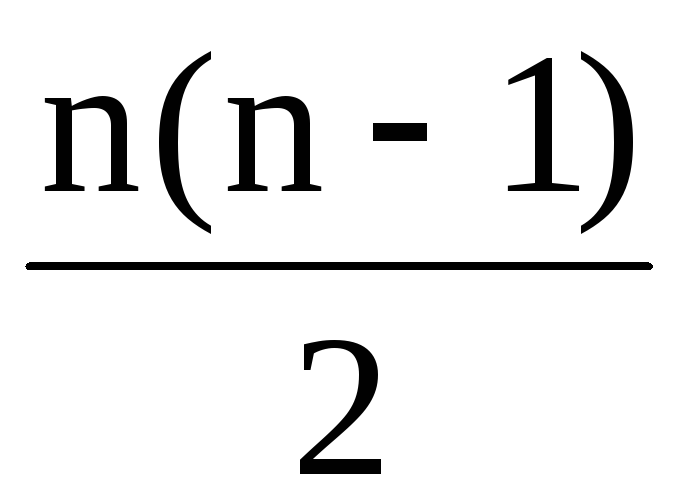 .
.
Однако
обратное преобразование всегда возможно
только при m
= n
= 3. Поэтому рассмотрим эквивалентное
преобразование Y  . замена
будет эквивалентной, если при одинаковых
потенциалах одноименных полюсов звезды
и треугольника токи, подходящие к этим
полюсам, также одинаковы, то есть при
одинаковых режимах работы сопротивления
между одними и теми же парами полюсов
звезды и треугольника равны.
. замена
будет эквивалентной, если при одинаковых
потенциалах одноименных полюсов звезды
и треугольника токи, подходящие к этим
полюсам, также одинаковы, то есть при
одинаковых режимах работы сопротивления
между одними и теми же парами полюсов
звезды и треугольника равны.
При выводе соотношений полагаем, что внешние токи I1, I2, I3 и потенциалы φ1, φ2 и φ3 для Y и одинаковы. Для цепи рис 6,а запишем основные уравнения для определения токов в первой и второй ветвях, а также потенциала φ0:
Ii = 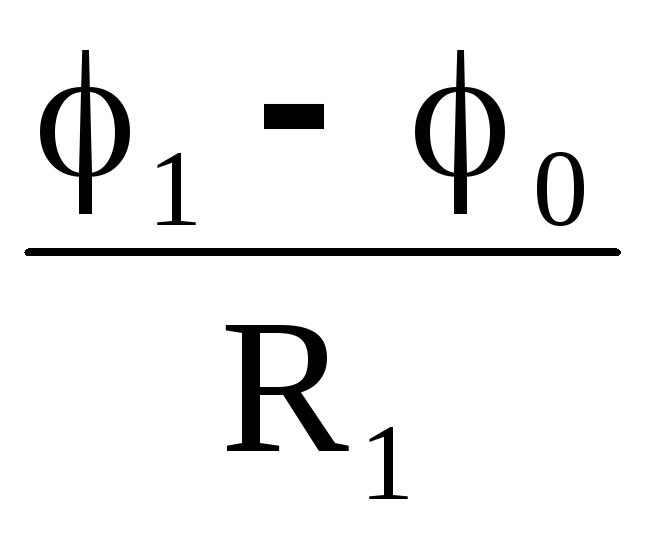 ; I2 =
; I2 = 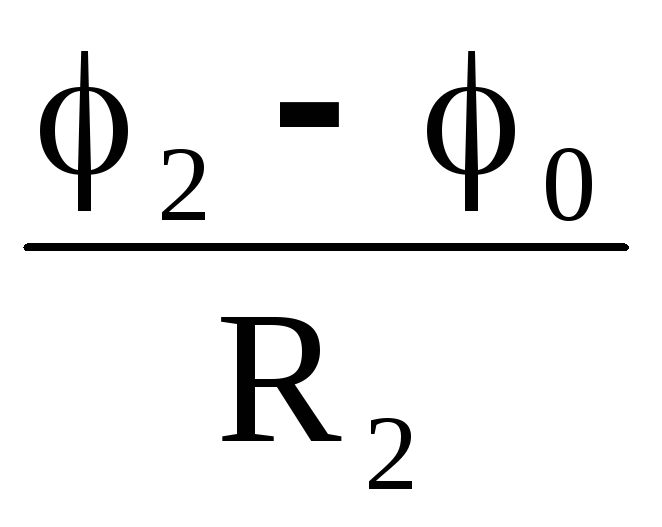 ; (15)
; (15)
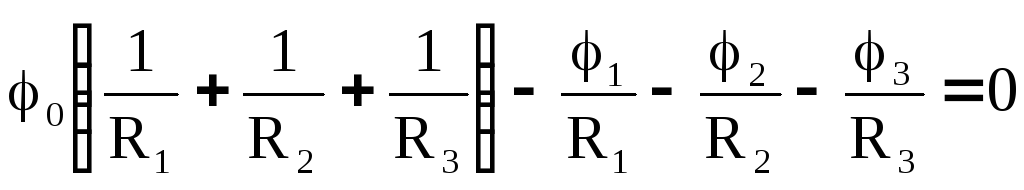 ; (16)
; (16)
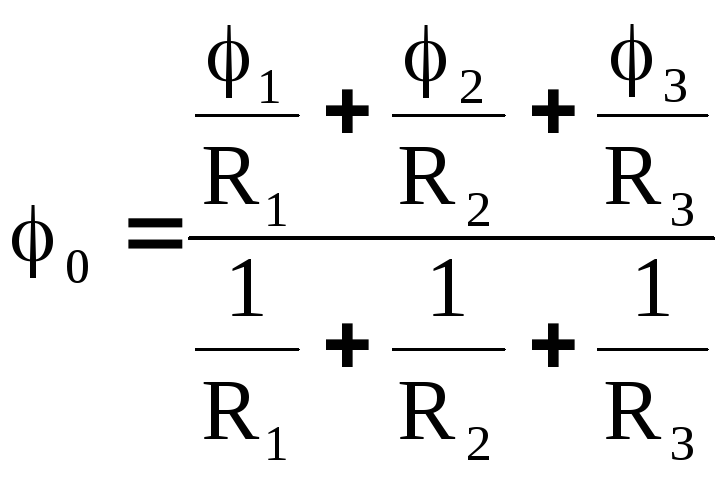 ; (17)
; (17)
Обозначим: 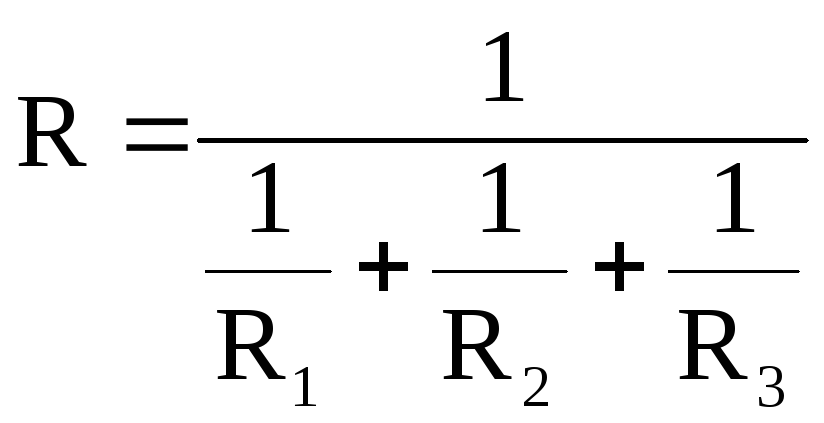
Подставим φ0 в (15) получим выражения для токов в «звезде»:
Ii = 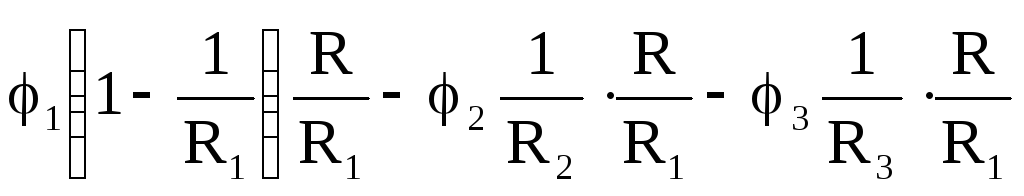 . (18)
. (18)
I2 = 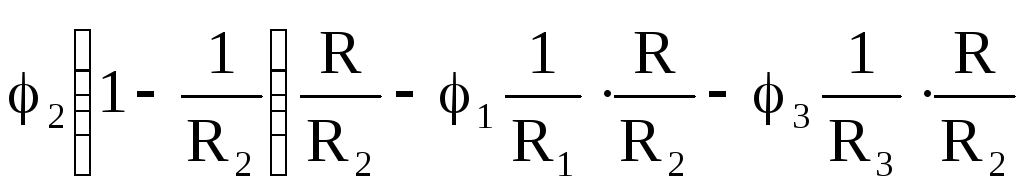 . (19)
. (19)
Для цепи рис 7,а запишем уравнения для токов в «треугольнике» :
I1 = I12 − I31 = 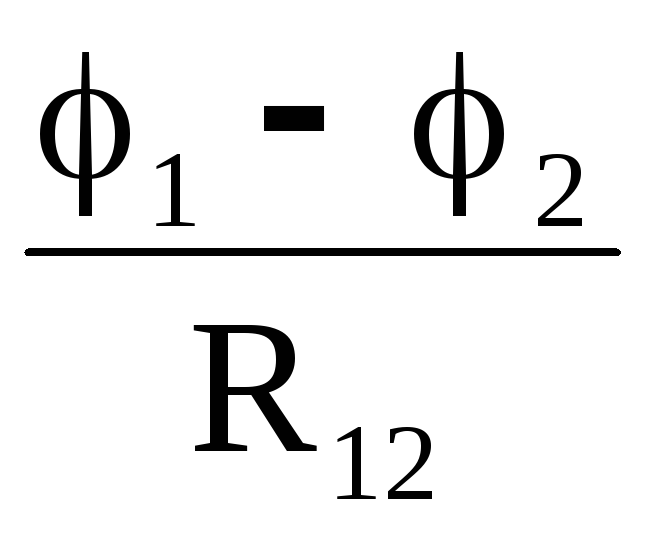 −
−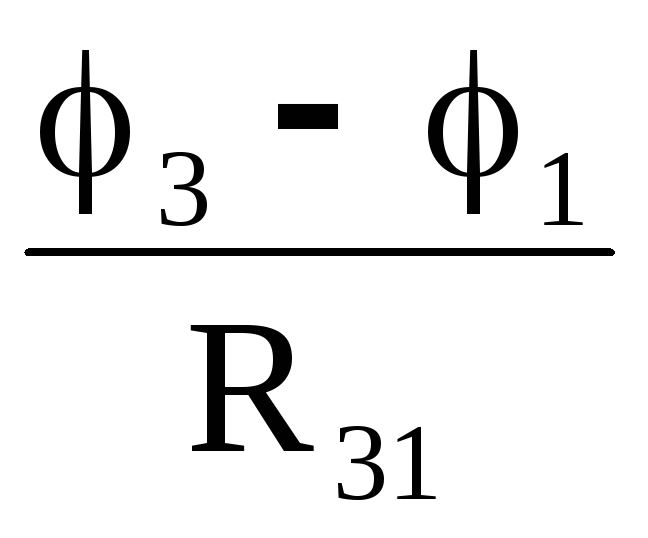 =
=  ; (20)
; (20)
I2 = I23 − I12 = 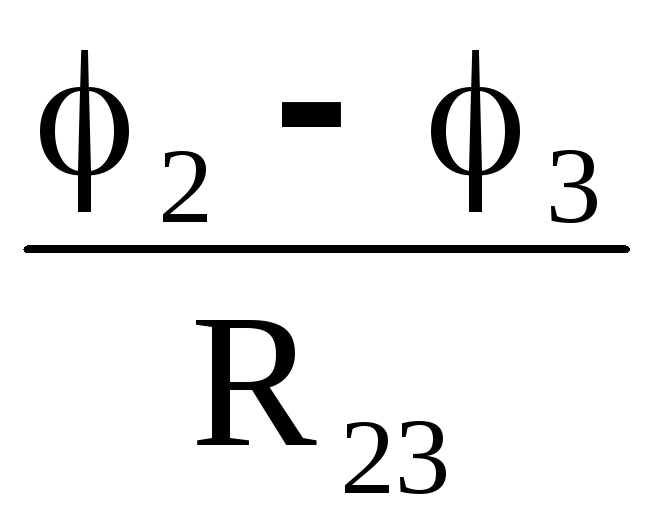 −
−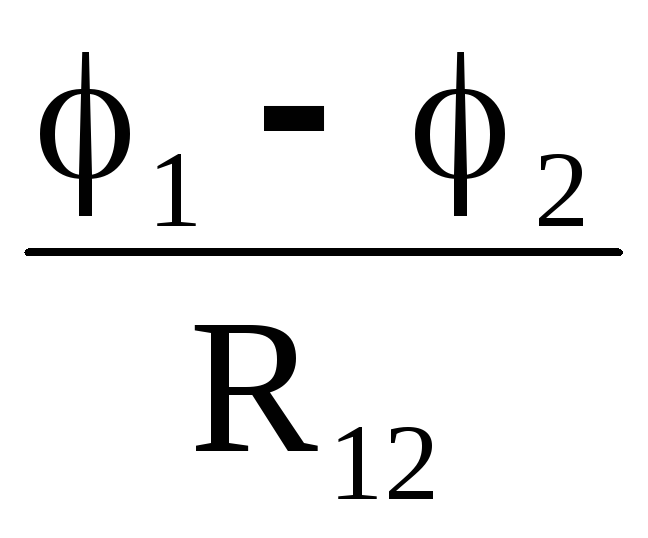 =
= 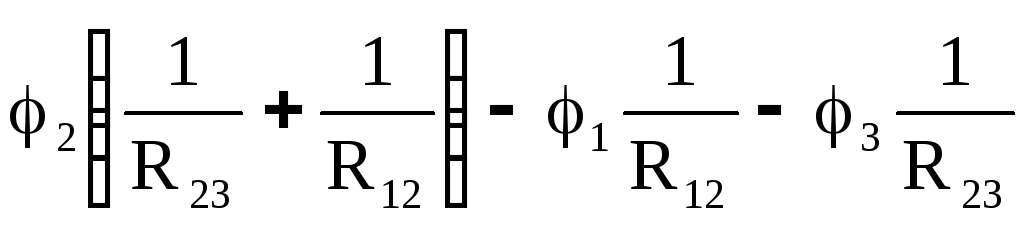 (21)
(21)
Приравняем коэффициенты при потенциалах φ2 и φ3 в (18) и (20) получим:
 ..=..
..=..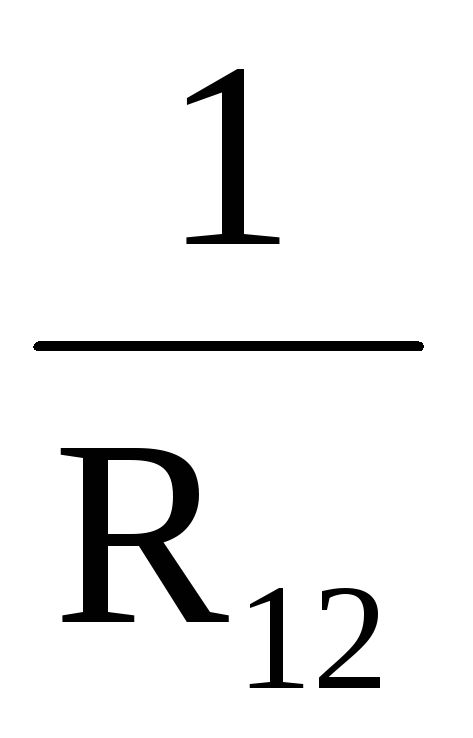 ; (22)
; (22)
 ..=..
..=..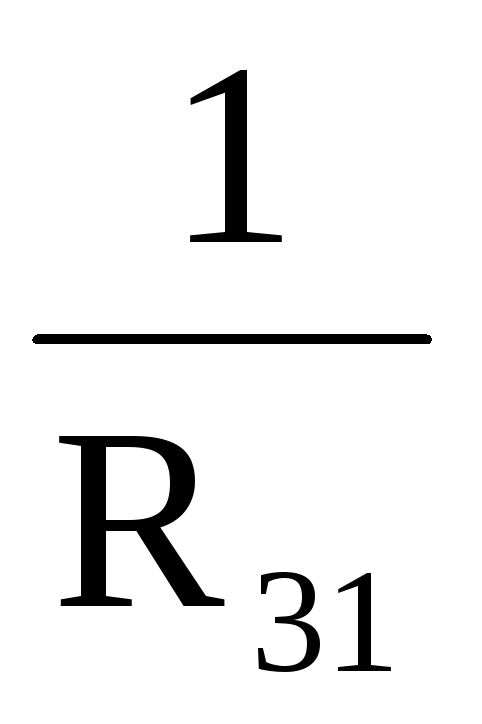 ; (23)
; (23)
Приравняем коэффициенты при потенциале φ3 в (19) и (21) получим:
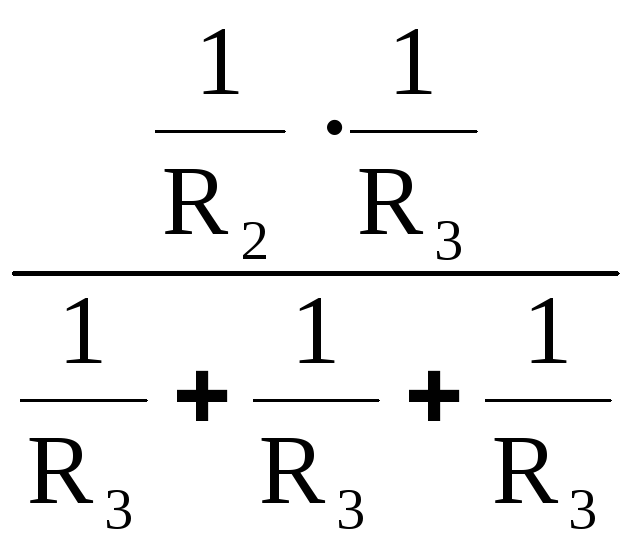 ..=..
..=..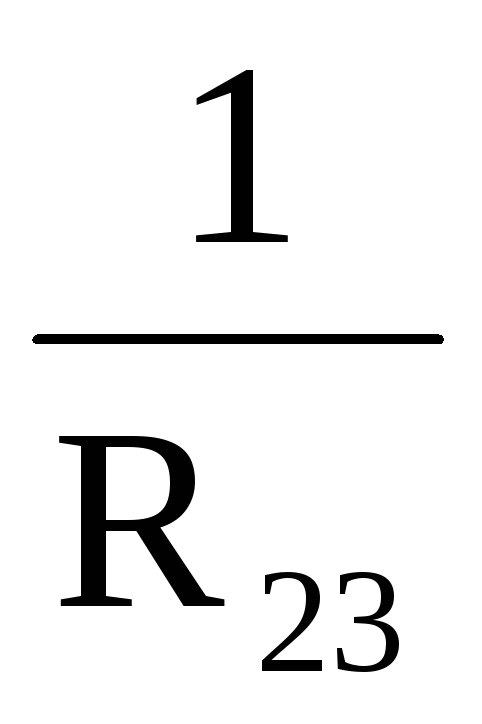 ; (24)
; (24)
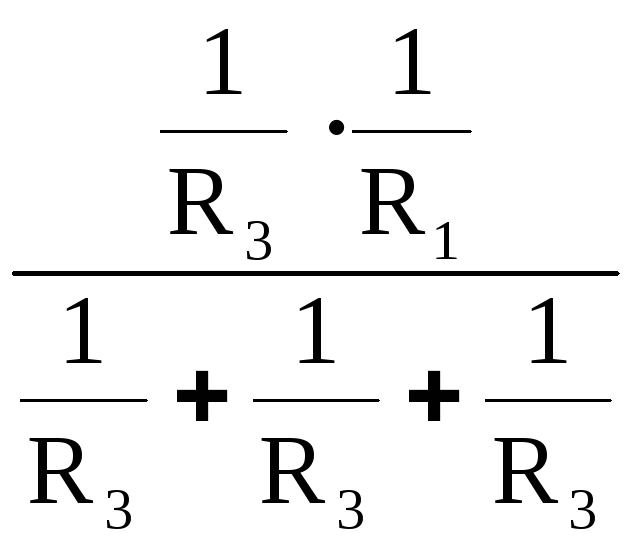
Преобразовав (22), (23) и (24) получим следующие формулы взаимного преобразования соединения «звезда» рис. 6 и «треугольник» рис. 7:
R1 =
 ;
;R2 =
 ;
;R3 =
 .
.R12 = R1 + R2 +
 ;
;R23 = R2 + R3 +
 ;
;R31 = R3 + R1 +
 .
.
Замена сопротивления с известным током, зависимым источником ЭДС (теорема о компенсации).

а б
Рис. 8
Согласно теореме о компенсации линейное сопротивление с известным током (рис. 8,а) можно заменить зависимым источником ЭДС, полярность которого совпадает с полярностью напряжения возникающего на зажимах сопротивления (рис. 8,б).
а б в
Рис. 9
Доказательство теоремы. В ветвь с линейным резистором рис. 9,а. включим два источника ЭДС E = I R, имеющих противоположное направление рис. 9,б. Так как напряжение на резисторе U=I R то разница потенциалов φ1 − φ3 = 0 и на схеме можно объединить точки 1 и 3 (на рис. 9,б показано пунктиром). В результате получим цепь рис. 9,в.
8
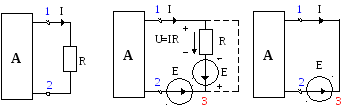
2. Источник эдс и источник тока
При расчёте и анализе электрических цепей источник электрической энергии заменяют расчётным эквивалентом. В качестве последнего может быть взят либо источник ЭДС, либо источник тока.
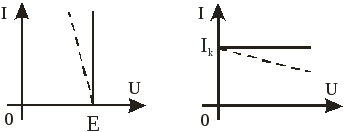
Под источником ЭДС условимся понимать такой идеализированный источник питания, ЭДС которого постоянна, не зависит от величины протекающего через него тока и равна ЭДС реального источника энергии. Очевидно, это может быть только в том случае, если внутреннее сопротивление Rв этого идеализированного источника равно нулю. ВАХ такого источника изображена на рис. 4, а (сплошная линия).
а)
б)
Рис. 4
Под источником тока понимают такой идеализированный источник питания, который даёт ток Ik, не зависящий от величины нагрузки цепи и равный частному от деления ЭДС реального источника на его внутреннее сопротивление Rв (Ik=Е/Rв).
Для того, чтобы источник тока мог давать ток Ik, не зависящий от величины сопротивления нагрузки, внутреннее сопротивление его должно стремиться к бесконечности. Но и ЭДС Е также должна стремиться к бесконечности, так как отношение двух бесконечных величин Е и Rв равно конечнойвеличине − току Ik. ВАХ такого источника показана на рис. 4, б (сплошная линия).
Физически осуществить эти идеализированные источники невозможно, поскольку внутреннее сопротивление реальных источников не может быть равно нулю и при конечном токе не может быть равно бесконечности.
Однако, если внутреннее сопротивление Rв реального источника питания на несколько порядков меньше сопротивления нагрузки, то источник питания будет работать в режиме, близком к режиму, характерному для источника ЭДС.
Так крупные генераторы, вырабатывающие электрическую энергию на различных электростанциях (ГЭС, ТЭЦ, атомных) практически являются источниками ЭДС, поскольку их внутреннее сопротивление Rв очень мало. В схему надо обязательно включить внутреннее сопротивление Rв (рис. 5).
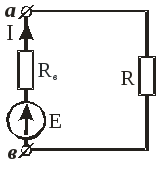
Рис. 5
Напряжение Uав на выходных зажимах источника ЭДС будет меньше ЭДС Е на величину падения напряжения на внутреннем сопротивлении Rв источника (Uав=Е−I Rв). С увеличением тока I напряжение на выходных зажимах источника будет уменьшаться, и ВАХ реального источника ЭДС будет выглядеть как наклонная линия (штриховая линия на рис. 4,а).
Аналогично, если внутреннее сопротивление Rв реального источника питания во всех возможных режимах работы схемы будет на несколько порядков больше сопротивления нагрузки, то источник питания будет работать в режиме, довольно близком к режиму, характерному для источника тока.
Так полупроводниковые генераторы имеют большое внутреннее сопротивление Rв, особенно если в их составе есть хотя бы один каскад на однопереходных транзисторах, особенностью которых является внутреннее сопротивление 3−5 Мом. Поэтому полупроводниковые генераторы такого типа практически являются источниками тока. Источник тока изображают с параллельно включенным с ним сопротивлением Rв (рис. 6), равным внутреннему сопротивлению реального источника энергии.

Рис. 6
Пусть, например, 
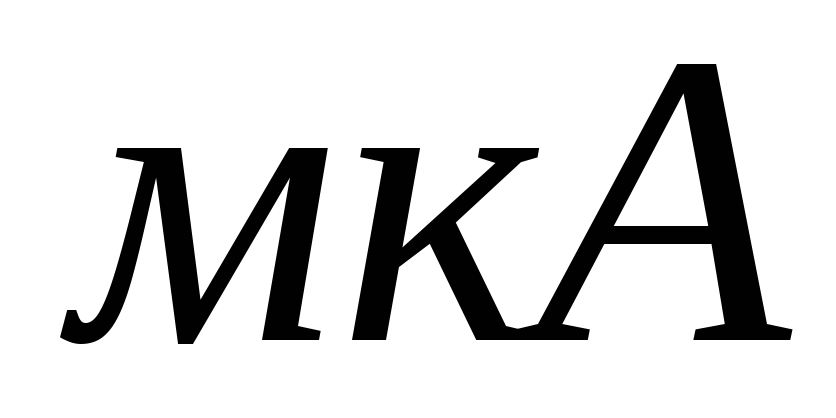 ,
,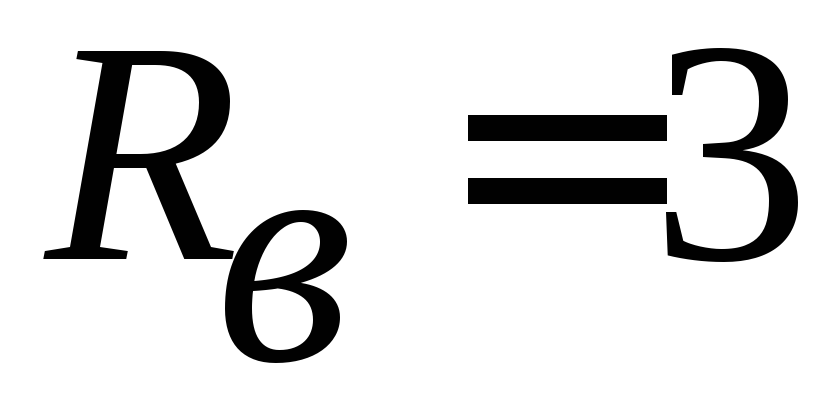
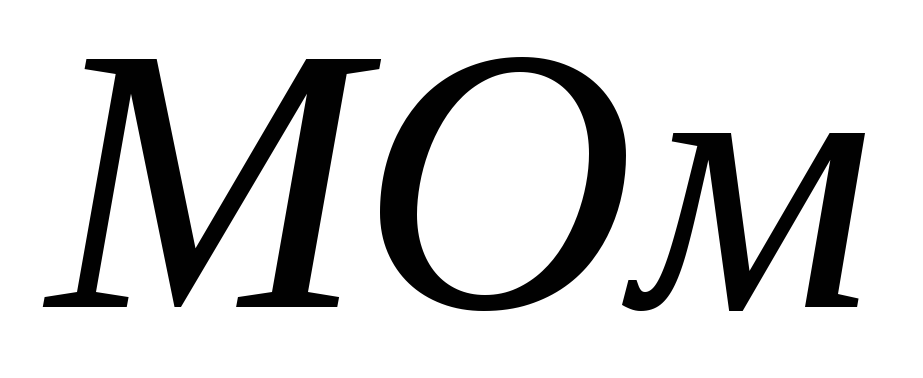 ,
а сопротивление нагрузки
,
а сопротивление нагрузки меняется в пределах от
меняется в пределах от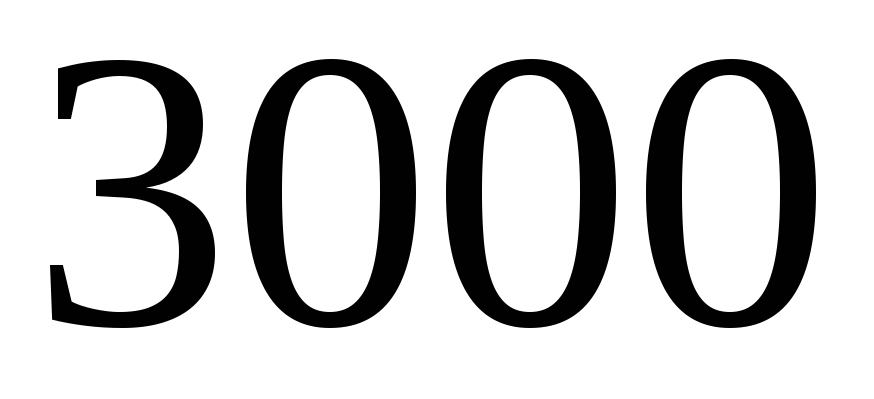
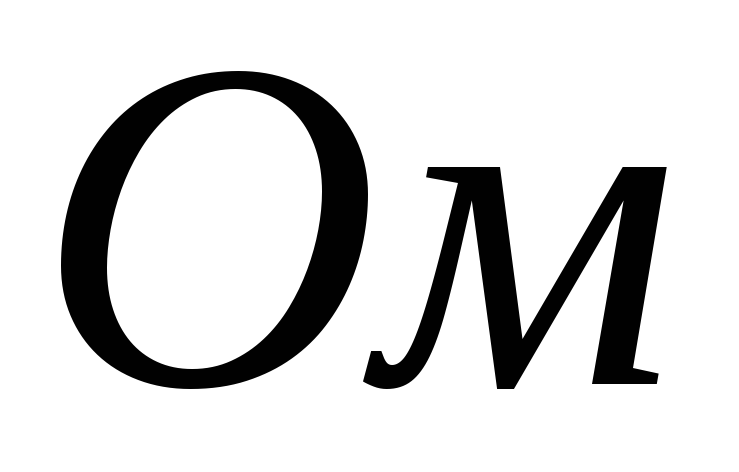 до
до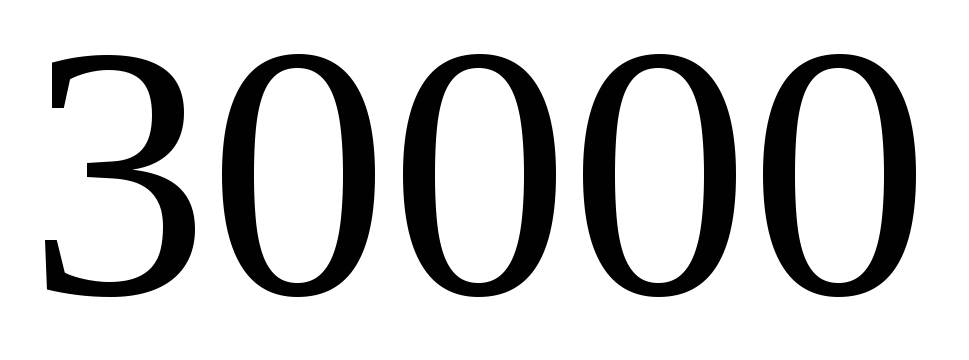
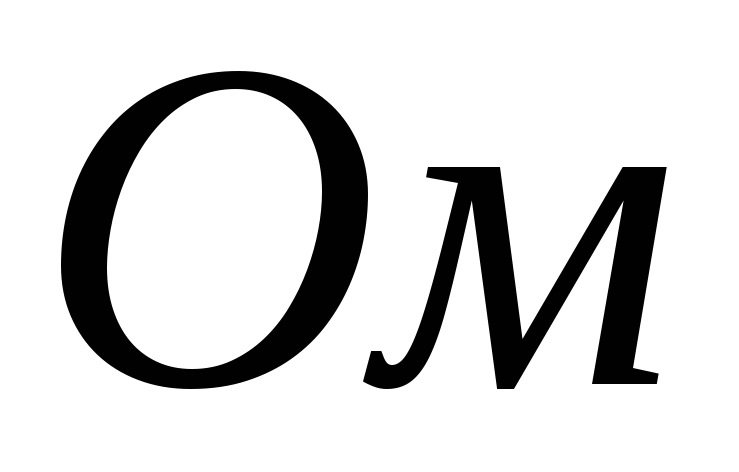 .
Тогда ЭДС источника будет
.
Тогда ЭДС источника будет
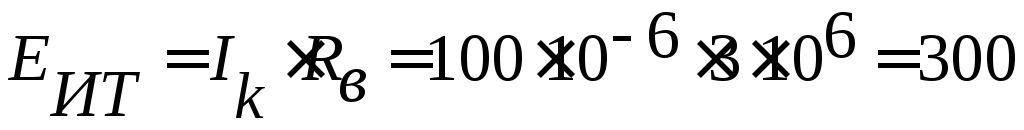
 ,
(1)
,
(1)
а ток I будет равен
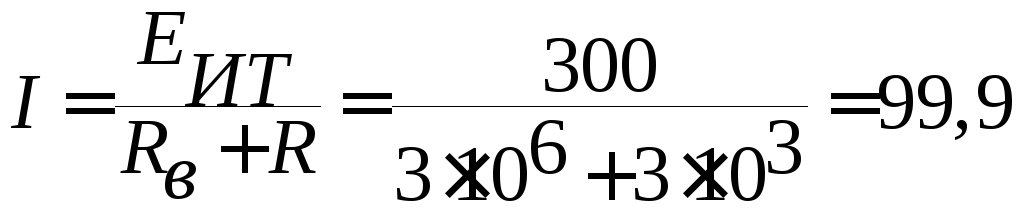
 (2)
(2)
при 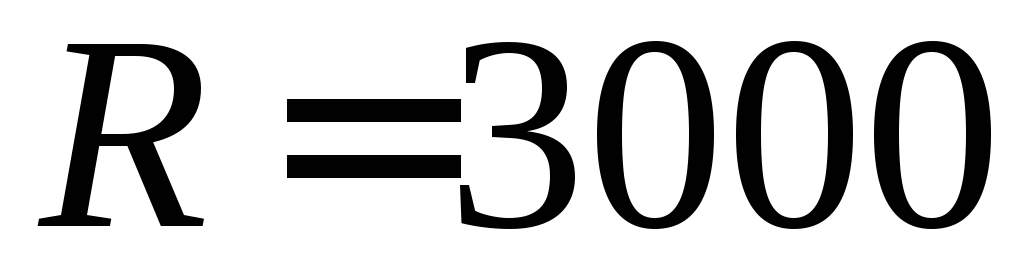
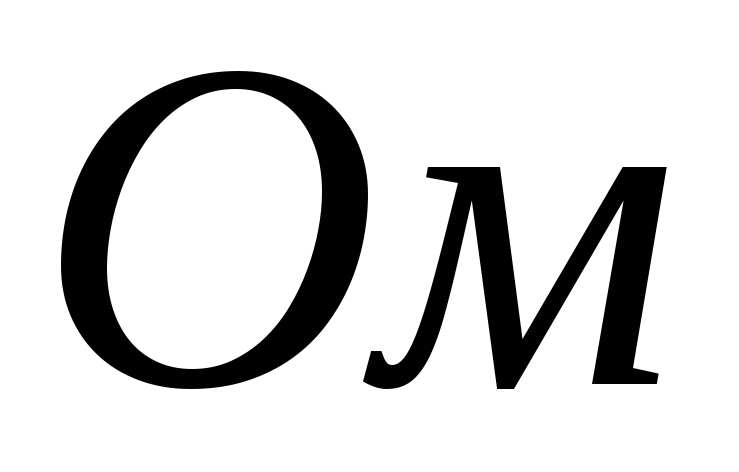 и
и

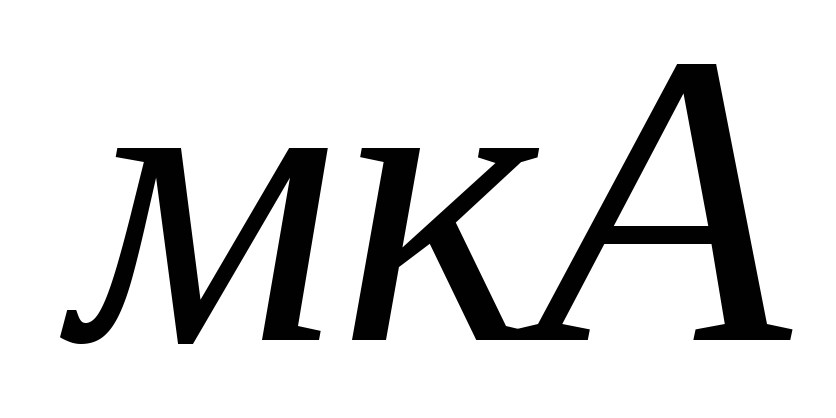 (3)
(3)
при  .
.
Таким образом, при
изменении сопротивления нагрузки  от
от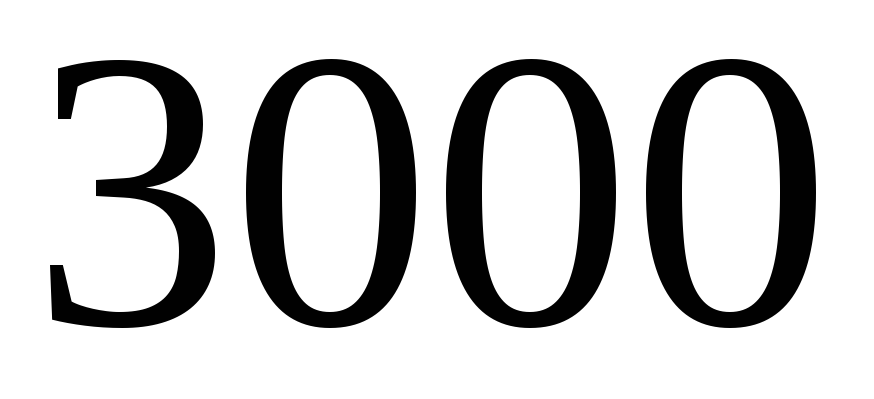
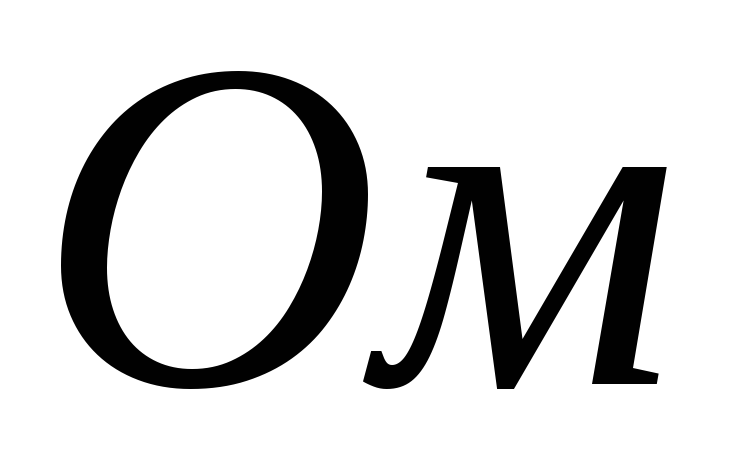 до
до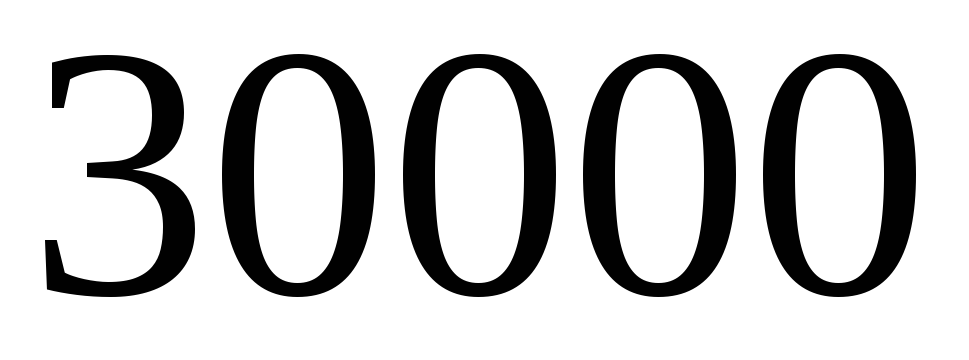
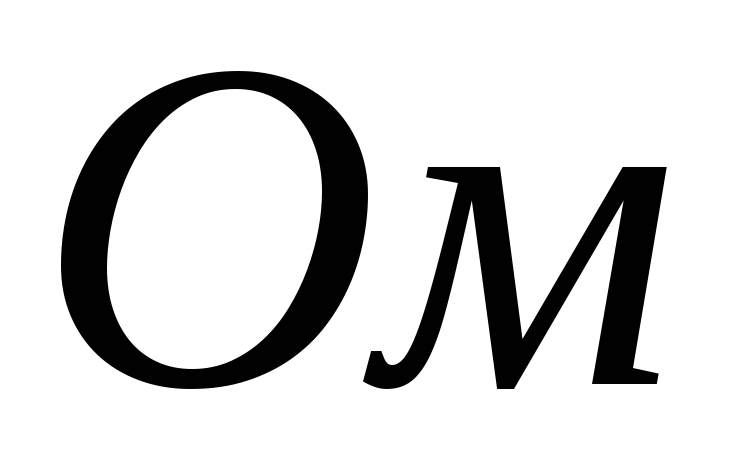 ток
ток практически не изменился.
практически не изменился.
Если же сопротивление
нагрузки будет меньше  на порядок и составит
на порядок и составит
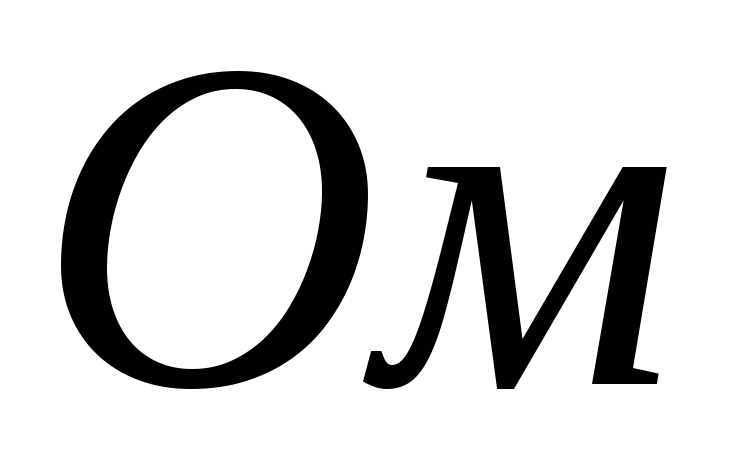 ,
то ток
,
то ток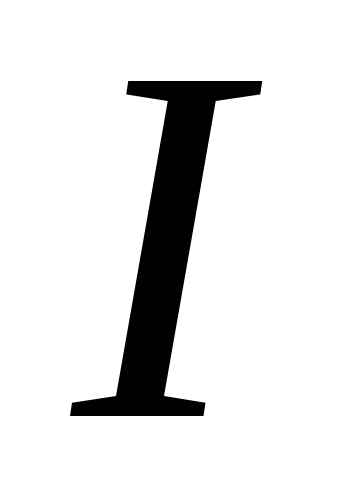 будет
будет
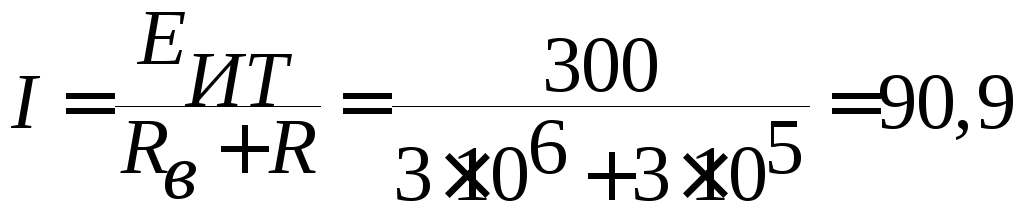
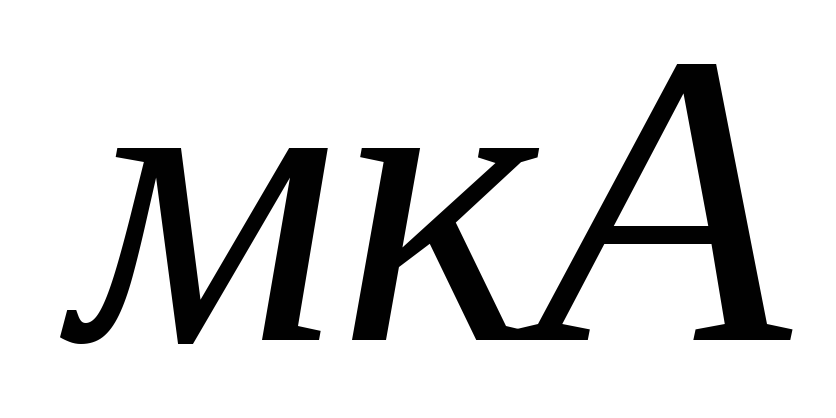 .
(4)
.
(4)
Ток в этом случае уменьшится на 9 %.
Таким образом,
рассматриваемый источник будет
практически работать в режиме источника
тока, если сопротивление нагрузки 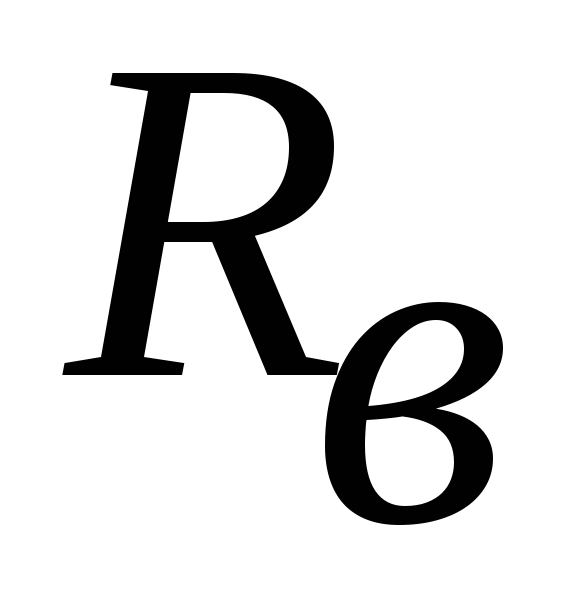 не менее чем на два порядка меньше
внутреннего сопротивления источника
не менее чем на два порядка меньше
внутреннего сопротивления источника .
При больших значениях сопротивления
нагрузки ВАХ источника получается
падающей (штриховая линия на рис. 4, б).
.
При больших значениях сопротивления
нагрузки ВАХ источника получается
падающей (штриховая линия на рис. 4, б).
Источник эдс и источник тока.
Под
идеализированным источником ЭДС
условимся понимать такой источник
питания, ЭДС которого постоянна, не
зависит от величины протекающего через
него тока. Очевидно, это может быть
только в том случае, если внутреннее
сопротивление 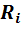 равно
нулю.
равно
нулю.
ВАХ такого источника ЭДС представляет прямую линию, параллельную оси тока (рис. 5).
На рисунке: 1 – ВАХ идеализированного источника ЭДС;
2 – ВАХ реального источника ЭДС.
Рис. 5. ВАХ идеализированного и реального источника ЭДС
Внутреннее
сопротивление  реального
источника ЭДС не может быть равно нулю.
Поэтому ВАХ реального источника ЭДС
представляет наклонную линию. С
увеличением тока напряжение на выходе
источника падает (линия 2 на рис. 5).
реального
источника ЭДС не может быть равно нулю.
Поэтому ВАХ реального источника ЭДС
представляет наклонную линию. С
увеличением тока напряжение на выходе
источника падает (линия 2 на рис. 5).
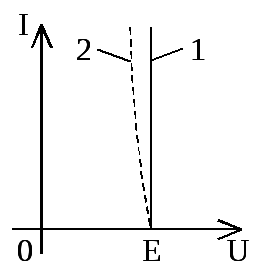
На рис. 6 представлена электрическая схема с реальным источником ЭДС.
Рис. 6. Электрическая схема с реальным источником ЭДС
Напряжение на выходе источника ЭДС меньше величины электродвижущей силы на величину падения напряжения на внутреннем сопротивлении источника:
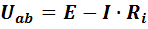 . (1)
. (1)
Под
идеализированным источником тока
понимают такой источник питания, который
даёт ток 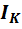 ,
не зависящий от величины нагрузки
,
не зависящий от величины нагрузки 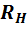 цепи и равный частному от деления ЭДС
реального источника на его внутреннее
сопротивление
цепи и равный частному от деления ЭДС
реального источника на его внутреннее
сопротивление  :
:
 . (2)
. (2)
Чтобы
такой источник тока мог давать ток 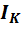 ,
не зависящий от величины сопротивления
нагрузки
,
не зависящий от величины сопротивления
нагрузки 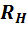 ,
внутреннее сопротивление его
,
внутреннее сопротивление его 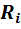 и его ЭДС теоретически должны стремиться
к бесконечности.
и его ЭДС теоретически должны стремиться
к бесконечности.
Внутреннее сопротивление реального источника тока не может быть равно бесконечности.
На рис. 7 представлена электрическая схема с реальным источником тока:

Рис. 7. Электрическая схема с реальным источником тока
По
определению идеализированный источник
тока даёт ток  ,
не зависящий от величины сопротивления
нагрузки
,
не зависящий от величины сопротивления
нагрузки 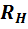 .
Другими словами, сопротивление
.
Другими словами, сопротивление 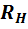 в схеме рис. 7 может быть равно нулю
(короткое замыкание) или равным
бесконечности (холостой ход), а ток
в схеме рис. 7 может быть равно нулю
(короткое замыкание) или равным
бесконечности (холостой ход), а ток 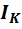 должен остаться неизменным. Рассмотрим,
при каких условиях это возможно. С этой
целью через
должен остаться неизменным. Рассмотрим,
при каких условиях это возможно. С этой
целью через 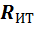 обозначим внутреннее сопротивление
источника тока, а через
обозначим внутреннее сопротивление
источника тока, а через 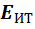 его ЭДС и запишем два уравнения,
описывающие работу схемы рис. 7 для двух
упомянутых крайних режимов работы.
его ЭДС и запишем два уравнения,
описывающие работу схемы рис. 7 для двух
упомянутых крайних режимов работы.
При 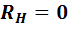
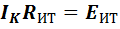 .
(3)
.
(3)
При 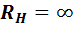
 или
или  . (4)
. (4)
Уравнения
(3) и (4) совместимы только в том случае,
если 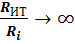 .
.
Однако
если внутреннее сопротивление 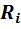 источника питания на несколько порядков
меньше сопротивления нагрузки
источника питания на несколько порядков
меньше сопротивления нагрузки  ,
то источник питания будет работать в
режиме, близком к режиму, характерному
для источника ЭДС.
,
то источник питания будет работать в
режиме, близком к режиму, характерному
для источника ЭДС.
Так, например, электромагнитные генераторы, вырабатывающие электрическую энергию на всех видах электрических станций ГЭС, ТЭЦ, АЭС и др., работают в режиме, характерном для источника ЭДС. Обмотка ротора и статора крупного генератора выполнена из довольно толстого провода, поэтому их сопротивление мало (десятые, сотые и даже тысячные доли Ома). Падение напряжения на внутреннем сопротивлении источника очень мало, поэтому и получается ВАХ, близкая к идеализированному источнику ЭДС.
Если
же внутреннее сопротивление 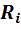 источника питания на несколько порядков
больше сопротивления нагрузки
источника питания на несколько порядков
больше сопротивления нагрузки 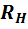 ,
то источник питания будет работать в
режиме, близком к режиму, характерному
для источника тока.
,
то источник питания будет работать в
режиме, близком к режиму, характерному
для источника тока.
Примером
могут служить полупроводниковые
высокочастотные генераторы, особенно,
если в их составе есть хотя бы один
каскад на однопереходных транзисторах.
Особенностью таких транзисторов является
их внутреннее сопротивление, составляющее
3-:-5 МОм (3-:-5 миллиона Ом). Собственно это
и будет внутреннее сопротивление
источника. ВАХ такого источника будет
близка к ВАХ идеализированного источника
тока, особенно в том случае, когда
сопротивление нагрузки 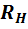 меняется в относительно небольших
пределах. Тогда нет необходимости
требовать, чтобы
меняется в относительно небольших
пределах. Тогда нет необходимости
требовать, чтобы 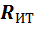 и
и 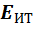 стремились к бесконечности.
стремились к бесконечности.
Следует
отметить, что схема рис. 7 эквивалента
схеме рис. 6 только в отношении энергии,
выделяющейся в сопротивлении нагрузки 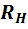 ,
и не эквивалентна ей в отношении энергии,
выделяющейся во внутреннем сопротивлении
источника тока.
,
и не эквивалентна ей в отношении энергии,
выделяющейся во внутреннем сопротивлении
источника тока.
Ток
в сопротивлении нагрузки 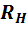 будет одинаков в обеих эквивалентных
схемах рис. 6 и рис. 7:
будет одинаков в обеих эквивалентных
схемах рис. 6 и рис. 7:
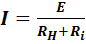 . (5)
. (5)
Для схемы рис. 6 это настолько очевидно, что не требует пояснений.
Убедимся
в этом для схемы рис. 7. Ток 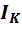 источника тока в этой схеме распределяется
обратно пропорционально сопротивлениям
двух параллельных ветвей с сопротивлениями
источника тока в этой схеме распределяется
обратно пропорционально сопротивлениям
двух параллельных ветвей с сопротивлениями 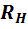 и
и 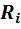 .
Ток
.
Ток  в нагрузке
в нагрузке 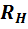 равен:
равен:
 . (6)
. (6)
Таким образом, совершенно безразлично, каким из рассмотренных эквивалентов пользоваться.
Пример.
В
схеме рис. 7 источник тока даёт ток 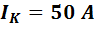 .
Шунтирующее его сопротивление
.
Шунтирующее его сопротивление 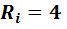 Ом.
Найти величину ЭДС эквивалентного
источника ЭДС в схеме рис. 6.
Ом.
Найти величину ЭДС эквивалентного
источника ЭДС в схеме рис. 6.
Решение:
ЭДС  .
.
Таким
образом, параметры эквивалентной схемы
рис. 6 таковы: 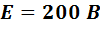 и
и 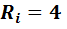 Ом.
Ом.
Источник эдс и источник тока — Мегаобучалка
Источник электродвижущей силы – источник электромагнитной энергии, характеризующихся электродвижущей силой и внутренним электрическим сопротивлением.
Часть схемы, обведенная на рис. 12 пунктиром, является источником ЭДС.
Направление действия ЭДС указывается от отрицательного зажима к положительному. Если к зажимам источника ЭДС присоединить приемник (нагрузить источник), то в цепи возникает ток. При этом напряжение (разность потенциалов) на зажимах 1 и 2 уже не будет равно ЭДС вследствие падения напряжения Uвн внутри источника энергии, т.е. на его внутреннем сопротивлении rвн:
т.е.
. (1.5)
Рис. 12 Источник ЭДС и его ВАХ
Зависимость напряжения источника от отдаваемого им тока называется внешней характеристикой источника или вольтамперной характеристикой элемента (рис.12).
Если и напряжение на зажимах источника, ЭДС убывает по линейному закону.
Кстати, направление действия напряжения принято обозначать от точки с большим потенциалом к точке с меньшим потенциалом.
Источник ЭДС, внутреннее сопротивление которого равно нулю называют идеальным источником ЭДС. Вольтамперная характеристика идеального источника ЭДС проходит параллельно оси абсцисс.
Представленная на рис. 12 схема называется схемой замещения источника ЭДС.
Источник тока.
Источник тока – источник электромагнитной энергии, характеризующийся током в нем и внутренней проводимостью. На рис. 13 показана схема замещения источника тока.
.
Рис 13 Источник тока и его ВАХ
Напряжение на зажимах источника тока с учетом того, что , а , равно:
(1.2)
При неизменных параметрах источника тока ( , ) его ВАХ выражается прямой линией (рис. 13).
В режиме короткого замыкания (R=0) весь генерируемый ток проходит через цепь нагрузки, т.е.
В режиме холостого хода (R=¥) ток источника проходит через . При этом напряжение холостого хода равно:
.
Так как — мала, то , что является опасным, аварийным.
Чем меньше , тем больше , тем больше угол наклона ВАХ. Когда =0, ВАХ – вертикальная прямая. Такой источник тока, внутренняя проводимость которого равна нулю, называется идеальным источником тока.
Для идеального источника тока ток нагрузки постоянен, а напряжение на нагрузке равно и может быть сколь угодно большим. В связи с этим, идеальный источник тока является источником бесконечно большой мощности.
Источник ЭДС целесообразно заменять эквивалентным источником тока в том случае, если сопротивление нагрузки в цепи (усилитель электронный).
1.6. Основные режимы работы электрической цепи
При рассмотрении основных режимов работыэлектрической цепи используем её ВАХ.
Источники электрической энергии постоянного тока характеризуются э.д.с. Е и внутренним сопротивлением rвн, а приемники – величиной их сопротивления. Для получения ВАХ электрической цепи воспользуемся законом Ома для полной цепи, изображенной на рис. 14
, откуда .
Данное выражение определяет зависимость напряжением на зажимах источника э.д.с. и током нагрузки. При постоянных параметрах Е и rвнвольтамперная характеристика представляет собой прямую линию проходящую через точки Е и Iкз (рис. 14.). Такой источник э.д.с. называется линейным.
Рис.14 Источник ЭДС и его ВАХ
Рассмотрим различные режимы работы источника электрической энергии.
Режим холостого хода (х.х.) – такой режим, при котором потребитель отключен от источника. Поэтому внешнее сопротивление цепи бесконечно велико ( ), а величина тока в цепи равна нулю (I=0), падение напряжения внутри источника так же будет равно нулю ( ). Напряжение на зажимах источника U будет равно э.д.с. Е.
Вывод: чтобы измерить э.д.с. источника, необходимо провести режим холостого хода (оборвать внешнюю цепь), тогда вольтметр, подключенный к зажимам источника покажет э.д.с. источника.
Режим короткого замыкания (к.з.) – такой режим, при котором зажимы источника соединены проводником с весьма малым сопротивлением, величиной которого можно пренебречь. При этом сопротивление всей цепи равно внутреннему сопротивлению источника, а ток в цепи будет наибольшим .
Напряжение на зажимах источника при коротком замыкании
.
Вывод: в режиме короткого замыкания ток в цепи наибольший, а напряжение на зажимах равно нулю.
Режим короткого замыкания опасен для большинства источников, так как при этом происходит перегрев источника, что может вывести его из строя.
Нагрузочный режим
Зависимость напряжения на зажимах источника от тока нагрузки выражается формулой , где Е и rвн – величины постоянные.
Графически (рис. 12) эта зависимость представляет собой наклонную прямую линию. Отрезок ОЕ, который отсекает данная прямая на вертикальной оси, соответствует точке I=0 (х.х.). При этом, как было показано выше Uхх=Е.
По мере увеличения тока падение напряжения внутри источника (Irвн) увеличивается, а напряжение на зажимах уменьшается. В точке Iкз напряжение на зажимах источника равно нулю (U=0). Эта точка соответствует режиму короткого замыкания.
Пользуясь данным графиком, можно для любого значения тока нагрузки определить соответствующее значение напряжения на зажимах источника.
Идеальный источник тока
Источники напряжения и тока, их свойства, характеристики и схемы замещения. Законы Ома и Кирхгофа.
Источник ЭДС (идеальный источник напряжения) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.
В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.
Реальные источники напряжения
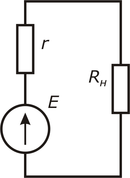

Рисунок 2
Идеальный
источник напряжения (источник ЭДС)
является физической абстракцией, то
есть подобное устройство не может
существовать. Если допустить существование
такого устройства, то электрический
ток I,
протекающий через него, стремился бы к
бесконечности при подключении нагрузки, сопротивление RH которой
стремится к нулю. Но при этом получается,
что мощность источника
ЭДС также стремится к бесконечности,
так как 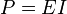 .
Но это невозможно, по той причине, что
мощность любого источника энергии
конечна.
.
Но это невозможно, по той причине, что
мощность любого источника энергии
конечна.
В реальности, любой источник напряжения обладает внутренним сопротивлением r, которое имеет обратную зависимость от мощности источника. То есть, чем больше мощность, тем меньше сопротивление (при заданном неизменном напряжении источника) и наоборот. Наличие внутреннего сопротивления отличает реальный источник напряжения от идеального. Следует отметить, что внутреннее сопротивление — это исключительно конструктивное свойство источника энергии. Эквивалентная схема реального источника напряжения представляет собой последовательное включение источника ЭДС — Е (идеального источника напряжения) и внутреннего сопротивления — r.
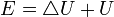
где
 —
падение напряжения
на внутреннем сопротивлении;
—
падение напряжения
на внутреннем сопротивлении;
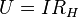 —
падение напряжения
на нагрузке.
—
падение напряжения
на нагрузке.
При
коротком замыкании ( )
)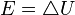 ,
то есть вся мощность источника энергии
рассеивается на его внутреннем
сопротивлении. В этом случае ток
,
то есть вся мощность источника энергии
рассеивается на его внутреннем
сопротивлении. В этом случае ток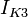 будет
максимальным для данного источника
ЭДС. Зная напряжение холостого хода и
ток короткого замыкания, можно вычислить
внутреннее сопротивление источника
напряжения:
будет
максимальным для данного источника
ЭДС. Зная напряжение холостого хода и
ток короткого замыкания, можно вычислить
внутреннее сопротивление источника
напряжения:
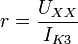
Исто́чник
то́ка (также генератор
тока) — двухполюсник,
который создаёт ток 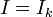 ,
не зависящий от сопротивления нагрузки,
к которой он присоединён. В быту
«источником тока» часто неточно называют
любой источник электрического напряжения
(батарею, генератор, розетку), но в строго
физическом смысле это не так, более
того, обычно используемые в быту источники
напряжения по своим характеристикам
гораздо ближе к источнику
ЭДС,
чем к источнику тока.
,
не зависящий от сопротивления нагрузки,
к которой он присоединён. В быту
«источником тока» часто неточно называют
любой источник электрического напряжения
(батарею, генератор, розетку), но в строго
физическом смысле это не так, более
того, обычно используемые в быту источники
напряжения по своим характеристикам
гораздо ближе к источнику
ЭДС,
чем к источнику тока.
Свойства:
Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи:

Мощность, отдаваемая источником тока в сеть, равна:
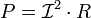
Так
как для источника тока 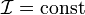 ,
напряжение и мощность, выделяемая им,
неограниченно растут при росте
сопротивления..
,
напряжение и мощность, выделяемая им,
неограниченно растут при росте
сопротивления..
Реальный источник тока
Реальный
источник тока, так же как и источник
ЭДС,
в линейном приближении может быть описан
таким параметром, как внутреннее
сопротивление  .
Отличие состоит в том, что чем больше
внутреннее сопротивление, тем ближе
источник тока к идеальному (источник
ЭДС, наоборот, чем ближе к идеальному,
тем меньше его внутреннее сопротивление).
Реальный источник тока с внутренним
сопротивлением
.
Отличие состоит в том, что чем больше
внутреннее сопротивление, тем ближе
источник тока к идеальному (источник
ЭДС, наоборот, чем ближе к идеальному,
тем меньше его внутреннее сопротивление).
Реальный источник тока с внутренним
сопротивлением  эквивалентен
реальному источнику ЭДС, имеющему
внутреннее сопротивление
эквивалентен
реальному источнику ЭДС, имеющему
внутреннее сопротивление  и
ЭДС
и
ЭДС 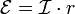 .
.
Напряжение на клеммах реального источника тока равно:
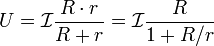
Сила тока в цепи равна:
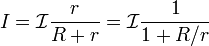
Мощность, отдаваемая реальным источником тока в сеть, равна:
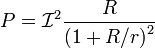
Схемы
замещения источников энергии Простейшая
электрическая цепь и ее схема замещения,
как указывалось, состоят из одного
источника энергии с ЭДС Е и внутренним
сопротивлением rвт и
одного приемника с сопротивлением r.
Ток
во внешней по отношению к источнику
энергии части цепи, т. е. в приемнике с
сопротивлением r,
принимается направленным от точки а с
большим потенциалом  к
точке b с
меньшим потенциалом
к
точке b с
меньшим потенциалом 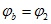 .
Направление
тока будем обозначать на схеме стрелкой
с просветом или указывать двумя индексами
у буквы I, такими
же, как и у соответствующих точек схемы.
Так, для схемы рис. 1.3 ток в приемнике I = Iаb,
где индексы а и b обозначают направление
тока от точки а к точке b.
Покажем,
что источник энергии с известными
ЭДС E и
внутренним сопротивлением rвт,
может быть представлен двумя
основными схемами замещения (эквивалентными
схемами).
Как
уже указывалось, с одной стороны,
напряжение на выводах источника энергии
меньше ЭДС на падение напряжения внутри
источника:
.
Направление
тока будем обозначать на схеме стрелкой
с просветом или указывать двумя индексами
у буквы I, такими
же, как и у соответствующих точек схемы.
Так, для схемы рис. 1.3 ток в приемнике I = Iаb,
где индексы а и b обозначают направление
тока от точки а к точке b.
Покажем,
что источник энергии с известными
ЭДС E и
внутренним сопротивлением rвт,
может быть представлен двумя
основными схемами замещения (эквивалентными
схемами).
Как
уже указывалось, с одной стороны,
напряжение на выводах источника энергии
меньше ЭДС на падение напряжения внутри
источника: 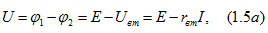 с
другой стороны, напряжение на
сопротивлении r
с
другой стороны, напряжение на
сопротивлении r 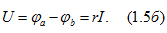 Ввиду
равенства
Ввиду
равенства 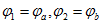 из
(1.5а) и (1.56) получается
из
(1.5а) и (1.56) получается 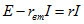 или
или 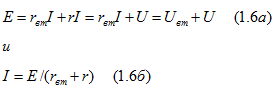 В
частности, при холостом ходе (разомкнутых
выводах а и b)
получается E=Uх,
т. е. ЭДС равна напряжению холостого
хода. При коротком замыкании (выводов
а и b)
ток
В
частности, при холостом ходе (разомкнутых
выводах а и b)
получается E=Uх,
т. е. ЭДС равна напряжению холостого
хода. При коротком замыкании (выводов
а и b)
ток 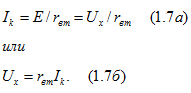
 Из
(1.7 6)
следует, что rвт источника
энергии, так же как и сопротивление
приемника, ограничивает ток.
На
схеме замещения можно показать элемент
схемы с rвт,
соединенным последовательно с элементом,
обозначающим ЭДС E (рис.
1.7, а). Напряжение U зависит от тока
приемника и равно разности между
ЭДС E источника
энергии и падением напряжения rвтI (1.6а).
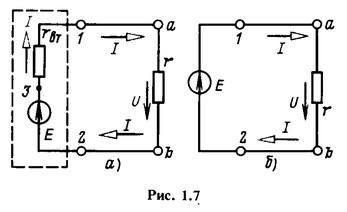
Схема источника энергии, показанная на
рис. 1.7, а, называется первой
схемой замещения или
схемой с источником ЭДС.
Если rвт<<r и
напряжение Uвт<<U,
т. е. источник электрической энергии
находится в режиме, близком к холостому
ходу, то можно практически пренебречь
внутренним падением напряжения и
принять Uвт = rвт =
0.
В этом случае для источника энергии
получается более простая эквивалентная
схема только с источником ЭДС, у которого
в отличие от реального источника
исключается режим короткого замыкания
(U =0). Такой источник энергии без внутреннего
сопротивления (rвт =
0),
обозначенный кружком со стрелкой внутри
и буквой E (рис.
1.7,6), называют идеальным
источником ЭДС или источником
напряжения (источником
с заданным напряжением). Напряжение на
выводах такого источника не зависит от
сопротивления приемника и всегда равно
ЭДС E.
Его внешняя характеристика — прямая,
параллельная оси абсцисс (штриховая
прямая ab на
рис. 1.4).
Из
(1.7 6)
следует, что rвт источника
энергии, так же как и сопротивление
приемника, ограничивает ток.
На
схеме замещения можно показать элемент
схемы с rвт,
соединенным последовательно с элементом,
обозначающим ЭДС E (рис.
1.7, а). Напряжение U зависит от тока
приемника и равно разности между
ЭДС E источника
энергии и падением напряжения rвтI (1.6а).
Схема источника энергии, показанная на
рис. 1.7, а, называется первой
схемой замещения или
схемой с источником ЭДС.
Если rвт<<r и
напряжение Uвт<<U,
т. е. источник электрической энергии
находится в режиме, близком к холостому
ходу, то можно практически пренебречь
внутренним падением напряжения и
принять Uвт = rвт =
0.
В этом случае для источника энергии
получается более простая эквивалентная
схема только с источником ЭДС, у которого
в отличие от реального источника
исключается режим короткого замыкания
(U =0). Такой источник энергии без внутреннего
сопротивления (rвт =
0),
обозначенный кружком со стрелкой внутри
и буквой E (рис.
1.7,6), называют идеальным
источником ЭДС или источником
напряжения (источником
с заданным напряжением). Напряжение на
выводах такого источника не зависит от
сопротивления приемника и всегда равно
ЭДС E.
Его внешняя характеристика — прямая,
параллельная оси абсцисс (штриховая
прямая ab на
рис. 1.4). 
Источник ЭДС и источник тока в электрических цепях — Мегаобучалка
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r0 заменяют расчетным эквивалентным источником ЭДС или источником тока.
Рис. 1.14
Источник ЭДС (рис. 1.14) имеет внутреннее сопротивление r0, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС.
Для данной цепи запишем соотношение по второму закону Кирхгофа
(1.10)
E=U+Ir0 или E=U−Ir0.
Эта зависимость напряжения U на зажимах реального источника от тока I определяется его вольт-амперной или внешней характеристикой (рис. 1.15). Уменьшение напряжения источника U при увеличении тока нагрузки I объясняется падением напряжения на его внутреннем сопротивлении r0.
| Рис. 1.15 | Рис. 1.16 |
У идеального источника ЭДС внутреннее сопротивление r0<<Rн (приближенно r0≈0). В этом случае его вольт-амперная характеристика представляет собой прямую линию (рис. 1.16), следовательно, напряжение U на его зажимах постоянно (U=E) и не зависит от величины сопротивления нагрузки Rн.
Рис. 1.17
Источник тока, заменяющий реальный источник электрической энергии, характеризуется неизменным по величине током Iк, равным току короткого замыкания источника ЭДС , и внутренним сопротивление r0, включенным параллельно (рис. 1.17).
Стрелка в кружке указывает положительное направление тока источника. Для данной цепи запишем соотношение по первому закону Кирхгофа
Iк=I0+I; .
В этом случае вольт-амперная (внешняя) характеристика I(U) источника тока определится соотношением
(1.11)
I=Iк−I0=Iк−U/r0
и представлена на рис. 1.18.
| Рис. 1.18 | Рис. 1.19 |
Уменьшение тока нагрузки I при увеличении напряжения U на зажимах ab источника тока, объясняется увеличением тока I0, замыкающегося в цепи источника тока.
В идеальном источнике тока r0>>Rн. В этом случае можно считать, что при изменении сопротивления нагрузки Rн потребителя I0≈0, а I≈Iк. Тогда из выражения (1.11) следует, что вольт-амперная характеристика I(U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I=Iк=E/r0 (рис. 1.19).
При сравнении внешних характеристик источника ЭДС (рис. 1.15) и источника тока (рис. 1.18) следует, что они одинаково реагируют на изменение величины сопротивления нагрузки. Покажем, что в обоих случаях ток I в нагрузке определяется одинаковым соотношением.
Ток в нагрузке Rн для схем источника ЭДС (рис. 1.14) и источника тока (рис. 1.17) одинаков и равен .
Для схемы (рис. 1.14) это следует из закона Ома, т.к. при последователь-ном соединении сопротивления r0 и Rн складываются. В схеме (рис. 1.17) ток распределяется обратно пропорционально сопротивлениям r0 и Rн двух параллельных ветвей. Ток в нагрузке Rн
,
т.е. совпадает по величине с током при подключении нагрузки к источнику ЭДС. Следовательно, схема источника тока (рис. 1.17) эквивалентна схеме источника ЭДС (рис. 1.14) в отношении энергии, выделяющейся в сопротивлении нагрузки Rн, но не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания.
Каким из двух эквивалентных источников питания пользоваться, не играет существенной роли. Однако на практике, особенно при расчете электротехнических устройств, чаще используется в качестве источника питания источник ЭДС с внутренним сопротивлением r0 и величиной электродвижущей силы E.
В тех случаях, когда номинальное напряжение или номинальный ток и мощность источника электрической энергии оказываются недостаточными для питания потребителей, вместо одного используют несколько источников. Существуют два основных способа соединения источников питания: последовательное и параллельное.
Последовательное включение источников питания (источников ЭДС) применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС (рис. 1.20).
Рис. 1.20
Для этой цепи на основании второго закона Кирхгофа можно записать
E1+E2+E3=I(r01+r02+r03+Rн),
откуда
.
Таким образом, электрическая цепь на рис. 1.20 может быть заменена цепью с эквивалентным источником питания (рис. 1.21), имеющим ЭДС Eэ и внутреннее сопротивление rэ.
| Рис. 1.21 | Рис. 1.22 |
При параллельном соединении источников (рис. 1.22) соединяются между собой положительные выводы всех источников, а также их отрицательные выводы. Характерным для параллельного соединения является одно и то же напряжение U на выводах всех источников. Для электрической цепи на рис. 1.22 можно записать следующие уравнения:
I=I1+I2+I3; P=P1+P2+P3=UI1+UI2+UI3=UI.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. Параллельное соединение источников применяется в первую очередь тогда, когда номинальные ток и мощность одного источника недостаточны для питания потребителей. На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями.
Основы электротехники и электроники: Курс лекций, страница 2
Величина, обратная сопротивлению, называется проводимостью (обозначается буквой g, имеет размерность Ом – 1 или См, Сименс).
В линейных цепях сопротивление ветвей постоянно, определяется лишь физическими свойствами материала проводников и не зависит от источников, токов и напряжений в ветвях.
Если источники в цепи создают на своих выводах напряжения и токи, которые не изменяются во времени, цепь называется электрической цепью постоянного тока. В цепи постоянного тока сопротивление индуктивностей равно нулю, сопротивление конденсаторов бесконечно велико.
Далее будут рассмотрены линейные цепи постоянного тока.
2. ИСТОЧНИКИ ЭДС И ИСТОЧНИКИ ТОКА
ЭДС – это максимальное напряжение, которое могут создать сторонние силы на выводах источника при отсутствии в цепи тока. В качестве сторонних сил могут выступать, например, химические реакции в гальванической батарее или момент на валу электрической машины, работающей в режиме генератора.
Для удобства анализа источники электрической энергии представляют либо с помощью идеального источника ЭДС, либо с помощью идеального источника тока. Идеальный источник ЭДС и идеальный источник тока называют также источниками бесконечно большой мощности.
На Рис. 2.1 а показана вольт-амперная характеристика идеального источника ЭДС. Этот источник отличается тем, что напряжение на его выводах равно значению ЭДС независимо от тока нагрузки. На Рис. 2.1 б показана вольт-амперная характеристика идеального источника тока. Он сохраняет постоянство тока вне зависимости от напряжения на своих выводах.
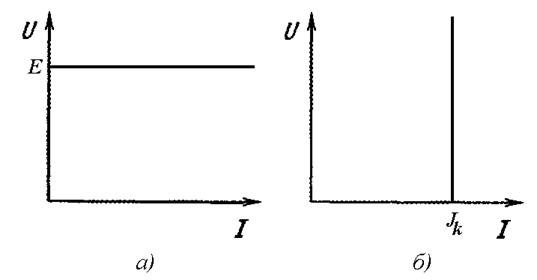
Рис. 2.1
Если к данным вольт-амперным характеристикам применить закон Ома (см. формулу (1.1))
 ,
,
можно сделать вывод, что сопротивление идеального источника ЭДС равно нулю, а сопротивление идеального источника тока равно бесконечности.
Реальный источник электрической энергии обладает конечным внутренним сопротивлением, его вольт-амперная характеристика показана на Рис. 2.2 и может быть описана выражением:
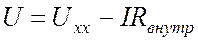 (2.1)
(2.1)
где  –
внутреннее сопротивление источника;
–
внутреннее сопротивление источника;
 – напряжение холостого хода
источника.
– напряжение холостого хода
источника.

Рис. 2.2
Когда источник
отключен от нагрузки, на его зажимах существует напряжение холостого хода  , равное ЭДС источника. Если
соединить накоротко зажимы источника, напряжение на зажимах будет равно нулю, а
ток между зажимами будет равен току короткого замыкания
, равное ЭДС источника. Если
соединить накоротко зажимы источника, напряжение на зажимах будет равно нулю, а
ток между зажимами будет равен току короткого замыкания 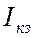 .
.
Сравнивая вольт-амперные характеристики идеальных источников и реального источника, можно заключить, что реальный источник можно смоделировать либо с помощью эквивалентного идеального источника ЭДС и последовательно включенного внутреннего сопротивления, либо с помощью эквивалентного идеального источника тока и параллельно включенного внутреннего сопротивления (Рис. 2.3).
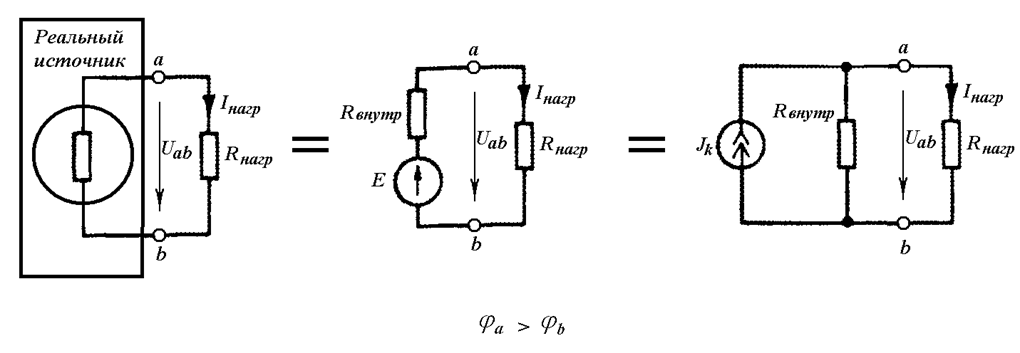
Рис. 2.3
Внутреннее сопротивление реального источника вычисляется как
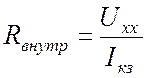 .
.
ЭДС эквивалентного источника ЭДС равна напряжению холостого хода реального источника.
Ток эквивалентного источника тока равен току короткого замыкания реального источника.
ЭДС эквивалентного источника ЭДС и ток эквивалентного источника тока связаны соотношением:
 (2.2)
(2.2)
Это соотношение говорит о том, что любой источник ЭДС с последовательно включенным сопротивлением может быть заменен источником тока с параллельно включенным таким же сопротивлением и наоборот.
Какой из двух эквивалентных замен воспользоваться, совершенно безразлично, и определяется лишь удобством расчета в каждом конкретном случае.
Заметим, что ЭДС идеального источника ЭДС всегда направлена от меньшего потенциала к большему, а ток идеального источника тока всегда направлен в ту же сторону, что и ток реального источника.
3. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ ЦЕПИ
Для упрощения расчетов электрическую цепь можно преобразовывать, уменьшая количество ветвей и узлов. При этом необходимо помнить, что после расчета преобразованной цепи следует выполнить обратное преобразование, чтобы вернуться к исходной цепи.
Любые преобразования цепей должны быть эквивалентными, то есть преобразование какого-либо участка цепи не должно изменять токораспределения в непреобразованной части схемы. А это возможно лишь тогда, когда в процессе преобразования потенциалы узлов в непреобразованной части схемы и токи, подтекающие извне к преобразованному участку, сохраняются неизменными.
Простейшими преобразованиями электрической цепи являются свертки последовательно-параллельных соединений элементов цепи.
При последовательном соединении элементов конец предыдущего соединяется с началом последующего (Рис. 3.1). Главный признак последовательного соединения – один и тот же ток в каждом из элементов.
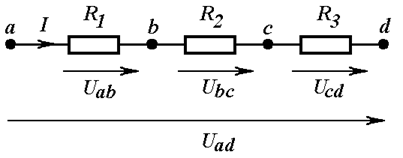
Рис. 3.1
Если к последовательному соединению элементов применить закон Ома (1.1), можно заключить, что напряжения на элементах распределяются прямо пропорционально сопротивлениям, а общее сопротивление последовательного соединения равно сумме сопротивлений элементов:
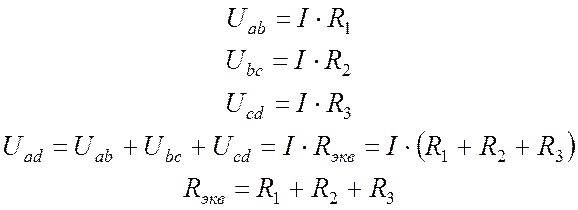 (3.1)
(3.1)
Итак, если на участке цепи несколько элементов соединены последовательно, они могут быть заменены одним эквивалентным элементом, сопротивление которого равно сумме сопротивлений отдельных элементов. ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ СОПРОТИВЛЕНИЯ СКЛАДЫВАЮТСЯ!
При параллельном соединении элементов начала всех элементов соединены в один узел, а концы всех элементов соединены в другой узел (Рис. 3.2).
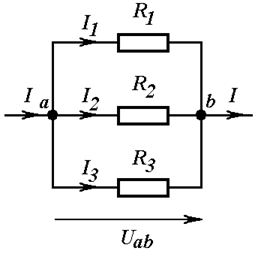
Рис. 3.2
Главный признак параллельного соединения – одно и то же напряжение на каждом из элементов.
Если на участке цепи несколько элементов соединены параллельно, они могут быть заменены одним эквивалентным элементом, проводимость которого равна сумме проводимостей отдельных элементов. ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ СКЛАДЫВАЮТСЯ ПРОВОДИМОСТИ!
 (3.2)
(3.2)


 амена
треугольника сопротивлений эквивалентной
звездой и наоборот.
амена
треугольника сопротивлений эквивалентной
звездой и наоборот.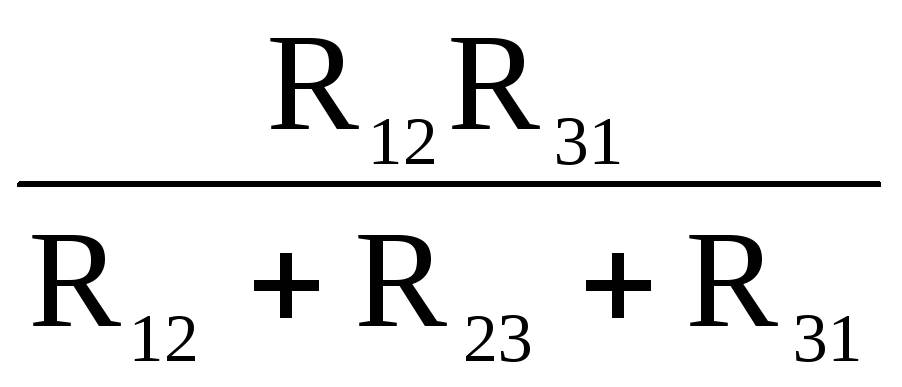 ;
;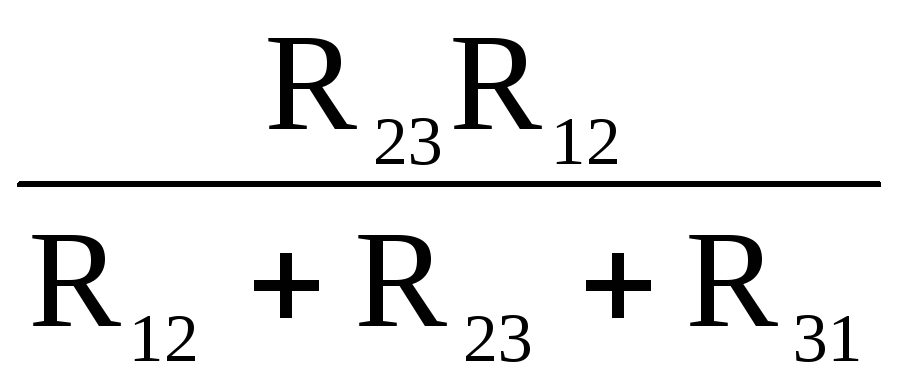 ;
; .
. ;
;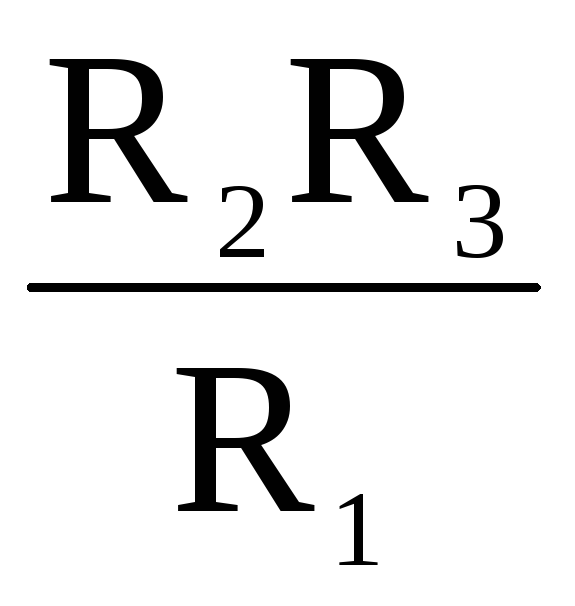 ;
;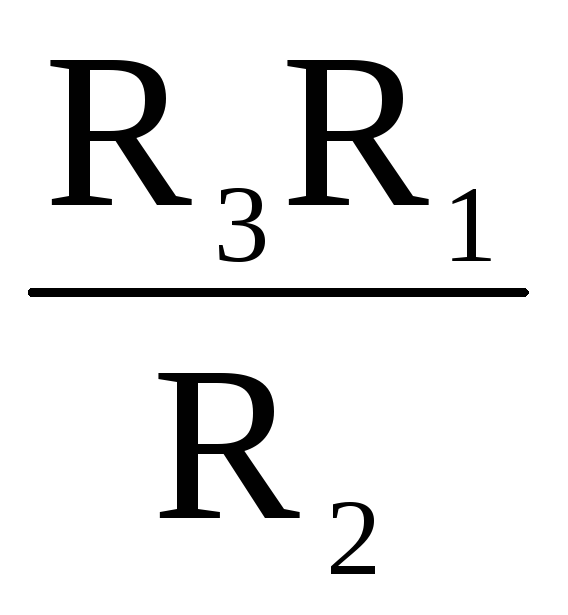 .
.