Как выразить векторы через другие векторы: Выразить вектор через векторы базиса. — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Часть I. Аналитическая геометрия

Глава 1. Векторы

§1. Сложение векторов и умножение на число

Напомним, что сумма двух векторов может быть найдена: а) по правилу треугольника; б) по правилу параллелограмма (см. рис. 1).

Рис.1.

Если векторы иколлинеарны (записывается это так:), то “работает” только первое правило. Кроме того, для любых точекплоскости или пространства имеет местоправило трёх точек: (см. рис. 2).

Рис.2.

Понятно, что равенства такого вида можно писать, даже не делая чертежа: и т.д. Если нам надо разложить какой-либо вектор (например,) в сумму, то можно попробовать разные варианты:и т.д.

Решим в качестве иллюстрации несколько задач.

Задача 1. Дан правильный шестиугольник Точка– середина стороныВыразить векторчерез векторы

Решение (см.

рис.3). Известно, что правильный шестиугольник разбивается диагоналями на 6 правильных треугольников.

Рис.3.

Поэтому Используя правило трёх точек, получим:

Задача 2. В параллелепипеде точка– центр граниВыразить векторчерез векторы

Решение (см. рис. 4).

Рис.4

Имеем:

В некоторых случаях для того, чтобы выразить какой-либо вектор через другие, приходится решать отдельно задачу из элементарной геометрии или систему уравнений. Рассмотрим несколько примеров.

Задача 3.

В окружности с центром проведены радиусыиРадиусделит уголпополам. Зная, чтоинайти вектор

Решение (см. рис. 5).

Рис.5.

Пусть – середина отрезкаТогдаТак как векторыимеют одинаковую длину, а векторобразует с ними одинаковые углы, топри некоторомОчевидно,Следовательно,Отсюда получаем:Таким образом,

Задача 4.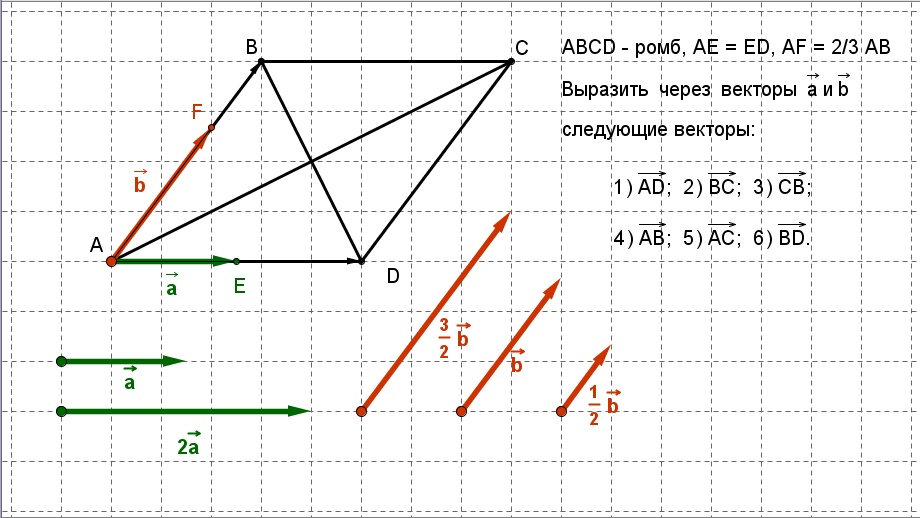 В параллелограмме и– середины сторонисоответственно. Выразить векторчерез векторы

Решение (см. рис 6).

Рис.6.

Введём векторы иВекторыиможно выразить черезии аналогичноНа эти равенства можно смотреть как на систему уравнений

Решим эту систему. Имеем: откуда получаем:т.е.ОтсюдаТаким образом,

Задача 5. В треугольнике – биссектриса углаВыразить векторчерез векторыи длины этих векторов.

Решение (см. рис. 7). По свойству биссектрисы имеем:

Рис.7.

Следовательно, Отсюда получаем:

Задача 6. Пусть – точка пересечения медиан треугольникаВычислить сумму

Решение (см. рис. 8).

Рис.8.

Пусть – середины сторонсоответственно. Продлим отрезокза точкуна величину, равнуюМы получим отрезокТак как диагонали четырёхугольникаточкой пересеченияделятся пополам, то этот четырёхугольник является параллелограммом. Следовательно, по правилу параллелограммаДалее, по свойству медианпоэтомуа значит,Теперь можно вычислить требуемую сумму:

Покажем, как с помощью векторов можно доказывать утверждения. Напомним, что пространственным четырёхугольником называется четырёхугольник, вершины которого могут не лежать в одной плоскости.

Задача 7. Доказать, что отрезки, соединяющие середины противоположных сторон пространственного четырёхугольника, а также отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся этой точкой пополам.

Решение (см. рис. 9).

Рис.9.

Пусть – середины сторонсоответственно. Обозначим черезисередины диагоналейисоответственно. Требуется доказать, что середины отрезковисовпадают. Пусть– середина отрезкаа– произвольная точка пространства. Тогда получаем:

Рассуждая аналогично, получим, что если – середина отрезкатоТаким образом,откуда следует, что точкиисовпадают. Обозначим черезсередину отрезкаИмеем:

Теперь ясно, что

Учебные материалы по математике | Разложение вектора по базису

4. – скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны или хотя бы один из них равен нулю.

5. – скалярный множитель можно выносить за знак скалярного произведения.

е) Разложение вектора по базису – это представление одного вектора через другие, называемые базисными.

Под базисом на плоскости подразумевается два неколлинеарных вектора плоскости, взятых в определенном порядке. Под базисом в пространстве понимается три некомпланарных вектора, взятых в определенном порядке.

Если на плоскости выбраны два базисных вектора и , то любой вектор плоскости может быть представлен в виде:

Аналогично в пространстве: если базисными будут векторы , то любой вектор пространства выражается так: . Если на плоскости или в пространстве выбрана прямоугольная декартовая система координат, в которой базисные векторы попарно перпендикулярны, то любой вектор можно записать так: или , где – единичные векторы соответствующих осей координат.

Пример 17. По сторонам ОА и ОВ прямоугольника ОАСВ отложены единичные векторы . Выразить через них векторы если длина .

Решение: Рассмотрим рис. 8 и найдем векторы:

Рис. 8

Пример 18. В равнобедренной трапеции ОАСВ угол ; M и N – середины сторон ВС и АС. Выразить векторы и через и — единичные векторы (рис. 9).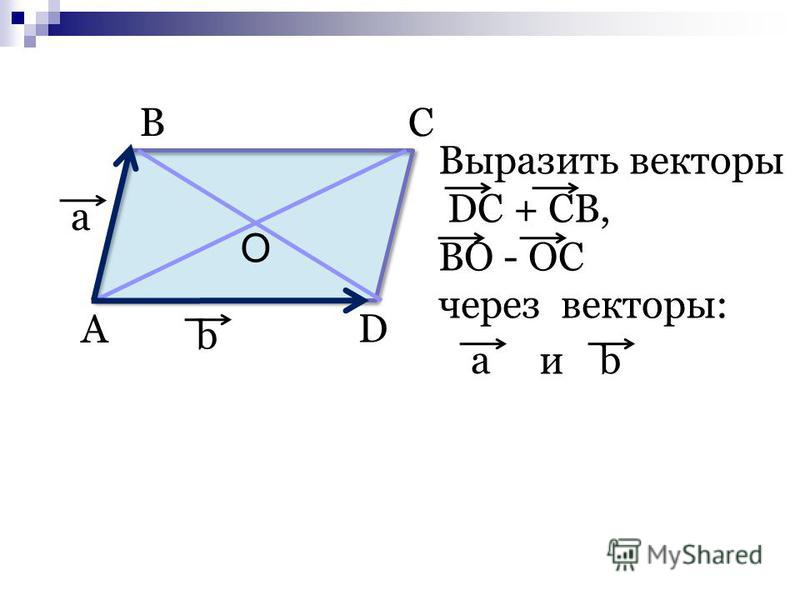

Рис. 9

Решение.

; ;

Пример 19. Три вектора расположены в одной плоскости. Известно, что векторы и составляют с вектором углы в 600. Определить угол между векторами и и длину вектора .

Решение. Векторы и могут находиться по одну сторону от , (тогда угол между ними равен ) и по разные стороны (тогда между ними угол в ):

Рис. 10

Рис. 11

Соответственно длина вектора для каждого случая будет своя:

а)

, .

б)

, .

Наташа

Автор

Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.

Выражение вектора в компонентной форме

Все ресурсы для предварительного исчисления

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Precalculus Help » Матрицы и векторы » Алгебраические векторы и параметрические уравнения » Выразите вектор в компонентной форме

Выразите следующий вектор в компонентной форме:

Возможные ответы: 9
Правильный ответ:
Объяснение:
При разделении вектора на составляющие его формы мы, по сути, создаем прямоугольный треугольник с вектором, являющимся гипотенузой.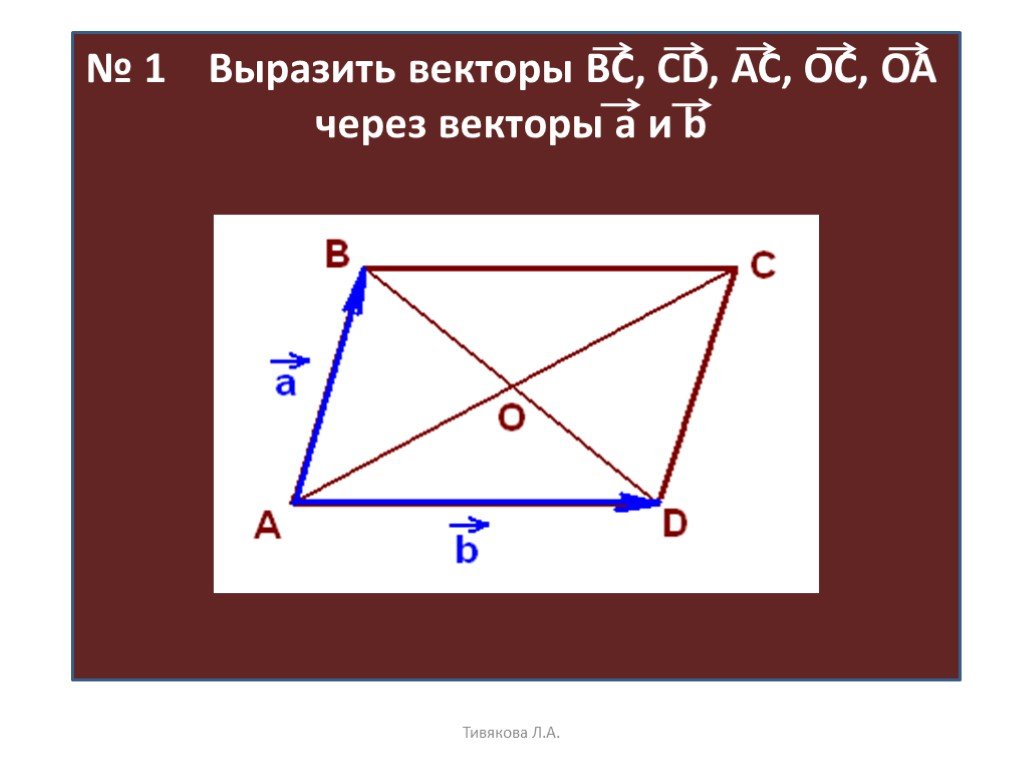
Следовательно, мы можем найти каждый компонент, используя функции cos (для компонента x) и sin (для компонента y):
Теперь мы можем представить эти два компонента вместе, используя обозначения i (для компонента x) и j (для компонента y).
Сообщить об ошибке
Найдите , затем найдите его величину. и оба являются векторами.
Возможные ответы:
Правильный ответ:
Объяснение:
При сложении векторов вы просто добавляете каждый компонент вектора друг к другу.
x компонент: .
компонент y: .
z компонент: .
Новый вектор:
.
Чтобы найти модуль, мы используем формулу
Таким образом, его модуль равен 5.
Сообщить об ошибке 004 начальная точка
и
конечная точка .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор в компонентной форме, зная начальную и конечную точки, просто вычтите начальную точку из конечной точки.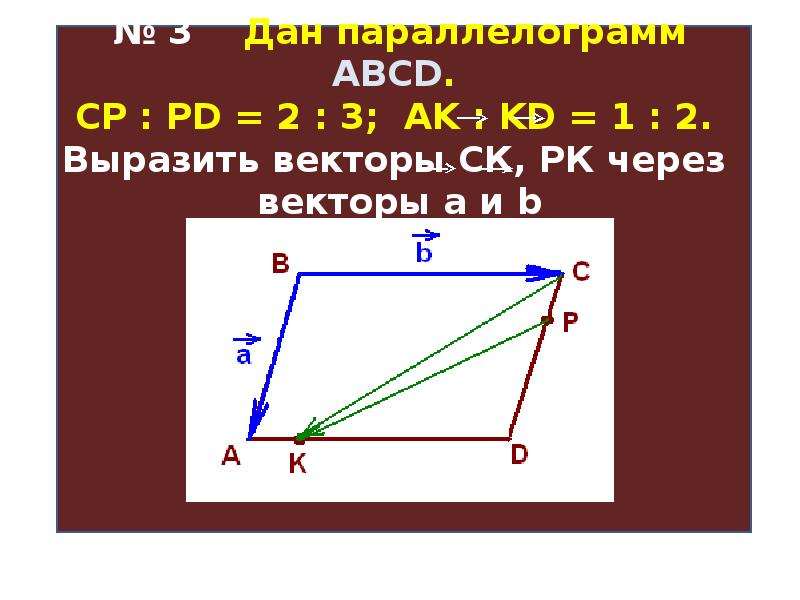
Сообщить об ошибке. 005 Правильный ответ:
Объяснение:
Чтобы найти вектор в компонентной форме с учетом начальной и конечной точек, просто вычтите начальную точку из конечной точки.
Сообщить об ошибке
Птица летит со скоростью 15 миль в час под углом 45 градусов к горизонтали. Какова скорость птицы в компонентной форме?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу для нахождения компонентов x и y вектора.
Подставьте значения скорости и тета в уравнения.
Вектор:

Сообщить об ошибке 3 Правильный ответ:

Объяснение:

Чтобы найти горизонтальную составляющую, составим уравнение, включающее косинус с 7 в качестве гипотенузы, поскольку сторона в подразумеваемом треугольнике, представляющая горизонтальную составляющую, примыкает к углу в 22 градуса:

Сначала найдите косинус числа 22, а затем умножьте на 7

Чтобы найти вертикальную составляющую, составьте уравнение, включающее синус, поскольку сторона в подразумеваемом треугольнике, представляющая вертикальную составляющую, противоположна углу в 22 градуса. :

Сначала найдите синус 22, затем умножьте на 7

Мы почти закончили, но нам нужно сделать небольшую корректировку. На рисунке показано, что вектор направлен вверх и влево, поэтому горизонтальная составляющая 6,49., должно быть отрицательным:

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы Precalculus

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Как определить, является ли вектор линейной комбинацией других векторов

Идея линейной комбинации векторов очень важна для изучения линейной алгебры. Мы можем использовать линейные комбинации для понимания остовных множеств, пространства столбцов матрицы и многих других тем. Одним из самых полезных навыков при работе с линейными комбинациями является определение того, когда один вектор является линейной комбинацией заданного набора векторов. n\) для некоторого \(n\), то на этот вопрос можно ответить, используя эквивалентную расширенную матрицу:

\(\left[ \begin{array}{ccc|c} \vec{a}_1 & \vec{a}_2 & \vec{a}_3 & \vec{v} \\ \end{array} \right]\)

Если эта матрица представляет собой непротиворечивую систему уравнений, то мы можем сказать, что \(\vec{v}\) является линейной комбинацией других векторов.

Пример

Определить, является ли вектор \(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) линейной комбинацией векторов:
\(\begin{bmatrix} 2 \ \ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix}\), \(\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix}\), и \(\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)

Решение

Помните, что это означает, что мы хотим найти константы \(x_{1}\), \(x_{2}\), \(x_{3}\) и \(x_{4}\) такое, что:

\(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = x_{1}\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + x_{2}\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + x_{3}\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + x_ {4}\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)

Это векторное уравнение эквивалентно расширенной матрице. Составляя эту матрицу и уменьшая количество строк, мы находим, что:

\(\left[ \begin{array}{cccc|c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \\
\end{array} \right]
\)

Эквивалентно:

\(\left[ \begin{array}{cccc|c} 1 & 0 & 0 & -\frac{103} {29} & -\frac{74}{29} \\
0 & 1 & 0 & \frac{42}{29} & \frac{13}{29} \\
0 & 0 & 1 & \frac {6}{29} & \frac{35}{29} \\
\end{массив}\right]\)

Хотя это и некрасиво, эта матрица НЕ содержит такой строки, как \(\begin{bmatrix} 0 & 0 & 0 & 0 & c \\ \end{bmatrix}\), где \(c \neq 0 \), что указывало бы на то, что базовая система несовместима. Следовательно, основная система непротиворечива (имеет решение), что означает, что векторное уравнение также непротиворечиво.

Итак, мы можем сказать, что \(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) является линейной комбинацией других векторов.

Пошаговый процесс

В общем, если вы хотите определить, является ли вектор \(\vec{u}\) линейной комбинацией векторов \(\vec{v}_{1}\), \(\vec{v}_ {2}\), … , \(\vec{v}_{p}\) (для любого целого числа \(p > 2\)) вы сделаете следующее.

Шаг 1

Настройка расширенной матрицы

\(\left[ \begin{array}{cccc|c} \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v} _p & \vec{u} \\ \end{array} \right]\)

и уменьшить строку.

Шаг 2

Используйте сокращенную форму матрицы, чтобы определить, представляет ли расширенная матрица непротиворечивую систему уравнений. Если это так, то \(\vec{u}\) является линейной комбинацией остальных. В противном случае это не так.

На втором этапе важно помнить, что система уравнений непротиворечива, если существует одно решение ИЛИ много решений. Количество решений не важно, главное, чтобы было хотя бы одно решение. Это означает, что существует по крайней мере один способ записать данный вектор как линейную комбинацию других.

Запись вектора в виде линейной комбинации других векторов

Иногда вас могут попросить записать вектор в виде линейной комбинации других векторов. Это требует той же работы, что и выше, с еще одним шагом. Вам нужно использовать решение векторного уравнения, чтобы написать, как векторы комбинируются, чтобы создать новый вектор.

Давайте начнем с более простого случая, чем тот, который мы делали раньше, а затем вернемся к нему, так как он немного сложнее.