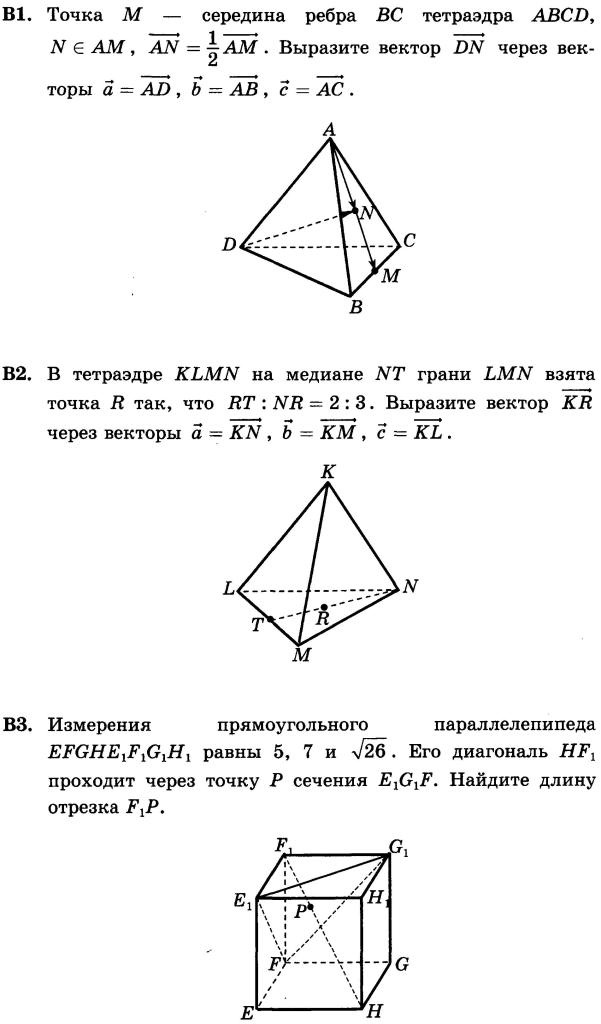
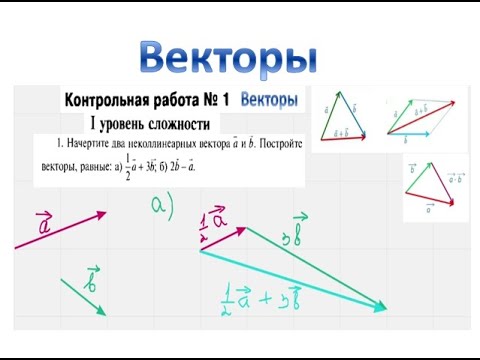
Как выразить вектор через векторы

Как выражать векторы через другие векторы?

Пробывал выразить через сумму/разность векторов AB и AD, вектор OP, но безрезультатно.

Как вариант решения:

Точка P распологается на векторе AD, следовательно:
AD = AP + PD.

Вектор BC равен вектору AD, как сторона параллелогамма, отсюда:
AD = CO + OB

Вектор AB = CD как сторона параллелограмма.

Вектор OP исходя из этого может быть выражен через сумму векторов:
OP = PD + DC + CO

Как выразить вектор

да, квадрат, который представляет собой трапецию — это сильно.

такие задачи решаются довольно просто: надо пройти из начала вектора в его конец по векторам, которые известны.

при этом векторы, соответствующие сонаправленным отрезкам одинаковой длины, считаются равными. например, SM = MR, TN = NU.
и если на пути встретился вектор, который придётся пройти «против шерсти», его надо взять с минусом.

получаем:
RS = RM + MS = -2 MR = -2a
ST = SM + MT = a + b
TN = TM + MN = -MT + MN = -b + c
RU = RM + MN + NU = -MR + MN + NU = -a + c + (-b + c) = -a -b + 2c
US = UR + RS = -RU + RS = -(-a -b + 2c) + (-2a) = a + b — 2c — 2a = -a + b — 2c

Большая теория по векторам

И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь (\(L\)).

А некоторые имеют и число, и направление — например, перемещение (\(\vec\)).

И сейчас ты узнаешь, почему это настолько важно.

Векторы — коротко о главном

Решать задачи с векторами — легко!

Векторы и… Колумб

В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.

Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.

Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?

О направлении

Направление – одна из важнейших характеристик движения.

Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.

Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.

Так вот, «просто числа» — это скалярные величины (их также называют скалярами).

А «числа с направлением» — это векторные величины (их иногда называют векторы).

В физике существует множество скалярных и векторных величин.

Что такое скалярная величина?

Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)

Это, например, время, длина, масса, температура (продолжи сам!)

Что такое векторная величина?

Векторная величина – это величина, которая определяется и значением, и направлением.

В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.

Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):

Как обозначаются векторы?

Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: \(\vec\)

Значение вектора – это модуль вектора, то есть его длина.

Обозначить это можно двумя способами: \(\left| > \right|\) или \(S\)

Операции над векторами

Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.

Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!

Умножение вектора на число

Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.

(Если направление противоположно, обозначаем так: \(\vec\uparrow \downarrow \vec\))

Рассмотрим на примере, используя клетку для точности построений:

Если вектор умножить на ноль, он станет нулевым.

Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:

Рассмотрим некоторые свойства нулевого вектора.

Если он нулевой, то его длина равна нулю! Логично, не правда ли?

А это значит, что его начало совпадает с концом, это просто какая-то точка.

Нулевой вектор – вектор, начало которого совпадает с концом.

Нулевой вектор принято считать сонаправленным любому вектору.

Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:

А если к любому вектору прибавит нулевой, ничего не изменится:

Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.

Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.

Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.

Две прямые параллельны: \(q\parallel p\)

Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:

Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:

Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:

\(\vec\uparrow \downarrow \vec\)

Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.

Параллельный перенос векторов

Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.

Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство – параллельный перенос.

Сложение векторов по правилу треугольника

Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:

Наша цель – найти такой вектор, который будет являться суммой двух данных:

Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:

Теперь достроим до треугольника.

Но как узнать направление нужного нам вектора?

Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:

Это называется правилом треугольника.

Больше двух слагаемых векторов. Сложение по правилу многоугольника

Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?

Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:

Это называется правилом многоугольника.

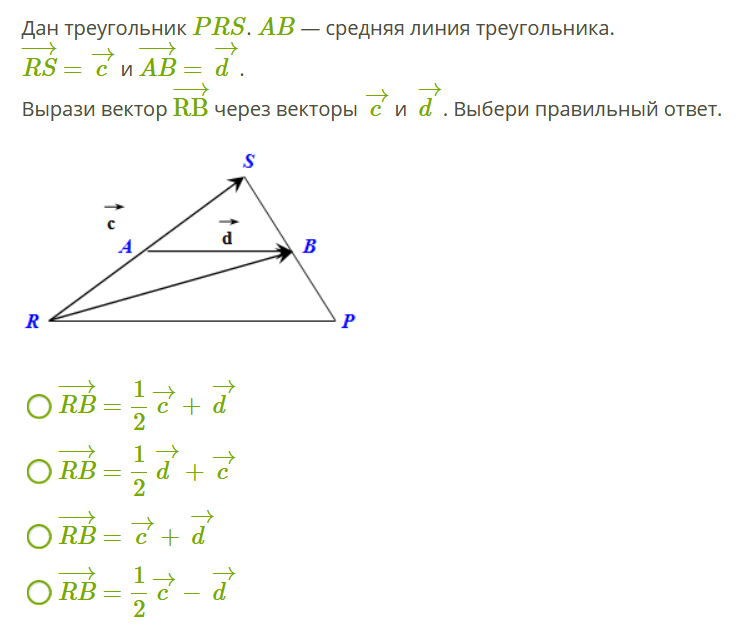
Вычитание векторов через сложение

Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:

Тогда нам лишь остается найти сумму с обратным вектором:

А сделать это очень легко по правилу треугольника:

Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.

Вычитание векторов через треугольник

Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.

Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:

Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.

Универсальное правило параллелограмма

Есть еще один способ сложения и вычитания векторов.

Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.

Ничего не напоминает?

Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.

В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:

Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:

Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.

Скалярное произведение векторов

Еще одной важной операцией является произведение векторов. Рассмотрим скалярное произведение. Его результатом является скаляр.

Уравнение очень простое: произведение длин этих векторов на косинус угла между ними.

Векторное произведение векторов

Векторное произведение векторов пригодится нам в электродинамике.

Его формула лишь немного отличается от предыдущей:

В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!

После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:

Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.

Об этом мы поговорим подробнее, когда будем изучать электродинамику.

Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.

Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.

Проекции векторов

Что такое проекция вектора и с чем ее едят?

Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.

Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.

Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.

Проекция вектора – словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.

Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.

Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.

Именно поэтому необходимо научиться работать с проекциями и осями.

Построение проекции. Определение знака

Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.

Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х₀) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.

Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, – большое заблуждение.

Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:

Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.

В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:

Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:

Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:

Пример на конкретных числах:

Рассмотрим еще один интересный случай.

Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!

Анализ углов

Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!

Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось.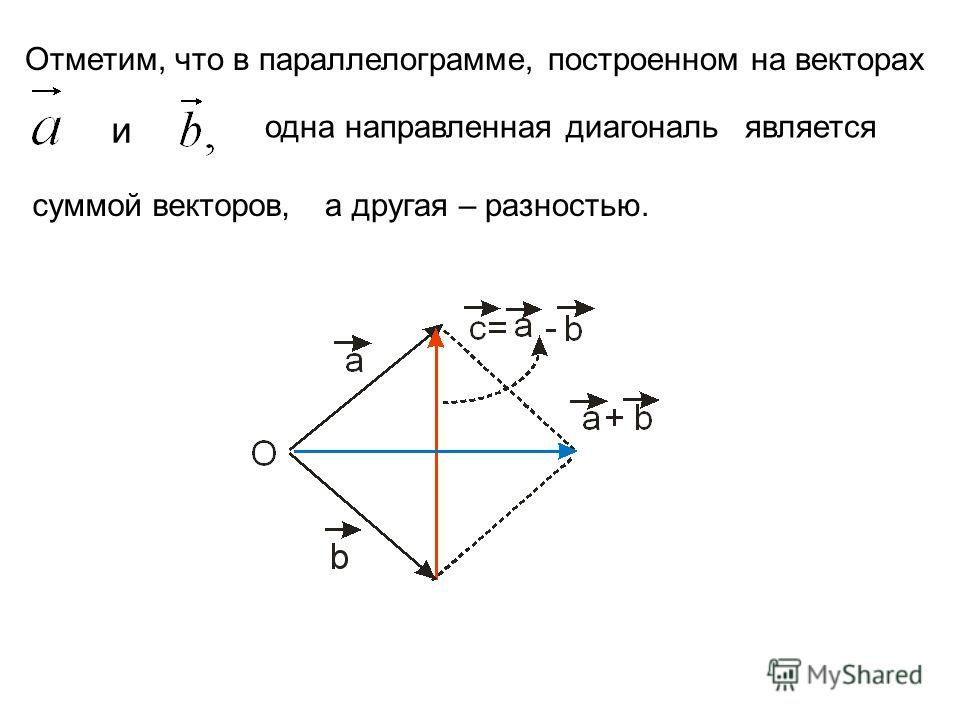 Получим угол между вектором и осью.

Если угол острый, проекция положительна:

Если угол тупой, проекция отрицательна:

Если угол прямой, она равна нулю:

Обрати особое внимание на то, какой именно угол является углом между вектором и осью!

Частные случаи проекции

Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.

Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180 О ). Это зависит от направления.

При этом длина проекции совпадает с длиной вектора! Смотри!

Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:

Если вектор направлен в другую сторону, проекция отрицательна:

Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.

Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.

Что? Почему раньше не сказал? А… Ну…

Хватит вопросов! Вот тебе пример:

\(\vec\) направлен противоположно оси. Его проекция отрицательна.

Еще один частный случай – работа с обратными векторами.

Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:

Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.

Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.

Прямоугольные треугольники равны по углу и гипотенузе.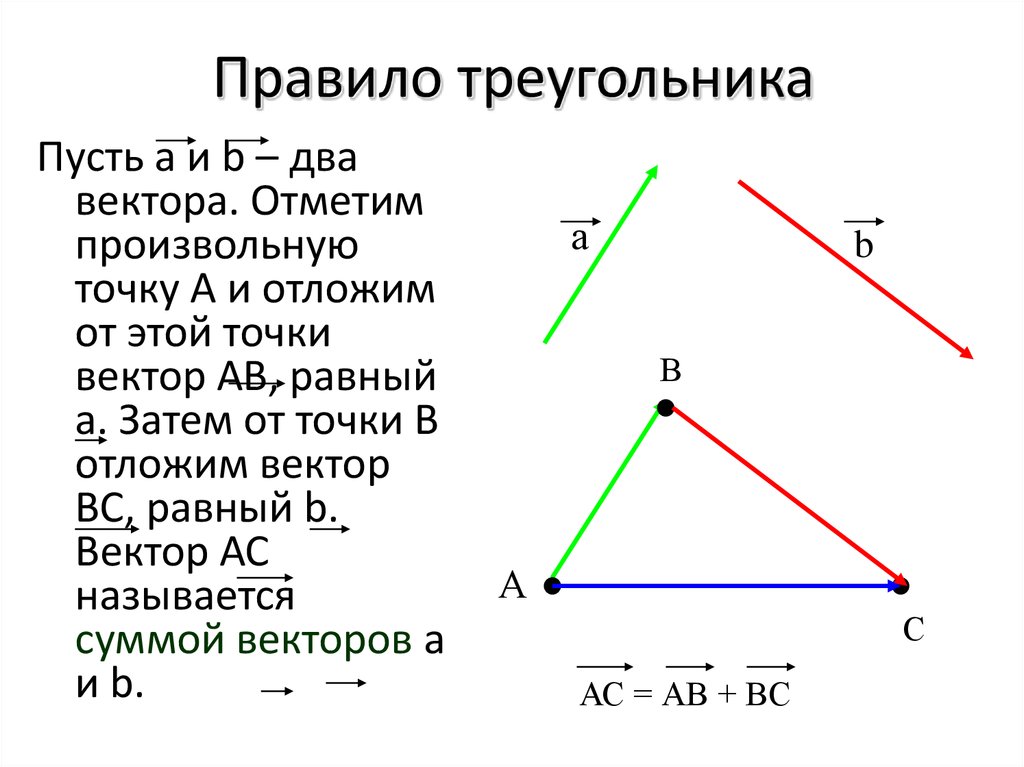 Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:

Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:

Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.

Проекции обратных векторов равны по модулю и противоположны по знаку.

Давайте еще раз уточним.

Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).

Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.

Проекция вектора бывает отрицательной. Это зависит от направления вектора.

Способы нахождения проекций и векторов с помощью тригонометрии

Зная угол между вектором и осью, можно не прибегать к координатам.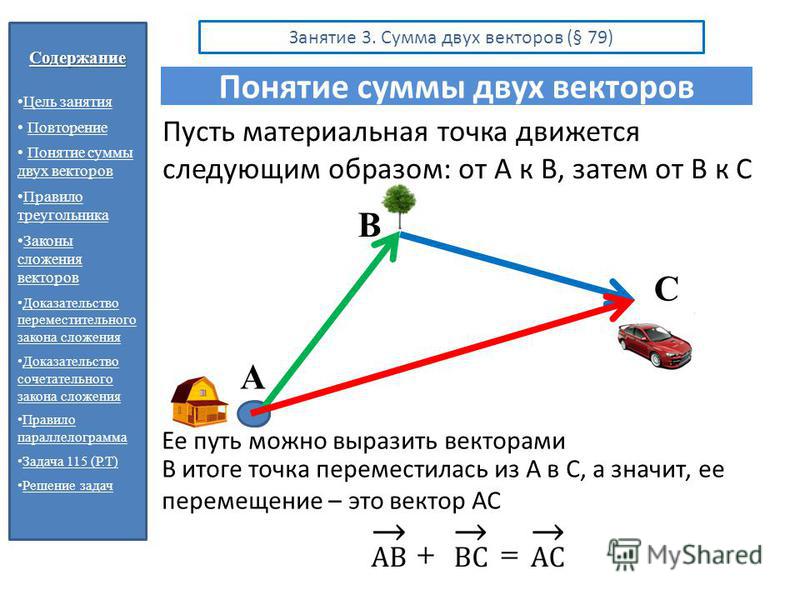 Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.

Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.

Рассмотрим вектор и его проекции на оси:

Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:

Тогда обозначим прямой угол и угол между вектором и осью:

Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.

Из этих уравнений легко выражаются проекции.

А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:

Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.

Действия над проекциями векторов. Решение задач

Умение применять свои знания на практике невероятно важны. Это касается не только физики.

Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.

Сложение проекций. Доказательство главного свойства

Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:

Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:

Давай посчитаем проекции векторов и проекцию вектора их суммы:

Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!

Намного важнее уметь доказывать гипотезы в общем виде.

Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!

Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:

Затем запишем, чему равна сумма этих векторов.

Мы доказали нашу гипотезу.

Но что насчет разности?

Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!

Проекция суммы векторов равна сумме проекций векторов.

Проекция разности векторов равна разности проекций векторов.

Или можно записать так:

Простейшие задачи на нахождение проекций

Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.

Давай научимся с ними работать.

Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.

Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.

В первом случае вектор направлен против оси Х.

Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.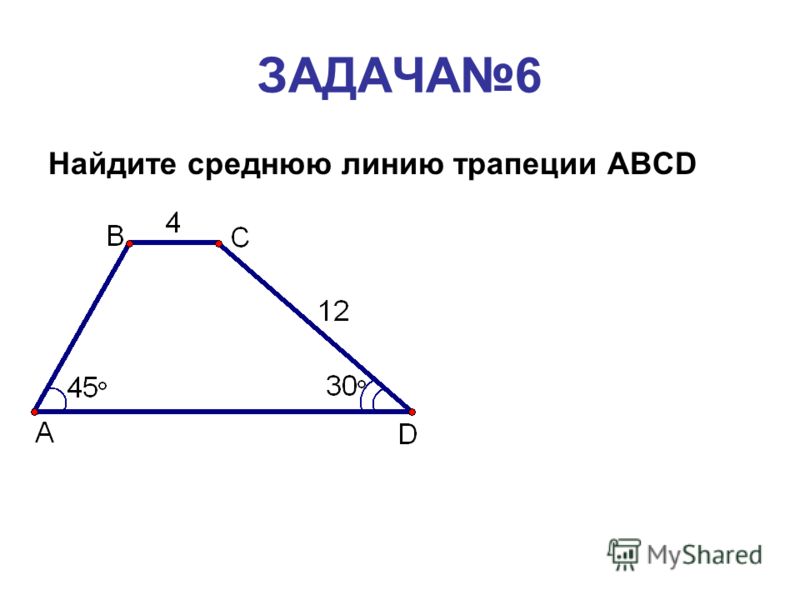

Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!

Рассмотрим второй вектор.

Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.

Убедимся в этом.

На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:

Рассмотрим \(\vec\). Заметим, что он является обратным для \(\vec\): их длины равны, а направления противоположны.

Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:

Поступаем с \(\vec\) так же, как поступали с первым вектором.

Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.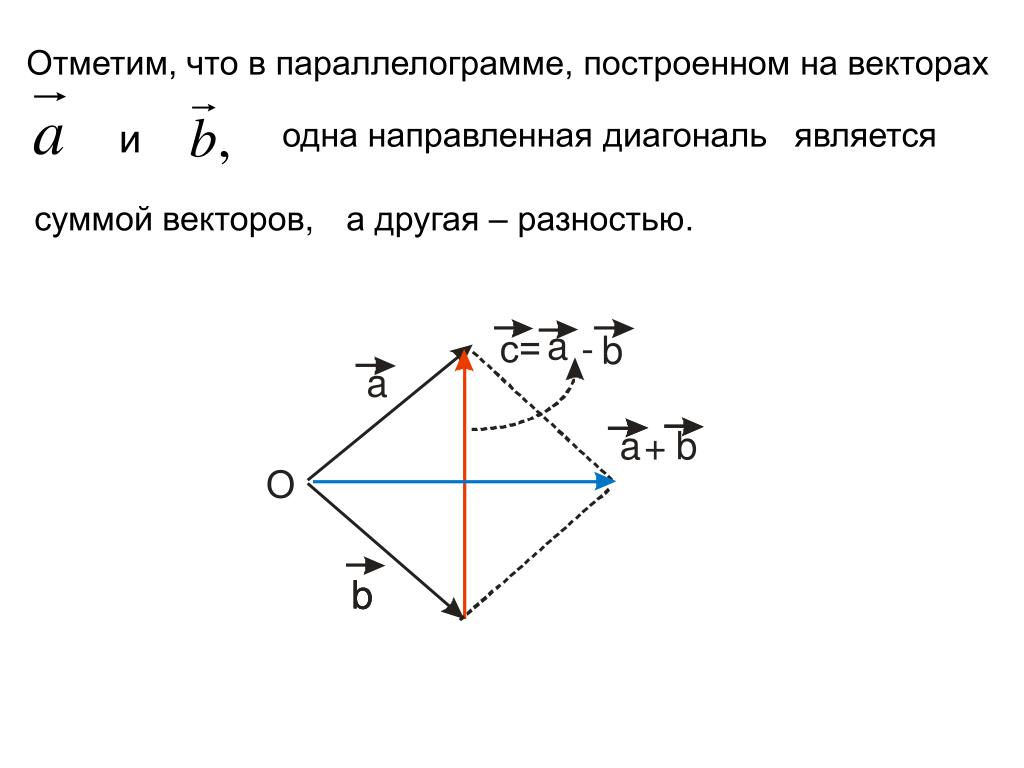

Проведя перпендикуляры, считаем проекцию на ось Y:

С \(\vec\) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:

Задачи на нахождение вектора и его угла с осью

С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.

Давай попробуем это сделать.

Даны проекции вектора на две оси. Для начала нарисуем оси:

Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.

С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?

Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.

Проекция на ось Y положительна.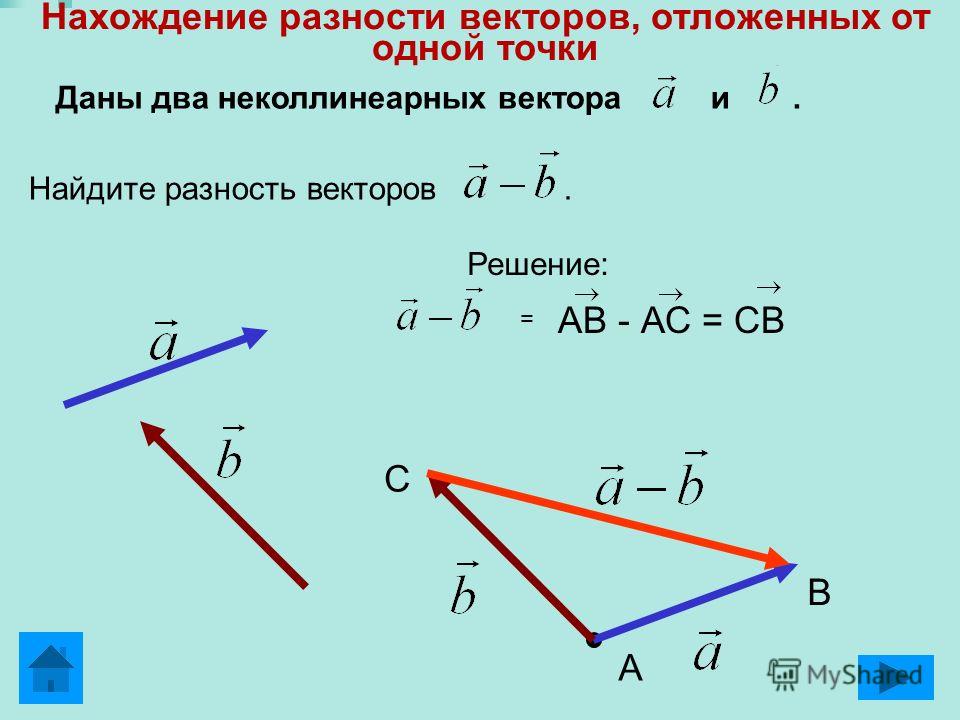 Вектор смотрит в ту же сторону, что и ось.

Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:

Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:

Обозначим угол \(\alpha \), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?

Рассмотрим смежный ему угол \(\beta \). Его найти гораздо проще, а в сумме они дадут 180 градусов.

Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла \(\beta \) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.

Вычитанием угла \(\beta \) из 180 градусов найдем угол \(\alpha \):

Главный метод работы с осями и проекциями в решении физических задач

В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.

Поэтому важно научиться искать проекции вектора и связывать их с ней.

Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):

Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.

Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.

Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.

Сделаем это для данного рисунка:

Мы видим, что остальные векторы расположены к осям под каким-то углом.

Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:

Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:

Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.

Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:

Переходим к векторам, которые расположены под углом.

Выглядит страшно, но это не так!

Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.

Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).

Обозначим, что является проекцией. Это катет:

Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.

Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.

Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…

Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Заключение

Итак, теперь мы знаем о векторах очень много! Мы выяснили, зачем они нужны и как с ними работать, а еще разобрали их роль в решении различных задач. Теперь векторы — наша прочная опора.

Именно из таких знаний складывается порой нечто более сложное и комплексное, что-то, что безусловно нам однажды поможет.

Применение векторов к решению задач (продолжение) 8 класс онлайн-подготовка на Ростелеком Лицей

Теорема о двух неколлинеарных векторах

 

В предыдущих уроках мы неоднократно решали следующую задачу: даны два неколлинеарных вектора, через которые в многоугольнике нужно выразить некоторые другие векторы. Выполним обобщение такого типа задач.

 

Теорема

Заданы векторы  и . Векторы неколлинеарны. Доказать, что любой третий вектор  однозначно выражается через векторы  и , то есть найдутся такие числа х и у, что: .

Если данная теорема будет доказана, то в некотором смысле можно сказать, что, зная два неколлинеарных вектора, мы владеем всеми остальными векторами на плоскости.

Доказательство:

Из точки С, конца вектора , проведем прямые, параллельные векторам  и . Получим точки А, В – пересечения построенных прямых с продолжениями векторов. Концы векторов обозначим за F и К соответственно (см. Рис. 1). Воспользуемся правилом треугольника и выразим вектор :

Вектор  коллинеарен вектору , так как они

Рис. 1

принадлежат одной прямой согласно построению. Отсюда найдется такое число х, которое в произведении с вектором  даст вектор : . С другой стороны, вектор  равен вектору  по построению, вектор  коллинеарен вектору , значит, аналогично сказанному ранее, .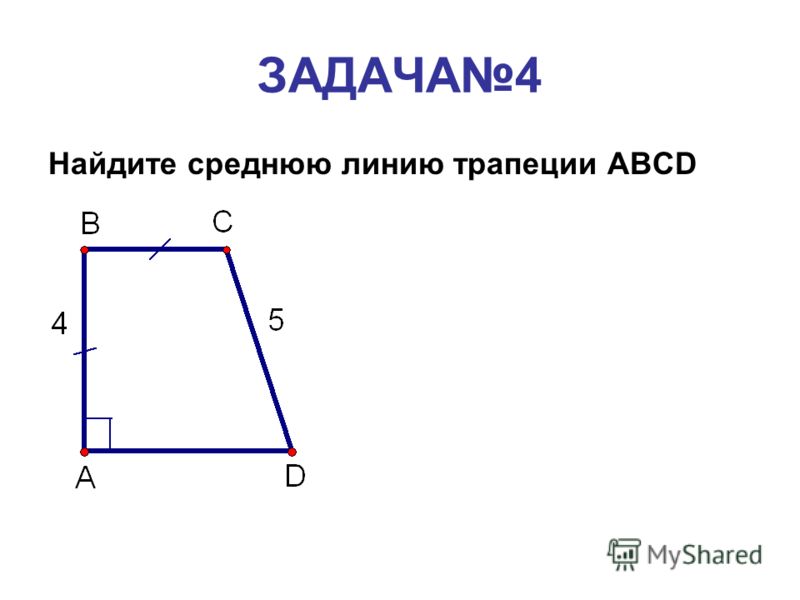

Таким образом, , то есть вектор  является линейной комбинацией неколлинеарных векторов  и . Кроме того, нашлась такая пара чисел х и у, с помощью которых любой вектор на плоскости можно выразить через два заданных неколлинеарных вектора.

Докажем, что такая пара единственная. Предположим противное: пусть существует такая пара чисел х₁ и у₁, что . Мы предположили, что есть еще одна линейная комбинация тех же двух неколлинеарных векторов для того же третьего вектора. Выполним вычитание полученных выражений:

Слева в выражении стоит нулевой вектор, справа – линейная комбинация двух неколлинеарных векторов, которые друг через друга не выражаются, таким образом, чтобы выполнялось равенство, коэффициенты при векторах в правой части должны быть нулевыми, то есть .

Вывод: разложение вектора  по двум неколлинеарным векторам однозначно.

 

Задача о трапеции

 

 

Пример 1 – задача 790: докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности (см.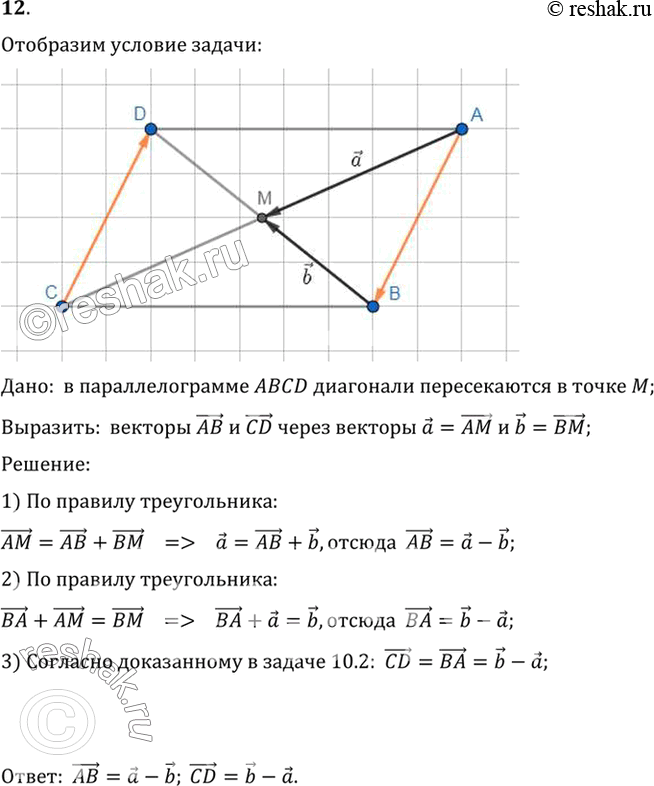 Рис. 2).

 

Доказать: ;  (при условии, что AD – большее основание, обозначим его за b, а ВС – меньшее основание, обозначим его за а).

Рис. 2

Доказательство:

Введем вектор . Выразим его через другие векторы, пользуясь правилом многоугольника. Напомним, что вектор , :

С другой стороны:

Выполним сложение полученных выражений:

Векторы  очевидно противоположны, и их сумма составляет нулевой вектор, аналогично и векторы  сокращаются. Получаем:

Поделим обе части выражения на два:

Из полученного равенства следует, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований. Кроме того, из равенства векторов в правой и левой частях следует, что они коллинеарны между собой, а также коллинеарны векторам  и , таким образом, отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям, что и требовалось доказать.

Обратим внимание, что несложно доказывается тот факт, что отрезок MN принадлежит средней линии трапеции, и данным фактом можно пользоваться при решении различных задач (см. Рис. 3).  Напомним, что отрезок средней линии ММ₁ – средняя линия треугольника , отсюда . Аналогично . Таким образом, можно найти длину отрезка, не пользуясь

Рис. 3

векторами, для этого следует вычесть из длины средней линии трапеции (она равна полусумме оснований) длины только что найденных отрезков:

Итак, мы рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.

 

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Terver.ru (Источник).
2. Cleverstudents.ru (Источник).

 

Домашнее задание

1. Задание 1: точки M и N – середины диагоналей АС и BD четырехугольника ABCD. Докажите, что

2. Задание 2: дан произвольный треугольник . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника

3. Задание 3: докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырехугольника, точкой пересечения делятся пополам.

 

Длина вектора — как найти? Формулы и примеры

Что такое векторы и какими они бывают

Как обычно, мы начнем с самого важного: с определения.

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Вектор обозначают знаком →, например . Как вы заметили, вектор можно выразить одной латинской буквой, а можно — сочетанием двух букв, которыми мы назовем точками начала и конца вектора.

Нулевой вектор — вектор, начало которого совпадает с его концом. Обозначается он так: .

Как вы уже знаете, векторы бывают коллинеарными и неколлинеарными, сонаправленными и противоположно направленными. Теперь давайте подумаем, что объединяет все виды векторов без исключения. Правильно, у всех есть длина! О том, что это такое, мы и поговорим дальше.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Длина вектора

Длиной или модулем вектора называется длина направленного отрезка, определяющего вектор.

Иногда в математике длину вектора называют модулем. Это легко запомнить, так как длина вектора обозначается с помощью знака | |. Например: . Альтернативное название длины вектора дает нам отличную подсказку: она не может быть отрицательной, в какую бы сторону вектор ни был направлен. А вот нулевой — пожалуйста!

Длина нулевого вектора всегда равна нулю.

Здесь вам может стать интересно, зачем нам нужно знать, как найти длину вектора, и это очень хороший вопрос. Причин может быть множество, но мы выделим несколько главных:

1. Чтобы определить равенство векторов, необходимо знать их длины. Векторы являются равными, если равны их длины, и сами векторы — сонаправленные.

2. Вычислив модуль вектора, мы можем рассчитать другие величины.

3. Например, в физике сила — это векторная величина, т. е. имеет направление. Если вычислить модуль силы, мы можем рассчитать массу тела, его ускорение и т. д.

4. В геометрии с помощью длины векторов мы можем определить угол между ними, их скалярное произведение.

Достаточно весомые аргументы для нахождения этой величины, правда? Самое время перейти от слов к делу: давайте научимся вычислять длину вектора через свои координаты!

Как можно найти длину вектора по его координатам

Используя прямоугольную систему координат, нарисуем вектор АВ (х, у) из точки (0; 0).

Тогда его можно будет считать радиус-вектором для векторов АВ₁ и АА₁.

Давайте обозначим длину вектора |АВ₁| = у, длину вектора |АА₁| = х. Треугольники АА₁В и АВ₁В являются прямоугольными, где АВ — гипотенуза. Теперь вспомните, как можно найти длину гипотенузы, зная длины катетов. Верно, через теорему Пифагора! Составим выражение для АВ:

Это значит, чтобы найти длину вектора нужно взять квадратный корень из суммы квадратов его координат. В общем виде эту формулу для длины вектора записывают так — длина вектора :

Если мы будем рассматривать векторы в трехмерном пространстве, формулу нахождения длины вектора можно рассчитать так:

Давайте разберемся, как работают эти формулы для нахождения длины вектора, на примерах. Вы можете решать задания самостоятельно, а потом свериться с нами: так будет еще эффективнее!

Пример № 1

Найдите модуль вектора .

Решение:

Ответ:

Пример № 2

Проведите вычисление длины вектора по его координатам {-2; 0; 5}.

Решение:

Ответ:

Пример № 3

Определите координату х вектора , если его координата по у равна 6, а длина вектора 10.

Решение:

,

,

,

.

,

,

,

.

Ответ: .

Уверены, что у вас все блестяще получилось!

Как найти длину вектора по двум точкам

Давайте подумаем, как решать задачи, если нам не даны координаты вектора. Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:

Пример № 4

Найти длину вектора , если В (4; 6), С (-2; 0).

Решение:

Ответ:

Как найти длину вектора по теореме косинусов

Пришло время разобраться, как длина вектора связана с теоремой косинусов. К сожалению, не во всех задачах дано нужное количество информации, чтобы определить длину вектора — тут-то нам и поможет теорема. Вспомним ее!

Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Итак, чтобы определить длину стороны треугольника, нужно сложить квадраты двух других сторон, вычесть удвоенное произведение длин сторон на косинус угла между ними и взять корень из полученного числа. Так мы получим формулу нахождения длины вектора через теорему косинусов.

Предположим, что нам необходимо узнать длину вектора или . Тогда, чтобы воспользоваться теоремой косинусов, нам нужно найти длину векторов и и угол между ними.

Пример № 5

Длины векторов и равны 5 и 12 соответственно, а угол между ними равен π/3. Проведите вычисление длины вектора .

Решение:

Ответ:

Сегодня мы обсудили с вами все основные моменты, которые касаются длины вектора: изучили теорию и дополнили ее базовыми задачами. Дело осталось за малым — выучить весь материал и практиковаться! В этом вам помогут курсы по профильной математике в школе Skysmart. Уникальная платформа, учителя-профессионалы, индивидуальная программа — уроки просто созданы для того, чтобы стать уверенными в математике. Ждем вас на занятиях и до новых встреч!

Базис векторного пространства

Пусть V будет подпространством R ⁿ для некоторого n . Коллекция B = { V ₁ , V ₂ ,…, V _R } векторов из V , как говорят, составляет базис. если B линейно независим и охватывает V . Если хотя бы один из этих критериев не выполняется, то коллекция не является основой для

В . Если набор векторов охватывает V , то он содержит столько векторов, что каждый вектор из V может быть записан как линейная комбинация векторов в наборе. Если набор линейно независим, то он не содержит столько векторов, чтобы одни становились зависимыми от других. Таким образом, интуитивно понятно, что базис имеет правильный размер: он достаточно велик, чтобы охватывать пространство, но не настолько велик, чтобы быть зависимым.

Пример 1 : Коллекция {

i, j } является базисом для R ² , поскольку он охватывает R ² , а векторы i и j линейно независимы (поскольку ни один из них не кратен другому). Это называется стандартной базой для R ² . Аналогично набор { i, j, k } называется стандартным базисом для R ³ и вообще

является стандартной основой для Р ^п .

Пример 2 : Набор { i, i+j , 2 j } не является основой для R ²

. Хотя он охватывает R ² , он не является линейно независимым. Никакая коллекция из 3 и более векторов из R ² не может быть независимой.

Пример 3 : Набор { i+j, j+k } не является основой для R ³ . Хотя он линейно независим, он не охватывает все Р ³ . Например, не существует линейной комбинации i + j и j + k , равной i + j + k .

Пример 4 : Набор { i + j, i − j

} является основой для R ² . Во-первых, оно линейно независимо, поскольку ни i + j , ни i − j не кратны другим. Во-вторых, он охватывает все R ² , потому что каждый вектор в R ² может быть выражено как линейная комбинация i + j и i − j . В частности, если A I + B J — любой вектор в R ² , тогда, если K ₁ = ½ ( A + B ) и K 988989898989898989818 гг. = ½( а — б ).

Пространство может иметь много разных оснований. Например, как { i, j }, так и { i + j, i − j } являются основаниями для Р ² . Фактически, любой набор , содержащий ровно два линейно независимых вектора из R ² , является основой для R ² . Точно так же любой набор, содержащий ровно три линейно независимых вектора из R ³ , является основой для R ³ и так далее. Хотя ни одно нетривиальное подпространство R ⁿ не имеет уникальной базы, есть нечто такое, что должно быть общим для всех баз данного пространства.

Пусть V будет подпространством R ⁿ для некоторого n . Если V имеет базис, содержащий ровно r векторов, то каждый базис для V содержит ровно r векторов. То есть выбор базисных векторов для данного пространства не уникален, но число базисных векторов является уникальным. Этот факт позволяет четко определить следующее понятие: число векторов в базисе векторного пространства V ⊆ R ⁿ называется размером из V , обозначается тусклый V .

Пример 5 : Поскольку стандартный базис для R ² , { i, j } содержит ровно 2 вектора, каждый базис для R ² содержит ровно 2 90 вектора, поэтому ² = 2. Аналогично, поскольку { i, j, k } является основой для R ³ , который содержит ровно 3 вектора, каждую основу для R ³ содержит ровно 3 вектора, поэтому DIM R ³ = 3. В целом, DIM R ^N = N для каждого натурального числа n .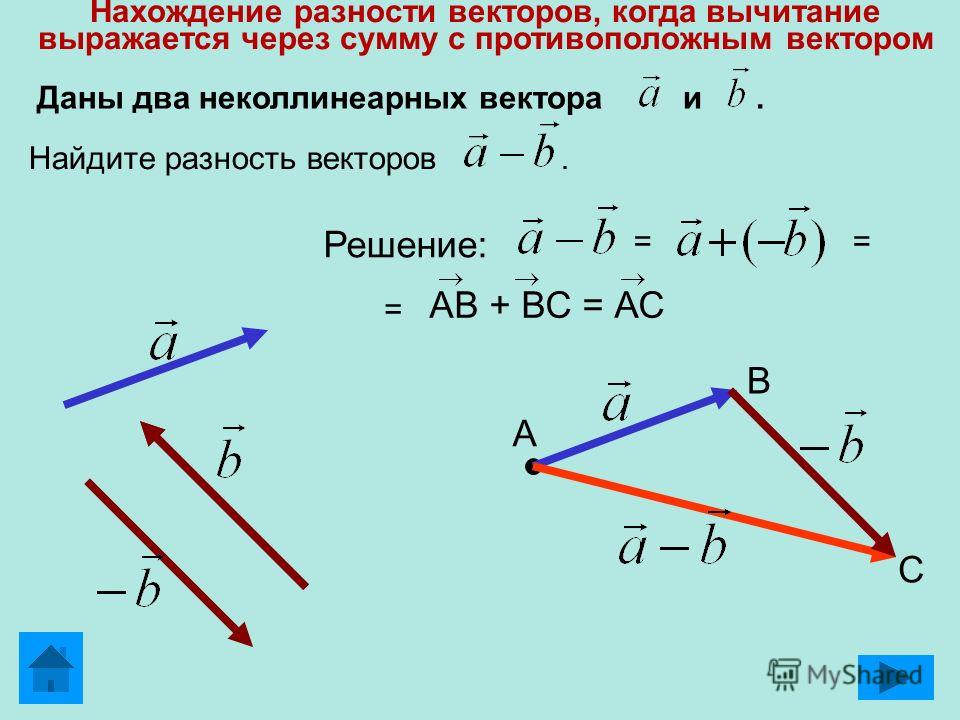

Пример 6 : В R ³ векторы i и k охватывают подпространство размерности 2. Это плоскость x−z , как показано на рисунке .

Рисунок 1

Пример 7: Одноэлементный набор { i + j = (1, 1)} является базой для одномерного подпространства V of R ² , состоящего из строки y = х . См. рис.

Рисунок 2

Пример 8 : Тривиальное подпространство { 0 } в R ⁿ имеет размерность 0. Следовательно, чтобы соответствовать определению размерности, основание для { 0 } должна быть коллекцией, не содержащей элементов; это пустой набор, ø.

Подпространства R ¹ , R ² и R ³ , некоторые из которых были проиллюстрированы в предыдущих примерах, можно резюмировать следующим образом:

  

Пример 9 : Найдите размерность подпространства V из R ⁴ , натянутого на векторы

 

The collection { v ₁ , v ₂ , v ₃ , v ₄ } is not a basis for V —and dim V is not 4— потому что { v ₁ , v ₂ , v ₃ , v ₄ } не является линейно независимым; см. расчет, предшествующий приведенному выше примеру. Отбрасывание v ₃ и v ₄ из этой коллекции не уменьшает пролет { V ₁ , V ₂ , V ₃ , V ₄ }, но REALTTIONTTIONTTIONTTIONTTIONTTIONTTION. ₁ , v ₂ }, линейно независима. Таким образом, { v ₁ , v ₂ } является основой для V , поэтому dim V = 2,

Пример 10 : Найдите размер промежутка векторов

 

Так как эти векторы находятся в R ⁵ , их диапазон, S , является подпространством R ⁵ . Однако это не трехмерное подпространство R ⁵ , поскольку три вектора w ₁ , w ₂ и w 3 _{не являются линейно независимыми1. Фактически, поскольку w 3 = 3w 1 + 2w 2 , вектор w 3 можно исключить из коллекции без уменьшения диапазона. Поскольку векторы w 1 и w 2 независимы — ни один из них не является скалярным кратным другого, набор { w 1 , w 1 , w 2 служит базисом1 для 2 } S , поэтому его размерность равна 2.}

Наиболее важным атрибутом базиса является возможность записать каждый вектор в пространстве в виде уникальный способ с точки зрения базисных векторов. Чтобы понять, почему это так, пусть B = { v ₁ , v ₂ , …, v _r } пространство является 9 базисом для a30 V }. Поскольку базис должен охватывать V , каждый вектор v в V может быть записан по крайней мере одним способом как линейная комбинация векторов в B . То есть существует скаляров k ₁ , k ₂ , …, k _r такие, что

Чтобы показать, что никакой другой выбор скалярных множителей не может дать v , предположим, что

также является линейной комбинацией базисных векторов, равной v .

Вычитание (*) из (**) дает

 

Это выражение представляет собой линейную комбинацию базисных векторов, которая дает нулевой вектор. Поскольку базисные векторы должны быть линейно независимыми, каждый из скаляров в (***) должен быть равен нулю:

 

Следовательно, K ′ ₁ = K ₁ , K ′ ₂ = K ₂ ,… и K ′ _R = K _R , это представление в = K _R , это представление в = K _R , так что представление в = K _R .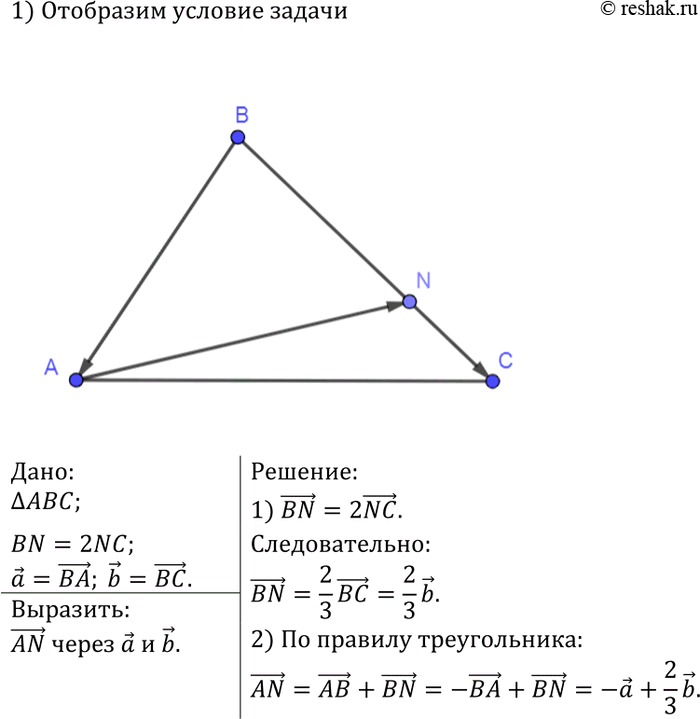 *) действительно уникален. Когда v записывается в виде линейной комбинации (*) базисных векторов v ₁ , v ₂ , …, v _r , скалярно определенный коэффициент0082 k ₁ , k ₂ , …, k _r называются компонентами из v относительно основы B . Вектор ряда ( K ₁ , K ₂ ,…, K _R ) называется Vector из V , относительно B и Denoteded ( V . ) _Б . Иногда удобно записать вектор компонентов в виде столбец вектор; В этом случае вектор компонентов ( K ₁ , K ₂ ,…, K _R ) ^T обозначено [ V ] _B .

Пример 11 : Рассмотрим набор C = { i, i + j , 2 j } векторов в R ² . Заметим, что вектор v = 3 i + 4 j можно записать как линейную комбинацию векторов в С следующим образом:

   

и

Тот факт, что существует более одного способа выразить вектор v в R ² в виде линейной комбинации векторов в C , еще раз указывает на то, что C не может быть основой для R ² . Если бы C были базисом, то вектор v можно было бы записать как линейную комбинацию векторов из C в одной девятке.0082 и только один способ .

Пример 12 : Рассмотрим базис B = { i + j , 2 i − j } числа R ² . Определить компоненты вектора v = 2 i − 7 j относительно B .

Компоненты v относительно B представляют собой скалярные коэффициенты k ₁ и k ₂ которые удовлетворяют уравнению

 

Это уравнение эквивалентно системе

 

Решение этой системы: k ₁ = −4 и k ₂ = 3, поэтому

 

Пример 13 : относительно стандартной основы { i, j, k } = { ê ₁ , ê ₂ , ê ₃ } для R ^{70007 3 3}

3

3

3

3

3

3

3

3

3 3

3

3

3 3 3

3 3 3

3 3 3

3 3

3 3 3 ₃ 0010 , компонентный вектор любого вектора v в R ³ равен самому v : ( v ) _B = v . Тот же результат справедлив для стандартного базиса { х ₁ , х ₂ ,…, х _n } для каждого R

Ортонормированные базисы . Если В = { v ₁ , v ₂ , …, v _n } является основой для векторного пространства V , тогда каждый вектор v может быть записан как линейная комбинация V базисных векторов одним и только одним способом:

 

Нахождение компонент v относительно базиса B — скалярные коэффициенты0083 в приведенном выше представлении — обычно включает решение системы уравнений. Однако, если базисные векторы ортонормированы , то есть взаимно ортогональные единичные векторы, то вычисление компонентов особенно легко. Вот почему. Предположим, что B = {vˆ ₁ ,vˆ ₂ ,…,vˆ _n } является ортонормированным базисом. Начиная с приведенного выше уравнения, где vˆ ₁ , vˆ ₂ ,…, vˆ _n вместо v ₁ , v ₂ , …, v _n , чтобы подчеркнуть, что базисные векторы теперь считаются единичными векторами — возьмите скалярное произведение обеих сторон с vˆ 5 ^{1 :} 0

 

В силу линейности скалярного произведения левая часть становится равной

.

 

Теперь, в силу ортогональности базисных векторов, vˆ _i · vˆ ₁ = 0 для i = 2 через n . Кроме того, поскольку vˆ — единичный вектор, vˆ ₁ · vˆ ₁ = ‖vˆ ₁ ‖1 ² = 1 ² = 1. Следовательно, приведенное выше уравнение упрощается до утверждения

в целом, если B = { Vˆ ₁ , Vˆ ₂ ,…, Vˆ _N } — это ортонормальная основа для векторного пространства V , тогда — это ортонормальная базис для векторного пространства V , тогда — это ортонормальная базис, а затем и ортонормальная основа, а затем — 9008, а затем — ортонормальная основа для вектора. k _i , любого вектора v относительно B находятся по простой формуле

 

Пример 14 : Рассмотрим векторы

из Р ³ . Эти векторы взаимно ортогональны, как вы можете легко проверить, проверив, что V ₁ · V ₂ = V ₁ · V ₃ = v V V v V . v ₃ = 0. Нормализуем эти векторы, тем самым получив ортонормированный базис для R ³ и затем найти компоненты вектора v = (1, 2, 3) относительно этого базиса.

Ненулевой вектор нормализуется — преобразуется в единичный вектор — путем деления его на длину. Следовательно,

 

с B = { Vˆ ₁ , Vˆ ₂ , Vˆ ₃ } — это ортонормальная основание для R ³ , что является представленным на основе, что выдержка выше, что выдвижение выше, что выясняется выше. 0047 v относительно B можно найти, просто взяв следующие скалярные произведения:

Следовательно, ( v ) _B = (5/3, 11/(3√2),3/√2), что означает, что единственное представление v в виде линейной комбинации базиса векторы читаются как v = 5/3 vˆ ₁ + 11/(3√2) vˆ ₂ + 3/√2 vˆ 3 900, как вы можете проверить.

Пример 15 : Докажите, что набор взаимно ортогональных ненулевых векторов линейно независим.

Доказательство . Let { V ₁ , V ₂ ,…, V _R } Будьте набора неэлевых векторов от некоторых R ^N , что является Mit MITEROG, что является MIT -MIRELIGULIN что нет v _i = 0 и v _i · v _j = 0 для i ≠ j . Пусть

   

— линейная комбинация векторов в этом наборе, дающая нулевой вектор. Цель состоит в том, чтобы показать, что k ₁ = k ₂ = … = k _r = 0. Для этого возьмем скалярное произведение обеих частей уравнения с v 1 :

Второе уравнение следует из первого в силу линейности скалярного произведения, третье уравнение следует из второго в силу ортогональности векторов, а итоговое уравнение является следствием того, что ‖ v ₁ ‖ ² ≠ 0 (начиная с v ₁ ≠ 0 ). Теперь легко видеть, что скалярное произведение обеих сторон (*) с v _i дает k _i = 0, устанавливая, что каждые скалярных коэффициента в (*) должны быть нулю, тем самым подтверждая, что векторы v ₁ , v ₂ , …, v _r действительно независимы.

Как найти единичные векторы и базисные векторы — Криста Кинг Математика

Что такое единичные векторы и базисные векторы?

Мы знаем, что каждый вектор по своему определению содержит информацию о своем направлении и величине (помните, что «величина» означает просто «длину»).

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Единичный вектор

Любой вектор с величиной ???1??? называется единичным вектором, ???\vec{u}???. В общем случае единичный вектор не обязательно должен указывать в определенном направлении. Пока вектор имеет длину в одну единицу, это единичный вектор.

Но часто нас интересует изменение определенного вектора ???\vec{v}??? (с длиной, отличной от ???1???), в соответствующий единичный вектор. В этом случае этот единичный вектор должен указывать в том же направлении, что и ???\vec{v}???. 92???.

Как найти единичный вектор и базисные векторы

Пройти курс

Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂

Нахождение единичного вектора в направлении некоторого другого вектора

Пример

Нахождение единичного вектора в направлении ???\vec{v}=(-4,-2)??? . 92}???

???||\vec{v}||=\sqrt{16+4}???

???||\vec{v}||=\sqrt{20}???

Единичный вектор ???\vec{u}??? ???1??? единица длины и находится прямо поверх ???\vec{v}???, указывая в том же направлении, что и ???\vec{v}???, так что это может выглядеть примерно так:

Меньший треугольник, образованный единичным вектором ???\vec{u}??? подобен большему треугольнику, образованному ???\vec{v}???. Итак, мы можем составить пропорцию, чтобы найти горизонтальную составляющую ???\vec{u}???.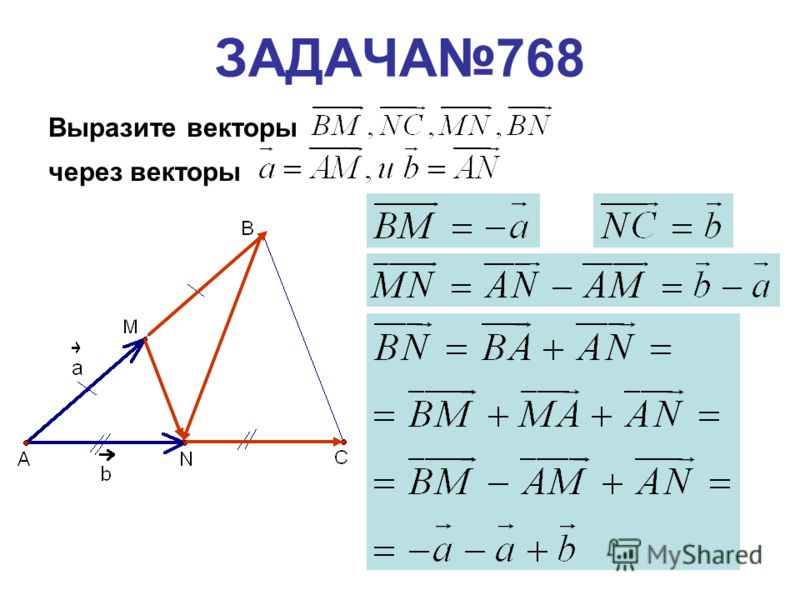

???\frac{-4}{\sqrt{20}}=\frac{a}{1}???

???a=\frac{-4}{\sqrt{20}}=-\frac{2}{\sqrt{5}}???

Установите соотношение, чтобы найти вертикальную составляющую единичного вектора.

???\frac{-2}{\sqrt{20}}=\frac{b}{1}???

???b=\frac{-2}{\sqrt{20}}=-\frac{1}{\sqrt{5}}???

Следовательно, мы можем сказать, что единичный вектор в сторону ???\vec{v}=(-4,-2)??? имеет компоненты

???\vec{u}=\left(-\frac{2}{\sqrt{5}},-\frac{1}{\sqrt{5}}\right)???

Если мы рационализируем здесь знаменатели (как мы научились делать это еще в алгебре), мы можем сказать, что единичный вектор, который указывает в том же направлении, что и ???\vec{v}=(-4,-2)? ??

???\vec{u}=\left(-\frac{2}{\sqrt{5}}\cdot\frac{\sqrt{5}}{\sqrt{5}},-\frac{ 1}{\sqrt{5}}\cdot\frac{\sqrt{5}}{\sqrt{5}}\right)???

???\vec{u}=\left(-\frac{2\sqrt{5}}{5},-\frac{\sqrt{5}}{5}\right)???

В этом последнем примере мы нашли единичный вектор, сначала используя теорему Пифагора, чтобы найти величину данного вектора, а затем используя долю подобных треугольников, чтобы найти компоненты ???\vec{u}? ???.

Но есть более простой способ найти единичный вектор, указывающий на ???\vec{v}???. Единичный вектор, указывающий в направлении ???\vec{v}??? всегда дается 92}=\sqrt{1+16+4}=\sqrt{21}???

Затем подключить ???||\vec{v}||??? и ???\vec{v}??? в формулу для ???\vec{u}??? найти направление ???\vec{v}???.

???\vec{u}=\frac{1}{||\vec{v}||}\vec{v}=\frac{1}{\sqrt{21}}\begin{bmatrix} 1\\4\\-2\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{21}}\\ \frac{4}{\sqrt{21}}\\-\frac {2}{\sqrt{21}}\end{bmatrix}???

Базисные векторы

Часто единичный вектор записывается как ???\hat{u}???, а не в типичном векторном обозначении ???\vec{u}???. Маленькая «шапочка» над ???u??? там, чтобы сказать нам, что длина вектора???1???. Каждый раз, когда вы видите вектор со «шляпой», это означает, что длина вектора равна ???1???, поэтому обычно это обозначение используется конкретно для единичного вектора.

Есть несколько специальных единичных векторов, которые мы будем часто использовать как в векторном исчислении, так и в линейной алгебре. Они называются стандартными базисными векторами.

В двумерном пространстве мы определяем два определенных базисных вектора, ???\hat{i}=(1,0)??? и ???\шляпа{j}=(0,1)???. Как видно из их компонентов, они оба имеют длину ???1???. В трехмерном пространстве базисные векторы равны ???\hat{i}=(1,0,0)???, ???\hat{j}=(0,1,0)???, и ???\шляпа{к}=(0,0,1)???.

Иногда вы увидите базисные векторы, представленные без «шляпы», так же, как выделенные полужирным шрифтом символы ???\bold{i}???, ???\bold{i}??? и ??? \жирный{я}???. 92??? в качестве отправной точки мы можем фактически построить каждый вектор в двумерном пространстве, просто добавляя масштабированные комбинации ???\hat{i}??? и ???\шляпа{j}???. Мы определим это более подробно позже, но эти масштабированные комбинации (суммы масштабированных векторов) называются линейными комбинациями.

Например, вектор ???\vec{a}=(6,4)??? движется ???6??? единиц в горизонтальном направлении, или ???\шляпа{i}??? раз ???4???. Он также движется ???4??? единиц в вертикальном направлении, или ???4??? раз ???\шляпа{j}???. Таким образом, мы могли бы написать линейную комбинацию, которая выражает вектор, где мы масштабируем ???\hat{i}=(1,0)??? на ???6??? и масштаб ???\hat{j}=(0,1)??? на ????4??.

???\vec{a}=(6,4)=6\begin{bmatrix}1\\0\end{bmatrix}+4\begin{bmatrix}0\\1\end{bmatrix}?? ?

???\vec{a}=(6,4)=\begin{bmatrix}6\\0\end{bmatrix}+\begin{bmatrix}0\\4\end{bmatrix}???

???\vec{a}=(6,4)=\begin{bmatrix}6+0\\0+4\end{bmatrix}???

???\vec{a}=(6,4)=\begin{bmatrix}6\\4\end{bmatrix}???

Это означает, что мы можем определить новую нотацию для выражения вектора:

???\vec{a}=(6,4)=6\hat{i}+4\hat{j}???

Мы выражали векторы как координатную точку, как матрицы строк и столбцов, а теперь как комбинацию базисных векторов ???\hat{i}??? и ???\шляпа{j}???. 93???, то есть ???\шляпа{i}=(1,0,0)???, ???\шляпа{j}=(0,1,0)???, и ?? ?\шляпа{к}=(0,0,1)???.

Переезжаем ???-3??? единиц в направлении оси ???x???, ???2??? единиц в направлении оси ???y???, а ???-1??? единиц в направлении оси ???z???.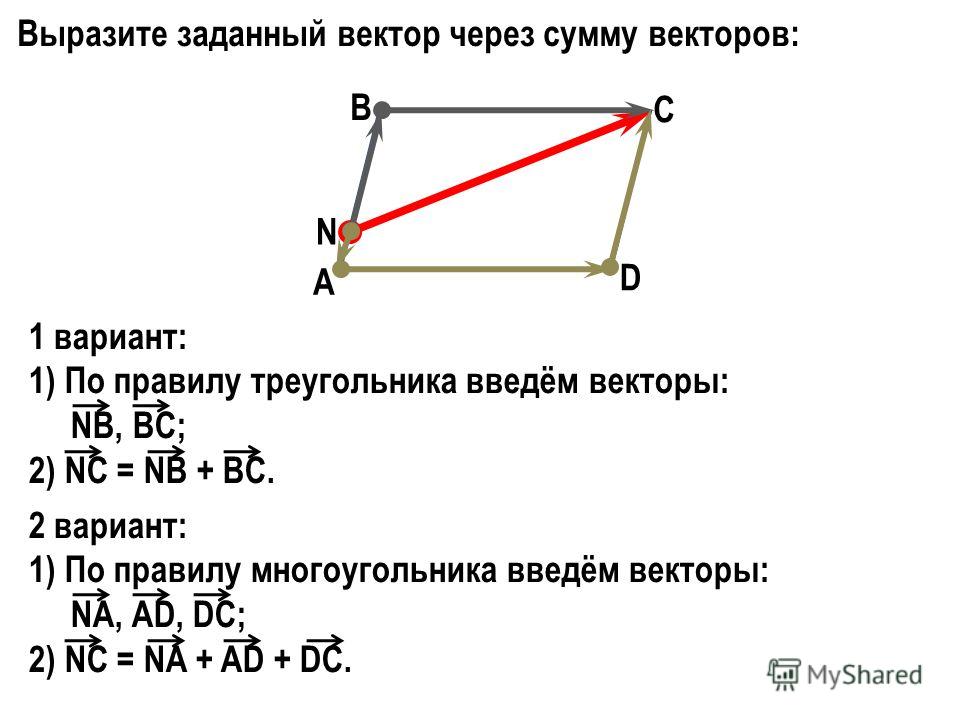

???\vec{a}=(-3,2,-1)=-3\begin{bmatrix}1\\0\\0\end{bmatrix}+2\begin{bmatrix}0\\ 1\\0\end{bmatrix}-1\begin{bmatrix}0\\0\\1\end{bmatrix}???

???\vec{a}=(-3,2,-1)=\begin{bmatrix}-3\\0\\0\end{bmatrix}+\begin{bmatrix}0\\2\ \0\end{bmatrix}+\begin{bmatrix}0\\0\\-1\end{bmatrix}???

???\vec{a}=(-3,2,-1)=\begin{bmatrix}-3+0+0\\ 0+2+0\\ 0+0-1\end{bmatrix }???

???\vec{a}=(-3,2,-1)=\begin{bmatrix}-3\\ 2\\ -1\end{bmatrix}???

Итак, мы можем выразить ???\vec{a}=(-3,2,-1)??? в терминах базисных векторов как

???\vec{a}=-3\hat{i}+2\hat{j}-\hat{k}???

Получите доступ к полному курсу линейной алгебры

Изучение математикиКриста Кинг 13 сентября 2021 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, линейная алгебра, единичные векторы, базисные векторы, линейные комбинации

0 лайков

Линейные комбинации

Марко Табога, доктор философии

Эта лекция посвящена линейным комбинациям векторы и матрицы.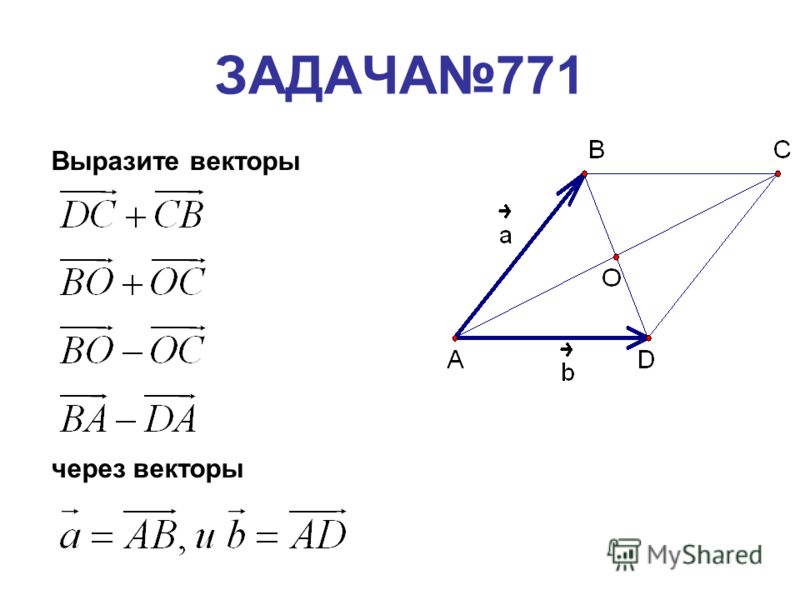 Линейный комбинации получаются умножением матриц на скаляры и добавлением их вместе. Поэтому, чтобы понять эту лекцию, нужно быть познакомиться с понятиями, введенными в лекциях по Сложение матриц и Умножение матрица скаляром.

Table of contents

1. Definition

2. Linear combinations of vectors

3. Solved exercises

   1. Exercise 1

   2. Exercise 2

   3. Exercise 3

Определение

Начнем с формального определения линейной комбинации.

Определение Позволять быть матрицы размерности . А матрица это линейная комбинация из тогда и только тогда, когда существуют скаляры , называется коэффициентов линейной комбинации, такой, что

Другими словами, если вы берете набор матриц, вы умножаете каждую из них на скаляр, и вы складываете все полученные таким образом продукты, то вы получаете линейная комбинация.

Обратите внимание, что все матрицы, участвующие в линейной комбинации, должны иметь той же размерности (иначе сложение матриц было бы невозможно).

Пример Позволять а также быть матрицы, определенные как следует: пусть а также быть двумя скалярами. Затем матрикс линейная комбинация а также . Он вычисляется как следующим образом:

Линейные комбинации векторов

В большинстве случаев в линейной алгебре мы имеем дело с линейными комбинациями векторы-столбцы (или векторы-строки), то есть матрицы, имеющие только один столбец (или только одну строку).

Пример Позволять , а также быть векторы-столбцы, определенные как следует: Пусть быть другим вектором-столбцом, определенным как есть линейная комбинация , а также ? Чтобы ответить на этот вопрос, заметим, что линейная комбинация , а также с коэффициентами , а также имеет следующее форма: Сейчас, представляет собой линейную комбинацию , а также тогда и только тогда, когда мы можем найти , а также такой, что который эквивалентен кНо мы знаем, что два вектора равны тогда и только тогда, когда их соответствующие элементы все равны между собой. Это означает, что приведенное выше уравнение удовлетворяется тогда и только тогда, когда следующие три уравнения одновременно удовлетворены: второе уравнение дает нам значение первого коэффициент:По подставив это значение в третье уравнение, получим получитьНаконец, подставив значение в первом уравнении мы получитьты можно легко проверить, что эти значения действительно представляют собой решение нашей проблема: Следовательно, ответ на наш вопрос утвердительный.

Решаемые упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Определите два матрицы а также в качестве следует: пусть а также быть двумя скалярами. Вычислить линейный комбинация

Решение

Вычисляется как следующим образом:

Упражнение 2

Позволять а также быть векторы:Вычислить значение линейного комбинация

Решение

Это делается как следующим образом:

Упражнение 3

Позволять быть следующим матрица:Есть в нуль вектора линейная комбинация рядов ?

Решение

Обозначим строки по , а также . Линейная комбинация , а также с коэффициентами , а также можно написать как сейчас, в нулевой вектор представляет собой линейную комбинацию , а также тогда и только тогда, когда существуют коэффициенты , а также такой, что который то же самое какПотому что два вектора равны тогда и только тогда, когда все их соответствующие элементы равны относительно друг друга, это уравнение выполняется тогда и только тогда, когда следующая система двух уравнений доволен: это можно переписать как это означает, что какое бы значение мы ни выбрали для , система удовлетворена, если мы установили а также . Например, если мы выбираем , тогда нам нужно setПоэтому, одно решение Если мы выбираем другое значение, скажем , то у нас другой решение:В таким же образом можно получить бесконечно много решений, выбирая различные значения и изменение а также соответственно.