Внешняя алгебра, которую мы заслужили. Часть 1 — симплексы и границы / Хабр

Мотивация

Это рассказ о том, что такое внешняя алгебра, из чего она состоит. Удивительно, но на Хабре почти нет статей о внешней алгебре при том, что ее прикладная ценность ничуть не меньше, например, реляционной алгебры. Внешняя алгебра — это смесь теории множеств, алгебры и комбинаторики. Она является основой для понимания пространств, поэтому в той или иной степени присутствует почти во всех разделах математики. При том, что ее постулаты исключительно просты.

Наше изложение отличается от традиционного, — ориентируемся не столько на точность формулировок, сколько на передачу сути. Осознанно используем отличные от общепринятых обозначения для упрощения формулировок. Это статья для того, чтобы ухватить основную суть. Тогда дальше будет проще.

В первой части определим пространство на основе правил внешнего произведения и сложения объектов. Во второй добавим пространству метрические свойства. В целом пройдем путь от внешнего произведения до представления произвольных графов в виде алгебраического выражения. По дороге познакомимся с основными идеями и инструментами внешней алгебры.

Внешнее произведение

Суть внешней алгебры в том, что объекты можно умножать. Если вас это не впечатлило, то еще раз — умножать можно любые объекты, а не только числа. Можно умножать людей, города, компьютеры, бухгалтерские счета и все остальное, что подходит под понятие объекта. Такое произведение объектов называется «внешним умножением». Это исторически сложившийся термин для того, чтобы отличать внешнее произведение от внутреннего, которым обычно обозначают скалярное произведение.

Обычно внешнее произведение математики обозначают клином (wedge). Но этот знак неудобен. Во-первых, его нет на клавиатуре. Во-вторых, никакого другого умножения, кроме внешнего, для произвольных объектов не существует. Поэтому будем обозначать внешнее произведение звездочкой. Вот оно, умножение элементана элемент: .

Выглядит знакомо, да? Но в отличие от привычного произведения чисел внешнее произведение антикоммутативно — проще говоря, меняет знак при перестановке множителей. Вот так:

Это важное свойство, которое является ключевым для внешней алгебры. Из него в частности следует, что внешнее произведение элемента на самого себя может быть только нулем — объектом без знака: .

Какой смысл несет в себе «внешнее произведение». По простому — это ничто иное, как объединение объектов в список. Поэтому, когда элементов много, то их удобно обозначить списком. Такой упорядоченный список выделим квадратными скобками:. При этом надо помнить про наличие знака у списка — при перестановке соседних элементов знак списка меняется на противоположный: . Ну и как следствие — в таком списке не может быть одинаковых элементов.

Список с такими свойствами будем называть симплексом. Симплекс из двух элементов — отрезок, из трех — треугольник, и т. д. (Только надо иметь ввиду, что это топологические отрезки и треугольники. У них нет длин, углов и прочих метрических параметров.). Количество элементов симплекса задает его порядок (грейд). Математики чаще используют понятие мерности. Размерность симплекса на 1 меньше его порядка. То есть отрезок является одномерным.

Симплексы можно умножать друг на друга — это будет эквивалентно объединению двух списков: . Но при наличии в множителях одинаковых элементов результатом объединения будет пустой список — нуль: .

Ну и еще одно полезное правило. При перестановке перемножаемых симплексов местами знак меняется на противоположный, если произведение порядков симплексов нечетное:

Здесь нижние индексы обозначают порядок симплексов.

Обратные элементы

В нашей алгебре не обойтись без понятия единицы. Единица — это такой элемент, при умножении на который с любой стороны симплекс остается без изменений: . В свою очередь наличие единицы позволяет расширить множество элементов, введя понятие обратных. Кратко обратные элементы именуют коэлементами. При умножении на обратный элемент обращается в единицу. Поскольку у нас не обычное умножение, а внешнее, то важно относительное положение множителей — при перемене мест элемента и обратного ему единица становится отрицательной. Для удобства (связанного с понятием граничного оператора) постулируем, что если обратный элемент расположен слева, то результатом произведения будет 1, а если справа, то -1. Это выглядит поначалу немного непривычно, но в целом окупается:

Здесь перед коэлементами стоит префикс в виде косой черты /. Если обратный элемент умножается на другой элемент, то результатом будет пустой симплекс — ноль: .

Коэлемент можно трактовать как отсутствие элемента. Это дырка в множестве. Но интересно, что с коэлементами можно обращаться так же как с обычными. Произведение коэлементов образует обратный симплекс (косимплекс). Для заданного симплекса можно определить обратный. Постулируем, что при умножении обратного слева на исходный должны получить 1 независимо от порядка симплекса: . Отсюда следует правило расположения элементов в обратном симплексе — в нем порядок элементов меняется на обратный. Таким образом если, то.

Если симплекс умножить на обратный справа, то результат зависит от четности порядка симплекса:

Если симплекс умножается на косимплекс, то взаимно обратные элементы должны сокращаться. Для того, чтобы правильно учесть знак необходимо элемент и обратный ему поставить рядом и выполнить сокращение с учетом их положения. Например: .

Если перемножаемые симплекс и косимплекс содержат элементы, которых нет в другом, то результатом произведения будет ноль: .

Отметим, что симплекса, образованного одновременно обычными и обратными элементами — не существует. Симплексы однородны по составу — либо симплекс полностью состоит из обычных элементов, либо из обратных. Данное свойство вытекает из правил перемножения симплексов. В этом смысле множества обычных элементов и коэлементов принадлежат разным пространствам.

Линейные комбинации и цепи

Элементы и симплексы можно не только умножать, но и складывать, образуя линейные комбинации. Перед каждым симплексом в комбинации может быть скалярный множитель (число). Пример линейной комбинации симплексов 2-го порядка:

.

Линейные комбинации тоже можно интерпретировать как список элементов (слагаемых). Однако в отличие от симплекса в линейных комбинациях допускается наличие произвольного количества одинаковых элементов. Коэффициенты линейной комбинации отражают кратность элементов списка, при этом допускаются и отрицательные кратности. Правила раскрытия двух видов списков отражаются законом дистрибутивности:

Но надо помнить, что умножение здесь внешнее (антикоммутативное). Поэтому некоторые привычные формулы выглядят иначе. Например, внезапно.

Линейную комбинацию симплексов одного порядка в топологии называют также цепью. Как правило, коэффициенты слагаемых цепи целочисленные. Поэтому в общем случае цепи являются подмножеством произвольных линейных комбинаций симплексов. Порядок цепи совпадает с порядком симплексов, из которых она состоит.

Линейную комбинацию можно рассматривать как разложение некоего объекта того же порядка по базисным. Например, если у нас есть два объектаи, то можно определить объект как их линейную комбинацию:

Полученный объект является зависимым, или производным. Отметим, что умножение производного объекта на симплекс его базиса, дает ноль:. То есть зависимые объекты не создают нового пространства. Ну или по другому — размерность пространства определяется количеством независимых элементов.

Коэффициенты разложения элемента по базисным могут быть определены через умножение на коэлементы базиса:

Получается, что внешнее произведение элементов и коэлементов является скалярным (в том смысле, что результат является скаляром). Но между самими элементами скалярное произведение не определено.

Аннулятор и граница

Мы определили симплексы как произведение элементов, определили обратные элементы и обратные симплексы, ввели понятие линейной комбинации симплексов.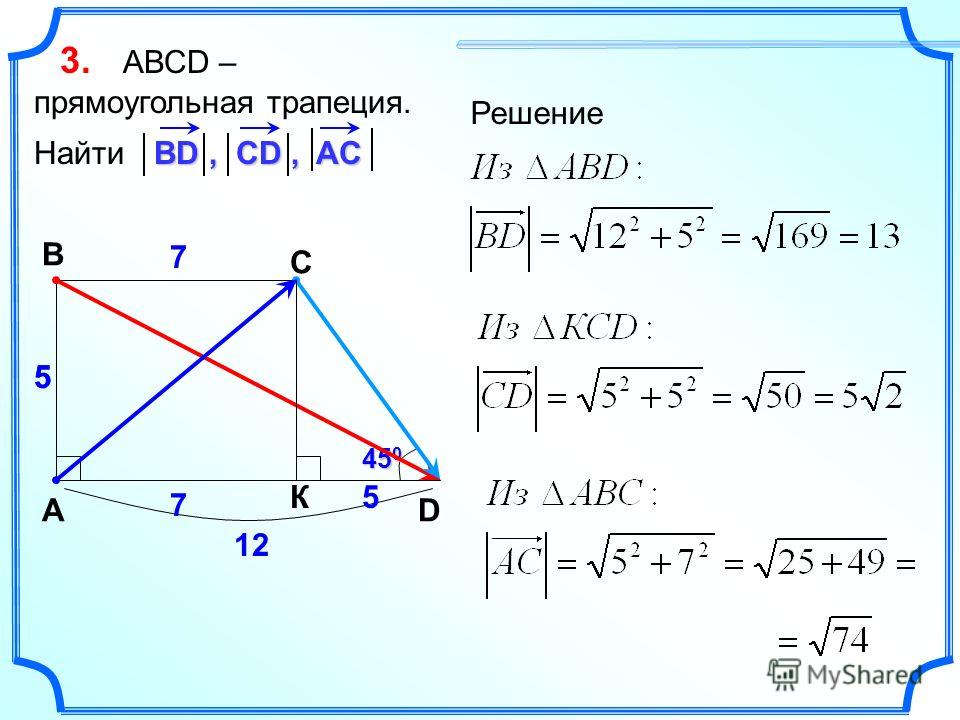 Пора разобраться с понятием вектор. Часто вектор появляется в учебниках как «черт из табакерки» — то есть явочным порядком. Но постулируя вектор как независимое понятие, мы препятствуем осмыслению его обобщения, создаем искусственный барьер в понимании «реальной картины мира». В нашей алгебре первично понятие объекта (элемента). Вектор — производное понятие, и сейчас мы его «произведем».

Вначале нам понадобится еще одно фундаментальное понятие, которое имеет разные названия, в зависимости от контекста в котором употребляется. Здесь для него используем абстрактный термин — аннулятор, хотя пока и непонятно, чего он там обнуляет. Пусть имеется некое конечное множество элементов, например, . Тогда аннулятором для данного множества является сумма обратных элементов данного множества:

Согласно определению аннулятор принадлежит копространству (пространству обратных элементов), поэтому для его обозначения используем косую черту. Поскольку у каждого симплекса есть множество образующих его элементов, то любому симплексу можно сопоставить аннулятор. При этом от знака симплекса аннулятор не зависит.

Аннулятор позволяет определить граничный оператор над симплексом как внешнее умножение аннулятора на симплекс. Результатом действия является граница. Вот она, граница симплекса:

Границы настолько важны, что не пожалеем для их обозначения отдельных скобок:

Аннулятор множества является также аннулятором всех его подмножеств. Поэтому граница симплекса может быть образована умножением не только на его аннулятор, но и на любой аннулятор надмножества. Пример:

Граница (симплекса) есть цепь — линейная комбинация симплексов. Порядок границы на 1 меньше порядка образующего ее симплекса. В частности, вектор — это граница 1-порядка, образованная отрезком (симплексом 2-го порядка):

Вектор 2-го порядка называют бивектором, 3-го — тривектором и т.д. Граница произвольного порядка может быть названа мульти- или поливектором.

Действие граничного оператора может быть отменено. Существует элемент, умножая на который границу симплекса, можно восстановить исходный симплекс. Данный элемент называется центроидом множества (или барицентром). Центроид — это среднее суммы элементов:

Здесь круглые скобки — это не обозначение границы, а группировка элементов (обычно смысл скобок понятен из контекста). Проверим действие центроида:

Умножение границы на центроид собирает несколько слагаемых в одно.

Основное свойство границ

Границы — это не просто цепи, фактически границы представляют собой новый тип данных со своими особыми свойствами. Главное из них — двойная граница равна нулю.

В традиционных учебниках граничный оператор вводят явочным порядком, и в этом случае приходится доказывать тот факт, что двойной граничный оператор дает ноль. Но в нашем изложении это очевидно ввиду того, что граничный оператор определен как умножение на аннулятор. Повторное умножение на тот же элемент дает ноль в соответствии со свойствами внешнего произведения.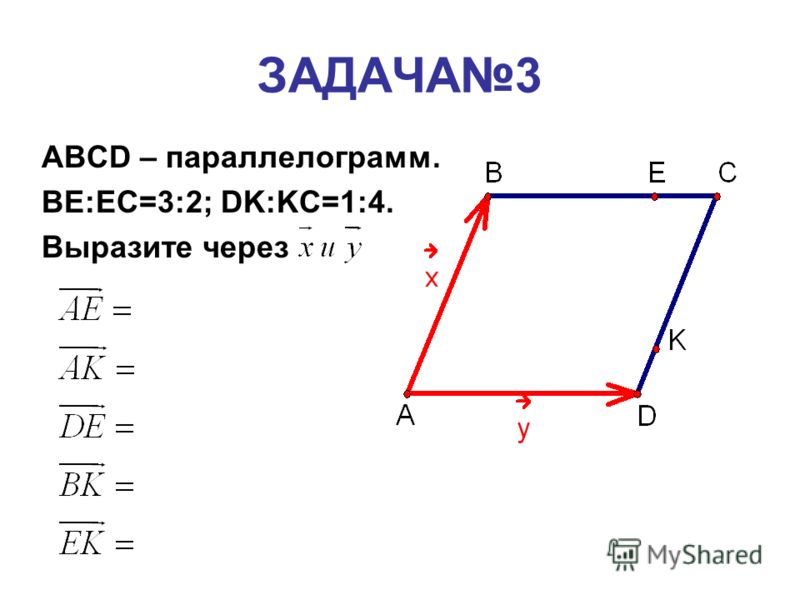

Данная формула раскрывает смысл термина «аннулятор» — при действии на границу аннулятор ее обнуляет. Раскрывая границу как линейную комбинацию симплексов и умножая каждый симплекс на аннулятор, получаем тождества границ:

Тождества границ играют ключевую роль в различных доказательствах и выводах, касающихся свойств границ. Например, из них вытекает полезные выражения исключения вершиныиз линейной комбинации границ:

Общий элементв правой части тождеств можно также интерпретировать как центр координат. На этом свойстве основано определение векторного пространства с общим центром, который всегда можно исключить. при выражении других границ пространства.

Становится понятно также, что двум различным цепям может соответствовать одна и та же граница при условии, что разность данных цепей является границей. Соответственно и восстановление цепи по границе (умножением на центроид) выполняется с точностью до произвольной границы.

Произведение границ

Обратимся к произведению границ.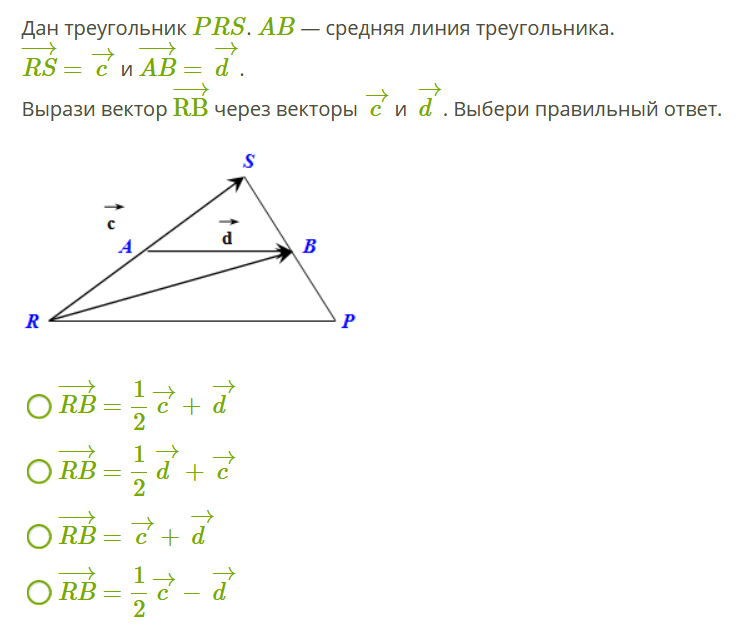 Произведение двух границ тоже является границей, но есть нюансы. Если перемножаемые границы имеют более одного общего элемента, то их произведение равно нулю. Это следствие свойств внешнего произведения. Пример:

Если границы имеют один общий элемент, то при умножении они сливаются в одну (компоненту) — это правило слияния границ. Пример слияния двух векторов в 2-границу (бивектор):

Если же перемножаемые границы не имеют общих элементов, то границы не сливаются. Получаем границу, состоящую из нескольких компонент связности. Пример такой границы, содержащей 4 элемента:. Поскольку под поливектором обычно понимают границу с одной компонентой связности, то строго говоря границы и поливекторы — это не одно и то же. Под поливектором будем понимать всегда границу из одной компоненты.

Итак, порядок границы зависит не только от количества образующих ее элементов , но и от количества ее компонент . Порядок границы равен 2, несмотря на то, что она содержит 4 элемента.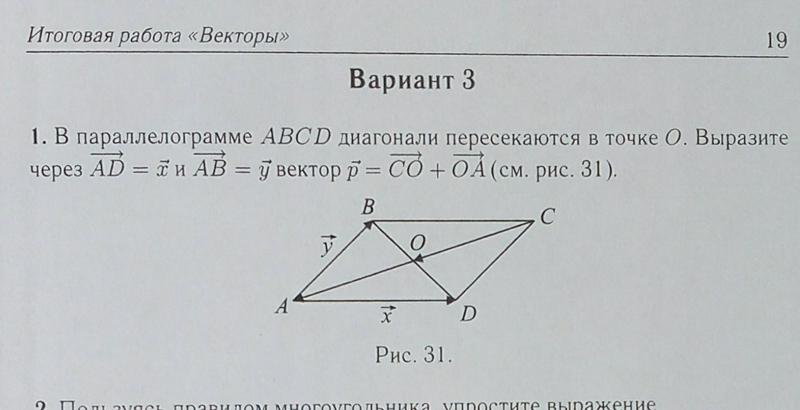 Для получения порядка границы надо из количества элементов вычесть количество компонент: .

Кроме того, одна и та же граница может быть образована произведением разных границ меньшего порядка. Например, граница может быть образована тремя разными парами векторов: . То есть произведение границ с общим элементом уничтожает информацию о том, какие именно границы умножались — границы сливаются в одну.

Для тех, кому интересны подробности, откуда все это следует

укажем, что в основе доказательства свойств произведения границ лежит правило Лейбница (цепочки), которое применительно к оператору границы можно записать в следующем виде:

Здесь граничный оператор (умножение на аннулятор слева обозначен как частная производная — это общепринятое обозначение. Используя данное тождество, можно показать, что. Проще всего это сделать раскрытием левой и правой частей по правилу Лейбница.

Немного линейной алгебры…

Пространство элементов, с которым мы тут возимся, принято называть аффинным. Это пространство, в котором есть элементы и их линейные комбинации, но нет метрики.

Насчет метрики следует уточнить. В нашем пространстве не определено скалярное произведение между элементами (и между границами тоже). Поэтому нет возможности определить, например, угол между векторами или сравнить длину (норму) двух произвольных векторов. Но. Из этого не следует, что в аффинном пространстве вообще невозможно ничего сравнивать. Мы вполне можем сравнить длину двух векторов, если они лежат на одной прямой. Мы можем сравнить площади двух бивекторов, если они лежат в одной плоскости и т.д. То есть полноценной метрики в аффинном пространстве нет, но есть полуметрика, которой вполне можно пользоваться. Полуметрика является следствием наличия скалярного произведения между элементами и коэлементами. То есть линейного разложения элементов через другие, базисные.

Рассмотрим пространство, образованное тремя элементами, среди которых выделим центр — общий элемент. Границей пространства будет бивектор базиса.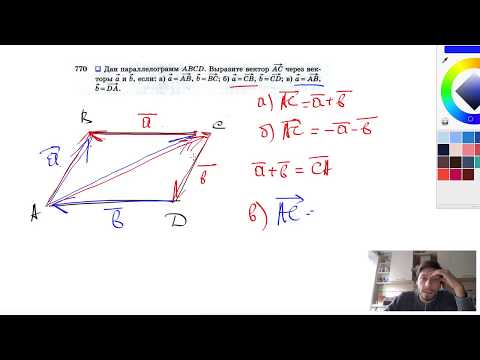 Пусть теперь в данном пространстве есть три элементас известными координатами относительно базисных элементов. Задача состоит в том, чтобы выразить бивекторчерез базисный.

Вначале выпишем координаты элементов. Учтем, что сумма коэффициентов разложения элемента по базисным должна быть равна единице — это следствие того, что граница любого элемента пространства должна быть равна 1: . Такие координаты называются барицентрическими. Тогда для базиса из 3-х элементов две координаты являются независимыми, а третья — выражается через них:

Данная формула может быть представлена как координаты вектора :

Аналогичным образом можно найти координаты векторови. Перемножая векторы, можно выразить координаты бивекторов через базисный бивектор:

Для нахождения искомого бивекторавоспользуемся тождеством границ из предыдущего раздела: . Подставляя в него координаты бивекторов, получаем итоговый ответ:

Значение скалярного коэффициента здесь как раз и будет отношением площадей искомого и базового бивекторов. Отметим, что коэффициент может быть и отрицательным, поскольку у бивекторов есть ориентация.

Аффинные координаты и площади

Коэффициент может быть также выражен как детерминант матрицы: . Значения матрицы координатравны произведению элементов и базисных коэлементов (за исключением центра координат):

Для вычисления относительного объема в матрицу добавляется дополнительная строка и колонка, соответствующие новому измерению.

Умение различать ситуации, где пространство является аффинным, является полезным навыком при анализе данных. Пусть, например, задано множество людей, для которых известны рост и вес. Данные свойства образуют два вектора аффинного пространства. Как показано выше, в таком пространстве можно сравнивать людей отдельно по росту или весу, но нет возможности оценить близость людей одновременно по «росто-весу», поскольку нет связи между данными свойствами, нет метрики. Но ничто не мешает сравнивать по «росто-весу» тройки людей. Координаты этих троек (вычисленные указанным выше способом) пропорциональны их относительной площади и не зависят от скалярного произведения свойств (угла между базисными векторами).

… и топологии

Про топологию говорят, что это геометрия без измерений. В том смысле, что конкретные координаты элементов топологам неинтересны. Поэтому коэффициенты топологических цепей всегда равны +-1. Алгебраические выражения границ симплекса можно интерпретировать топологически. В качестве примера приведем разрезание (топологического) квадрата с вершинами на два треугольника. Треугольники в данном случае должны быть ориентированы, то есть иметь знак. Тогда квадрат можно представить как сумму (склейку) треугольников:. Применив к данной цепи граничный оператор, получим цепь из 4-х 2-симплексов — это граница квадрата:

Склейка симплексов

При сложении 2-границ общая сторона треугольников сократилась. В общем случае, можно продолжать склейку треугольников, получая произвольные топологические многогранники. Кажется, что можно любую поверхность представить как сумму треугольников, но на самом деле нет. При покрытии треугольниками поверхности ленты Мёбиуса не удается сократить внутренние границы!

Мы определили границу симплексакак результат действия граничного оператора (умножение аннулятора) на некий симплекс. Повторное взятие границы, как уже отмечалось дает ноль:

Но вообще говоря, возможны и другие цепи (линейные комбинации симплексов), граница которых нулевая. Цепи с нулевой границей называют циклами. Инвариант циклов:

Циклы — это более общее подмножество цепей, чем границы. В общем случае существуют циклы, которые не являются границами какого-либо симплекса. Их называют гомологиями:

Говоря про циклы, снова оговоримся — это топологические циклы. Так же как в топологическом треугольнике нет величины сторон и углов, так и в топологическом цикле нет величины связи между элементами цикла.

Топология — огромный раздел современной математики. Тут мы лишь показали, как порождаются и связываются направления математики через одну простую операцию — внешнее умножение.

Коцепи и дуальность

Для заданного конечного множества независимых элементов существует симплекс предельного порядка, определяемый как произведение всех элементов.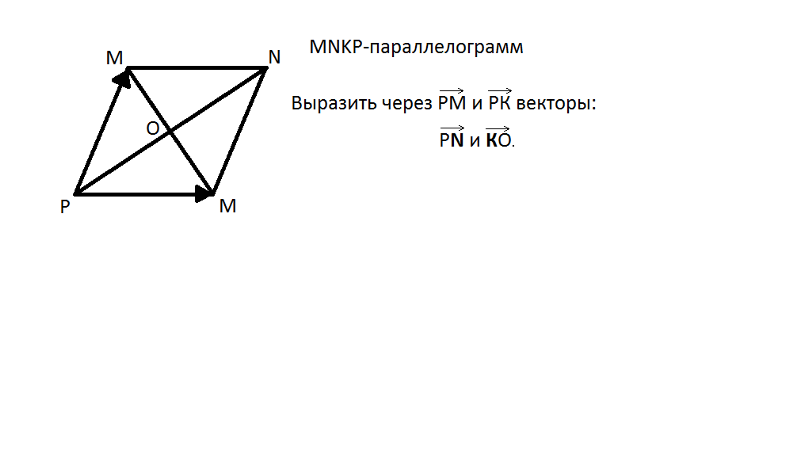 Граница данного симплекса называется предельной границей пространства — она имеет максимальный порядок из всех возможных границ на данном множестве. Предельная граница для множества 4-х элементов : .

Предельная граница множества всегда связна (имеет только одну компоненту). Умножение предельной границы на коэлементы понижает ее порядок, но оставляет границу связной: . Умножение предельной границы на сумму коэлементов порождает границы, состоящие из компонент. Например,

Здесь мы видим коцепи 1-го порядка — это линейные комбинации коэлементов. Встречаются также коцепи более высокого порядка. Например, граница из трех компонент может быть получена умножением предельной границы на аннуляторы двух произвольных компонент:

Здесь- предельная граница 6 элементов. Коцепь 2-го порядка:

Видим, что разным коцепям может соответствовать одна и та же граница. Из данных соотношений следует, что границуна конечном множестве элементов можно задать через коцепь. Умножая коцепь на предельную границу, переходим из копространства в обычное:

Преобразование коцепей в границы называется дуальным преобразованием.

Дуальное преобразование и звездочка Ходжа — это не одно и тоже!

Для тех, кто вообще в курсе про оператор Ходжа. Оператор Ходжа преобразует одни (поли)векторы пространства в другие векторы того же пространства. Дуальное преобразование преобразует коцепи в границы.

Чтобы определить в пространстве оператор Ходжа, надо договориться об общем элементе всех границ. То есть задать начало координат. Такое возможно, поскольку произвольная граница всегда может быть выражена через линейную комбинацию границ с общим элементом (см. граничные тождества). В этом случае становится однозначным дополнение поливектора до предельной границы пространства, которое и называется звездочкой Ходжа.

Можно определить и обратное дуальное преобразование — от границ (цепей) к коцепям. Пусть дана некая граница (в общем случае произвольная цепь). Надо построить дуальную ей коцепь для заданного пространства (симплекса) с предельной границей .

Алгоритм построения может быть таким. Для цепи определяем центроид (средняя сумма элементов, образующих цепь). «Интегрируем» цепь умножением слева на центроид. Переводим полученный «интеграл» из пространства в копространство умножением на косимплекс пространства. Косимплекс пространства однозначно определяется предельной границей. Полученная коцепь и будет искомой:

В данной формуле круглые скобки обозначают порядок операций.

На этом завершаем. Надеюсь, что общее представление о том, что такое внешняя алгебра, читатели получили. Самое странное, что все эти «игры с абстрактными символами» отражают свойства вполне реального окружающего мира. В следующей статье рассмотрим пространства со скалярным произведением между элементами.

Помогите решить / разобраться (Ф)

Nesalvador в сообщении #1087327 писал(а): Я не математик, и не физик, но мне необходимо понять — почему вектор момента импульса и момента силы направлен перпендикулярно плоскости всех действий при стандартных условиях? Nesalvador Полагаю, это можно понять, пристально разглядывая рисунки с вращающимися телами. Например, пусть два шарика (точнее говоря, две материальные точки и ) с одинаковыми массами вращаются по инерции, скреплённые невесомым жёстким стержнем. Для 3-мерности рисунка изобразил ещё и плоскость с круговой орбитой шаров в виде поверхности стола, хотя никакого стола в этом примере нет 🙂 Здесь ось вращения очевидным образом перпендикулярна плоскости орбиты, т.е. в каждый момент времени ось вращения перпендикулярна вектору скорости шара и перпендикулярна радиус-вектору шара проведённому из середины стержня (будем следить за шаром а для второго шара всё будет аналогично). При этом в каждый момент времени векторы скорости перпендикулярны радиус-векторам шариков. Наличие оси вращения люди условились выражать вектором угловой скорости Величина его равна угловой скорости вращения а его направление символизирует направление оси вращения. Более строго говоря, вектор угловой скорости это псевдовектор (его также называют аксиальным вектором): «начало» и «конец» на оси вращения выбраны условно — так, чтобы глядя с «конца» вектора мы видели вращение против часовой стрелки. Какой формулой выражается взаимосвязь векторов и ? Сначала найдём связь между числовыми величинами этих векторов. Если шар движется по круговой орбите с постоянной скоростью то всю длину окружности он проходит за время — за это время шар совершает один орбитальный оборот, т.е. поворачивается вокруг точки на угол Значит, величина орбитальной угловой скорости, определяемая как есть Эту же взаимосвязь числовых величин можем описать равенством: А для того, чтобы из такой формулы была видна не только указанная связь величин, но и направления векторов относительно друг друга, запишем вместо (1) следующее векторное равенство с символом векторного произведения Мы условимся здесь, что направление векторных сомножителей и векторного произведения друг относительно друга именно такое, какое показано выше на рисунке; все три вектора там взаимно перпендикулярны. Если представить себе ещё один шарик — в виде материальной точки расположенной на оси вращения первых двух шаров над (или под) плоскостью их орбиты, — то его скорость а радиус-вектор параллелен Значит, векторное произведение (2) взаимно параллельных (или антипараллельных) векторов равно нулю. Можно заметить также, что если изобразить новую картинку, где на месте прежнего вектора будет нарисован новый , а на месте прежнего будет новый то новая скорость окажется противоположной к прежней; значит, векторное произведение меняет свой знак при перестановке сомножителей: Очевидно также, что если в прежней плоскости орбиты включить на короткое время пару противоположных сил, которые увеличат (или уменьшат) скорость показанных выше двух шаров, то увеличится (или уменьшится) угловая скорость шаров , а направление оси вращения останется прежним. Т.е. вектор угловой скорости удлинится (или укоротится) на какой-то вектор без изменения своего направления. Этот факт ведёт нас к представлению о некоем «векторе момента сил», вызывающем изменение вектора угловой скорости . В данном примере естественно думать, что вектор момента сил параллелен оси вращения, поскольку вызванное им изменение параллельно оси вращения. Попробуем это записать в форме векторного равенства. Представим себе вектор силы параллельный вектору скорости шара За короткое время сила изменяет вектор импульса шара на так что (это второй закон Ньютона): Чтобы представить это равенство как равенство векторов, параллельных оси вращения шаров, умножим векторно левую и правую сторону этого равенства на радиус-вектор шара Обозначив здесь левую сторону как — это у нас будет вектор скорости изменения «момента импульса», а правую сторону обозначив как — это у нас будет вектор «момента сил», можем записать равенство (5) в виде: В качестве не сильно сложного упражнения проверяется, что при этом сам орбитальный момент импульса материальной точки можно определить формулой: В нашем примере орбитальный момент импульса одного шарика-точки есть Система двух шариков и имеет вдвое больший момент импульса. Рассмотрим теперь другую ситуацию. Пусть до включения пары сил шарики и покоились, а затем на короткое время включалась пара сил, перпендикулярных той же плоскости, которая была показана на предыдущем рисунке: Очевидно, что здесь за время шарики приобрели угловую скорость в направлении «на нас». Соответствующее этому факту изменение момента импульса одного шарика есть где Наконец, можем попытаться «просуммировать» эту ситуацию с самой первой ситуацией, где шарики вращались вокруг вертикальной оси (см. первый рисунок). Мы видим, что показанная на втором рисунке пара сил стремится повернуть стержень в плоскости рисунка, т.е. эта пара сил как бы «стремится наклонить ось вращения налево». Однако, векторы и параллелльные вертикальной оси вращения, при этом получают добавки и направленные «на нас», и превращаются в слегка наклонённые «на нас» векторы и (С Новым Годом!) (Если чё-ньть слегка напутал, прошу извинить, всё ж таки Новый Год. Всех с Новым Годом! 🙂

Вопрос Видео: Использование операций над векторами для выражения вектора через два других вектора выразить вектор 𝐂, равный отрицательной восьмерке, отрицательной единице, через векторы 𝐀 и 𝐁.

Здесь нас попросили выразить один вектор 𝐂 через два других вектора 𝐀 и 𝐁. Это означает, что мы хотим записать 𝐂 как 𝑚𝐀 плюс 𝑘𝐁 для некоторых скалярных значений 𝑚 и 𝑘. То есть некоторое кратное 𝐀 плюс некоторое кратное 𝐁. Мы можем заменить 𝐀, 𝐁 и 𝐂 их компонентами, и мы получим векторное уравнение. Вектор минус восемь, минус один равен 𝑚, умноженному на вектор минус четыре, минус один плюс 𝑘, умноженному на вектор минус два, минус один. Затем мы вспоминаем, что для умножения вектора на скаляр мы просто умножаем каждый из его компонентов на этот скаляр.

Итак, чтобы умножить вектор минус четыре, минус один на 𝑚, мы сначала умножим 𝑚 на минус четыре, получив первую компоненту минус четыре 𝑚. А затем мы умножаем 𝑚 на отрицательную единицу, получая вторую составляющую отрицательной 𝑚. Точно так же, чтобы умножить вектор минус два, минус один на 𝑘, мы сначала умножаем 𝑘 на минус два, давая первый компонент минус два 𝑘. А затем мы умножаем 𝑘 на отрицательную единицу, получая вторую составляющую отрицательной 𝑘. Далее нам нужно сложить вместе два вектора в правой части. А для этого напомним, что мы можем просто добавлять составные части.

Итак, первый компонент вектора в правой части будет суммой первых компонентов. Это минус четыре 𝑚 плюс минус два 𝑘, что мы можем записать как минус четыре 𝑚 минус два 𝑘. И тогда второй компонент будет суммой второго компонента в каждом векторе. Это минус 𝑚 плюс минус 𝑘, который мы можем записать как минус 𝑚 минус 𝑘. Итак, теперь мы имеем, что вектор минус восемь, минус единица равен вектору минус четыре 𝑚 минус два 𝑘, минус 𝑚 минус 𝑘. Здесь мы вспоминаем, что если два вектора равны, то это должно означать, что их отдельные компоненты равны.

Итак, первый компонент вектора в левой части должен быть равен первому компоненту в правой части. Это дает нам уравнение без каких-либо векторов. Минус восемь равен минус четыре 𝑚 минус два 𝑘. Таким же образом, приравнивая вторые компоненты в наших векторах, получаем уравнение отрицательной единицы равно отрицательному 𝑚 минус 𝑘. Теперь у нас есть пара линейных одновременных уравнений относительно скаляров 𝑚 и 𝑘. Итак, мы можем решить эти одновременные уравнения, чтобы найти их значения.

Во-первых, мы можем немного упростить каждое уравнение. Первое уравнение можно разделить на минус два, чтобы получить упрощенное уравнение два 𝑚 плюс 𝑘 равно четырем. А второе уравнение можно разделить на отрицательное, чтобы получить упрощенное уравнение 𝑚 плюс 𝑘 равно единице. Затем мы видим, что у нас есть одинаковый коэффициент 𝑘 в каждом из наших уравнений. Итак, если мы вычтем второе уравнение из первого, это устранит члены 𝑘. В левой части два 𝑚 плюс 𝑘 минус 𝑚 минус 𝑘 оставят нам 𝑚. А в правой части четыре минус один равно трем. Итак, по сути, мы нашли значение 𝑚. 𝑚 равно трем.

Затем мы можем подставить это значение 𝑚 в наше простейшее уравнение, которое представляет собой уравнение 𝑚 плюс 𝑘 равно единице. Итак, у нас есть три плюс 𝑘 равно одному. И это уравнение можно решить, вычитая по три с каждой стороны, чтобы получить 𝑘 равно минус два.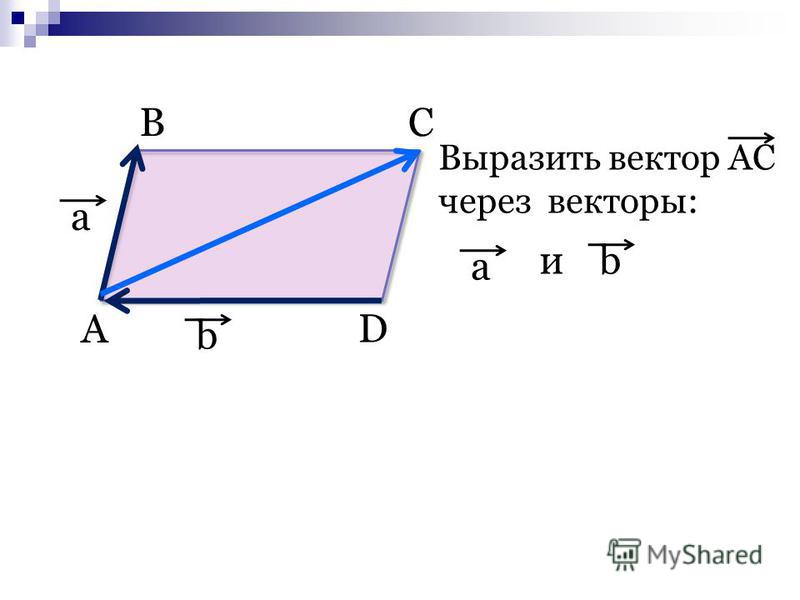 Таким образом, мы нашли значения наших двух скаляров 𝑚 и 𝑘. Наконец, мы можем вернуться к утверждению, с которого начали, а именно, что вектор 𝐂 равен некоторому скаляру, умноженному на 𝐀, плюс некоторому скаляру, умноженному на 𝐁, и подставить значения 𝑚 и 𝑘.

Затем мы обнаружили, что вектор 𝐂 может быть выражен через векторы 𝐀 и 𝐁 как 𝐂 равно трем 𝐀 минус два 𝐁. Мы можем, конечно, проверить это вручную, пересчитав вектор три 𝐀 минус два 𝐁. И если мы это сделаем, то обнаружим, что получаем вектор минус восемь, минус единица, который действительно равен вектору 𝐂. Итак, наш ответ правильный.

Линейная комбинация векторов — определение деловых терминов

Линейная комбинация векторов имеет место, когда вектор может быть выражен в виде линейной функции других векторов, которые линейно независимы.

Другими словами, линейная комбинация векторов состоит в том, что вектор может быть выражен как линейная комбинация других векторов, линейно независимых друг от друга.

Требования к линейной комбинации векторов

Линейная комбинация векторов должна удовлетворять двум требованиям:

1. Вектор может быть выражен как линейная комбинация других векторов.
2. Пусть эти другие векторы линейно независимы друг от друга.

Линейная комбинация в исчислении

В базовой математике мы часто видим линейные комбинации, не осознавая этого. Например, линия представляет собой комбинацию одной переменной по отношению к другой, такую, что:

Общее уравнение для прямой линии

Но корни, логарифмы, экспоненциальные функции … уже не являются линейными комбинациями, поскольку пропорции не остаются постоянными для целая функция:

Нелинейные комбинации

Итак, если мы говорим о линейной комбинации векторов, то структура уравнения будет иметь следующий вид:

Общее уравнение для прямой

Так как мы говорим о векторах, а предыдущее уравнение относится к переменным, то для построения комбинации векторов нам нужно только заменить переменные на векторы.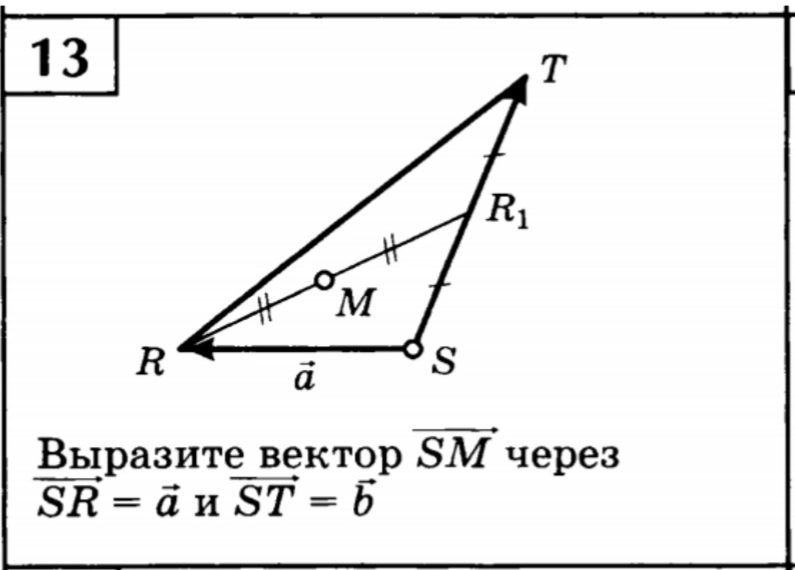 Пусть следующие векторы будут:

Мультяшный вектор

Итак, мы можем записать их в виде линейной комбинации следующим образом:

Уравнение прямой и линейная комбинация векторов

Векторы линейно независимы друг от друга.

Греческая буква лямбда действует как параметр m в общем уравнении линии. Лямбда будет любым действительным числом, и, если оно не появляется, говорят, что его значение равно 1.

То, что векторы линейно независимы, означает, что ни один из векторов не может быть выражен как линейная комбинация других. Известно, что независимые векторы составляют основу пространства, и зависимый вектор также принадлежит этому пространству.

Пример параллелепипеда

Предположим, что у нас есть три вектора, и мы хотим выразить их в виде линейной комбинации. Мы также знаем, что каждый вектор исходит из одной и той же вершины и составляет абсциссу этой вершины. Геометрическая фигура представляет собой параллелепипед.