Нулевой вектор — Википедия
Нулевой вектор (нуль-вектор) — вектор, начало которого совпадает с его концом. Нулевой вектор имеет норму 0 и обозначается 0→{\displaystyle {\vec {0}}} или 0{\displaystyle \mathbf {0} }.
Нулевой вектор определяет тождественное движение пространства, при котором каждая точка пространства переходит в себя.
С нулевым вектором не связывают никакого направления в пространстве. Нулевой вектор принято считать сонаправленным любому вектору. Можно считать, что нулевой вектор одновременно коллинеарен и ортогонален любому вектору пространства (легко выводится из определения).
Все координаты нулевого вектора в любой аффинной системе координат равны нулю.
С точки зрения линейной алгебры, в линейном пространстве должен существовать специальный вектор 0→{\displaystyle {\vec {0}}}, обладающий следующими свойствами:
- a→+0→=a→{\displaystyle {\vec {a}}+{\vec {0}}={\vec {a}}}
Для любого вещественного числа c{\displaystyle c}
- c⋅0→=0→{\displaystyle c\cdot {\vec {0}}={\vec {0}}}
Для всякого вектора a→{\displaystyle {\vec {a}}}, найдется такой вектор −a→{\displaystyle -{\vec {a}}}, что:
- a→+(−a→)=0→{\displaystyle {\vec {a}}+(-{\vec {a}})={\vec {0}}}.
- Нейтральный элемент
- Ноль
- Винберг Э.Б. курс высшей алгебры. М.: Факториал, 2001
 | Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её. |
Векторы и матрицы | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Векторы |
| ||||||||
| Матрицы |
| ||||||||
| |||||||||
Векторы на плоскости, формулы и примеры
Если начало и конец вектора – это точки и , то вектор обозначается как . Также для обозначения векторов используются строчные латинские буквы:
Нулевой вектор
Нулевым вектором называется вектор, у которого начало совпадает с концом (рис. 1).
Длинойили модулем вектора называется неотрицательное число, равное длине отрезка , который задает вектор.
Коллинеарные и неколлинеарные векторы на плоскости
Сонаправленные и противоположно направленные векторы на плоскости
Два коллинеарных вектора и называются сонаправленными, если их направления совпадают. Сонаправленные векторы обозначаются следующим образом: . Два коллинеарные вектора и называются противоположно направленными, если их направления противоположны. Обозначение .
Два вектора плоскости называются равными, если они сонаправлены и их длины равны (рис. 3):
Вектор называется противоположным
Отложим от некоторой точки на плоскости два произвольных вектора и (рис. 4). Лучи, исходящие из этой точки образуют угол , который называется углом между векторами и :
Два вектора и называются ортогональными (или перпендикулярными), если угол между ними равен ( радиан) (рис. 5).
| Понравился сайт? Расскажи друзьям! | |||
Презентация на тему: ВЕКТОРЫ.

ВЕКТОРЫ НА ПЛОСКОСТИ.

История возникновения
понятия вектора
Одним из фундаментальных понятий современной математики являются вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике. Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение. Почти одновременно с ним
исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман . Англичанин Уильям Клиффорд сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса который в 1901 году опубликовал обширный учебник по векторному анализу. Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной математике.
Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением.

Векторы вокруг нас.
Векторы в повседневной жизни.С уверенностью можно сказать,что мало кто из людей задумывается о том,что векторы окружают нас повсюду и помогают нам повседневной жизни.Так например, ель можно рассматривать как пример вектора в пространстве:нижняя её часть- начало вектора,а верхушка дерева является концом вектора

Векторы вокруг нас.
Векторы в знаках дорожного движения.
Каждый день ,выходя из дома,мы становимся участниками дорожного движения в роли пешехода либо в роли водителей.В жизни всё взаимосвязано и,даже в простейших предписываюших знаках дорожного движения,мы видим указательные стрелки движения,в математике называемые-ВЕКТОРАМИ

Векторы на плоскости
Отрезок,для которого указано,какая его граничная точка является началом,а какая –концом,называется направленным отрезком или вектором
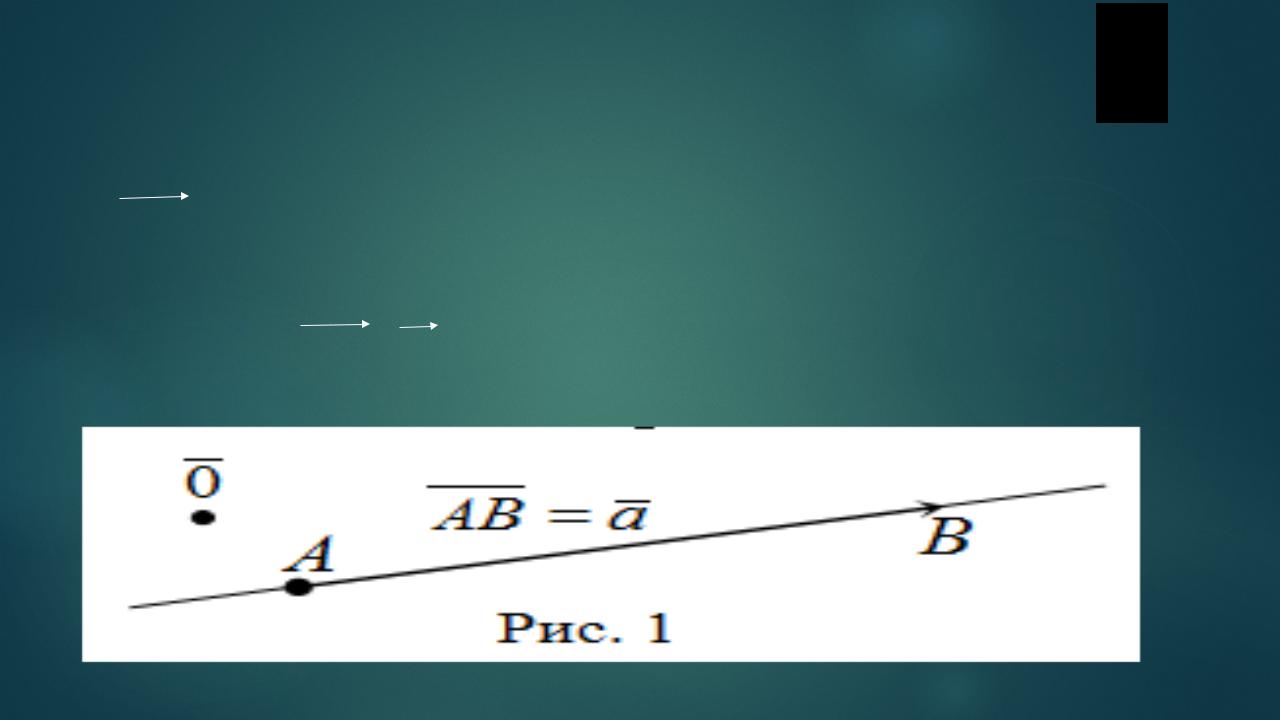
Если начало и конец вектора – это точки А и B,то вектор обозначается
точки А и B,то вектор обозначается
как AB. Также для обозначения
векторов используются строчные латинские буквы: AB=а

1. Нулевым вектором 0 называется вектор, у которого начало совпадает с
вектор, у которого начало совпадает с
концом.ПРИМЕЧАНИЕ!!!
Нулевому вектору 0 придают любое
направление на плоскости. Длиной или
модулем AB вектора AB называется неотрицательное число, равное длине
отрезка AB который задаёт вектор.

ПРИМЕЧАНИЕ!!!
Длина нулевого вектора равна нулю.
2.Коллинеарные и неколлинеарные векторы на плоскости
Два вектора на плоскости называют коллинеарными ,если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2). В противном случае векторы называются неколлинеарными.
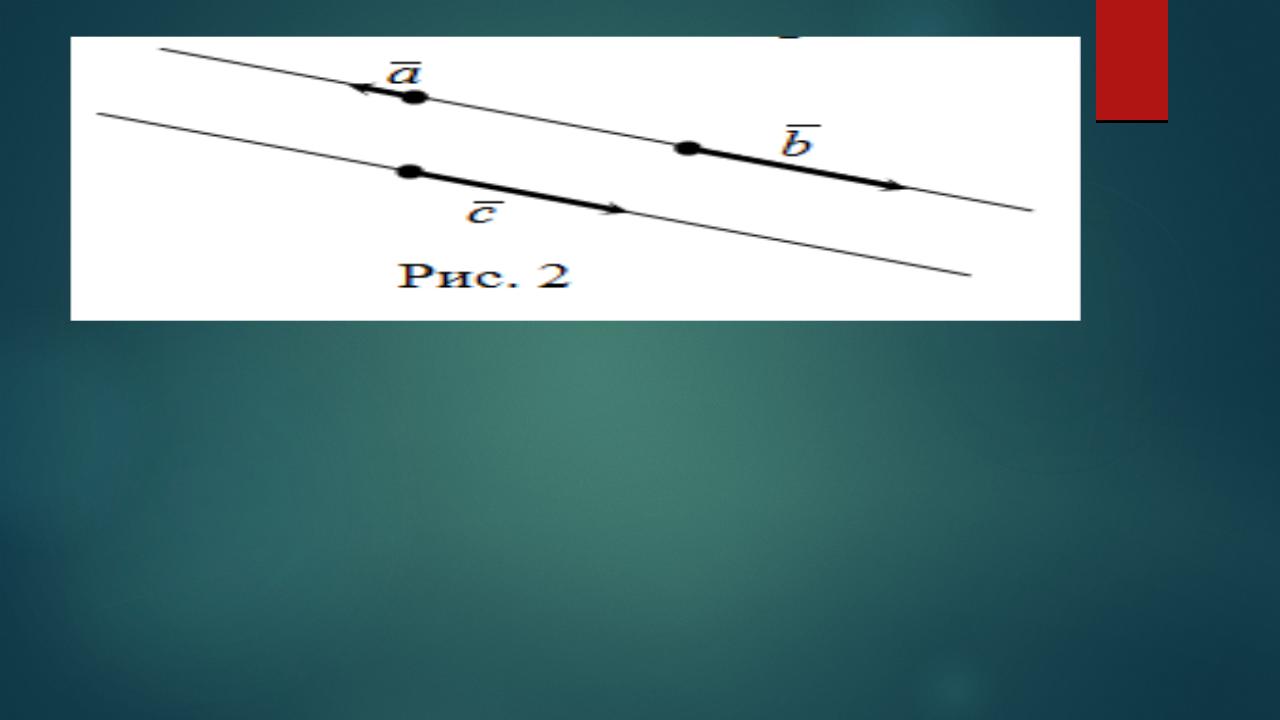
В противном случае векторы называются неколлинеарными.
ПРИМЕЧАНИЕ!!!
Нулевой вектор коллинеарен любому другому вектору плоскости.

3. Сонаправленные и противоположно направленные векторы на плоскости. Два коллинеарных вектора называются сонаправленными
когда и только тогда, если их направления совпадают. Сонаправленные векторы обозначаются следующим образом:а b. 
Свойства векторов
Предварительные сведения
Перед тем как вводить свойства векторов, введем, непосредственно, понятие вектора, а также понятия их сложения, умножения на число и их равенства.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ — (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Чтобы ввести определение равенства двух векторов, сначала нужно разобраться с такими понятиями, как коллинеарность, сонаправленность, противоположная направленность двух векторов, а также длину вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}↑↑\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↑↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Осталось ввести понятие сложения векторов, а также их умножения на число.
Определение 8
Суммой векторов $\overline{a+b}$ будем называть вектор $\overline{c}=\overline{AC}$, который построен следующим образом: От произвольной точки A отложем $\overline{AB}=\overline{a}$, далее от точки $B$ отложем $\overline{BC}=\overline{b}$ и соединим точку $A$ c точкой $C$ (рис. 6).
Определение 9
Произведением вектора $\overline{a}$ на $k∈R$ будем называть вектор $\overline{b}$ который будет удовлетворять условиям:
- $|\overline{b}|=|k||\overline{a}|$;
- $\overline{a}↑↑\overline{b}$ при $k≥0$ и, $\overline{a}↑↓\overline{b}$ при $k
Свойства сложения векторов
Введем свойства сложения для трех векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$:
Коммутативность сложения векторов:
$\overline{α}+\overline{β}=\overline{β}+\overline{α}$
Ассоциативность трех векторов по сложению:
$(\overline{α}+\overline{β})+\overline{γ}=\overline{α}+(\overline{β}+\overline{γ})$
Сложение с нулевым вектором:
$\overline{α}+\overline{0}=\overline{α}$
Сложение противоположных векторов
$\overline{α}+(\overline{-α})=\overline{0}$
Все эти свойства можно легко проверить с помощью построений таких векторов с помощью определения 8. В двух первых сравнением построенных векторов с правой и левой частей равенства, а в третьем и четвертом с помощью построения вектора с левой стороны.
Свойства умножения вектора на число
Введем свойства умножения для двух векторов $\overline{α}$, $\overline{β}$ и чисел $a$ и $b$.
- $a(\overline{α}+\overline{β})=a\overline{α}+a\overline{β}$
- $\overline{α}(a+b)=\overline{α}a+\overline{α}b$
- $(ab)\overline{α}=a(b\overline{α})=b(a\overline{α})$
- $1\cdot \overline{α}=\overline{α}$
Все эти свойства можно легко проверить с использованием определений 8 и 9. В двух первых сравнением построенных векторов с правой и левой частей равенства, в третьем сравнением всех векторов, входящих в равенство, и в четвертом с помощью построения вектора с левой стороны.
Пример задачи
Пример 1
Провести сложение векторов
$2\overline{AB}+(2\overline{BC}+3\overline{AC})$
Решение.
Используя свойство сложения 2, получим:
$2\overline{AB}+(2\overline{BC}+3\overline{AC})=(2\overline{AB}+2\overline{BC})+3\overline{AC}$
Используя свойство умножения на число 1, получим:
$(2\overline{AB}+2\overline{BC})+3\overline{AC}=2(\overline{AB}+\overline{BC})+3\overline{AC}=2\overline{BC}+3\overline{AC}=5\overline{AC}$
Ответ: $5\overline{AC}$.
Нулевой вектор, формулы и примеры
Определение и формулы нулевого вектора
Длина нулевого вектора равна нулю:
С нулевым вектором не связано никакое направление в пространстве. Нулевой вектор считается сонаправленным любому вектору. Нулевой вектор одновременно коллинеарен и ортогонален любому вектору пространства.
Все координаты нулевого вектора в любой аффинной системе координат равны нулю. Например, в трехмерном пространстве
Свойства нулевого вектора
Нулевой вектор обладает следующими свойствами:
1) ;
2) ;
3) для любого вектора существует такой вектор , что
Вектор называется противоположным к вектору .
| Понравился сайт? Расскажи друзьям! | |||


 точки А и B,то вектор обозначается
точки А и B,то вектор обозначается вектор, у которого начало совпадает с
вектор, у которого начало совпадает с