Физика. 8 класс
Физика. 8 класс
ОглавлениеГлава 1. Общие сведения о движении§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4.  § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23.  УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ§ 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ  СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ§ 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7.  Элементы статики§ 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36.  КИНЕТИЧЕСКАЯ ЭНЕРГИЯ§ 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям |
Подробный обзор вычитания векторов
Можно выполнять математические операции с векторами в определенной степени. Некоторые из этих операций — сложение, вычитание и умножение. Разделение векторов не должно иметь большого значения. Это так, потому что деление векторов может быть определено как функция обратного умножения данных векторов.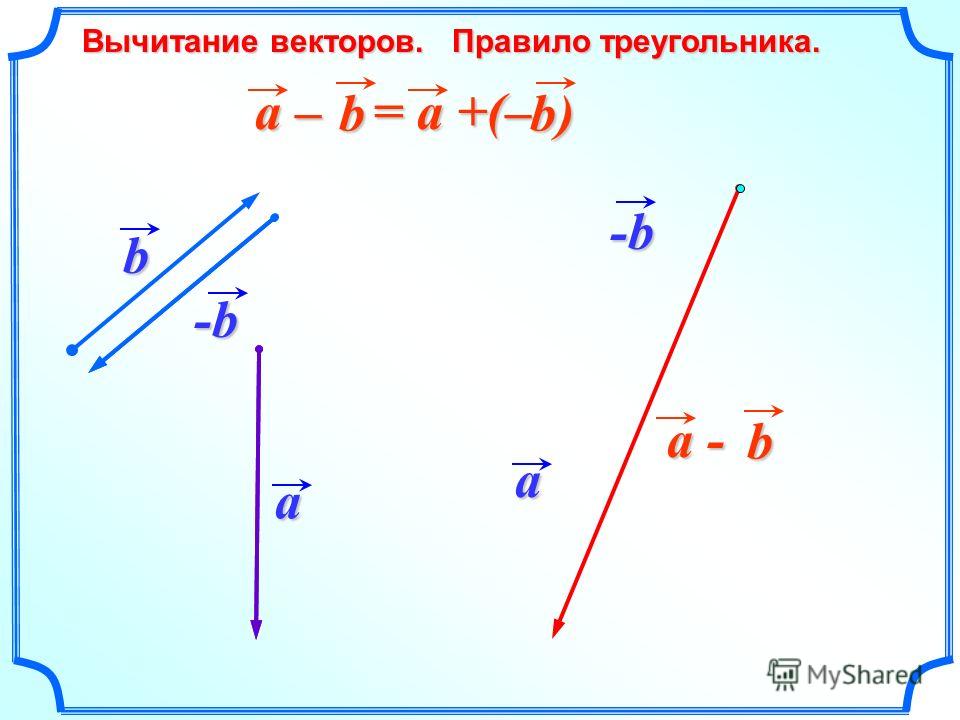
Точно так же вычитание векторов также можно рассматривать как функцию сложения векторов. Просто в этом случае нам нужно сделать один из заданных векторов отрицательным.
Что такое вычитание векторов?
Вычитание векторов — это вычитание двух векторов. При этом негатив одного вектора добавляется к другому вектору, который нам предоставили. Следовательно, вычитание векторов также можно определить как сложение одного из векторов с минусом другого данного вектора. Следует отметить, что результат, который мы получим после вычитания двух векторов, также будет вектором.
Свойство вычитания векторов можно применять только к объектам, которые сами являются векторами. Это означает, что обе величины, которые мы вычитаем, должны быть векторами. Если хотя бы одна из заданных величин является скалярной, то к ней не будет применяться формула вычитания векторов.
Кроме того, вычитаемые векторы должны представлять ту же физическую величину, которой они принадлежат.
Если их физические величины или единицы различны, то эти два вектора нельзя будет вычесть. Следовательно, вычитание этих векторов будет невозможно. Этот принцип очень похож на сложение векторов. Оба заданных вектора должны иметь одни и те же единицы, чтобы они могли дать результирующую, которая несет одну и ту же единицу.
Какова формула вычитания векторов?
Вычитание двух заданных векторов просто представляется как:
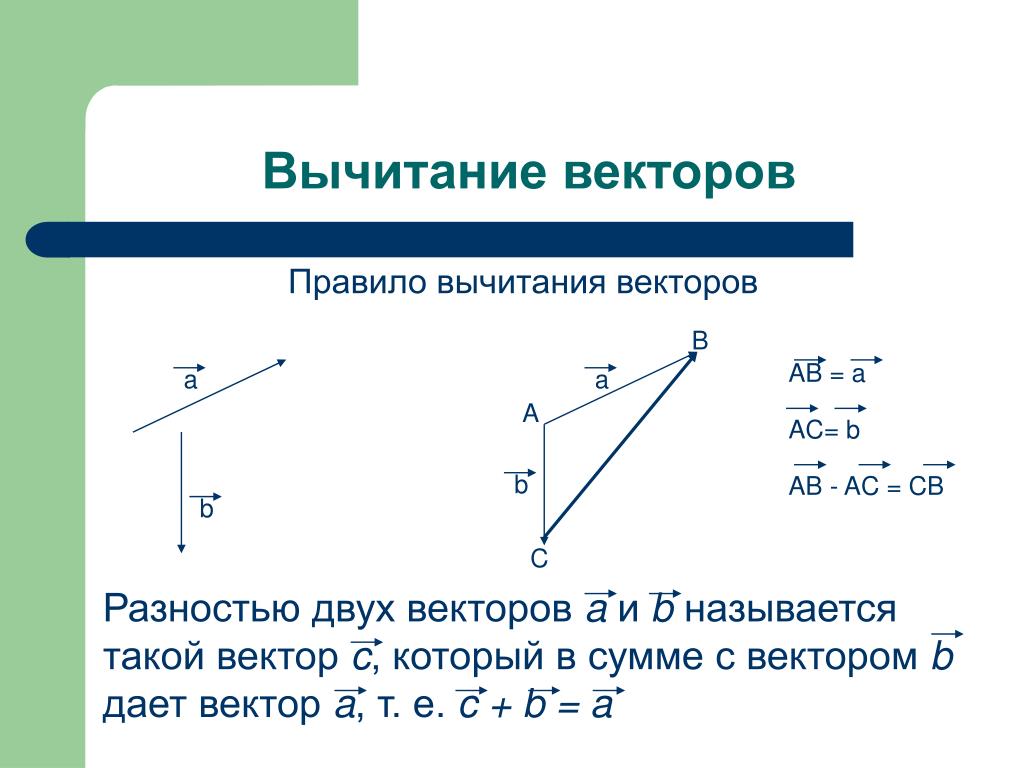
Используя треугольный закон вычитания векторов;
Разница между двумя векторами даст равнодействующую двух заданных векторов.
Результирующая =
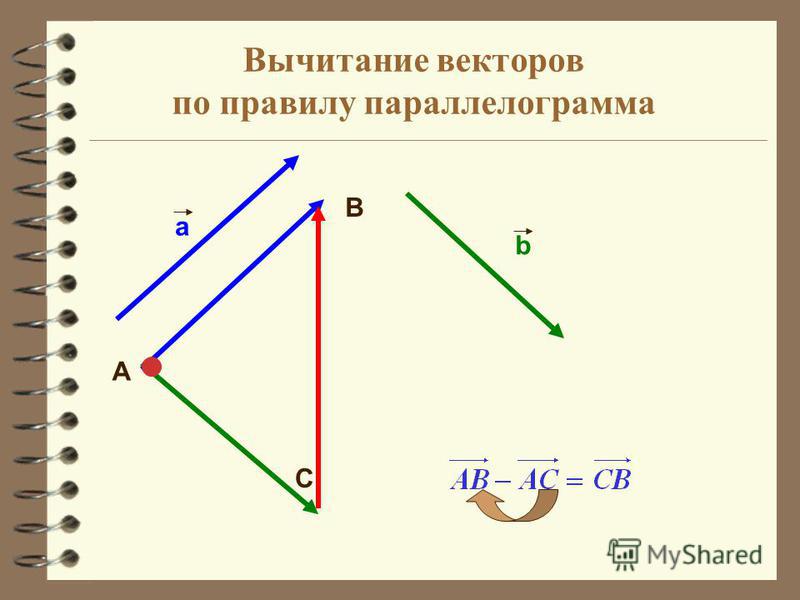
Аналогично, для закона вычитания векторов параллелограмма;
Если данные векторы действуют в двух разных направлениях, то равнодействующая их разности будет иметь следующий вид:
Resultant =
Случай сложения векторов останется тем же, если результирующий вектора не лежит между заданными двумя векторами.
Свойства вычитания векторов
Вычитание векторов относится к этому алгебраическому свойству. Учитывая, что и «a», и «b» имеют одинаковые единицы измерения, их биномиальное разложение приведет к одному и тому же результату.
Это также может быть определено как произведение двух результатов вычитания векторов. Если к этим двум применить теорему о биномиальном расширении, результат, который мы получим, будет таким же.
Как задачи с левой, так и с правой стороны приведут к двум разным результатам. Следовательно, можно сказать, что свойство ассоциативности не сохраняется при вычислениях вычитания векторов.
Проблемы по обе стороны от знака «не равно» — это две разные величины. Результаты, которые мы получим из этих двух расчетов, не будут одинаковыми. Следовательно, мы можем сказать, что вычитание векторов не коммутативно.
Этот результат будет содержать любой вектор ‘a → ’.
Заключение
Вычитание двух векторов можно определить как функцию сложения двух векторов. Методы, которые используются для нахождения вычитания векторов, такие же, как и методы, которые используются для нахождения суммы векторов. Этими методами являются векторный закон треугольника и векторный закон параллелограмма. Векторы не следуют свойствам коммутативности и ассоциативности в случае вычитания. А для вычитания векторов оба объекта должны быть векторами.
Сложение и вычитание векторов: графические методы | Физика |
Векторы в двух измерениях
Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т.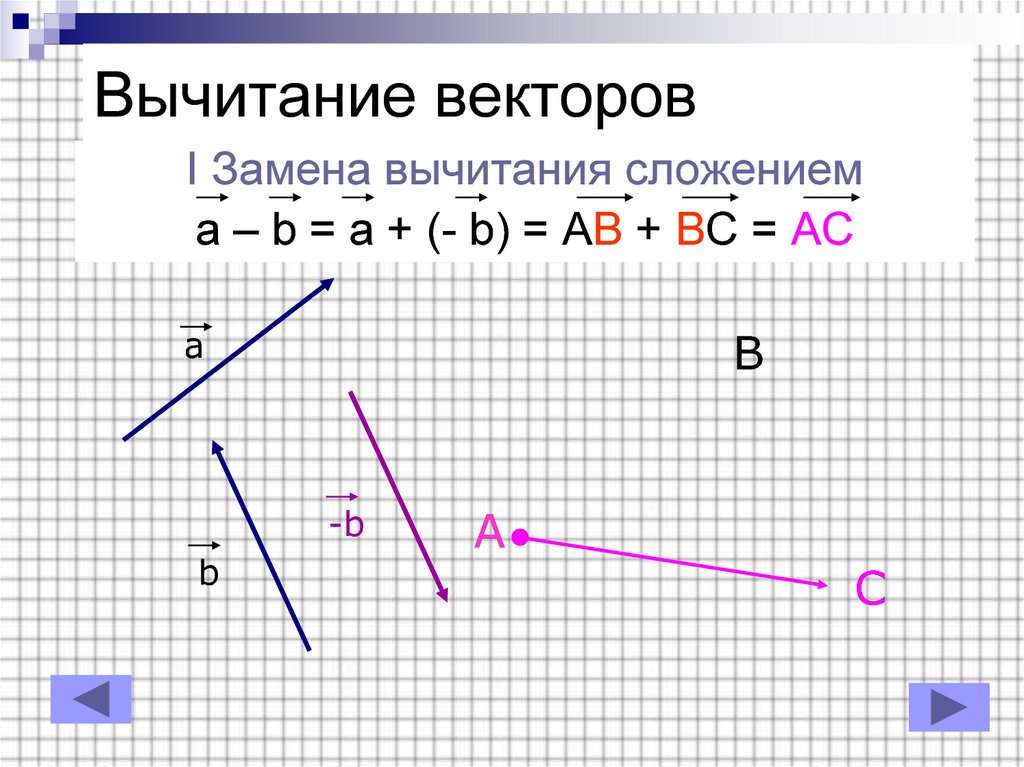
На рисунке 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный символ, такой как D , обозначает вектор. Его величина представлена курсивным символом D , а его направление — θ .
Векторы в этом тексте В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором
Рисунок 2.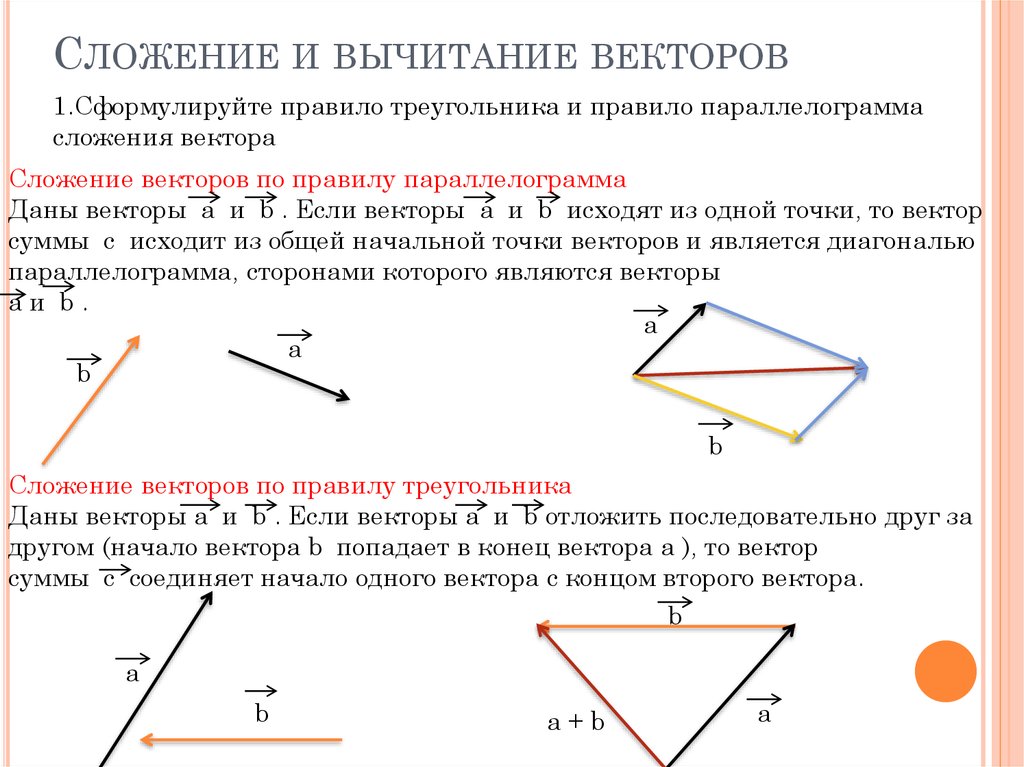
Человек проходит 9 кварталов на восток и 5 кварталов на север. Смещение 10,3 блока под углом 29,1º к северу от востока.
Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, изображенному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения
Сложение векторов: метод «голова к хвосту»
Метод «голова к хвосту» – это графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. хвост вектора является начальной точкой вектора, а начало (или кончик) вектора является конечным заостренным концом стрелки.
Рис. 4. Метод «голова к хвосту». Метод графического сложения векторов «голова к хвосту» проиллюстрирован для двух перемещений человека, идущего по городу, показанного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или
Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 5
Шаг 2. Теперь нарисуйте стрелку, обозначающую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6
Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7
Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.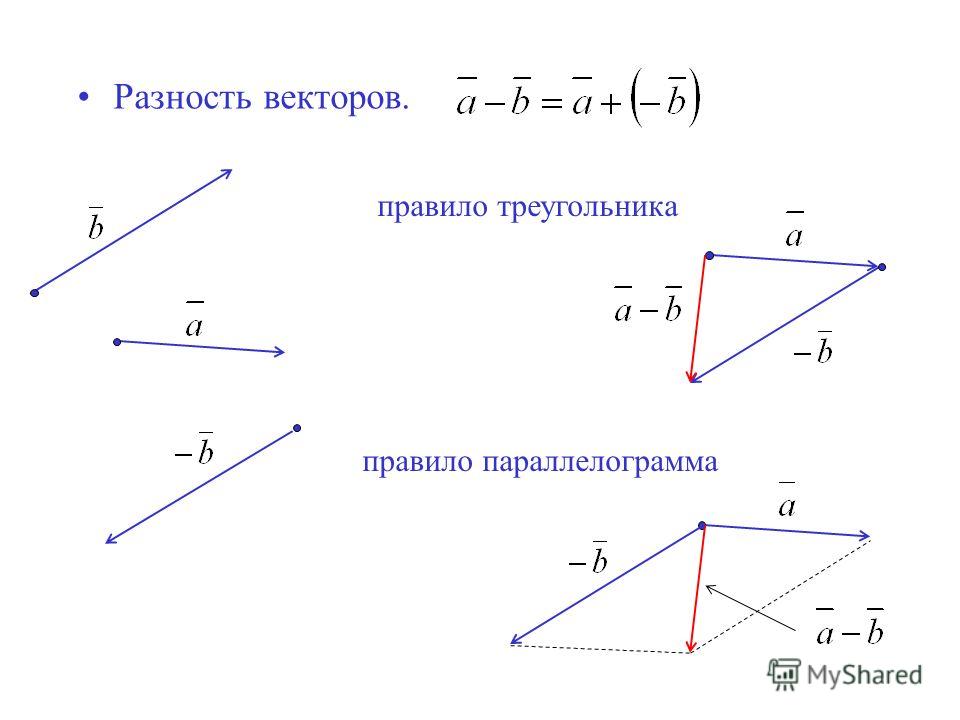
) Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.) Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов с использованием метода «голова к хвосту»: женщина прогуливается
Используйте графический метод сложения векторов, чтобы найти полное перемещение человека, который проходит следующие три пути (перемещения) по плоскому полю. Сначала она проходит 25,0 м в направлении 49..0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.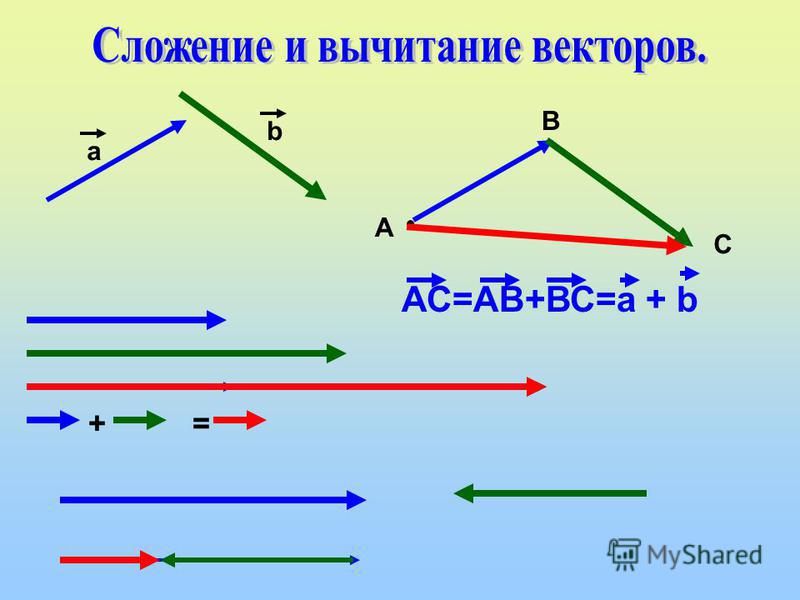
Представьте каждый вектор смещения графически со стрелкой, обозначив первый A , второй B и третий C , сделав длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволит определить величину и направление результирующего смещения, обозначенного цифрой 9.0083 Р .
Раствор(1) Нарисуйте три вектора смещения.
Рис. 8.
(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рис. 9.
(3) Нарисуйте результирующий вектор R .
Рис. 10.
(4) Используйте линейку для измерения величины R и транспортир для измерения направления R .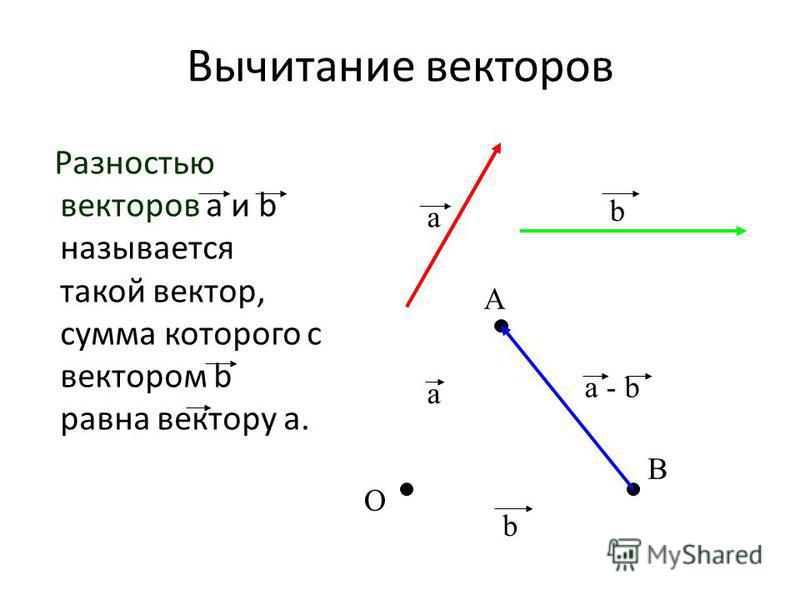
Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.
Рисунок 11
В этом случае видно, что полное смещение R имеет величину 50,0 м и направлено в направлении 7,0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0º к югу от востока.
Обсуждение Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Таким образом, мы можем добавлять векторы в любом порядке, как показано на рисунке 12, и все равно получим то же решение.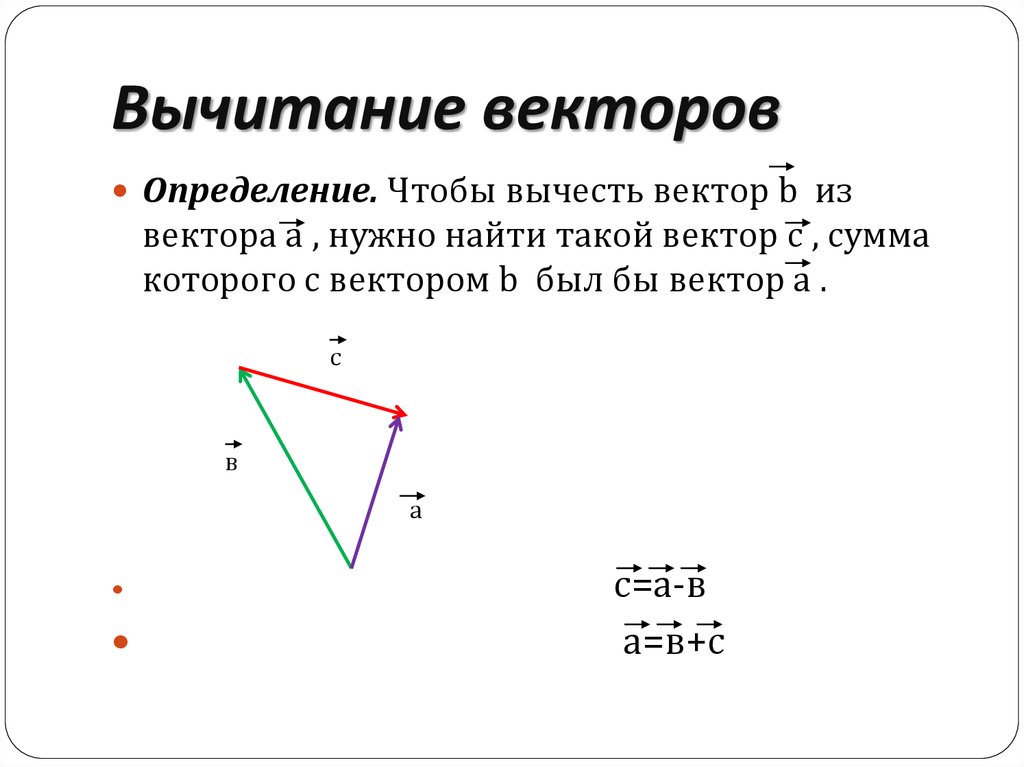
Рисунок 12.
Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.
А + В = В + А.
(Это верно и для сложения обычных чисел — вы получите один и тот же результат, сложите ли вы, например, 2 + 3 или 3 + 2 ).
Это видео можно использовать для просмотра. Он включает в себя основы работы с векторами — рисование векторов/добавление векторов. Вы узнаете об основном понятии вектора, о том, как графически складывать векторы, а также о том, что графически означает умножение вектора на скаляр.
Вычитание векторов Вычитание векторов — это прямое расширение сложения векторов.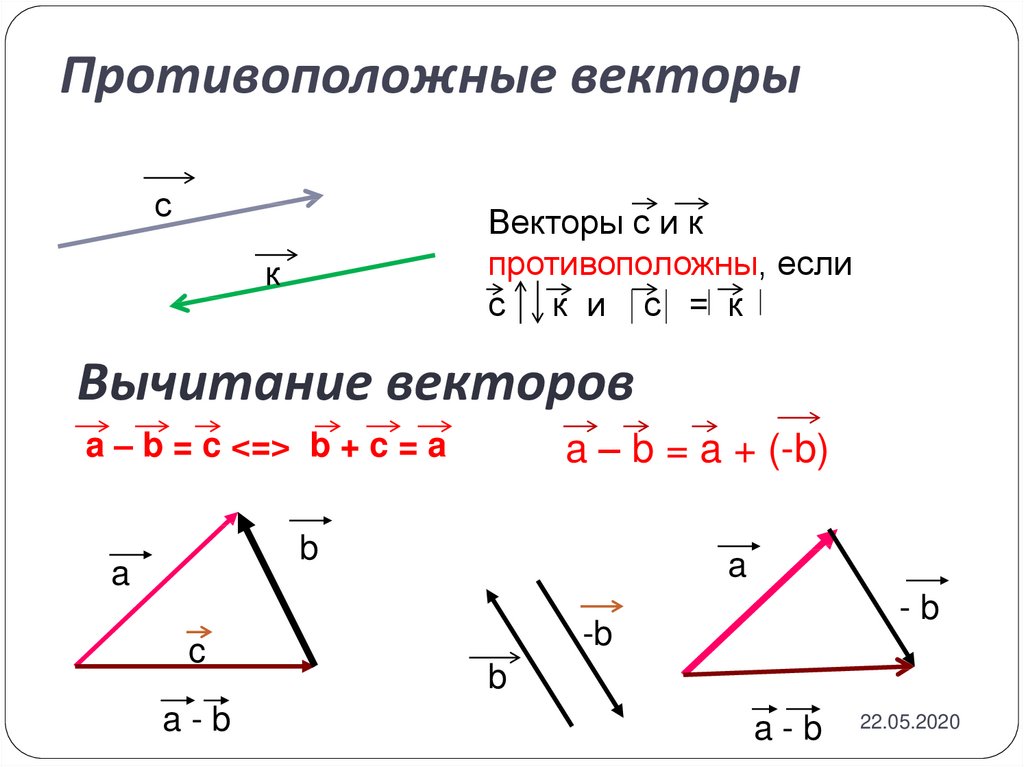
Чтобы определить вычитание (скажем, мы хотим вычесть B из A, записанного A – B), мы должны сначала определить, что мы подразумеваем под вычитанием.0077 минус вектора B определяется как –B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, B имеет ту же длину, что и -B, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Рис. 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, B является минусом 9.0083 –В ; он имеет ту же длину, но противоположное направление.
Вычитание вектора B из вектора A определяется просто как сложение –B с A .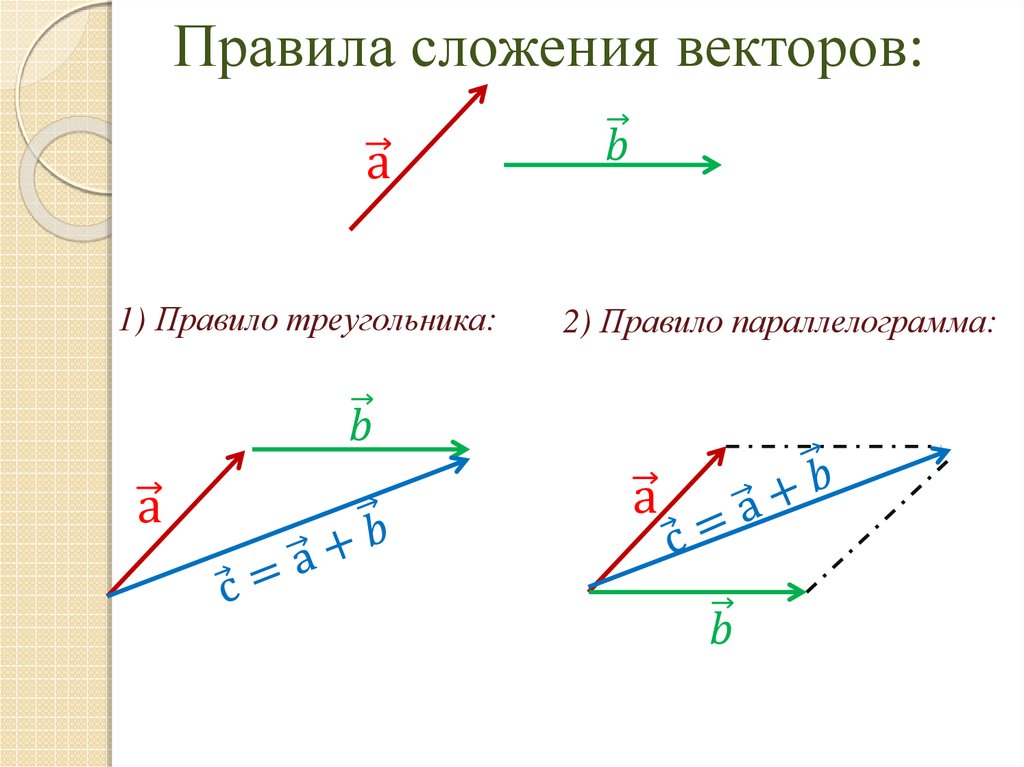
Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.
А — В = А + (-В)
Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2)). Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.
Пример 2. Графическое вычитание векторов: женщина, плывущая на лодке
Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0º к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112º к северу от востока (или 22,0º к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном , на втором этапе пути, где она окажется? Сравните это место с расположением дока.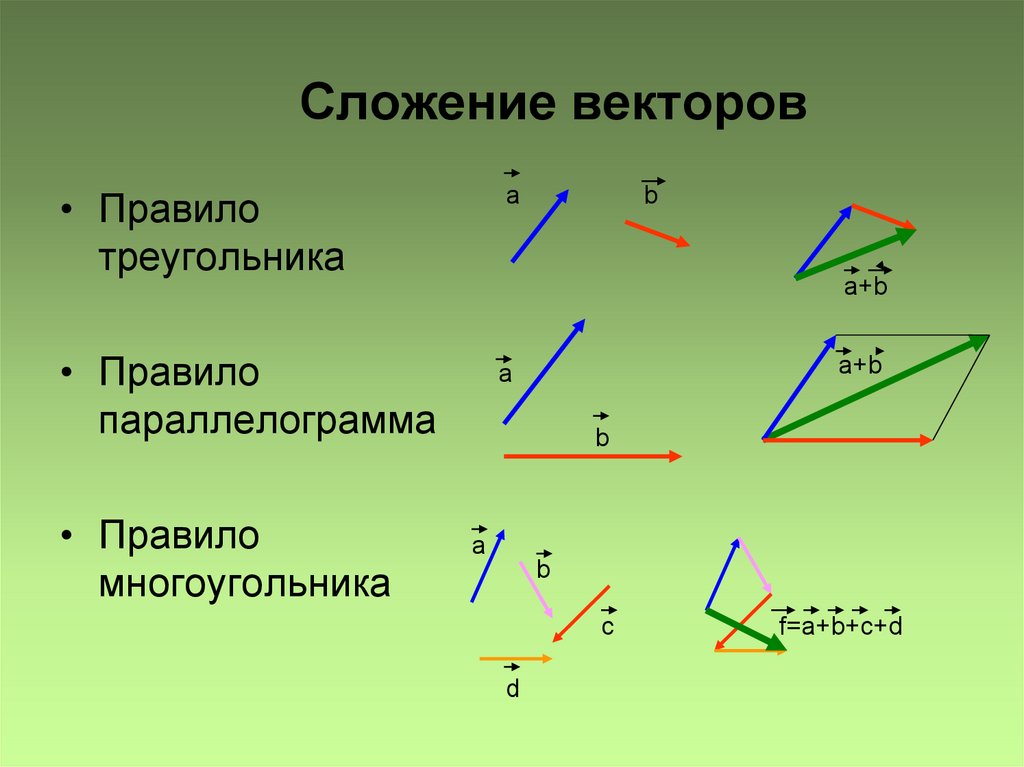
Рисунок 14.
СтратегияМы можем представить первый отрезок пути вектором A , а второй отрезок пути вектором B . Док находится по адресу A + B . Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от востока. Мы представляем это как –B , как показано ниже. Вектор –B имеет ту же величину, что и B, но направлен в противоположную сторону. Таким образом, она окажется в локации A + (–B) , или A – B .
Рисунок 15
Выполним сложение векторов, чтобы сравнить местоположение причала, A + B , с местоположением, в которое по ошибке прибыла женщина, A + (-B) .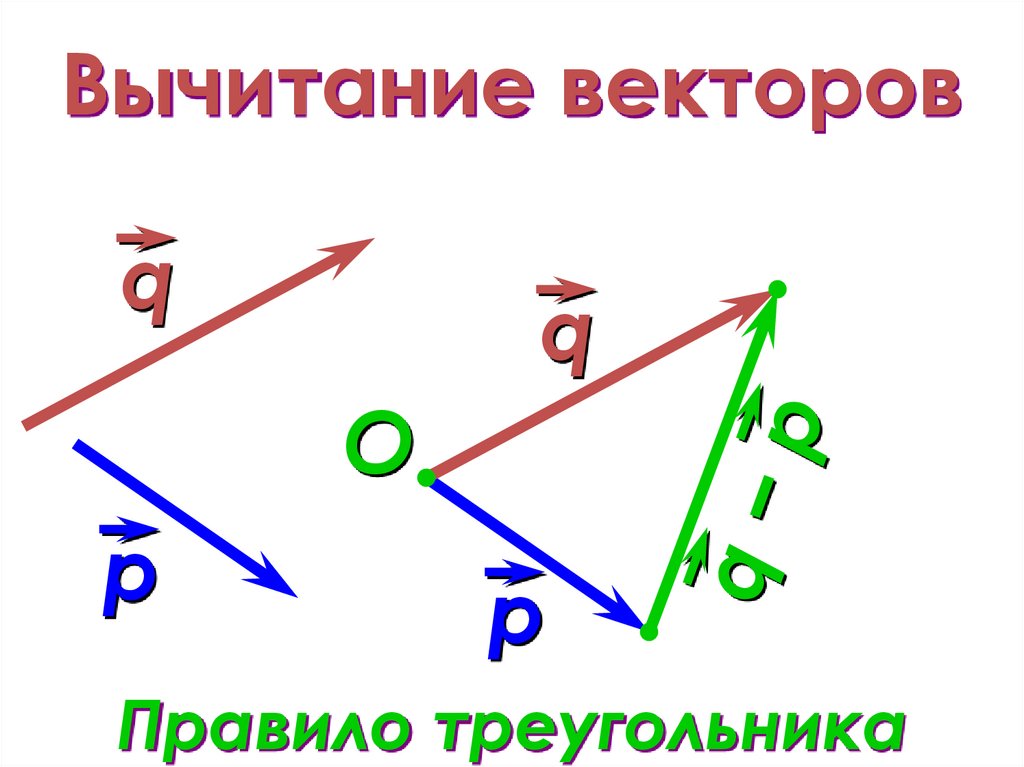
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы А и –В .
(2) Разместите векторы лицом к хвосту.
(3) Нарисуйте результирующий вектор R .
(4) С помощью линейки и транспортира измерьте величину и направление R .
Рисунок 16
В этом случае R = 23 . 0 м и θ = 7 . 5º к югу от востока.
(5) Чтобы определить местоположение дока, мы повторяем этот метод, чтобы добавить векторы A и B . Получаем результирующий вектор R’ :
Рисунок 17
В этом случае R = 52,9 м и θ = 90,1° к северу от востока.
Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.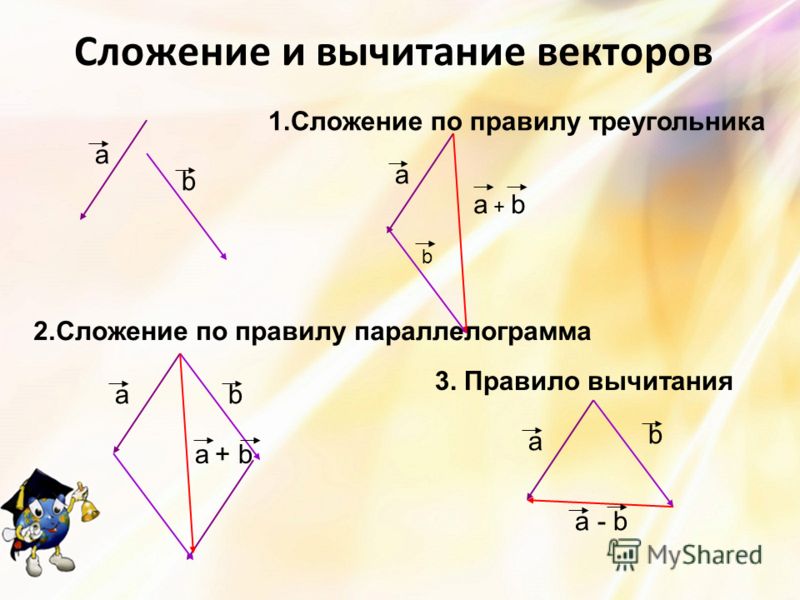
Поскольку вычитание вектора — это то же самое, что сложение вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Умножение векторов и скаляров
Если бы мы решили пройти в три раза большее расстояние на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м, или 82,5 м, в направлении 66,0º к северу от востока. Это пример умножения вектора на положительный скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор A умножается на скаляр c ,
- , величина вектора становится абсолютной величиной c A , .
- если c положительно, направление вектора не меняется,
- , если c отрицательно, направление меняется на противоположное.
В нашем случае c = 3 и A = 27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр от 0 до 1.
Разложение вектора на компоненты
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это связано с определением перпендикуляра компоненты одного вектора, например x — и y -компоненты, или компоненты север-юг и восток-запад.
Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0º к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
Исследования PhET: Игра в лабиринт
Узнайте о положении, скорости и ускорении на «Арене боли».
Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Нажмите, чтобы загрузить. Запуск с использованием Java.
Резюме
- Графический метод сложения векторов A и B включает в себя рисование векторов на графике и их сложение методом «голова к хвосту». Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.
- Графический метод вычитания вектора B из A включает добавление противоположного вектора B , который определяется как -B . В этом случае A — B = A + (-B) = R . Затем обычным образом применяют метод сложения «голова к хвосту» для получения результирующего вектора R .
- Сложение векторов коммутативно, так что A + B = B + A .
- Метод сложения векторов «голова к хвосту» заключается в том, что первый вектор рисуется на графике, а хвост каждого последующего вектора помещается в начало предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
- Если вектор A умножить на скалярную величину c , величина произведения будет равна cA . Если c положительно, направление произведения указывает на то же направление, что и A ; если c отрицательно, то направление произведения указывает на направление, противоположное A .
Концептуальные вопросы
1. Что из следующего является вектором: рост человека, высота на Эвересте, возраст Земли, температура кипения воды, стоимость этой книги, население Земли, ускорение свободного падения?
2.
Приведите конкретный пример вектора, указав его величину, единицы измерения и направление.
3. Что общего между векторами и скалярами? Чем они отличаются?
4. Двое отдыхающих в национальном парке отправляются из своей хижины в одно и то же место на озере, каждый из которых идет своим путем, как показано ниже. Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста?
Рис. 18.
5. Если пилоту самолета велят пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на рисунке 19. Какая еще информация ему потребуется, чтобы добраться до Сакраменто. ?
Рисунок 19.
6. Предположим, вы делаете два шага A и B (то есть два ненулевых смещения). При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут сложиться, чтобы получить ноль? Максимальное расстояние, на котором вы можете оказаться от начальной точки A + B сумма длин двух шагов?
7.
Объясните, почему нельзя добавить скаляр к вектору.
8. Если вы сделаете два шага разной длины, сможете ли вы оказаться в исходной точке? В более общем смысле, могут ли два вектора с разными величинами дать в сумме ноль? Можно три или больше?
Задачи и упражнения
Используйте графические методы для решения этих задач. Вы можете предположить, что данные, взятые из графиков, имеют точность до трех цифр.
1. Найдите следующее для пути А на рис. 20: (а) общее пройденное расстояние и (б) величину и направление смещения от начала до конца.
Рисунок 20. Различные линии обозначают пути, по которым идут разные люди, идущие по городу. Все блоки со стороной 120 м.
2. Найдите следующее для пути B на рисунке 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.
3. Найдите северную и восточную составляющие смещения для туристов, показанных на Рисунок 20.
4. Предположим, вы идете 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 21, то эта задача требует от вас найти их сумму R = A + B .
Рисунок 21. Два смещение A и B добавить, чтобы получить общее смещение R с величиной R и направлением θ .
5. Предположим, вы сначала прошли 12,0 м в направлении 20° к западу от севера, а затем 20,0 м в направлении 40,0° к югу от запада. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представите два этапа прогулки как векторные смещения A и B , как на рисунке 22, то эта задача найдет их сумму R = A + B .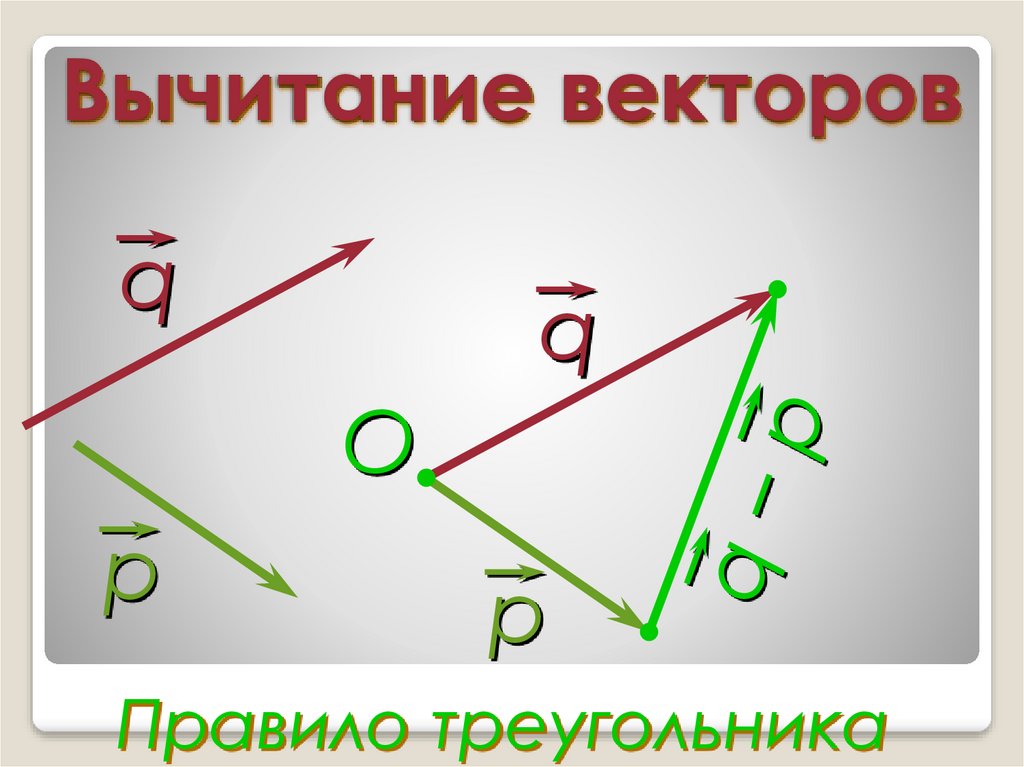
)
Рис. 22.
6. Повторите описанную выше задачу, но поменяйте порядок двух шагов ходьбы; показать, что вы получаете тот же конечный результат. То есть вы сначала проходите отрезок B , который составляет 20,0 м в направлении точно на 40º к югу от запада, а затем проходите отрезок A , который составляет 12,0 м в направлении ровно 12,0 к западу от севера. (Эта задача показывает, что A + B = B + A .)
7. (a) Повторите задачу двумя предыдущими задачами, но на втором этапе вы пройдете 20,0 м в направлении 40° к северу от востока (что эквивалентно вычесть B от A — то есть к нахождению R’ = A — B ). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала проходите 20,0 м в направлении на 40º к югу от запада, а затем 12,0 м в направлении на 20º к востоку от юга (что эквивалентно вычитанию A из B — это R» = B — A = R’ Покажите, что это так.
8. Покажите, что порядок сложения трех векторов не влияет на их сумму. Покажите это свойство с помощью выбор любых трех векторов A , B , C и
C\mathbf{C}C
, все они имеют разную длину и направление. Найдите сумму A + B + C , затем найдите их сумму при сложении в другом порядке и покажите, что результат тот же. (Есть пять других заказов, в которые можно добавить A , B и C ; выберите только один.) 9. Покажите, что сумма векторов, рассмотренных в примере 2, дает результат, показанный на рисунке 17.
10. Найдите модули скоростей V A и V B на рисунке 23.
Рисунок 23. Две скорости V A и V B 0 ADD ADS ARTA ALI AI AS AIS AIS AIS AIS AIS AIS AIS AIS AIS AIS AIS AIS AI AS AI AS AIS AIA A ADAI AIS AIA A ADAI AI AS AIS AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI AI A ADAI A
11.
