Презентация «Сложение и вычитание векторов» | Презентация к уроку по геометрии (9 класс) по теме:
Опубликовано 24.09.2013 — 15:44 — Погребняк Татьяна Николаевна
Данная презентация содержит несколько кадров, которые помогут наглядно показать правило сложения и вычитания векторов. Слайды содержат необходимые определения для выполнения указанных действий.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
ГОУ лицей № 408 Пушкинского района Санкт- Петербурга.
Слайд 2
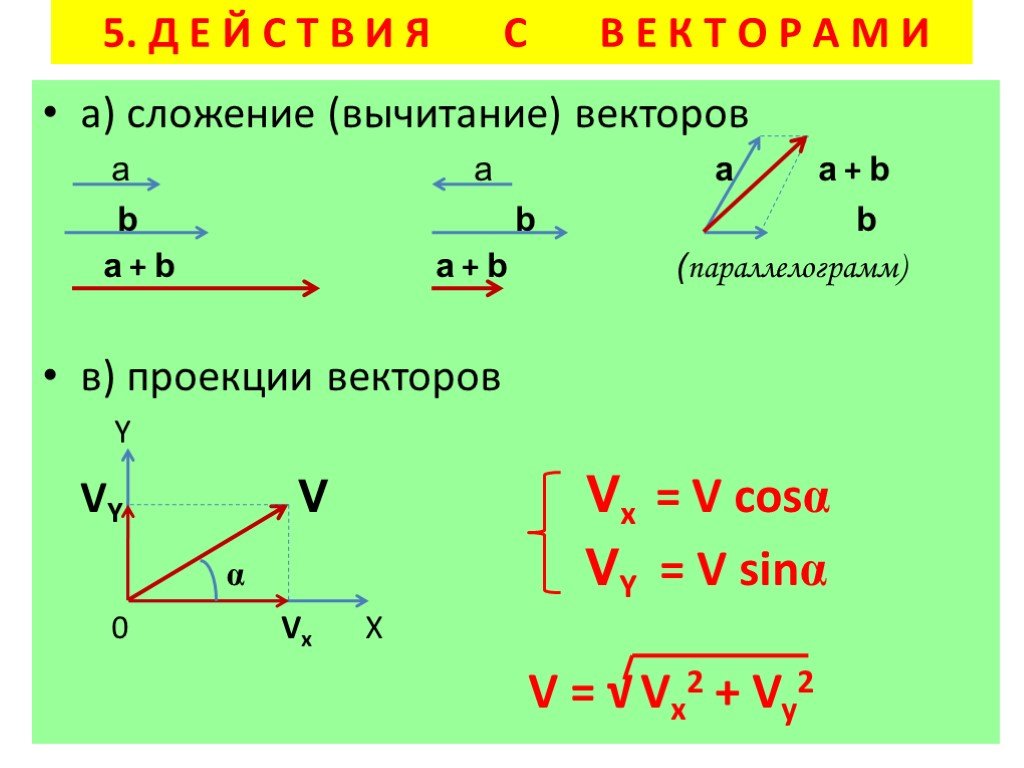
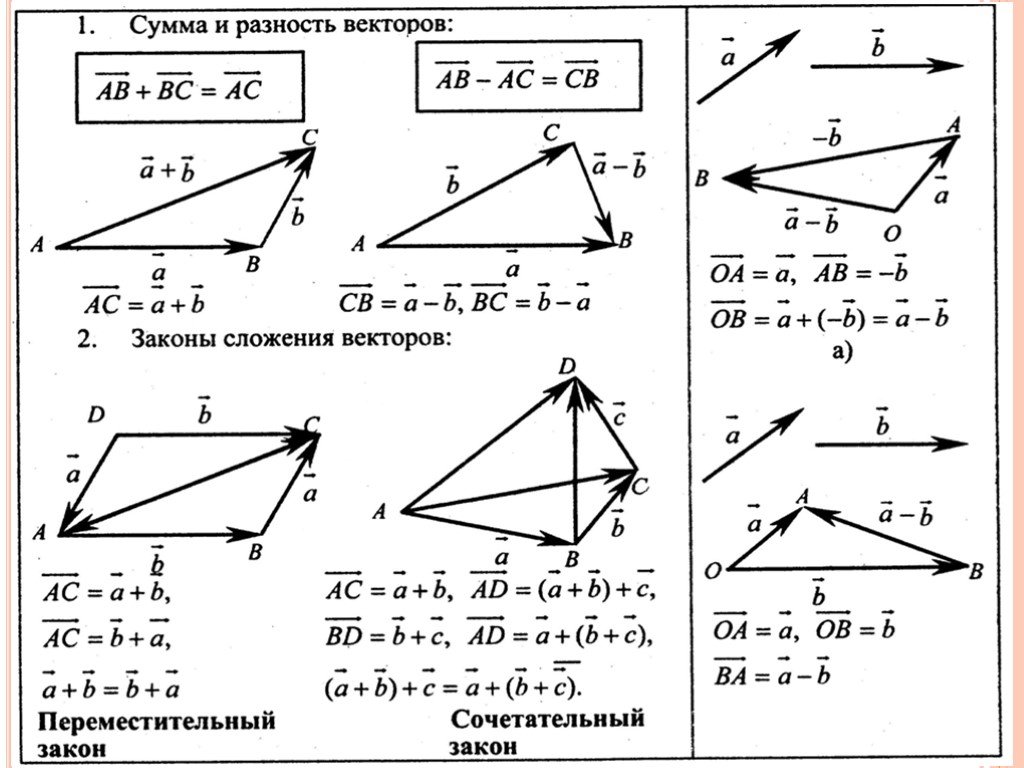
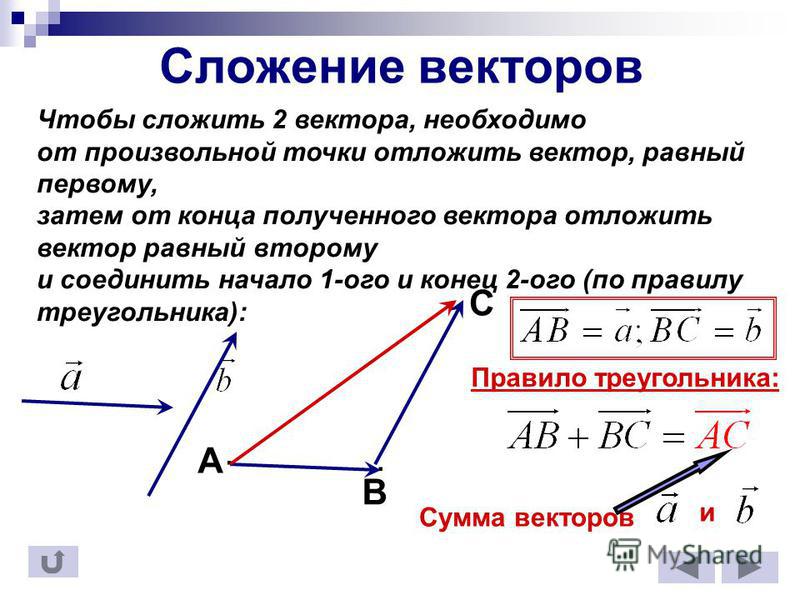
Сумма двух векторов Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Слайд 3
Правило параллелограмма Правило параллелограмма. Для сложения двух неколлинеарных векторов u и v , нужно отложить от какой- либо точки А векторы равные данным и построить параллелограмм АВС D. Тогда диагональ АС и будет суммой двух векторов.
Слайд 5
Правило треугольника Правило треугольника.
Для сложения двух векторов по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Слайд 7
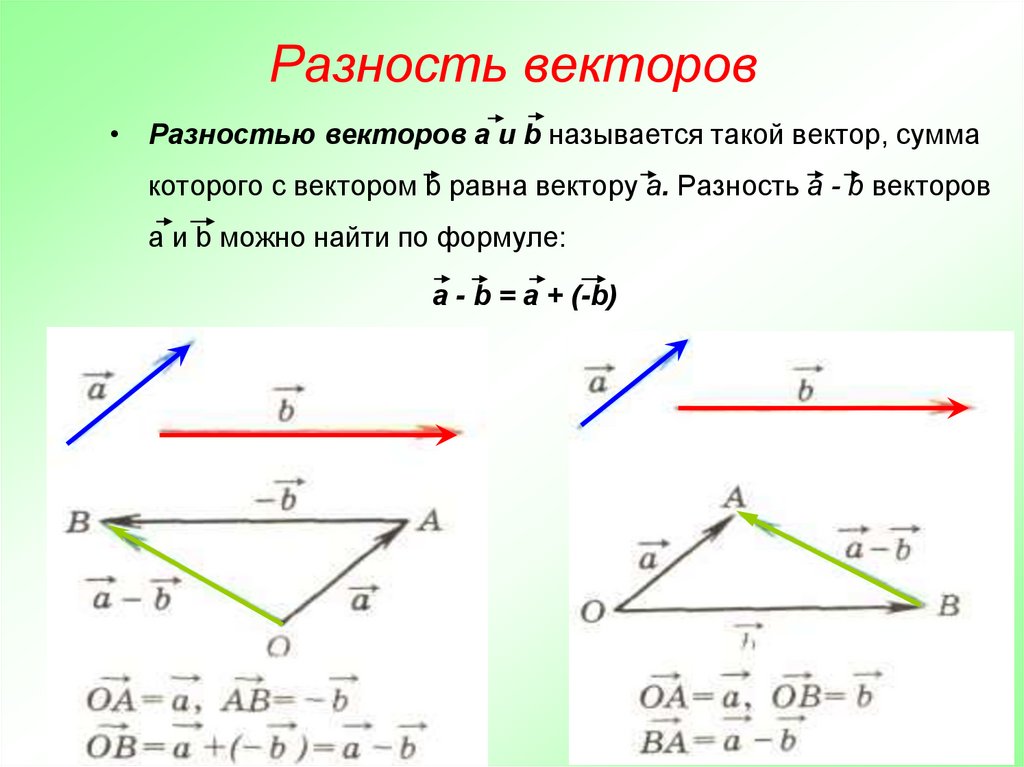
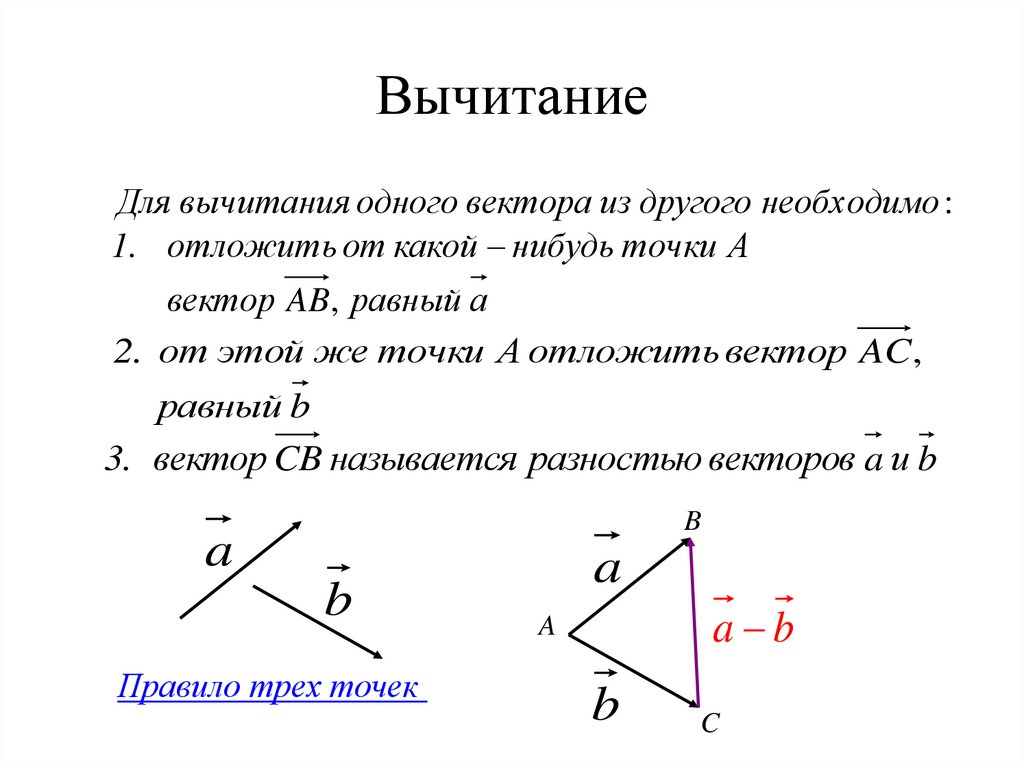
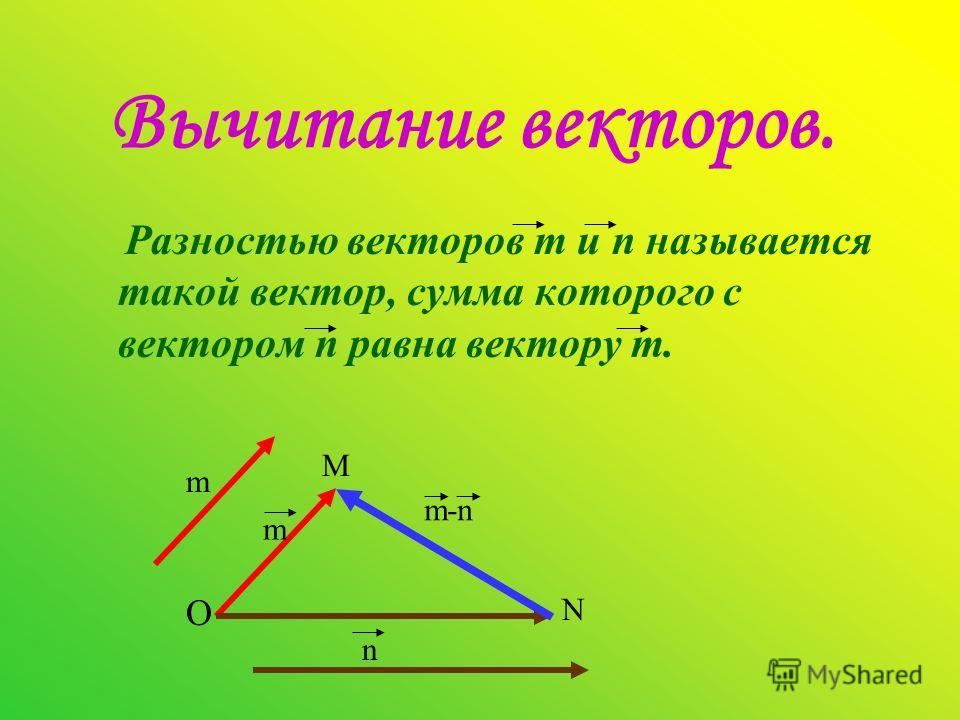
Вычитание векторов Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор , противоположный вектору b . Полученный в результате этой операции вектор с и будет являться разностью векторов а и b . Таким образом, с = а − b = а + (− b ).
Слайд 8
Спасибо за внимание!!! Учитель математики: Т.Н.Погребняк.
По теме: методические разработки, презентации и конспекты
презентация к уроку «Сложение и вычитание векторов» 9 класс.
Презентация к уроку » Сложение и вычитание векторов» 8 класс. Изучение правила треугольника,параллелограмма,многоугольника. Вычитание векторов. Решение задач….
конспект урока»Сложение и вычитание векторов» 9 класс
Конспект урока » Сложение и вычитание векторов» 9 класс.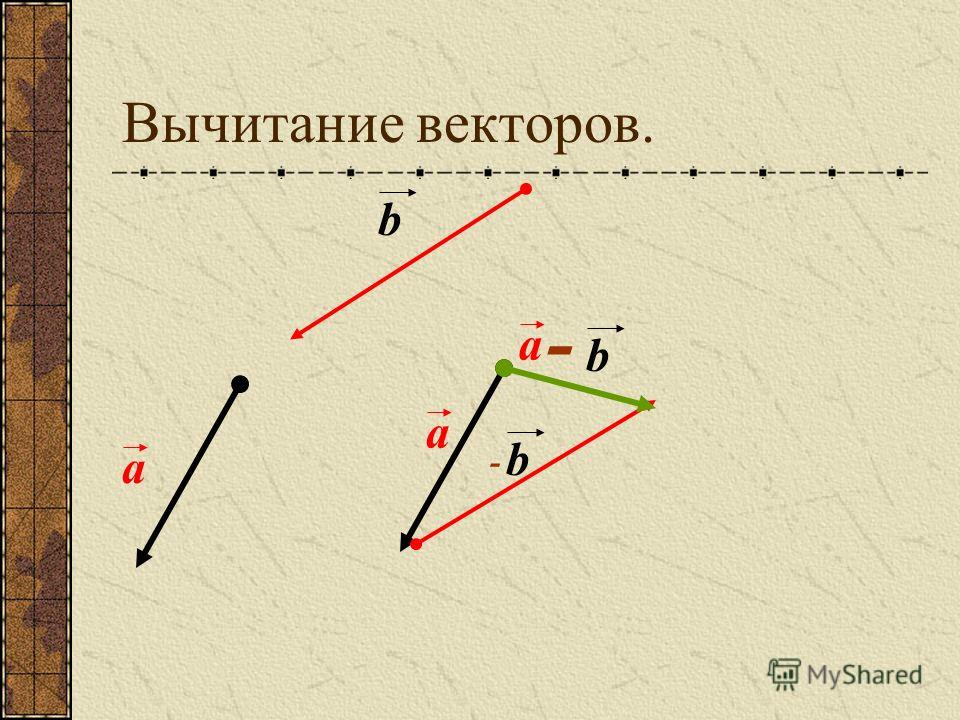
…
Презентация на тему — Сложение и вычитание векторов
Презентация на тему — Сложение и вычитание векторовПрезентацию подготовила ученица 10 класса — Сисейкина АнастасияРуководитель: Давтян Римма Артемовна…
Сложение и вычитание векторов
Урок геометирии 9 класс…
38. Интерактивный тест по теме: «Сложение и вычитание векторов. Умножение вектора на число».
Данный тест с автоматизированной проверкой ответа может быть использован на занятиях промежуточного, обобщающего или итогового контроля знаний учащихся. Для корректной работы теста, необходимо установ…
Диктант по теме: «Вектор. Сложение и вычитание векторов».
Презентация для проведения диктантов по геометрии….
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА (Понятие вектора. Сложение и вычитание векторов.)
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Геометрии 10класс (Понятие вектора. Сложение и вычитание векторов.)…
Поделиться:
Раздел 2 .
Вектора и метод координат в пространстве.Тема 2.1. Вектора.
1. Классификация векторов
| Вектора |
| Неколлинеарные |
| Коллинеарные (2 вектора) Лежат на параллельных прямых или на одной прямой |
| Сонаправленные Направлены в одну сторону |
| Противонаправленные Направленны в разные стороны |
| Равные Равные по длине Равные по длине |
| Противоположенные Равные по длине |
| Компланарные (3 вектора) Лежат на параллельных плоскостях или в одной плоскости |
| Некомпланарные Не лежат в одной плоскости |
2 .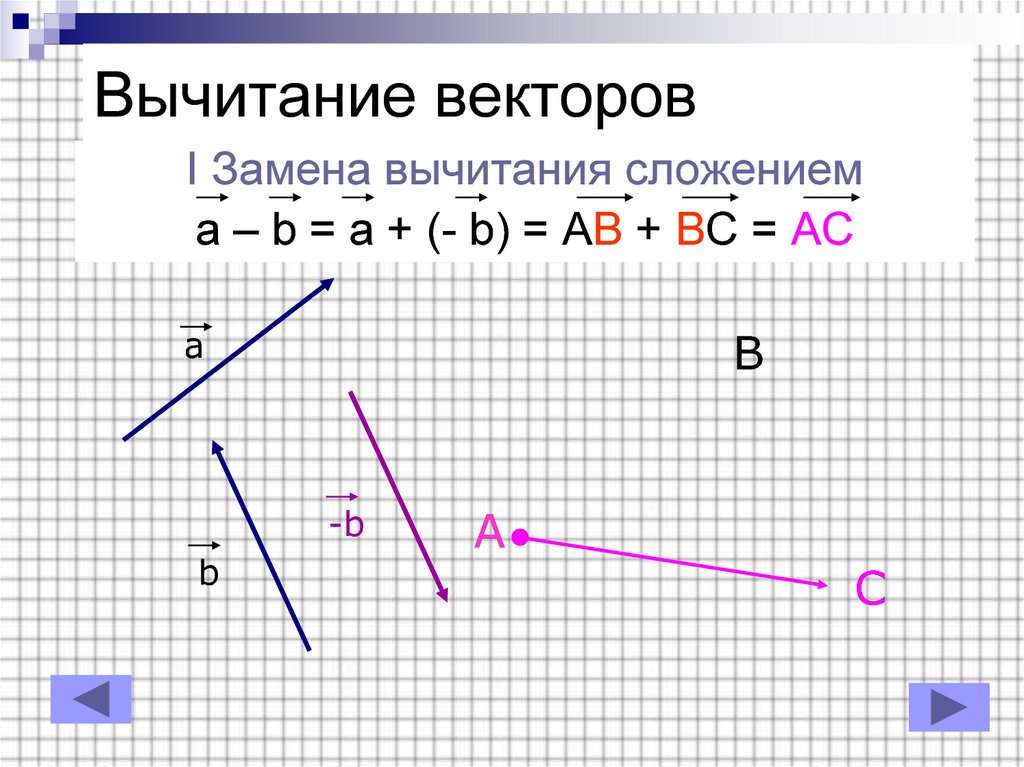
Сложение трех некомпланарных векторов (правило параллелепипеда)
Чтобы сложить три вектора и , надо построить параллелепипед так, что бы отрезки были его ребрами.
Суммой этих векторов является диагональ этого параллелепипеда.
Если надо вычесть вектор, то надо прибавить противоположенный ему вектор.
4. Выразить вектор через три некомпланарных вектора
K
B C
A D
=
5.
правило сложения векторов
(заменяем вектор на противоположенный
(меняем местами вектора)
правило вычитания векторов
(заменяем вектор на противоположенный
(группируем вектора)
(группируем вектора)
Тренажер 2.1.1. Вектора в пространстве.
1. Задать три произвольных вектора . Построить результирующий вектор
а) для неколлениарных векторов на плоскости
б) для коллиниарных векторов на плоскости
в) для некомпланарных векторов в пространстве
2. Упростить выражение с векторами.
а).
б)
в)
3. В параллелепипеде точка . Разложить
а) вектор через вектора
б) вектор через вектора
в) вектор через вектора
4. В параллелепипеде найти результирующий вектор,применяя параллельный перенос вектора на равный ему вектор.
а)
б)
с)
Тема 2.2 . Метод координат
1. Нахождение координаты вектора В
и В А
Равные вектора имеют равные координаты.
2. Нахождение координаты середины отрезка
А М B
3. Нахождение длины отрезка АВ
4. Сложение векторов
Вычитание векторов
5.
Умножение вектора на число
6. Длина вектора или модуль вектора
7. Разложение вектора по единичным векторам
y
x
8. Скалярное произведение векторов
Определение
В координатах
9.
Нахождение косинуса угла между векторами
10. Свойства скалярного произведения
1). если
и
2). если угол между векторами острый
3). если угол между векторами тупой
11. Если вектора перпендикулярны, то их скалярное произведение равно нулю
если вектора коллинеарные
если
если
12. Уравнение окружности где
13. Уравнение сферы
14. Уравнение прямой, проходящей через две точки А и В
находим угловой коэффициент
решаем уравнение
15.
Если две прямые параллельны, то их угловые коэффициенты равны
если две прямые перпендикулярны, то
16. Что бы найти точку пересечения двух прямых и , надо
приравнять их правые части и найти абсциссу ( ) точки
пересечения. Подставив полученное в любое из данных уравнений, найдем
ординату ( ).
17. Что бы найти координаты точки пересечения прямой с осью абсцисс
(Ох), надо найти
Что бы найти координаты точки пересечения прямой с осью ординат
(Оу), надо подставить в уравнение прямой и найти
18. Что бы найти точку пересечения окружности и
прямой , надо решить подстановкой систему двух уравнений
и найти .
19. Если точка А лежит на оси ОХ, то ее координаты (х, 0, 0)
если точка В лежит на оси ОУ, то ее координаты (0, у, 0)
если точка С лежит на оси ОZ, то ее координаты (0, 0, z
Тренажер 2.
2.1. Метод координ ат
1.Вектора перпендикулярны. Длина вектора равна 2, а длины векторов и равны 1. Угол между векторами и равен 30 Найти величину скалярного произведения +
2. В прямоугольном параллелепипеде и диагональ наклонена к основанию под углом 60 . Найти скалярные произведения:
3. Дан куб с ребром равным 2. Найти угол между прямыми , расстояние между серединами
4. При каких длина вектора равна 11?
5. Даны два вектора . При каких ветора перпендикулярны и при каких угол между векторами острый?
6. Даны два вектора . При каких ветора коллинеарны?
7. Найти координаты точки М, лежащей на оси ОУ, если расстояние от нее до точки
равно расстоянию от нее до точки
8. Даны три точки ). Найти координаты точки лежащий на оси ОZ, так, что бы
9. Доказать, что четырехугольник АВСD является ромбом, если ) и . Найти площадь ромба и радиус, вписанной в ромб окружности.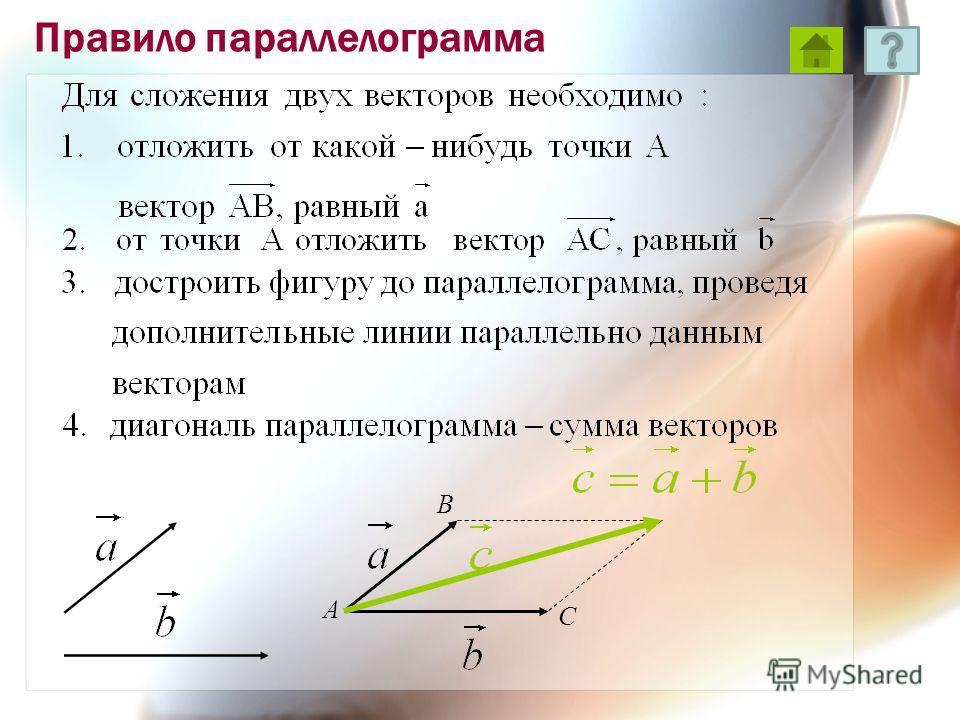
10. Даны точки ), которые являются тремя вершинами параллелограмма. Найти координаты четвертой вершины параллелограмма, его площадь и угол А.
11. Дан треугольник , при чем Найти угол между медианой и основанием треугольника и площадь треугольника .
12. Дан треугольник , при чем Найти расстояние от начала координат и до центра окружности, описанной около треугольника и площадь треугольника.
13. Найти расстояние от центра окружности до точки пересечения прямых .
14. Составить уравнение прямой, проходящей через точку пересечения прямых
и центр окружности .
15. Прямая пересекает окружность в точка А и В. Найти расстояние от середины отрезка АВ до центра окружнлости.
16. Дан треугольник , при чем Определить вид треугольника АВС и составить уравнение прямой, содержащией высоту, опущенную на основание треугольника.
Тема 2.3. Применение метода координат при решении задач по стереометрии.
Комбинации векторов (сложение и вычитание векторов) — Криста Кинг Математика
Создание комбинации
Когда мы хотим найти комбинацию двух векторов, мы просто сопоставляем начальную точку второго вектора с конечной точкой первого вектора, а затем рисуем новый третий вектор из начальной точки первого до конечной точки второго.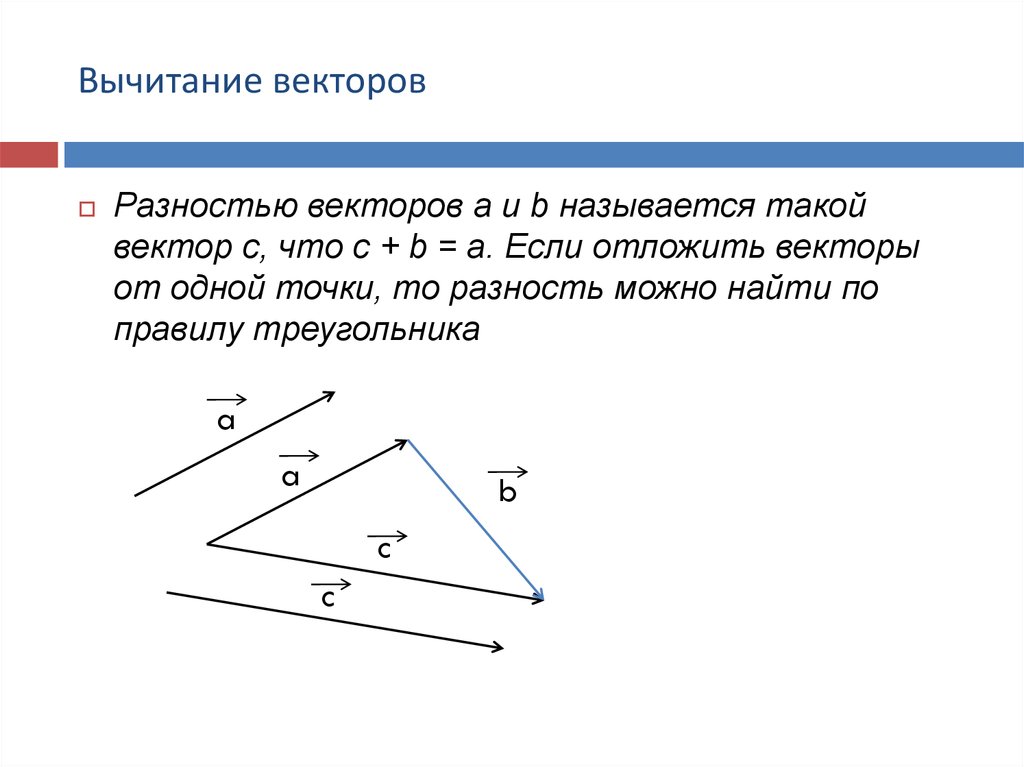
Другими словами, сочетание серого и синего — фиолетовый:
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов. В приведенном выше примере серый + синий = фиолетовый. Мы также можем вычитать векторы. Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору. В приведенном ниже примере серый — синий = фиолетовый. Сплошной синий вектор — исходный вектор, но поскольку мы вычитаем, мы движемся в противоположном направлении.
Как рассчитать комбинацию векторов
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого.
🙂Учить больше
Объединение трех векторов
Пример
Найдите комбинации векторов.
???\vec{AB}+\vec{BC}???
???\vec{BC}-\vec{AC}???
???\vec{AC}+\vec{CB}-\vec{DB}???
Для ???\vec{AB}+\vec{BC}???:
Начальная точка ???\vec{AB}??? ???A???, а его конечная точка ???B???. Начальная точка ???\vec{BC}??? это б??? (конечная точка ???A???), а его конечная точка ???C???. Следовательно, комбинация этих двух векторов от начальной точки первого до конечной точки последнего равна
???\vec{AB}+\vec{BC}=\vec{AC}???
Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору.
Для ???\vec{BC}-\vec{AC}???:
Когда два вектора вычитаются, мы можем изменить отрицательный вектор на положительный, изменив направление вектора. В этом случае ???-\vec{AC}??? становится ???+\vec{CA}???. Затем мы просто объединяем их, как обычно.
???\vec{BC}-\vec{AC}=\vec{BC}+\vec{CA}???
???\vec{BC}-\vec{AC}=\vec{BA}???
Для ???\vec{AC}+\vec{CB}-\vec{DB}???:
Начнем с изменения отрицательного вектора на положительный, изменив направление вектора. В этом случае ???-\vec{DB}??? становится ???+\vec{BD}???. Мы избавимся от негатива, а затем объединим векторы по два за раз.
???\vec{AC}+\vec{CB}-\vec{DB}=\vec{AC}+\vec{CB}+\vec{BD}???
???\vec{AC}+\vec{CB}-\vec{DB}=\vec{AB}+\vec{BD}???
???\vec{AC}+\vec{CB}-\vec{DB}=\vec{AD}???
Получить доступ к полному курсу Calculus 3
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление 3, исчисление iii, векторы, векторное исчисление, комбинации векторов, сложение векторов, вычитание векторов, объединение векторов
0 лайковвекторное вычитание — GCSE Math
Введение
Что такое векторное вычитание?
Как вычесть векторы
Рабочие листы векторного вычитания
Распространенные заблуждения
Практические вопросы по вычитанию векторов
Вычитание векторов Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое векторное вычитание?
Как вычесть векторы
Рабочие листы векторного вычитания
Распространенные заблуждения
Практические вопросы по вычитанию векторов
Вопросы GCSE по векторному вычитанию
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о вычитании векторов.
Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое вычитание векторов?
Вычитание вектора вычитание одного вектора из другого вектора.
Для этого мы вычитаем горизонтальные компоненты (верхние числа) вектора-столбца и вычитаем вертикальные компоненты (нижние числа) вектора-столбца.
Напр.
Давайте посмотрим на вектор a и вектор b .
\[\textbf{а}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) \четверка \textbf{b}= \left(\begin{массив}{1} 3\\ 1\\ \end{массив}\right)\]
\[\textbf{a}-\textbf{b}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) – \left(\begin{массив}{1} 3\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 3\\ \end{array}\right)\]
Вычитание векторов основано на сложении векторов.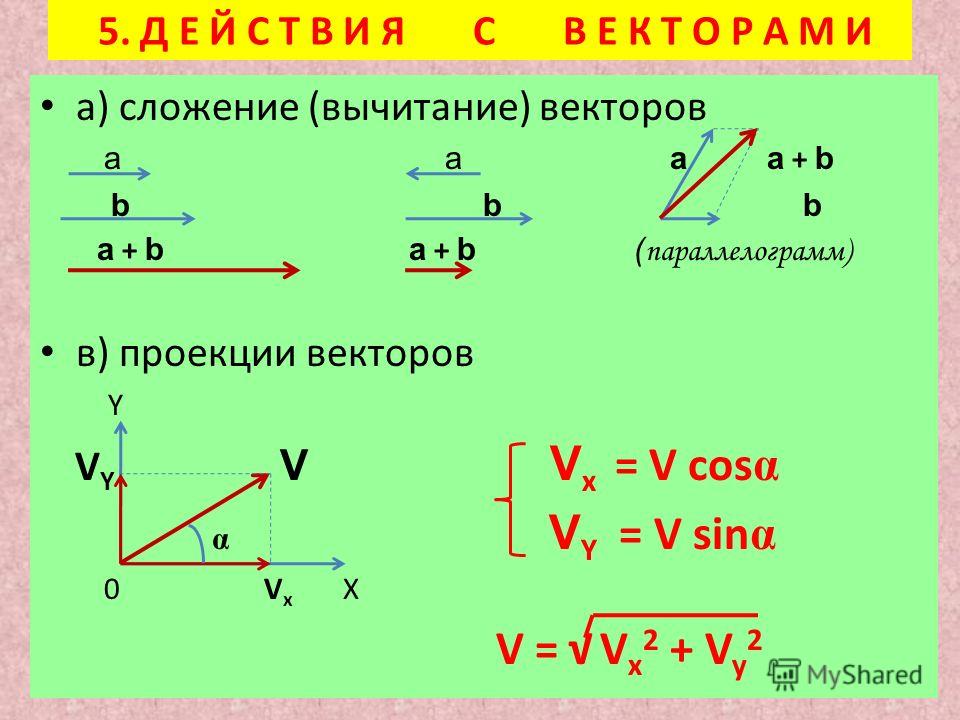
Первый вектор остается прежним, но второй вектор меняет направление на противоположное, становясь отрицательным вектором.
\mathbf{a}-\mathbf{b}=\mathbf{a}+-\mathbf{b}
Используя вектор a и вектор b , посмотрим, что получится.
\[\textbf{а}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа)\]
\[\textbf{b}= \left(\begin{массив}{1} 3\\ 1\\ \end{array}\right)\]
Нам нужен вектор – b . Направление вектора – b противоположно направлению исходного вектора b (но имеет ту же величину).
\[-\textbf{b}= \left(\begin{массив}{1} -3\\ -1\\ \end{массив}\right)\]
Итак,
\textbf{a} — \textbf{b}= \textbf{a}+ — \textbf{b}
Из сложения векторов мы знаем, что при сложении двух векторов второй добавляется к концу первого, как показано здесь:
Окончательный ответ известен как результирующий вектор.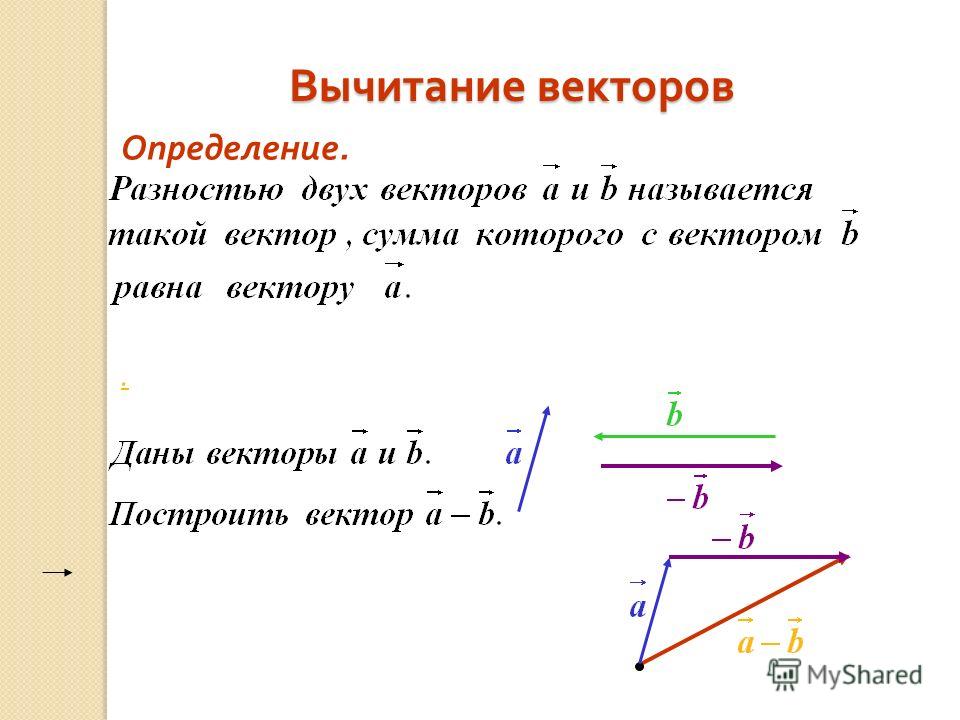
\[\textbf{a}-\textbf{b}=\textbf{a}+ -\textbf{b}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) +\ \left(\begin{массив}{1} -3\\ -1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 3\\ \конец{массив}\справа)\]
Следовательно,
\[\textbf{a} – \textbf{b}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 3\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 3\\ \end{массив}\right)\]
Что такое вычитание векторов?
Как вычесть вектор
Чтобы вычесть вектор из исходного вектора:
- Вычтите компоненты размером x .
- Вычесть 9Компоненты 0028 и .
- Запишите результирующий вектор.
Как вычитать векторы
Лист векторов (включая вычитание векторов)
Получите бесплатный лист вычитания векторов из 20+ вопросов и ответов по векторам.
Включает рассуждения и прикладные вопросы.
СКОРО
ИксЛист векторов (включает вычитание векторов)
Получите бесплатный лист вычитания векторов из 20+ вопросов и ответов по векторам. Включает рассуждения и прикладные вопросы.
СКОРО
Связанные уроки по векторам
Вычитание векторов является частью нашей серии уроков для поддержки пересмотра векторов . Возможно, вам будет полезно начать с урока по основным векторам, чтобы получить общее представление о том, чего ожидать, или воспользоваться пошаговыми руководствами, приведенными ниже, для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
- Векторы
- Величина вектора
- Вектор-столбец
- Векторное обозначение
- Умножение на вектор
- Добавление вектора
- Векторные проблемы
Примеры вычитания векторов
Пример 1: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 6\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 4\\ 3\\ \end{массив}\right)\]
- Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
6-4=2
2 Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
4-3=1
3 Запишите результирующий вектор.
\[\left(\begin{массив}{1} 6\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 4\\ 3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 1\\ \end{array}\right)\]
Пример 2: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 3\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 5\\ 1\\ \конец{массив}\справа)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
3-5=-2
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
2-1=1
Запишите результирующий вектор.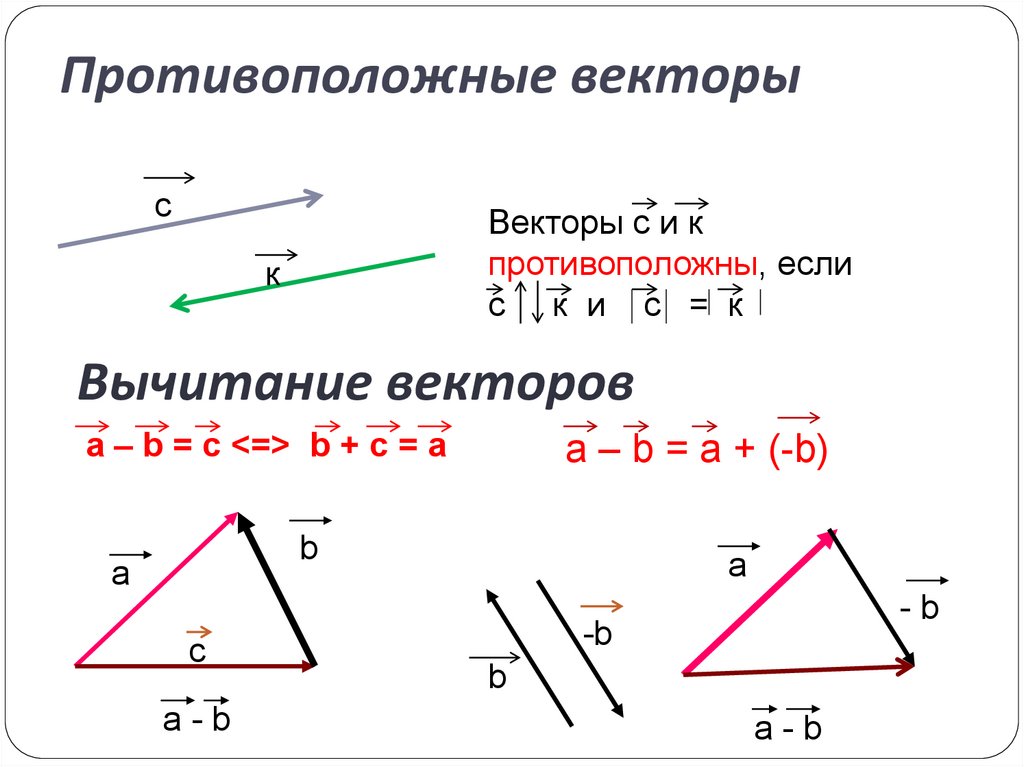
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} 3\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 5\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -2\\ 1\\ \конец{массив}\справа)\]
Пример 3: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 2\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 6\\ \end{массив}\right)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
2-2=0
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
4-6=-2
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} 2\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 6\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 0\\ -2\\ \end{array}\right)\]
Пример 4: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} -4\\ 3\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 1\\ \end{массив}\right)\]
Вычесть 9Компоненты 0028 x .
Вычесть второе верхнее число из первого верхнего числа
-4-2=-6
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
3-1=2
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} -4\\ 3\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -6\\ 2\\ \конец{массив}\справа)\]
Пример 5: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} -5\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -3\\ -2\\ \end{массив}\right)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
-5-(-3)=-2
Вычесть компоненты и .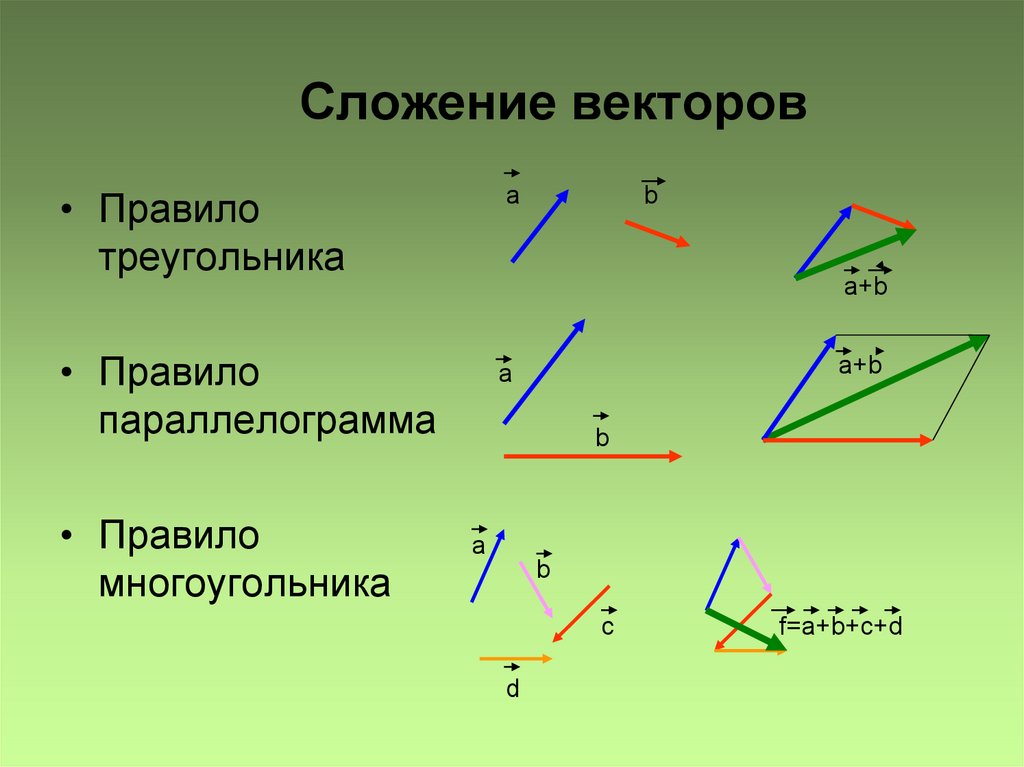
Вычесть второе нижнее число из первого нижнего числа
2-(-2)=4
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} -5\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -3\\ -2\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -2\\ 4\\ \end{array}\right)\]
Пример 6: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 2\\ -1\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -4\\ -3\\ \конец{массив}\справа)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
2-(-4)=6
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
-1-(-3)=2
Запишите результирующий вектор.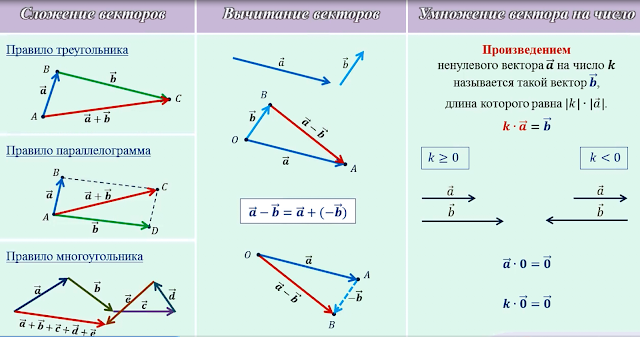
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} 2\\ -1\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -4\\ -3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 6\\ 2\\ \конец{массив}\справа)\]
Распространенные заблуждения
- Вычитание отрицательных целых чисел
При вычитании отрицательных целых чисел легко допустить ошибку.
Убедитесь, что навыки работы с отрицательными числами хорошо отработаны.
3-(-4)=3+4=7
- Порядок вычитания
Порядок вычитания очень важен. Вычитание векторов НЕ является коммутативным и должно выполняться в указанном порядке.
и т. д.
а — б ≠ б — а
- Обозначение векторов столбцов
Векторы-столбцы имеют только 2 числа в скобках: верхнее и нижнее число.
Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой, и нет необходимости в черте для разделения чисел.
- Окончательный ответ 0
Компонент x или компонент y может быть равен 0 . Если обе компоненты вектора равны 0, то конечным результирующим вектором будет вектор 0 . Это известно как нулевой вектор или нулевой вектор.
Напр.
\[\left(\begin{массив}{1} 3\\ 7\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 3\\ 7\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 0\\ 0\\ \end{array}\right)\]
Практические вопросы по вычитанию векторов
\begin{pmatrix} \; 3 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -3 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -3 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; 3 \;\\ \; -2\; \end{pmatrix}
\textbf{v}-\textbf{w}= \begin{pmatrix} \; 7 \;\\\; 3 \; \end{pmatrix} – \begin{pmatrix} \; 4 \;\\\; 1 \; \end{pmatrix} = \begin{pmatrix} \; 3 \;\\ \; 2\; \end{pматрица}
\begin{pmatrix} \; -3 \;\\ \; 5 \; \end{pmatrix}
\begin{pmatrix} \; -3 \;\\ \; -5 \; \end{pmatrix}
\begin{pmatrix} \; 3 \;\\ \; -5 \; \end{pmatrix}
\begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix}
\textbf{c}-\textbf{d}= \begin{pmatrix} \; 6 \;\\\; 2\; \end{pmatrix} – \begin{pmatrix} \; 3 \;\\ \; 7\; \end{pmatrix} = \begin{pmatrix} \; 3 \;\\ \; -5 \; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -6 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; -6 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; -2\; \end{pmatrix}
\textbf{b}-\textbf{a}= \begin{pmatrix} \; 5 \;\\\; 4\; \end{pmatrix} – \begin{pmatrix} \; -1 \;\\\; 6\; \end{pmatrix} = \begin{pmatrix} \; 6 \;\\\; -2\; \end{pmatrix}
\begin{pmatrix} \; -1 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; -1 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; 2\; \end{pmatrix}
\textbf{p}-\textbf{q}= \begin{pmatrix} \; -3 \;\\\; 6\; \end{pmatrix} – \begin{pmatrix} \; -2 \;\\\; 4\; \end{pmatrix} = \begin{pmatrix} \; -1 \;\\\; 2\; \end{pmatrix}
\begin{pmatrix} \; -5 \;\\ \; 6\; \end{pmatrix}
\begin{pmatrix} \; -5 \;\\ \; -6 \; \end{pmatrix}
\begin{pmatrix} \; 5 \;\\ \; 6\; \end{pmatrix}
\begin{pmatrix} \; 5 \;\\ \; -6 \; \end{pматрица}
\textbf{s}-\textbf{r}= \begin{pmatrix} \; -2 \;\\\; -1\; \end{pmatrix} – \begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix} = \begin{pmatrix} \; -5 \;\\\; -6 \; \end{pmatrix}
\begin{pmatrix} \; 2 \;\\ \; -3\; \end{pmatrix}
\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -2 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -2 \;\\ \; -3\; \end{pmatrix}
\textbf{e}-\textbf{d}= \begin{pmatrix} \; -4\;\\\; 3 \; \end{pmatrix} – \begin{pmatrix} \; -2 \;\\\; 6\; \end{pmatrix} = \begin{pmatrix} \; -2 \;\\\; -3\; \end{pматрица}
Вопросы GCSE по векторному вычитанию
1.
Вектор \textbf{v} равен \begin{pmatrix}
\; 3 \;\\
\; 1 \;
\end{pматрица}
Вектор \textbf{w} равен \begin{pmatrix} \; 2 \;\\ \; 4\; \end{pматрица}
Какой из следующих векторов является ответом на \textbf{w}-\textbf{v} ?
| А | \ четырехъядерный \ четырехъядерный | Б | \ четырехъядерный \ четырехъядерный | С | \квадратный \четверный | Д |
| \begin{pmatrix} \; -1 \;\\ \; 3 \; \end{pmatrix} | \ четырехъядерный \ четырехъядерный | \begin{pmatrix} \; 1 \;\\ \; 3 \; \end{pmatrix} | \ четырехъядерный \ четырехъядерный | \begin{pmatrix} \; 1 \;\\ \; -3\; \end{pmatrix} | \ четырехъядерный \ четырехъядерный | \begin{pmatrix} \; -1 \;\\ \; -3\; \end{pmatrix} |
(1 балл)
Показать ответ
2. Вот два вектора.
\textbf{m}= \begin{pmatrix} \; 2 \;\\ \; -4\; \end{pmatrix} \; а также \; \textbf{n}= \begin{pmatrix} \; 3 \;\\ \; -6 \; \end{pматрица}
Выработка \; \textbf{n}-\textbf{m}
(2 балла)
Показать ответ
\textbf{n}-\textbf{m}= \begin{pmatrix} \; 3 \;\\ \; -6 \; \end{pmatrix} – \begin{pmatrix} \; 2 \;\\\; -4\; \end{pmatrix} = \begin{pmatrix} \; 1 \;\\ \; -2\; \end{pматрица}
для компонента x (верхний номер)
(1)
для компонента Y (нижний номер)
(1)
3.
Вот векторное вычтение
\begin{pmatrix} \; \текст{а} \;\\ \; -1\; \end{pматрица} – \begin{pmatrix} \; 2 \;\\ \; \текст{б} \; \end{pматрица} знак равно \begin{pmatrix} \; 4 \;\\ \; 2\; \end{pматрица}
(a) Найдите значение a .
(b) Найдите значение b .
(2 балла)
Показать ответ
(a)
а=6
(1)
(б)
б=-3
(1)
Контрольный список для обучения
Теперь вы научились:
- Вычитать векторы
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
